Computational Fluid Dynamics and Visualisation of Coastal Flows in Tidal Channels Supporting Ocean Energy Development
Abstract
:1. Introduction
2. Theory and Method
2.1. Standard k-ϵ Turbulence Model
2.2. Large Eddy Simulation (LES)
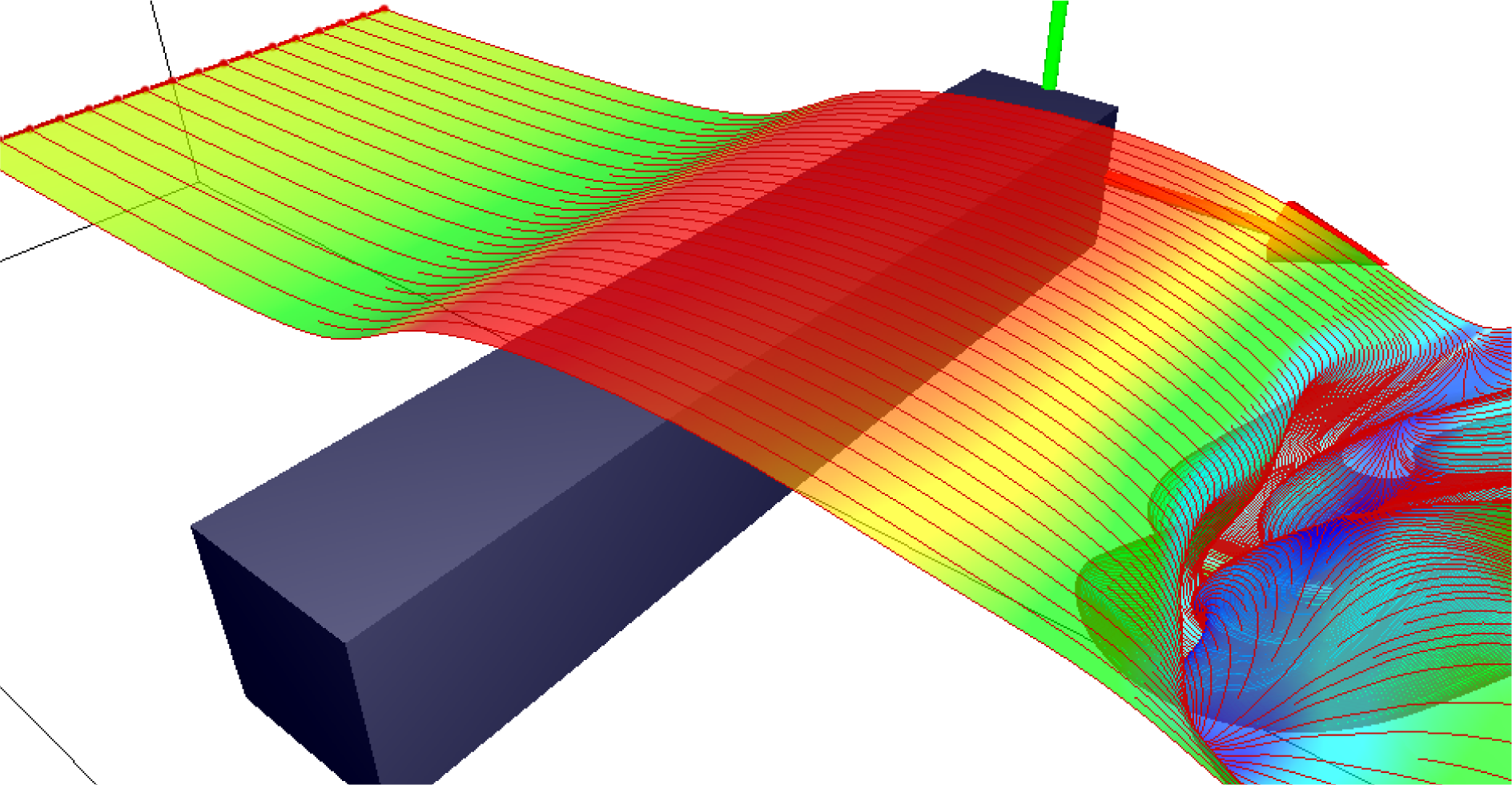
2.3. Visualisation Technique
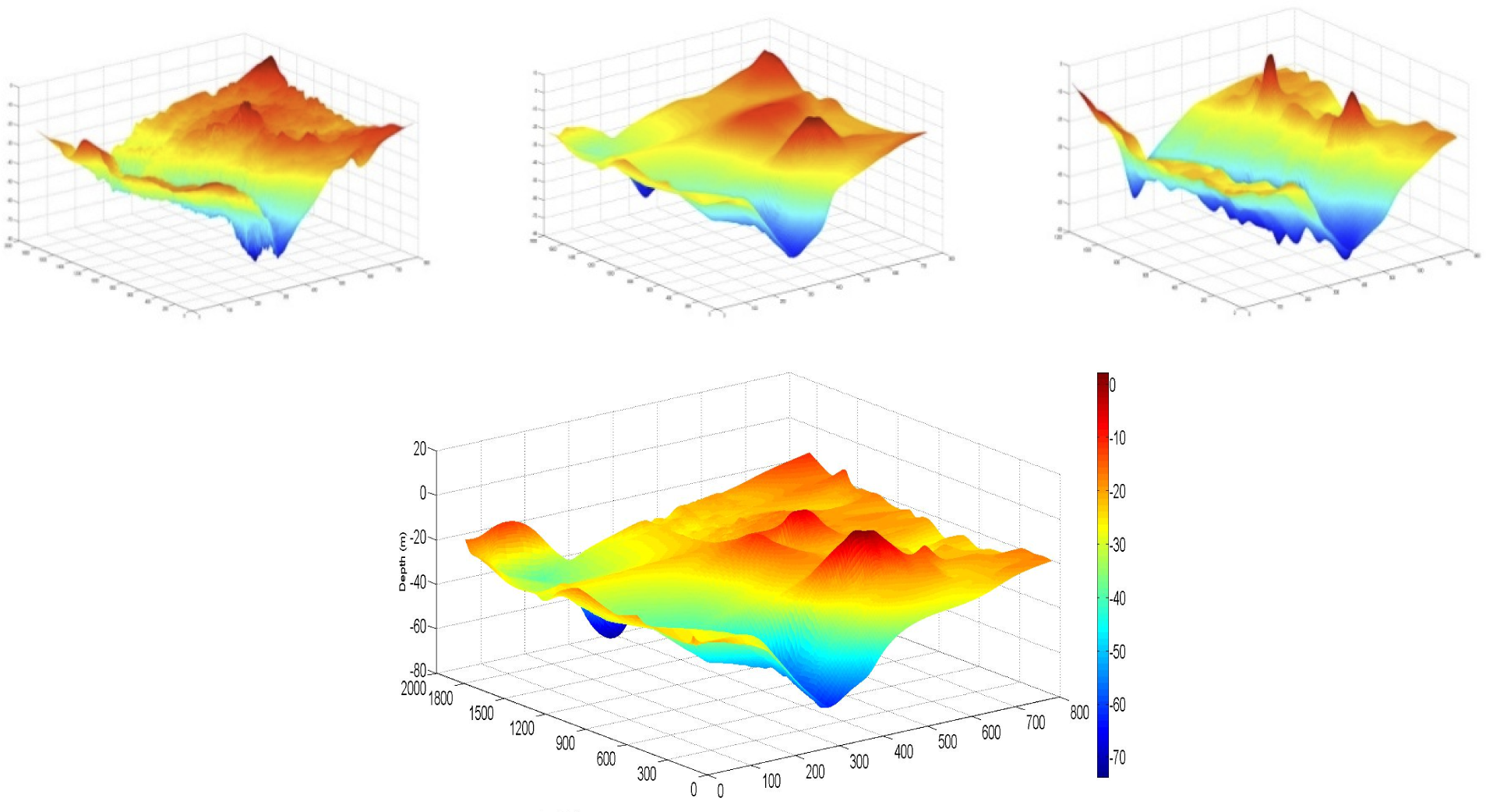
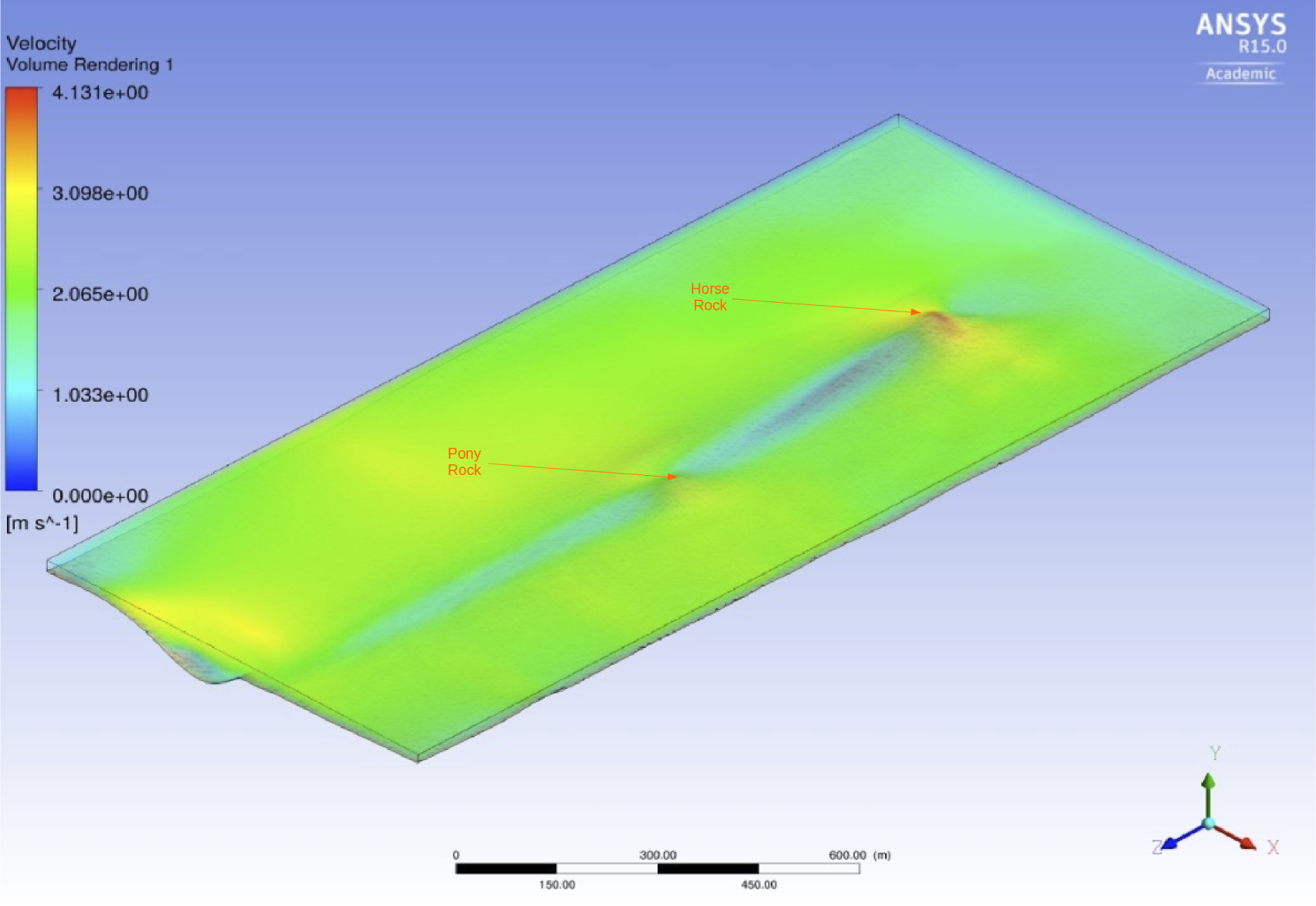
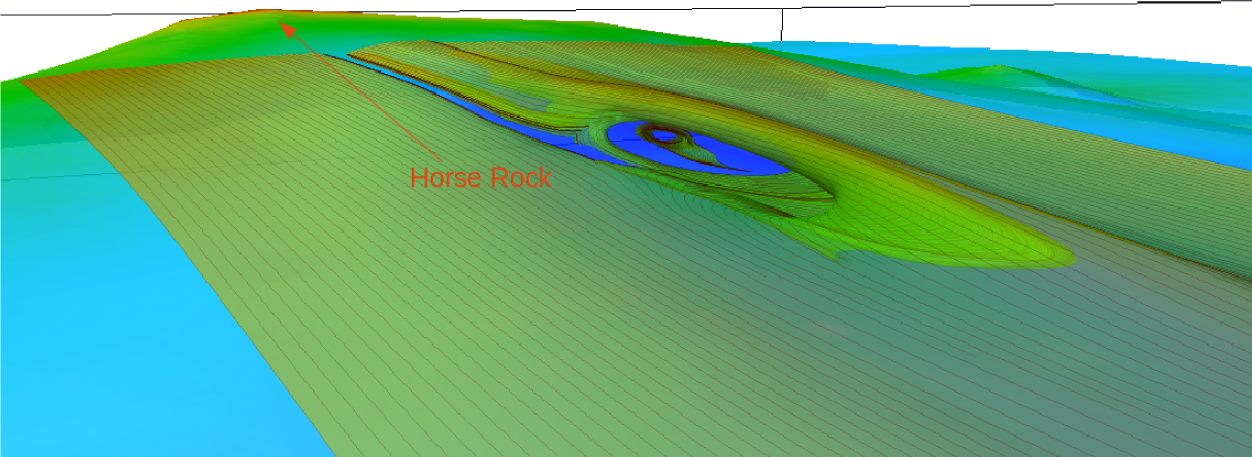
3. Domain
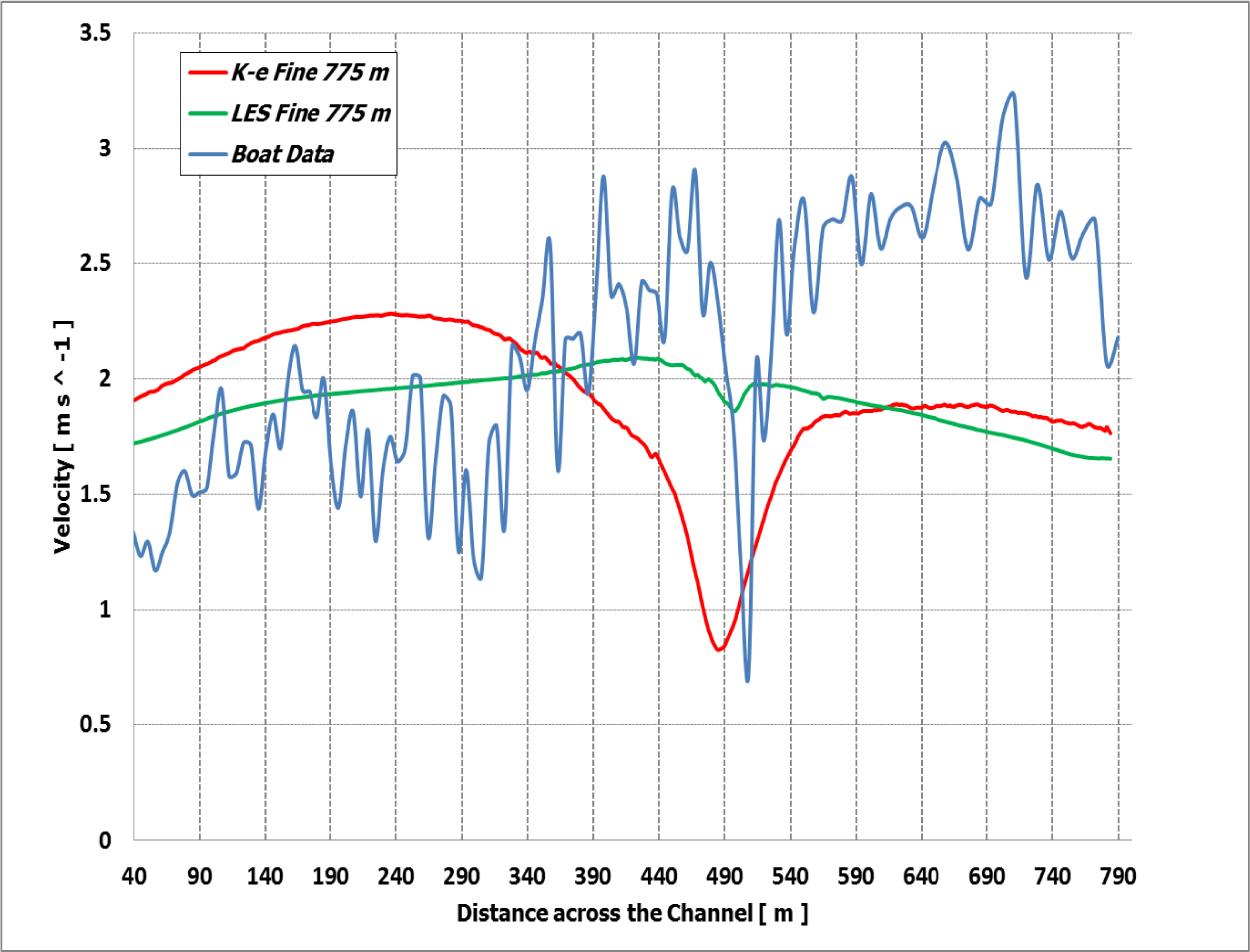
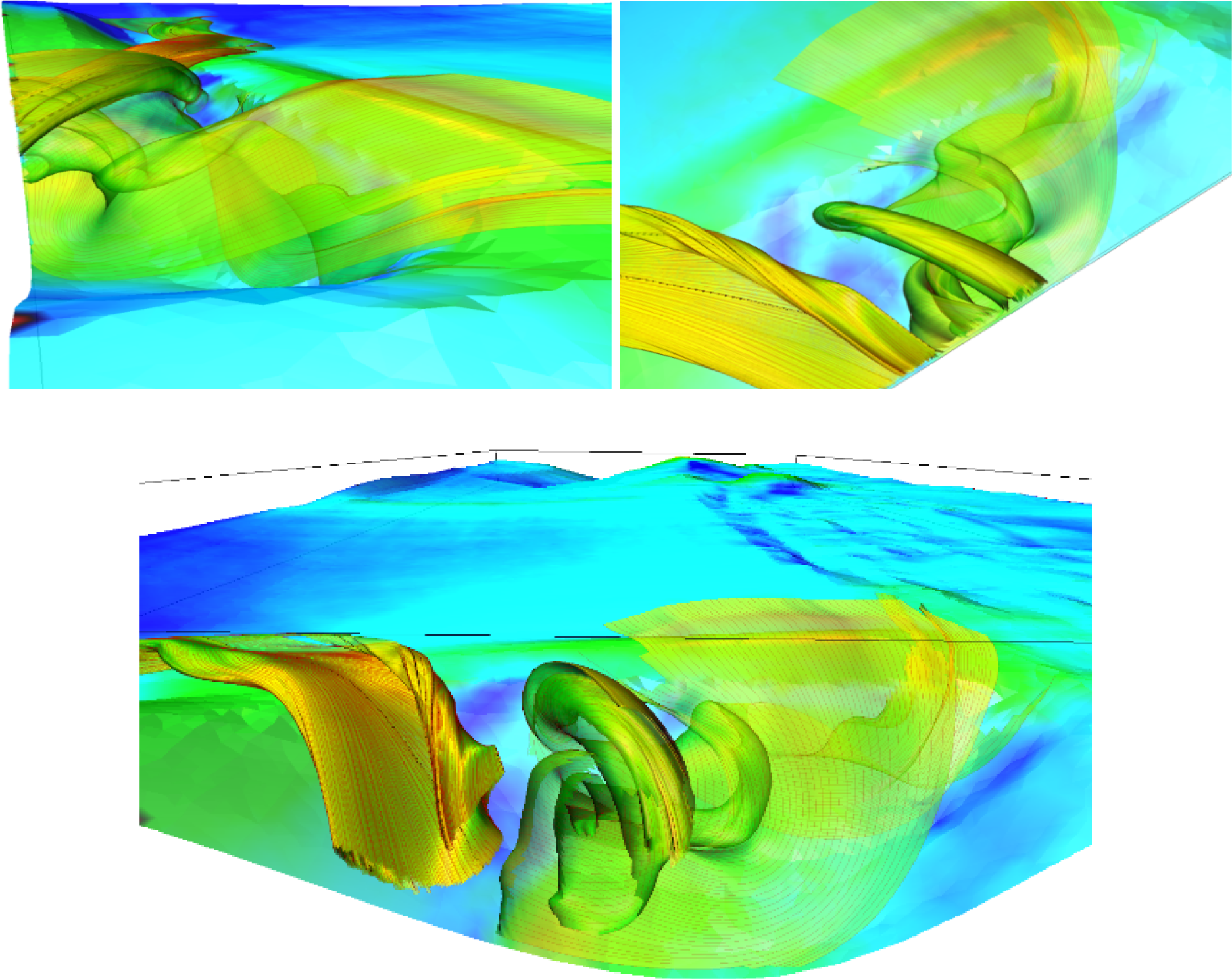
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Edmunds, M.; Laramee, R.S.; Chen, G.; Max, N.; Zhang, E.; Ware, C. Surface-based flow visualization. Comput. Graph 2012, 36, 974–990. [Google Scholar]
- Val, D.V.; Chernin, L.; Yurchenko, D.V. Reliability analysis of rotor blades of tidal stream turbines. Reliab. Eng. Syst. Saf. 2014, 121, 26–33. [Google Scholar]
- Sicot, C.; Devinant, P.; Loyer, S.; Hureau, J. Rotational and turbulence effects on a wind turbine blade. Investigation of the stall mechanisms. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1320–1331. [Google Scholar]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part II: Two interacting turbines. Renew. Energy 2014, 68, 876–892. [Google Scholar]
- Milne, I.; Sharma, R.; Flay, R.; Bickerton, S. Characteristics of the turbulence in the flow at a tidal stream power site. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371. [Google Scholar] [CrossRef]
- Lu, Y.; Lueck, R.G. Using a broadband ADCP in a tidal channel. Part II: Turbulence. J. Atmos. Ocean. Technol. 1999, 16, 1568–1579. [Google Scholar]
- Lorke, A.; Wüest, A. Application of coherent ADCP for turbulence measurements in the bottom boundary layer. J. Atmos. Ocean. Technol. 2005, 22, 1821–1828. [Google Scholar]
- Masters, I.; Chapman, J.; Orme, J.; Willis, M. A robust blade element momentum theory model for tidal stream turbines including tip and hub loss corrections. J. Mar. Eng. Technol. 2011, 10, 25–35. [Google Scholar]
- Togneri, M.; Masters, I.; Orme, J. Incorporating turbulent inflow conditions in a blade element momentum model of tidal stream turbines, In Proceedings of the 21st 2011 International Offshore and Polar Engineering Conference (ISOPE), 19–24 June 2011; Maui: HI, USA.
- Black and Veatch Limited. Tidal Stream Energy Resource and Technology Summary Report; Technical Report 107799/D/2200/04; Black and Veatch Limited: Middlesex, UK, 2005. [Google Scholar]
- Fraenkel, P.I.; Musgrove, P.J. Tidal and river current energy systems, Proceedings of the IEEE International Conference on Future Energy Concepts, 30 January –1 February 1979; London, UK; pp. 114–117.
- Binnie and partners, Sir Robert McAlpine & Sons Ltd and IT Power Ltd. Tidal Stream Energy Review; Technical report etsu-t-05/00155/rep, dti; Harwell Laboratory, Energy Technology Support Unit ETSU: Brighton, UK, 1993. [Google Scholar]
- European Commission. The Exploitation of Tidal and Marine Currents; Technical Report EUR 16683 EN; Wave Energy, Project Results; Directorate-General for Science, Research and Development: Brussels, Belgium, 1996. [Google Scholar]
- Blunden, L.; Bahaj, A. Tidal energy resource assessment for tidal stream generators. Proc. Inst. Mech. Eng. A J. Power Energy 2007, 221, 137–146. [Google Scholar]
- Evans, P.; Mason-Jones, A.; Wilson, C.; Wooldridge, C.; O’Doherty, T.; O’Doherty, D. Constraints on extractable power from energetic tidal straits. Renew. Energy 2015, 81, 707–722. [Google Scholar]
- Galland, J.C.; Goutal, N.; Hervouet, J.M. TELEMAC: A new numerical model for solving shallow water equations. Adv. Water Resour 1991, 14, 138–148. [Google Scholar]
- IMCS, Ocean Modelling Group. Regional Ocean Modelling System (ROMS). Available online: http://www.myroms.org/(accessed accessed on 4 Sptember 2014.
- Ahmadian, R.; Falconer, R.; Lin, B. Hydro-environmental modeling of proposed Severn barrage, UK. Proc. ICE-Energy 2010, 163, 107–117. [Google Scholar]
- Brammer, J.; Falconer, R.; Ellis, C.; Ahmadian, R. Physical and numerical modelling of the Severn Barrage. Sci. China Technol 2014, 57, 1471–1481. [Google Scholar]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar]
- Burchard, H.; Bolding, K.; Villarreal, M.R. GOTM, A General Ocean Turbulence Model: Theory, Implementation and Test Cases; Space Applications Institute: Athens, Greece, 1999. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed; DCW Industries: La Cañada Flintridge, CA, USA, 1998. [Google Scholar]
- Schlichting, H.; Gersten, K.; Gersten, K. Boundary-Layer Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Sarkar, A.; So, R. A critical evaluation of near-wall two-equation models against direct numerical simulation data. Int. J. Heat Fluid Flow 1997, 18, 197–208. [Google Scholar]
- Bomminayuni, S.; Stoesser, T. Turbulence statistics in an open-channel flow over a rough bed. J. Hydraul. Eng. 2011, 137, 1347–1358. [Google Scholar]
- Kuban, L.; Laval, J.P.; Elsner, W.; Tyliszczak, A.; Marquillie, M. LES modeling of converging-diverging turbulent channel flow. J. Turbul 2012, 13. [Google Scholar] [CrossRef]
- Edmunds, M.; Laramee, R.; Malki, R.; Masters, I.; Croft, T.; Chen, G.; Zhang, E. Automatic stream surface seeding: A feature centered approach. Comput. Graph. Forum. 2012, 31, 1095–1104. [Google Scholar]
- Launder, B.; Spalding, D. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Launder, B.E.; Spalding, D. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: New York, NY, USA, 2007. [Google Scholar]
- Jones, W.; Launder, B. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf 1972, 15, 301–314. [Google Scholar]
- Zangiabadi, E.; Masters, I.; Williams, A. Characterisation of the coastal hydrology of oceans using 3D computational fluid dynamics, Proceedings of the 4th International Conference on Ocean Energy, Dublin, Ireland, 17 October 2012.
- ANSYS Inc. ANSYS FLUENT Theory Guide; ANSYS Inc: Canonsburg, PA, USA, 2010. [Google Scholar]
- Benhamadouche, S.; Jarrin, N.; Addad, Y.; Laurence, D. Synthetic turbulent inflow conditions based on a vortex method for large-eddy simulation. Prog. Comput. Fluid Dyn. Int. J. 2006, 6, 50–57. [Google Scholar]
- Moeng, C.H.; Sullivan, P. Large eddy simulation. Encycl. Atmos. Sci. 2002, 1140, 1150. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev 1963, 91, 99–164. [Google Scholar]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar]
- Sergent, E. Vers une Methodologie de Couplage Entre la Simulation des Grandes Echelles et les Modeles Statistiques. Ph.D. Thesis, Ecole centrale de Lyon, Ecully, France, 2002. [Google Scholar]
- Langevin, P. On the theory of Brownian motion. C. R. Acad. Sci. (Paris) 1908, 146, 530–533. [Google Scholar]
- Zangiabadi, E. Using 3D-CFD Methods to Investigate Hydrology of Oceans and Fish Passage through Tidal Stream Turbines. Ph.D. Thesis, Swansea University, Swansea, UK, 2015. [Google Scholar]
- Edmunds, M.; Tong, C.; Laramee, R.S. Design of a flow visualisation framework. Computers 2015, 4, 24–38. [Google Scholar]
- Evans, P.; Armstrong, S.; Wilson, C.; Fairley, I.; Wooldridge, C.; Masters, I. Characterisation of a highly energetic tidal energy site with specific reference to hydrodynamics and bathymetry. Proceedings of the European Wave and Tidal Energy Conference EWTEC, Aalborg, Denmark, 2–5 September 2013.
- Fairley, I.; Neill, S.; Wrobelowski, T.; Willis, M.; Masters, I. Potential array sites for tidal stream electricity generation off the pembrokeshire coast. Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011.
- Fairley, I.; Evans, P.; Wooldridge, C.; Willis, M.; Masters, I. Evaluation of tidal stream resource in a potential array area via direct measurements. Renew. Energy 2013, 57, 70–78. [Google Scholar]
- Tidal Energy Limited. Wales’ First Full-Scale Tidal Energy Generator Unveiled Ahead of Its Installation in Welsh Waters. Available online: http://www.tidalenergyltd.com/?p=2191 accessed on 30 September 2014.
- Sandwell, D.T. Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data. Geophys. Res. Lett. 1987, 14, 139–142. [Google Scholar]
- Pattanapol, W.; Wakes, S.J.; Hilton, M.J.; Dickinson, K.J. Modeling of surface roughness for flow over a complex vegetated surface. Int. J. Math. Phys. Eng. Sci. 2008, 2, 18–26. [Google Scholar]
- Yue, W.; Lin, C.L.; Patel, V.C. Large-eddy simulation of turbulent flow over a fixed two-dimensional dune. J. Hydraul. Eng. 2006, 132, 643–651. [Google Scholar]
- Stoesser, T.; Braun, C.; Garcia-Villalba, M.; Rodi, W. Turbulence structures in flow over two-dimensional dunes. J. Hydraul. Eng. 2008, 134, 42–55. [Google Scholar]
- Xie, Z.; Lin, B.; Falconer, R.A. Turbulence characteristics in free-surface flow over two-dimensional dunes. J. Hydro-Environ. Res. 2014, 8, 200–209. [Google Scholar]
- Malki, R.; Masters, I.; Williams, A.J.; Croft, T.N. A numerical investigation into tidal stream turbine wake dynamics and device performance in non-uniform flows, Proceedings of the 22nd 2012 International Offshore and Polar Engineering Conference, 17–23 June 2012; ISOPE, Rhodes: Greece.
- Masters, I.; Malki, R.; Williams, A.J.; Croft, T.N. The influence of flow acceleration on tidal stream turbine wake dynamics: A numerical study using a coupled BEM–CFD model. Appl. Math. Model. 2013, 37, 7905–7918. [Google Scholar]


© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zangiabadi, E.; Edmunds, M.; Fairley, I.A.; Togneri, M.; Williams, A.J.; Masters, I.; Croft, N. Computational Fluid Dynamics and Visualisation of Coastal Flows in Tidal Channels Supporting Ocean Energy Development. Energies 2015, 8, 5997-6012. https://doi.org/10.3390/en8065997
Zangiabadi E, Edmunds M, Fairley IA, Togneri M, Williams AJ, Masters I, Croft N. Computational Fluid Dynamics and Visualisation of Coastal Flows in Tidal Channels Supporting Ocean Energy Development. Energies. 2015; 8(6):5997-6012. https://doi.org/10.3390/en8065997
Chicago/Turabian StyleZangiabadi, Enayatollah, Matt Edmunds, Iain A. Fairley, Michael Togneri, Alison J. Williams, Ian Masters, and Nick Croft. 2015. "Computational Fluid Dynamics and Visualisation of Coastal Flows in Tidal Channels Supporting Ocean Energy Development" Energies 8, no. 6: 5997-6012. https://doi.org/10.3390/en8065997
APA StyleZangiabadi, E., Edmunds, M., Fairley, I. A., Togneri, M., Williams, A. J., Masters, I., & Croft, N. (2015). Computational Fluid Dynamics and Visualisation of Coastal Flows in Tidal Channels Supporting Ocean Energy Development. Energies, 8(6), 5997-6012. https://doi.org/10.3390/en8065997




