Effects of Surface Wettability and Roughness on the Heat Transfer Performance of Fluid Flowing through Microchannels
Abstract
:1. Introduction
2. Lattice Boltzmann Method
2.1. LB Flow Field Equations
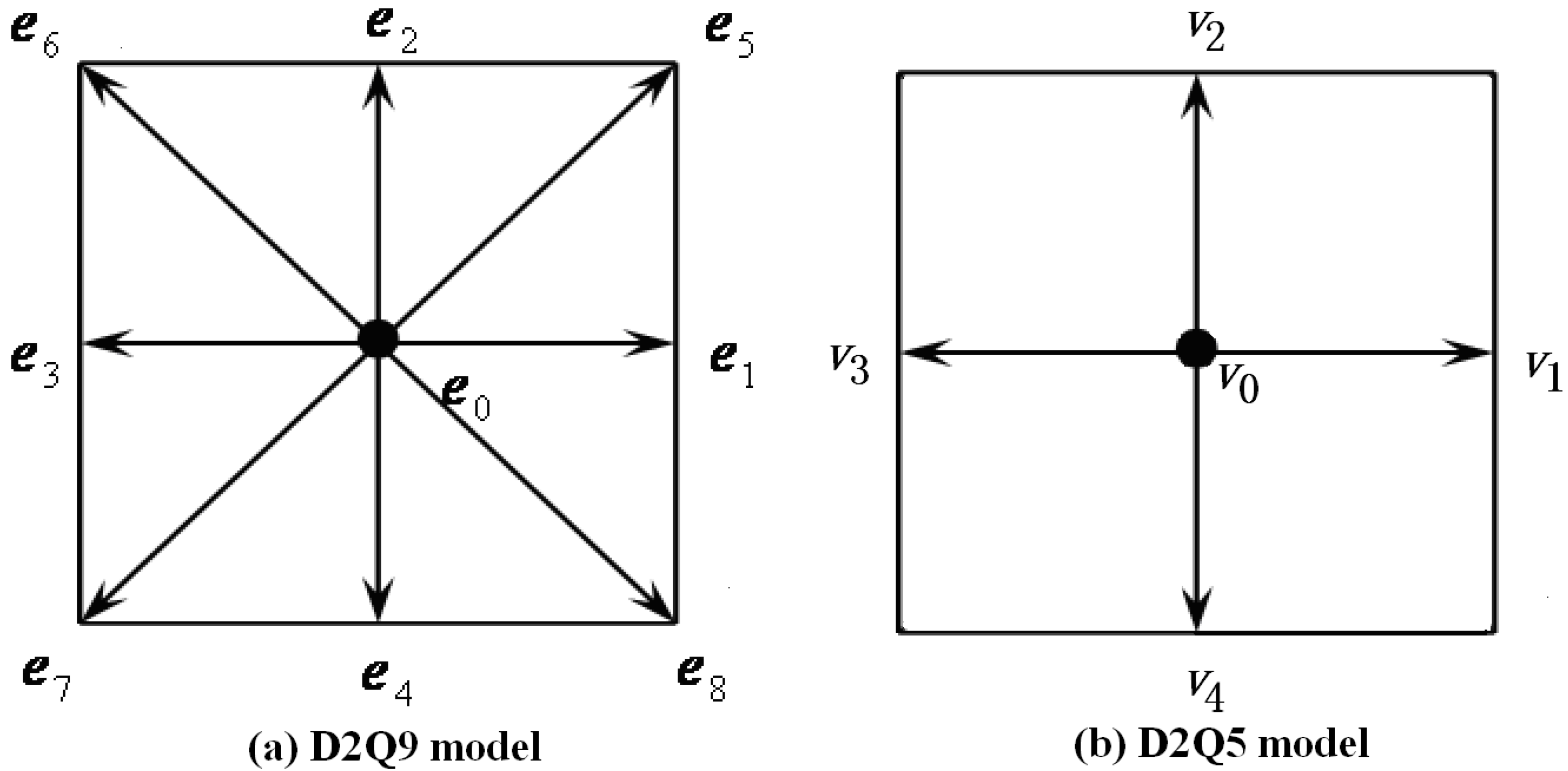
2.2. LB Equations for Temperature Field
2.3. Variable Relaxation Times Treatment
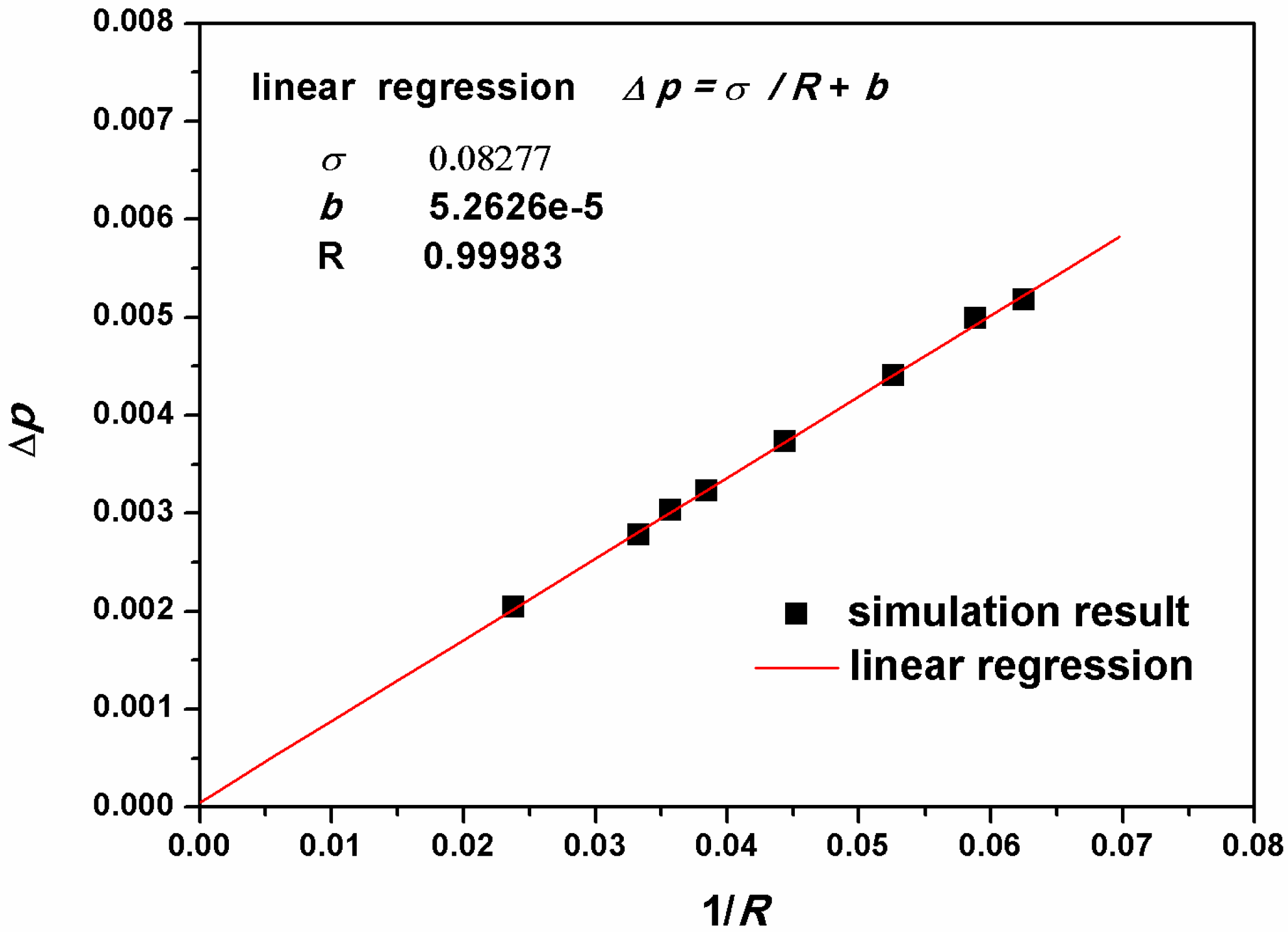
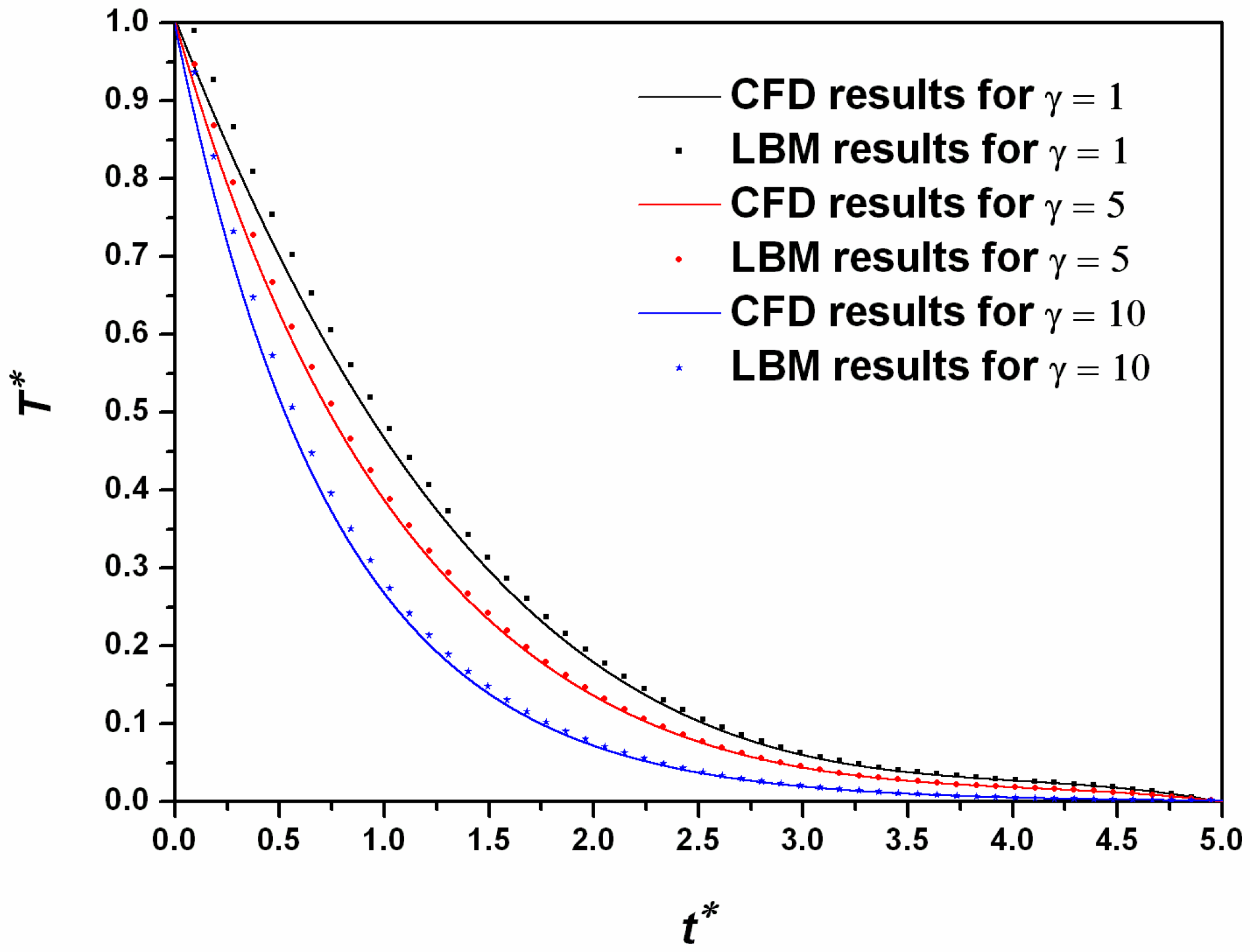
3. Benchmark Tests
4. Numerical Simulation
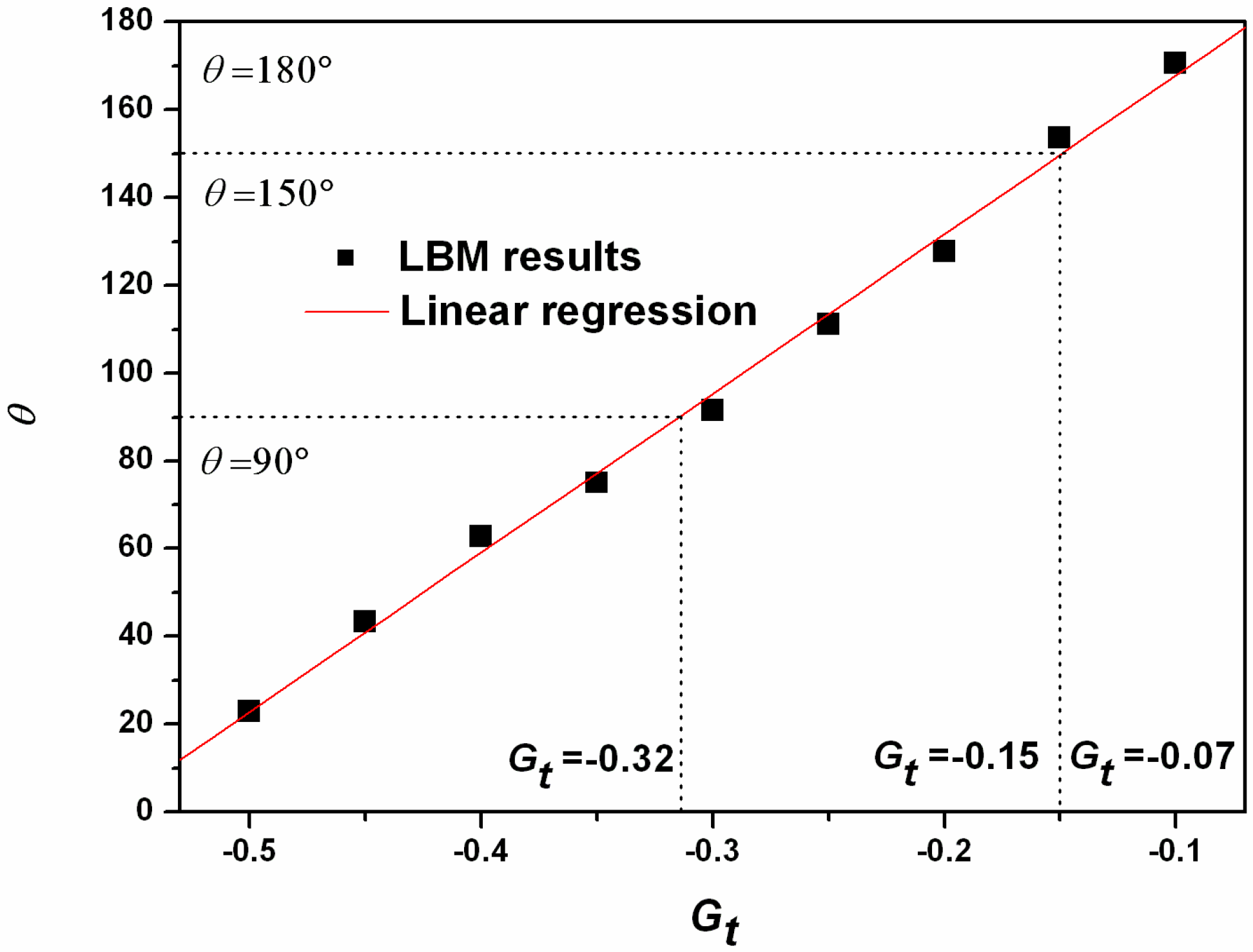
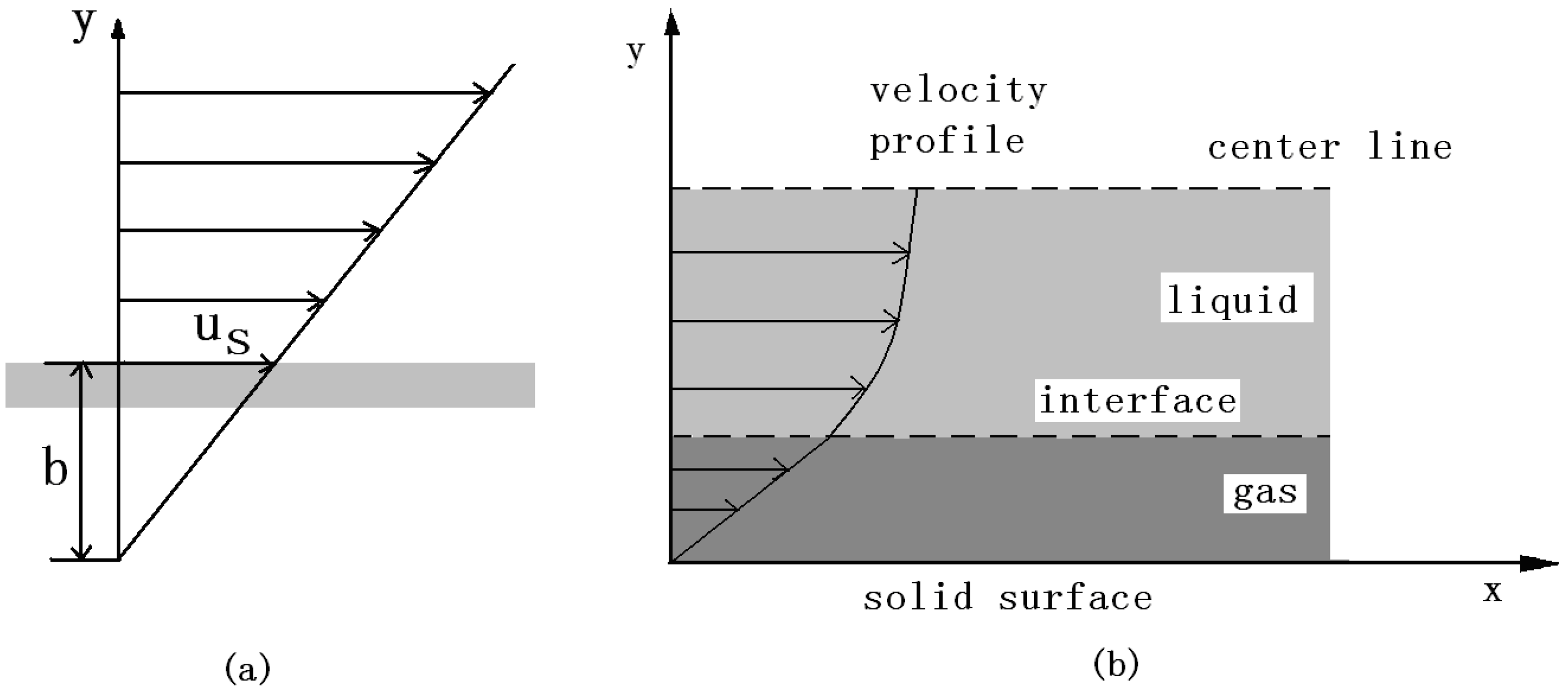
4.1. Different Wettabilities Treatment
4.2. Solution Scheme and Procedure
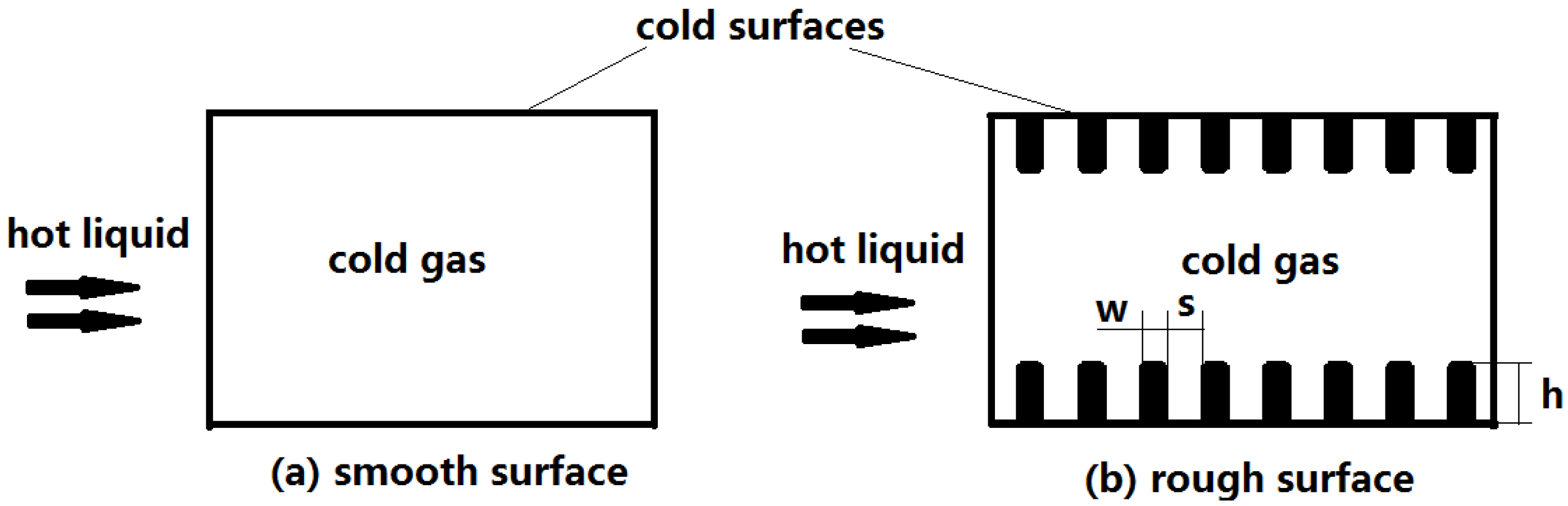
| Smooth Channel Flow | Rough Channel Flow | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lattice number | Average temperature | Lattice number | Average temperature | |||||||||
| nx | ny | 200th | 400th | nx | ny | nw | ns | ny | 200th | 400th | ||
| Grid 1 | 100 | 15 | 0.3669 | 0.7261 | Grid 1 | 100 | 25 | 2 | 3 | 5 | 0.3059 | 0.6627 |
| Grid 2 | 200 | 15 | 0.3292 | 0.7058 | Grid 2 | 150 | 25 | 4 | 4 | 5 | 0.3136 | 0.6795 |
| Grid 3 | 200 | 30 | 0.3892 | 0.7658 | Grid 3 | 150 | 50 | 4 | 4 | 10 | 0.3029 | 0.6573 |
| Grid 4 | 400 | 30 | 0.3856 | 0.7620 | Grid 4 | 200 | 50 | 5 | 5 | 10 | 0.3221 | 0.6853 |
| Grid 5 | 400 | 60 | 0.3801 | 0.7592 | Grid 5 | 400 | 100 | 10 | 10 | 20 | 0.3202 | 0.6823 |
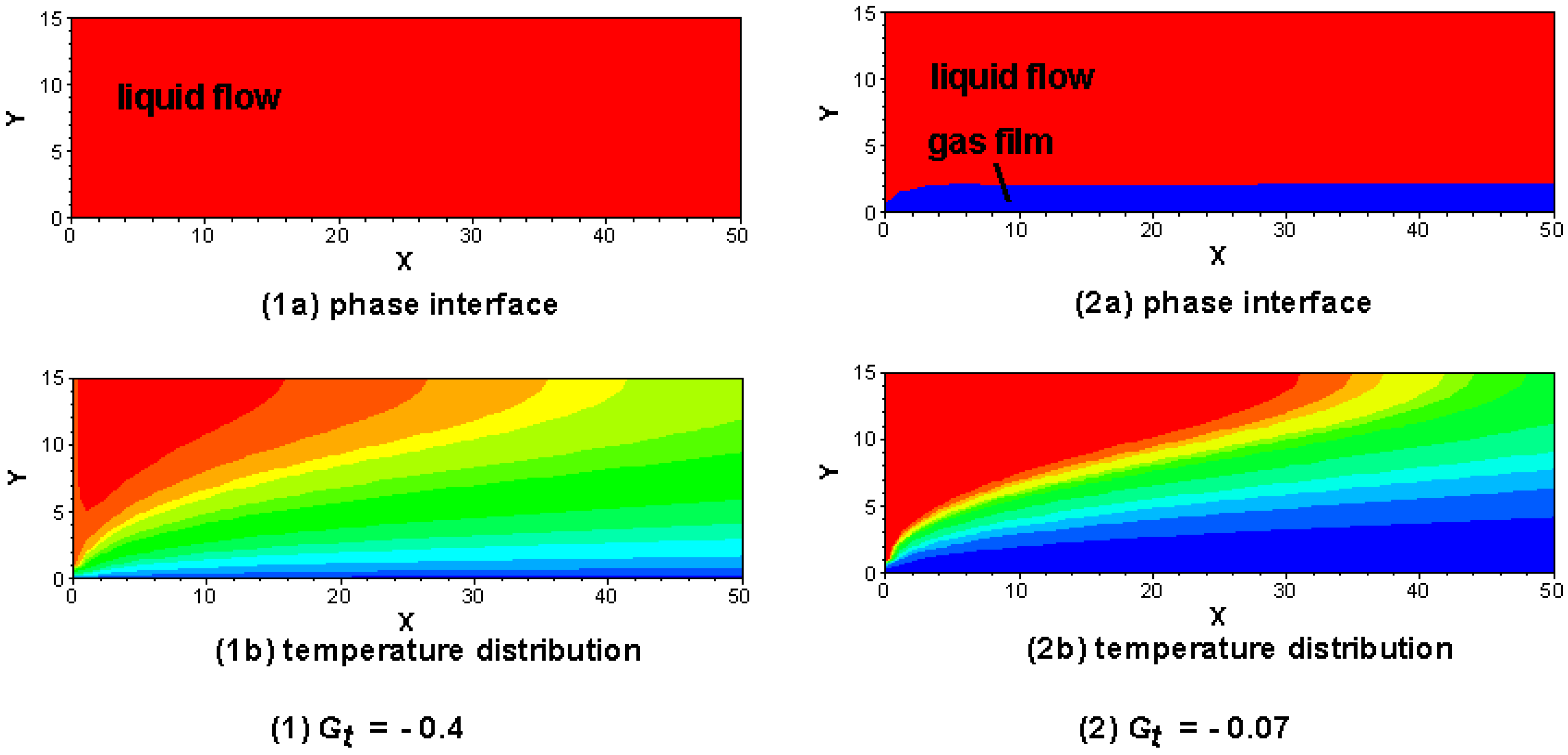
4.3. Simulation Results
4.4. Model Validation
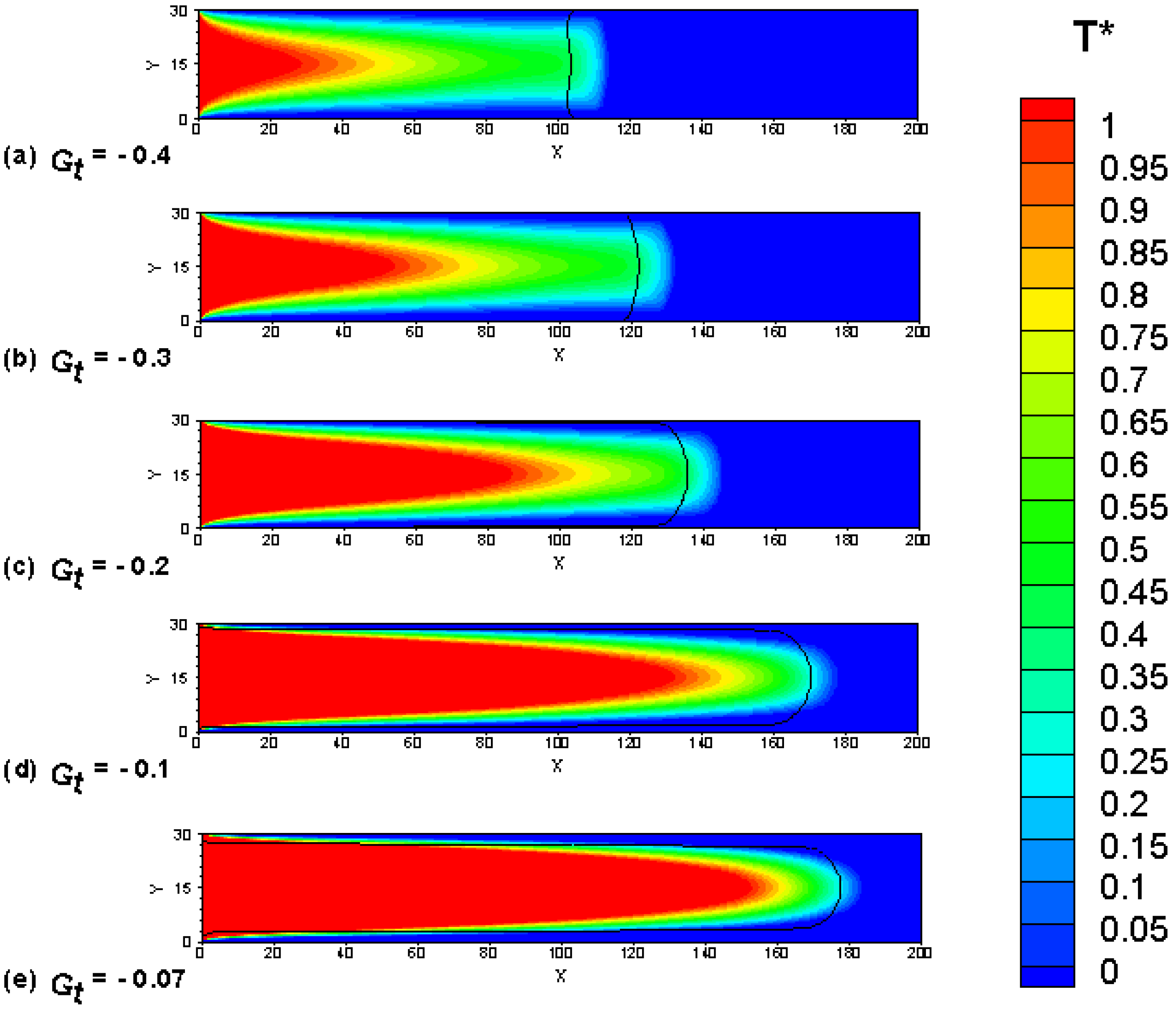
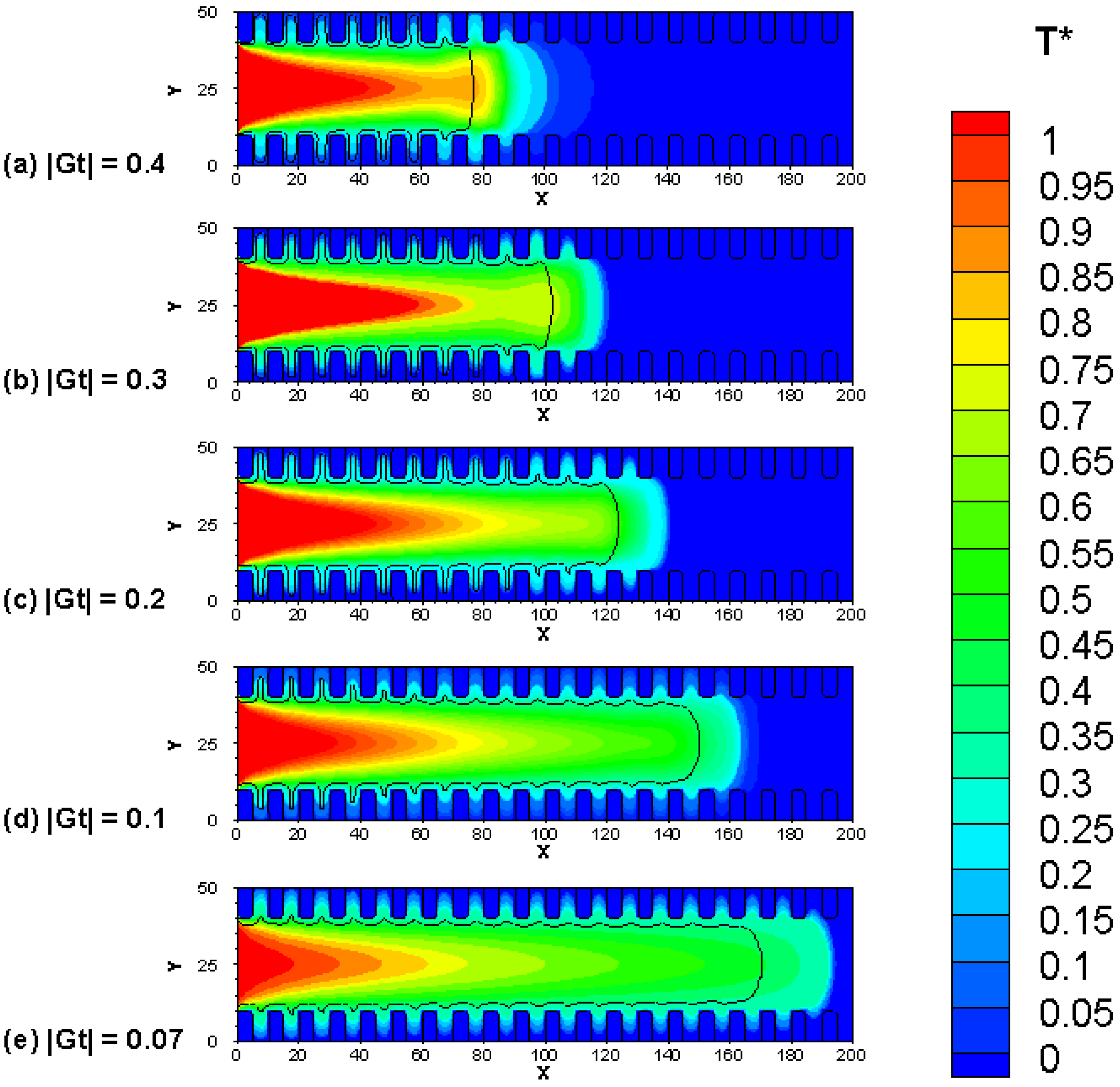
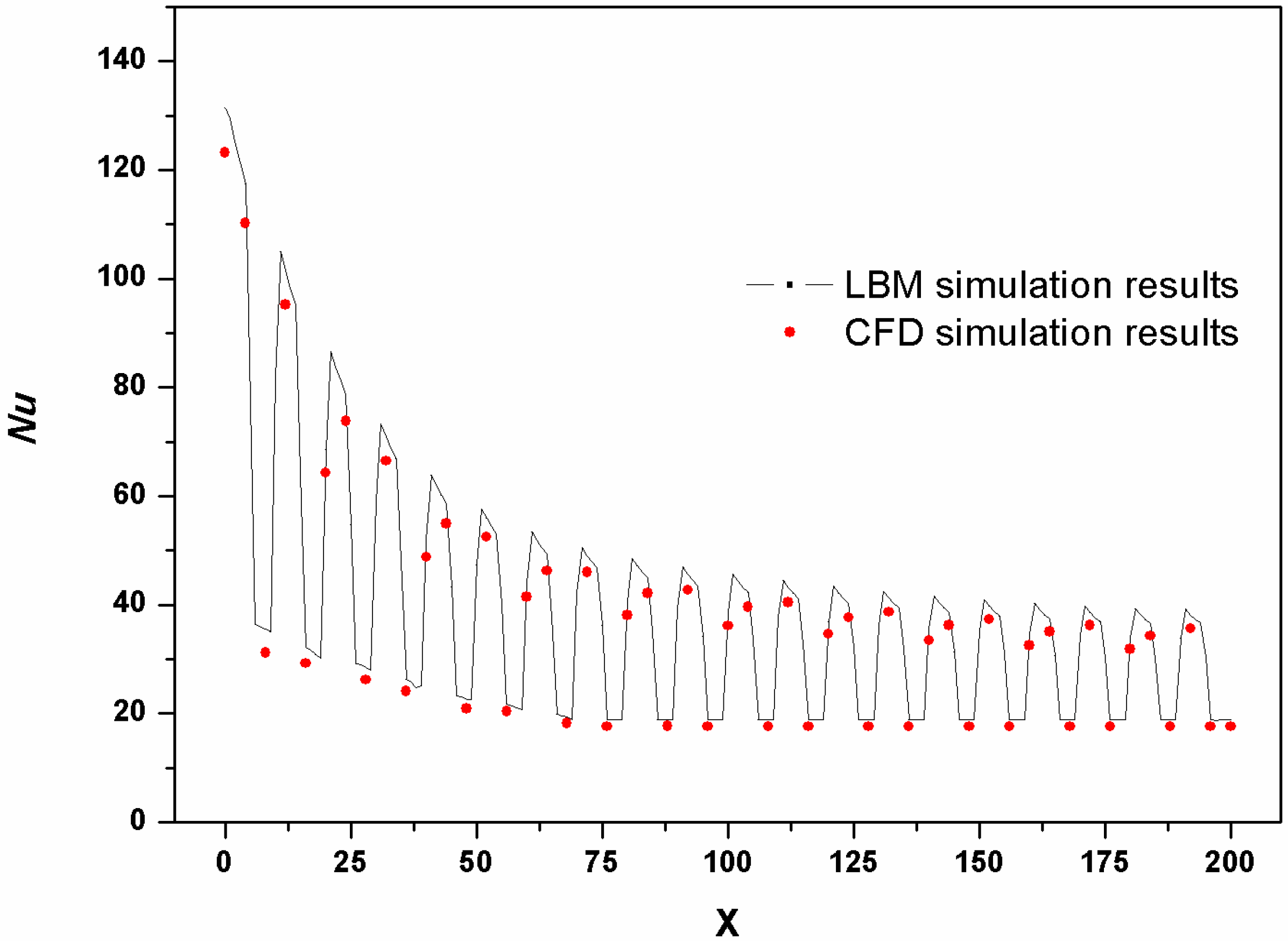
4.5. Quantitative Analysis and Discussion
4.5.1. Heat Exchanger Performance
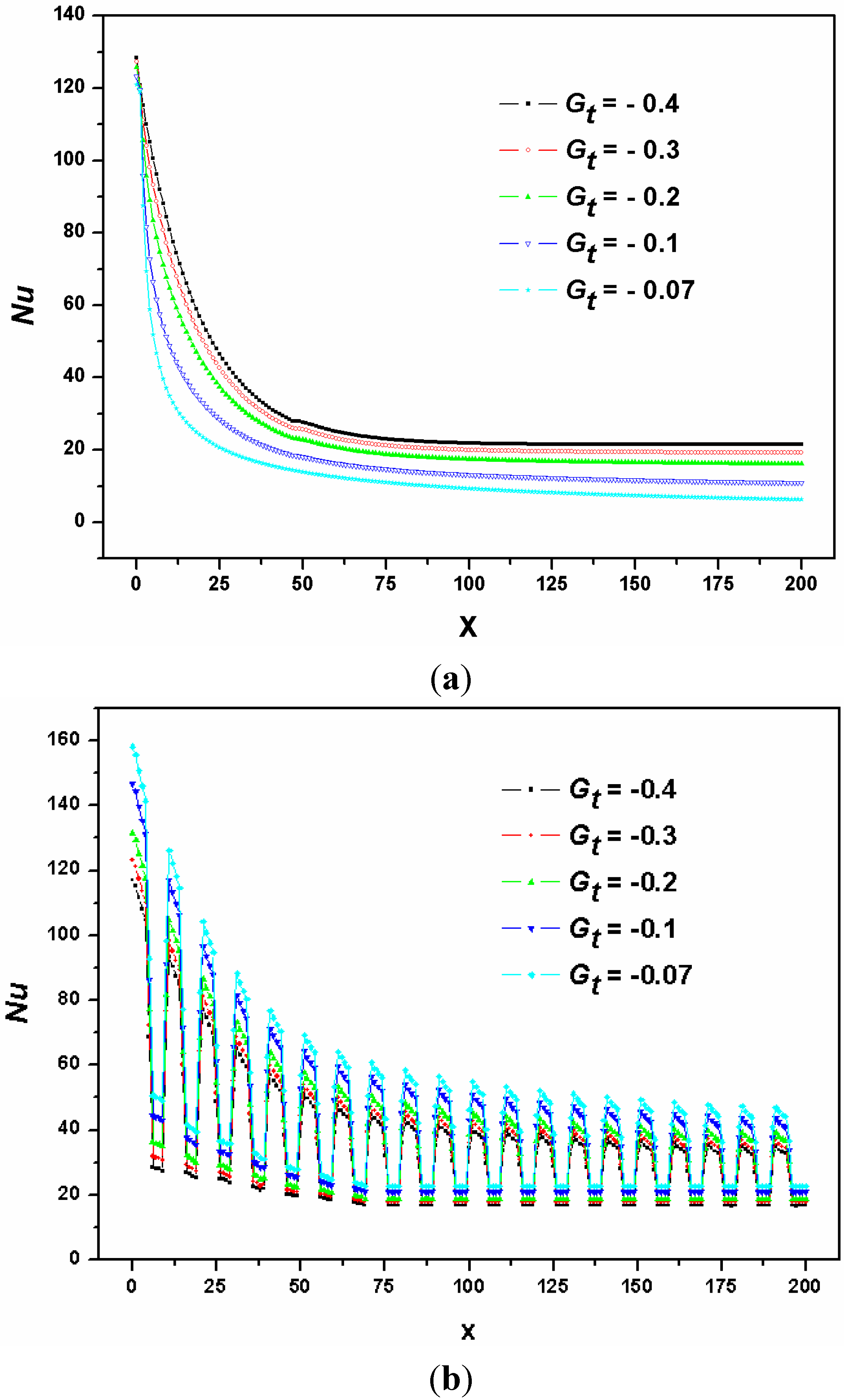
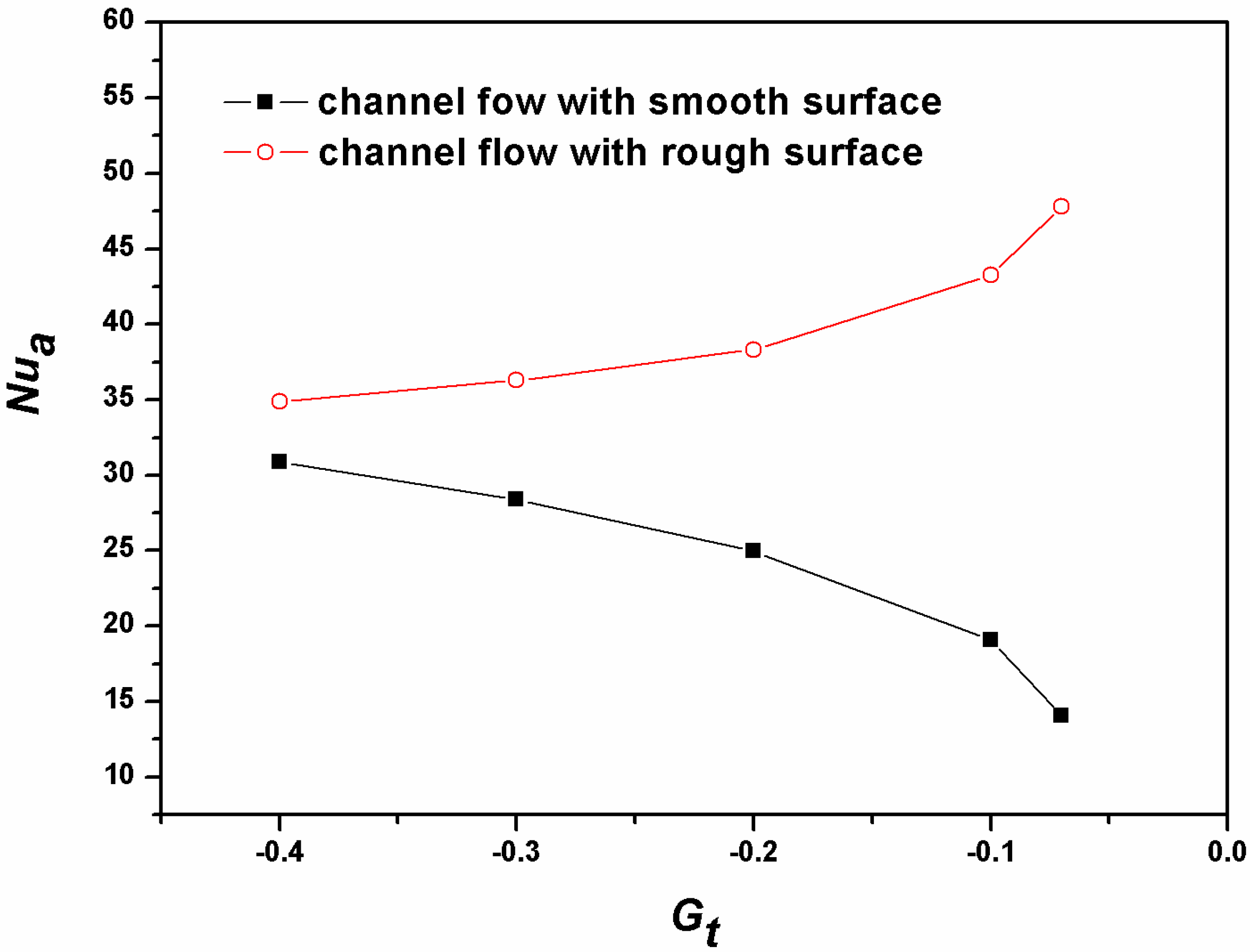
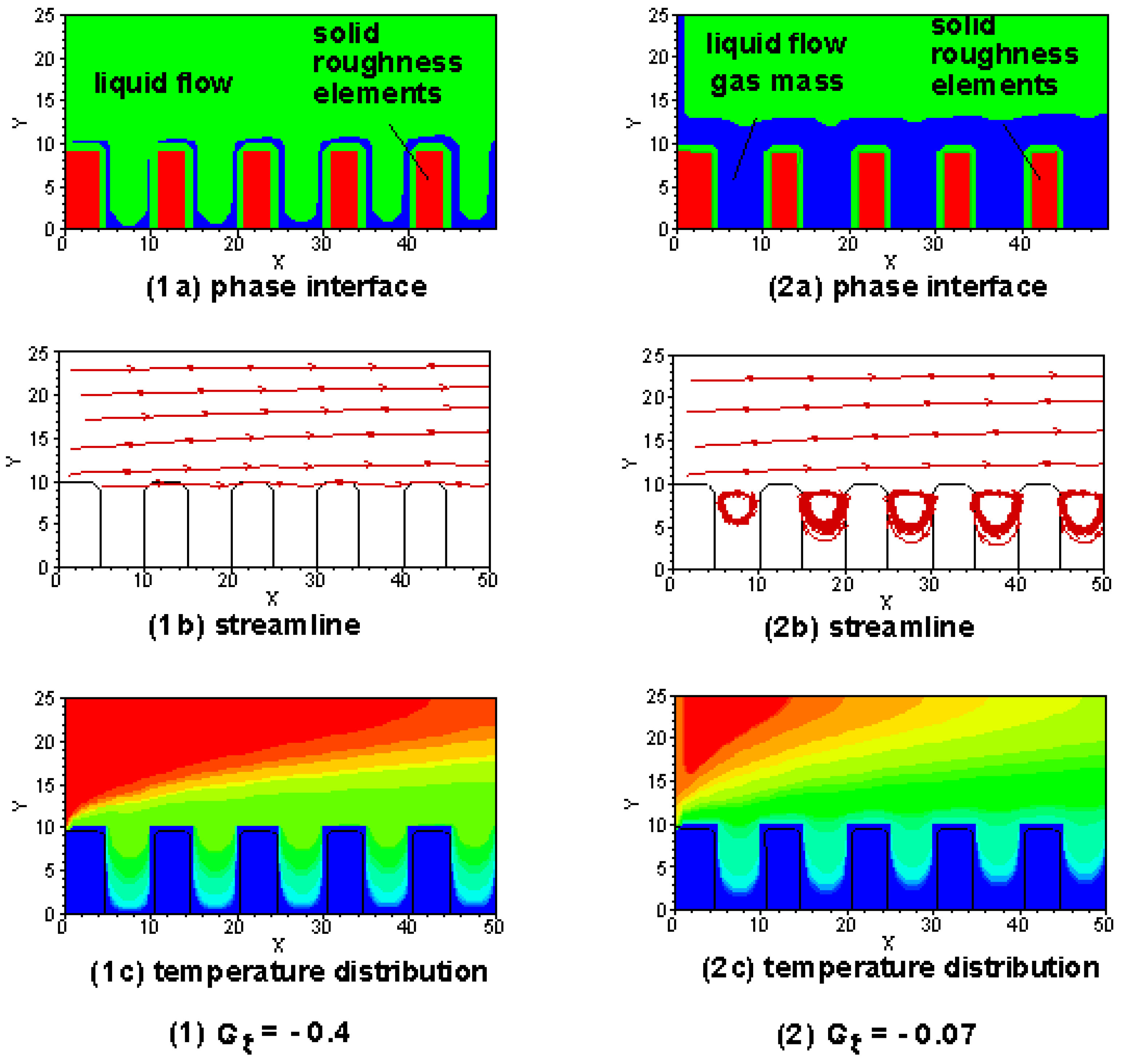
4.5.2. Pressure Drop
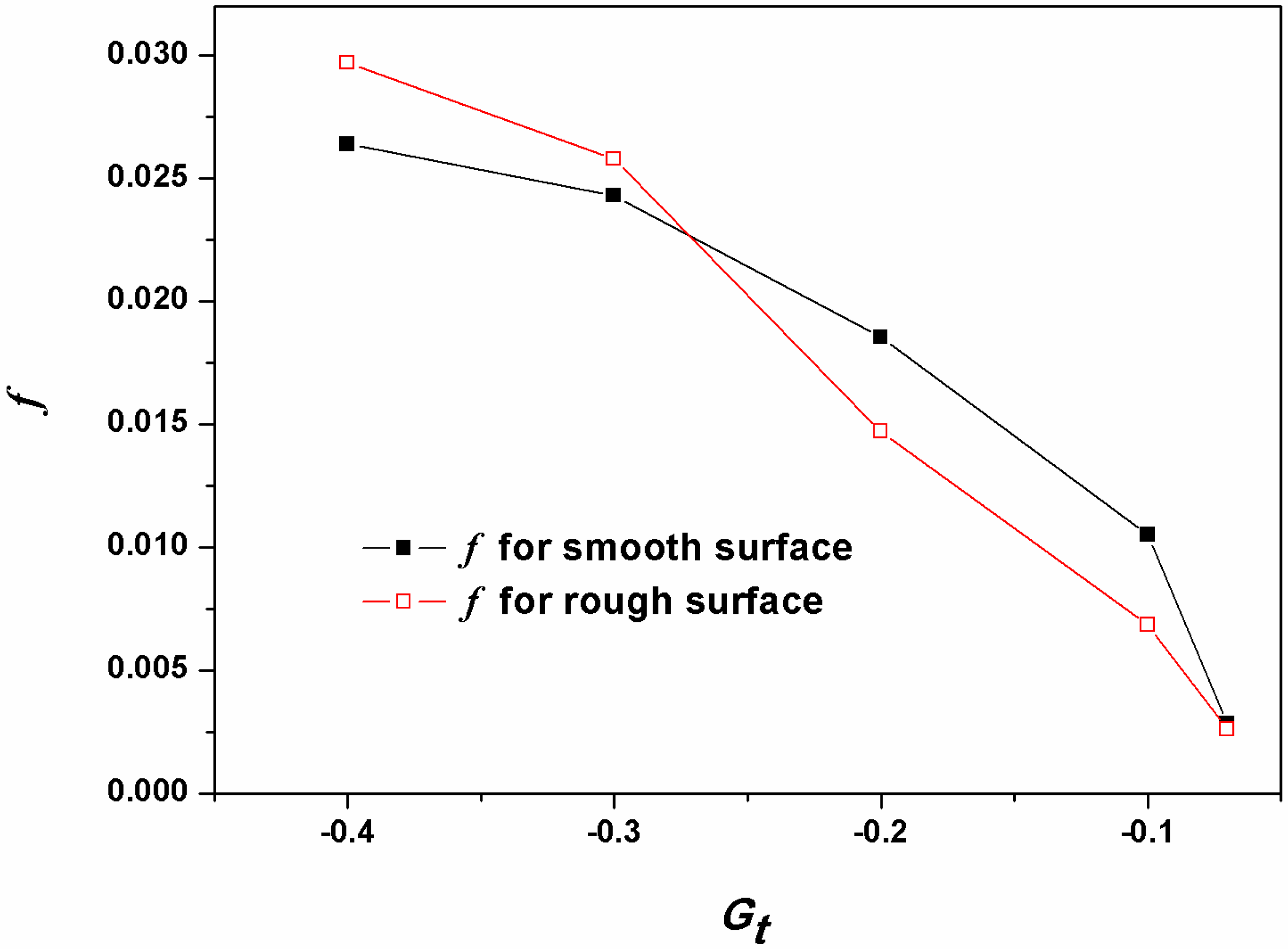
5. Conclusions
- (1)
- For the smooth-surface channel flow, the pressure drop could be reduced by using hydrophobic surfaces because a very thin gas film is formed between the fluid and superhydrophobic wall and the liquid/solid interface is replaced by a gas/liquid one. However the heat transfer performance is worsened when the surface is hydrophobic compared to the hydrophilic surface flow. This is because that the velocity of liquid-phase flow is larger when the hydrophobic properties are better. The flow time is therefore less for the hydrophobic-surface channel flow, masking the heat transfer insufficient compared with the hydrophilic-surface channel flow.
- (2)
- As to the rough-surface channel flow, the pressure drop for the hydrophobic-surface flow is much less because the liquid sweeps over the grooves and the contact area is reduced in the case of hydrophobic-surface flow. Moreover, the better the hydrophobic surface is, the better the heat transfer performance becomes. For the superhydrophobic surface channel flow, liquid sweeps over the roughness bumps and gas squeezes into the spaces and being subject to vertical movement owing to the drag force at the top side of the gap caused by the liquid flow in the main region, which will produce heat convection, a superior kind of heat exchange mechanism, to enhance the heat transfer performance.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, J.; Kwok, D.Y. Contact line and contact angle dynamics in superhydrophobic channels. Langmuir 2006, 22, 4998–5004. [Google Scholar] [CrossRef] [PubMed]
- Jeffs, K.; Maynes, D.; Webb, B.W. Prediction of turbulent channel flow with superhydrophobic walls consisting of micro-ribs and cavities oriented parallel to the flow direction. Int. J. Heat Mass Transf. 2010, 53, 786–796. [Google Scholar] [CrossRef]
- Chibbaro, S.; Costa, E.; Dimitrov, D.I.; Diotallevi, F.; Milchev, A.; Palmieri, D.; Pontrelli, G.; Succi, S. Capillary Filling in Microchannels with Wall Corrugations: A Comparative Study of the Concus-Finn Criterion by Continuum, Kinetic, and Atomistic Approaches. Langmuir 2013, 25, 12653–12660. [Google Scholar] [CrossRef] [PubMed]
- Lauga, E.; Stone, H.A. Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 2003, 489, 55–77. [Google Scholar] [CrossRef]
- Ybert, C.; Barentin, C.; Cottin-Bizonne, C.; Joseph, P.; Bocquet, L. Achieving large slip with superhydrophobic surfaces: Scaling laws for generic geometries. Phys. Fluids 2013, 19, 123601. [Google Scholar] [CrossRef]
- Davies, J.; Maynes, D.; Webb, B.W.; Woolford, B. Laminar flow in a microchannel with superhydrophobic walls exhibiting transverse ribs. Phys. Fluids 2006, 18, 087110. [Google Scholar] [CrossRef]
- Ou, J.; Perot, B.; Rothstein, J.P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 2004, 16, 4635. [Google Scholar] [CrossRef]
- Cui, J.; Li, W.; Lam, W.H. Numerical investigation on drag reduction with superhydrophobic surfaces by lattice-Boltzmann method. Comput. Math. Appl. 2011, 61, 3678–3689. [Google Scholar] [CrossRef]
- Öner, D.; McCarthy, T.J. Ultrahydrophobic surfaces. Effects of topography length scales on wettability. Langmuir 2000, 16, 7777–7782. [Google Scholar] [CrossRef]
- Extrand, C.W. Model for contact angles and hysteresis on rough and ultraphobic surfaces. Langmuir 2002, 18, 7991–7999. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Alexander, F.J.; Chen, S.; Sterling, J.D. Lattice boltzmann thermohydrodynamics. Phys. Rev. E 1993, 47, 2249–2252. [Google Scholar] [CrossRef]
- Chen, Y.; Ohashi, H.; Akiyama, M. Thermal lattice Bhatnagar-Gross-Krook model without nonlinear deviations in macrodynamic equations. Phys. Rev. E 1994, 50, 2776–2783. [Google Scholar] [CrossRef]
- Bartoloni, A.; Battista, C.; Gabasino, S.; Paolucci, P.S. LBE simulations of Rayleigh-Bénard convection on the APE100 parallel processor. Int. J. Mod. Phys. C 1993, 4, 993–1006. [Google Scholar] [CrossRef]
- Shan, X. Simulation of Rayleigh-Benard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780–2788. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Doolen, G.D. A Novel Thermal Model for the Lattice Boltzmann Method in Incompressible Limit. J. Comput. Phys. 1998, 146, 282–300. [Google Scholar] [CrossRef]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef] [PubMed]
- Swift, M.R.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 1995, 75, 830–833. [Google Scholar] [CrossRef] [PubMed]
- Swift, M.R.; Orlandini, E.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 1996, 54, 5041–5052. [Google Scholar] [CrossRef]
- Luo, L.S. Unified theory of lattice Boltzmann models for nonideal gases. Phys. Rev. Lett. 1998, 81, 1618–1621. [Google Scholar] [CrossRef]
- Luo, L.S. Some recent results on discrete velocity models and ramifications for lattice Boltzmann equation. Comput. Phys. Commun. 2000, 129, 63–74. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Qian, Y.H.; d'Humieres, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. EPL (Europhys. Lett.) 1992, 17, 479. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Raiskinmäki, P.; Shakib-Manesh, A.; Jasberg, A.; Koponen, A.; Merikoski, J.; Timonen, J. Lattice-Boltzmann simulation of capillary rise dynamics. J. Stat. Phys. 2002, 107, 143–158. [Google Scholar] [CrossRef]
- Hyväluoma, J.; Raiskinmäki, P.; Jäsberg, A.; Koponen, A.; Kataja, M.; Timonen, J. Evaluation of a lattice-Boltzmann method for mercury intrusion porosimetry simulations. Future Gener. Comput. Syst. 2004, 20, 1003–1011. [Google Scholar] [CrossRef]
- Chopard, B.; Droz, M. Cellular Automata Modeling of Physical Systems; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equation. Phys. Rev. Lett. 1986, 56, 1505–1508. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Pan, N. Modeling and prediction of the effective thermal conductivity of random open-cell porous foams. Int. J. Heat Mass Transf. 2008, 51, 1325–1331. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, J.; Cui, Y. Effects of Surface Wettability and Roughness on the Heat Transfer Performance of Fluid Flowing through Microchannels. Energies 2015, 8, 5704-5724. https://doi.org/10.3390/en8065704
Cui J, Cui Y. Effects of Surface Wettability and Roughness on the Heat Transfer Performance of Fluid Flowing through Microchannels. Energies. 2015; 8(6):5704-5724. https://doi.org/10.3390/en8065704
Chicago/Turabian StyleCui, Jing, and Yanyu Cui. 2015. "Effects of Surface Wettability and Roughness on the Heat Transfer Performance of Fluid Flowing through Microchannels" Energies 8, no. 6: 5704-5724. https://doi.org/10.3390/en8065704
APA StyleCui, J., & Cui, Y. (2015). Effects of Surface Wettability and Roughness on the Heat Transfer Performance of Fluid Flowing through Microchannels. Energies, 8(6), 5704-5724. https://doi.org/10.3390/en8065704





