Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery
Abstract
:1. Introduction
| Reference | Objective Function | Cycle Architecture |
|---|---|---|
| Hettiarachchi et al. [26] (2007) | Heat exchange area per unit power (m2/kWe) | SCORC |
| Cayer et al. [27] (2010) | Relative cost per unit power (€/kWe) | TCORC |
| Shengjun et al. [28] (2011) | Levelized energy cost ($/kWh) Heat exchange area per unit power (m2/kWe) | SCORC, TCORC |
| Quoilin et al. [29] (2011) | Specific investment cost (€/kWe) | SCORC |
| Wang et al. [17] (2012) | Linear combination of area per unit power (m2/kWe) and heat recovery efficiency (%) | SCORC |
| Wang et al. [30] (2013) | Heat exchange area per unit power (m2/kWe) | SCORC |
| Wang et al. 1 [31] (2013) | Exergy efficiency (%) vs. total investment cost (€/kWe) | SCORC |
| Lecompte et al. [32] (2013) | Specific investment cost (€/kWe) | SCORC |
| Pierobon et al. 1 [33] (2013) | Net present value (€) vs. volume (m3) Volume (m3) vs. thermal efficiency (%) | SCORC |
| Astolfi et al. [34] (2013) | Plant total specific cost (k€/kW) | TCORC |
| Shu et al. [35] (2014) | Net present value ($) Deprecated payback period (years) Heat exchange area per unit power (m2/kWe) | SCORC TCORC |
| Li et al. [36] (2014) | Electricity production cost ($/kWh) | SCORC ZM |
| Li et al. [37] (2014) | Electricity production cost ($/kWh) | SCORC |
| Muhammad et al. [38] (2014) | Specific investment cost ($/kW) | SCORC |
| Nusiaputra et al. [39] (2014) | Specific investment cost ($/kW) Mean cash flow ($/year) | SCORC |
| Li et al. [40] (2014) | Total area (m2) Relative cost per unit power ($/W) Ratio heat exchanger cost tot total cost (%) | SCORC |
| Toffolo et al. [41] (2014) | Specific investment cost ($/kW) Levelized cost of electricity ($/kWh) | SCORC TCORC |
| Meinel et al. [42] (2014) | Specific costs per kilowatt hour (€/kWh) | SCORC |
| Objective Function | Formula | Comments |
|---|---|---|
| Min. specific area (SA) |
| |
| Min. specific investment cost (SIC) |
| |
| Min. simple payback period (PB) |
| |
| Max. net present value (NPV) |
| |
| Min. levelized cost of electricity (LCOE) |
|
2. Description of the Thermodynamic Cycles and Cases
2.1. Description Subcritical and Transcritical ORC

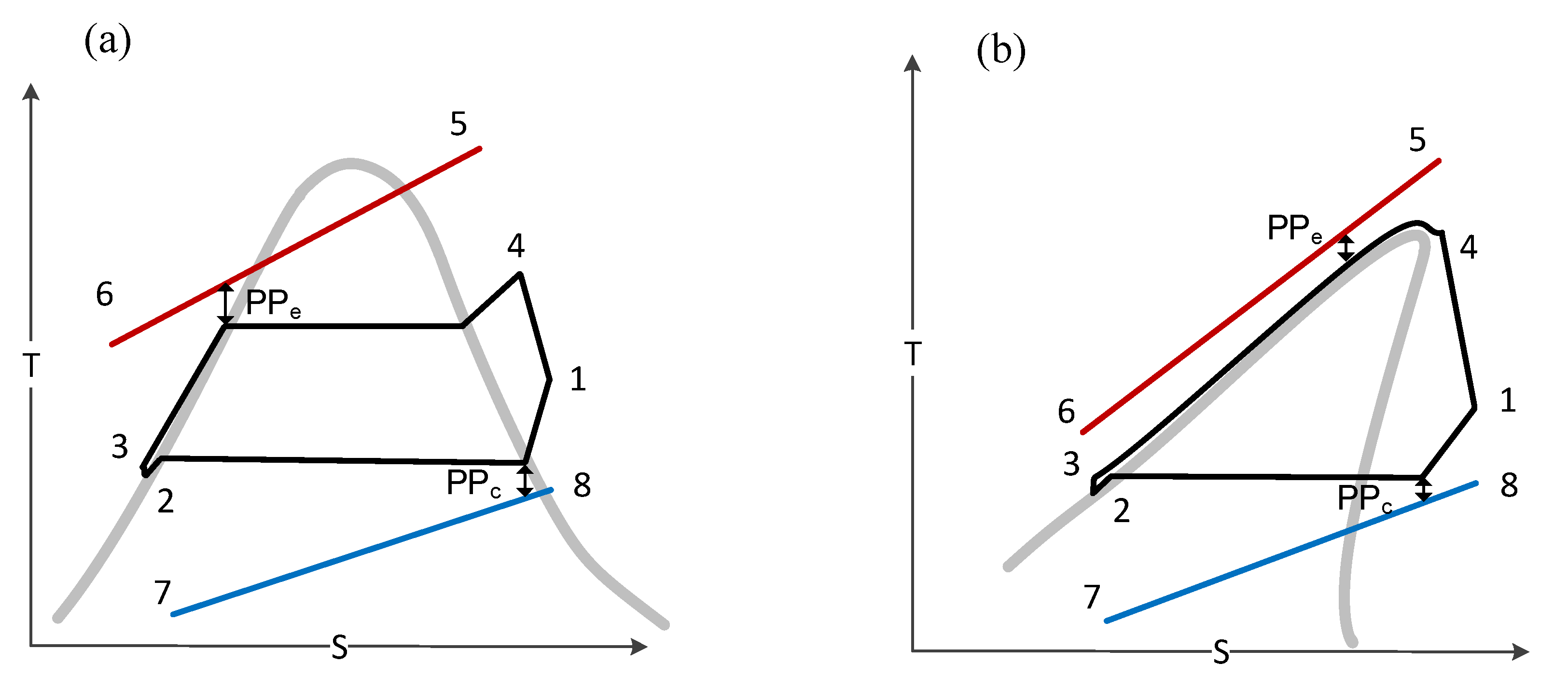
2.2. Case Definition
3. Model and Assumptions
3.1. Cycle Assumptions
| Variable | Description | Value |
|---|---|---|
| PPe | Pinch point temperature difference evaporator (°C) | Optimized |
| PPc | Pinch point temperature difference condenser (°C) | Optimized |
| T7 | Inlet temperature cooling fluid condenser (°C) | 25 |
| T4 | Inlet temperature turbine (°C) | Optimized 1 |
| pe | Evaporation pressure (Pa) | Optimized 2 |
| pc | Condensation pressure (Pa) | Optimized |
| εturbine | Isentropic efficiency turbine (-) | 0.7 |
| εpumps | Isentropic efficiency pumps (-) | 0.6 |
| εgenerator | Generator efficiency (-) | 0.98 |
| ΔTsub | Temperature subcooling (°C) | 3 |
| ΔTsup | Temperature superheating (°C) | 5 2 |
3.2. Heat Exchanger Models
| Variable | Description | Value |
|---|---|---|
| Hydraulic diameter (m) | 0.0035 | |
| Plate thickness (m) | 0.0005 | |
| Chevron angle (°) | 45 | |
| Plate thermal conductivity (W/m/K) | 13.56 | |
| Corrugation pitch (m) | 0.007 |
3.3. Cost Models
| Component | B | K1 | K2 | K3 | Valid Range |
|---|---|---|---|---|---|
| Plate heat exchangers | Area (m2) | 4.6656 | −0.1557 | 0.1547 | 10–1000 (m2) |
| Turbine | Fluid power (kW) | 2.2476 | 1.4965 | −0.1618 | 100–1500 (kW) |
| Pumps (centrifugal) | Shaft power (kW) | 3.3892 | 0.0536 | 0.1538 | 1–300 (kW) |
| Electrical motor pump | Shaft power (kW) | 2.4604 | 1.4191 | −0.1798 | 75–2600 (kW) |
| Electrical generator [41] | Shaft power (kW) | ||||
| Component | B1 | B2 | C1 | C2 | C3 | Fm | FBM |
|---|---|---|---|---|---|---|---|
| Plate heat exchangers p (bar) < 19 | 0.96 | 1.21 | 0 | 0 | 0 | 1 | - |
| Turbine | - | - | - | - | - | - | 3.5 |
| Pumps (centrifugal) 10 < p (bar) < 100 | 1.89 | 1.35 | −0.3935 | 0.3957 | −0.00226 | 1 | - |
| Pumps (centrifugal) p (bar) < 10 | 1.89 | 1.35 | 0 | 0 | 0 | 1 | - |
| Electrical motor pump | - | - | - | - | - | - | 1.5 |
| Electrical generator [41] | - | - | - | - | - | - | 1.5 |
3.4. Working Fluid Selection
| Variable | Uncertainty |
|---|---|
| Density | 0.1% (liquid phase, temperature <400 K and pressure <30 MPa) 0.2% (liquid phase, temperature >310 K and pressure >30 MPa) 1% (liquid phase, temperature <310 K and pressure >30 MPa) 1% (vapor phase, temperature >400 K) |
| Vapor pressure | 0.2% (temperature >250 K) 0.35% (temperature >370 K) |
| Liquid phase heat capacity | 5% |
3.5. Expander Considerations
4. Optimization Strategy
| Variable | Description | Lower | Upper |
|---|---|---|---|
| Mass flux working fluid condenser (kg/m2/s) | 20 | 100 | |
| Mass flux working fluid evaporator (kg/m2/s) | 20, 100 1 | 50, 200 1 | |
| Pinch point temperature difference condenser (°C) | 3 | 10 | |
| Pinch point temperature difference evaporator (°C) | 3 | 10 | |
| Liquid saturation temperature condenser (°C) | 35 | 50 | |
| 2 | Liquid saturation temperature evaporator (°C) | 100 | 148.5 |
| T71 | Turbine inlet temperature (°C) | 150 | 175 |
| Number of passes hot fluid side evaporator (-) | 1 | 3 | |
| Number of passes cold fluid side condenser (-) | 1 | 3 |
| Parameter | Value |
|---|---|
| Generations | 50 |
| Population size | 120 |
| Crossover rate | 0.8 |
| Migration rate | 0.2 |
| Mutation type | Gaussian (shrink = 1, scale = 1) |
5. Results and Discussion
5.1. Pareto Fronts and Specific Investment Cost
| Variable | Minimum SIC | Maximum Net Power Output | ||
|---|---|---|---|---|
| SCORC | TCORC | SCORC | TCORC | |
| (kWe) | 681.8 | 681.3 | 791.5 | 1040 |
| (%) | 10.47 | 11.20 | 10.9 | 11.1 |
| (°C) | 5.9 | 8.2 | 3 | 3 |
| (°C) | 8.0 | 7.0 | 3 | 3 |
| (°C) | 128.8 | - | 124.5 | - |
| (°C) | 41.1 | 39.85 | 35.2 | 37.0 |
| (°C) | 128.8 | 161.6 | 124.5 | 160.0 |
| (k€) | 2805 | 3436 | 3725 | 8162 |
| (€/kWe) | 4114 | 5044 | 4707 | 8137 |
| (m2) | 258 | 879 | 418 | 1205 |
| (m2) | 398 | 385 | 888 | 756 |
| (-) | 2 | 2 | 2 | 2 |
| (-) | 2 | 2 | 2 | 2 |
| (kg/s) | 28.58 | 26.7 | 28.9 | 40.52 |
| (kg/s) | 205.30 | 150 | 217 | 255 |
| (kg/s/m2) | 91.0 | 187 | 70.3 | 175.0 |
| (kg/s/m2) | 54.0 | 53.5 | 22.4 | 46.1 |
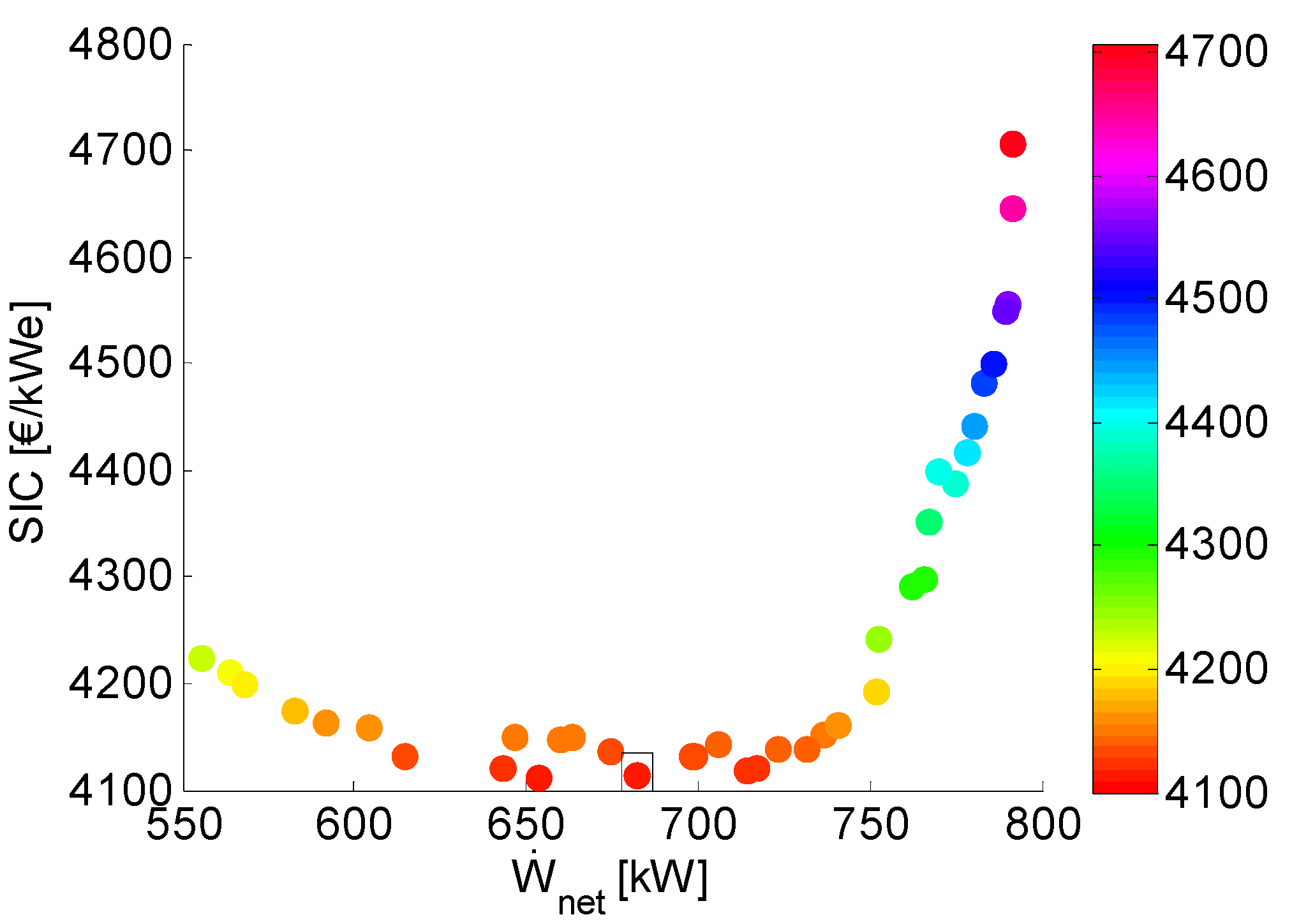
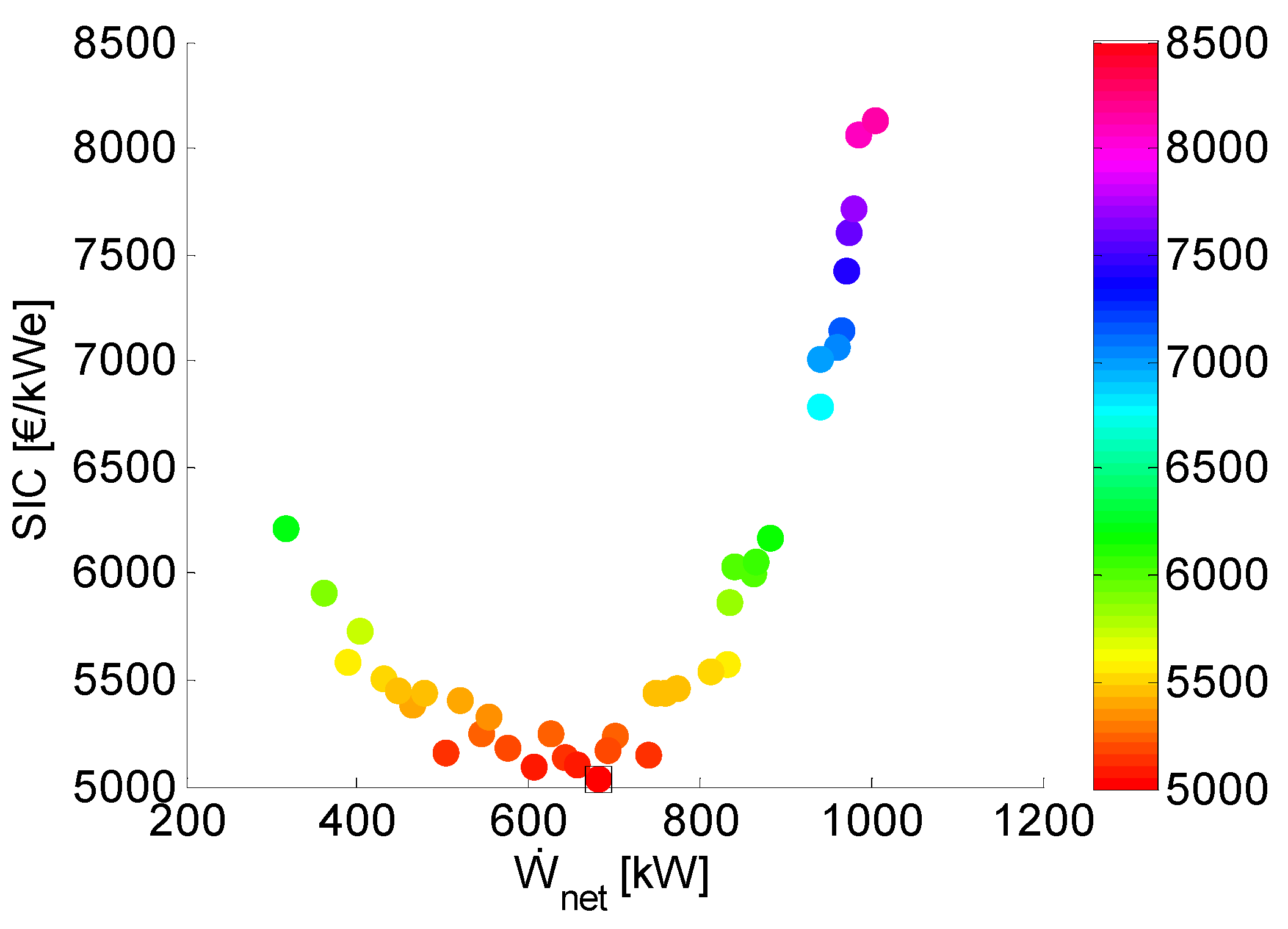
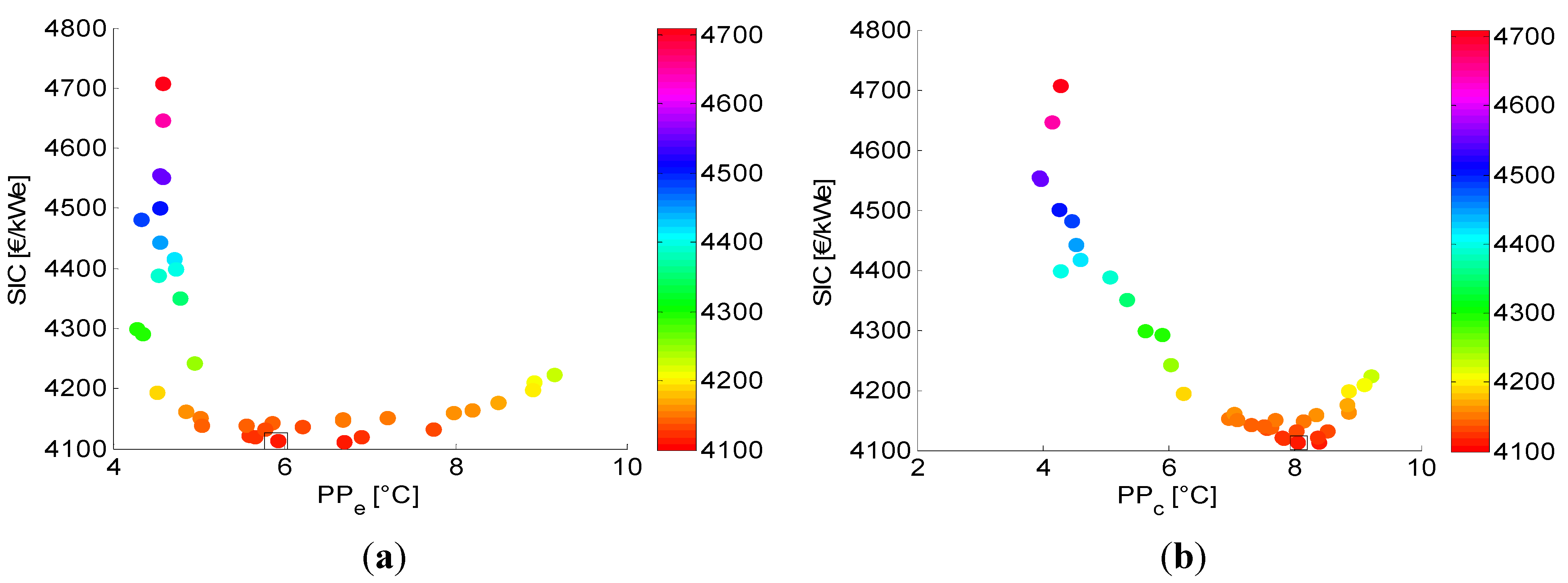

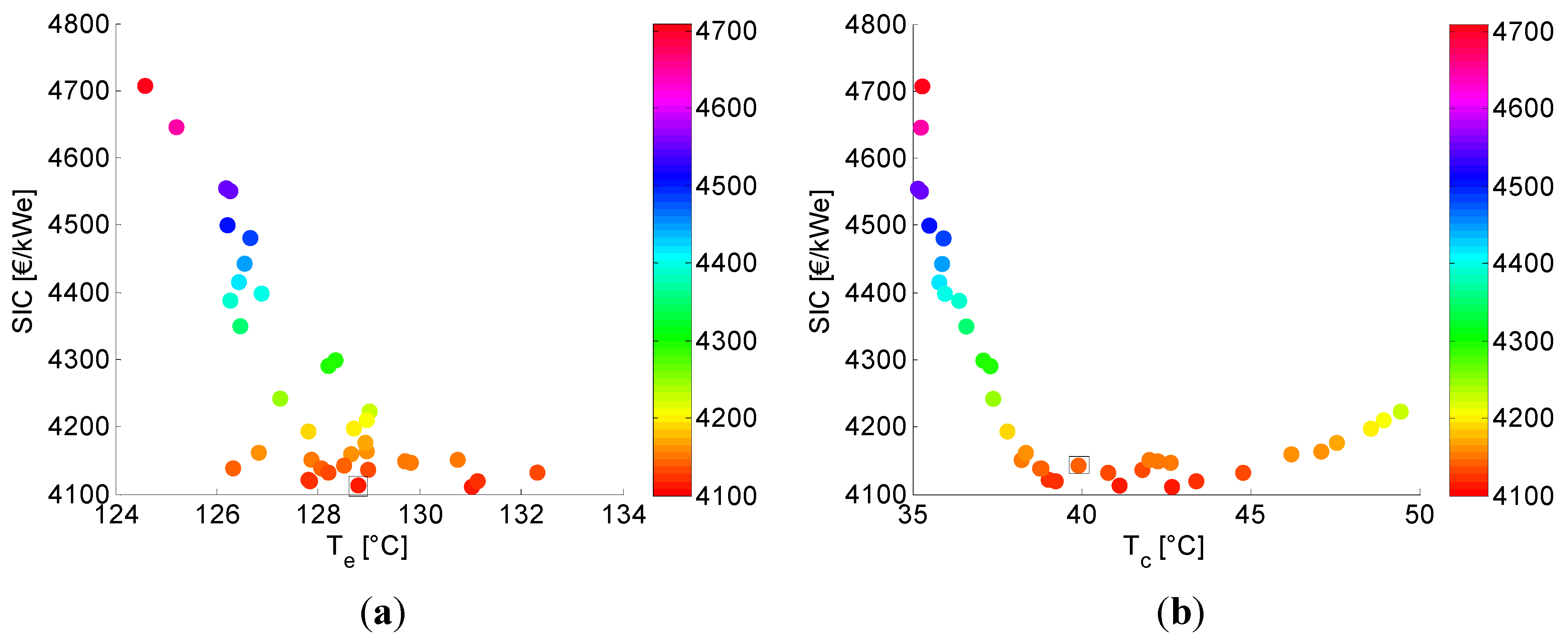
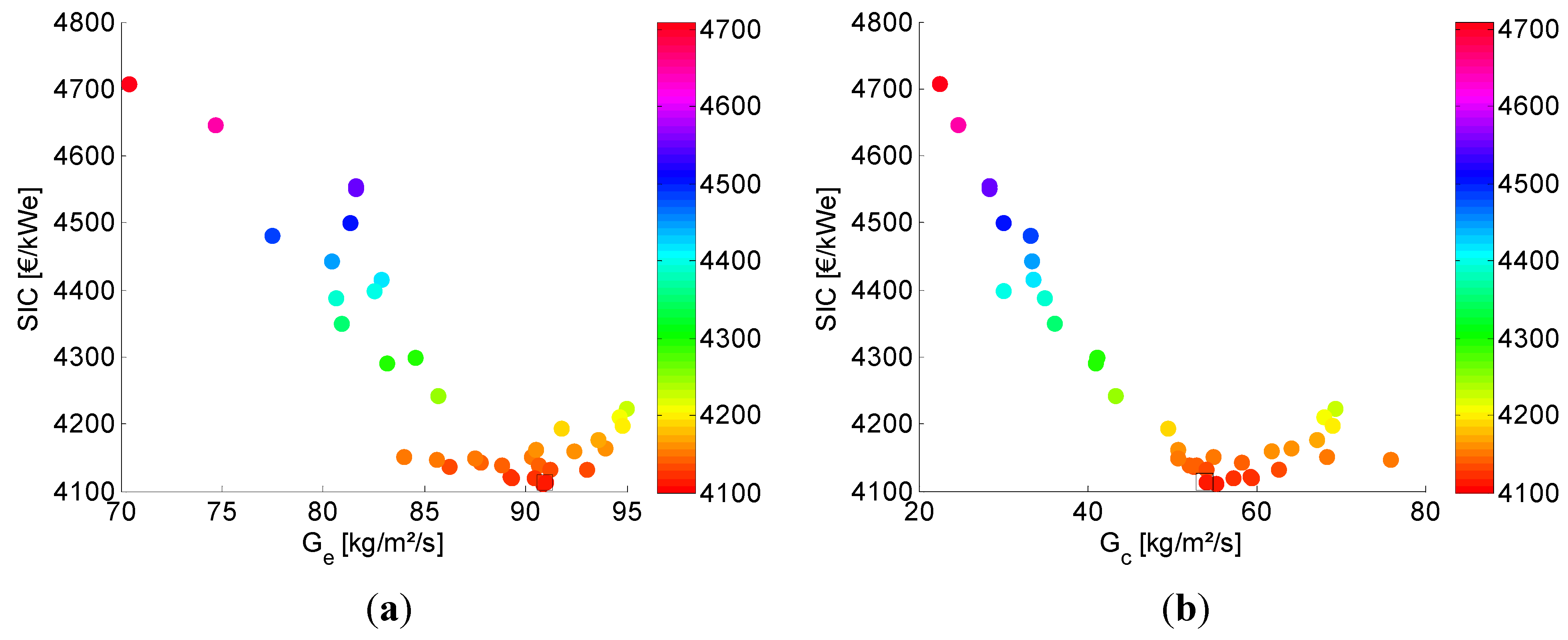
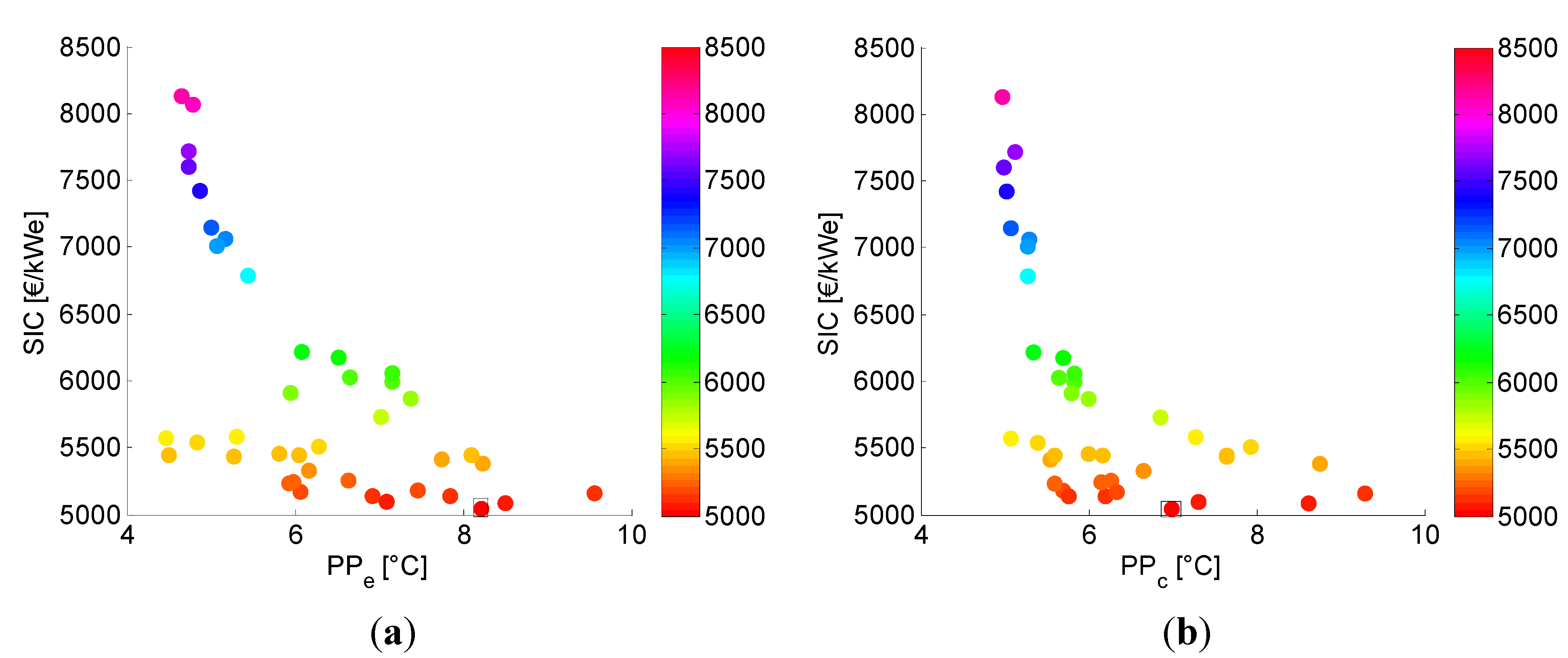
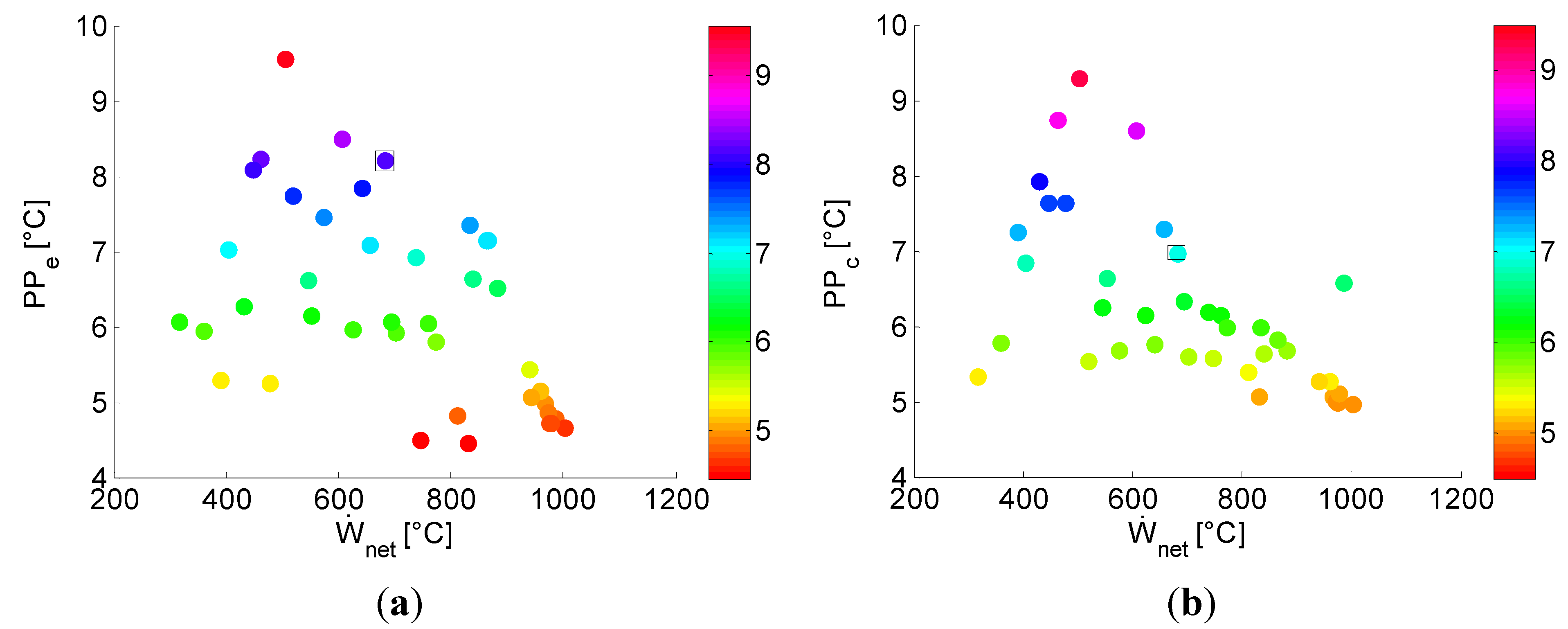
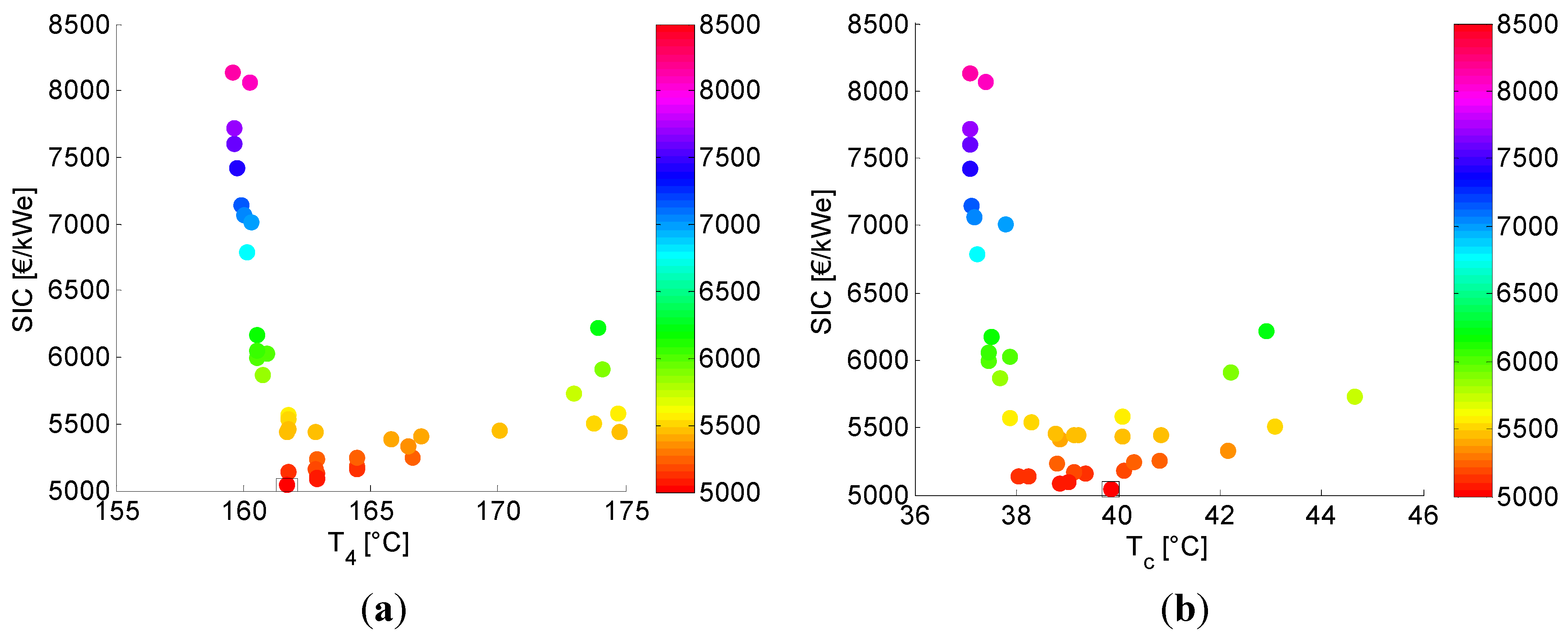
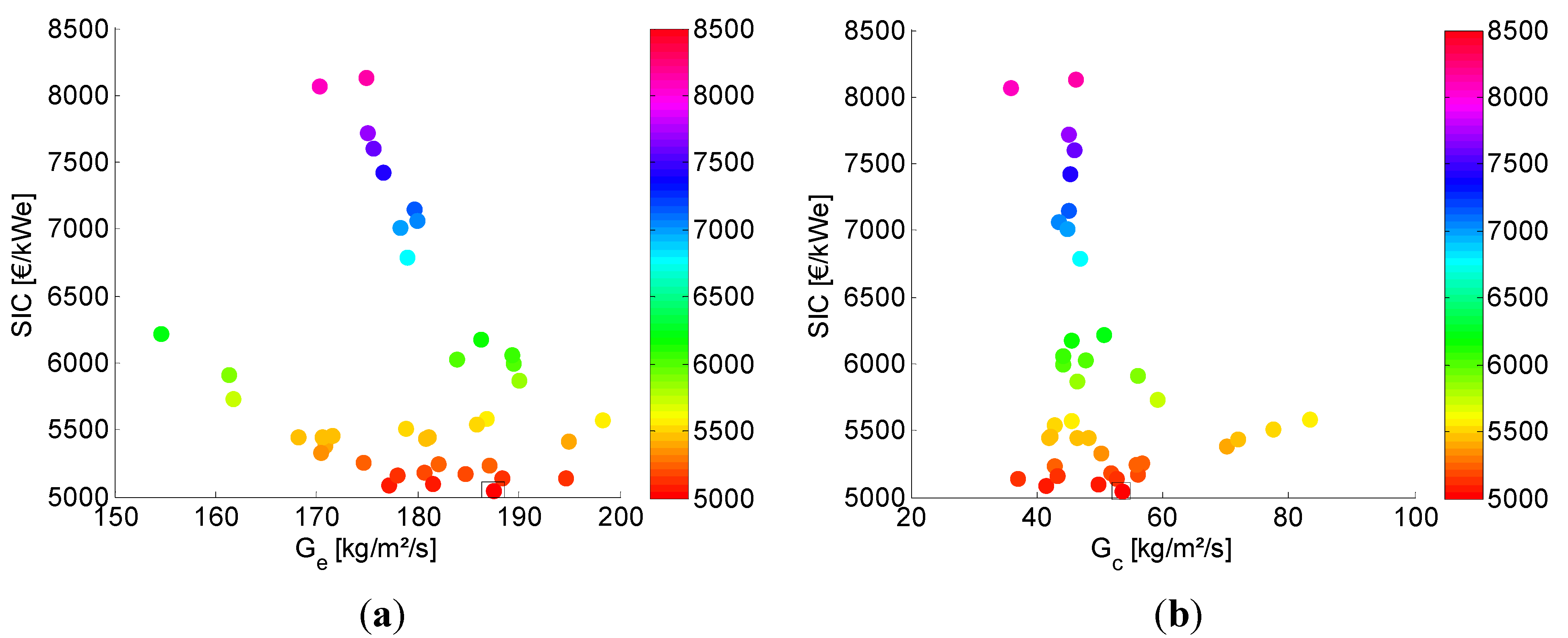
5.2. Analysis of the Parameter Space
5.3. Turbine Performance Parameters
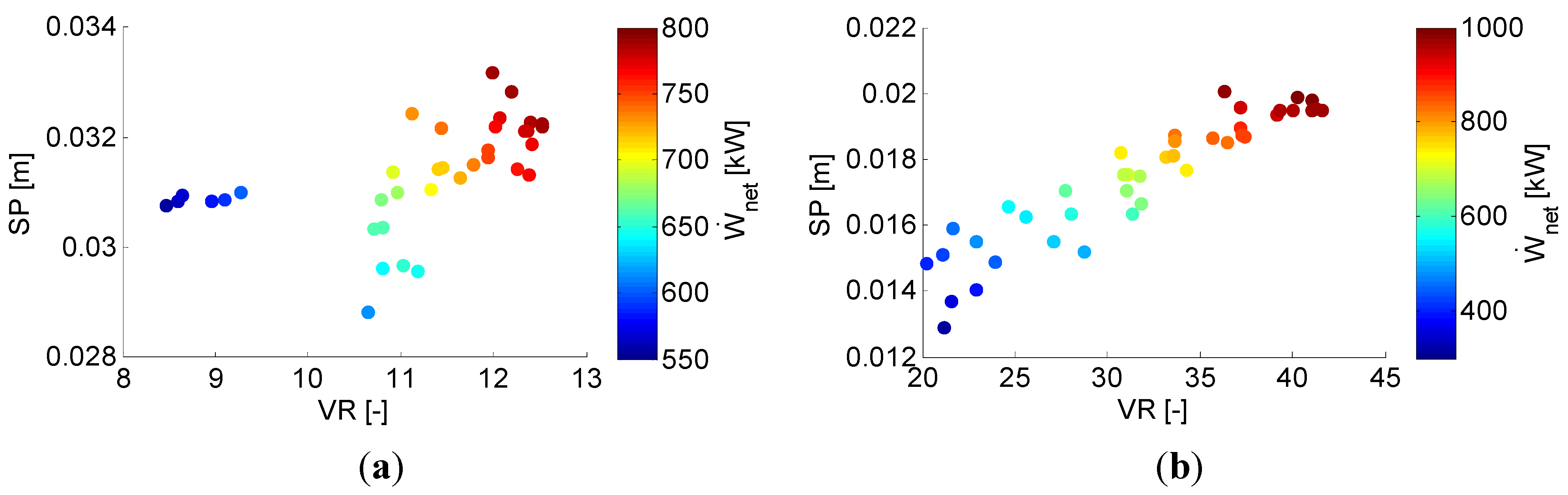
5.4. Distribution of the Costs
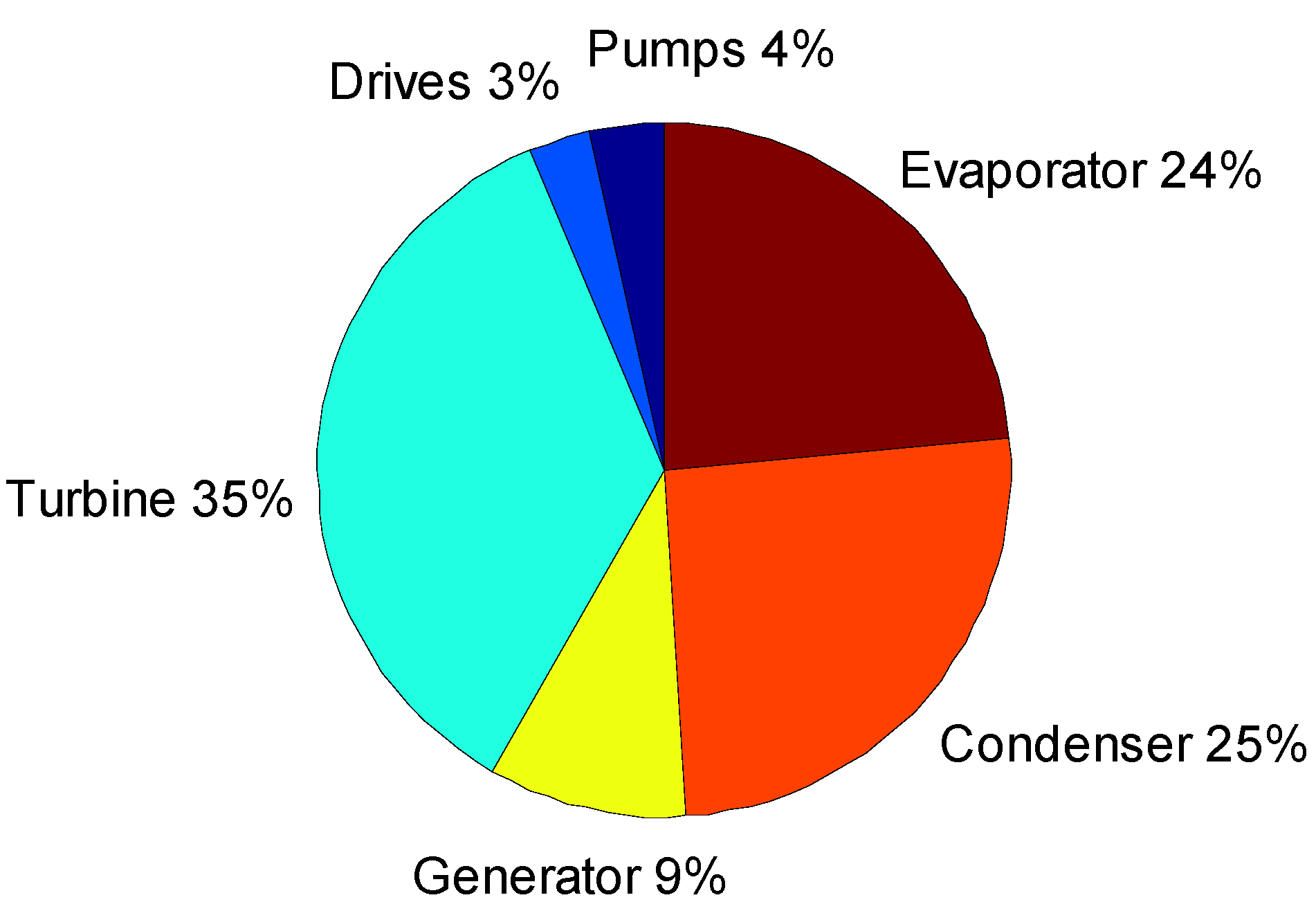

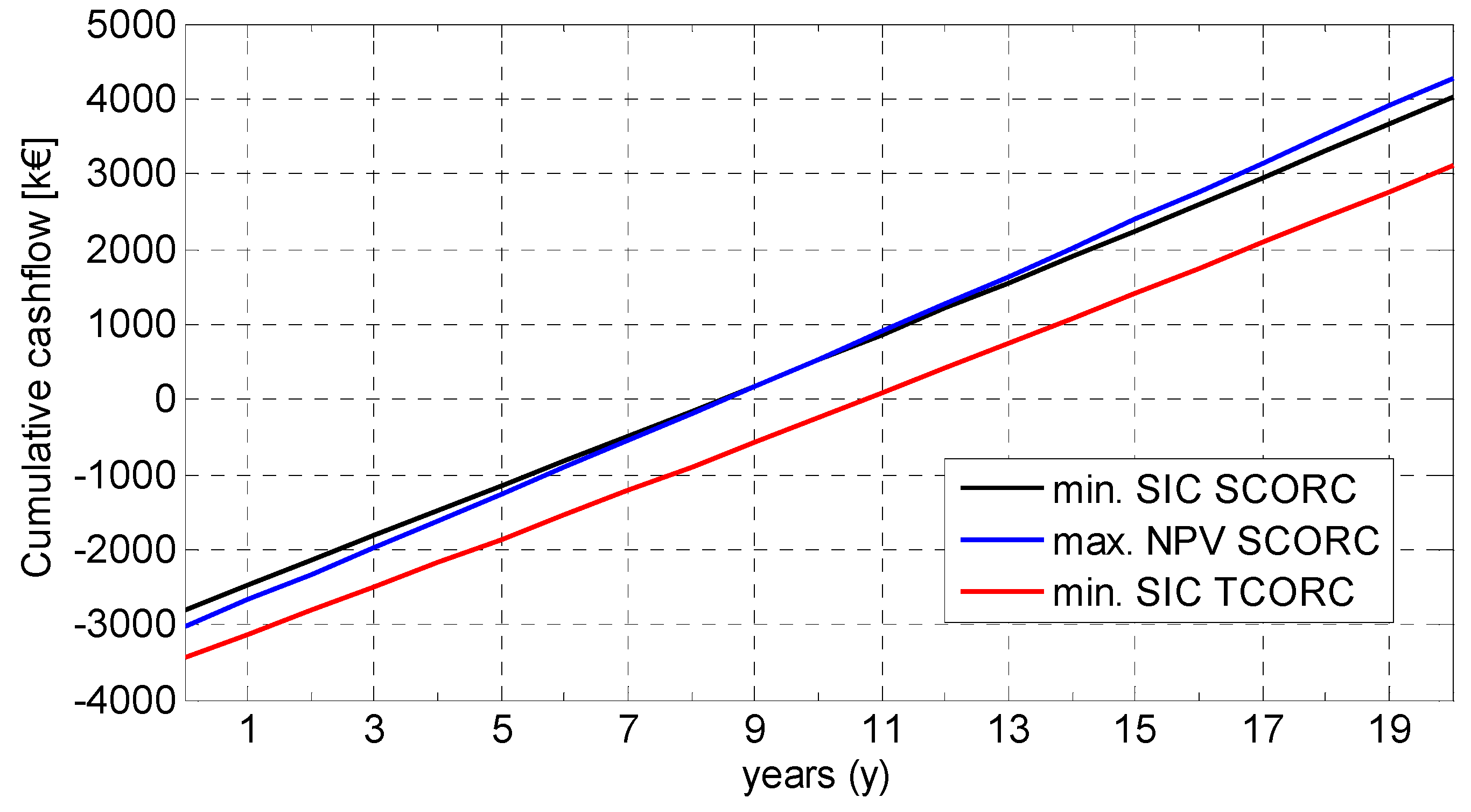
5.5. Financial Analysis and Decision Making
| Parameter | Value |
|---|---|
| ORC lifetime (y) | 20 |
| discount rate (%) | 6 |
| production hours (h/y) | 8000 |
| price electricity (€/MWh) | 69.6 |
| increase electricity price (%/y) | 0.50 |
| maintenance cost () | 0.02 |
| Case | (kW) | SIC (€/kWe) | NPV (k€) | Payback Time (y) |
|---|---|---|---|---|
| Min. SIC SCORC | 681.8 | 4114 | 1070 | 8.46 |
| Min. SIC TCORC | 681.3 | 5044 | 284 | 10.70 |
| Max. NPV SCORC | 731.3 | 4138 | 1126 | 8.52 |
| Max. NPV TCORC | 681.3 | 5044 | 284 | 10.70 |
6. Conclusions
Acknowledgments
Author Contributions
Nomenclature
| A | heat transfer area (m2) |
| Bo | boiling number (-) |
| C | cost (€) |
| Cp | isobaric specific heat capacity (J/kg·K) |
mean isobaric specific heat capacity (hb-hw)/(Tb-Tw) (J/kg·K) | |
| Dh | hydraulic diameter (m) |
| F | LMTD correction factor |
| Fm | material correction factor (-) |
| Fp | pressure correction factor (-) |
| f | friction factor (-) |
| G | mass flux (kg/m2·s) |
| h | enthalpy (J/kg) |
| I | number of segments (-) |
| K | number of paths (-) |
| k | thermal conductivity (W/m·K) |
| ṁ | mass flow rate (kg/s) |
| N | number of passes (-) |
| Nu | Nusselt number (-) |
| p | pressure (bar) |
| pco | corrugation pitch (m) |
| Pr | Prandtl number (-) |
| PP | pinch point temperature difference (°C) |
| Q̇ | heat transfer rate (W) |
| R | yearly cash flow (€/y) |
| r | discount rate (-) |
| Re | Reynolds number |
| SP | size parameter (m) |
| T | temperature (°C) |
| t | plate thickness (m) |
| U | overall heat transfer coefficient (W/m2/K) |
| V̇ | volume flow rate (m3/s) |
| v | specific volume (m3/kg) |
| VR | volume ratio (-) |
| x | vapor fraction (-) |
Greek letters
| α | heat transfer coefficient (W/m2/K) |
| β | chevron angle (°) |
| γ | thermal conductivity plate (W/m/K) |
| ε | isentropic efficiency (-) |
| μ | dynamic viscosity (kg/m/s) |
Subscripts
| b | bulk |
| c | condenser |
| cf | cooling fluid |
| e | evaporator |
| eq | equivalent |
| hf | heat carrier |
| in | inlet |
| inv | investment |
| out | outlet |
| sub | subcooled |
| sup | superheated |
| wl | wall |
| wf | working fluid |
Abbreviations
| BM | bare module |
| CPCI | Chemical Engineering Plant Cost Index |
| EES | Engineering Equation Solver |
| GR | grass root |
| LMTD | log mean temperature difference |
| ORC | organic Rankine cycle |
| PEC | purchased equipment cost |
| SA | specific area (m2/kW) |
| SCORC | subcritical organic Rankine cycle |
| SIC | specific investment cost (€/kW) |
| TCORC | transcritical organic Rankine cycle |
| TLC | triangular cycle |
| TM | total module |
Conflicts of Interest
References
- Bronicki, L. Short review of the long history of ORC power systems. In Proceedings of the ORC2013, Rotterdam, The Netherlands, 7–8 October 2013.
- Tchanche, B.F.; Pétrissans, M.; Papadakis, G. Heat resources and organic Rankine cycle machines. Renew. Sustain. Energy Rev. 2014, 39, 1185–1199. [Google Scholar]
- Quoilin, S.; Broek, M.V.D.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles–A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Lai, N.A.; Fischer, J. Efficiencies of power flash cycles. Energy 2012, 44, 1017–1027. [Google Scholar] [CrossRef]
- Fischer, J. Comparison of trilateral cycles and organic Rankine cycles. Energy 2011, 36, 6208–6219. [Google Scholar] [CrossRef]
- Smith, I.K. Development of the trilateral flash cycle system Part1: Fundamental considerations. Proc. Inst. Mech. Eng. Part A J. Power Energy 1993, 207, 179–194. [Google Scholar] [CrossRef]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in Organic Rankine Cycles for low-enthalpy geothermal resources. Renew. Energy 2012, 37, 364–370. [Google Scholar] [CrossRef]
- Lecompte, S.; Ameel, B.; Ziviani, D.; van den Broek, M.; de Paepe, M. Exergy analysis of zeotropic mixtures as working fluids in Organic Rankine Cycles. Energy Convers. Manag. 2014, 85, 727–739. [Google Scholar] [CrossRef]
- Chys, M.; van den Broek, M.; Vanslambrouck, B.; Paepe, M.D. Potential of zeotropic mixtures as working fluids in organic Rankine cycles. Energy 2012, 44, 623–632. [Google Scholar] [CrossRef]
- Stijepovic, M.Z.; Papadopoulos, A.I.; Linke, P.; Grujic, A.S.; Seferlis, P. An exergy composite curves approach for the design of optimum multi-pressure organic Rankine cycle processes. Energy 2014, 69, 285–298. [Google Scholar] [CrossRef]
- Gnutek, Z.; Bryszewska-Mazurek, A. The thermodynamic analysis of multicycle ORC engine. Energy 2001, 26, 1075–1082. [Google Scholar] [CrossRef]
- Angelino, G.; Colonna, P. Multicomponent working fluids for organic Rankine cycles (ORCs). Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Schuster, A.; Karellas, S.; Aumann, R. Efficiency optimization potential in supercritical Organic Rankine Cycles. Energy 2010, 35, 1033–1039. [Google Scholar] [CrossRef]
- Karellas, S.; Schuster, A.; Leontaritis, A.-D. Influence of supercritical ORC parameters on plate heat exchanger design. Appl. Therm. Eng. 2012, 33–34, 70–76. [Google Scholar]
- Wang, Z.Q.; Zhou, N.J.; Guo, J.; Wang, X.Y. Fluid selection and parametric optimization of organic Rankine cycle using low temperature waste heat. Energy 2012, 40, 107–115. [Google Scholar] [CrossRef]
- Yamada, N.; Mohamad, M.N.A.; Kien, T.T. Study on thermal efficiency of low- to medium-temperature organic Rankine cycles using HFO−1234yf. Renew. Energy 2012, 41, 368–375. [Google Scholar] [CrossRef]
- Liu, B.-T.; Chien, K.-H.; Wang, C.-C. Effect of working fluids on organic Rankine cycle for waste heat recovery. Energy 2004, 29, 1207–1217. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, J.; Gao, L. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery. Energy Convers. Manag. 2009, 50, 576–582. [Google Scholar] [CrossRef]
- Hung, T.C.; Wang, S.K.; Kuo, C.H.; Pei, B.S.; Tsai, K.F. A study of organic working fluids on system efficiency of an ORC using low-grade energy sources. Energy 2010, 35, 1403–1411. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Ho, T.; Mao, S.S.; Greif, R. Comparison of the Organic Flash Cycle (OFC) to other advanced vapor cycles for intermediate and high temperature waste heat reclamation and solar thermal energy. Energy 2012, 42, 213–223. [Google Scholar] [CrossRef]
- Öhman, H.; Lundqvist, P. Comparison and analysis of performance using Low Temperature Power Cycles. Appl. Therm. Eng. 2013, 52, 160–169. [Google Scholar] [CrossRef]
- Brigham, E.F.; Ehrhardt, M.C. Financial Management: Theory and Practice, 14th ed.; South-Western Cengage Learning: Mason, USA, 2014. [Google Scholar]
- Madhawa Hettiarachchi, H.D.; Golubovic, M.; Worek, W.M.; Ikegami, Y. Optimum design criteria for an Organic Rankine cycle using low-temperature geothermal heat sources. Energy 2007, 32, 1698–1706. [Google Scholar]
- Cayer, E.; Galanis, N.; Nesreddine, H. Parametric study and optimization of a transcritical power cycle using a low temperature source. Appl. Energy 2010, 87, 1349–1357. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Guo, T. Performance comparison and parametric optimization of subcritical Organic Rankine Cycle (ORC) and transcritical power cycle system for low-temperature geothermal power generation. Appl. Energy 2011, 88, 2740–2754. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Wang, M.; Ma, S.; Dai, Y. Thermodynamic analysis and optimization of an (organic Rankine cycle) ORC using low grade heat source. Energy 2013, 49, 356–365. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Wang, M.; Li, M.; Dai, Y. Multi-objective optimization of an organic Rankine cycle (ORC) for low grade waste heat recovery using evolutionary algorithm. Energy Convers. Manag. 2013, 71, 146–158. [Google Scholar] [CrossRef]
- Lecompte, S.; Huisseune, H.; van den Broek, M.; de Schampheleire, S.; de Paepe, M. Part load based thermo-economic optimization of the Organic Rankine Cycle (ORC) applied to a combined heat and power (CHP) system. Appl. Energy 2013, 111, 871–881. [Google Scholar] [CrossRef]
- Pierobon, L.; Nguyen, T.-V.; Larsen, U.; Haglind, F.; Elmegaard, B. Multi-objective optimization of organic Rankine cycles for waste heat recovery: Application in an offshore platform. Energy 2013, 58, 538–549. [Google Scholar] [CrossRef]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (Organic Rankine Cycles) power plants for the exploitation of medium–low temperature geothermal sources–Part B: Techno-economic optimization. Energy 2014, 66, 435–446. [Google Scholar]
- Shu, G.; Yu, G.; Tian, H.; Wei, H.; Liang, X. A Multi-Approach Evaluation System (MA-ES) of Organic Rankine Cycles (ORC) used in waste heat utilization. Appl. Energy 2014, 132, 325–338. [Google Scholar] [CrossRef]
- Li, Y.-R.; Du, M.-T.; Wu, C.-M.; Wu, S.-Y.; Liu, C. Potential of organic Rankine cycle using zeotropic mixtures as working fluids for waste heat recovery. Energy 2014, 77, 509–519. [Google Scholar] [CrossRef]
- Li, Y.-R.; Du, M.-T.; Wu, C.-M.; Wu, S.-Y.; Liu, C.; Xu, J.-L. Economical evaluation and optimization of subcritical organic Rankine cycle based on temperature matching analysis. Energy 2014, 68, 238–247. [Google Scholar] [CrossRef]
- Imran, M.; Park, B.S.; Kim, H.J.; Lee, D.H.; Usman, M.; Heo, M. Thermo-economic optimization of Regenerative Organic Rankine Cycle for waste heat recovery applications. Energy Convers. Manag. 2014, 87, 107–118. [Google Scholar] [CrossRef]
- Nusiaputra, Y.Y.; Wiemer, H.-J.; Kuhn, D. Thermal-Economic modularization of small, organic Rankine cycle power plants for mid-enthalpy geothermal fields. Energies 2014, 7, 4221–4240. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; Li, S.; Wang, X.; He, W.; Dai, Y. Thermo-economic analysis and comparison of a CO2 transcritical power cycle and an organic Rankine cycle. Geothermics 2014, 50, 101–111. [Google Scholar] [CrossRef]
- Toffolo, A.; Lazzaretto, A.; Manente, G.; Paci, M. A multi-criteria approach for the optimal selection of working fluid and design parameters in Organic Rankine Cycle systems. Appl. Energy 2014, 121, 219–232. [Google Scholar] [CrossRef]
- Meinel, D.; Wieland, C.; Spliethoff, H. Economic comparison of ORC (Organic Rankine cycle) processes at different scales. Energy 2014, 74, 694–706. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; Wiley: Chicester, West Sussex, UK, 2001. [Google Scholar]
- Mago, P.J.; Chamra, L.M.; Srinivasan, K.; Somayaji, C. An examination of regenerative organic Rankine cycles using dry fluids. Appl. Therm. Eng. 2008, 28, 998–1007. [Google Scholar] [CrossRef]
- Hung, T.C.; Shai, T.Y.; Wang, S.K. A review of organic rankine cycles (ORCs) for the recovery of low-grade waste heat. Energy 1997, 22, 661–667. [Google Scholar] [CrossRef]
- Lai, N.A.; Wendland, M.; Fischer, J. Working fluids for high-temperature organic Rankine cycles. Energy 2011, 36, 199–211. [Google Scholar] [CrossRef]
- Martin, H. Economic optimization of compact heat exchangers. In Proceedings of the EF-Conference on Compact Heat Exchangers and Enhancement Technology for the Process Industries, Banff, AB, Canada, 18–23 July 1999.
- Han, D.-H.; Lee, K.-J.; Kim, Y.-H. Experiments on the characteristics of evaporation of R410A in brazed plate heat exchangers with different geometric configurations. Appl. Therm. Eng. 2003, 23, 1209–1225. [Google Scholar] [CrossRef]
- Han, D.; Lee, K.; Kim, Y. The characteristics of condensation in brazed plate heat and exchangers with different chevron angles. J. Korean Phys. Soc. 2003, 43, 66–73. [Google Scholar]
- Hsieh, Y.Y.; Lin, T.F. Evaporation heat transfer and pressure drop of refrigerant R-410A flow in a vertical plate heat exchanger. J. Heat Transf. 2003, 125, 852–857. [Google Scholar] [CrossRef]
- Yan, Y.Y.; Lin, T.F. Evaporation heat transfer and pressure drop of refrigerant R-134a in a plate heat exchanger. J. Heat Transf. 1999, 121, 118–127. [Google Scholar] [CrossRef]
- Kuo, C.-R.; Hsu, S.-W.; Chang, K.-H.; Wang, C.-C. Analysis of a 50kW organic Rankine cycle system. Energy 2011, 36, 5877–5885. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Comparison of shell-and-tube with plate heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 87, 227–237. [Google Scholar] [CrossRef]
- García-Cascales, J.R.; Vera-García, F.; Corberán-Salvador, J.M.; Gonzálvez-Maciá, J. Assessment of boiling and condensation heat transfer correlations in the modelling of plate heat exchangers. Int. J. Refrig. 2007, 30, 1029–1041. [Google Scholar] [CrossRef]
- Petukhov, B.S.; Krasnoschekov, E.A.; Protopopov, V.S. An investigation of heat transfer to fluid flowing in pipes under supercritical conditions. In Proceedings of the International Developments in Heat Transfer, University of Colorado, Boulder, CO, USA, 8–12 January 1961; Volume 67, pp. 569–578.
- Wang, L.; Sundén, B.; Manglik, R.M. Plate Heat Exchangers: Design, Applications and Performance; WIT Press: Southampton, UK, 2007. [Google Scholar]
- Barbazza, L.; Pierobon, L.; Mirandola, A.; Haglind, F. Optimal design of compact organic Rankine cycle units for domestic solar applications. Therm. Sci. 2014, 18, 811–822. [Google Scholar] [CrossRef]
- Wang, L.; Sundén, B. Optimal design of plate heat exchangers with and without pressure drop specifications. Appl. Therm. Eng. 2003, 23, 295–311. [Google Scholar] [CrossRef]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.; Bhattacharyya, D. Analysis, Synthesis and Design of Chemical Processes, 4th ed.; Pearson Education: Ann Arbor, MI, USA, 2013. [Google Scholar]
- Lee, Y.-R.; Kuo, C.-R.; Wang, C.-C. Transient response of a 50 kW organic Rankine cycle system. Energy 2012, 48, 532–538. [Google Scholar] [CrossRef]
- Declaye, S.; Quoilin, S.; Guillaume, L.; Lemort, V. Experimental study on an open-drive scroll expander integrated into an ORC (Organic Rankine Cycle) system with R245fa as working fluid. Energy 2013, 55, 173–183. [Google Scholar] [CrossRef]
- Sauret, E.; Rowlands, A.S. Candidate radial-inflow turbines and high-density working fluids for geothermal power systems. Energy 2011, 36, 4460–4467. [Google Scholar] [CrossRef]
- Kang, S.H. Design and experimental study of ORC (organic Rankine cycle) and radial turbine using R245fa working fluid. Energy 2012, 41, 514–524. [Google Scholar] [CrossRef]
- Luján, J.M.; Serrano, J.R.; Dolz, V.; Sánchez, J. Model of the expansion process for R245fa in an Organic Rankine Cycle (ORC). Appl. Therm. Eng. 2012, 40, 248–257. [Google Scholar] [CrossRef]
- Da Lio, L.; Manente, G.; Lazzaretto, A. New efficiency charts for the optimum design of axial flow turbines for organic Rankine cycles. Energy 2014, 77, 447–459. [Google Scholar] [CrossRef]
- Klein, S.A. Engineering Equation Solver; F-Chart Software: Middleton, WI, USA, 2010. [Google Scholar]
- Lemmon, E.W.; Span, R. Short fundamental equations of state for 20 industrial fluids. J. Chem. Eng. Data 2006, 51, 785–850. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 9.1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013.
- Huber, M.L.; Laesecke, A.; Perkins, R.A. Model for the viscosity and thermal conductivity of refrigerants, including a new correlation for the viscosity of R134a. Ind. Eng. Chem. Res. 2003, 42, 3163–3178. [Google Scholar] [CrossRef]
- Marsh, K.N.; Perkins, R.A.; Ramires, M.L.V. Measurement and correlation of the thermal conductivity of propane from 86 to 600 K at pressures to 70 MPa. J. Chem. Eng. Data 2002, 47, 932–940. [Google Scholar] [CrossRef]
- Macchi, E. The choice of working fluid: The most important step for a successful organic Rankine cycle (and an efficient turbine), Keynote lecture. In Proceedings of the ASME ORC2013, Rotterdam, The Netherlands, 7–8 October 2013.
- Maraver, D.; Royo, J.; Lemort, V.; Quoilin, S. Systematic optimization of subcritical and transcritical organic Rankine cycles (ORCs) constrained by technical parameters in multiple applications. Appl. Energy 2014, 117, 11–29. [Google Scholar] [CrossRef]
- Shah, R.K.; Subbarao, E.C.; Mashelkar, R.A. Heat Transfer Equipment Design; CRC Press: New York, NY, USA, 1988. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algoritm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, Y.; Li, B.; Yang, J.; Shi, Y. Sensitivity analysis and thermoeconomic comparison of ORCs (organic Rankine cycles) for low temperature waste heat recovery. Energy 2015, 82, 664–677. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Thermodynamic modeling and multi-objective evolutionary-based optimization of a new multigeneration energy system. Energy Convers. Manag. 2013, 76, 282–300. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Thermoeconomic multi-objective optimization of a novel biomass-based integrated energy system. Energy 2014, 68, 958–970. [Google Scholar] [CrossRef]
- Hajabdollahi, Z.; Hajabdollahi, F.; Tehrani, M.; Hajabdollahi, H. Thermo-economic environmental optimization of Organic Rankine Cycle for diesel waste heat recovery. Energy 2013, 63, 142–151. [Google Scholar] [CrossRef]
- MATLAB Release 2013b, The MathWorks, Inc.: Natick, MA, USA.
- Lemmens, S.; Lecompte, S.; de Paepe, M. Workshop Financial Appraisal of ORC Systems. In Presented at ORCNext Project, Antwerp, Belgium, 18 September 2014.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lecompte, S.; Lemmens, S.; Huisseune, H.; Van den Broek, M.; De Paepe, M. Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery. Energies 2015, 8, 2714-2741. https://doi.org/10.3390/en8042714
Lecompte S, Lemmens S, Huisseune H, Van den Broek M, De Paepe M. Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery. Energies. 2015; 8(4):2714-2741. https://doi.org/10.3390/en8042714
Chicago/Turabian StyleLecompte, Steven, Sanne Lemmens, Henk Huisseune, Martijn Van den Broek, and Michel De Paepe. 2015. "Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery" Energies 8, no. 4: 2714-2741. https://doi.org/10.3390/en8042714
APA StyleLecompte, S., Lemmens, S., Huisseune, H., Van den Broek, M., & De Paepe, M. (2015). Multi-Objective Thermo-Economic Optimization Strategy for ORCs Applied to Subcritical and Transcritical Cycles for Waste Heat Recovery. Energies, 8(4), 2714-2741. https://doi.org/10.3390/en8042714






