Methodologies and Advancements in the Calibration of Building Energy Models
Abstract
:1. Introduction
2. Typical Calibration Issues
| Calibration Levels | Building Input Data Available | |||||
|---|---|---|---|---|---|---|
| Utility Bills | As-Built Data | Site Visit or Inspection | Detailed Audit | Short-Term Monitoring | Long-Term Monitoring | |
| Level 1 | X | X | ||||
| Level 2 | X | X | X | |||
| Level 3 | X | X | X | X | ||
| Level 4 | X | X | X | X | X | |
| Level 5 | X | X | X | X | X | X |
- -
- Standardization. Statistical criteria are used for assessing whether or not a building model can be considered calibrated. They do not provide a method about how calibrating a building model. Therefore, so far, there is no formal and recognized standard methodology or guidelines for CS, which is usually carried out based on users’ judgment and experience.
- -
- Calibration costs. The modeling process does not represent an easy task, even for building simulation that does not require calibration. Calibrated models are far more complicated and require higher expenses than “uncalibrated” models. Calibration, as no automated procedure has been defined yet, is highly time-consuming indeed. Furthermore time and expense for collecting sub-metered data, contribute to CS costs.
- -
- Model complexity. Depending on the type of energy model created and on the model complexity, the number of input data considered may vary. Normative quasi-steady models are simpler than transient energy models, created within energy simulation program (e.g., EnergyPlus, TRNSYS (Transient System Simulation Tool), etc.). The degree of simplification of the building model concerns directly the input data, as the more complex the models is, the larger amount of input data are required.
- -
- Model input data. Large quantity of input data are always involved in the building modeling process. However, the quantity may vary depending on the level of detail pursued in the model definition and on the data availability (e.g., problems of data quality). Measured data are sometime used for providing the model with further information (e.g., building occupancy, temperature set point, etc.) during validation of the calibrated model based on statistical indices.
- -
- Uncertainty in building models. When manual calibration is carried out, a deterministic approach is usually adopted. However as not all input data affect the investigated energy consumption in the same ways, it is important to identify, throughout a screening analysis, the parameters that influence the most the building model, and define their level of uncertainty.
- -
- Discrepancies identification. Issues concerning the reason of discrepancies between simulated consumption and measured consumption is often encountered during CS. Experienced users may be able to detect the underlying causes of the mismatch due to their building simulation skills and knowledge. These disagreements may be linked to a chain of causes or imputation errors in building model definition or also to measurements errors.
- -
- Automation. So far, no approved automated methodology for calibration has been presented. Various CS application, based on users’ experience and manual approach, can be listed. An automated methodology will so far reduce expenses and also attempt to wider the knowledge of calibration to other professionals.
- -
- User’s experience. Another issue that should be taken into consideration is the user’s experience. Reddy et al. [17] claims that “calibration is highly dependent on the personal judgment of the analyst doing the calibration”. Since from the first stages of simulation, the user’s experience can affect calibration results. Even with a systematic and automated procedure, users are still responsible of CS and a more than basic knowledge of the building simulation domain is required for applying the procedure. A deep sensibility towards the modeling process may in fact reduce calibration expenses, in terms of timing and avoiding mistakes.
3. Criteria for the Model Goodness-of-Fit
- -
- M is the measured energy data point during the time interval; and
- -
- S is the simulated energy data point during the same time interval.
| Statistical Indices | Monthly Calibration | Hourly Calibration | ||||
|---|---|---|---|---|---|---|
| St. 14 | IPMVP | FEMP | St. 14 | IPMVP | FEMP | |
| MBE [%] | ±5 | ±20 | ±5 | ±10 | ±5 | ±10 |
| Cv(RMSE) [%] | 15 | - | 15 | 30 | 20 | 30 |
4. Calibration Methodologies for Building Simulation Models
- (1)
- manual calibration methods based on an iterative approach;
- (2)
- graphical-based calibration methods;
- (3)
- calibration based on special tests and analysis procedures; and
- (4)
- automated techniques for calibration, based on analytical and mathematical approaches.
4.1. Manual Calibration
4.2. Graphical Techniques
- -
- 3D comparative plots; and
- -
- calibration and Characteristic signature.
4.2.1. 3D Comparative Plots
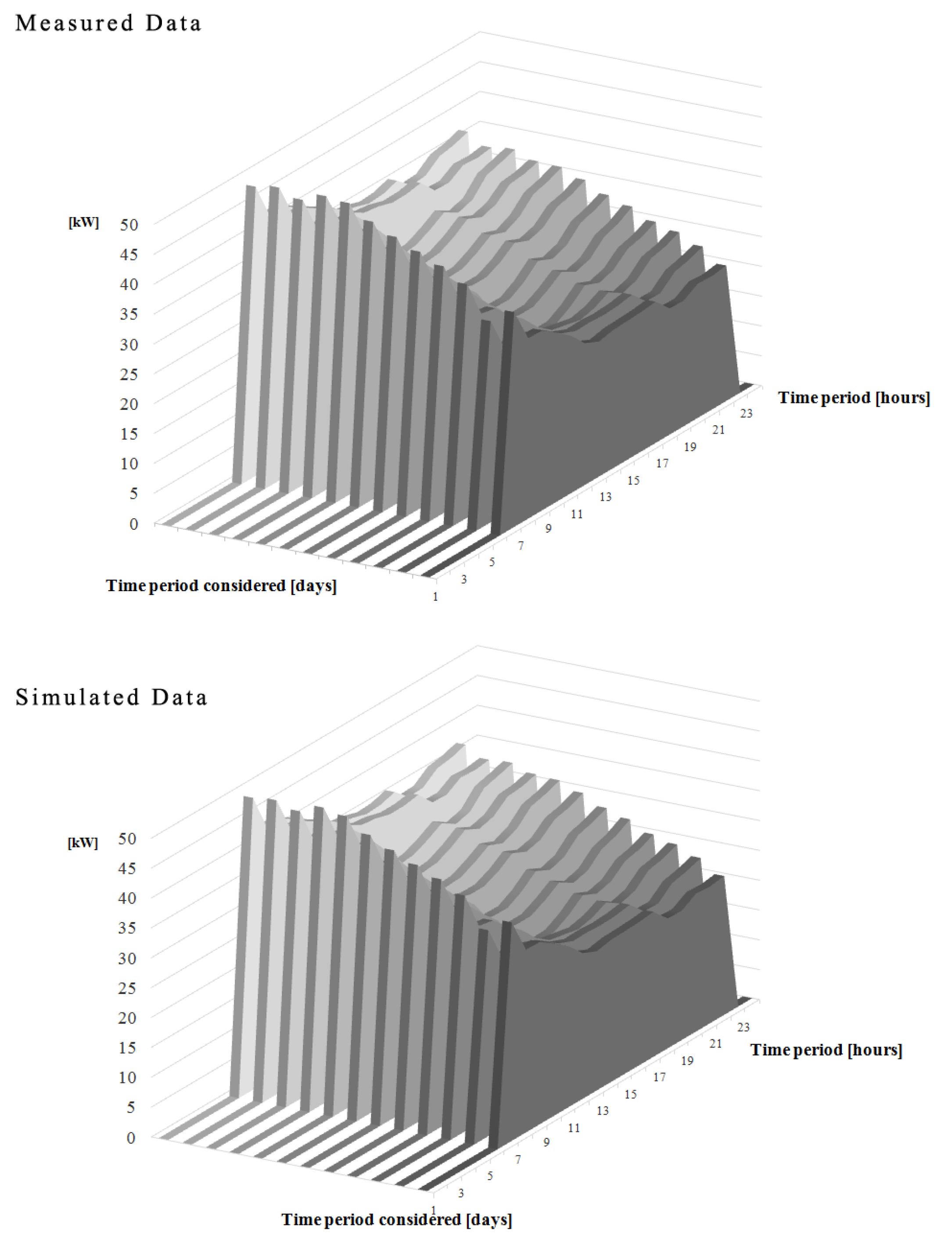
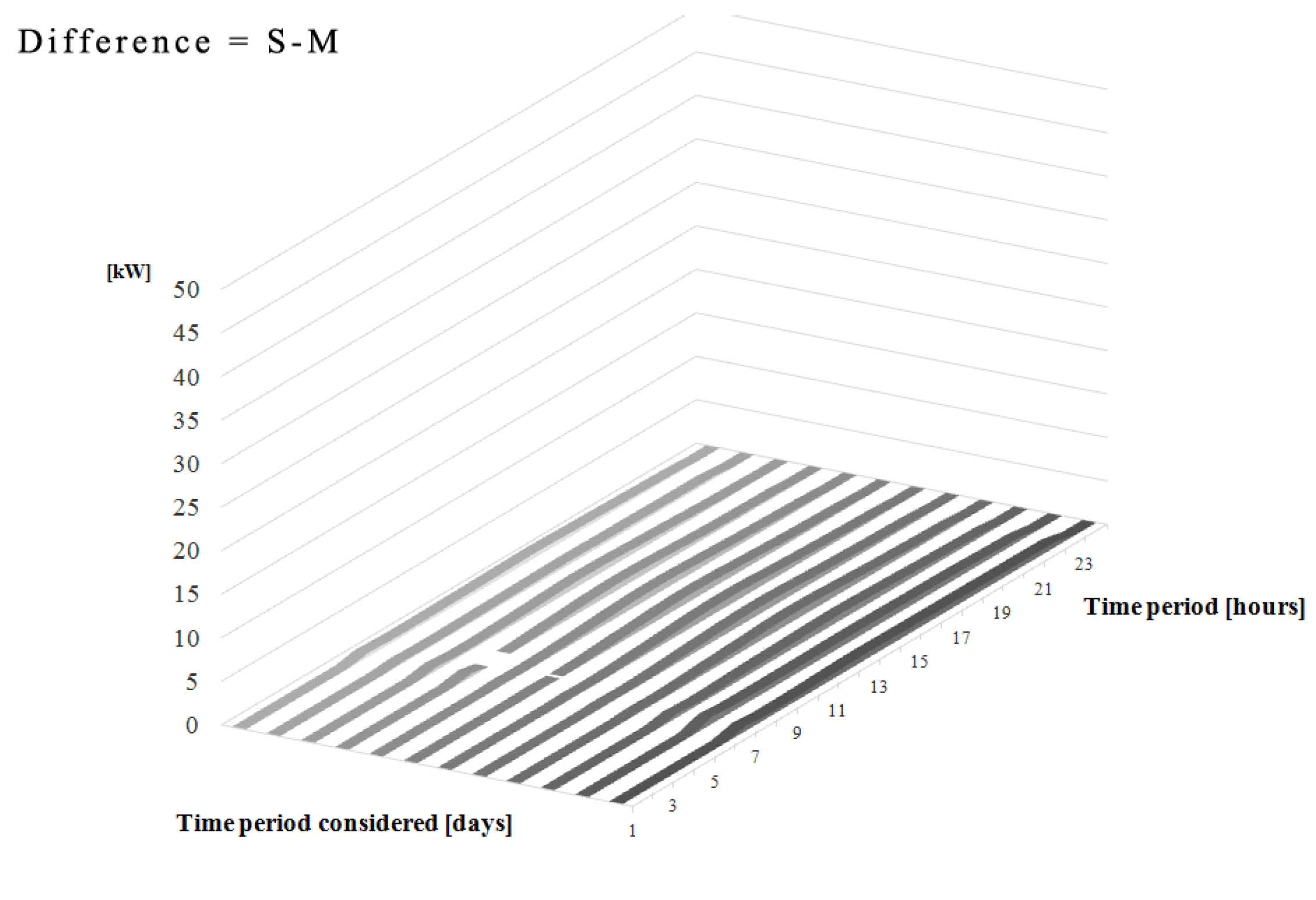
4.2.2. Calibration Signature
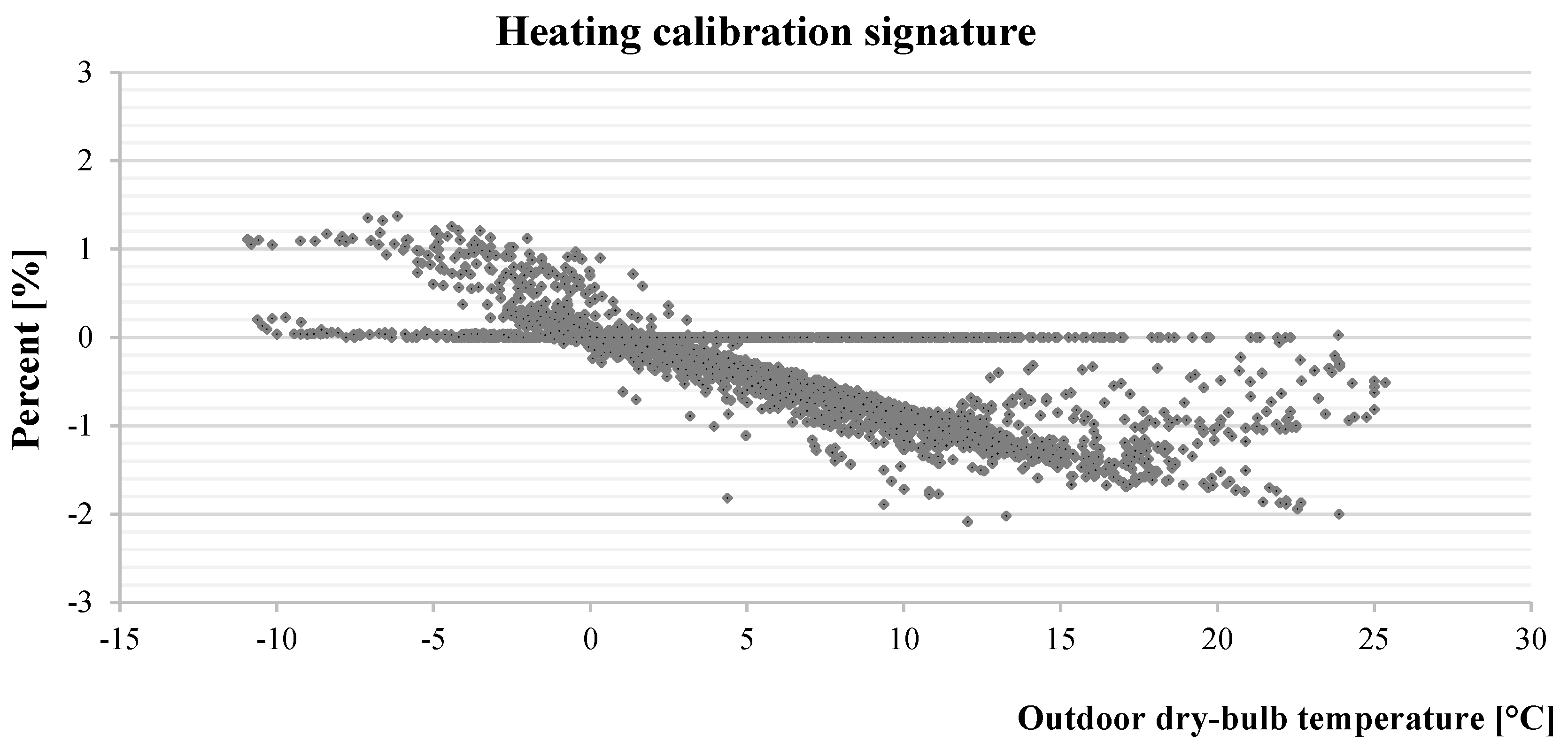
- subscripts HTG and CLG refer, respectively, to the heating and cooling time intervals considered;
- RSME is the Root Mean Squared Error calculated as in Equation (3); and
- MBE is the Mean Bias Error calculated as in compliance with Equation (1).
4.3. Calibration Based on Analytical Procedures
4.4. Automated Techniques for Calibration Based on Analytical and Mathematical Approaches
4.4.1. Bayesian Calibration
4.4.2. Meta-Modeling
4.4.3. Optimization-Based Methods
5. Model Uncertainties
| Category | Factors |
|---|---|
| Scenario uncertainty | Outdoor weather conditions |
| Building usage/occupancy schedule | |
| Building physical/operational uncertainty | Building envelope properties |
| Internal gains | |
| HVAC systems | |
| Operation and control settings | |
| Model inadequacy | Modeling assumptions |
| Simplification in the model algorithm | |
| Ignored phenomena in the algorithm | |
| Observation error | Metered data accuracy |
5.1. Screening-Based Method
5.1.1. Sensitivity Index
5.1.2. Differential Sensitivity Analysis
- OP is the output data value;
- IP is the input data value; and
- the subscript bc indicates the values referring to the baseline model.
5.1.3. Elementary Effects
- Y is the system output evaluated before and after the variation of the ith parameter; and
- Δ is an incremental effect that is a multiple of 1/(p − 1).
5.2. Regression Analysis
5.3. Variance-Based Method
- -
- first-order index, Si, which represents the effect of the input parameter Xi on output variation y;
- -
- total order index, STi, that measures the effect of the parameter alone and the sensitivity of the interaction of the parameter with all other parameters, as described in Equation (16).
5.3.1. ANOVA
5.3.2. FAST
5.4. Monte Carlo Method
6. Calibrated Simulation Applications
- -
- the calibration methodology adopted;
- -
- the calibration level pursued;
- -
- the model complexity;
- -
- the simulation tool used; and
- -
- the integration of SA/UA in the calibration process.
7. Conclusions
| Author | Title | Year | Journal/Conference | Ref. | Calibration Characterization | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model type | Calibration level | Calibration Method | SA/UA | Monitoring period | Simulation tool or Standard | ||||||||
| Palomo del Barrio, E.; Guyon, G. | Application of parameters space analysis tools for empirical model validation | 2004 | Energy and Buildings, 36, 23-33 | [89] | - | whole building model | - | - | Optmi-zation | SA | - | CLIM2000 | |
| Liu, S.; Henze, G.P. | Calibration of building models for supervisory control of commercial building | 2005 | 9th International Building Simulation Association (IBPSA) Conference 2005 | [48] | Detailed | whole building model | - | Automated | Optmi-zation | - | - | EnergyPlus, GenOpt | |
| Pan, Y.; Huang, Z.; Wu, G. | Calibrated building energy simulation and its application in a high-rise commercial building in Shanghai | 2007 | Energy and Buildings, 39, 651-657 | [12] | Detailed | whole building model | Level 3 | Manual | Iterative | - | - | DOE-2 | |
| Reddy, T.A.; Maor, I.; Panjapornpon, C. | Calibrating Detailed Building Energy Simulation Programs with Measured Data–Part II: Application to Three Case Study Office Buildings (RP-1051) | 2007 | HVAC and Research, 13, 221-241 | [16] | Detailed | whole building model | Level 4 | Mathema-tical | - | Montecarlo | N.A. | DOE-2 | |
| Hassan, M.A.; Shebl, S.S.; Ibrahim, E.A.; Aglan, H.A. | Modeling and validation of the thermal performance of an affordable, energy efficient, healthy dwelling unit | 2011 | Journal of Building Simulation 4, 255-262 | [24] | Detailed | whole building model | Level 4-5 | Manual | Iterative | - | Short-term | Visual DOE-4 | |
| Liu, G.; Liu, M. | A rapid calibration procedure and case study for simplified simulation models of commonly used HVAC systems | 2011 | Building and Environment 46, 409-420 | [28] | - | whole building model | Level 4 | Graphical | Calibration Signature | NA | Short-term | - | |
| Raftery, P.; Keane, M.; Costa, A. | Calibrating whole building energy models: Detailed case study using hourly measured data | 2011 | Energy and Buildings 2011, 43, 3666-3679 | [85] | Detailed | whole building model | Level 4 | Manual | Iterative | - | Long-term | EnergyPlus | |
| Bertagnolio, S.; Randaxhe, F.; Lemort, V. | Evidence-based calibration of a building energy simulation model: Application to an office building in Belgium | 2012 | 12th International Conference for Enhanced Building Operations, Manchester, UK | [83] | Normative (quasi-steady) | whole building model | Level 1 to 4 | - | evidence-based | Morris Method | Short-term | ISO 13790 | |
| Heo, Y.; Choudhary, R.; Augenbroe, G.A. | Calibration of building energy models for retrofit analysis under uncertainty | 2012 | Energy and Buildings 47, 550-560 | [38] | Normative (quasi-steady) | whole building model | - | Mathema-tical | Bayesian | Morris Method | - | ISO 13790 | |
| Fontanella,G.; Basciotti, D.; Dubisch, F.; Judex, F.; Preisler, A.; Hettfleisch, C.; Vukovic, V.; Selke, T. | Calibration and validation of a solar thermal system model in Modelica | 2012 | Journal of Building Simulation 5, 293-300 | [25] | Detailed | Solar System | Level 4 | - | Optmiza-tion | - | Short-term | Modelica (Dymola), GenOpt | |
| Maile, T.; Bazjanac, T.; Fischer, M. | A method to compare simulated and measured data to assess building energy performance | 2012 | Building and Environment 56, 241-251 | [90] | Detailed | whole building model | N.A. | Manual | Iterative | - | Long-term | Not specified | |
| Parker, J.; Cropper, P.; Shao, L. | A calibrated whole building simulation approach to assessing retrofit options for Birmingham airport | 2012 | IBPSA-England, 1st Building Simulation and Optimization Conference, Loughborough, UK | [91] | Detailed | whole building model | Level 2 | Manual (Raftery et al.) | Iterative | - | Long-term | IES | |
| Kim, Y.; Yoon, S.; Park, C. | Stochastic comparison between simplified energy calculation and dynamic simulation | 2013 | Energy and Buildings 64, 332-342 | [59] | Simplified (A), detailed (B) | whole building model | - | Matema-tical | Bayesian | SA-Morris Method | - | ISO 13790 (A), EnergyPlus (B) | |
| Manfren, M.; Aste, N.; Moshksar, R. | Calibration and uncertainty analysis for computer models–A meta-model based approach for integrated building energy simulation | 2013 | Applied Energy 103, 627-641 | [39] | Simplified and detailed | whole building model | Level 4 | Mathema-tical | Bayesian, Meta-modelling | with Bayesian calibration | Short-term | - | |
| O’Neill, Z.; Eisenhower, B. | Leveraging the analysis of parametric uncertainty for building energy model calibration | 2013 | Journal of Building Simulation 5, 365-377 | [13] | meta-model | whole building model | Levels 4-5 | Automated | Optmi-zation | quasi-Montecarlo approach | Long-term | EnergyPlus, Design-Builder | |
| Taheri, M.; Tahmasebi, F.; Mahdavi, A. | A case study of optimization-aided thermal building performance simulation calibration | 2013 | 13th Conference of IBPSA Chambéry, France | [51] | Dynamic | whole building model | Level 4 | Automated | Optmi-zation | - | Short-term | EnergyPlus, GenOpt | |
| Mihai, A.; Zmeureanu, R. | Calibration of an energy model of a new research center building | 2014 | 13th Conference of IBPSA Chambéry, France | [92] | Dynamic | whole building model | Level 4 | Manual | evidence-based | - | Short-term | eQuest | |
| Mustafaraj, G.; Marini, D.; Costa, A.; Keane, M. | Model calibration for building energy efficiency simulation | 2014 | Applied Energy 130, 72-85 | [93] | Dynamic | whole building model | Level 3-4 | Manual | Iterative (based on Bertagnolio and Raftery methods) | SA | Short-term | Design-Builder, EnergyPlus | |
| Penna, P.; Gasparella, A.; Cappelletti, F.; Tahmasebi, F.; Mahdavi A. | Optimization-based calibration of a school building based on short-term monitoring data | 2014 | 10th European Conference on Product and Process Modeling | [88] | Detailed | whole building model | Level 3-4 | Automated | Optmiza-tion | - | Short-term | TRNSYS, GenOPt | |
Conflicts of Interest
References
- Clarke, J.A. Energy Simulation in Building Design, 2nd ed.; Butterworth Heinemann: Oxford, UK, 2001. [Google Scholar]
- Hensen, J.L.M.; Lamberts, R. Introduction to building performance simulation. In Building Performance Simulation for Design and Operation, 1st ed.; Hensen, J.L.M., Lamberts, R., Eds.; Spon Press: Oxfordshire, UK, 2011. [Google Scholar]
- Claridge, D.E. Building simulation for practical operational optmization. In Building Performance Simulation for Design and Operation, 1st ed.; Hensen, J.L.M., Lamberts, R., Eds.; Spon Press: Oxfordshire, UK, 2011. [Google Scholar]
- Emily, M.; Ryan, E.M.; Sanquist, T.F. Validation of building energy modeling tools under idealized and realistic conditions. Energy Build. 2012, 47, 375–382. [Google Scholar] [CrossRef]
- Dall’O’, G.; Sarto, L.; Sanna, N.; Martucci, A. Comparison between predicted and actual energy performance for summer cooling in high-performance residential buildings in the Lombardy region (Italy). Energy Build. 2012, 54, 234–242. [Google Scholar] [CrossRef]
- Reddy, T.A.; Maor, I.; Panjapornpon, C. Calibrating detailed building energy simulation programs with measured data—Part I: General methodology (RP-1051). HVAC&R Res. 2007, 13, 221–241. [Google Scholar] [CrossRef]
- Claridge, D.E. Using simulation models for building commissioning. In Proceedings of the Fourth International Conference for Enhanced Building Operations, Paris, France, 18–19 October 2004.
- Tian, Z.; Love, J.A. Energy performance optimization of radiant slab cooling using building simulation and field measurements. Energy Build. 2009, 41, 320–330. [Google Scholar] [CrossRef]
- Morrison, L.; Azebergi, R.; Walker, A. Energy modeling for measurement and verification. In Proceedings of the SimBuild 2008—Third National conference of IBPSA-USA, Berkley, CA, USA, 30 July–1 August 2008.
- IPMVP New Construction Subcommittee. International Performance Measurement & Verification Protocol: Concepts and Option for Determining Energy Savings in New Construction, Volume III; Efficiency Valuation Organization (EVO): Washington, DC, USA, 2003. [Google Scholar]
- FEMP. Federal Energy Management Program, M&V Guidelines: Measurement and Verification for Federal Energy Projects Version 3.0; U.S. Department of Energy Federal Energy Management Program: Washington, DC, USA, 2008. [Google Scholar]
- Pan, Y.; Huang, Z.; Wu, G. Calibrated building energy simulation and its application in a high-rise commercial building in Shanghai. Energy Build. 2007, 39, 651–657. [Google Scholar] [CrossRef]
- O’Neill, Z.; Eisenhower, B. Leveraging the analysis of parametric uncertainty for building energy model calibration. Build. Simul. 2013, 6, 365–377. [Google Scholar] [CrossRef]
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Carroll, W.L.; Hitchcock, R.J. Tuning simulate building description to match actual utility data: Methods and implementation. ASHRAE Trans. 1993, 99, 982–993. [Google Scholar]
- Reddy, T.A.; Maor, I.; Panjapornpon, C. Calibrating detailed building energy simulation programs with measured data—Part II: Application to three case study office buildings (RP-1051). HVAC&R Res. 2007, 13, 221–241. [Google Scholar] [CrossRef]
- Reddy, T.A. Literature review on calibration of building energy simulation programs: Uses, problems, procedures, uncertainty and tools. ASHRAE Trans. 2006, 112, 226–240. [Google Scholar]
- Bertagnolio, S. Evidence-based model calibration for efficient building energy services. Ph.D. Thesis, University of Liège, Liège, Belgium, June 2012. [Google Scholar]
- Coakley, D.; Raftery, P.; Keane, M. A review of methods to match building energy simulation models to measured data. Renew. Sustain. Energy Rev. 2014, 37, 123–141. [Google Scholar] [CrossRef]
- Maile, T. Comparing measured and simulated building energy performance data. Ph.D. Thesis, Stanford University, Stanford, CA, USA, August 2010. [Google Scholar]
- ASHRAE. ASHRAE Guideline 14-2002: Measurement of Energy Demand and Savings; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2002. [Google Scholar]
- Clarke, J.A.; Strachan, P.; Pernot, C. An approach to the calibration of building energy simulation models. ASHRAE Trans. 1993, 99, 917–927. [Google Scholar]
- Pedrini, A.; Westphal, F.S.; Lamberts, R. A methodology for building energy modelling and calibration. Build. Environ. 2002, 37, 903–912. [Google Scholar] [CrossRef]
- Hassan, M.A.; Shebl, S.S.; Ibrahim, E.A.; Aglan, H.A. Modeling and validation of the thermal performance of an affordable, energy efficient, healthy dwelling unit. J. Build. Simul. 2011, 4, 255–262. [Google Scholar] [CrossRef]
- Fontanella, G.; Basciotti, D.; Dubisch, F.; Judex, F.; Preisler, A.; Hettfleisch, C.; Vukovic, V.; Selke, T. Calibration and validation of a solar thermal system model in Modelica. J. Build. Simul. 2012, 5, 293–300. [Google Scholar] [CrossRef]
- Haberl, J.S.J.; Bou-Saada, T.E. Procedures for calibrating hourly simulation models to measured building energy and environmental data. J. Sol. Energy Eng. 1998, 120, 193–204. [Google Scholar] [CrossRef]
- Liu, M.; Claridge, D.E.; Bensouda, N.; Heinemeier, K.; Uk Lee, S.; Wei, G. High Performance Commercial Building Systems: Manual of Procedures for Calibrating Simulations of Building Systems; Lawrence Berkeley National Laboratory, 2003. Available online: http://buildings.lbl.gov/cec/pubs/E5P23T2b.pdf (accessed on 23 March 2015).
- Liu, G.; Liu, M. A rapid calibration procedure and case study for simplified simulation models of commonly used HVAC systems. Build. Environ. 2011, 46, 409–420. [Google Scholar] [CrossRef]
- Bensouda, N. Extending and formalizing the energy signature method for calibrating simulation and illustrating with application for three California climates. Master’s Thesis, Texas A&M University, College Station, TX, USA, August 2004. [Google Scholar]
- Kandil, A.; Love, J.A. Signature analysis calibration of a school energy model using hourly data. J. Build. Perform. Simul. 2014, 7, 326–345. [Google Scholar] [CrossRef]
- Claridge, D.E. Using Whole Building Simulation Models in Commissioning. IEA Annex 40 Working Paper. Available online: http://www.commissioning-hvac.org/files/doc/A40-D2-M4-US-TAMU-02.pdf (accessed on 23 March 2015).
- Subbarao, K. PSTAR—Primary and Secondary Terms Analysis and Renormalization. A Unified Approach to Building Energy Simulations and Short-Term Monitoring; SERI/TR-254-3175; Solar Energy Research Institute: Golden, CO, USA, 1988. [Google Scholar]
- Booth, A.T.; Choudhary, R.; Spiegelhalter, D.J. Handling uncertainty in housing stock models. Build. Environ. 2012, 48, 35–47. [Google Scholar] [CrossRef]
- Heo, Y. Bayesian calibration of building energy models for energy retrofit decision-making under uncertainty. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, December 2011. [Google Scholar]
- Tierney, J.E.; Tingley, M.P. A Bayesian, spatially-varying calibration model for the TEX86 proxy. Geochim. Cosmochim. Acta 2014, 127, 83–106. [Google Scholar] [CrossRef]
- Zhang, W.; Arhonditsis, G.B. Predicting the Frequency of Water Quality Standard Violations Using Bayesian Calibration of Eutrophication Models. J. Gt. Lakes Res. 2008, 34, 698–720. [Google Scholar] [CrossRef]
- Rahn, K.; Butterbach-Bahl, K.; Werner, C. Selection of likelihood parameters for complex models determines the effectiveness of Bayesian calibration. Ecol. Inform. 2011, 6, 333–340. [Google Scholar] [CrossRef]
- Heo, Y.; Choudhary, R.; Augenbroe, G.A. Calibration of building energy models for retrofit analysis under uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Manfren, M.; Aste, N.; Moshksar, R. Calibration and uncertainty analysis for computer models—A meta-model based approach for integrated building energy simulation. Appl. Energy 2013, 103, 627–641. [Google Scholar] [CrossRef]
- Pavlak, G.S.; Florita, A.R.; Henze, G.P.; Rajagopalan, B. Comparison of Traditional and Bayesian Calibration Techniques for Gray-Box Modeling. J. Arch. Eng. 2014, 20. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models, 1st ed.; John Wiley & Sons Ltd.: Chichester, UK, 2004. [Google Scholar]
- Van Gelder, L.; Das, P.; Janssen, H.; Roels, S. Comparative study of metamodelling techniques in building energy simulation: Guidelines for practitioners. Simul. Model. Pract. Theory 2014, 49, 245–257. [Google Scholar] [CrossRef]
- Eisenhower, B.; O’Neill, Z.; Narayanan, S.; Fonoberov, V.A.; Mezic, I. A methodology for meta-model based optimization in building energy models. Energy Build. 2012, 47, 292–301. [Google Scholar] [CrossRef]
- Nguyen, A.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimization methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Attia, S. Computational optimization zero energy building design: Interviews with 28 international experts. In International Energy Agency (IEA) Task 40: Towards Net Zero Energy Buildings Subtask, B; Université Catholique de Louvain: Louvain la Neuve, Belgium, 2012. [Google Scholar]
- Machairasetal, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Liu, S.; Henze, G.P. Calibration of building models for supervisory control of commercial building. In Proceedings of the Ninth International IBPSA Conference 2005, Montréal, QC, Canada, 15–18 August 2005.
- Hani, A.; Koiv, T. Optimization of office building façades in a warm summer continental climate. Smart Grid Renew. Energy 2012, 3, 222–230. [Google Scholar] [CrossRef]
- Ferrara, M.; Fabrizio, E.; Virgone, J.; Filippi, M. A simulation-based optimization method for cost-optimal analysis of nearly Zero Energy Buildings. Energy Build. 2014, 84, 442–457. [Google Scholar] [CrossRef]
- Taheri, M.; Tahmasebi, F.; Mahdavi, A. A case study of optimization-aided thermal building performance simulation calibration. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambéry, France, 25–28 August 2013.
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity analysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar] [CrossRef]
- Spitz, C. Analyse de la Fiabilité des Outils de Simulation et des Incertitudes de Métrologue Appliquée à L’efficacité Energétique des Bâtiments. Master’s Thesis, Universitè de Grenoble, Grenoble, France, March 2012. [Google Scholar]
- Campolongo, F.; Saltelli, A.; Cariboni, J. From screening to quantitative analysis. A unified approach. Comput. Phys. Commun. 2011, 182, 978–988. [Google Scholar] [CrossRef]
- Macdonald, I.A. Quantifying the Effects of Uncertainty in Building Simulation. Ph.D. Thesis, Department of Mechanical Engineering, University of Strathclyde, Glasgow, UK, 2002. [Google Scholar]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.F.; Campolongo, J.; Cariboni, D.; Gatelli, M.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Hopfe, C.J. Uncertainty and sensitivity analysis in building performance simulation for decision support and design optimization. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2009. [Google Scholar]
- Kim, Y.-J.; Yoon, S.-H.; Park, C.-S. Stochastic comparison between simplified energy calculation and dynamic simulation. Energy Build. 2013, 64, 332–342. [Google Scholar] [CrossRef]
- De Wit, S.; Augenbroe, G. Analysis of uncertainty in building design evaluations and its implications. Energy Build. 2002, 34, 951–958. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K. A quantitative, model independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Wang, M.; Wright, J.; Buswell, R.; Brownlee, A. A comparison of approaches to stepwise regression for global sensitivity analysis used with evolutionary optimization. In Proceedings of the BS2013,13th Conference of International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013.
- Dedovic, N.; Igic, S.; Janic, T.; Matic-Kekic, S.; Ponjican, O.; Tomic, M.; Savin, L. Efficiency of small scale manually fed boilers—mathematical models. Energies 2012, 5, 1470–1489. [Google Scholar] [CrossRef]
- Heiselberg, P.; Brohus, H.; Hesselholt, A.; Rasmussen, H.; Seinre, E.; Thomas, S. Application of sensitivity analysis in design of sustainable buildings. Renew. Energy 2009, 34, 2030–2036. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Corrado, V.; Mechri, H.E. Uncertainty and sensitivity analysis for building energy rating. J. Build. Phys. 2009, 33, 125–156. [Google Scholar] [CrossRef]
- Sanchez, D.G.; Lacarrièrea, B.; Musy, M.; Bourgesa, B. Application of sensitivity analysis in building energy simulations: Combining first- and second-order elementary effects methods. Energy Build. 2014, 68, 741–750. [Google Scholar] [CrossRef]
- Calleja Rodríguez, G.; Carrillo Andrés, A.; Domínguez Muñoz, F.; Cejudo López, J.M.; Zhang, Y. Uncertainties and sensitivity analysis in building energy simulation using macroparameters. Energy Build. 2013, 67, 79–87. [Google Scholar] [CrossRef]
- Domínguez-Muñoz, F.; Cejudo-López, J.M.; Carrillo-Andrés, A. Uncertainty in peak cooling load calculations. Energy Build. 2010, 42, 1010–1018. [Google Scholar] [CrossRef]
- Encinas, F.; de Herde, A. Sensitivity analysis in building performance simulation for summer comfort assessment of apartments from the real estate market. Energy Build. 2013, 65, 55–65. [Google Scholar] [CrossRef]
- Archer, G.; Saltelli, A.; Sobol, I. Sensitivity measures, ANOVA-like techniques and the use of bootstrap. J. Stat. Comput. Simul. 1997, 58, 99–120. [Google Scholar] [CrossRef]
- Cukier, R.I.; Levine, H.B.; Schuler, K.E. Nonlinear sensitivity analysis of multiparameter model systems. J. Comput. Phys. 1978, 26, 1–42. [Google Scholar] [CrossRef]
- Saltelli, A.; Bolado, R. An alternative way to compute Fourier amplitude sensitivity test (FAST). Comput. Stat. Data Anal. 1998, 26, 445–460. [Google Scholar] [CrossRef]
- Janssen, H. Monte-Carlo based uncertainty analysis: Sampling efficiency and sampling convergence. Reliab. Eng. Syst. Saf. 2013, 109, 123–132. [Google Scholar] [CrossRef]
- Sun, Y.; Gu, L.; Wu, C.F.W.; Augenbroe, G. Exploring HVAC system sizing under uncertainty. Energy Build. 2014, 81, 243–252. [Google Scholar] [CrossRef]
- Spitz, C.; Mora, L.; Wurtz, E.; Jay, A. Practical application of uncertainty analysis and sensitivity analysis on an experimental house. Energy Build. 2014, 55, 459–470. [Google Scholar] [CrossRef]
- Lomas, K.J.; Eppel, H. Sensitivity analysis techniques for building thermal simulation programs. Energy Build. 1992, 19, 21–44. [Google Scholar] [CrossRef]
- Macdonald, I.A. Comparison of sampling techniques on the performance of Monte-Carlo based sensitivity analysis. In Proceedings of the 9th Conference of International Building Performance Simulation Association, Glasgow, UK, 27–30 July 2009.
- Sun, J.; Reddy, T.A. Calibration of building energy simulation programs using the analytic optimization approach (RP-1051). HVAC&R Res. 2006, 12. [Google Scholar] [CrossRef]
- McKay, M.D.; BeckMan, R.L.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Gestwick, M.J.; Love, J.A. Trial application of ASHRAE 1051-RP: Calibration method for building energy simulation. J. Build. Perform. Simul. 2014, 7, 346–359. [Google Scholar] [CrossRef]
- Collis, J.; Robertson, J.; Polly, B. Evaluation of Automated Model Calibration Techniques for Residential Building Energy Simulation; Technical Report NREL/TP-5500-60127; National Renewable Energy Laboratory: Golden, CO, USA, 2013. [Google Scholar]
- Bertagnolio, S.; Randaxhe, F.; Lemort, V. Evidence-based calibration of a building energy simulation model: Application to an office building in Belgium. In Proceedings of the Twelfth International Conference for Enhanced Building Operations, Manchester, UK, 23–26 October 2012.
- Raftery, P.; Keane, M.; O’Donnell, J. Calibrating whole building energy models: An evidence-based methodology. Energy Build. 2011, 43, 2356–2364. [Google Scholar] [CrossRef]
- Raftery, P.; Keane, M.; Costa, A. Calibrating whole building energy models: Detailed case study using hourly measured data. Energy Build. 2011, 43, 3666–3679. [Google Scholar] [CrossRef]
- Tahmasebi, F.; Mahdavi, A. A two-staged simulation model calibration approach to virtual sensors for building performance data. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambéry, France, 25–28 August 2013.
- Tahmasebi, F.; Mahdavi, A. An optimization-based approach to recurrent calibration of building performance simulation models. In Proceedings of the ECPPM2012 eWork and eBusiness in Architecture, Engineering and Construction, Vienna, Austria, 17–19 September 2014.
- Penna, P.; Gasparella, A.; Cappelletti, F.; Tahmasebi, F.; Mahdavi, A. Optimization-based calibration of a school building based on short-term monitoring data. In Proceedings of the eWork and eBusiness in Architecture, Engineering and Construction: ECPPM 2014, Vienna, Austria, 17–19 September 2014.
- Palomo del Barrio, E.; Guyon, G. Application of parameters space analysis tools for empirical model validation. Energy Build. 2004, 36, 23–33. [Google Scholar] [CrossRef]
- Maile, T.; Bazjanac, T.; Fischer, M. A method to compare simulated and measured data to assess building energy performance. Build. Environ. 2012, 56, 241–251. [Google Scholar] [CrossRef]
- Parker, J.; Cropper, P.; Shao, L. A calibrated whole building simulation approach to assessing retrofit options for Birmingham airport. In Proceedings of the IBPSA—England 2012,First Building Simulation and Optimization Conference, Loughborough, UK, 10–11 September 2012.
- Mihai, A.; Zmeureanu, R. Calibration of an energy model of a new research center building. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambéry, France, 25–28 August 2013.
- Mustafaraj, G.; Marini, D.; Costa, A.; Keane, M. Model calibration for building energy efficiency simulation. Appl. Energy 2014, 130, 72–85. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabrizio, E.; Monetti, V. Methodologies and Advancements in the Calibration of Building Energy Models. Energies 2015, 8, 2548-2574. https://doi.org/10.3390/en8042548
Fabrizio E, Monetti V. Methodologies and Advancements in the Calibration of Building Energy Models. Energies. 2015; 8(4):2548-2574. https://doi.org/10.3390/en8042548
Chicago/Turabian StyleFabrizio, Enrico, and Valentina Monetti. 2015. "Methodologies and Advancements in the Calibration of Building Energy Models" Energies 8, no. 4: 2548-2574. https://doi.org/10.3390/en8042548
APA StyleFabrizio, E., & Monetti, V. (2015). Methodologies and Advancements in the Calibration of Building Energy Models. Energies, 8(4), 2548-2574. https://doi.org/10.3390/en8042548






