1. Introduction
Due to technological and regulatory innovations, the micro-grid has become an alternate choice to compete with traditional centralized electricity plants for its small-scale and on-site distributed energy providing capability. A typical micro-grid consists of distributed generation sources, e.g., diesel generators or micro-turbines, loads, and renewable sources [
1,
2]. A micro-grid can be operated in two modes,
i.e., isolated mode or grid-connected mode [
3]. If a micro-grid is grid-connected, the loads can be supplied by the connected electrical power system. Otherwise, the distributed generation has to cope with varying load and fluctuating renewable energy sources in the isolated mode, which requires proper control of micro-grid to ensure frequency and voltage stability in order to supply high-quality power to customers. However, because of fluctuations of renewable sources and limited capacity of distributed generation sources, it is difficult to achieve active power balance between generations and loads that is important for critical installations.
Electric vehicles (EV) are an inevitable trend in the automotive industry’s development of energy-saving and environmentally friendly cars [
4,
5]. EV technology represents a good option for significant reductions in gasoline consumption, smog precursors and emission of greenhouse gases. When EVs are connected to an electric distribution grid, the power flow between EVs and the power grid can be bidirectional: a charging EV is a load for the grid [
6], whereas a discharging EV is a power source for the grid [
7]. Statistical data of car usage show that private cars are sitting idle 95% of the day, which mean most electric vehicles remain connected to the grid in charging or idle mode. With the rapid development of EVs, the controllable energy stored in on-board batteries could be enormous. By utilizing vehicle to grid (V2G) technique, EVs can act as distributed energy storage units. Thus, in order to improve the support ability of load balance and the operation flexibility, EV can be a good solution to stable operation of isolated micro-grids. As mentioned before, the critical issue in such isolated micro-grids is large frequency fluctuation caused by intermittent renewable energy in an isolate operating micro-gird, where the load-frequency control (LFC) capacity is not enough to compensate the unbalance of generation and load demand. In this paper, we focus on the design of a power system frequency oscillation damping controller using EVs. By providing active power to load or absorbing extra active power from generations, EVs could quickly compensate the active power gap between generation and load, thus improving the power grid frequency stability [
8].
Load frequency control methods have been applied in traditional thermal power generation systems and hydro power generation systems. Optimal control [
9], fuzzy control, adaptive control [
10] and robust control have improved the load frequency control performance greatly. In [
11], an optimal output feedback method was proposed for the load frequency control in the deregulated environment. In [
12] a combined
H ∞/
μ approach to design a robust feedback load frequency controller for multi-area power system was proposed. The authors of [
13] proposed a coordinated control of blade pitch angle of wind turbine generators and plug-in hybrid electric vehicles (PHEVs) for load frequency control of micro-grid using model predictive controls (MPCs). In order to reduce the number of PHEVs, a smoothing technique of wind power production by pitch angle control using MPC method is proposed and is coordinated with PHEVs control in this literature. In [
14], a proportional integral (PI) controller was applied in wind diesel hybrid power systems, and its parameters were optimized by integral square error (ISE). In [
15], an aggregated EV-based battery storage representing a V2G system was modeled for long-term dynamic power system simulations, and the performance of a PI controller for LFC was evaluated. However, since the PI controller with fixed gains has been designed at nominal operating conditions, it could not provide good control performance over a wide range of operating conditions. In [
16], a typical city distribution system was modeled to demonstrate V2G capabilities for frequency regulation and voltage sag reduction using a FUZZY logic controller. However, it can only demonstrated good dynamics when some specific membership functions were selected, whose application can be limited in reality.
In an isolated micro-grid with fluctuating renewable sources and EVs, the system state parameters and operating conditions are changing rapidly. Traditional controllers are not optimized for the whole set of possible operating conditions and configurations, so they cannot guarantee the control of system frequency through coordinating V2G and other units for all operating conditions. Also, there are some constraints in the LFC units including capacity constraints and generation rate constraints, which are difficult to be considered in the controller design. So, a controller with robust performance over a wide range of system operating conditions is greatly expected for LFC in isolated micro-grids.
To overcome the aforementioned problems, this paper proposes a new coordinated LFC controller based on multivariable generalized predictive control (MGPC). With the control procedure of multi-step prediction, rolling optimization and feedback correction [
17], MGPC can effectively solve multivariable optimal control problem with constraints even without an accurate system model, so that the rapid change of system operation status can be tracked quickly. In this controller design, the LFC signal is dispatched to diesel generator (DG) and EVs according to the response speed and the controllable capacity; moreover, the wind turbine generator is modeled as a random fluctuating resource in this paper.
The rest of this paper is organized as follows:
Section 2 provides the description and analysis of the models in an isolated grid, including EVs, DG and wind power. In
Section 3, the coordinated LFC controller based on MGPC is proposed. In
Section 4, effectiveness and robustness of the proposed coordinated controller is demonstrated by numerical simulations on a benchmark power system with EVs. Conclusions are drawn in
Section 5.
2. Model of an Isolated Micro-Grid
2.1. Model of the Benchmark Micro-Grid
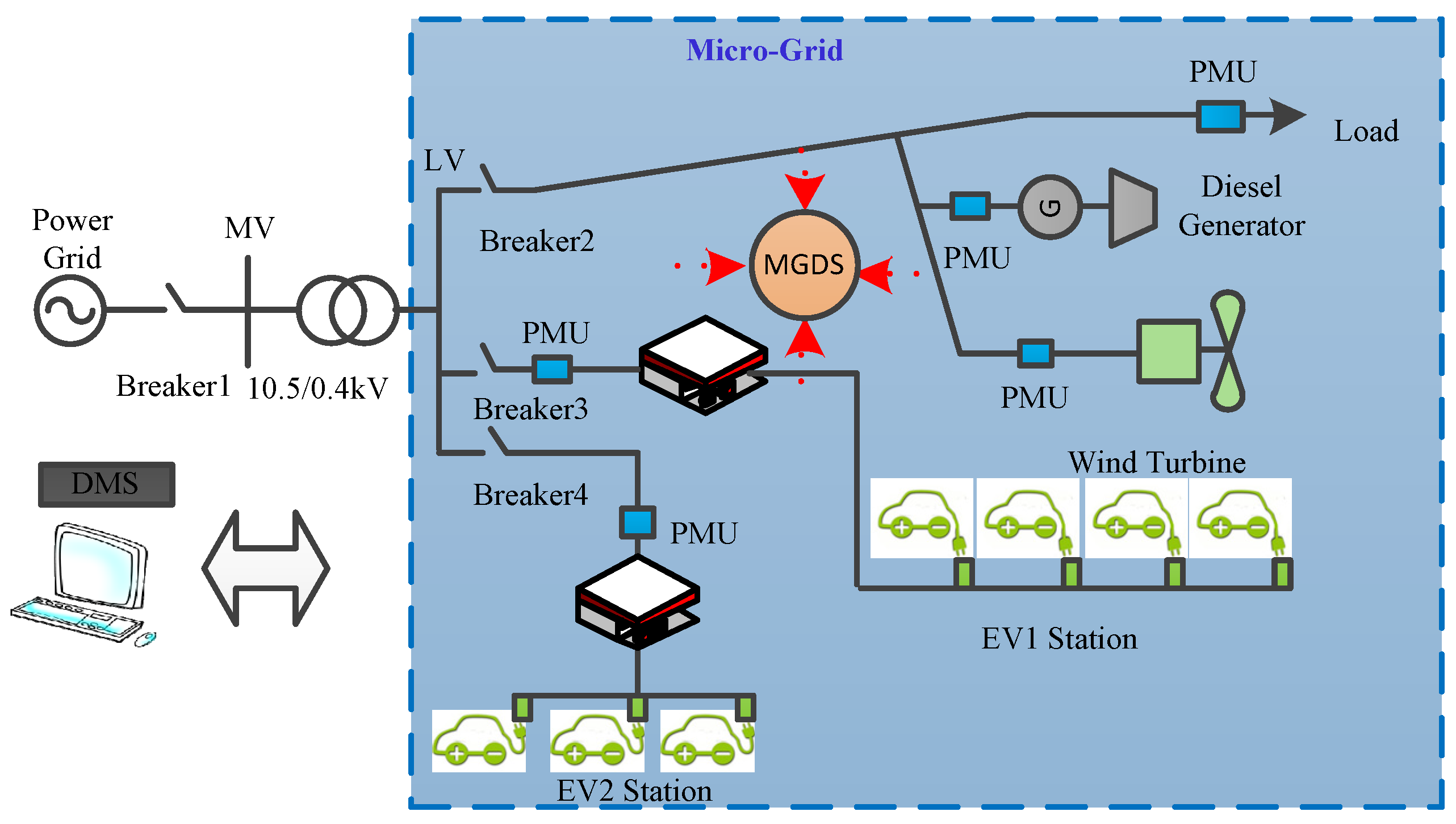
As shown in
Figure 1, a micro-grid is composed of a single bus-bar, a wind turbine, a diesel generator, EVs and loads. The power grid is managed by a distribution management system (DMS), and the micro-grid operation is controlled by a micro-grid dispatch system (MGDS). Phasor measurement units (PMUs) are installed in this micro-grid to measure the real-time information of circuit breakers, distributed generation sources, EVs, and loads. With the same model, the micro-grid can be operated in two alternative modes,
i.e., the isolated mode and the grid-connected mode. By controlling the circuit breaker “Breaker1” in
Figure 1, the micro-grid can switch from one mode to the other mode. If the micro-grid is grid-connected, the majority of loads can be supplied by the connected electrical power system. Otherwise, in the isolated mode, the loads will be supplied by coordinated control of EVs and the diesel generator.
Figure 1.
The model of the benchmark micro-grid.
Figure 1.
The model of the benchmark micro-grid.
2.2. Benchmark Micro-Grid with LFC Controller
Figure 2 shows the framework of the proposed LFC controller in an isolated micro-gird, which consists of a DG, two equivalent EVs (
i.e., EV1 and EV2), and power disturbance
. In this paper,
consists of load disturbance
and the fluctuation of wind power generation
. Also, in the figure,
represents the equivalent inertia constant of the isolated micro-grid, which consists of inertias for all the directly connected generators and motor loads [
18].
Figure 2.
The control model of the micro-grid including LFC controller.
Figure 2.
The control model of the micro-grid including LFC controller.
Based on this model, the state space can be denoted as follows:
where:
The matrixes A, B, D, C are the system state matrix, the input matrix, the disturbance matrix and the output matrix, respectively. x, u, w are the state variables, the controlled input and the uncontrolled input (power disturbance), respectively.
2.3. The Electric Vehicle Model
Since there are different numbers of EVs in each EV station, we can consider an equivalent EV model that parameterizes each EV with different inverter capacities. Details of the equivalent EV model including battery and charger based on the charging and discharging characteristics can be found in literature [
19].
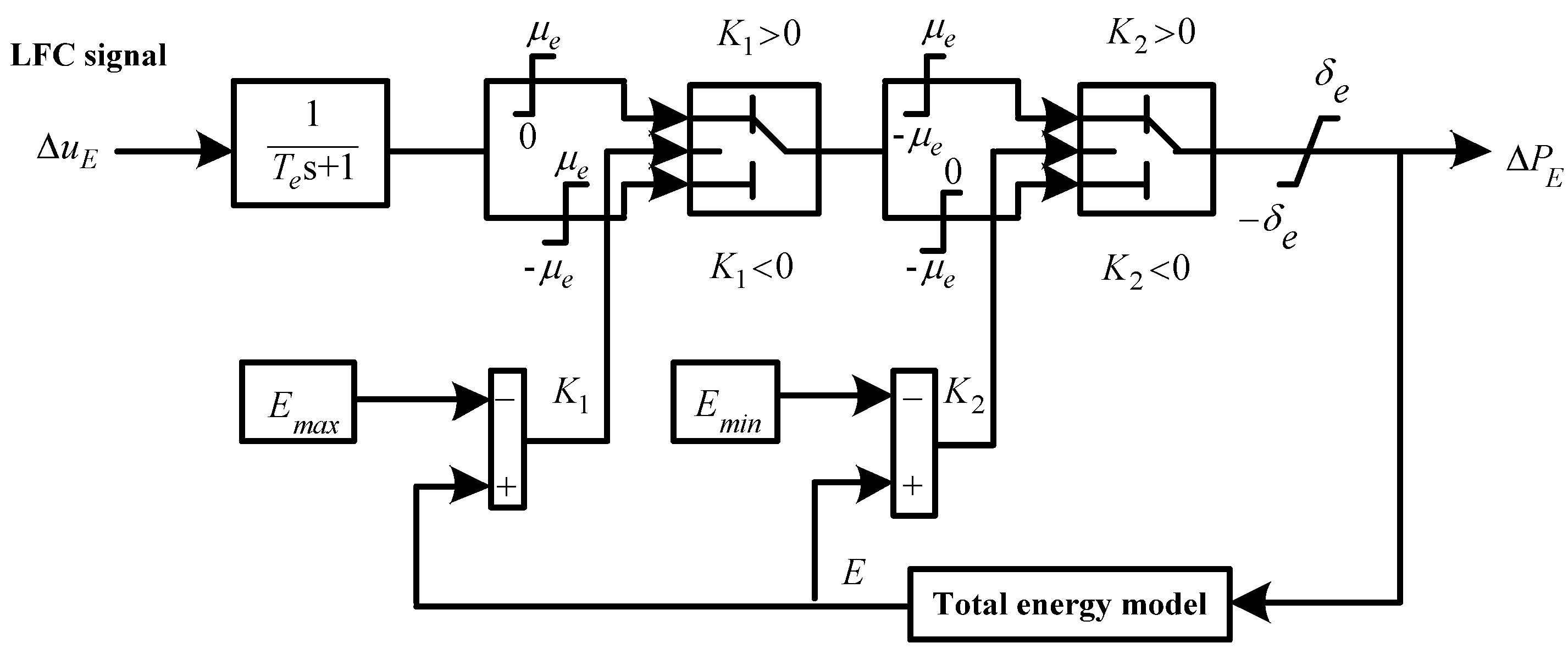
Figure 3 from [
16] shows the model and how it can be used for load frequency control. It represents the behavior of the battery characteristic of one EV, where the total charging or discharging power in controllable state can be calculated accordingly.
Figure 3.
The equivalent EV model for LFC [
16].
Figure 3.
The equivalent EV model for LFC [
16].
In this figure, is the time constant of EV, is the LFC signal dispatched to EV, are the inverter capacity limits, and are the power ramp rate limits. s is the complex frequency and . is the current energy of the EV battery. and are the maximum and minimum controllable energy of the EV battery, respectively. and are the difference between limited energy and current energy of the EV battery, respectively. They can be calculated as and . Finally, is the charging/discharging power. means EV is in the idle state, means EV is in the discharging state and means EV is in the charging state.
The EV can be charged and discharged only within the range of . However, if the energy of the EV exceeds the upper limit (i.e., Emax), the EV can only be discharged within the range of (0~). Also, if the energy of the EV is under the lower limit (i.e., Emin), the EV can only be charged within the range of (~0).
2.4. Diesel Generator Model
A diesel generator (DG) is a small-scale power generation equipment with the characteristics of fast starting speed, durability and high efficiency. DG can follow load demand variations by power control mechanisms within short intervals of time [
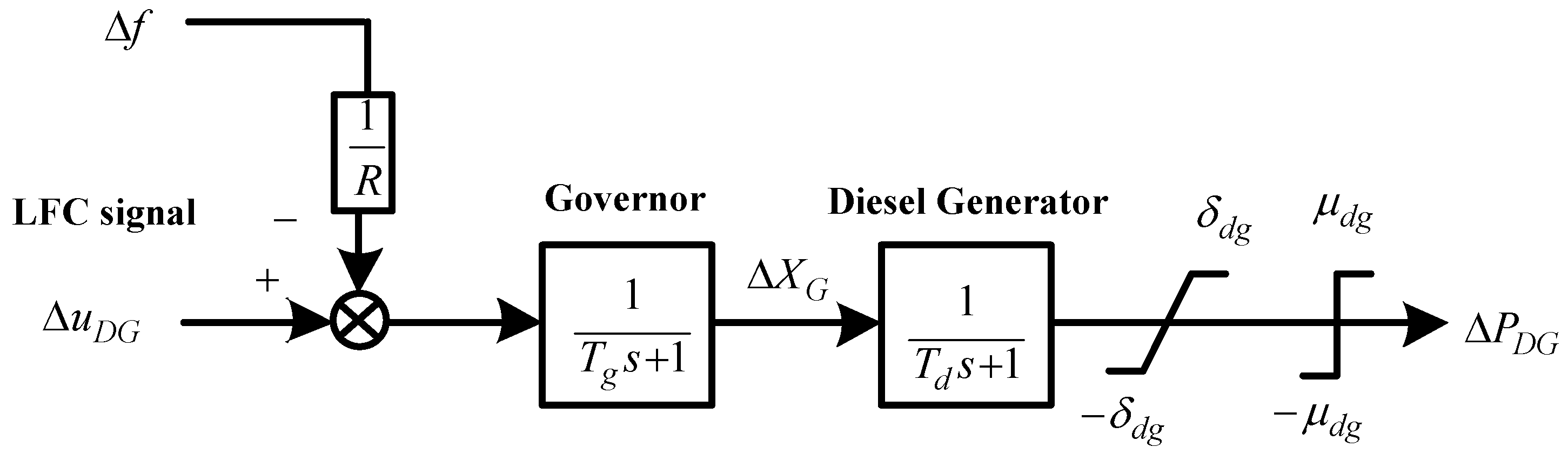
20]. When power demand fluctuates, the DG varies its output via the fuel regulation. The continuous time transfer function model of the DG for LFC is shown in
Figure 4. The relationship between LFC signal and the output power of DG is represented in this figure. It consists of a governor and a generator, which are denoted by first-order inertia plants respectively.
Figure 4.
The transfer function model of DG for LFC [
20].
Figure 4.
The transfer function model of DG for LFC [
20].
In this figure, is the frequency deviation, is the LFC signal dispatched to DG, is the valve position increment of the governor, is the time constant of the governor, is the time constant of the DG, is the speed regulation coefficient of the DG, are the power ramp rate limits and are the power increment limits. In this paper, DG is a generator and the output of the DG is always positive. If there is a very small load with a high wind power, EVs can absorb active power and DG still works as the generator. In the practical system, the DG output is limited to prevent overload status; if there is a very large load, EVs and DG can provide active power together. is the output power increment. If , the output power of DG is a threshold value that balances the load without grid disturbance, indicated as . In general, the threshold value is determined by the power balance of the grid. means that the output power of DG is larger than the threshold value, where means that the output power of DG is smaller than the threshold value.
2.5. Wind Turbine Model
As a natural source, the output power of a wind turbine is fluctuating due to the time-variant wind direction and the wind speed [
21]. When the performance of controllers for EV and DG is considered, the inner characteristics of wind turbine have little effect on LFC of the micro-grid, so the wind power can be simplified as a power fluctuation source of the isolated gird in this paper [
22].
3. The Coordinated LFC Controller Based on Multivariable Generalized Predictive Control
When the isolated grid suffers from a power disturbance, the goal of LFC is to regulate the frequency deviation to zero as soon as possible by controlling the input signal of DG and EVs. According to system state and disturbance characteristic, an online closed-loop control system can be established considering the constraints of DG and EVs. Therefore, we propose a coordinated LFC controller based on multivariable generalized predictive control (MGPC). As shown in
Figure 5, this controller is composed of two layers: a coordinated control layer and a local frequency control layer. Based on frequency deviation and active power deviation, the coordinated control layer first provides the real time LFC signal to the local frequency control layer; then the local frequency control layer controls the DG and the EVs to quickly damp the system frequency oscillation.
Figure 5.
The structure of the proposed coordinated LFC controller based on MGPC.
Figure 5.
The structure of the proposed coordinated LFC controller based on MGPC.
The operation flow of the proposed controller can be divided into following three steps:
- Step 1
State monitoring. The real-time state information measured by PMUs, including , , , and , is collected by MGDS, and then sent to the proposed coordinated controller.
- Step 2
Future prediction. Based on the real time state information from MGDS, the coordinated controller will predict the dynamic trajectory of
using the controlled auto-regressive and integrated moving average (CARIMA) model [
23]. Then the relationship between control variables
,
,
and the predicted variable
is established.
- Step 3
Optimal control. Based on the result from step 2, the coordinated controller will calculate , and according to the objective function considering the constraints of EVs and DG.
Based on these general steps for the proposed LFC controllers, the detailed control theory and implementation are presented in the following sections.
3.1. CARIMA Model for Isolated Micro-Grid
In the MGPC algorithm, the process to be controlled is described by the CARIMA model. This model is suitable for unstable system and is easier to be recognized online. In addition to stable process and integration process, the unstable process can also be described by CARIMA. Moreover, the measurable disturbance, immeasurable disturbance, and measurable noise can be taken into account by the introduction of disturbance and noise models. Integral action in CARIMA is adopted to eliminate the steady-state error.
In order to obtain the LFC CARIMA model of the micro-grid, the LFC state space model in Equation (1) can be transformed into a transfer function model as follows:
where
,
,
,
,
.
and
represent the transfer function matrix from input variables to output variables,
i.e., from load disturbance variables to output variables.
By using a zero-order hold (ZOH), the CARIMA model can be obtained from Equation (2) as follows:
where
is defined as
,
and
are the output sequence and the control sequence, respectively.
is the measurable disturbances sequence that includes load disturbance and wind power disturbance.
is a n-dimensional zero mean white noise sequence.
,
and
are the polynomial matrixes of the backward shift operator
as follows:
where
,
, and
are the coefficients.
are the orders of the polynomial, respectively.
3.2. State Monitoring and Output Prediction
Based on CARIMA model for the isolated grid, the coordinated controller can predict the dynamic trajectory of output variable at time
using real time information measured by PMUs. In order to export the output of
-step prediction, a Diophantine equation is used.
where
,
and
are denoted as follows:
Multiplying Equation (3) by
leads to:
Considering Equation (5) and Equation (7), then:
The
-step output prediction of the process is described below:
and
are considered as:
Then we can denote Equation (9) as:
where
is the free response which can be calculated as follows:
As a result, Equation (11) can be represented as follows:
where
,
,
,
is the prediction horizon, and
is the control horizon.
3.3. Optimal Control
In order to track the set reference value
in the predicted output, we can calculate the control vectors using optimization techniques based on the following objective function.
where
and
are the positive definite weighting matrixes,
is the future reference trajectory for the output signal.
is an optimal
-step prediction of the system output based on data up to time
.
According to Equation (13), Equation (14) can be written as follows:
Assuming there is no constraint on the control signals, the minimum of
can be obtained from
, so:
The control signal in this process is the first element of vector
, which is presented as:
where
is the first row of matrix
.
As mentioned previously, the constraints of inverter capacity limit of equivalent EVs, ramp rate and power increment limit of DG, can be formulated as follows:
where
is the sampling interval.
These constraints can be expressed by a compact form as:
To get the optimal control signals, we need to solve a standard quadratic programming problem with constraints as follows:
There are many algorithms to solve this quadratic programming problem, such as the interior-point method, the active-set method, the ellipsoid method, etc. In this paper, we use the function “quadprog” provided by Matlab to solve the optimization problem in Equation (20). Since the optimization variables are only three-dimensional, the computation time will be significantly reduced.
Equation (20) sets up the quadratic object function to optimize the coordinated control between EVs and DG with corresponding constraints listed in Equation (19). Optimization results shown in the following sections illustrate that the results of control are consistent with practical operating situations in real power grid.
4. Simulation Studies
In order to investigate the performance of the proposed MGPC based controller for LFC, the module of the micro-grid in
Figure 1 is established in the Matlab/Simulink environment. Also, a well-tuned PID controller and a FUZZY controller have also been studied in the simulation. The system parameters are provided in
Table A1 [
18,
19,
24], and the parameters of controllers are presented in
Table A2 [
25].
In this paper, three cases have been analyzed to investigate the performance of the proposed controller on different disturbances. In case A, we assume that the output power of wind generation is a constant and only load disturbance is considered. In case B, the load demand is a constant with varying wind power based on real wind power data. In case C, both load disturbance and wind power fluctuation are considered in the simulation.
4.1. Case A: The Dynamic Response to Load Disturbance
In this case, the isolated grid is in steady state at the beginning of the simulation, and the performance of the proposed controller on load disturbance is investigated. In this case, we assume that the output power of wind generation is a constant with stable wind speed during a short period, which is denoted as .
Without considering the constraints of EVs and DG, a load step disturbance Δ
PL = 0.05
pu is applied at
t = 20 s. The system frequency deviation using PID control, FUZZY control and MGPC control is shown in
Figure 6a. The outputs of the DG and EVs under different control are shown in
Figure 6b.
Figure 6.
(a) The frequency deviation of the micro-grid without constraints using PID control, FUZZY control and MGPC control; (b) The output power increment of DG, EV1 and EV2 without constraints using PID control, FUZZY control and MGPC control.
Figure 6.
(a) The frequency deviation of the micro-grid without constraints using PID control, FUZZY control and MGPC control; (b) The output power increment of DG, EV1 and EV2 without constraints using PID control, FUZZY control and MGPC control.
As shown in
Figure 6a, compared with the PID controller and the FUZZY controller, the peak value in the first swing has significantly decreased and the proposed MGPC controller has quickly damped the system frequency oscillation.
Figure 6b shows that MGPC obtains stable output power of EVs and DG in shorter time and with less adjustment frequency, which is beneficial for a longer equipment life of EV batteries and DG.
Because the EVs have been considered as an equivalent power source in this paper, different structures of EVs have no impact on the controller. The impact of different EV capacity on the load frequency control is determined by the constraints of inverter capacity limit of equivalent EVs. Without considering the constraints of inverter capacity limit of EVs, EVs of different capacities control the frequency with the same output power, which is shown in
Figure 6b.
Then, considering the constraints of EVs and DG (given in
Table A1), a load step disturbance
is applied at
t = 10 s, and EV2 will be removed from the LFC system as soon as its energy is smaller than
at
t = 60 s. The system frequency deviation using PID control, FUZZY control and MGPC control is shown in
Figure 7a. The outputs of the DG, EVs under PID control, FUZZY control and MGPC control are shown in
Figure 7b, respectively.
Figure 7.
(a) The frequency deviation of the micro-grid with constraints using PID control, FUZZY control and MGPC control; (b) The output power increment of DG, EV1 and EV2 with constraints using PID control, FUZZY control and MGPC control.
Figure 7.
(a) The frequency deviation of the micro-grid with constraints using PID control, FUZZY control and MGPC control; (b) The output power increment of DG, EV1 and EV2 with constraints using PID control, FUZZY control and MGPC control.
Due to the constraints, as shown in
Figure 7a, the system can damp the frequency oscillation under disturbance. Nevertheless, the MGPC controller still demonstrates superior damping performance over the PID controller and the FUZZY controller. As shown in
Figure 7b, the output power increments of the two EVs are different by using different constraints. In the well-tuned PID controller and the FUZZY controller, the output power increment of EV1 and EV2 hit their inverter capacity limits and remains saturated for a relative long time. In addition, MGPC obtains more stable output power of EVs than the PID controller and the FUZZY controller. It is observed that, all the EVs and DG participate in damping frequency oscillation under different controls considering constraints. As shown in
Figure 7b, if constraints of inverter capacity limit of EVs are considered, the output power of EVs is determined by constrains. EVs require longer time to damp the frequency oscillation under the same disturbance because of constraints.
When the total energy of EV2 hits at t = 60 s, the grid loses a controllable unit. As a result, the response speed of the LFC system slows down, but the MGPC based controller still damps the frequency oscillation well with remain controllable units (i.e., EV1 and DG).
4.2. Case B: The Dynamic Response to Wind Power Fluctuation
In this case, the load demand in isolated mode is set as a constant,
i.e.,
. Because the output power of wind generation will fluctuate according to the change of weather condition, a power fluctuation
is applied to the system. As shown in
Figure 8a, the data of
is from an offshore wind farm in Denmark [
26], where
means the wind power is equal to the average wind power during the period. The simulation results are shown in
Figure 8b–e, and the scenarios with and without constraints are compared.
Figure 8.
(a) The power fluctuation of wind power generation; (b) The frequency deviation of the micro-grid without constraints; (c) The frequency deviation of the micro-grid with constraints; (d) The output power increment of DG, EV1 and EV2 without constraints; (e) The output power increment of DG, EV1 and EV2 with constraints.
Figure 8.
(a) The power fluctuation of wind power generation; (b) The frequency deviation of the micro-grid without constraints; (c) The frequency deviation of the micro-grid with constraints; (d) The output power increment of DG, EV1 and EV2 without constraints; (e) The output power increment of DG, EV1 and EV2 with constraints.
Figure 8b,c show that the proposed MGPC based controller effectively restrains the frequency fluctuation caused by wind generation, and it also demonstrates superior damping performance over PID controller and FUZZY controller. From
Figure 8d and
Figure 8e, the output power curve of DG is smoother than that of EVs, because the inertia constant of DG is much larger than that of EVs. Also, when constraints are considered in the system, DG and EVs have less output power fluctuation by using the MGPC control.
4.3. Case C: The Dynamic Response to Both Load Disturbance and Wind Power Fluctuation
In this case, both load disturbance and wind power fluctuation are applied to the system. When a fault occurs in the connected power grid at 19.5 s, the circuit breaker “Breaker1” in
Figure 1 will trip to isolate the micro-grid from the power grid, and the micro-grid enters isolated mode from gird-connected mode at 20 s. We assume that the power provided to the micro-grid by grid is 0.03
pu, so there is a power shortage of 0.03
pu in the micro-grid at 20 s. Also, a load step disturbance of −0.03
pu is applied at 50 s. The same wind power fluctuation in Case B is also applied in this case. The power disturbances are shown in
Figure 9a, and the simulation results with and without constraints are compared in
Figure 9b–e.
Figure 9.
(a) The power disturbances applied in case C; (b) The frequency deviation of the micro-grid without constraints; (c) The frequency deviation of the micro-grid with constraints; (d) The output power increment of DG, EV1 and EV2 without constraints; (e) The output power increment of DG, EV1 and EV2 with constraints.
Figure 9.
(a) The power disturbances applied in case C; (b) The frequency deviation of the micro-grid without constraints; (c) The frequency deviation of the micro-grid with constraints; (d) The output power increment of DG, EV1 and EV2 without constraints; (e) The output power increment of DG, EV1 and EV2 with constraints.
Figure 9b shows that the MGPC has good performance on the frequency deviation caused by both wind power fluctuation and load disturbances without considering constraints. Also, as shown in
Figure 9d, the output power curve of EVs is less smooth than that of DG because of smaller inertia constant. And, compared with PID and FUZZY, the MGPC can obtain more stable output power of EVs and DG. When the constraints of EVs and DG are considered,
Figure 9c shows that the MGPC still quickly damps the frequency deviation, although the peak value of frequency deviation is a little larger than FUZZY at first swing and second swing. The allowed frequency fluctuation is ±0.2
Hz of distribution grid in China, so the frequency deviation under MGPC control can meet the need of frequency limit.
Figure 9e shows that when the output power of EVs and DG are constrained, the MGPC can still obtain more stable output power of EVs and DG.
5. Conclusions
Load frequency stability is an important issue in micro-grid, especially for the power fluctuation caused by renewable energy sources. In this paper, a coordinated controller based on MGPC theory for LFC in an isolated micro-grid with V2G technique has been proposed under varying operation conditions with fluctuating renewable energy generation and load disturbance. Using the online monitoring data from PMUs, the MGPC based controller can coordinate the output of EVs and DG through a process of multi-step prediction, rolling optimization and feedback compensation. Moreover, the constraints of control variables can be easily implemented in the proposed controller design. Time-domain simulations with different micro-grid operation conditions are employed to investigate the effectiveness and robustness of the proposed controller. Comparing with PID controller and FUZZY controller, simulation results demonstrate that the proposed controller can obtain better robust performance on LFC with complex operation situations, namely, random renewable energy generation and continuous load disturbances.
According to the control model of the micro-grid including LFC controller, both load disturbance and the output power of renewable source are considered as ΔP. So the proposed controller can be used in different configurations of micro-grid, including different loads, renewable sources and grid topologies. With DMS, MGDS and PMUs, almost all the electrical information of the micro-grid can be obtained online. The parameters of controllable generation sources and EVs can be determined offline. This has shown the feasibility to implement the proposed method in real power system. On the other hand, only active power controls of DG and EVs for the purpose of LFC are presented in the proposed model. Bus voltage regulation by controlling the reactive power with intelligent solution will be studied in the future work. Also, the optimal decisions of the proposed coordinated controller depend on real-time information from MGDS. Therefore, the communication delay may have an impact on the performance of the controller, which poses further challenges and research directions along this topic.