3.2. Reliability of Fluid Properties
Regarding the reliability of fluid properties for pure working fluids and mixtures, predicted vapour pressure, VLE and density data are compared to experimental data. Exemplarily,
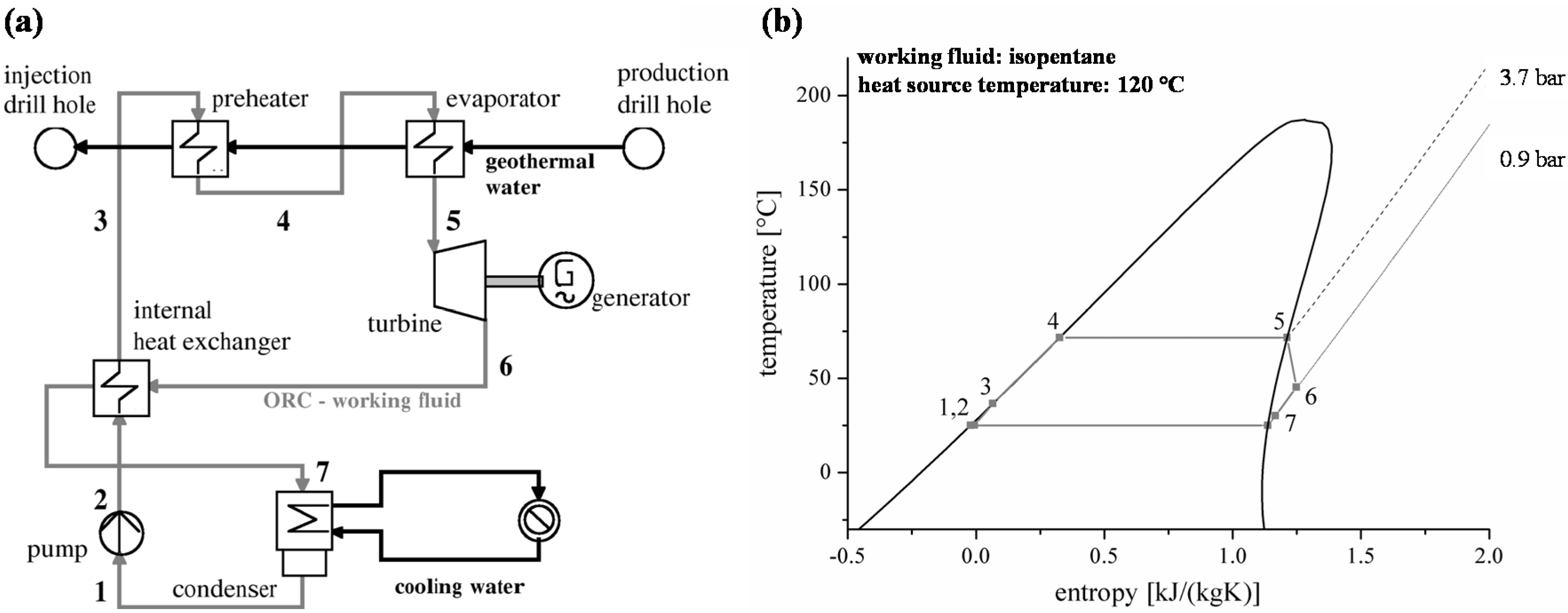
Figure 2 shows the vapour pressure for R134a,
n-butane, R245fa and
n-pentane calculated by REFPROP [
60,
61,
62,
63]. For R134a, the experimental data of Valtz
et al. [
64] and the prediction model are in good agreement. The mean relative deviation is 0.2% and the maximum relative deviation of 0.5% occurs for high temperatures. In case of
n-butane, the experimental data of Warowny [
65] show a maximum deviation of 3.0% and a mean relative deviation of 2.3%. For
n-pentane, the vapour pressure measured by Abdulagatov und Rasulov [
66] lead to a mean relative deviation of 1.4% compared to REFPROP.
Figure 2.
Vapour pressure calculated by REFPROP compared to experimental data for selected ORC working fluids.
Figure 2.
Vapour pressure calculated by REFPROP compared to experimental data for selected ORC working fluids.
The maximum relative deviation of −2.4% arise near critical conditions (
Tcrit = 196.6 °C). Vapour pressure measurements of R245fa by Feng
et al. [
67] show a mean relative deviation of 0.4% compared to REFPROP. The maximum relative deviation of −2.1% is related to low temperatures.
In the case of the evaluation of fluid properties for the considered mixtures, a distinction between natural hydrocarbons and fluorinated hydrocarbons has to be made. In case of natural hydrocarbons as mixture components, the required binary coefficients for the mixing rule of Kunz
et al. [
59] are available in literature and implemented in REFPROP.
N-pentane/isohexane represents the only exception for mixtures of this class of substance. In this case, as well as for mixtures of fluorinated components, the generalized factors and mixture parameters for the equation of state are estimated by REFPROP. Regarding natural hydrocarbons,
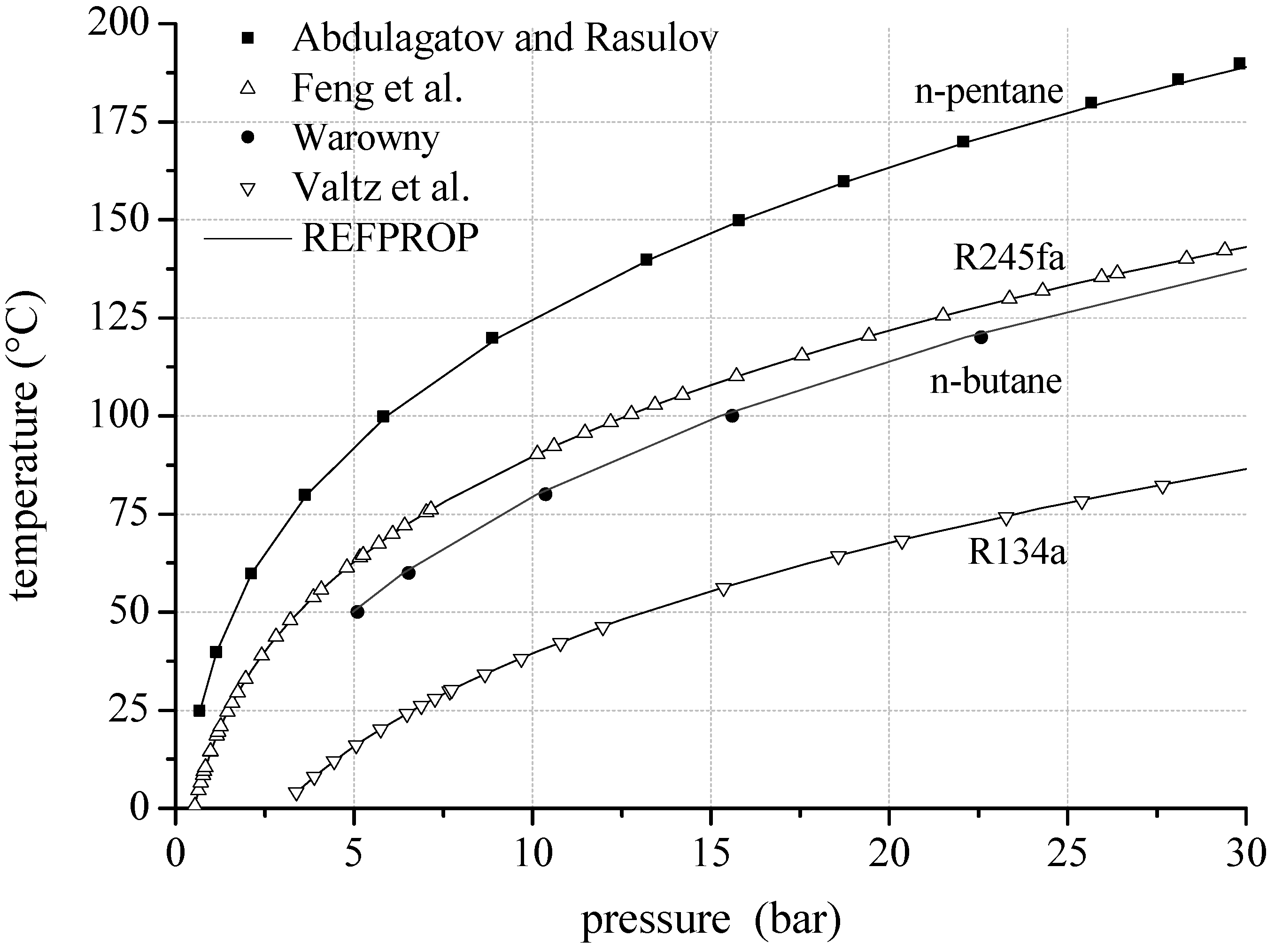
Figure 3 shows experimental and theoretical VLE data of the binary mixtures
n-butane/
n-pentane and propane/isobutane. The measurements of Calingaert and Hitchcock [
68] lead to a mean relative deviation of 3.4% compared to REFPROP. The maximum relative deviation is 10.8%. In case of propane/isobutane the mean relative deviation is 0.8% compared to the experimental data of Lim
et al. [
69].
Figure 3.
VLE data calculated by REFPROP compared to experimental data for fluid mixtures considering natural hydrocarbons as mixture components.
Figure 3.
VLE data calculated by REFPROP compared to experimental data for fluid mixtures considering natural hydrocarbons as mixture components.
To evaluate the uncertainties resulting from predicted mixing factors and parameters,
Figure 4 shows VLE data of mixtures consisting of fluorinated components compared to REFPROP. In case of R134a/R245fa, experimental data of Bobbo
et al. [
70] show a mean relative deviation of 4.7% compared to REFPROP. Regarding the liquid phase, the mean relative deviation is 5.1% and for the gaseous phase 4.4%. The maximum relative deviation of −11.0% arises in the liquid phase. For R134a/R236fa a mean relative deviation of 4.9% is determined comparing data of Bobbo
et al. [
71] and REFPROP. The maximum relative deviation of −10.1% occurs in the gaseous phase. Additionally, fluid properties of R142b/R134a are compared to experimental VLE data of Kleiber [
72]. Here, a mean relative deviation of 3.3% is obtained. For the examined zeotropic mixtures consisting of fluorocarbons, the comparisons show similar deviations as determined for mixtures with natural hydrocarbon components.
Figure 4.
VLE data calculated by REFPROP compared to experimental data for fluid mixtures regarding fluorinated hydrocarbons as mixture components.
Figure 4.
VLE data calculated by REFPROP compared to experimental data for fluid mixtures regarding fluorinated hydrocarbons as mixture components.
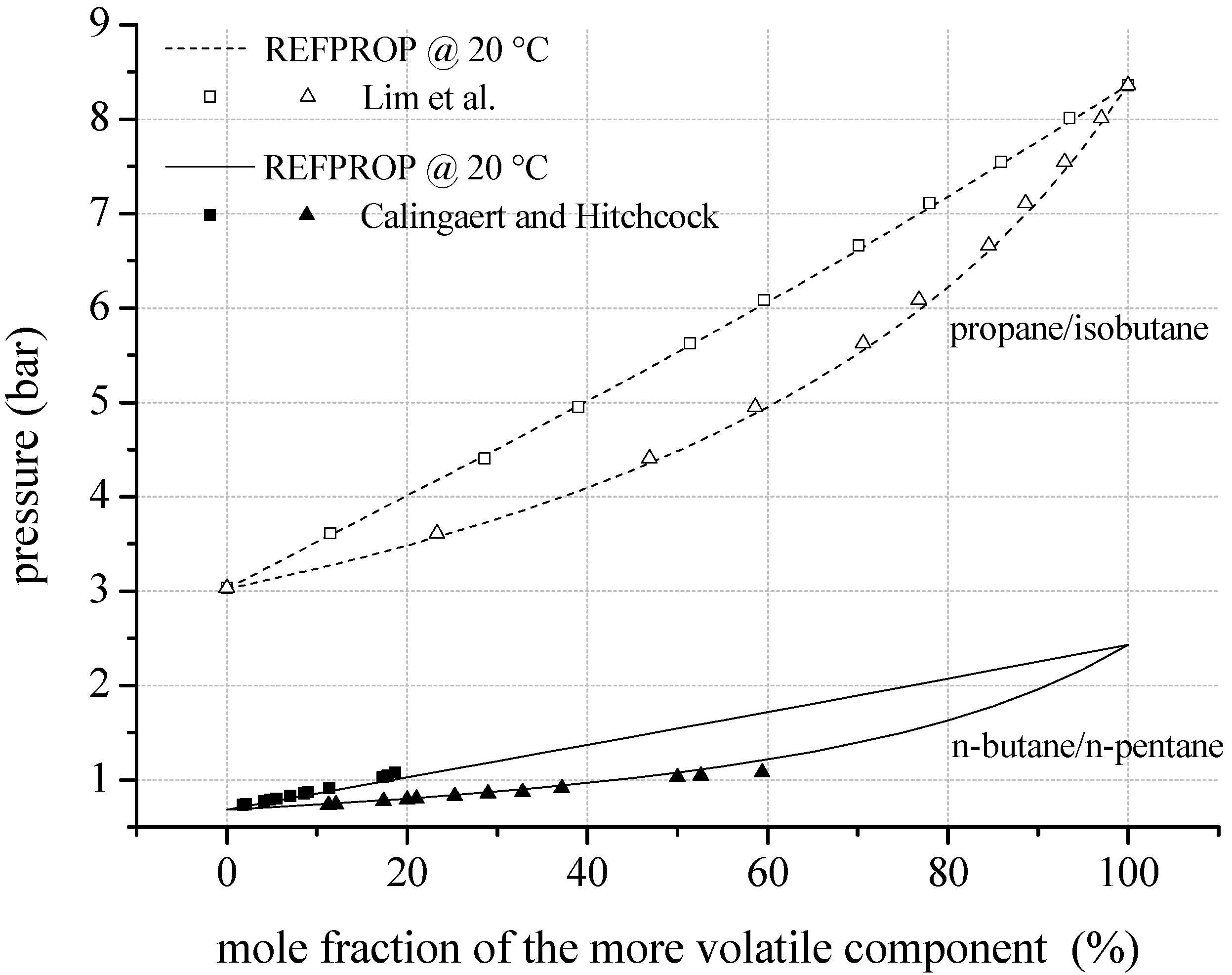
As an alternative to vapour pressure and VLE–data, experimental data for density are analyzed. According to
Figure 5a, gaseous density for
n-pentane measured by Abdulagatov and Rasulov [
66] show a mean relative deviation of 2.6% to REFPROP. In case of liquid density, mean relative deviation is 1.0%. The uncertainties increase with increasing temperature. Near critical conditions the maximum relative deviation is 10.8%. A limitation of the maximum ORC process pressure according to
Table 1 leads to a maximum relative deviation of 1.8% in the gaseous phase and 0.4% in the liquid phase. Experimental data for density of the selected zeotropic mixtures are available for propane/isobutane. Kayukawa and Watanabe [
73] examined the liquid density at constant temperature depending on pressure for three mixture compositions.
Figure 5b shows the liquid density for 26.85 °C as a function of mixture composition and pressure. Considering the complete available data set, a mean relative deviation of 0.15% is determined.
Figure 5.
(a) Predicted liquid and gaseous density depending on temperature compared to experimental data for n-pentane; (b) liquid density as a function of mixture composition and pressure calculated by REFPROP compared to experimental data for propane/isobutane.
Figure 5.
(a) Predicted liquid and gaseous density depending on temperature compared to experimental data for n-pentane; (b) liquid density as a function of mixture composition and pressure calculated by REFPROP compared to experimental data for propane/isobutane.
In general the experimental data show a good agreement to the predictions models. In this context, REFPROP is suitable for process simulations of ORC systems using pure working fluids and zeotropic mixtures. For pure fluids, the determined deviations correspond quiet well with the uncertainties of prediction models, which range between 0.2% and 1.0% for density as well as for vapour pressure. Higher deviations are only obtained near critical conditions and for those mixtures, where mixture parameters for the equation of state are estimated.
3.3. Second Law Analysis
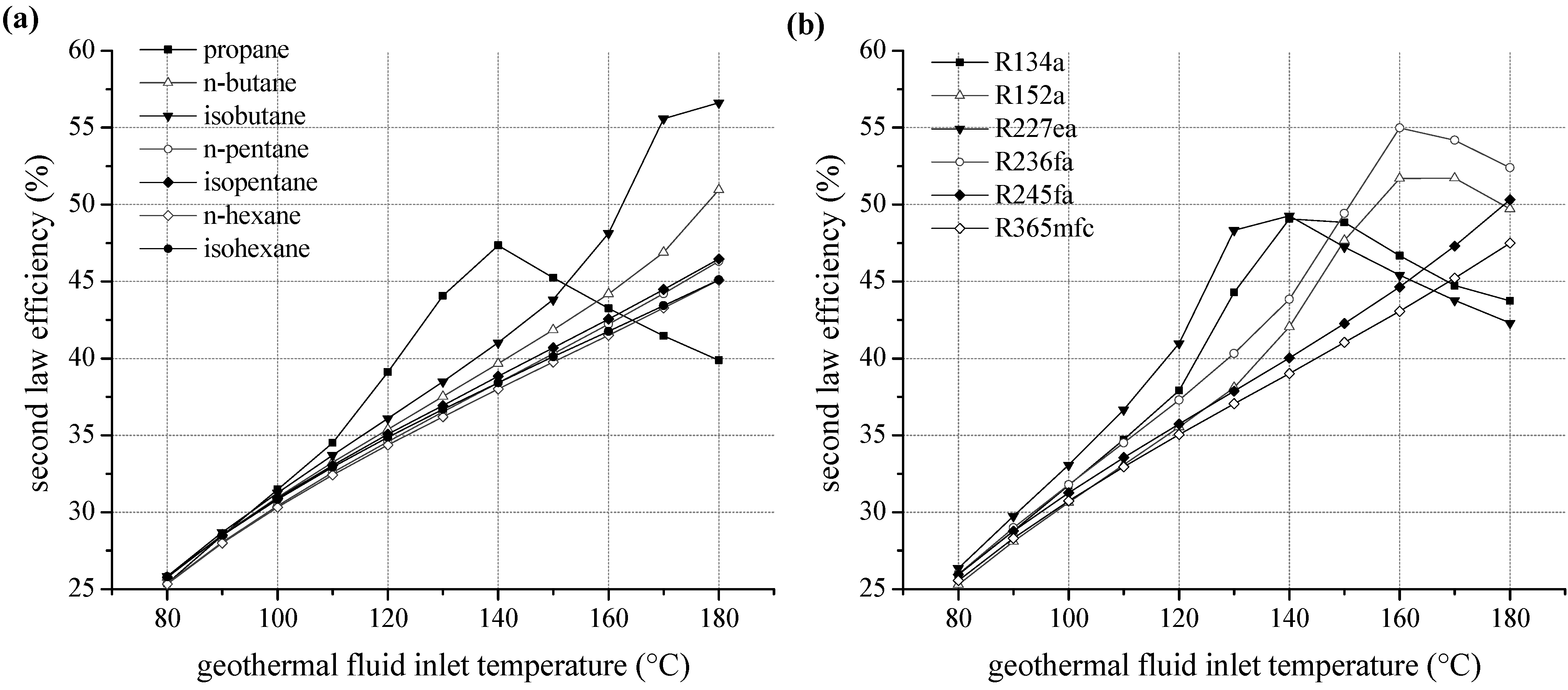
We examined the second law efficiency of the ORC depending on inlet temperature of the geothermal fluid in the range of 80 and 180 °C.
Figure 6a shows the exergetic efficiency as a function of heat source temperature for ORC systems using pure natural hydrocarbons as working fluids. For temperatures below 130 °C, relative differences of second law efficiency are maximal 5%. Considering the homologous series of alkanes, starting from isobutane, the margin of fluctuation related to fluid selection is low. More volatile components lead to more efficient cycles; this is also applicable for higher heat source temperatures. The ranking correlates with the critical temperature, too. Second law efficiency increases with rising temperature except choosing propane as a working fluid. For propane, an efficiency optimum at 140 °C is obtained due to a shift of the pinch-point from the preheater outlet to the inlet. Additionally, an expansion into the two-phase region has to be taken into account, evaluating propane as working fluid. A minimal vapour quality of 94.9% at the turbine outlet is determined for 130 °C inlet temperature of the geothermal fluid. However, compared to isopentane the second law efficiency is increased by up to 21.9% for the use of propane as a working fluid. For temperatures higher than 150 °C, the efficiency decreases below alternatively considered hydrocarbons.
Figure 6.
Second law efficiency as a function of heat source temperature for ORC systems using pure working fluids (a) natural hydrocarbons (b) fluorinated hydrocarbons.
Figure 6.
Second law efficiency as a function of heat source temperature for ORC systems using pure working fluids (a) natural hydrocarbons (b) fluorinated hydrocarbons.
For fluorinated hydrocarbons a correlation between critical temperature and second law efficiency is obtained, too (see
Figure 6b). For temperatures up to 140 °C the working fluids R134a and R227ea, with the lowest critical temperatures, lead to the highest efficiency. In analogy to propane, the fluids R227ea, R134a, R152a and R236fa show an efficiency optimum of the ORC. In case of R227ea, second law efficiency at 130 °C is 27.6% higher compared to the common working fluid R245fa. In general, the optimum is shifted to higher heat source temperatures for fluids with higher critical temperatures. Again, the significant efficiency increase is accompanied by a shift of the pinch-point from the preheater outlet to the inlet. As a consequence, a better match of temperature profiles regarding the ORC and the heat source is obtained. Therefore, the reinjection temperature sinks and a higher amount of thermal power is coupled to the ORC.
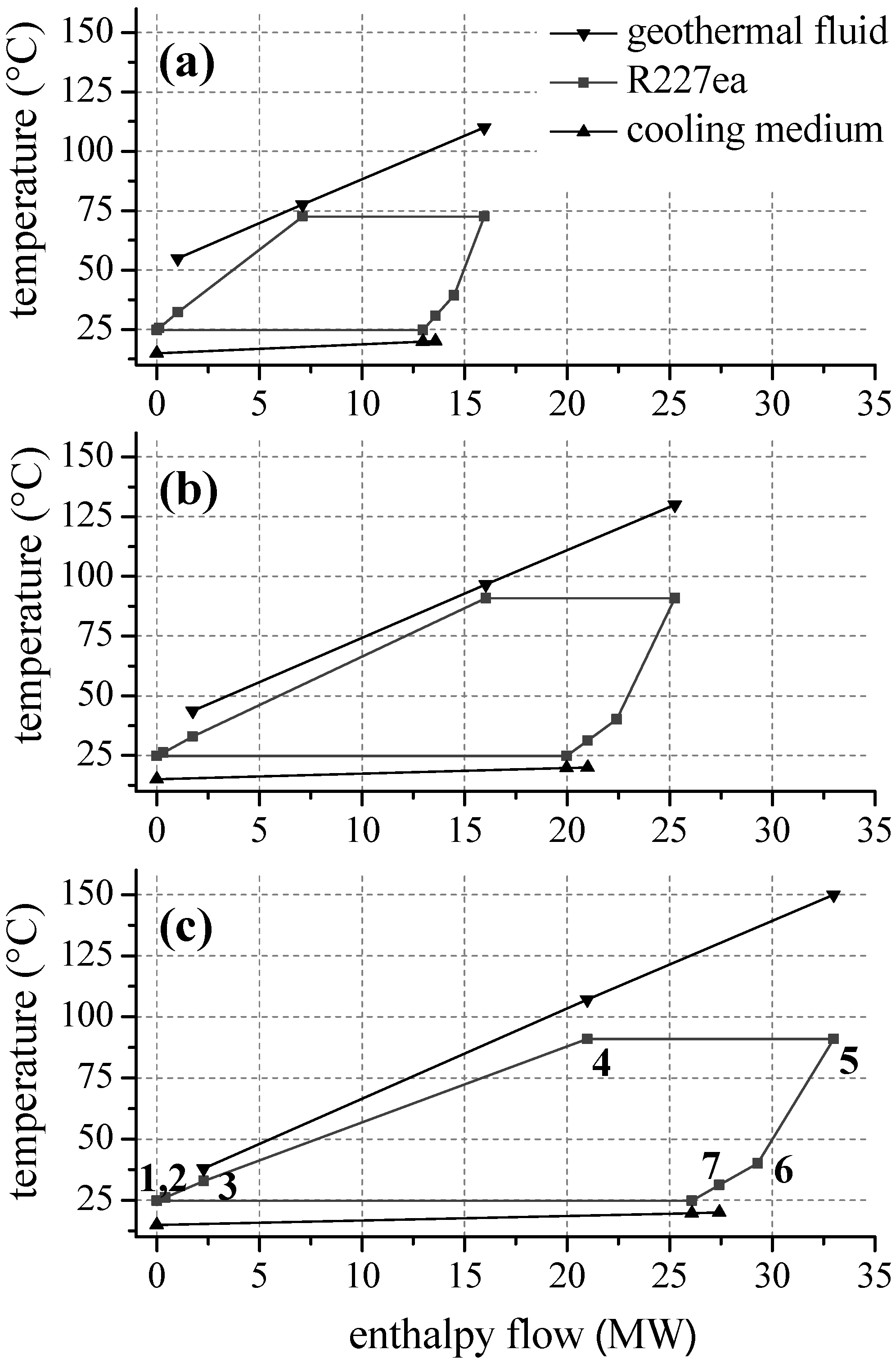
Figure 7 illustrates this effect by means of a temperature–enthalpy flow-diagram for the cycle with R227ea as ORC working fluid. In case of a heat source temperature of 110 °C (
Figure 7a), the ORC is limited by the minimal temperature difference between heat source and cycle at the pinch point, here state point 4. The process pressure
p4 of 15.8 bar is below the maximum value of 0.8·
pcrit. In case of an inlet temperature of the geothermal fluid of 130 °C (
Figure 7b), the maximum pressure of 23.4 bar is reached. The pinch-point is still at state point 4. For a temperature of 140 °C, the pinch point shifts to the inlet of the preheater, while
p4 and
T4 stay constant. This allows a reduction of the reinjection temperature to 37.9 °C and an efficiency maximum can be observed (see
Figure 6b). For R245fa, at same conditions, a reinjection temperature of 65.2 °C is determined. Thus, 7.4 MW more thermal power is transferred to the ORC using R227ea as a working fluid. The gross power output is 0.9 MW higher compared to R245fa.
Figure 7.
Temperature-enthalpy flow-diagram for the ORC with R227 at different inlet temperature of the geothermal fluid of (a) 110 °C; (b) 130 °C; and (c) 150 °C.
Figure 7.
Temperature-enthalpy flow-diagram for the ORC with R227 at different inlet temperature of the geothermal fluid of (a) 110 °C; (b) 130 °C; and (c) 150 °C.
Regarding geothermal fluid temperatures higher than 140 °C, an adaption of the ORC using R227ea to the heat source characteristics exclusively takes place by increasing the ORC mass flow. Upper process pressure and temperature of the ORC as well as reinjection temperature stay constant (see
Figure 7c). As a result, the net second law efficiency decreases.
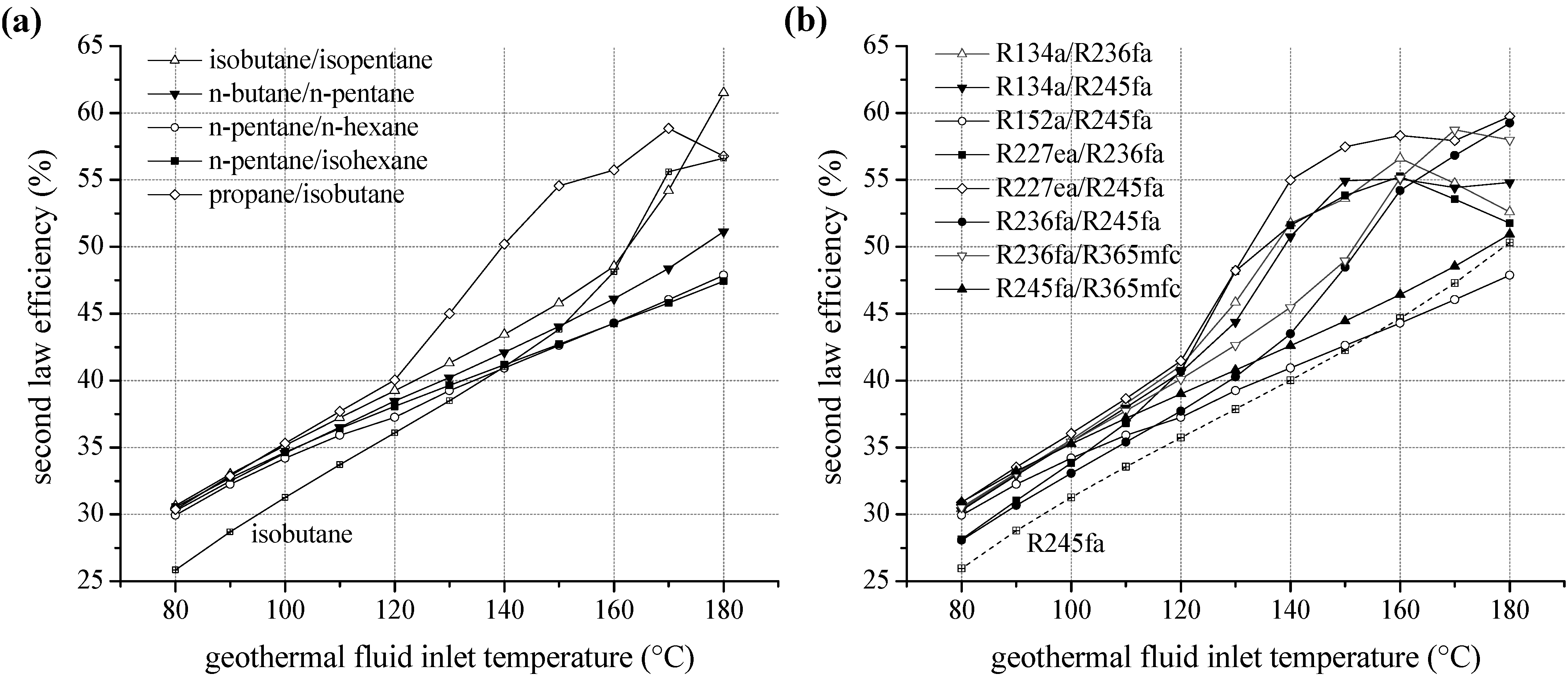
For ORC systems using zeotropic mixtures as a working fluid, second law efficiency as a function of the inlet temperature of the geothermal fluid is illustrated in
Figure 8. Only the most efficient mixture compositions are included in the diagram. In
Table 4 and
Table 5 the corresponding mole fractions are listed. Regarding natural hydrocarbons as mixture components (see
Figure 8a), a significant efficiency increase compared to the most efficient pure component is obtained. For heat source temperatures lower than 100 °C isobutane/isopentane leads to an efficiency increase between 12.2% and 18.6% in relation to isobutane. For higher temperatures propane/isobutane is suitable as working fluid. Compared to propane, a higher efficiency in the range of 2.1% and 20.6% is obtained. Considering fluorinated hydrocarbons as ORC working fluids a comparable efficiency increase is observed.
Figure 8b shows the second law efficiency for the considered zeotropic mixtures based on fluorocarbons depending on inlet temperature of the geothermal fluid. For the examined temperature range, R227ea/R245fa leads to high exergetic efficiencies. Compared to the most efficient pure fluid, the increase is up to 17.3%. Only for a heat source temperature of 130 °C, pure R227ea is the most efficient working fluid due to the described shift of the pinch-point. Otherwise zeotropic mixtures lead to an efficiency increase of minimal 5.4% and maximal 20.6%. Considering geothermal fluid temperatures below 130 °C additionally R134a/R236fa and R134a/R245fa are favourable. In the case of higher temperatures, next to R227ea/R245fa, R236fa/R365mfc and R236fa/R245fa are suitable.
Figure 8.
Second law efficiency as a function of heat source temperature for ORC systems using zeotropic mixtures as working fluids (a) natural hydrocarbons (b) fluorinated hydrocarbons.
Figure 8.
Second law efficiency as a function of heat source temperature for ORC systems using zeotropic mixtures as working fluids (a) natural hydrocarbons (b) fluorinated hydrocarbons.
Table 4.
Most efficient mixture compositions (mole fractions) corresponding to
Figure 8a.
Table 4.
Most efficient mixture compositions (mole fractions) corresponding to Figure 8a.
| TGF,in (°C) | Isobutane/Isopentane | n-Butane/n-Pentane | n-Pentane/n-Hexane | n-Pentane/Isohexane | Propane/Isobutane |
|---|
| 80 | 90/10 | 80/20 | 80/20 | 50/50 | 80/20 |
| 90 | 90/10 | 90/10 | 80/20 | 50/50 | 80/20 |
| 100 | 90/10 | 90/10 | 80/20 | 50/50 | 80/20 |
| 110 | 90/10 | 90/10 | 80/20 | 50/50 | 80/20 |
| 120 | 90/10 | 90/10 | 80/20 | 50/50 | 80/20 |
| 130 | 90/10 | 90/10 | 80/20 | 50/50 | 90/10 |
| 140 | 90/10 | 90/10 | 80/20 | 50/50 | 80/20 |
| 150 | 90/10 | 90/10 | 80/20 | 50/50 | 80/20 |
| 160 | 90/10 | 90/10 | 80/20 | 50/50 | 50/50 |
| 170 | 90/10 | 90/10 | 80/20 | 50/50 | 20/80 |
| 180 | 90/10 | 90/10 | 80/20 | 50/50 | 10/90 |
Table 5.
Most efficient mixture compositions (mole fractions) corresponding to
Figure 8b.
Table 5.
Most efficient mixture compositions (mole fractions) corresponding to Figure 8b.
| TGF,in (°C) | R134a/R236fa | R134a/R245fa | R152a/R245fa | R227ea/R236fa | R227ea/R245fa | R236fa/R245fa | R236fa/R365mfc | R245fa/R365mfc |
|---|
| 80 | 60/40 | 80/20 | 80/20 | 30/70 | 70/30 | 40/60 | 90/10 | 60/40 |
| 90 | 60/40 | 90/10 | 80/20 | 30/70 | 70/30 | 40/60 | 90/10 | 60/40 |
| 100 | 60/40 | 90/10 | 80/20 | 40/60 | 70/30 | 40/60 | 90/10 | 60/40 |
| 110 | 60/40 | 90/10 | 80/20 | 50/50 | 70/30 | 40/60 | 90/10 | 60/40 |
| 120 | 60/40 | 90/10 | 80/20 | 90/10 | 80/20 | 40/60 | 90/10 | 60/40 |
| 130 | 60/40 | 90/10 | 80/20 | 90/10 | 90/10 | 90/10 | 90/10 | 60/40 |
| 140 | 60/40 | 90/10 | 80/20 | 60/40 | 80/20 | 90/10 | 90/10 | 60/40 |
| 150 | 20/80 | 90/10 | 90/10 | 20/80 | 70/30 | 90/10 | 90/10 | 60/40 |
| 160 | 20/80 | 70/30 | 90/10 | 10/90 | 50/50 | 90/10 | 90/10 | 60/40 |
| 170 | 10/90 | 60/40 | 80/20 | 10/90 | 40/60 | 70/30 | 90/10 | 60/40 |
| 180 | 10/90 | 30/70 | 50/50 | 10/90 | 20/80 | 40/60 | 80/20 | 60/40 |
The selected boundary conditions of our study are in good agreement to Andreasen
et al. [
28]. Except of the hot fluid mass flow and the minimal temperature difference in the preheater the assumptions are nearly identical. Andreasen
et al. [
28] identify the most efficient fluids for a heat source temperature at 120 °C. Regarding the considered subcritical cycles, propane/isobutane and isobutane/isopentane were also determined as efficient mixtures. Slight deviations for the most efficient mixture composition occur due to the mentioned differences of boundary conditions and due to the fact we use discrete mole fractions in the sensitivity analysis.
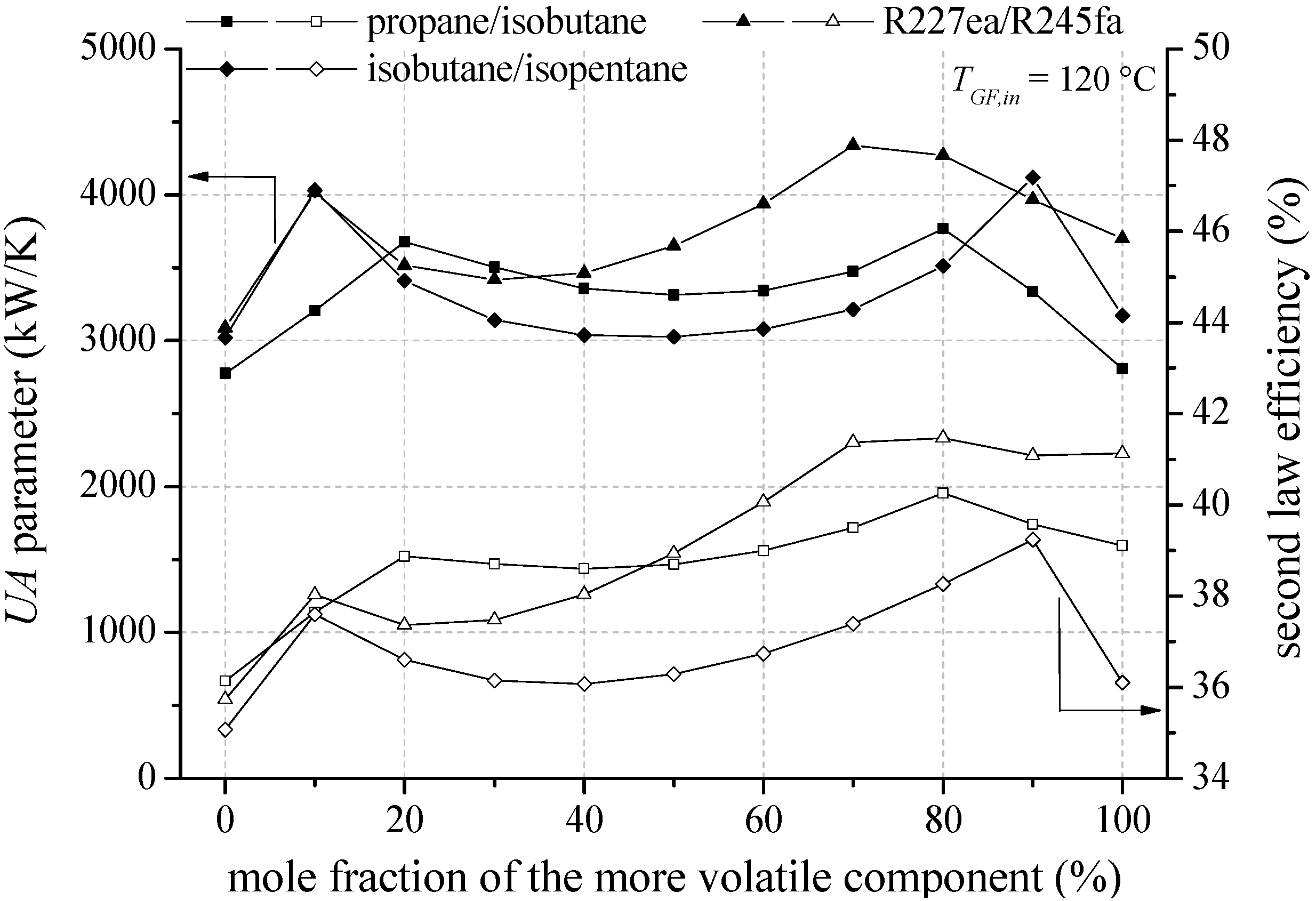
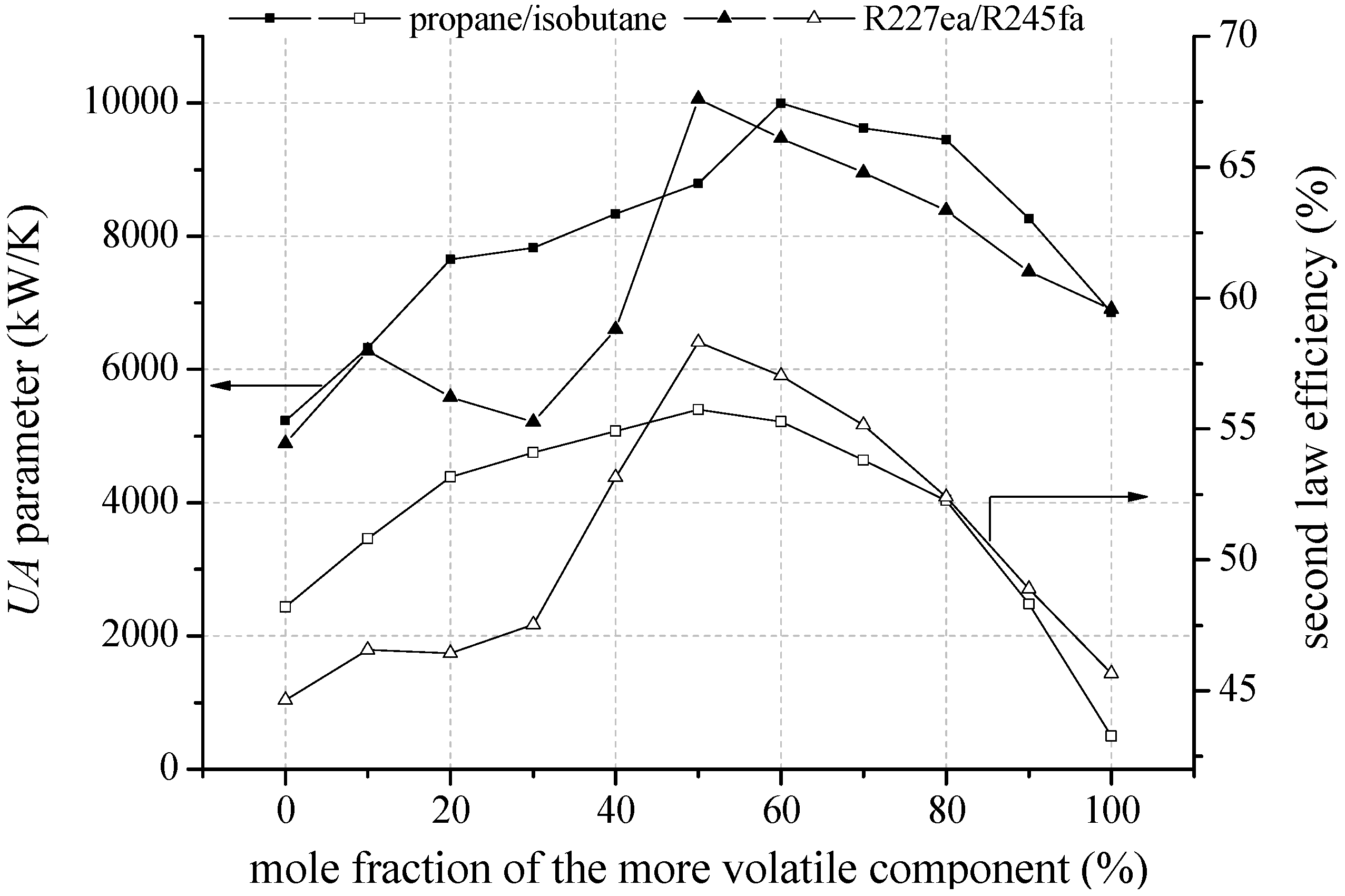
In the following, heat source temperatures of 120 °C and 160 °C are selected representatively to analyse the influence of mixture composition on second law efficiency, total
UA parameter and economic parameters. In
Figure 9 the second law efficiency and the total
UA parameter depending on mixture composition are shown for the most efficient zeotropic mixtures in case of a geothermal fluid temperature of 120 °C.
Figure 9.
Second law efficiency and UA parameter depending on mixture composition for the most efficient zeotropic mixtures and a geothermal fluid temperature of 120 °C.
Figure 9.
Second law efficiency and UA parameter depending on mixture composition for the most efficient zeotropic mixtures and a geothermal fluid temperature of 120 °C.
Considering the mixture isobutane/isopentane, a mole fraction of 90% isobutane leads to the highest second law efficiency. For propane/isobutane, a mole fraction of 80% propane is the most efficient mixture composition. For the mentioned mixture compositions, a glide match of ORC working fluid at condensation occurs. Previous investigations have confirmed that a reduction of irreversibilities in the condenser is mainly responsible for the efficiency increase [
18,
29]. In contrast, R227ea/R245fa does not show the efficiency maximum at a mixture composition, at which a good glide match takes place. The highest exergetic efficiency is determined for a mole fraction of 80% R227ea, while the best glide match of the temperature profile arises for a mole fraction of 30% R227ea. For fluid mixtures, which show a shift of the pinch-point, the possibility to influence this effect to higher heat source temperatures by adding a less volatile component is of primary importance. Accordingly, for R227ea/R245fa the mole fraction of R245fa increases with increasing heat source temperature starting from 130 °C (see
Table 5). This principle can also be observed in
Table 4 for propane/isobutane in case of heat source temperatures higher than 150 °C. If a shift of the pinch point does not occur, like for isobutane/isopentane or R245fa/R365mfc, the most efficient mixture composition is independent from the heat source temperature (see
Table 4 and
Table 5). For these mixtures a mole fraction is suitable, which leads to a ratio of
TG,Cond/Δ
TCM equal 1.
In general, the most efficient mixture composition leads to the highest total
UA parameters,
Figure 10 shows that the total
UA parameter is mainly influenced by the condenser. In case of isobutane/isopentane up to 76.7% of the total
UA parameter is related to the condenser. This is due to a high amount of transferred thermal energy and a low logarithmic temperature difference. In case of zeotropic mixtures the logarithmic temperature difference is even reduced in context of the good glide match. Consequently, pure components in conjunction with the pinch point at the outlet of the preheater lead to low
UA parameter due to an isothermal phase-change. The correlation of high efficiency for specific mixture compositions and high
UA parameter emphasize the importance of a thermo-economic analysis to clarify if the increase in power output overcompensates the additional heat transfer surface.
Figure 10.
UA parameter for the considered heat exchanger depending on mixture composition of isobutane/isopentane at a geothermal fluid temperature of 120 °C.
Figure 10.
UA parameter for the considered heat exchanger depending on mixture composition of isobutane/isopentane at a geothermal fluid temperature of 120 °C.
For an inlet temperature of the geothermal fluid of 160 °C the described principles are transferable.
Figure 11 shows that high second law efficiency correlates with high
UA parameters. For R227ea/R245a, the efficiency optimum occurs at equimolar composition. As mentioned before, the shift of the pinch point is delayed by adding a higher amount of R245fa. Compared to pure R227ea, the second law efficiency can be increased by up to 28.4%. However, the
UA parameter is 45.7% higher in case of the equimolar mixture.
Figure 11.
Second law efficiency and UA parameter depending on mixture composition for selected zeotropic mixtures and a geothermal fluid temperature of 160 °C.
Figure 11.
Second law efficiency and UA parameter depending on mixture composition for selected zeotropic mixtures and a geothermal fluid temperature of 160 °C.
Finally, the size parameter of the turbine and the volume flow ratio at the expansion are calculated depending on mixture composition. Regarding isobutane/isopentane and a heat source temperature of 120 °C, the size parameter introduced by Angelino
et al. [
74] varies in the range of 0.15 and 0.26, the volume ratio is in the range of 3.6 and 4.0. According to Lazzaretto and Manente [
75], these parameters would lead to an isentropic efficiency of a radial turbine between 84.0% and 86.5%. A similar range for isentropic efficiency is obtained for the alternative considered working fluids. Exemplarily, the use of R227ea/R245fa shows isentropic turbine efficiencies between 83.0% and 86.0%. Here, the size parameter varies in the range of 0.17 and 0.24 and the volume ratio is in the range of 4.5 and 7.6. Regarding the mixture butane/pentane, the turbine efficiency ranges between 84.0% and 86.75%. This justifies the assumption of a constant isentropic efficiency of the turbine in this study.
3.4. Heat Exchanger Design
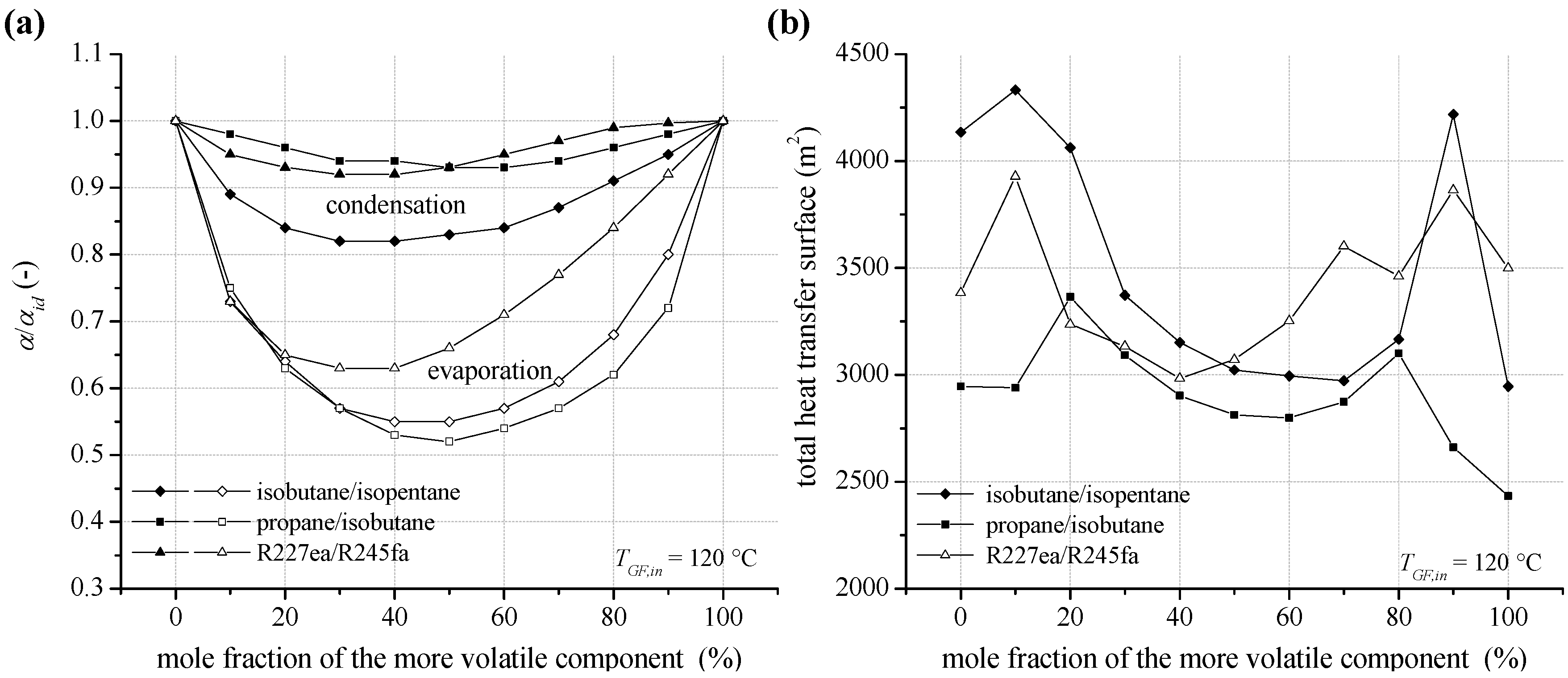
In
Figure 12a the ratio between the heat transfer coefficient at condensation and evaporation and the ideal value α
id is shown for the selected zeotropic mixtures isobutane/isopentane, propane/isobutane and R227ea/R245fa at a heat source temperature of 120 °C. In general, the results show a slight reduction of the heat transfer characteristics in case of condensation. For isobutane/isopentane the most distinctive reduction with up to 18% is obtained. This is due to a low mass flux density and high enthalpy difference at condensation. In case of high mass flux densities, like for propane/isobutane and R227ea/R245fa, the reduction is less pronounced with maximal 8%. The general behavior agrees with literature for experimental investigations of flow condensation of zeotropic mixtures [
76,
77]. In contrast, the reduction of pool boiling heat transfer coefficient is more significant. For isobutane/isopentane and propane/isobutane a minimum for α/α
id is obtained in case of an equimolar fraction. The reduction is 45% and 48%. In case of R227ea /R245fa, the reduction is 37% at 40 mol% R245fa. In principle, high heat transfer coefficients are obtained for more volatile working fluids with higher process pressures and thus higher gaseous density.
Figure 12b illustrates the total heat transfer surface of the ORC power plant, including internal heat exchanger, preheater, evaporator and condenser, depending on mixture composition at inlet temperature of the geothermal fluid of 120 °C. The local maxima for the total heat transfer surface correspond to the
UA-parameter in
Figure 9. The total heat exchange surface is mainly affected by the condenser dimensions. In this context, additionally to the reduction of the heat transfer coefficient at condensation, a low logarithmic mean temperature difference leads to high required heat transfer surfaces for efficient compositions.
In contrast, the logarithmic temperature difference for the evaporator and preheater differs only slightly for a variation of mixture composition (see
Table 6). For isobutane/isopentane depending on mole fraction the logarithmic temperature difference of the preheater differs only up to 5% and in case of the evaporator 13%. Differences in heat transfer surfaces of up to 47% for the preheater and up to 227% for the evaporator are due to a variation of thermodynamic characteristics as a function of mole fraction. More volatile working fluids show higher heat transfer surfaces for the preheater and for less volatile concentrations the evaporation heat transfer is dominant. As a consequence the sum of heat transfer surfaces concerning the heat input, preheater and evaporator differs only by 30% as a function of mixture composition. For the same mixture, a mole fraction of 90 mol% isobutane leads to the highest power output. Due to the good glide match in the condenser the logarithmic mean temperature difference is 5.1 K. As a result, the total heat transfer surface of 4218.1 m
2 is relatively high. In case of an equimolar concentration, a logarithmic mean temperature difference of 8.1 K and a total heat transfer surface of 3,021.4 m
2 are determined. The most efficient pure component isobutane leads to a logarithmic mean temperature difference of 7.2 K and a total heat transfer surface of 2,996.0 m
2.
Figure 12.
(a) Reduction of the heat transfer coefficient at condensation and evaporation (pool boiling) for zeotropic mixture depending on mixture composition (b) total heat transfer surface of the ORC power plant for a geothermal fluid temperature of 120 °C.
Figure 12.
(a) Reduction of the heat transfer coefficient at condensation and evaporation (pool boiling) for zeotropic mixture depending on mixture composition (b) total heat transfer surface of the ORC power plant for a geothermal fluid temperature of 120 °C.
Table 6.
Heat exchange surface, mean logarithmic temperature difference and transferred amount of thermal energy for each heat exchanger depending on mixture composition (isobutane/isopentane).
Table 6.
Heat exchange surface, mean logarithmic temperature difference and transferred amount of thermal energy for each heat exchanger depending on mixture composition (isobutane/isopentane).
| Parameter | 0/100 | 10/90 | 20/80 | 30/70 | 40/60 | 50/50 | 60/40 | 70/30 | 80/20 | 90/10 | 100/0 |
|---|
| APHE (m2) | 280.6 | 272.2 | 301.4 | 294.5 | 302.1 | 312.4 | 329.4 | 342.4 | 366.1 | 390.4 | 411.3 |
| ΔTlog,PHE (K) | 13.5 | 13.9 | 13.4 | 13.2 | 13.3 | 13.4 | 13.2 | 13.5 | 13.4 | 13.6 | 13.9 |
| Q̇PHE (MW) | 3.44 | 3.42 | 3.38 | 3.48 | 3.56 | 3.68 | 3.81 | 4.01 | 4.22 | 4.53 | 4.85 |
| AEVP (m2) | 495.8 | 518.3 | 600.2 | 622.5 | 614.8 | 587.7 | 537.0 | 473.1 | 404.5 | 330.4 | 274.3 |
| ΔTlog,EVP (K) | 19.2 | 17.6 | 18.7 | 17.2 | 16.9 | 16.8 | 17.2 | 17.2 | 17.8 | 18.3 | 18.5 |
| Q̇EVP (MW) | 12.02 | 11.55 | 13.53 | 12.56 | 12.54 | 12.50 | 12.72 | 12.39 | 12.48 | 12.14 | 11.39 |
| ACOND (m2) | 2638.5 | 3541.1 | 3160.9 | 2455.2 | 2234.6 | 2121.8 | 2128.3 | 2156.8 | 2396.0 | 2915.9 | 1911.0 |
| ΔTlog,COND (K) | 7.2 | 5.1 | 6.4 | 7.5 | 8.0 | 8.1 | 8.0 | 7.4 | 6.5 | 5.1 | 7.2 |
| Q̇COND (MW) | 13.94 | 13.34 | 15.32 | 14.46 | 14.53 | 14.60 | 14.92 | 14.76 | 15.02 | 14.96 | 14.66 |
| AIR (m2) | 719.5 | 917.8 | 568.3 | 448.5 | 388.0 | 359.7 | 353.2 | 374.7 | 442.4 | 581.4 | 349.43 |
| ΔTlog,IR (K) | 6.5 | 7.2 | 10.3 | 12.6 | 13.7 | 13.9 | 13.3 | 11.9 | 9.5 | 6.6 | 5.9 |
| Q̇IR (MW) | 0.94 | 1.36 | 1.29 | 1.29 | 1.25 | 1.22 | 1.17 | 1.14 | 1.11 | 1040.3 | 0.60 |
| Atotal (m2) | 4134.3 | 4331.6 | 4062.5 | 3372.2 | 3151.5 | 3021.9 | 2994.7 | 2972.3 | 3166.7 | 4218.1 | 2946.0 |
| PT (kW) | 1520.7 | 1623.0 | 1587.7 | 1581.3 | 1583.5 | 1598.3 | 1623.1 | 1659.0 | 1704.0 | 1755.3 | 1631.5 |
| PP (kW) | 27.8 | 34.2 | 35.6 | 42.3 | 47.6 | 53.4 | 59.1 | 66.9 | 74.5 | 84.7 | 94.6 |
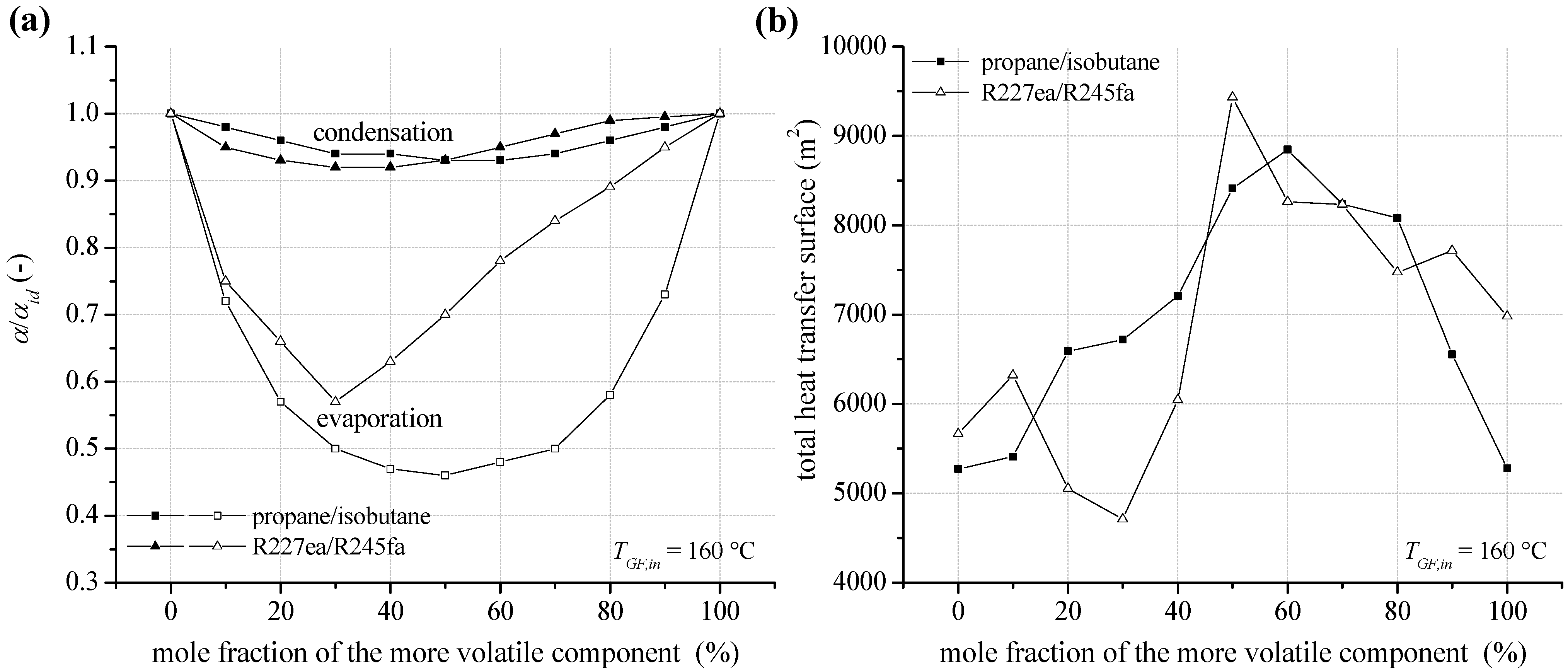
In case of a heat source temperature of 160 °C, the reduction of heat transfer coefficient at condensation and evaporation depending on mixture composition for propane/isobutane and R227ea/R245fa is shown in
Figure 13a. Compared to a heat source temperature of 120 °C, relevant parameters regarding condensation heat transfer like
Reg, differ only slightly. This is due to the assumption of a constant flow velocity in the pipes. In addition,
Prl or
Prg show only a low dependence on the increased process pressure. As a result, the reduction of condensation heat transfer coefficients is almost identical compared to the geothermal inlet temperature of 120 °C. Regarding the evaporation heat transfer, a more pronounced reduction for fluid mixtures can be observed. In case of an equimolar concentration for propane/isobutane, a reduction of 54% is calculated. Considering the mixture R227ea/R245fa the maximal reduction is 43%. Again, not mole fractions with the most evident reduction of heat transfer characteristics lead to the highest heat transfer surface (see
Figure 13b). High total heat transfer surfaces for propane/isobutane and R227ea/R245fa occur for the most efficient mixture compositions. For these concentrations the ORC leads to a minimal reinjection temperature for the geothermal fluid and, therefore, a maximum for heat input to the ORC is obtained. Exemplarily, for the equimolar mixture R227ea/R245fa a higher amount of 29.0% thermal energy is transferred to the ORC compared to pure R245fa. As a consequence and taken into account the reduction of heat transfer characteristics, a 66.5% higher total heat transfer surface results. Local maxima for the total heat transfer surface can be observed for mole fractions, which lead to a good match of the temperature profiles in the condenser. In this context, 90 mol% R227ea could be mentioned exemplarily.
Figure 13.
(a) Reduction of the heat transfer coefficient at condensation and evaporation (pool boiling) for zeotropic mixtures depending on composition; (b) total heat transfer surface of the ORC power plant for a geothermal fluid temperature of 160 °C.
Figure 13.
(a) Reduction of the heat transfer coefficient at condensation and evaporation (pool boiling) for zeotropic mixtures depending on composition; (b) total heat transfer surface of the ORC power plant for a geothermal fluid temperature of 160 °C.
3.5. Economic Parameters
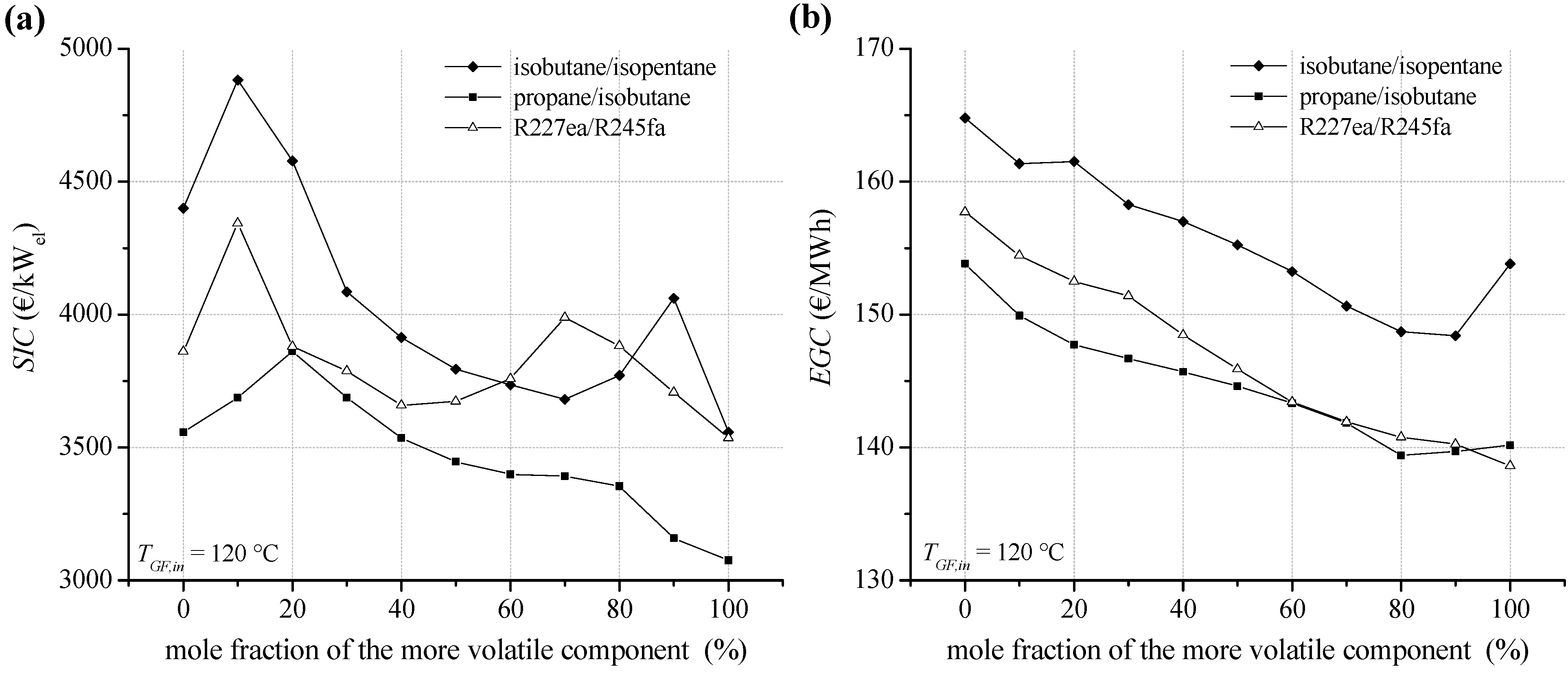
In the case of a heat source temperature of 120 °C,
SIC for the ORC module depending on mole fraction of the considered fluid mixtures are shown in
Figure 14a.
The total capital investment for an ORC system is determined according to Equation (15). In general,
PEC are dominated by costs for heat exchangers. In case of isobutane as a working fluid, 57.0% of the
PEC are costs for the preheater, evaporator, condenser and internal heat exchanger. A detailed overview for the
PEC of the major components depending on mixture composition of isobutane/isopentane is listed in
Table 7. For the considered pure media and fluid mixtures, the heat exchanger costs in relation to total
PEC are in the range of 54.1% and 59.8%. Therefore, working fluids showing a high total heat transfer surface lead to high
SIC. For the examined heat source temperature of 120 °C,
SIC range between 4,882 €/kW for isobutane/isopentane (90/10) and 3,076 €/kW in case of pure propane. The resulting costs for electricity generation (
EGC) are shown in
Figure 14b. Due to high drilling costs concerning the exploration of a geothermal resource, high
SIC could be overcompensated by an efficient ORC module. In case of the mixture isobutane/isopentane, a mole fraction of 90% isobutane leads to
EGC of 148.4 €/MWh. Compared to pure isobutane (153.8 €/MWh), 14% higher
SIC could be considerably overcompensated. Also, in case of the mixture propane/isobutane higher
SIC for a mole concentration of 80% propane are overcompensated compared to propane. However, R227ea leads to the lowest
EGC with 138.6 €/MWh.
Figure 14.
(a) Specific investment costs for the ORC power plant depending on mixture composition for a geothermal fluid temperature of 120 °C; (b) electricity generation costs.
Figure 14.
(a) Specific investment costs for the ORC power plant depending on mixture composition for a geothermal fluid temperature of 120 °C; (b) electricity generation costs.
Table 7.
PEC for the major components depending on mixture composition (isobutane/isopentane) at a geothermal fluid temperature of 120 °C.
Table 7.
PEC for the major components depending on mixture composition (isobutane/isopentane) at a geothermal fluid temperature of 120 °C.
| Parameter | 0/100 | 10/90 | 20/80 | 30/70 | 40/60 | 50/50 | 60/40 | 70/30 | 80/20 | 90/10 | 100/0 |
|---|
| CIR (k€) | 115.9 | 148.0 | 92.9 | 75.6 | 67.1 | 63.2 | 62.3 | 65.3 | 74.7 | 94.9 | 61.8 |
| CPHE (k€) | 52.6 | 51.5 | 55.3 | 54.4 | 55.4 | 56.8 | 59.1 | 60.9 | 64.1 | 67.5 | 70.4 |
| CEVP (k€) | 82.3 | 85.6 | 97.7 | 101.0 | 99.9 | 95.8 | 88.3 | 79.1 | 69.4 | 59.3 | 51.7 |
| CK (k€) | 427.3 | 573.5 | 511.9 | 397.7 | 361.9 | 343.6 | 344.7 | 349.3 | 388.1 | 472.3 | 309.5 |
| CT (k€) | 354.0 | 360.9 | 358.3 | 357.4 | 357.2 | 357.8 | 359.2 | 361.1 | 363.6 | 366.3 | 357.2 |
| CPump (k€) | 7.1 | 7.9 | 8.0 | 8.8 | 9.4 | 10.1 | 10.7 | 11.6 | 12.4 | 13.4 | 14.4 |
| Ctotal,ORC (k€) | 6568.4 | 7756.9 | 7105.4 | 6288.0 | 6010.2 | 5861.3 | 5841.9 | 5860.3 | 6145.1 | 6785.2 | 5467.5 |
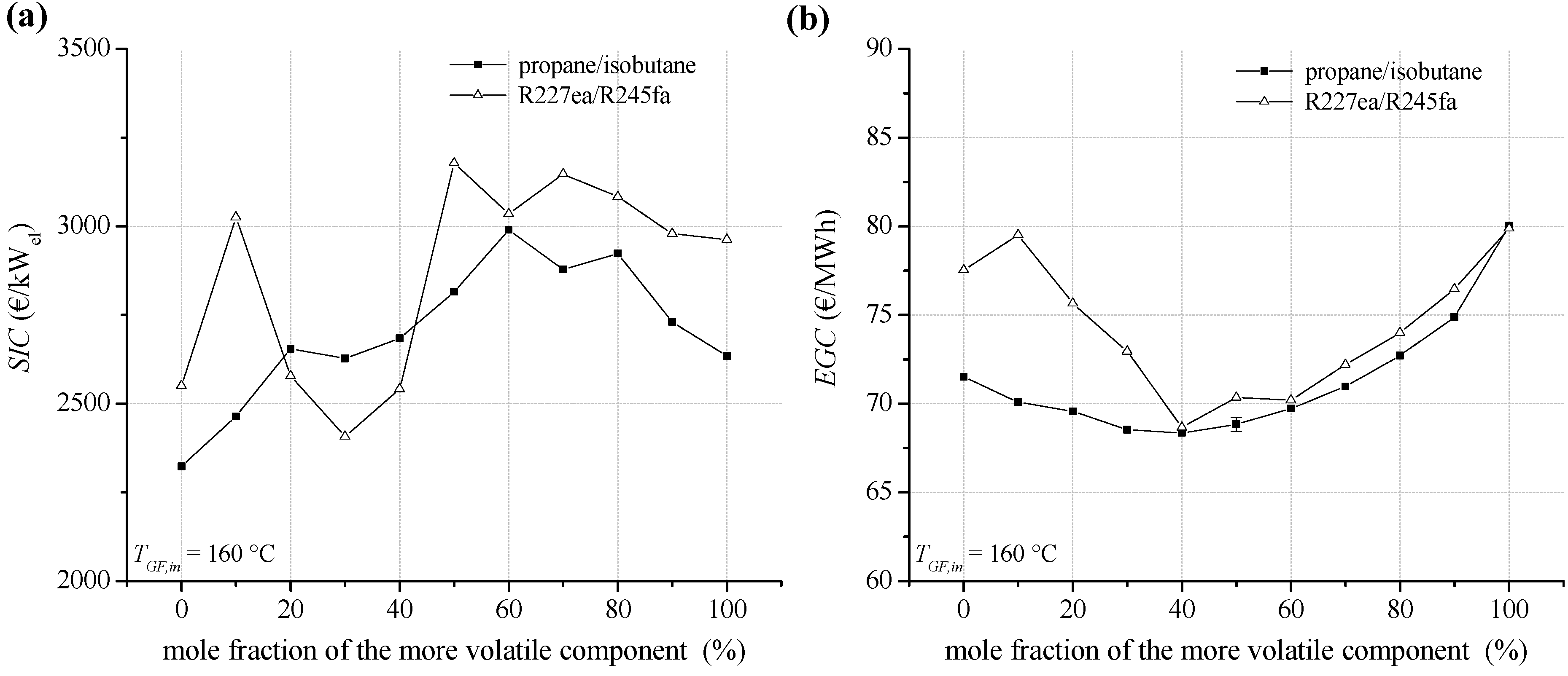
Regarding a heat source temperature of 160 °C,
SIC and
EGC are illustrated in
Figure 15a,b. Compared to lower heat source temperatures, the level and the bandwidth of
SIC are decreased. Compared to geothermal inlet temperature of 120 °C, the percentage of heat exchanger costs is even increased. For the considered working fluids 62.3% to 77.1% of the total
PEC are related to heat exchangers. For propane/isobutane
SIC range between 2,322 and 2,990 €/kW, in case of R227ea/R245fa between 2,407 €/kW and 3,147 €/kW. Considering
EGC, fluid mixtures as ORC working fluids lead to a significant improvement of economic conditions for geothermal power generation. Compared to the most cost-efficient pure component R245fa, a decrease of 10.0% for
EGC is determined in case of R227ea/R245fa (60/40). The lowest
EGC of 68.4 €/MWh are obtained for propane/isobutane. A mole fraction of 60% isobutane leads to a reduction of
EGC of 4.0% compared to propane. In general, the obtained
SIC are in a good agreement to the mentioned investigations [
40,
41,
42,
43].
Figure 15.
(a) Specific investment costs for the ORC power plant depending on mixture composition (b) electricity generation costs for a geothermal fluid temperature of 160 °C.
Figure 15.
(a) Specific investment costs for the ORC power plant depending on mixture composition (b) electricity generation costs for a geothermal fluid temperature of 160 °C.
In the context of the uncertainties of fluid properties, a sensitivity analysis is conducted for propane/isobutane (50/50). Based on the results of
Section 3.2Section 3.2, where a maximal mean deviation of 4.7% is obtained for VLE-data of R134a/R245fa, the relevant fluid properties for heat exchanger design like density, heat capacity or viscosity are varied within a range of −5% and +5%. In case of lower values (−5%) an increase of the total heat transfer surface of 3.4% results. This leads to a rise of SIC by 2.4% and finally EGC increase by 0.9% to 69.4 €/MWh. For 5% higher fluid properties, a reduction of
EGC by 0.8% results.
For further work, the implementation of a turbine model and pressure loss models for the heat exchangers would lead to a more comprehensive analysis. In addition, advanced heat exchanger design and alternative cost estimations models could be investigated. Furthermore, the adaption of the described methodology to alternative heat sources seems to be interesting due to differing temperature levels and exploitation costs. Finally, a validation and adaption of the considered heat transfer correlations for potential ORC working fluids would reduce additional uncertainties in heat exchanger design. In analogy, the measurement of fluid properties, especially for fluid mixtures, could lead to a more reliable heat exchanger design.