Microgrid Stability Controller Based on Adaptive Robust Total SMC

Abstract

This paper presents a microgrid stability controller (MSC) in order to provide existing distributed generation units (DGs) the additional functionality of working in islanding mode without changing their control strategies in grid-connected mode and to enhance the stability of the microgrid. Microgrid operating characteristics and mathematical models of the MSC indicate that the system is inherently nonlinear and time-variable. Therefore, this paper proposes an adaptive robust total sliding-mode control (ARTSMC) system for the MSC. It is proved that the ARTSMC system is insensitive to parametric uncertainties and external disturbances. The MSC provides fast dynamic response and robustness to the microgrid. When the system is operating in grid-connected mode, it is able to improve the controllability of the exchanged power between the microgrid and the utility grid, while smoothing the DGs’ output power. When the microgrid is operating in islanded mode, it provides voltage and frequency support, while guaranteeing seamless transition between the two operation modes. Simulation and experimental results show the effectiveness of the proposed approach.

1. Introduction

Features such as low investment, environmental friendliness, high reliability and flexibility make distributed generation (DG) systems an interesting and promising technological option [1,2,3]. As power systems are seeing an increasing DG penetration level, beside the aforementioned advantages, DG units may also bring problems to the utility grid like bidirectional power flow, voltage deviations, and voltage fluctuations. In this sense, a microgrid, which consists on a cluster of loads and parallel-connected DG units in a local area [4,5] is a suitable solution to problems caused by the high DG penetration, thus making possible large-scale DG penetration [6,7]. A microgrid can be connected to the utility grid at the point of common coupling (PCC), being able to flexibly import/export energy from/to the grid by controlling active and reactive power flows [8,9]. When there is a fault in the utility grid or during maintenance, according to IEEE standard 1547.4 [10], the microgrid must be disconnected from the utility grid, thus operating in islanded mode in order to guarantee the electrical power supply to the critical loads [11,12].

In general, the normal DG operation mode is performed connected to the grid, since in this case maximum produced power can be injected into the grid [13,14]. The control algorithms for grid-connected DGs have been developed and refined over the years [15,16]. Blaabjerg [17,18] presented an overview of different control and synchronization techniques for DG systems [19]. Different control strategies for DG systems under unbalanced condition are given in. Savaghebi, Castilla and Twining [20,21,22] proposed different controllers for DG systems to compensate harmonic components. Guerrero designed control schemes for parallel connected DGs [23,24,25], hierarchical control is discussed in [26,27]. Nowadays these control schemes are mature technologies that are available on the market. Therefore, a real microgrid plant often uses commercial DG systems and adds extra customized equipment to provide extra functionalities.

This paper proposes a “microgrid stability controller” (MSC) based on energy storage equipment, which provides islanding operation functionality to conventional DG systems without changing their grid-connected control strategies. In addition, in grid-connected mode, the MSC can smooth the exchanged power at the PCC, thus avoiding voltage fluctuations and other power quality issues in the main grid. This feature is important when prime movers are renewable energy sources which are characterized by having a stochastic and intermittent behavior.

The MSC is expected to operate with high efficiency, low output current total harmonics distortion, and sinusoidal output voltage with a specified frequency and amplitude in all operation modes. In addition to this requirement, the MSC must be robust against disturbances, having good voltage regulation and fast dynamic response. In that sense, many control techniques have been proposed for pulse width modulation (PWM) converters to achieve good dynamic response under different types of loads, including proportional-integral-derivative control, model-based linear control, robust control, and internal model principle based control [28,29,30]. However, uncertainties caused by the operation mode transitions and DG disturbances make the MSC a nonlinear, time-variable system. Therefore, it is difficult to reach ideal control objectives with conventional control techniques due to their multivariable structure and highly coupled nonlinearity of the system. Most of the conventional control techniques only guarantee the desired closed-loop response at the expected operating point, thus degrading their performances outside this point. Hence, it seems natural to explore other nonlinear controls that can overcome the uncertainties problem, and to achieve better compensation and global stability in large-signal sense [31].

For instance, sliding mode control (SMC) is one of the most effective nonlinear robust control approaches, since it provides to the system a dynamics with an invariance property to uncertainties once the system dynamics is controlled in the sliding mode [32,33,34,35,36]. Reference [37] applies the SMC scheme to a three-phase AC-to-DC voltage source boost converter to provide a constant level output voltage while keeping unity power factor. Reference [38] applies SMC in a single phase inverter and designs different control schemes in stand-alone and grid connected modes. Reference [39] uses SMC in the voltage control loop of a voltage-sourced rectifier, which provides quasi unity power factor operation, low harmonic content and fast dynamic response. While hysteretic control is applied in the current control loop, so that the switching frequency is variable, also named chattering.

In practical control systems, parameter variation, uncertainties, external disturbances and the limitation of detection make it difficult to acquire an accurate mathematical model. Consequently, the traditional SMC can hardly achieve outstanding results. Therefore, this work proposes an adaptive robust total sliding-mode control (ARTSMC) system for the MSC, which colligates the advantages of adaptive control and SMC. The total sliding surface eliminates the control error and gets a sliding motion through the whole state trajectory [40,41]. Furthermore, the use of PWM avoids variable switching frequency.

This paper is organized as follows: in Section 2 the configuration of a microgrid including the proposed MSC is presented. In Section 3 the model of the proposed MSC is derived for the system operating in both islanded and grid-connected modes. Section 4 presents the ARTSMC system for both voltage control and current control used in islanded and grid-connected modes respectively. Section 5 validates the proposed approach by means of simulation results, and Section 6 present the experimental results extracted by an AERTSMC-controlled MSC of 3 kVA. Finally, Section 7 concludes the paper.

2. Proposed MSC-Based Microgrid

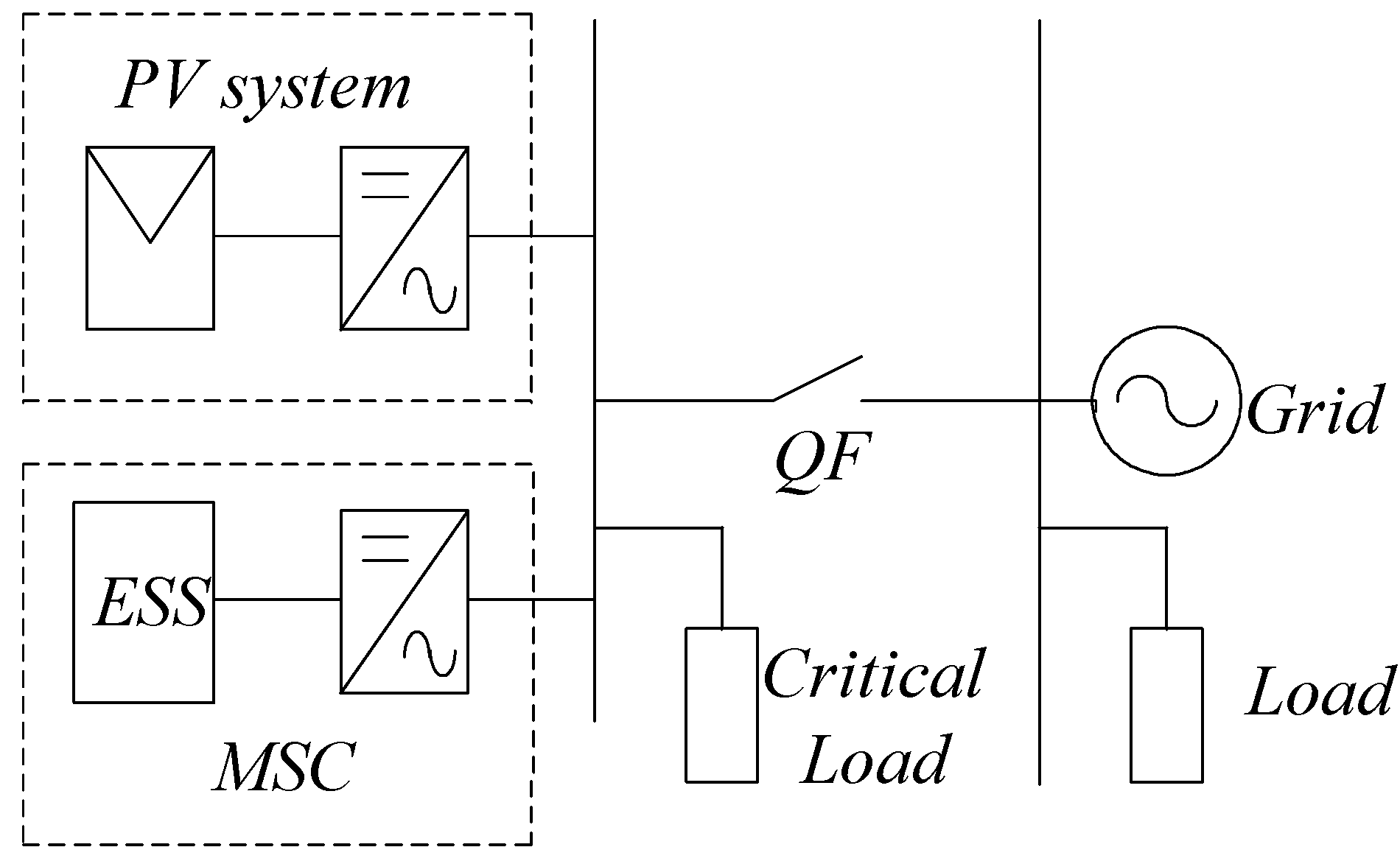
Figure 1 shows the circuit topology of a microgrid including a photovoltaic (PV)-based DG unit and critical loads connected to an AC bus. The microgrid is connected to the electrical distribution network through a circuit breaker QF. The MSC, which consists of an energy storage system, a bidirectional DC-to-AC converter with an inductor-capacitor (LC) filter, is connected to the AC bus together with the DG unit and the critical load inside the microgrid.

Figure 1. Microgrid including the proposed MSC.

Figure 1. Microgrid including the proposed MSC.

As the MSC is based on an energy storage system (ESS) and full controlled converter, it can flexibly import/export power from/to the grid. When the microgrid operates in grid-connected mode, the MSC can compensate the power variations or reduce the power fluctuations caused by the DG unit or the critical loads inside the microgrid. When the microgrid is disconnected from the main grid, thus operating in islanded mode, the MSC fixes the microgrid output voltage and frequency, which are the references to be used by the DG. Note that when the microgrid operates in islanded mode, it is a weak AC power system, consequently, the DG output power variations or load disturbances are more likely to cause voltage fluctuations or voltage sags. These problems may enforce DG units and/or sensitive load disconnection from the AC line. Therefore, it is necessary to use the MSC to balance active and reactive in the microgrid in order to maintain voltage and power quality.

3. MSC Modeling

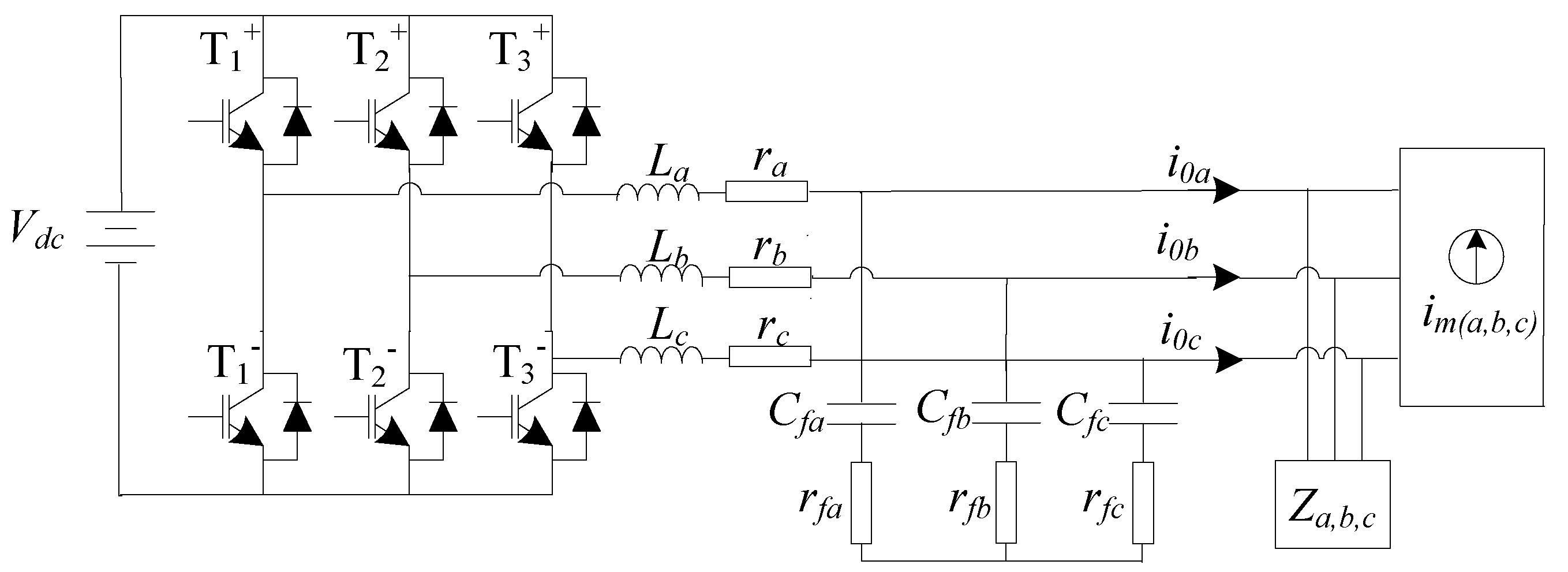
Figure 2 shows the power stage of the MSC when the microgrid operates in islanded mode. In this figure, v_0a, v_0b, v_0c are the AC bus voltages (per phase) and i_0a, i_0b, i_0c are the AC currents (per phase) of the MSC; L_a, L_b, L_c and C_fa, C_fb, C_fc are the filter inductor and capacitor values, respectively; r_a, r_b, r_c represent the equivalent series resistor (ESR) of the converter, inductor, and power line; r_fa, r_fb, r_fc represent the ESR of the filter capacitor; and i_ma, i_mb, i_mc represent the aforementioned disturbances in the microgrid.

Figure 2. Power stage of the MSC.

Figure 2. Power stage of the MSC.

The states of the switches of the n-th leg (n = 1, 2, 3) can be represented by the time-dependent variable S_n, defined as:

$$S_n=\{\begin{array}{c}1\to if {T_n}^{+} is on and {T_n}^{-} is off\\ 0\to if {T_n}^{\text{-}} is on and {T_n}^{+} is off\end{array}$$

(1)

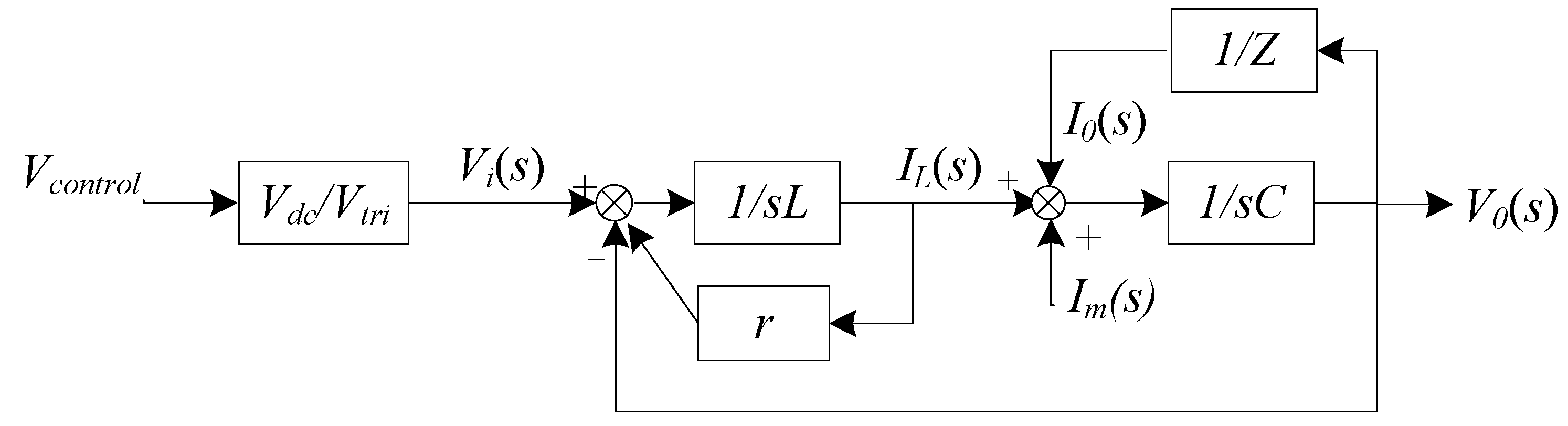
This switching strategy, together with a small dead-time generator, will avoid internal shorts between the two switches of each bridge leg, as the switches will always be in complementary states. Assuming that the switching frequency is high enough compared to the modulation and natural frequencies, the equivalent dynamic model of Figure 2 can be obtained as shown in Figure 3, where s is the Laplace operator, the power gain can be defined as k_PWM = V_d/v_tri, and v_tri is the amplitude of a triangular carrier signal.

Figure 3. Equivalent dynamic model.

Figure 3. Equivalent dynamic model.

3.1. System Modeling in Islanding Mode

When the microgrid operates in islanded mode, the dynamic Equation of the MSC during the positive-half period can be represented as:

$${\dot{X}}_k=A_k{X}_k+B_k{U}_k+D_k{I}_0{}_k+F_k{I}_m{}_k$$

(2)

where ${\dot{X}}_k={\left[\begin{array}{cc}{\dot{v}}_{0k}& {\ddot{v}}_{0k}\end{array}\right]}^T$, $A_k=\left[\begin{array}{cc}0& 1\\ \frac{-1}{L_k{C}_{fk}}& \frac{-r_k}{L_k}\end{array}\right]$, $X_k={\left[\begin{array}{cc}{v}_{0k}& {\dot{v}}_{0k}\end{array}\right]}^{\mathrm{T}}$, $B_k={\left[\begin{array}{cc}0& \frac{k_{PWM}}{L_k{C}_{fk}}\end{array}\right]}^T$, $U_k=\left[u_{control1k}\right]$, $D_k=\left[\begin{array}{cc}0& 0\\ \frac{-r_k}{L_k{C}_{fk}}& \frac{-1}{C_{fk}}\end{array}\right]$, $I_{0k}={\left[\begin{array}{cc}{i}_{0k}& {\dot{i}}_{0k}\end{array}\right]}^T$, $F_k=\left[\begin{array}{cc}0& 0\\ \frac{r_k}{L_k{C}_{fk}}& \frac{1}{C_{fk}}\end{array}\right]$, $I_{mk}={\left[\begin{array}{cc}{i}_{mk}& {\dot{i}}_{mk}\end{array}\right]}^T$, v_control1k is the control signal, k = a, b, c.

According to the aforementioned discussion, the microgrid is a nonlinear, time-variable system and there are uncertainties in the MSC system, which are caused by parametric variations or external disturbances. Therefore, Equation (2) should be modified as follows:

$${\dot{X}}_k=(A_k+\Delta A_k)X_k+(B_k+\Delta B_k)U_k+(D_k+\Delta D_k)I_0{}_k+F_k{I}_{mk}$$

(3)

∆A_k, ∆B_k, ∆D_k represent the system parameter variations and they satisfy the matching condition which is ∆A_k = B_kG_k, ∆B_k = B_kH_k, ∆D_k = B_kJ_k, F_kI_mk = B_kK_k. In order to analyze conveniently, define:

$$W_k=G_k{X}_k+H_k{U}_k+J_k{I}_0{}_k+F_k{I}_{mk}$$

(4)

Thus, rearranging Equation (4) as:

$${\dot{X}}_k=A_k{X}_k+D_k{I}_0{}_k+B_k(U_k+W_k)$$

(5)

The bound of the uncertainty is assumed to meet the following inequality:

$$\Vert W_k\Vert \le q_{1k}+q_{2k}\Vert e_k\Vert$$

(6)

where q_1k and q_2k are unknown positive constants and e_k is the voltage control error, which is defined as:

$$e_k=\left[\begin{array}{c}{v}_{0k}-v_{refk}\\ {\dot{v}}_{0k}-{\dot{v}}_{refk}\end{array}\right]=\left[\begin{array}{c}{e}_{vk}\\ {\dot{e}}_{vk}\end{array}\right]$$

(7)

where v_refk is the output voltage reference, which is set to the nominal value.

3.2. System Modeling in Grid-Connected Mode

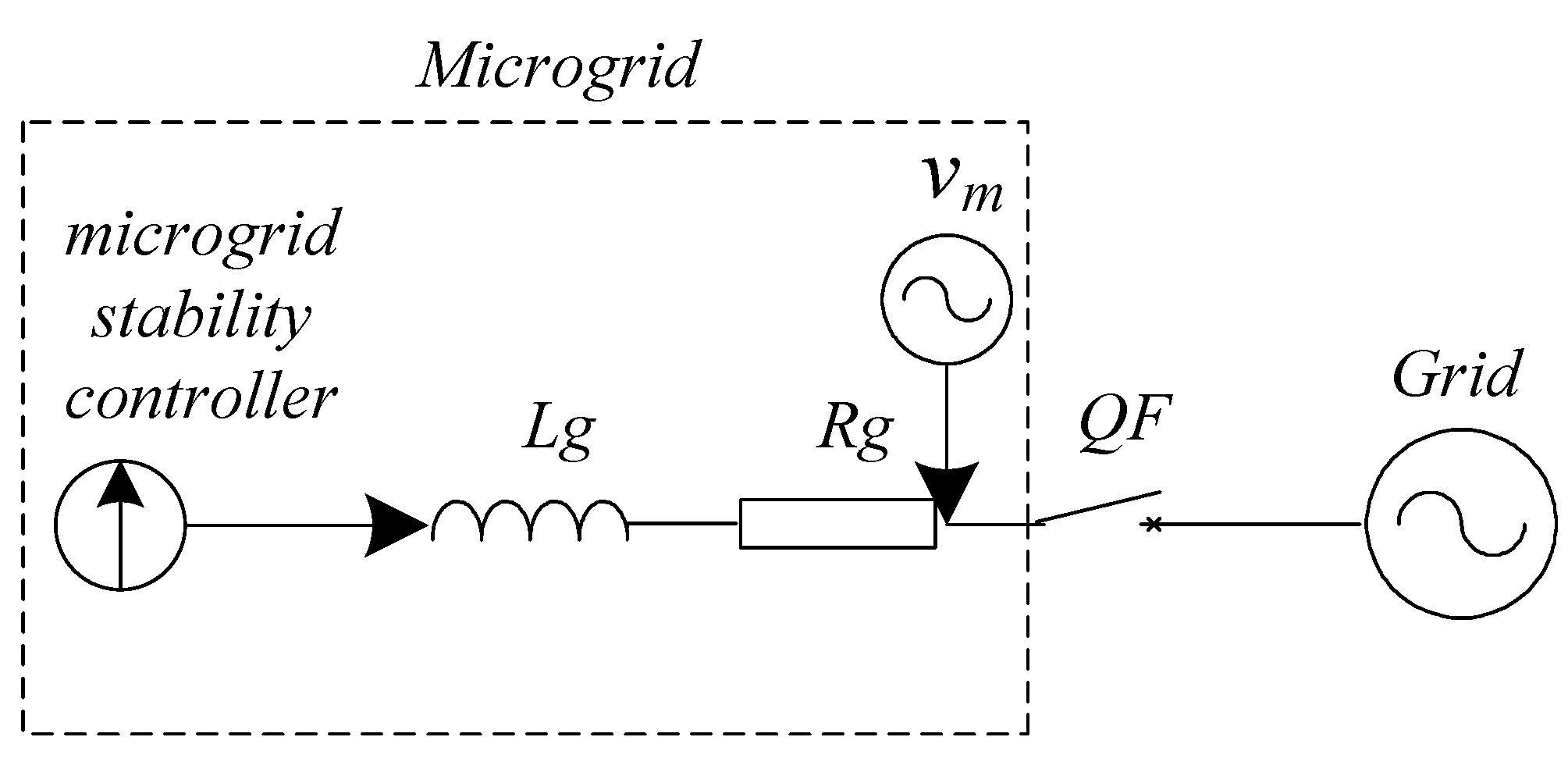
When the microgrid operates in grid-connected mode, it is connected to the utility grid through QF as shown in Figure 4.

Figure 4. Block diagram of the grid-connected microgrid.

Figure 4. Block diagram of the grid-connected microgrid.

In order to provide the desired power to the grid, we propose use the MSC to compensate power variations and to reduce power fluctuations caused by the DGs and/or loads in the microgrid. The dynamic Equation of the MSC during the positive-half period is represented as:

$$L_g{\dot{i}}_0=k_{PWM}{u}_{control2}-R_g{i}_0-v_0-v_m$$

(8)

Equation (8) can be rearranged as follows:

$${\dot{i}}_0=-\frac{R_g}{L_g}{i}_0\text{+}\frac{k_{PWM}}{L_g}{u}_{control2}\text{+}\frac{1}{L_g}{v}_0\text{+}\frac{1}{L_g}{v}_m$$

(9)

where L_g = diag(L_ga, L_gb, L_gc), i₀ = diag(i_0a, i_0b, i_0c), R_g = diag(R_ga, R_gb, R_gc), ${\stackrel{·}{i}}_0=diag({\stackrel{·}{i}}_{0a} {\stackrel{·}{i}}_{0b} {\stackrel{·}{i}}_{0c})$, v₀ = diag(v_0a, v_0b, v_0c), v_m = diag(v_ma, v_mb, v_mc), being u_control2 = diag(u_control2a, u_control2b, u_control2c) the control signal; L_ga, L_gb, L_gc and R_ga, R_gb, R_gc represent inductors and their respective ESRs; v_0a, v_0b, v_0c and i_0a, i_0b, i_0c are the AC voltage and current (per phase) respectively; and v_ma, v_mb, v_mc represent disturbances or uncertainties in the microgrid. Equation (9) can be rearranged as:

$${\dot{i}}_0=a{i}_0\text{+}b{u}_{control2}\text{+}c{v}_0\text{+}c{v}_m$$

(10)

where a = diag(−R_ga/L_ga, −R_gb/L_gb, −R_gc/L_gc), b = diag(k_PWM/L_ga, k_PWM/L_gb, k_PWM/L_gc), c = diag(−1/L_ga, −1/L_gb, −1/L_gc). Due to the parametric variations or external disturbances, Equation (10) should be modified as:

$${\dot{i}}_0=(a+\Delta a)i_0+(b+\Delta b)u_{control2}+(c+\Delta c)v_0+\frac{1}{L_g}{v}_m$$

(11)

∆a, ∆b, ∆c represent the system parameter variations and they satisfy the matching condition which is ∆a = bf, ∆b = bm, ∆c = bn, v_m/L_g = bg. In order to analyze conveniently, define:

$$w=f{i}_0+m{u}_{control2}+n{v}_0+g$$

(12)

where w is the uncertainty. Therefore Equation (11) is modified as:

$${\dot{i}}_0=a{i}_0+c{v}_0+b(u_{control2}+w)$$

(13)

The bound of the uncertainty is assumed to meet the following inequality:

$$\left|w\right|\le q$$

(14)

Being q = diag(q_a, q_b,q _c) an unknown positive constant.

4. ARTSMC System

The proposed ARTSMC is insensitive to parametric uncertainties and external disturbances. The total sliding surface ensures stability and robustness through the entire state trajectory. Hence, the system dynamics in the reaching phase is not influenced by uncertainties. The control law encompasses a state feedback term, a robust control term, and an adaptive compensation term. The state feedback term takes advantage of the pole assignment and state feedback, while simplifying the sliding surface design. The robust control term decides the basic structure of the uncertain nonlinear system. Uncertainties in the MSC system do not have a fixed value, so that it is difficult and impractical to measure real-time uncertainties. Thus, a logical solution is to apply an adaptive strategy. Instead of fixing a boundary of uncertainties, an adaptive compensation term is introduced in order to adjust the uncertainties in real-time. According to the difference between the nominal nonlinear system and the uncertain nonlinear system, the sliding surface and other parameters compose the adaptive law which satisfies the global Lyapunov stability condition.

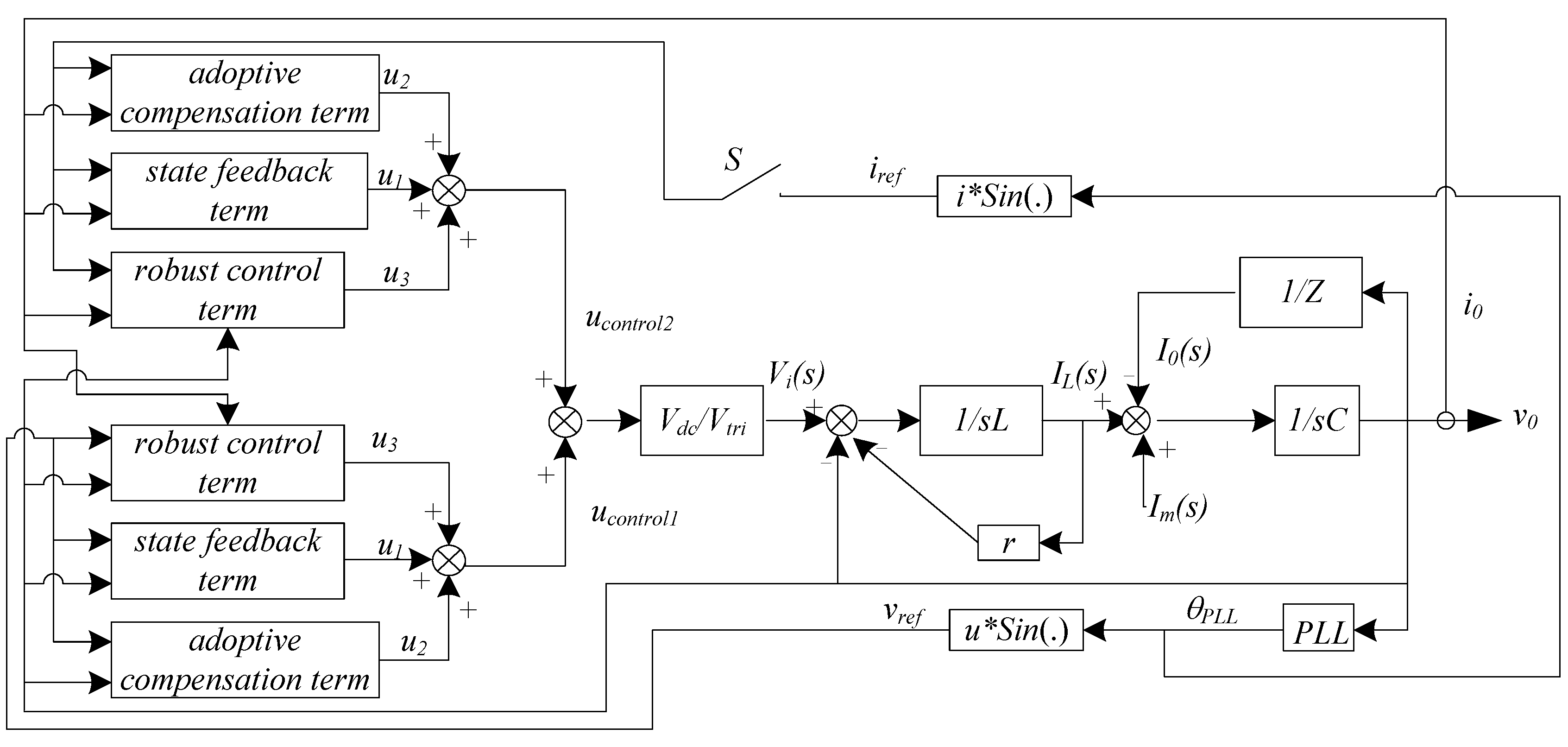
The proposed ARTSMC system is divided into two main parts, as illustrated in Figure 5. The first part is the ARTSMC based voltage control loop, which produces the control signals u_control1a, u_control1b and u_control1c. The second part is the ARTSMC based current control loop, which produces the control signals u_control2a, u_control2b, and u_control2c. When the microgrid operates in grid-connected mode, the current control loop determines the output power of the MSC by controlling its output current. In this scenario, its output voltage v_0a, v_0b, and v_0c is equal to the grid voltage (v_ga, v_gb, v_gc), which is assumed to be the nominal value, meaning that v_0a, v_0b, v_0c equal to v_refa, v_refb, v_refc, thus the voltage control loop is automatically disabled. When the microgrid operates in islanded mode, the voltage control loop enforces the output voltage of the MSC to track the reference value v_refa, v_refb, v_refc and to keep the microgrid voltage constant. The output power of the MSC is determined by the power balance among DGs, loads, and losses in the microgrid. Under this circumstance, the current control loop is not necessary and therefore the switch S is open.

Figure 5. Block diagram of the MSC model and its ARTSMC.

Figure 5. Block diagram of the MSC model and its ARTSMC.

4.1. ARTSMC Based Current Control Loop

The main task of the ARTSMC-based current control loop is to control the output power of the MSC by regulating its AC current. Specifically, it has to enforce i_0a, i_0b, i_0c to track the output current reference i_refa, i_refb, i_refc. Thus, a PLL structure is applied in order to generate the output current reference i_refa, i_refb, i_refc, to achieve unity power factor. It is important to notice that the power factor can be adjusted by modifying θ_PLL. The current control loop is synthesized as follows. The first step is to define a sliding surface [35,36]:

$$s=e_i-e_{i0}-{\displaystyle {\int }_0^t(a-\text{β}b)e_{i}ds}$$

(15)

where e_i = diag(i_0a−i_refa, i_0b−i_refb, i_0c−i_refc), s = diag(s_a, s_b, s_c) and β is the state feedback coefficient. e_io is the initial state of e_i. The second step is to design the control to enforce the system state trajectories to go toward the sliding surface (15) and to stay on it:

$$u_{control2}=u_1+u_2+u_3$$

(16)

where:

$$u_1=-\text{β}{e}_i$$

(17)

$$u_2=-b^{-1}(a{i}_{ref}+c{v}_0+{\dot{i}}_{ref}+\text{ε}sign(s))$$

(18)

$$u_3=-bs\cdot abs{\left(bs\right)}^{-1}\widehat{q}$$

(19)

Being u₁ the state feedback term, u₂ the robust control term, and u₃ the adaptive compensation term; ε is a small positive constant number; sign(s) = diag(sign(s_a), sign(s_b), sign(s_b)) and sign(·) is the sign function; abs(·) is the absolute value function; $\widehat{q}$ is the estimated value of q; the parameter deviation is defined as $\tilde{q}=\widehat{q}-q$; and the adaptive law is:

$$\dot{\widehat{q}}=abs\left(bs\right)$$

(20)

Proof: The existence condition of the sliding mode can be derived by using Lyapunov stability analysis, by consider the Lyapunov function candidate as:

$$V=\frac{s^2+{\tilde{q}}^2}{2}$$

(21)

$$\dot{V}=s\dot{s}+\tilde{q}\dot{\tilde{q}}$$

(22)

By taking the derivative of Equation (15) along Equation (13) and substituting Equation (16) and Equation (20) into Equation (22), it yields:

$$\dot{V}=s(b{u}_3+w-\epsilon sign(s))+\tilde{q}\dot{\tilde{q}}\le \epsilon \cdot abs(s)$$

Therefore, $\dot{V}<0$, when $abs(s)\ne 0$. It implies that the asymptotically stable behavior for the sliding mode system on the sliding surface (15) can be ensured.

Once the system trajectory reaches the sliding surface, $s=\stackrel{·}{s}=0$:

$$\dot{s}=a{i}_{ref}+b{u}_{control2}+c{v}_0-{\dot{i}}_{ref}+w+\text{β}b{e}_i=0$$

(23)

Then, the equivalent control can be obtained from the following equation:

$$u_{eq}=-b^{-1}(a{i}_{ref}+c{v}_0-{\dot{i}}_{ref}+w+\text{β}b{e}_i)$$

(24)

By substituting Equation (24) into Equation (13), it yields:

$${\dot{e}}_i=(a-\text{β}b)e_i$$

(25)

It implies that by properly selecting the state feedback coefficient β, the robustness of sliding mode (25) can be guaranteed, and the main dynamics features of the MSC such as rising time and maximum overshoot can easily be designed.

4.2. ARTSMC Based for Voltage Control Loop

The main function of the ARTSMC-based voltage control loop is to force the MSC output voltage to track its reference value v_refa, v_refb, v_refc, thus keeping the microgrid voltage constant when the microgrid operates in islanded mode. In order to eliminate the control error and to get a sliding motion through the entire state trajectory, let us define a sliding surface as:

$$s_{uk}=C{e}_k-C{e}_{k0}-C{\displaystyle {\int }_0^t(A_k-B_k\beta )e_{k}ds}$$

(26)

where C is a full rank constant matrix, CB is nonsingular, and β is state feedback control coefficient matrix, e_ko is the initial value of e_k. The system state trajectories are forced toward the sliding surface (26) and stay on it, by designing the control scheme as follows such that:

$$u_{control1k}=u_{1k}+u_{2k}+u_{3k}$$

(27)

where:

$$u_{1k}=-\beta e_k$$

(28)

$$u_{2k}=-{(C{B}_k)}^{-1}(C{A}_k{X}_{rk}-C{\dot{X}}_{rk}+C{D}_k{I}_{0k}+\text{ε}sign(s_{uk}))$$

(29)

$$u_{3k}=-({B_k}^T{C}^T{s}_{uk}){\Vert {s_{uk}}^{T}C{B}_k\Vert }^{-1}({\widehat{q}}_{1k}+{\widehat{q}}_{2k}\Vert e_k\Vert )$$

(30)

where u_1k is the state feedback term, u_2k is the robust control term, u_3k is the adaptive compensation term; $X_{rk}={\left[\begin{array}{cc}{v}_{refk}& {\dot{v}}_{refk}\end{array}\right]}^{\mathrm{T}}$; ε is a small positive constant and sign(·) is the sign function; ${\widehat{q}}_{1k}$, ${\widehat{q}}_{2k}$ are estimated values of $q_{1k}$, $q_{2k}$. The parameter deviations are ${\tilde{q}}_{1k}={\widehat{q}}_{1k}-q_{1k}$, ${\tilde{q}}_{2k}={\widehat{q}}_{2k}-q_{2k}$. Choose adaptive law as:

$${\dot{\widehat{q}}}_{1k}=\Vert s_{uk}{}^{T}C{B}_k\Vert \text{,} {\dot{\widehat{q}}}_{2k}=\Vert s_{uk}{}^{T}C{B}_k\Vert \cdot \Vert e_k\Vert$$

Proof: By considering a Lyapunov function candidate as:

$$V_k=\frac{{s_{uk}}^T{s}_{uk}+{{\tilde{q}}_{1k}}^2+{{\tilde{q}}_{2k}}^2}{2}$$

(31)

Taking the derivative of Equation (31):

$$\begin{array}{l}{\dot{V}}_k={s_{uk}}^T{\dot{s}}_{uk}+{\tilde{q}}_{1k}{\dot{\tilde{q}}}_{1k}+{\tilde{q}}_{2k}{\dot{\tilde{q}}}_{2k}\\ ={s_{uk}}^T(C{B}_k{W}_k-\text{ε}sign(s_{uk})+C{B}_k{u}_{3k})+{\tilde{q}}_{1k}{\dot{\tilde{q}}}_{1k}+{\tilde{q}}_{2k}{\dot{\tilde{q}}}_{2k}\\ ={s_{uk}}^T(C{B}_k{W}_k-\text{ε}sign(s_{uk}))-\Vert {s_{uk}}^{T}C{B}_k\Vert (q_{1k}+q_{2k}\Vert e_k\Vert )\end{array}$$

(32)

Substituting Equation (27) into (32), it yields:

$${\dot{V}}_k\le -\text{ε}\Vert s_{uk}\Vert$$

$$\text{Therefore}{\dot{V}}_k<0,\text{when}\Vert s_{uk}\Vert \ne 0$$

Consequently, the asymptotically stable behavior for the sliding mode system on the sliding surface (26) can be guaranteed.

Once the system trajectory reaches the sliding surface:

$$s{}_{uk}={\dot{s}}_{uk}=0$$

$${\dot{s}}_{uk}=C{A}_k{X}_{rk}-C{\dot{X}}_{rk}+C{D}_k{I}_{0k}+C{B}_k{U}_k+C{B}_k{W}_k+C{B}_k\beta e_k=0$$

(33)

Therefore, the equivalent control can be obtained from Equation (34) which is:

$$U_{eqk}=-{(C{B}_k)}^{-1}(C{A}_k{X}_{rk}-C{\dot{X}}_{rk}+C{D}_k{I}_{0k}+C{B}_k{W}_k+C{B}_k\beta e_k)$$

(34)

Substituting Equation (34) into Equation (5), it yields:

$${\dot{e}}_k=A_k{e}_k-B_k\beta e_k=(A_k-B_k\beta )e_k$$

(35)

This implies that with a properly designed state feedback coefficient β, the robustness of sliding mode (35) can be determined. The strictly logical and rigorous proof illustrates the ARTSMC system is insensitive to parametric uncertainties and external disturbances.

5. Simulation Results

A simulation platform under PSCAD/EMTDC environment is developed based on Figure 1 to study the performance of the MSC and to verify the proposed ARTSMC system. Table 1 shows the electrical parameters of MSC under study. The AC output voltage reference v_ref is set to 220 V at 50 Hz, and the AC output current reference i_ref is set according to the desired power exchange value at the PCC. Based on the sliding surfaces (15) and (26), the state feedback coefficients are designed to guarantee the robustness of the sliding modes (25) and (35), while determining the control performance and system stability, the parameters are given as: β = 30, β = [0.00270]. The DG_PV system in Figure 1 is connected to the same AC bus with the MSC through a DC-to-AC inverter, which is in phase with the grid voltage, and injecting power to the microgrid.

Table 1. Parameters of the MSC.

Parameter	Value
DC voltage (Energy storage equipment)	800 V
filter capacitance	3 μF
filter inductance	1.5 mH
output voltage (RMS) (phase)	220 V
output frequency	50 Hz

Table 1. Parameters of the MSC.

Parameter	Value
DC voltage (Energy storage equipment)	800 V
filter capacitance	3 μF
filter inductance	1.5 mH
output voltage (RMS) (phase)	220 V
output frequency	50 Hz

The microgrid operates in grid-connected mode and delivers 30 kW to the power grid. The output power of DG_PV is set to 40 kW and the critical load inside the microgrid is 30 kW. At 0.5 s, the output power of DG_PV increases to 50 kW and at 1 s the microgrid disconnects from the utility, thus operating in islanded mode. At 1.5 s the output power of DG_PV decreases to 20 kW, and at 1.75 s the 30 kW critical load is connected to the microgrid.

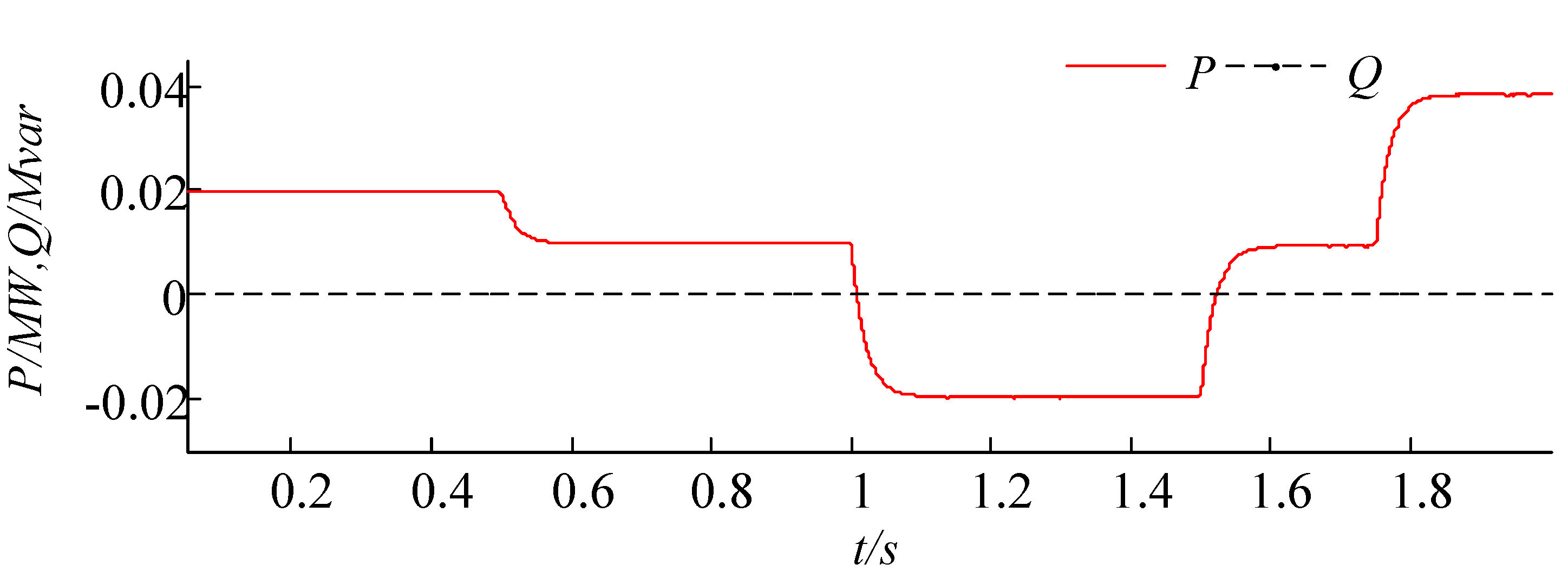
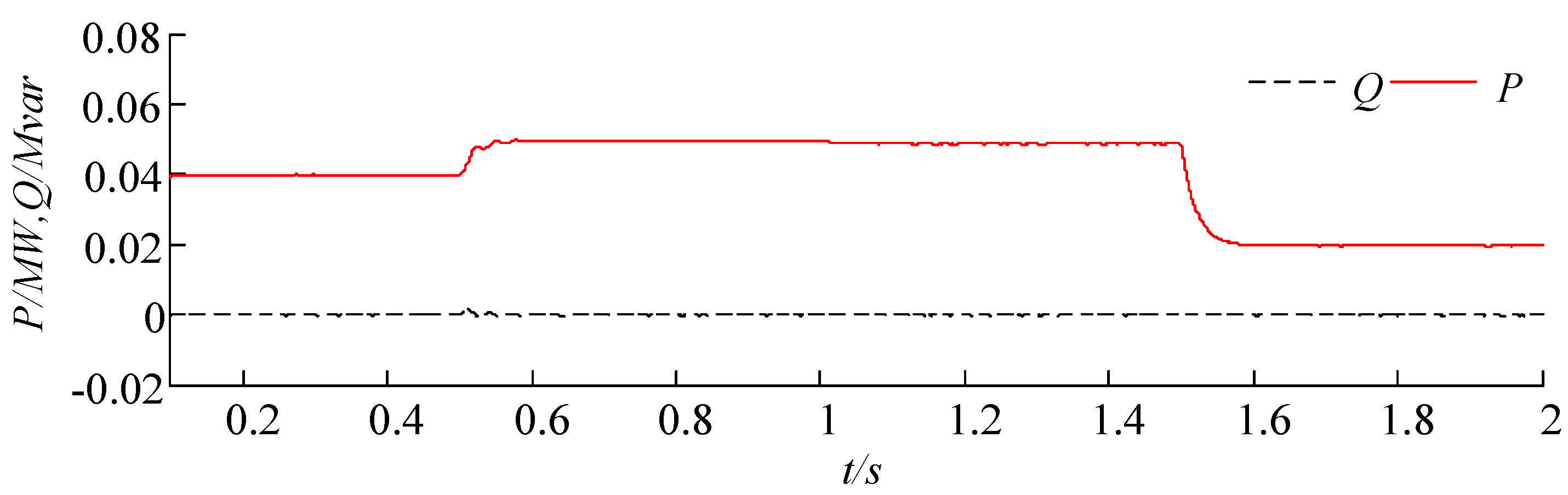
Figure 6 presents output power of the MSC, which is 20 kW at the beginning, and then it goes down to 10 kW at 0.5 s. The MSC switches to charge mode at 1 s as there is 20 kW excess of power when the microgrid operates in islanded mode from 1 s. When the output power of DG_PV decreases to 20 kW at 1.5 s, the MSC starts injecting 10 kW of active power to the microgrid, and its output power raise to 40 kW as the critical load in the microgrid increases to 60 kW at 1.75 s, while the output power of the DG_PV remains constant.

Output active and reactive powers of the MSC.

Figure 6. Output active and reactive powers of the MSC.

Figure 6. Output active and reactive powers of the MSC.

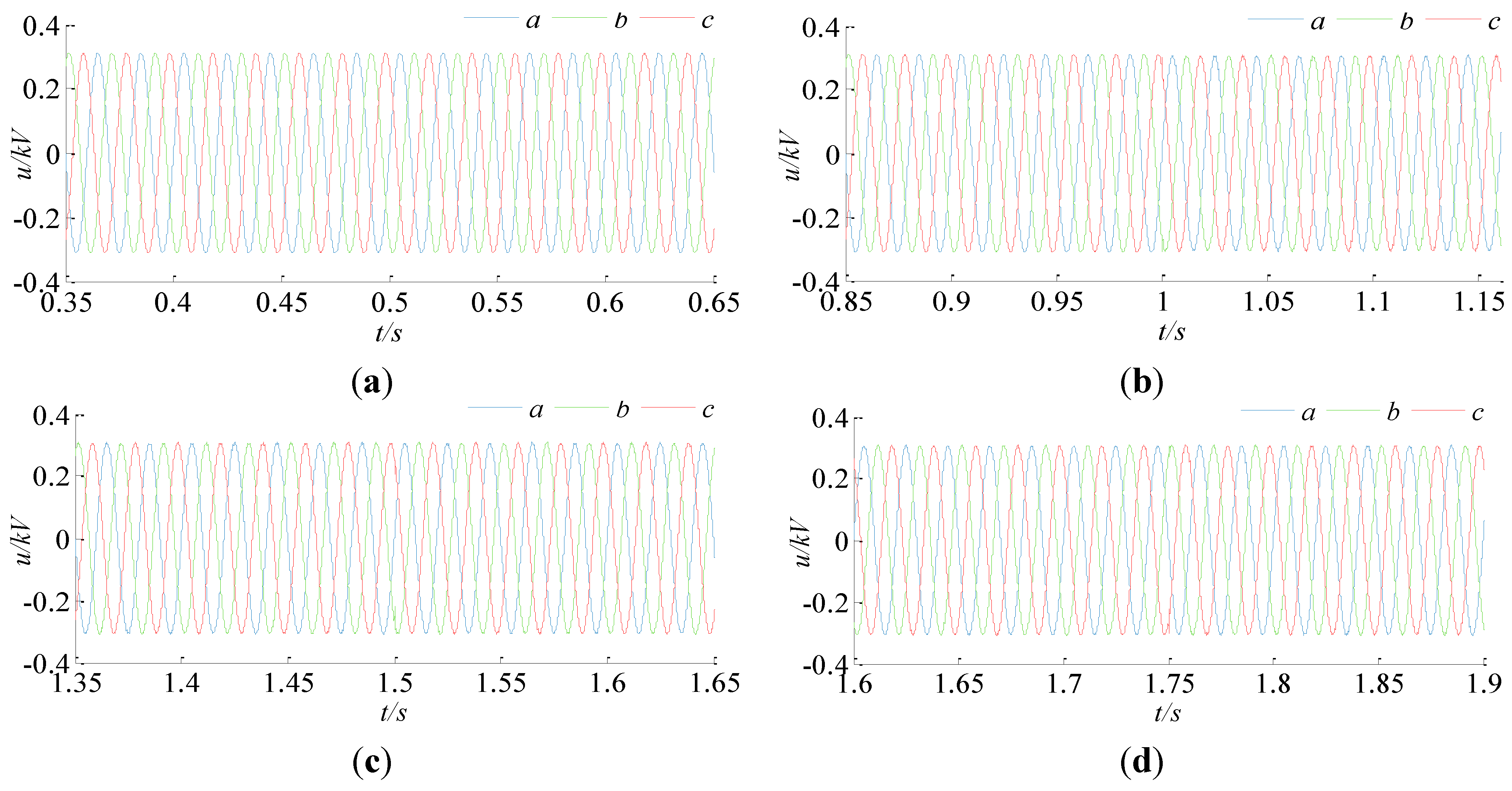
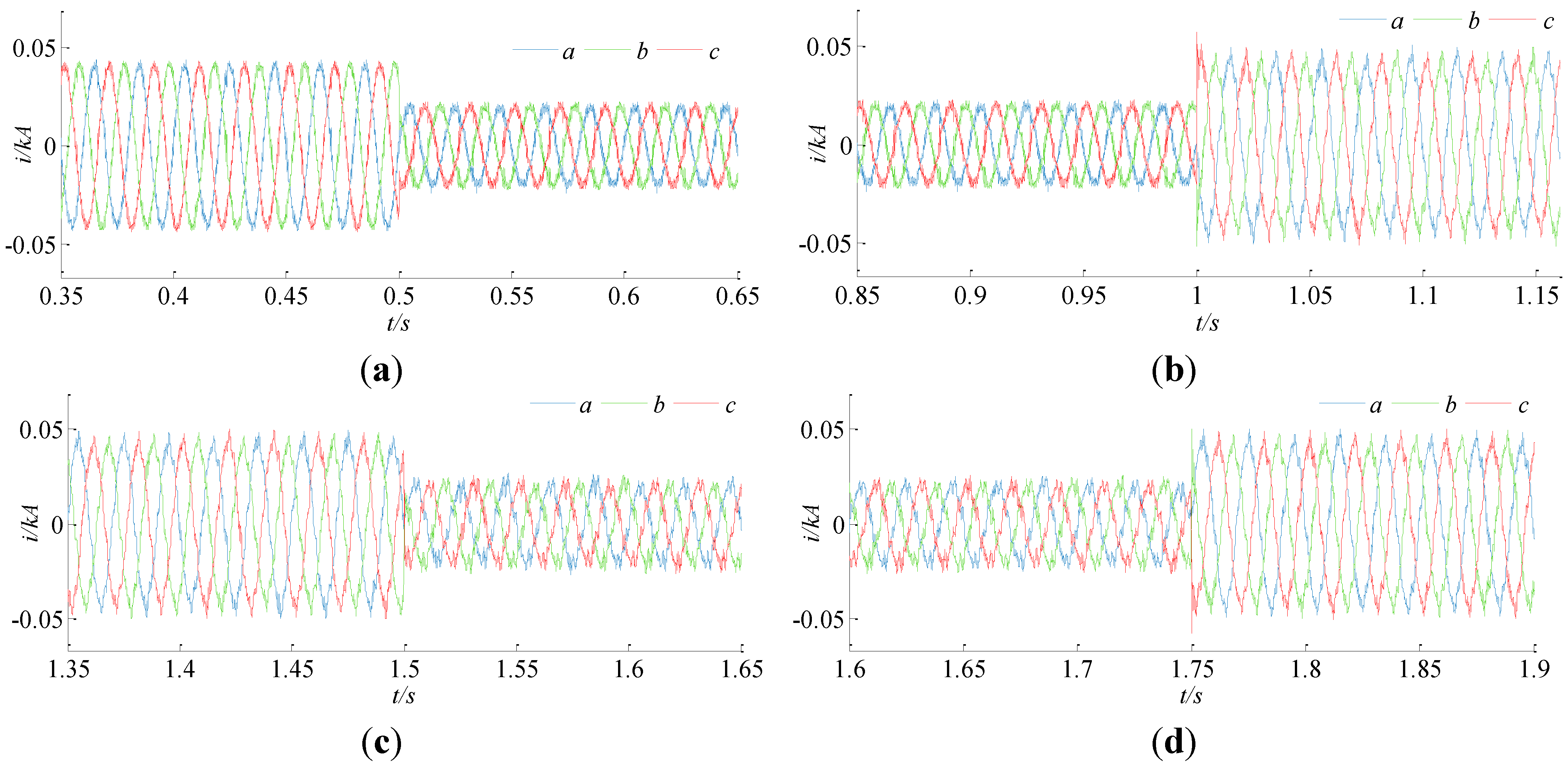
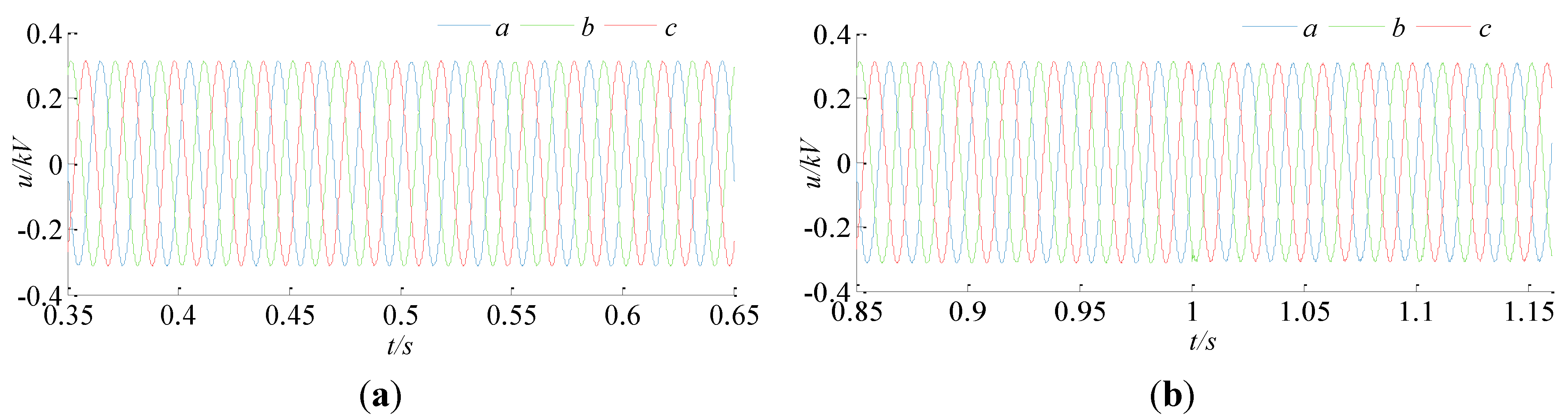
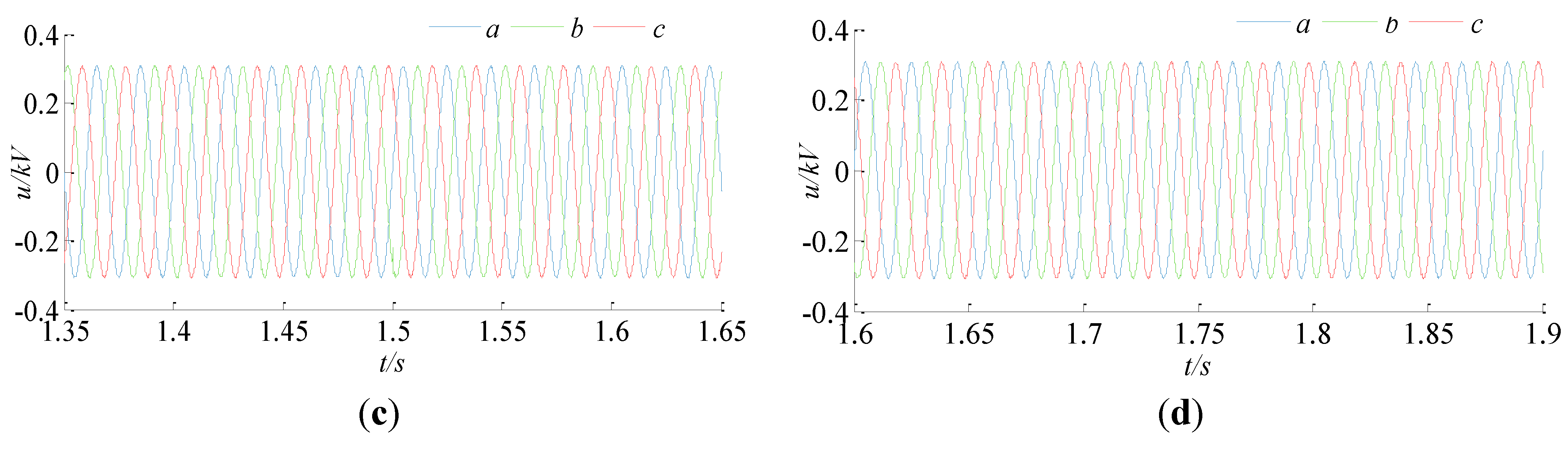
The voltage and current waveforms of the MSC at its AC side are shown in Figure 7 and Figure 8. The output current of the MSC does not have any inrush spikes during the entire transition period. Furthermore, there is no voltage perturbation along the operation. Due to the parallel connection of the MSC, the critical load and the DG_PV, the microgrid voltage remains stable in all situations.

Figure 7. (a) Voltage waveform of the MSC between 0.35 s and 0.65 s; (b) Voltage waveforms of the MSC between 0.85 s and 1.15 s; (c) Voltage waveforms of the MSC between 1.35 s and 1.65 s; (d) Voltage waveforms of the MSC between 1.6 s and 1.9 s.

Figure 7. (a) Voltage waveform of the MSC between 0.35 s and 0.65 s; (b) Voltage waveforms of the MSC between 0.85 s and 1.15 s; (c) Voltage waveforms of the MSC between 1.35 s and 1.65 s; (d) Voltage waveforms of the MSC between 1.6 s and 1.9 s.

Figure 8. (a) Current waveforms of the MSC between 0.35 s and 0.65 s; (b) Current waveforms of the MSC between 0.85 s and 1.15 s; (c) Current waveforms of the MSC between 1.35 s and 1.65 s; (d) Current waveforms of the MSC between 1.6 s and 1.9 s.

Figure 8. (a) Current waveforms of the MSC between 0.35 s and 0.65 s; (b) Current waveforms of the MSC between 0.85 s and 1.15 s; (c) Current waveforms of the MSC between 1.35 s and 1.65 s; (d) Current waveforms of the MSC between 1.6 s and 1.9 s.

Figure 9 gives the output power of the DG_PV. Figure 10 and Figure 11 present the output voltage and current waveforms of the DG_PV. Their output voltage keep steady, while the output current increases at 0.5 s and reduces at 1.5 s with no inrush current. The simulation results indicate smooth transaction and stable operation of the DG system. It shows that MSC provides DG_PV additional islanded operation functionality without changing their inner control strategies conceived for grid-connected mode.

Figure 9. Output power of the MSC.

Figure 9. Output power of the MSC.

Figure 10. (a) Output voltage waveforms of DG_PV between 0.35 s and 0.65 s; (b) Output voltage waveforms of DG_PV between 0.85 s and 1.15 s; (c) Output voltage waveforms of DG_PV between 1.35 s and 1.65 s; (d) Output voltage waveforms of DG_PV between 1.6 s and 1.9 s.

Figure 10. (a) Output voltage waveforms of DG_PV between 0.35 s and 0.65 s; (b) Output voltage waveforms of DG_PV between 0.85 s and 1.15 s; (c) Output voltage waveforms of DG_PV between 1.35 s and 1.65 s; (d) Output voltage waveforms of DG_PV between 1.6 s and 1.9 s.

Figure 11. (a) Output current waveforms of DG_PV between 0.35 s and 0.65 s; (b) Output current waveforms of DG_PV between 0.85 s and 1.15 s; (c) Output current waveforms of DG_PV between 1.35 s and 1.65 s; (d) Output current waveforms of DG_PV between 1.6 s and 1.9 s.

Figure 11. (a) Output current waveforms of DG_PV between 0.35 s and 0.65 s; (b) Output current waveforms of DG_PV between 0.85 s and 1.15 s; (c) Output current waveforms of DG_PV between 1.35 s and 1.65 s; (d) Output current waveforms of DG_PV between 1.6 s and 1.9 s.

6. Experimental Results

A 3kVA experimental MSC setup is shown in Figure 12. The converter used in the MSC is built based on IGBTs and the proposed control strategy is carried out by using a digital signal processor (DSP) TMS320F28335 produced by Texas Instruments Inc. (Dallas, TX, USA). The switching frequency of the PWM gating signal is 12 kHz, and the main circuit devices have the same value as in the simulation model. Figure 13 and Figure 14 give experimental results of the MSC under different conditions. The upper waveform is the voltage waveform of the MSC at the AC side and the lower one is the current waveform of phase A.

Figure 12. Laboratory setup to test the controller performance.

Figure 12. Laboratory setup to test the controller performance.

Figure 13. (a) Experimental results from grid-connected to islanding modes; (b) Experimental results from islanded to grid-connected modes.

Figure 13. (a) Experimental results from grid-connected to islanding modes; (b) Experimental results from islanded to grid-connected modes.

Figure 14. (a) Experimental results in grid-connected mode; (b) Experimental results in islanded mode.

Figure 14. (a) Experimental results in grid-connected mode; (b) Experimental results in islanded mode.

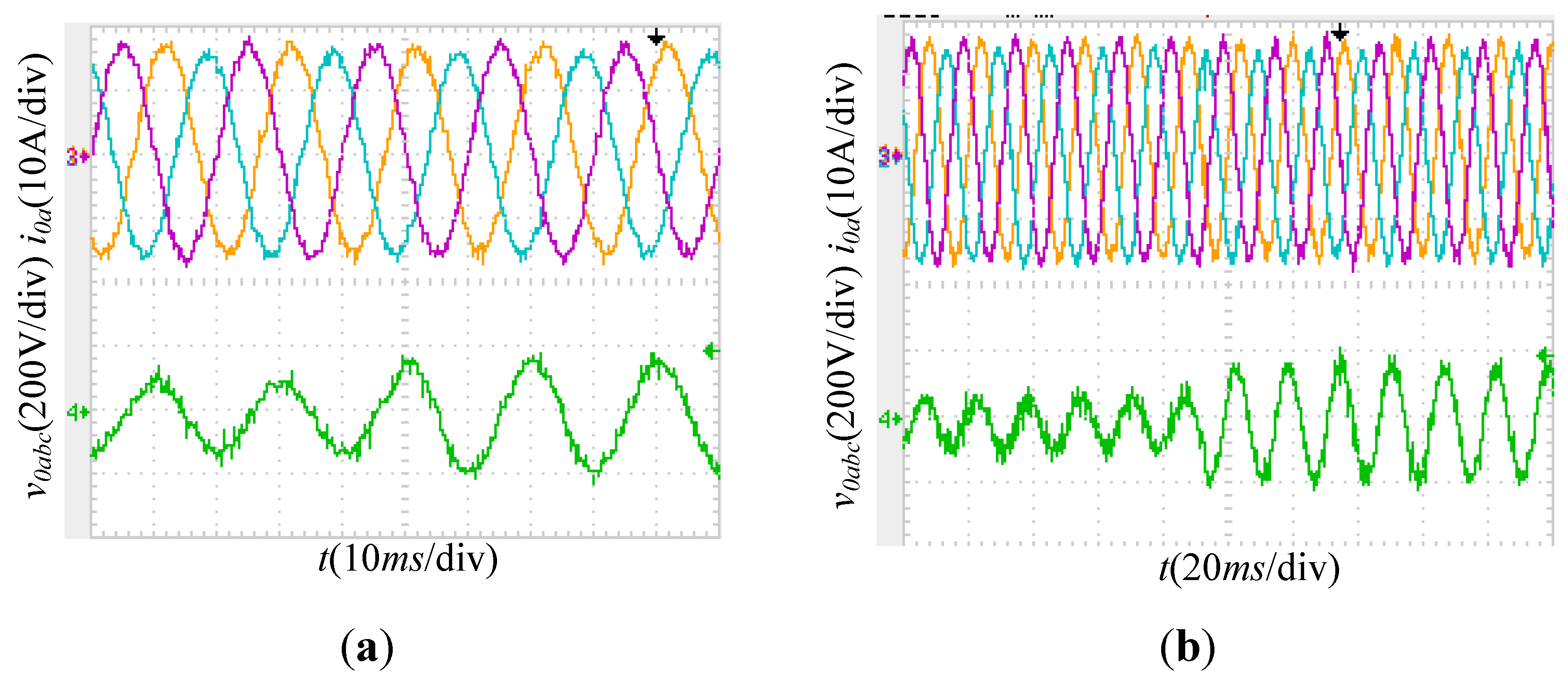
The experimental results of MSC when the microgrid transfers between the two operation modes are shown in Figure 13. In Figure 13a, the microgrid operates in grid-connected mode and transfers to islanded mode, while in Figure 13b the microgrid operates in islanded mode and reconnects to the utility. The output power reference of the MSC is set at 2 kW when the microgrid operates in grid-connected mode. If it is disconnected from the utility grid, the MSC supplies a 3 kW load. It can be seen that in Figure 13 the output power is controlled to be follow the reference value, and the voltage is controlled to track the voltage reference (220 V, 50 Hz). Note that the output voltage and current of the MSC do not have any inrush spikes during the entire transition period, thus indicating a smooth transition.

Figure 14a presents the experimental results when the microgrid operates in grid-connected mode, the output power reference value of MSC is set at 2.5 kW at first and then increases to 3 kW. Note that its output current is increased and the output voltage is stable. During islanded mode, the MSC feed a 1.5 kW load, and then another 1.5 kW load is connected to the microgrid. The experimental results are given in Figure 14b, showing clearly that the voltage remains stable during the whole period.

7. Conclusions

As the MSC in a microgrid is inherently nonlinear, time-variable, the authors proposed to employ the ARTSMC scheme in order to ensure its stability and dynamics. The ARTSMC system is developed after analyzing the microgrid operating characteristics and the mathematical models of the MSC. The rigorous proof illustrates the ARTSMC system is insensitive to parametric uncertainties and external disturbances. Simulation and experimental results have shown the fast dynamic response and robustness performance of the MSC, while guaranteeing stable operation of the microgrid in grid-connected and islanded modes, as well as automatic and seamless transition between these two operation modes. The MSC improves the reliability and power quality of the microgrid, thus providing additional islanded mode functionality without changing DG inner control strategies. The MSC is suitable for existing DGs to extend their function and to form a microgrid to supply critical loads. The proposed solution is quite independent from the use of third-party commercial DG units, such as PV inverters, so that no specific customized DGs are necessary.