1. Introduction
The design of offshore wind turbines and their support structures is based on load simulations, in which the response of the turbine to the different loads encountered in its environment is simulated and assessed [
1]. Loads typically consist of wind and wave loads, and the relevant standards prescribe a large number of load cases and scenarios that have to be evaluated [
2]. The validity of the design is then checked regarding fatigue damage, ultimate capacity and compliance with other criteria, such as service limits and behavior under accident conditions (e.g., ship collisions).
In this short note, we consider only the ultimate limit state (ULS) and, more specifically, its assessment for the support structure of a fixed-bottom wind turbine, such as a monopile or a jacket foundation. The standard assessment is based on a hybrid approach, in which both operational load cases, e.g., International Electrotechnical Commission (IEC) Design Load Case (DLC) 1.1: power production under normal turbulence, as well as extreme load cases, e.g., IEC DLC 1.3: power production under extreme turbulence and DLC 6.1: idling under extreme wind speed and/or extreme sea state, are considered. It is traditional in engineering to report the extreme loads acting on the wind turbine in an ultimate loads table, first for each load case and then as a summary over all load cases. These tables, one for each load case, show both the minimum and maximum values for each degree of freedom (forces
,
,
and moments
,
,
) acting on a specific location of the wind turbine, typically the tower bottom. The summary table identifies for each of these degrees of freedom the load case with the highest load in this particular variable and reports the minima and maxima of all of the other variables in the same load case (Table 4-2 in [
3] is a typical example). Apart from total loads on the structure, also the stress resultants for each structural detail or member can be reported in such a format. For a tubular member modeled as a beam, these consist of axial force
and the two bending moments
and
(
Table 1). These tables are used extensively in the preliminary design of support structures. During the final design phase, the loads on the support structure are then assessed for each simulated time step individually, and extensive code checks are performed in which the ULS condition is evaluated.
Table 1.
Example ultimate loads table. This shows typical results from a structural response analysis for a brace member at the bottom of the Offshore Code Comparison Collaboration Continuation (OC4) jacket support structure. Both contemporaneous loads (for each variable) and the standard approach using univariate maxima/minima are shown, the latter in the two bottom rows. These numbers correspond with the time series shown in
Figure 1. F, force; M, moment.
Table 1.
Example ultimate loads table. This shows typical results from a structural response analysis for a brace member at the bottom of the Offshore Code Comparison Collaboration Continuation (OC4) jacket support structure. Both contemporaneous loads (for each variable) and the standard approach using univariate maxima/minima are shown, the latter in the two bottom rows. These numbers correspond with the time series shown in Figure 1. F, force; M, moment.
| Variable | | | | | |
|---|
| (MN) | (MNm) | (MNm) | (MNm) |
|---|
| Maximum | 8.542 | −0.298 | −0.069 | 0.306 |
| Minimum | 5.317 | −0.013 | 0.248 | 0.248 |
| Maximum | 6.537 | 0.140 | 0.389 | 0.414 |
| Minimum | 7.204 | −0.434 | −0.229 | 0.490 |
| Maximum | 6.537 | 0.140 | 0.389 | 0.414 |
| Minimum | 7.204 | −0.434 | −0.229 | 0.490 |
| Maximum | 7.204 | −0.434 | −0.229 | 0.490 |
| Minimum | 5.670 | −0.087 | −0.089 | 0.125 |
| Overall | Maximum | 8.542 | 0.140 | 0.389 | 0.490 |
| Minimum | 5.317 | −0.434 | −0.229 | 0.125 |
This approach has two important limitations, both of which are addressed here. First, the ultimate loads table gives the impression that the maxima of individual loads appear together at the same time, which is normally not the case.
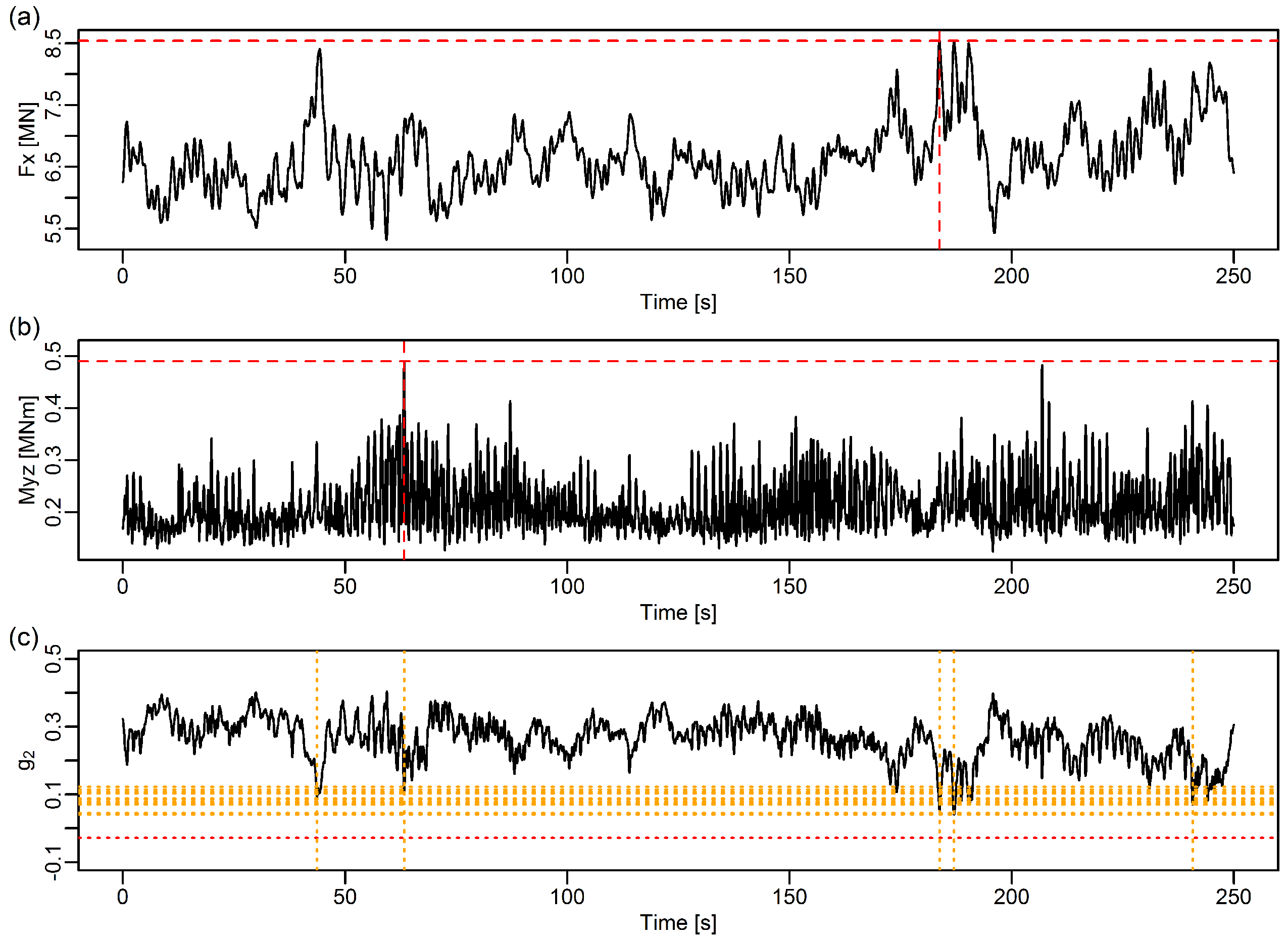
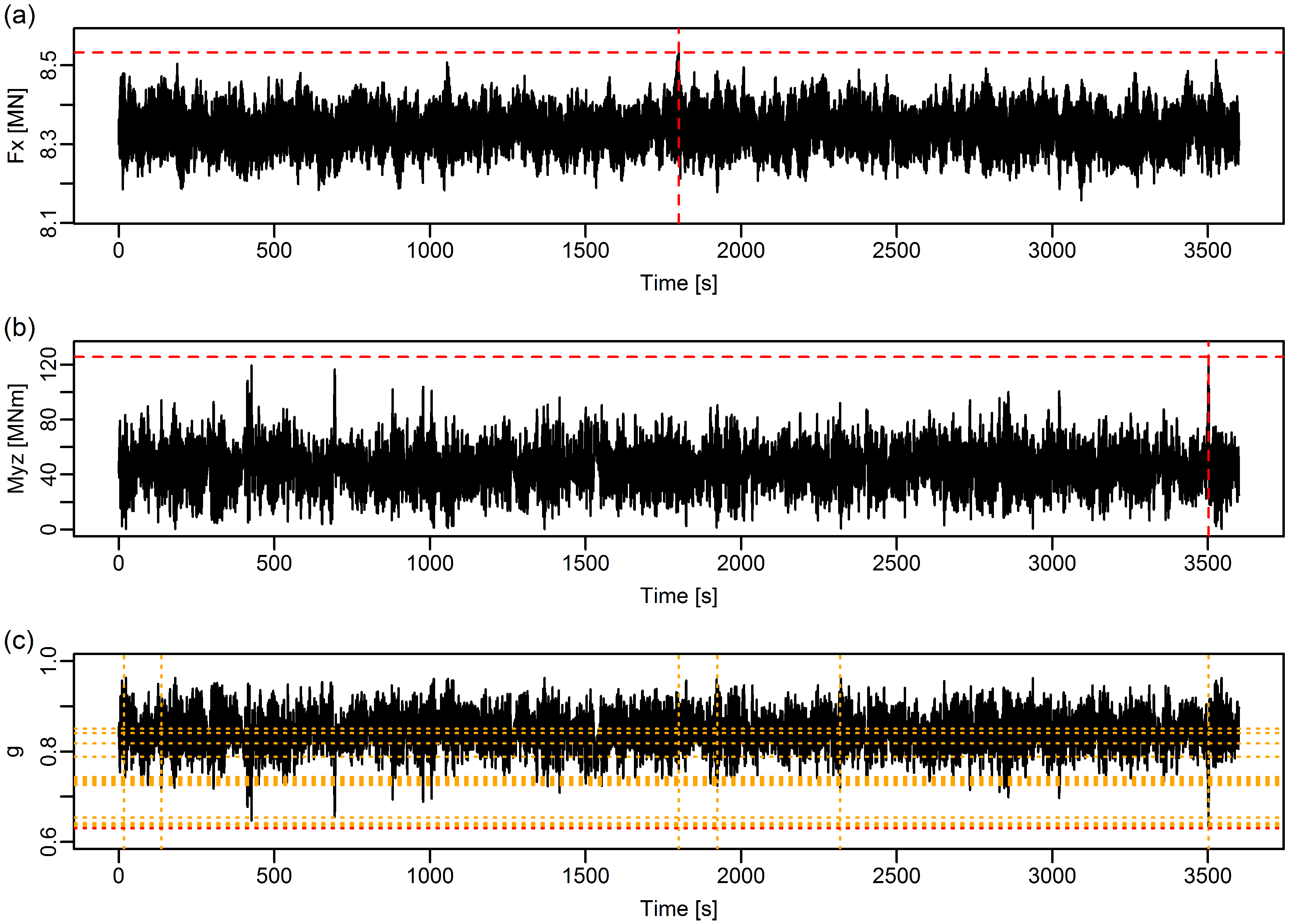
Figure 1 illustrates this for axial forces and bending moments in a joint of a jacket structure (at the location indicated in
Figure 2). The maximum of the axial force is obtained at time
s (
Figure 1a), whereas the maximum of the total bending moment is obtained at time
s (
Figure 1b). In both cases, the other variable takes on significantly lower values than one can infer from the ultimate loads table. This means that reporting all individual maxima together leads to a conservative assessment of the loads. This limitation has been addressed in the last revision of the IEC 61400-1 standard [
4], where
Appendix H advocates the use of contemporaneous loads: for each variable, the maximum/minimum is determined and combined with the values of the other variables at the same time (see
Table 1 for an example). However, as will be shown below, this approach is typically non-conservative.
The other limitation is that, when the actual loads are used, the amount of data that needs to be processed tends to be very large. This is of particular concern when one tries to assess the structural reliability of the support structure [
5]. In this case, one has to perform a probabilistic assessment, in which the various uncertainties about the design, the loads and the materials have to be considered. A straightforward way is a Monte Carlo simulation in which variations of important parameters, e.g., the steel yield strength, are randomly generated. These parameters are then used together with the loads in a limit state equation, and the probability of structural failure is evaluated by determining how many of these samples result in values that are outside of the safe region. As this is a time-consuming process, it cannot be performed for each time step individually.
There is thus a need for a more representative overview of the defining loads in wind turbine structural analysis. This is addressed here by introducing the concept of Pareto-optimal loads. These are defined in
Section 2, which also discusses typical ULS functions and presents details about the computational model used for a demonstration.
Section 3 presents some exemplary results from a simplified analysis of both a monopile and a jacket support structure. Finally, the findings are summarized and discussed in
Section 4.
Figure 1.
Illustration of the difference between Pareto-optimal loads and the standard approach for the bottom joint in the OC4 jacket support structure, at rated wind speed. (a) axial force. (b) total bending moment. The broken red lines indicate the locations and values of the univariate maxima. (c) limit state function for combined bending and compression (Equation (5)). The broken red line indicates the value for the conservative combination of univariate maxima. The dotted orange lines indicate the locations and values at the Pareto-optimal points. Note that only a small part of the total time series has been shown, for the purposes of better visualization.
Figure 1.
Illustration of the difference between Pareto-optimal loads and the standard approach for the bottom joint in the OC4 jacket support structure, at rated wind speed. (a) axial force. (b) total bending moment. The broken red lines indicate the locations and values of the univariate maxima. (c) limit state function for combined bending and compression (Equation (5)). The broken red line indicates the value for the conservative combination of univariate maxima. The dotted orange lines indicate the locations and values at the Pareto-optimal points. Note that only a small part of the total time series has been shown, for the purposes of better visualization.
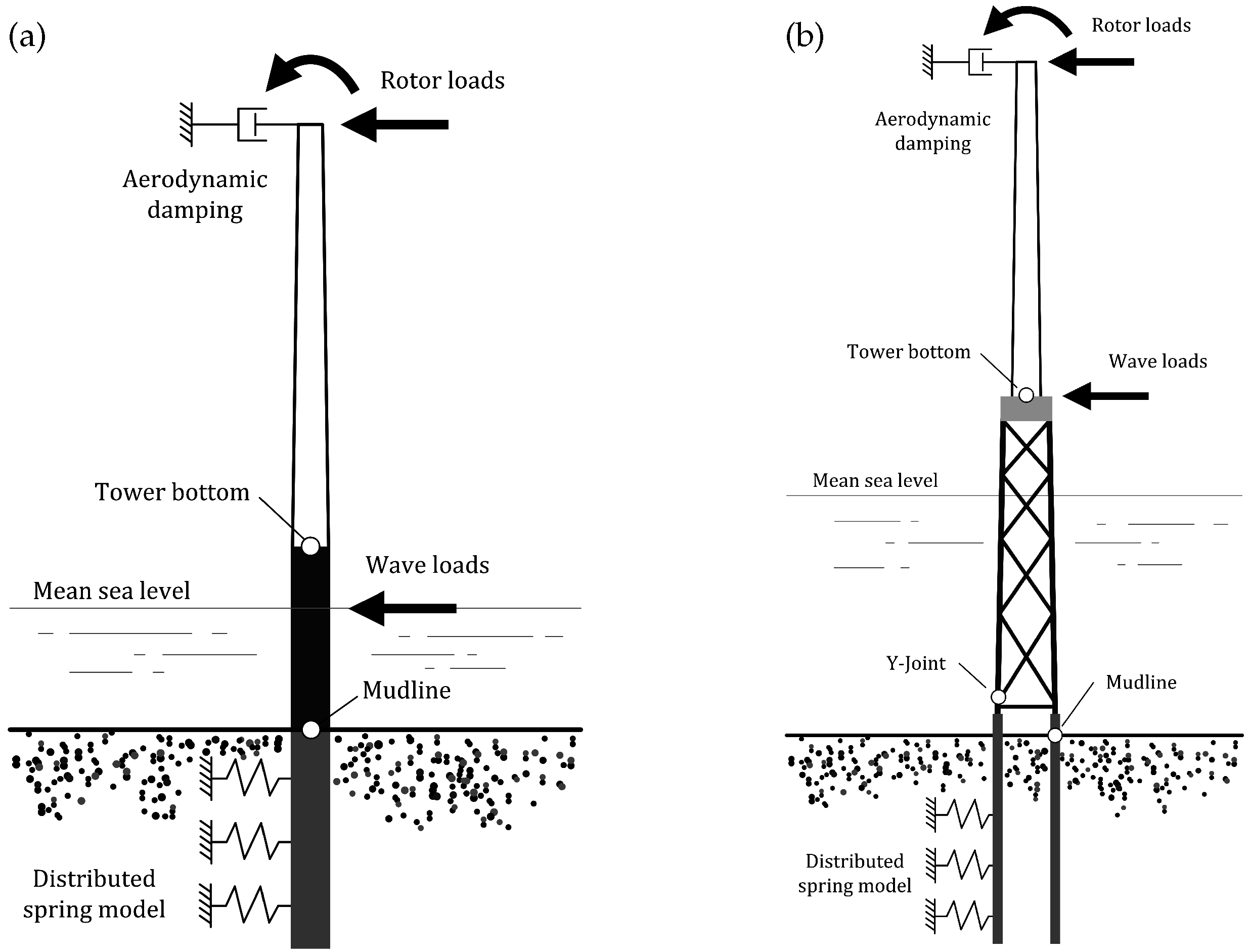
Figure 2.
Illustration of numerical models used for example calculations. (a) OC3 monopile. (b) OC4 jacket with additional soil model. Output locations are indicated.
Figure 2.
Illustration of numerical models used for example calculations. (a) OC3 monopile. (b) OC4 jacket with additional soil model. Output locations are indicated.
2. Methods
2.1. Pareto-Optimal Loads
The concept of Pareto optimality is a generalization of the idea of the maximum value. The basis of both concepts is an ordering of elements. When confronted with a univariate (one-dimensional) record of
n observations
, the standard order relation for numerical values (denoted by
) allows one to sort the samples according to their size and thereby identifies a maximal element
, which has the defining property that:
When confronted with a multivariate record,
i.e., a number of
d-dimensional vectors
of observations, it is not immediately clear how to order these. In fact, typically, no linear order exists,
i.e., there exists no simple order relationship that allows one to compare each element with each other in a consistent way. The straightforward generalization of the order
for univariate records to
d-dimensional observations is to define:
In other words, a vector x is less or equal to a vector y if all elements of x are less or equal to all corresponding elements in the vector y. We say that the vector y dominates the vector x.
This dominance order, unfortunately, only defines a partial order,
i.e., there exist many combinations of elements that cannot be compared. The concept of a maximal element still exists, if we define a maximal element as an
, such that:
or in other words, there exists no other observation that dominates
x. However, now, the maximum is not unique anymore, and there can be many maximal elements.
Finding all Pareto-optimal elements is easily done by iterating through all observations. The most important cases in practice are for two- and three-dimensional vectors of observations (e.g., axial force and the two bending moments in a structural member). The straightforward algorithms are given in the
Appendix, for use with the open-source statistical analysis software R [
6], and can be easily adapted into other programming or scripting languages.
Let us illustrate the method with an example.
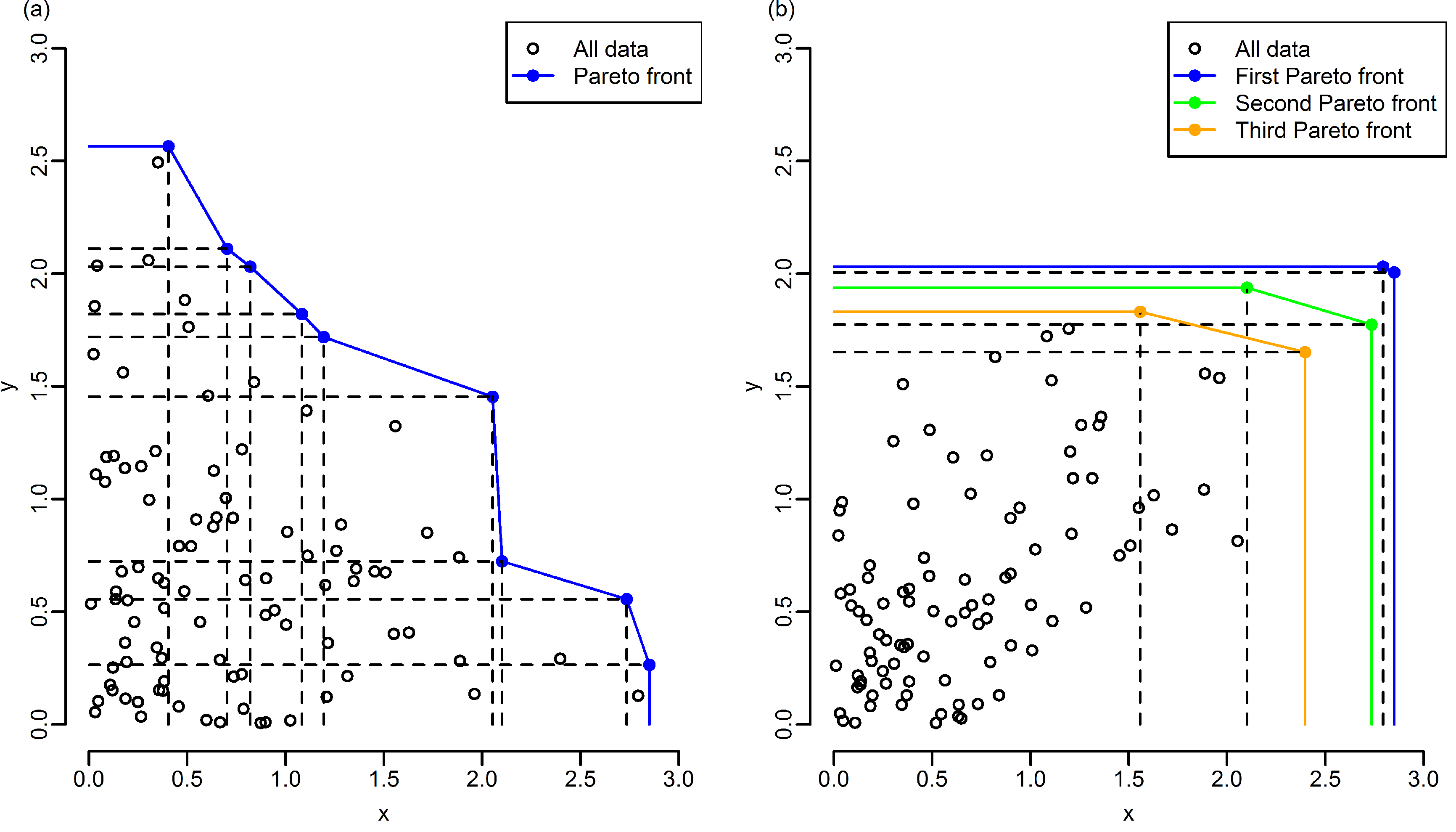
Figure 3a shows a scatterplot of
pairs, where the two elements in each observation have been generated randomly and independently, from a standard Gaussian distribution (for simplicity, only elements with positive values are shown). The elements in blue are the maximal elements. For each of them, the broken lines indicate the regions that are dominated by them. Together, the blue elements form the so-called Pareto front. As can be seen, a relatively small number of such Pareto-optimal elements (nine points, to be precise) covers the entire dataset (consisting of 100 points).
Figure 3b shows a similar scatterplot of
pairs, where now, a significant positive correlation exists between the
x- and
y-values. In this case, the Pareto front is rather simple and consists of only two elements. As the figure illustrates, it is also possible to define higher-order Pareto fronts. These are determined by successively removing all elements from the Pareto front and then finding the Pareto-optimal elements of the remaining points. Repeating this process, the first three Pareto fronts so obtained are shown in the figure.
The concept of Pareto optimality is used extensively in economic analysis and multi-criteria optimization, including structural optimization (see, e.g., [
7,
8,
9]).
Figure 3.
Illustration of Pareto optimality. (a) Samples from two independent Gaussian distributions. The Pareto front consists of the blue points. The broken lines show the regions of the space that are dominated by each Pareto-optimal point. (b) Samples from two strongly-correlated Gaussian distributions. A number of higher-order Pareto fronts are indicated as well (see the text for details).
Figure 3.
Illustration of Pareto optimality. (a) Samples from two independent Gaussian distributions. The Pareto front consists of the blue points. The broken lines show the regions of the space that are dominated by each Pareto-optimal point. (b) Samples from two strongly-correlated Gaussian distributions. A number of higher-order Pareto fronts are indicated as well (see the text for details).
2.2. Ultimate Limit State Equations
Whether a design fulfills the ULS condition is assessed by performing a number of checks. The structure of these tests is highly standardized. Typically, a limit-state equation is used, and values of the limit-state equation below zero signify structural failure.
The relevant standards specify a vast number of such checks, and their formulations differ significantly. We consider here only the most important and common features. The following is based on the Norsk Sokkels Konkurranseposisjon (NORSOK) offshore standard “Design of Steel Structures” [
10].
Focusing on tubular members, a number of checks only use univariate data. For example, each member has to be assessed for sufficient capacity to resist tensile and compressive loads and bending moments,
here,
A denotes the cross-sectional area,
W the elastic section modulus;
γ is a material factor (with a typical value of 1.15);
is the steel yield strength;
is the characteristic axial compressive strength (which depends on a number of factors, such as Young’s modulus of the material and the length of the member); and
is the characteristic bending strength (which is proportional to the yield strength). The actual loads are
(normal force) and
(total bending moment). These univariate conditions are monotonous (in fact, linear) in the load effects
and
, and for these equations, the knowledge of the univariate maximum for each component of the loads is sufficient.
In contrast to this, a number of combined conditions exist that are often defining for the elements. We only consider compression here, being the most important condition in many cases. In the NORSOK standard, this is assessed with two limit state equations:
here,
is the resistance to bending (as in Equation (3));
is the axial resistance to compression (as in Equation (2)), whereas
is the resistance to local buckling. Here, the local characteristic buckling strength
depends on both the yield strength (in a non-linear way), Young’s modulus, as well as on the thickness to diameter ratio of each element. The Euler buckling strengths
depend mainly on Young’s modulus and member length, and the reduction factors
depend on the type of structural element and details about the loading, but can be taken to be 0.85 in most cases.
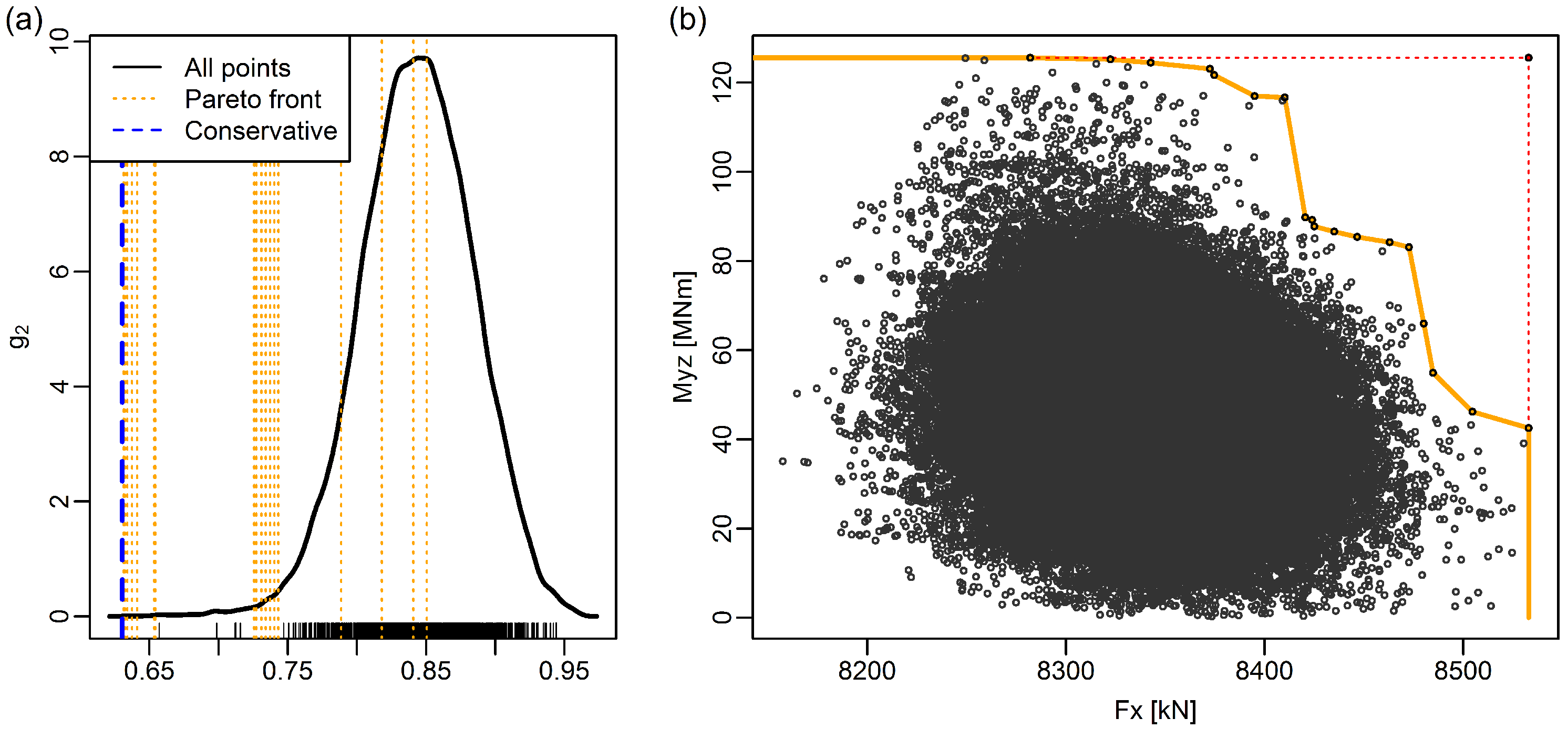
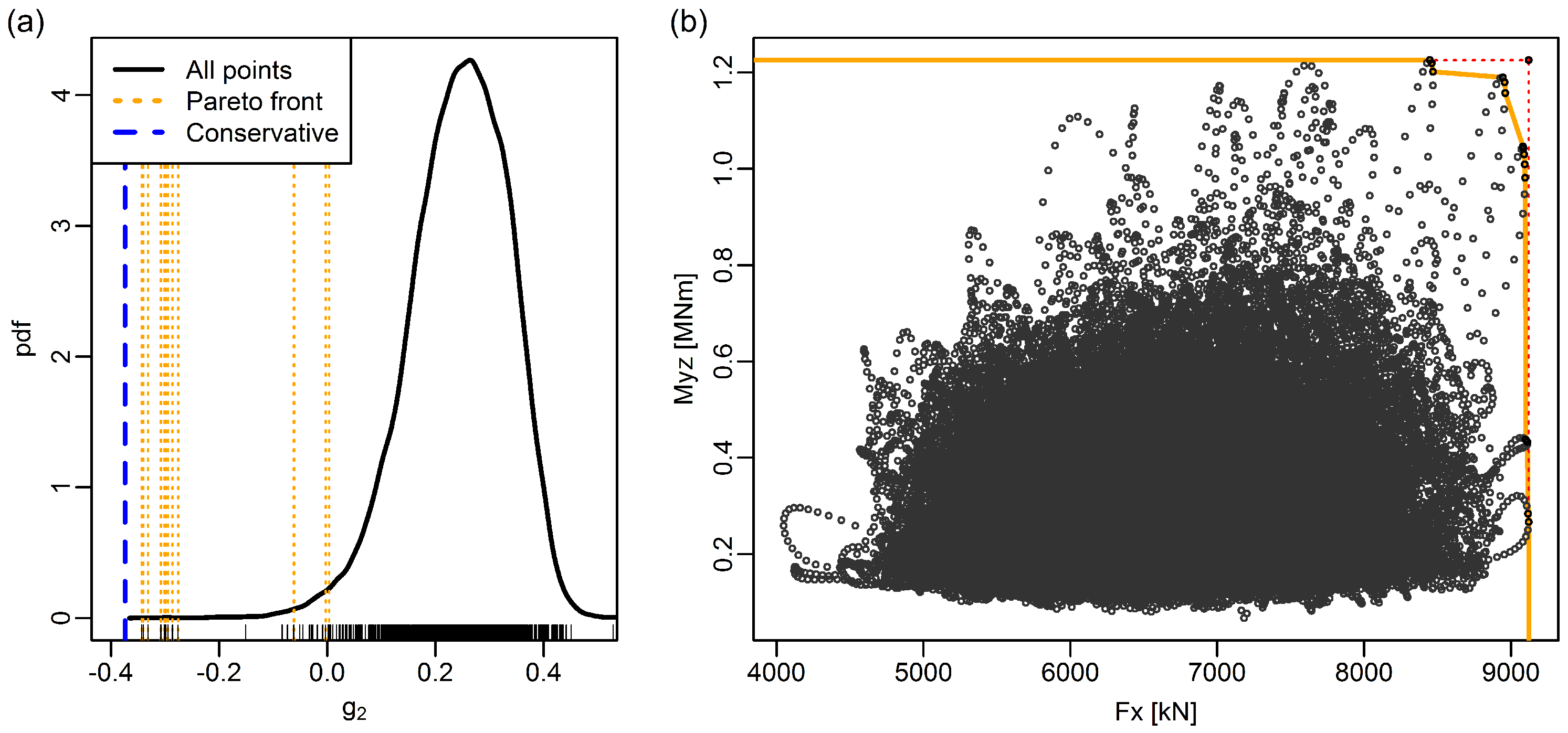
Although the value of the limit state equations Equations (4)–(5) depends in a complex and nonlinear way on the load components, this relationship is monotonic for each component. In other words, larger values of either axial force or bending moment will lead to lower values of the limit state equation, all other things being kept equal. Therefore, it is clear that Pareto-optimal load vectors result in the lowest possible values of the equations, compared to the elements that are dominated by these vectors, although it is not clear which Pareto-optimal vector (
i.e., which specific combination of loads) leads to the lowest value overall. In comparison, the use of contemporaneous load vectors [
4] (
Appendix H) is identical to the use of only two of the Pareto-optimal load vectors, the ones with the highest value for either the axial force or the bending moment.
As the local characteristic buckling strength is less than the axial resistance to compression, the value of the limit state equation is typically lower than the corresponding value of . For simplicity, we therefore only consider the function in the following examples, although a realistic application has to implement both checks. Furthermore, no (additional safety factors have been considered.
2.3. Computational Model
In order to discuss the relevance of the methodology, an example case was implemented. Two different support structures were evaluated, a monopile and a jacket support structure (
Figure 2). The monopile is identical to the Offshore Code Comparison Collaboration (OC3) monopile developed within the International Energy Agency (IEA) Task 23 [
11]. The jacket structure is the OC4 jacket developed within IEA Task 30 [
12], but for more realistic results, a soil model based on the p-y approach [
13] has been included.
Load simulations were performed with the elastic-multibody simulation tool Finite Element Dynamics in Elastic Mechanisms (Fedem) Windpower (Version 7.1; Fedem AS, Trondheim) under turbulent wind and irregular linear wave loads. A standard set of lumped load cases was assessed during a previous study, which should be consulted for more details on the simulation model [
5]. This set includes both DLC 1.1 and DLC 6.1. Additional simulations were performed here with the extreme turbulence model (DLC 1.3). All simulations were performed with rotor load time series and additional aerodynamic damping implemented as a linear viscous damping, but are more or less similar to what one would obtain with an integrated analysis. For demonstration purposes, only results from eight of these load cases are discussed here. Simulations were 3 h long, with a time step of 0.025 s. An additional, initial transient of 240 s was removed before analysis, during which the turbine did speed up and reached steady-state operational conditions.
2.4. Reliability Assessment
As mentioned previously, one important application of this method is to reduce the computational effort for structural reliability calculations. As an example, let us here consider two sources of uncertainty about the resistances.
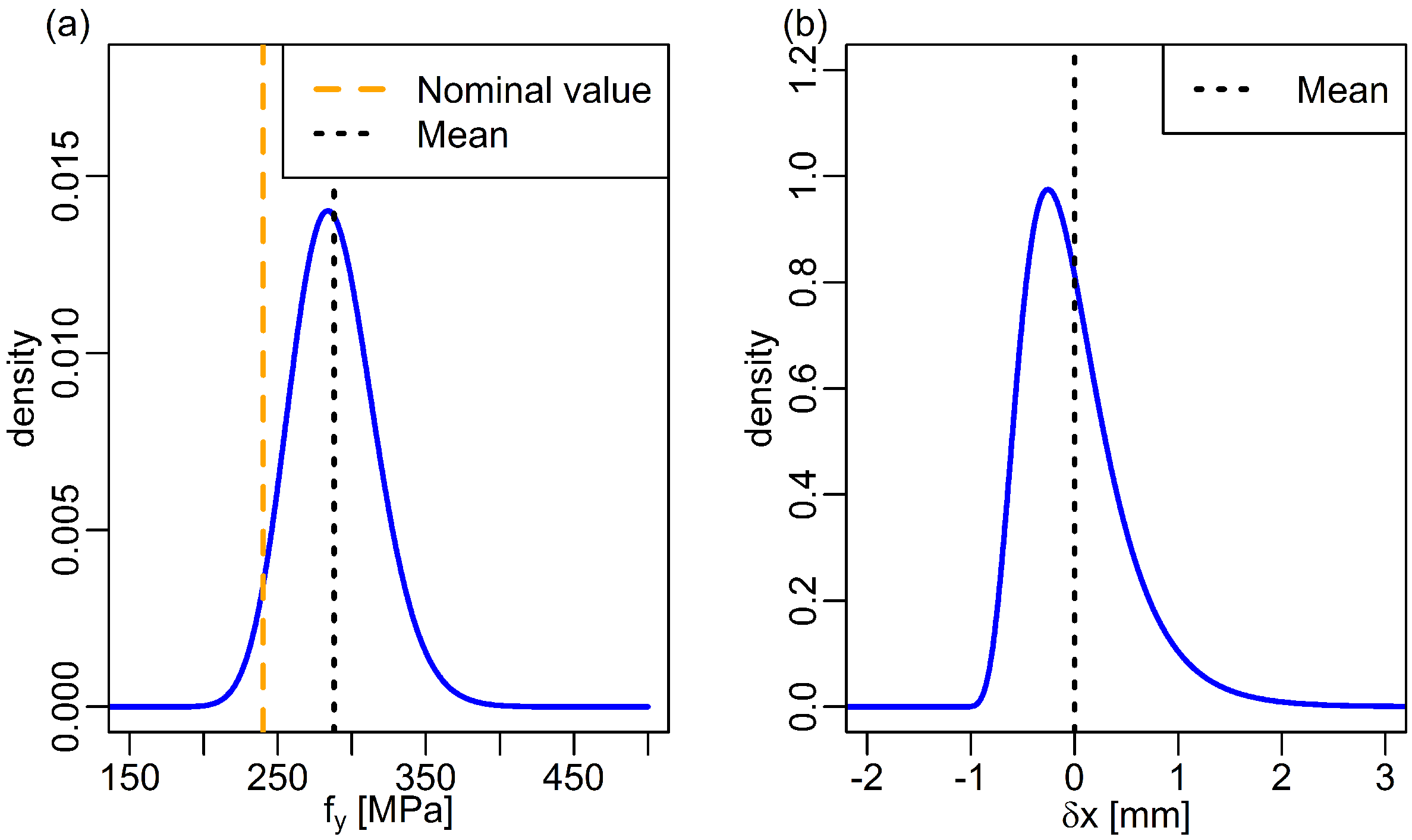
The yield strength of the steel for the two models studied has a nominal value of 240 MPa. In a probabilistic assessment, it is often modeled with a log-normal distribution [
5,
14,
15]. We chose a mean of 1.2-times the nominal value and a coefficient of variation (COV) of 0.1, which results in the probability distribution shown in
Figure 4a. Similarly, we model the manufacturing uncertainties (in units of mm) by another log-normal distribution, with a mean of 1.2 and COV of 0.5, shifted by 1.0 mm toward the right (
Figure 4b). We propose this distribution here based on discussions with relevant industry. It is skewed toward the right, as manufacturers prefer to deliver more material than less, as this is considered conservative and therefore more acceptable to their clients.
Figure 4.
Models for important sources of uncertainty. (a) Probability distribution of yield strength. Both the nominal value (orange) and the actual mean (black) are indicated. (b) Probability distribution of manufacturing uncertainties.
Figure 4.
Models for important sources of uncertainty. (a) Probability distribution of yield strength. Both the nominal value (orange) and the actual mean (black) are indicated. (b) Probability distribution of manufacturing uncertainties.
The limit state function (Equation (5)) is evaluated with Monte Carlo samples from these two distributions, for each combination of loads considered, and these results are then transformed into a failure probability for the structural member in question. For this example, we did not correct for the probability of occurrence of the different load cases or the project lifetime, but simply report these numbers for each single 3-h load simulation, as a highly simplified estimate of the probability of failure due to a certain loading scenario. Variations in dimensions due to manufacturing uncertainty are also assumed not to change the stress resultants, in order to avoid performing additional, expensive load simulations for each sample. The effect of this approximation is assumed to be relatively minor compared to the changes in resistance due to the changing area and moments of inertia.
4. Discussion
We have introduced the concept of Pareto-optimal loads as a tool for obtaining an efficient representation of extreme loads. The classical way of using univariate maxima is adequate in the case that one load component dominates all others. This is the case for the OC3 monopile, for example, where the bending moment more or less determines the value of the limit state equations. This also holds for the OC4 jacket at the larger elements, such as the tower bottom or mudline (results not shown). However, in the smaller structural details, such as the braces of the jacket, the contribution of the different load components in the limit state equation becomes more similar, and the use of univariate maxima is then very conservative. The recent edition of the IEC 61400-1 standard [
4] introduced the concept of contemporaneous load vectors, in order to address this issue. However, it was found here that these lead to non-conservative results.
The example considered only two reference support structures. If designs are optimized, the likelihood increases that the univariate maxima are over-predicting the actual loads.
However, the main issue in favor of the proposed approach is structural reliability and reliability-based design optimization. Determining the probability of structural failure (due to extreme loads) accurately becomes very challenging and can only be performed for a small number of extreme loads. As seen in
Section 2.2, the Pareto-optimal points are excellent candidates for this.
One advanced issue that we have neglected in this story so far is the statistical extrapolation of responses and loads. It is common practice to fit an extreme value distribution to the univariate extremes observed in simulations of operational load cases (DLC 1.1) and to predict a 50-year extreme response or load from this curve [
16,
17]. In detail, either block maxima (one value for each 10-min load case with a different random realization of wind and waves) or the exceedances over a high threshold are used [
18]. This approach breaks down when multivariate extremes are considered, such as is the case here, and other methods, such as the inverse First Order Reliability Method (FORM), need to be used [
19,
20], with well-known limitations (such as being computationally much more involved). However, the method allows for consistently dealing with dynamic problems [
21]. Using Pareto-optimal points for extrapolating multivariate extremes potentially offers an interesting alternative here, as well, but the details are left for future work.
5. Conclusions
The proposed method is easy to implement and use and can offer a significant advantage, both in the early design phases of a support structure, as well as during an assessment of structural reliability and probabilistic design. In the simple example case studied here, it effectively reduced the information contained in 144,000 time points into around 20 Pareto-optimal pairs of values that completely characterized the structure of the extreme loads, preserving in particular the non-trivial correlation between different load components.
For designs that are dominated by one load component, it is not necessary to consider the Pareto-optimal elements. Typical monopiles seem to fall into this category, as do larger members in jacket structures. However, both for smaller elements in jackets, as well as when performing structural optimization [
22,
23], it becomes important to evaluate the ULS condition with realistic loads. If this cannot be done for each time step simulated, such as in a computationally-involved reliability assessment, the Pareto-optimal points offer a safe and efficient alternative.
Other applications of the concept of Pareto-optimal vectors can be envisaged, as well. We already mentioned the accurate extrapolation of multivariate, correlated extremes for large return levels, but we also foresee applications in, e.g., condition monitoring of wind turbines.