Predicting Iron Losses in Laminated Steel with Given Non-Sinusoidal Waveforms of Flux Density
Abstract
:1. Introduction
2. Specimen and Measurement System
- induced voltage of the B-coil;
- turn number of the B-coil;
- S
- section area of the magnetic core.

| Item | Parameter |
|---|---|
| Model | 50WW470 |
| Inner diameter | 230 mm |
| Outer diameter | 250 mm |
| Thickness | 10 mm (20 sheets) |
| Air gap | 2 mm |
| Turn number of exciting coil | 1000 turns |
| Turn number of B-coil | 1000 turns |
| Magnetic path length | 751.55 mm |
| Resistance of exciting coil | 0.3615 Ω |
| Cross-sectional area of exciting coil | 6.627 mm |
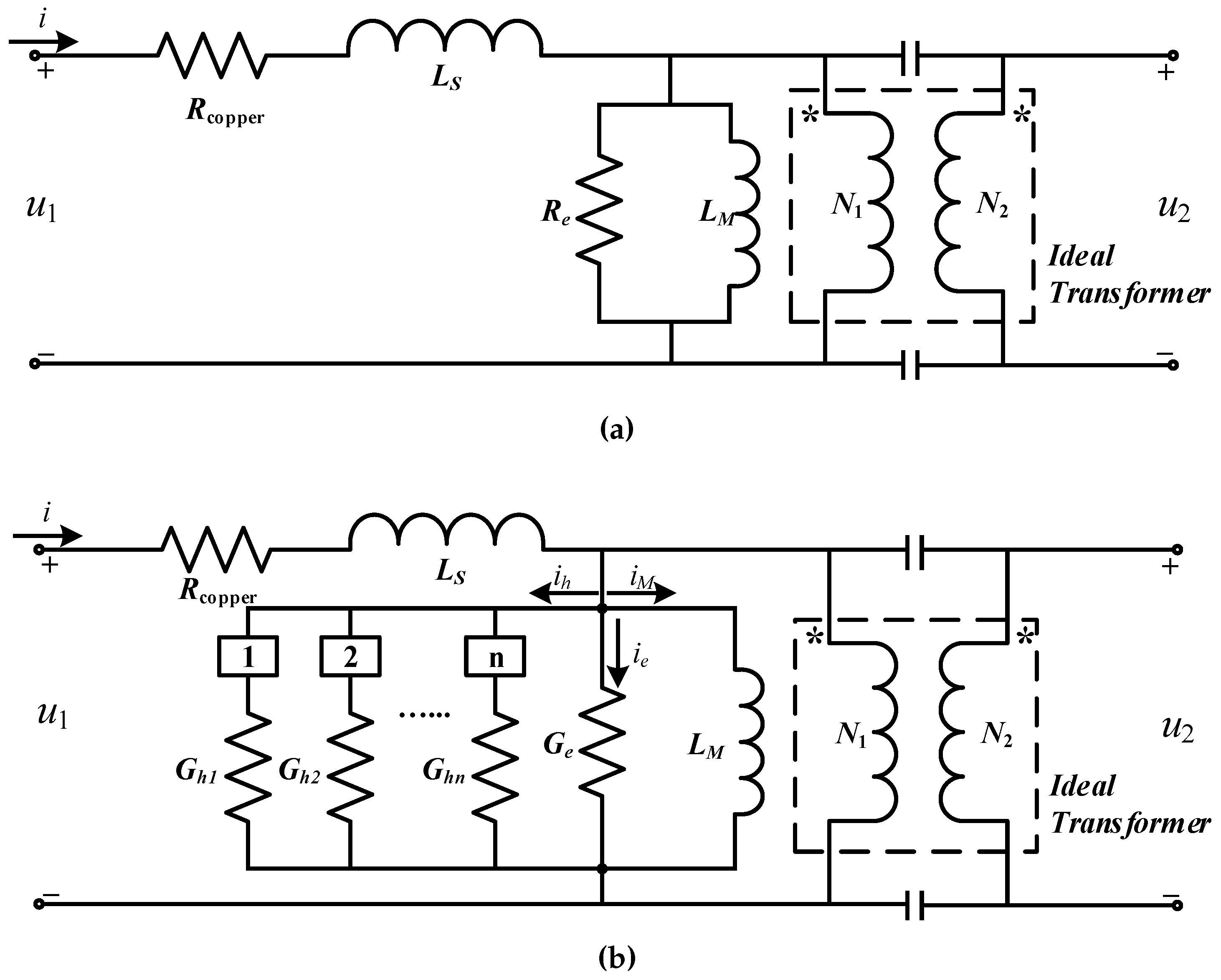
3. Engineering Model for the Iron Loss Calculation
3.1. Sinusoidal Excitations
- exciting voltage;
- i
- exciting current;
- number of turns of the exciting coil;
- induced voltage transformed to the primary side;
- P
- average iron loss in one cycle.

- amplitude of the induced voltage;
- ω
- angular frequency;
- amplitude of the flux density.
- parameters of the three-order polynomials;
- corresponding phase angle of the knee points.

- harmonic magnitude;
- harmonic amplitude of the exciting current;
- harmonic phase angle of the exciting current;
- harmonic amplitude of the induced voltage;
- harmonic phase angle difference between the induced voltage and exciting current;
- M
- mass of the specimen.
3.2. Non-Sinusoidal Excitations
- harmonic content of the induced voltage;
- harmonic phase angle of the induced voltage;
- harmonic component of the flux density.
- Step (1)
- Obtain describing functions in the same form as Equation (6) with various frequencies and values by multi-frequency tests under sinusoidal excitations.
- Step (2)
- Convert the non-sinusoidal waveforms of flux density into a series of sinusoidal waves and sample all waves with an interval time .
- Step (3)
- Initialize fundamental and harmonics of the exciting current as follows:where is a random value and .
- Step (4)
- Define as follows,The position of in the corresponding curve as shown in Figure 4 is found using the value of . The corresponding describing function is applied to calculate the change of the n-th harmonic of the exciting current by:
- Step (5)
- Calculate the average value of the n-th harmonic of the exciting current, . As no DC-bias is involved in the waveforms of flux density, the average value should be equal to zero, which suggests that:
- Step (6)
- Apply FFT on the sum of the harmonics of the exciting current to obtain amplitude and phase angles, which are substituted into Equation (8) to calculate the iron loss.
4. Verification of the Engineering Model
4.1. Magnetic Properties under Sinusoidal Excitations
- Ψ
- flux linkage of the exciting coil.
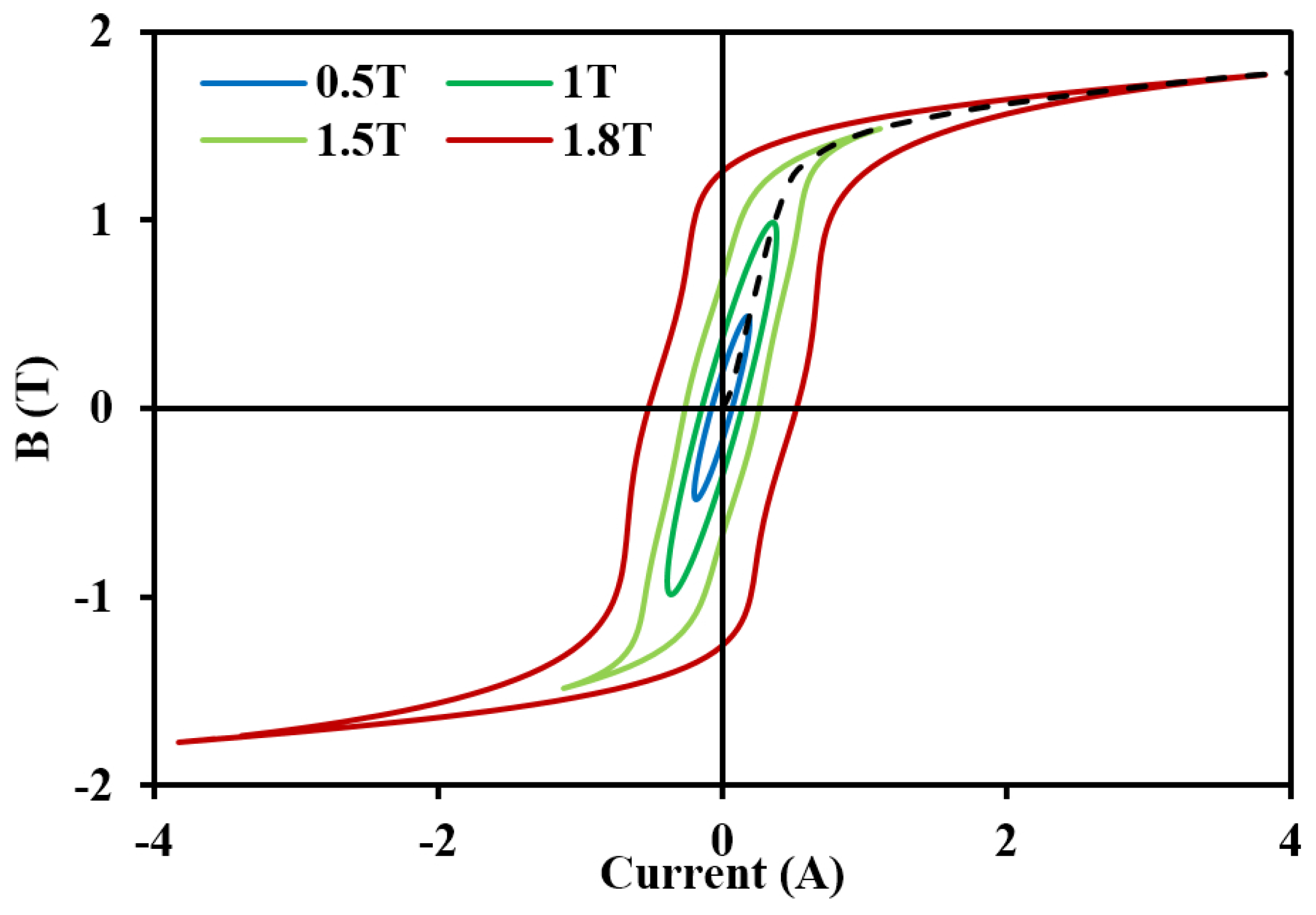

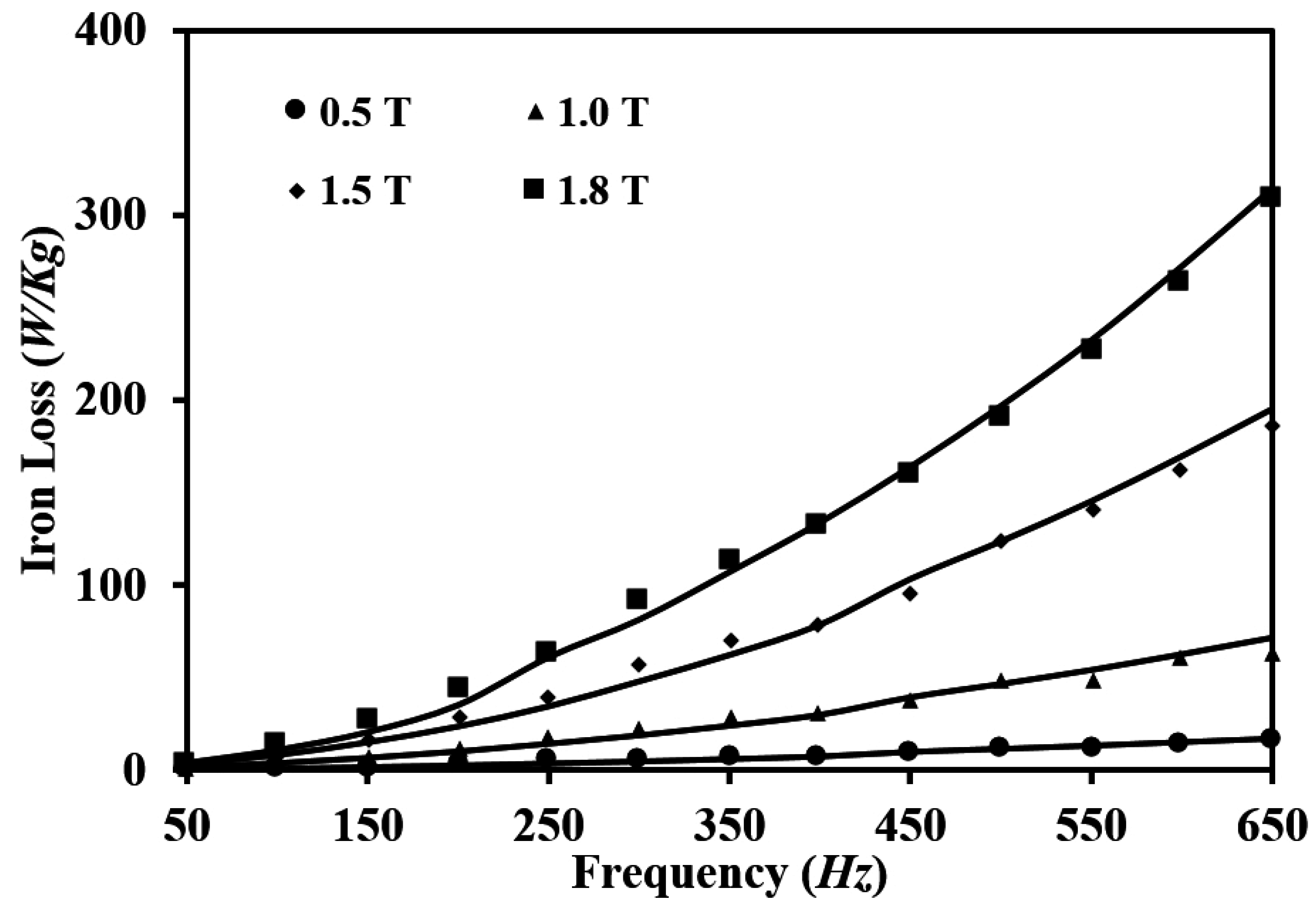
4.2. Single Harmonic Injections
| Content | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (A) | Simu. | 0.3795 | 0.3766 | 0.3737 | 0.3709 | 0.3681 | 0.3654 | 0.3627 | 0.3600 | 0.3574 | 0.3548 |
| Meas. | 0.3832 | 0.3824 | 0.3813 | 0.3801 | 0.3781 | 0.3774 | 0.3755 | 0.3737 | 0.3721 | 0.3700 | |
| (rad) | Simu. | −1.191 | −1.190 | −1.189 | −1.188 | −1.187 | −1.186 | −1.185 | −1.184 | −1.183 | −1.182 |
| Meas. | −1.210 | −1.212 | −1.213 | −1.209 | −1.211 | −1.214 | −1.215 | −1.216 | −1.210 | −1.213 | |
| (W/kg) | Simu. | 1.505 | 1.487 | 1.469 | 1.451 | 1.433 | 1.417 | 1.399 | 1.383 | 1.367 | 1.355 |
| Meas. | 1.453 | 1.432 | 1.414 | 1.415 | 1.390 | 1.367 | 1.347 | 1.328 | 1.335 | 1.318 | |
| Error (%) | 3.62 | 3.84 | 3.89 | 2.56 | 3.13 | 3.71 | 3.87 | 4.14 | 2.41 | 2.79 | |
| (A) | Simu. | 0.0060 | 0.0118 | 0.0176 | 0.0234 | 0.0290 | 0.0346 | 0.0400 | 0.0454 | 0.0508 | 0.0560 |
| Meas. | 0.0063 | 0.0122 | 0.0184 | 0.0242 | 0.0290 | 0.0335 | 0.0390 | 0.0458 | 0.0516 | 0.0540 | |
| (rad) | Simu. | −0.835 | −0.835 | −0.835 | −0.835 | −0.835 | −0.835 | −0.835 | −0.835 | −0.835 | −0.835 |
| Meas. | −0.690 | −0.759 | −0.739 | −0.732 | −0.826 | −0.878 | −0.838 | −0.838 | −0.884 | −0.907 | |
| (W/kg) | Simu. | 0.0022 | 0.0084 | 0.0187 | 0.0332 | 0.0505 | 0.0707 | 0.0965 | 0.1243 | 0.1553 | 0.1847 |
| Meas. | 0.0025 | 0.0092 | 0.0208 | 0.0369 | 0.0512 | 0.0667 | 0.0942 | 0.1253 | 0.1496 | 0.1705 | |
| Error (%) | 12.37 | 8.42 | 9.97 | 9.93 | 1.44 | 5.93 | 2.42 | 0.75 | 3.77 | 8.36 | |
| (W/kg) | Simu. | 1.508 | 1.495 | 1.487 | 1.484 | 1.484 | 1.488 | 1.496 | 1.507 | 1.522 | 1.540 |
| Meas. | 1.455 | 1.441 | 1.435 | 1.452 | 1.441 | 1.433 | 1.441 | 1.453 | 1.484 | 1.489 | |
| Error (%) | 3.59 | 3.75 | 3.63 | 2.15 | 2.97 | 3.82 | 3.78 | 3.72 | 2.54 | 3.45 | |

4.3. Square Wave Excitations
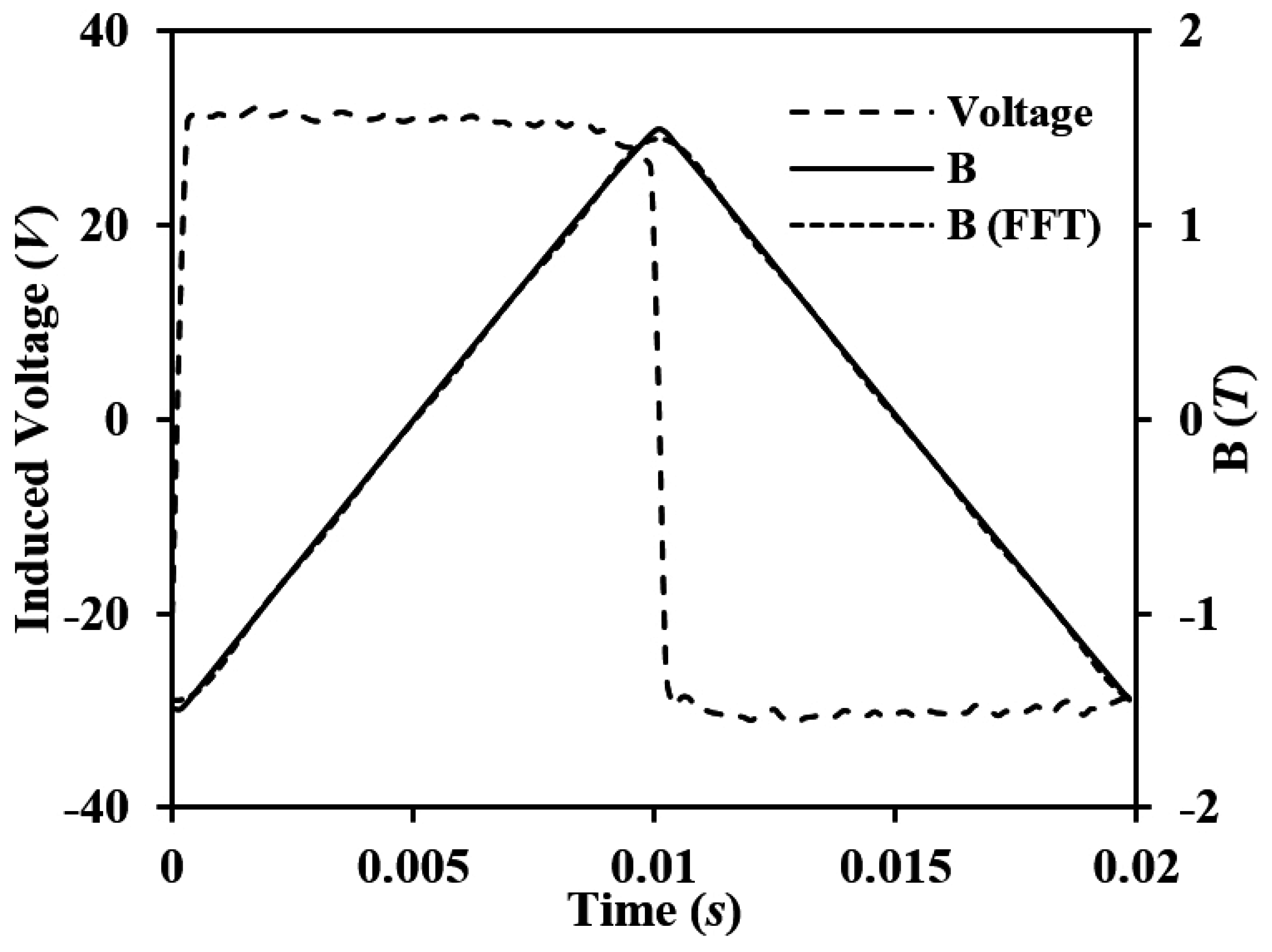
| Harmonic Order | Amplitude (A) | Phase Angle (rad) | ||
|---|---|---|---|---|
| Simulation | Measurement | Simulation | Measurement | |
| 1st | 0.6983 | 0.6976 | −1.276 | −1.276 |
| 3rd | 0.2617 | 0.3097 | −1.564 | −1.588 |
| 5th | 0.1134 | 0.1130 | −1.754 | −1.751 |
| 7th | 0.0300 | 0.0299 | −2.060 | −2.056 |
| Loss (W/kg) | 2.733 | 2.698 | Error | 1.29 |

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| B (T) | 1.0 | 1.5 | ||||
|---|---|---|---|---|---|---|
| f (Hz) | 50 | 350 | 50 | 150 | 250 | 350 |
| −0.793 | −0.985 | 11.545 | 10.715 | 0.825 | 5.745 | |
| −2.457 | −1.766 | 32.270 | 31.015 | 4.781 | 19.915 | |
| −3.941 | −3.878 | 28.825 | 28.055 | 4.722 | 19.610 | |
| −1.912 | −2.389 | 8.640 | 8.520 | 1.665 | 6.540 | |
| −0.139 | −0.519 | −0.255 | −0.381 | −0.426 | −0.523 | |
| 0.358 | 0.655 | 0.310 | 0.449 | 0.563 | 0.662 | |
| 0.079 | 0.287 | 0.051 | 0.069 | 0.066 | 0.069 | |
| 0.013 | 0.051 | 0.034 | 0.003 | −0.040 | 0.019 | |
| −5.320 | −5.635 | −6.675 | −4.102 | 2.564 | −0.281 | |
| 19.315 | 2.065 | 19.230 | 12.545 | −8.145 | 1.116 | |
| −23.010 | −28.040 | −18.610 | −13.140 | 7.755 | −2.274 | |
| 9.375 | 12.795 | 6.190 | 4.845 | −1.907 | 1.728 | |
| 0.956 | 1.109 | 0.565 | 0.823 | 1.098 | 0.564 | |
| 2.417 | 2.265 | 2.374 | 2.278 | 2.189 | 2.061 | |
References
- Steinmetz, C.P. On the Law of Hysteresis. Am. Inst. Electr. Eng. Trans. 1892, 9, 3–64. [Google Scholar]
- Bertotti, G. Hysteresis in Magnetism; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Lin, D.; Zhou, P.; Fu, W.; Badics, Z.; Cendes, Z. A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis. IEEE Trans. Magn. 2004, 40, 1318–1321. [Google Scholar] [CrossRef]
- Popescu, M.; Ionel, D.; Boglietti, A.; Cavagnino, A.; Cossar, C.; McGilp, M. A General Model for Estimating the Laminated Steel Losses under PWM Voltage Supply. IEEE Trans. Ind. Appl. 2010, 46, 1389–1396. [Google Scholar] [CrossRef]
- Amar, M.; Kaczmarek, R. A General Formula for Prediction of Iron Losses under Nonsinusoidal Voltage Waveform. IEEE Trans. Magn. 1995, 31, 2504–2509. [Google Scholar] [CrossRef]
- Kaczmarek, R.; Amar, M.; Protat, F. Iron Loss under PWM Voltage Supply on Epstein Frame and in Induction Motor Core. IEEE Trans. Magn. 1996, 32, 189–194. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. Predicting Iron Losses in Soft Magnetic Materials with Arbitrary Voltage Supply: An Engineering Approach. IEEE Trans. Magn. 2003, 39, 981–989. [Google Scholar] [CrossRef]
- Patsios, C.; Tsampouris, E.; Beniakar, M.; Rovolis, P.; Kladas, A. Dynamic Finite Element Hysteresis Model for Iron Loss Calculation in Non-Oriented Grain Iron Laminations under PWM Excitation. IEEE Trans. Magn. 2011, 47, 1130–1133. [Google Scholar] [CrossRef]
- Liu, C.T.; Lin, H.Y.; Hsu, Y.W.; Lin, S.Y. A Module-Based Iron Loss Evaluation Scheme for Electric Machinery Products. IEEE Trans. Ind. Appl. 2013, 49, 778–783. [Google Scholar]
- Boglietti, A.; Lazzari, M.; Pastorelli, M. Iron Losses Prediction with PWM Inverter Supply Using Steel Producer Data Sheets. In Proceedings of the 1997 IEEE Industry Applications Conference on Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; Volume 1, pp. 83–88.
- Stupakov, O.; Perevertov, O.; Stoyka, V.; Wood, R. Correlation between Hysteresis and Barkhausen Noise Parameters of Electrical Steels. IEEE Trans. Magn. 2010, 46, 517–520. [Google Scholar] [CrossRef]
- Albach, M.; Durbaum, T.; Brockmeyer, A. Calculating core losses in transformers for arbitrary magnetizing currents a comparison of different approaches. In Proceedings of the 27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, 23–27 June 1996; Volume 2, pp. 1463–1468.
- Reinert, J.; Brockmeyer, A.; de Doncker, R. Calculation of Losses in Ferro- and Ferrimagnetic Materials Based on the Modified Steinmetz Equation. IEEE Trans. Ind. Appl. 2001, 37, 1055–1061. [Google Scholar] [CrossRef]
- Chen, Y.; Pillay, P. An improved formula for lamination core loss calculations in machines operating with high frequency and high flux density excitation. In Proceedings of the 37th IAS Annual Meeting, Conference Record of the Industry Applications Conference, Pittsburgh, PA, USA, 13–18 October 2002; Volume 2, pp. 759–766.
- Li, J.; Abdallah, T.; Sullivan, C. Improved Calculation of Core Loss with Nonsinusoidal Waveforms. In Proceedings of the 2001 IEEE Industry Applications Conference on 36th IAS Annual Meeting, Chicago, IL, USA, 30 September–04 October 2001; Volume 4, pp. 2203–2210.
- Liu, J.; Wilson, T.; Wong, R.; Wunderlich, R.; Lee, F. A method for inductor core loss estimation in power factor correction applications. In Proceedings of the 17th Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 10–14 March 2002; Volume 1, pp. 439–445.
- Venkatachalam, K.; Sullivan, C.; Abdallah, T.; Tacca, H. Accurate Prediction of Ferrite Core Loss with Nonsinusoidal Waveforms Using only Steinmetz Parameters. In Proceedings of the 2002 IEEE Workshop on Computers in Power Electronics, Mayaguez, Puerto Rico, 3–4 June 2002; pp. 36–41.
- Ionel, D.; Popescu, M.; McGilp, M.; Miller, T.; Dellinger, S.; Heideman, R. Computation of Core Losses in Electrical Machines Using Improved Models for Laminated Steel. IEEE Trans. Ind. Appl. 2007, 43, 1554–1564. [Google Scholar] [CrossRef]
- Rasilo, P.; Dlala, E.; Fonteyn, K.; Pippuri, J.; Belahcen, A.; Arkkio, A. Model of Laminated Ferromagnetic Cores for Loss Prediction in Electrical Machines. IET Electr. Power Appl. 2011, 5, 580–588. [Google Scholar] [CrossRef]
- Nakamura, K.; Fujita, K.; Ichinokura, O. Magnetic-Circuit-Based Iron Loss Estimation under Square Wave Excitation with Various Duty Ratios. IEEE Trans. Magn. 2013, 49, 3997–4000. [Google Scholar] [CrossRef]
- Greene, J.; Gross, C. Nonlinear Modeling of Transformers. IEEE Trans. Ind. Appl. 1988, 24, 434–438. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Ma, J.; Huang, X.; Fang, Y. Predicting Iron Losses in Laminated Steel with Given Non-Sinusoidal Waveforms of Flux Density. Energies 2015, 8, 13726-13740. https://doi.org/10.3390/en81212384
Chen W, Ma J, Huang X, Fang Y. Predicting Iron Losses in Laminated Steel with Given Non-Sinusoidal Waveforms of Flux Density. Energies. 2015; 8(12):13726-13740. https://doi.org/10.3390/en81212384
Chicago/Turabian StyleChen, Wei, Jien Ma, Xiaoyan Huang, and Youtong Fang. 2015. "Predicting Iron Losses in Laminated Steel with Given Non-Sinusoidal Waveforms of Flux Density" Energies 8, no. 12: 13726-13740. https://doi.org/10.3390/en81212384
APA StyleChen, W., Ma, J., Huang, X., & Fang, Y. (2015). Predicting Iron Losses in Laminated Steel with Given Non-Sinusoidal Waveforms of Flux Density. Energies, 8(12), 13726-13740. https://doi.org/10.3390/en81212384






