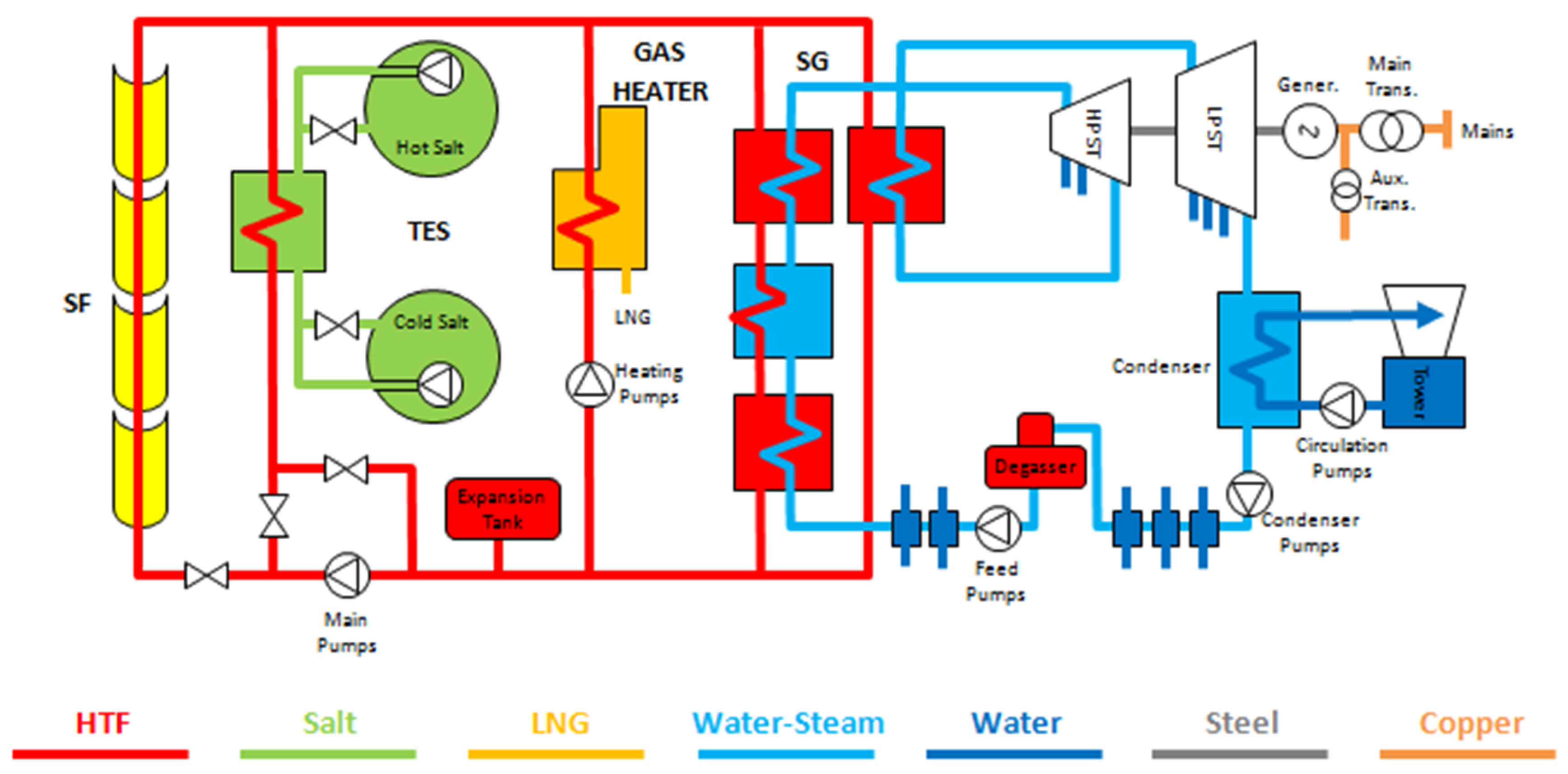
2.1. Description of the Solar Field (SF)
In order to adequately model the thermal-fluid heating process, it is mandatory to understand the main elements of the HTF system. This system contains several solar collector assemblies (SCA),
Figure 2 formed by solar collector elements (SCE),
Figure 3. Each SCE has mirrors (28 mirrors in
Figure 3) as well as absorber pipes arranged in such a way that the SCE is parabolic-trough shaped and the pipes are placed in its focal axis.
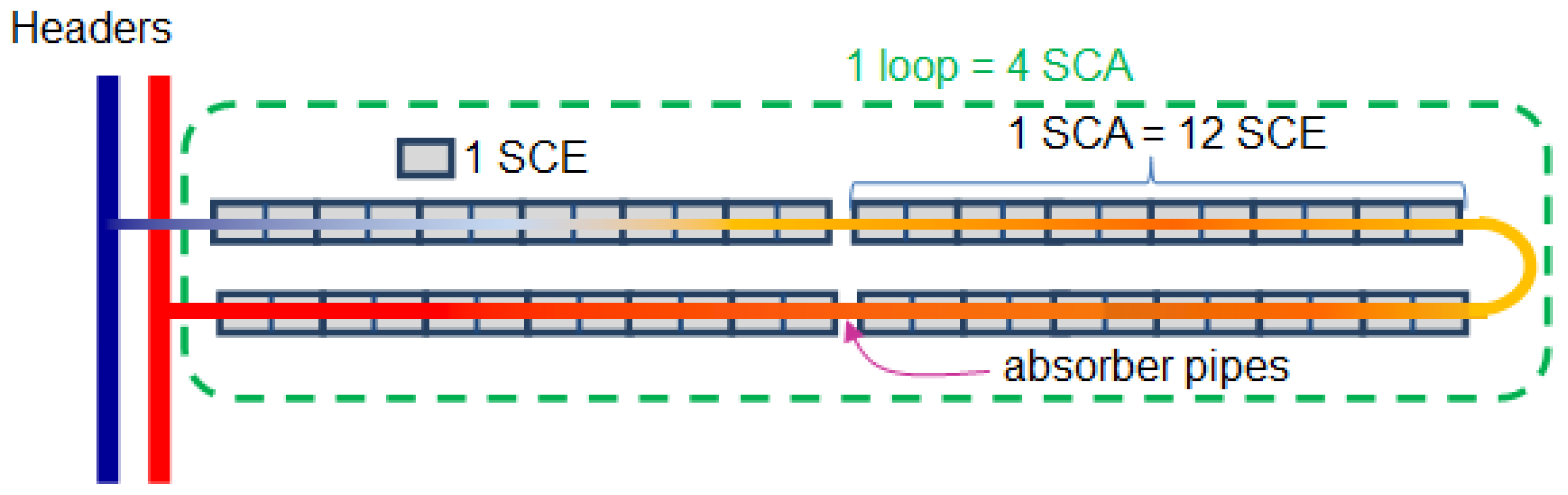
Depending on the solar thermal plant, the SCA may have six, eight or 12 SCEs. The dynamic model developed in this paper is based on the HTF system of the PTC solar plant “La Africana”, located in Cordoba, Spain. In the SF of “La Africana”, each SCE has three absorber tubes arranged in series and each SCA is formed by 12 SCEs.
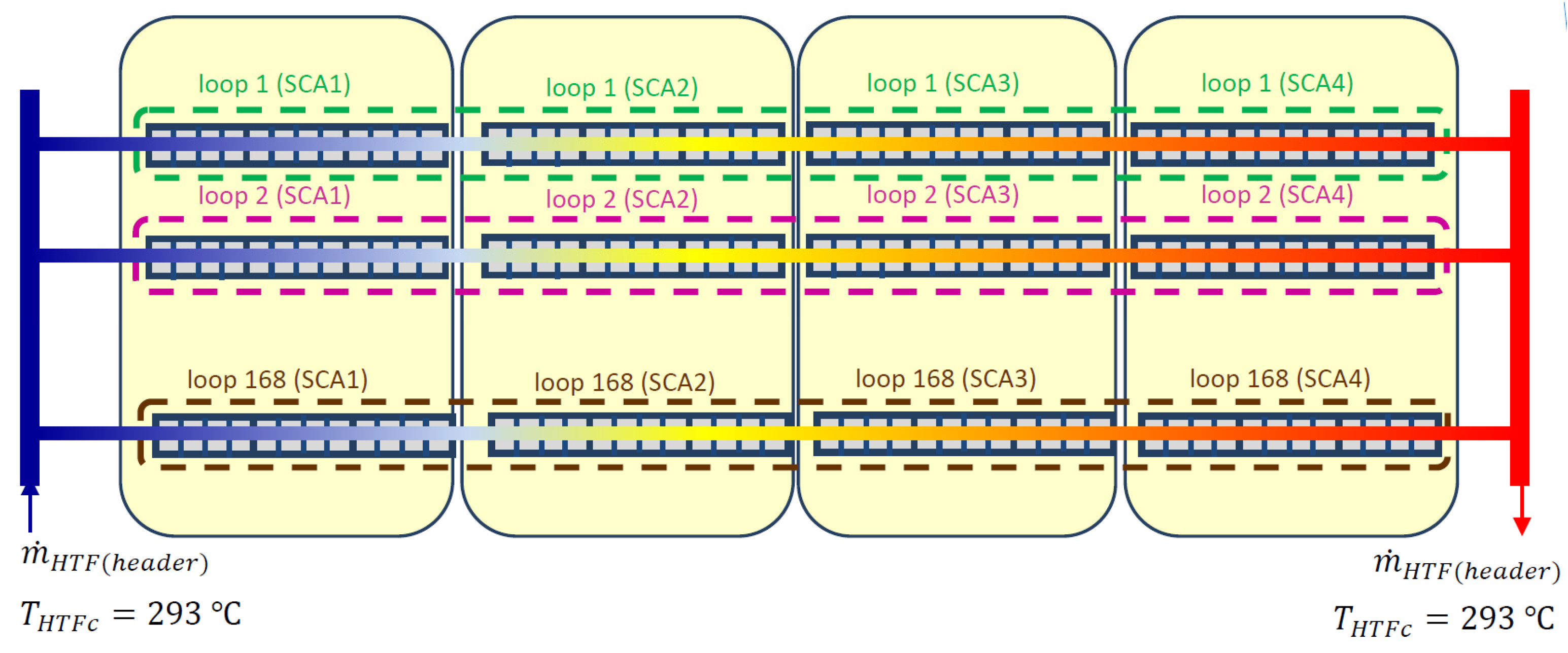
SCAs are arranged in series forming loops. These loops can be U-shaped or W-shaped. In the model described, U-shaped loops with four SCAs each are considered.
Figure 2.
Solar collector assembly (SCA).
Figure 2.
Solar collector assembly (SCA).
Figure 3.
Solar collector element (SCE) with 28 mirrors and three absorber pipes.
Figure 3.
Solar collector element (SCE) with 28 mirrors and three absorber pipes.
The beginning of the loop is linked to a large diameter pipe (cold header) that contains cold HTF (HTF that has not been heated by the solar radiation yet). The end of the loop is linked to another large diameter pipe (hot header) in such a way that, once the fluid coming out of the loops has been heated, it is transported to the steam generator system (SGS) and/or the TES system, depending on the operation mode.
Figure 4 shows one of these loops.
Figure 4.
U-Shaped loop in PTC solar plants.
Figure 4.
U-Shaped loop in PTC solar plants.
The elements included in the HTF system, also referred to as SF, modeled in this paper has 168 loops with 4 SCA per loop. Each SCA consists on 12 SCE that contains 3 absorber pipes. Therefore, this HTF systems has 24.192 absorber pipes transporting the fluid.
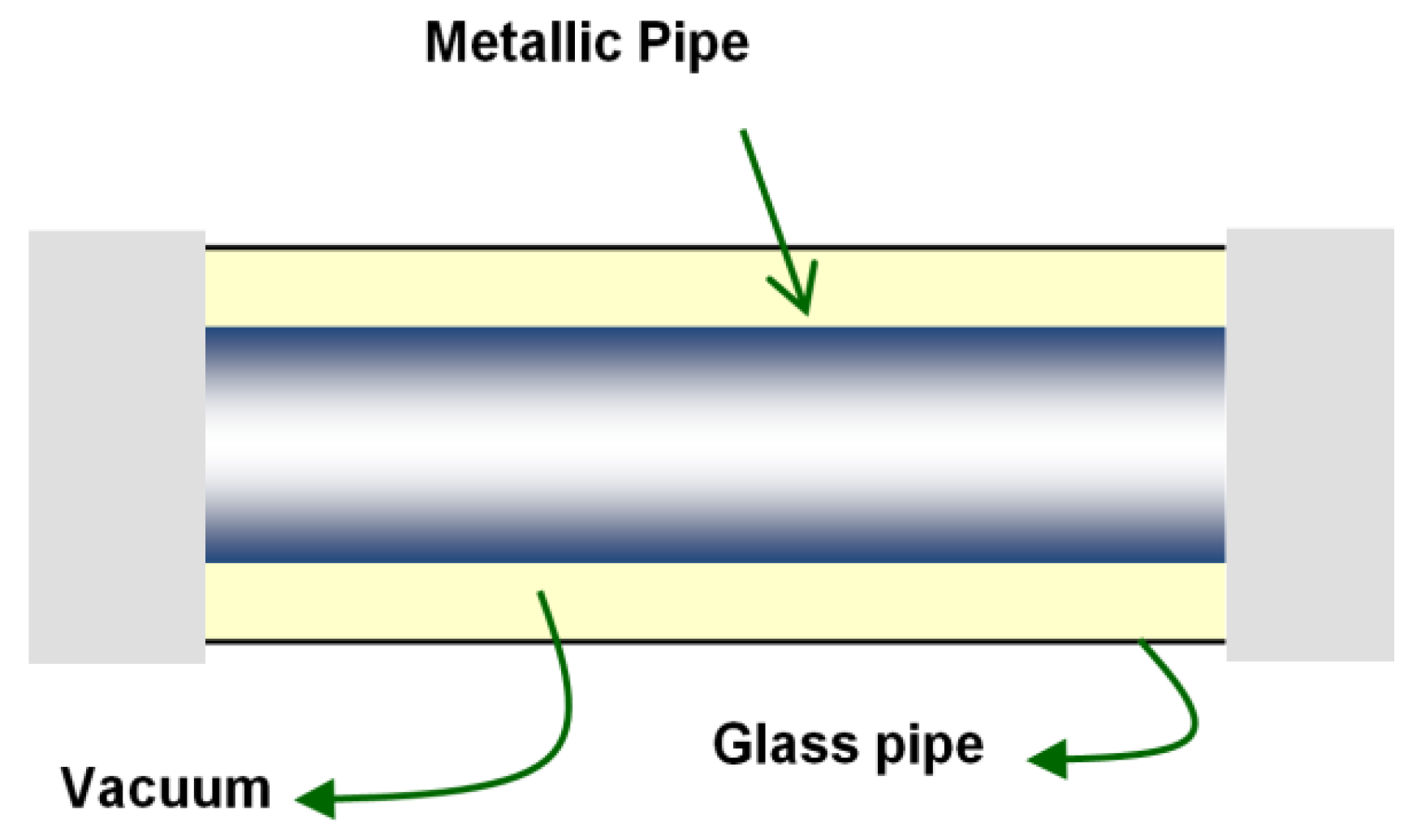
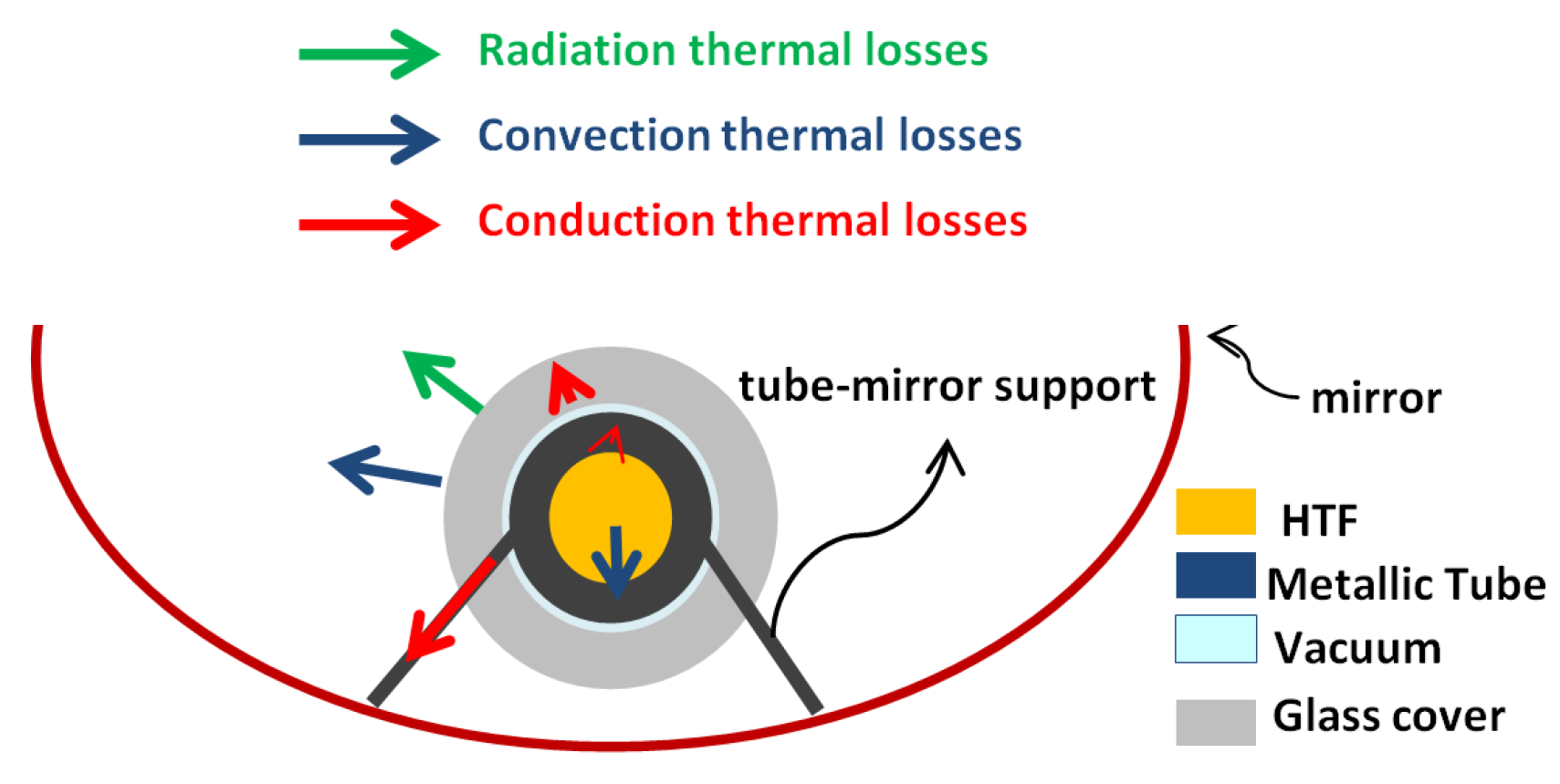
The most important elements to take into account in the modeling of this process are the absorber pipes, shown in
Figure 5 They are in charge of absorbing the solar radiation and turning it into thermal energy. Thanks to the fluid that flows through them, they also transport that thermal energy to the rest of the plant where needed.
They consist of two concentric pipes. The inner one is metallic with a blue film to minimize radiation thermal losses, whereas the outer pipe is made of glass. Vacuum is created between them in order to avoid convention and conduction thermal losses.
Figure 6 shows the main parts of an absorber pipe.
2.2. Description of the Heat Transfer Fluid (HTF)-Heating Process
The solar radiation is reflected by the mirrors over the absorber pipes, thus heating the HTF. A comparative study of the different thermal fluids most currently used in PTC power plants (oil, molten salt and water steam) is presented in [
7]. The authors conclude that direct steam generation is more efficient than the other two. In spite of that, and although other alternatives are being studied [
8,
9,
10,
11,
12,
13,
14], most of the PTC plants use some sort of synthetic oil, mainly due to its lower freezing point (around 12 °C) when compared to other HTFs.
According to the literature, there are different kinds of fluids that have been or are being analyzed to be used as HTF. One of them is molten salt. Taking into account that they are used to store thermal energy in the TES, it would be relatively easy to use it also in the SF. The main problem is its high freezing point (around 140 °C). Due to the small internal diameter of the absorber pipes, having part of the molten salts freeze would cause blockages that could cause the pipes to break. Other installations use direct steam generators (DGS) instead, in which water acts as HTF. The main advantages of this technology are its lower thermal losses and, therefore, its higher cycle efficiency. Its drawbacks are the higher pressures required and the more complex control needed. These drawbacks are also present in installations that use gas and air as HTF. Two new research lines are emerging nowadays: nanofluids and ionic fluids. The first one consists of adding metallic nanoparticles or carbon nanotubes in order to improve its optical and thermal properties. Ionic fluids are very promising. They are formed by joining anions and cations so that they can result in billions of different ionic fluids for multiple applications.
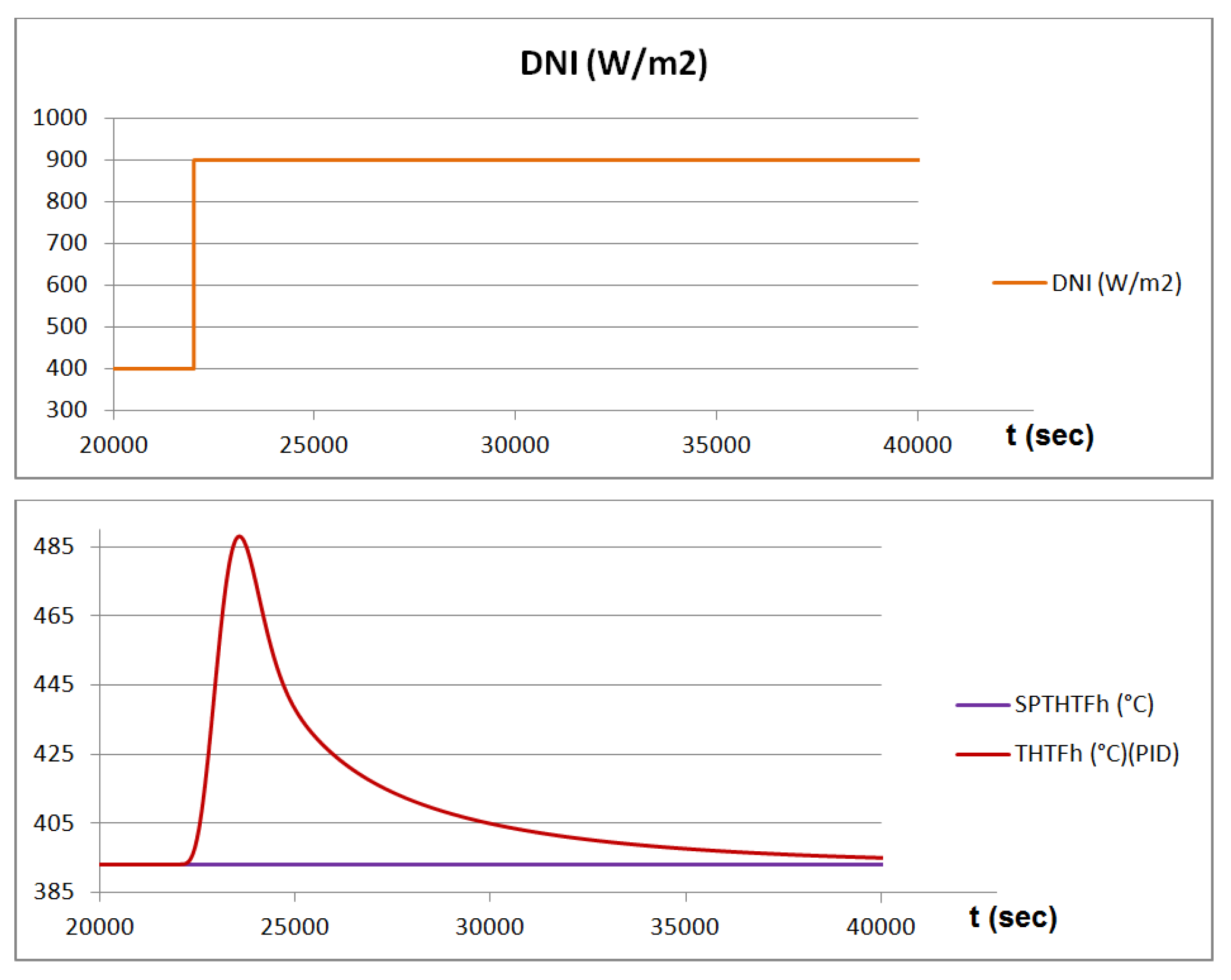
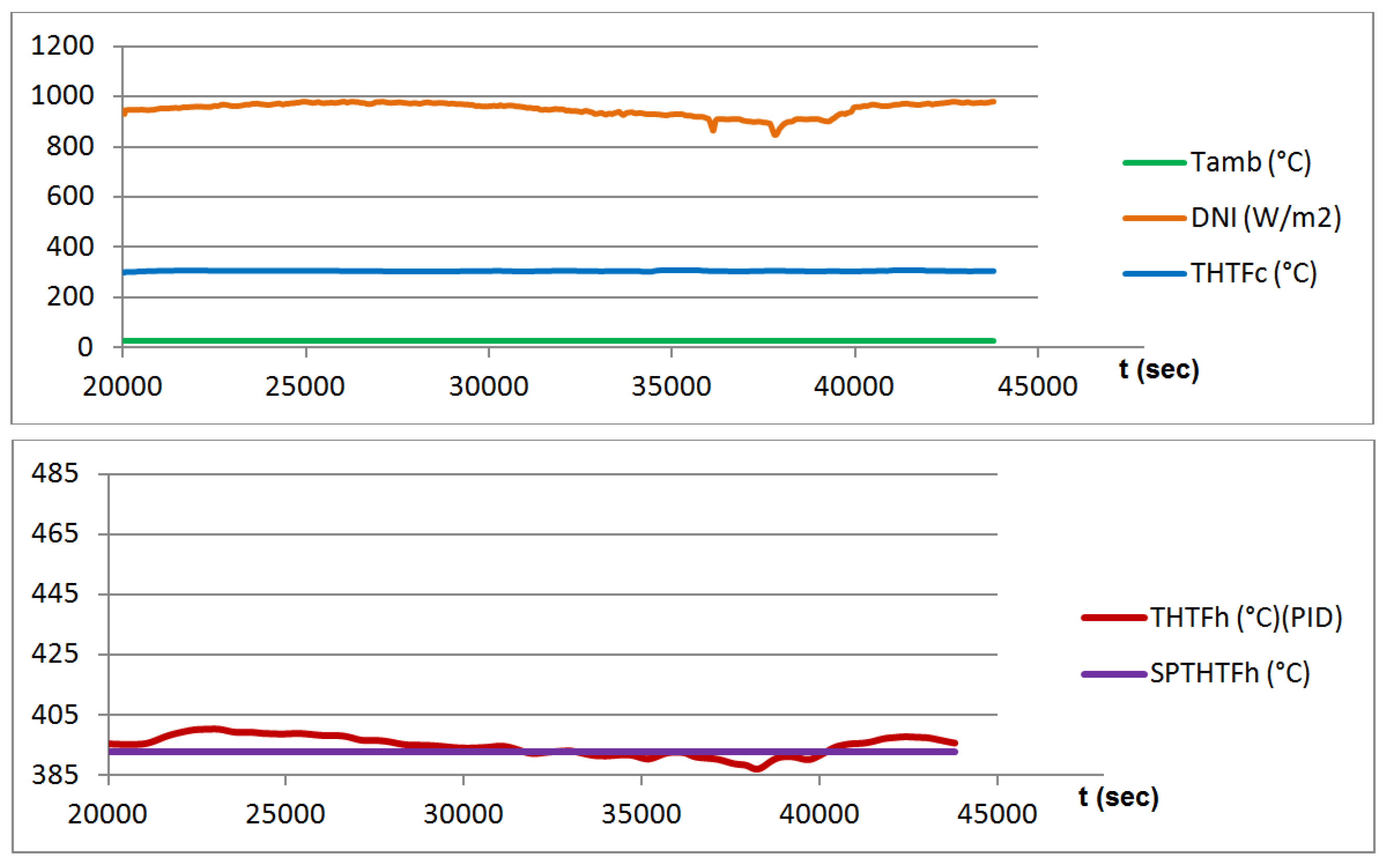
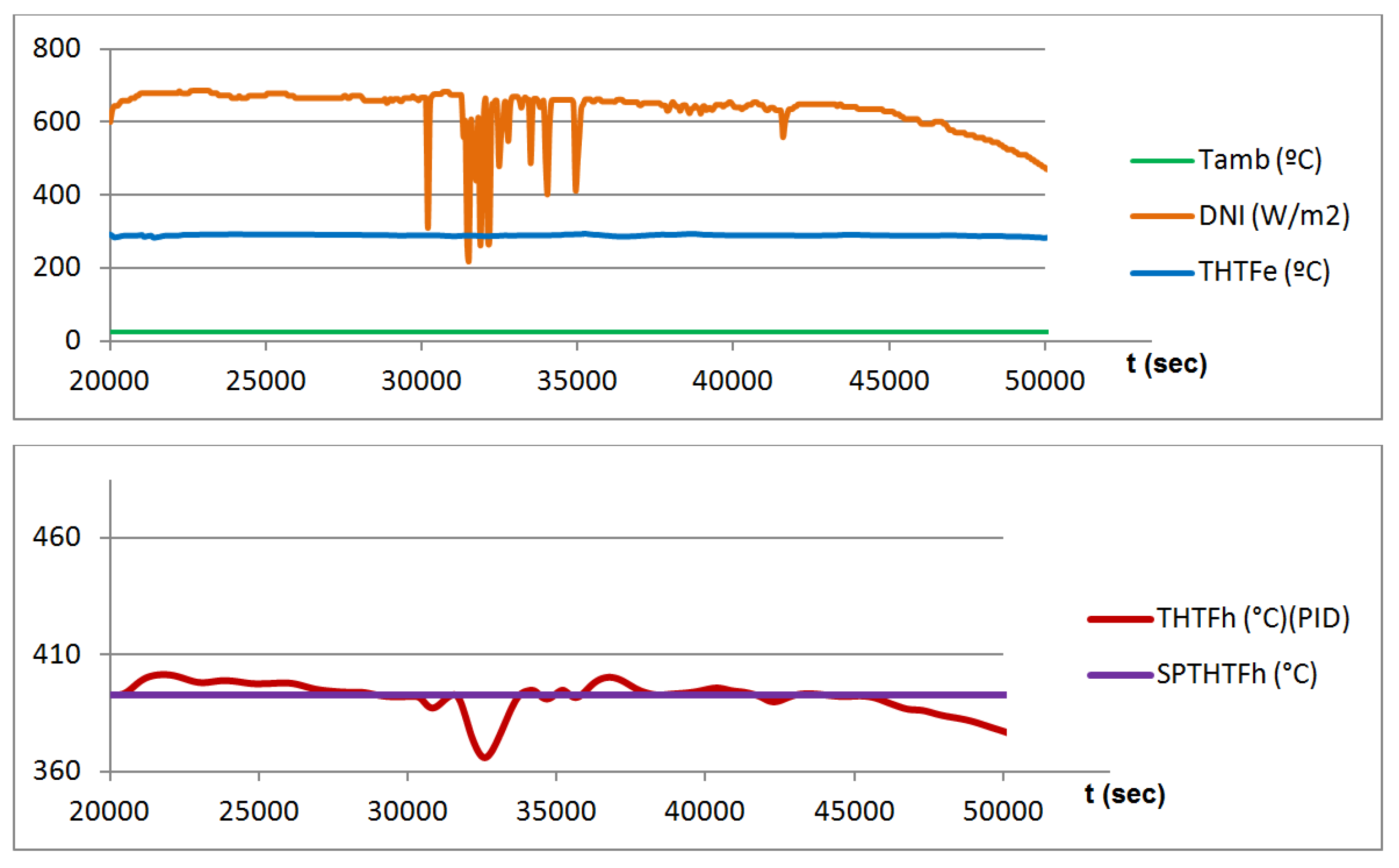
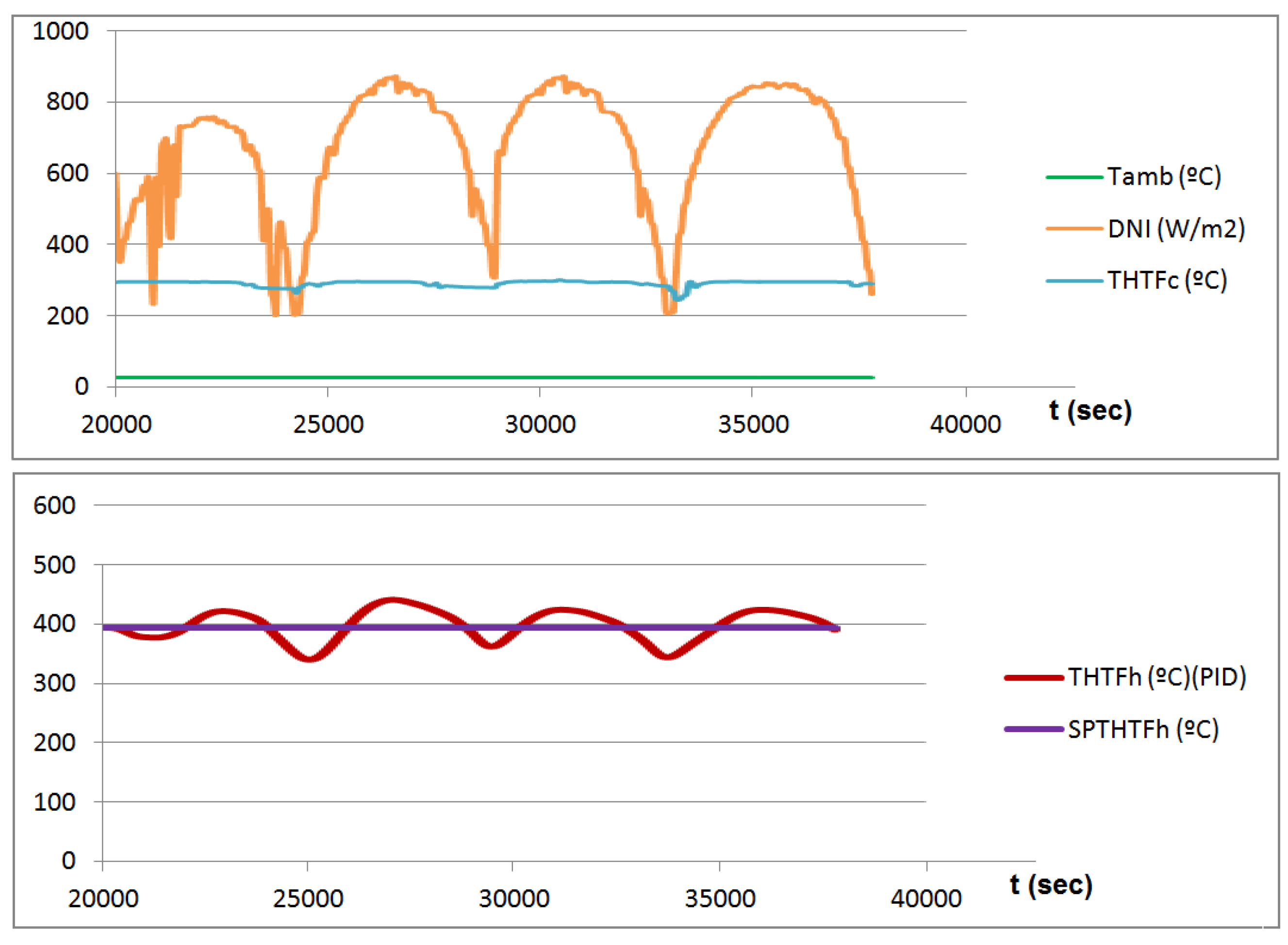
Using synthetic oil as HTF also has drawbacks, the main one being its maximum operation temperature, which is around only 400 °C in the best-case scenario. This critical point can be easily exceeded when direct solar irradiation (DNI) is high. Given that solar radiation is a phenomenon that can vary widely in a short space of time, a good regulation method is necessary. This method should allow the oil to leave the SF with the highest possible temperature while, at the same time, preventing the oil from exceeding its maximum operating point.
To meet this goal, the control method varies the mass flow of the fluid in such a way that, if the oil temperature exceeds a given set point (393 °C in the case considered), the mass flow will increase. Thus, the time the fluid stays in the SF will be shorter and its temperature will drop. Similarly, if the oil temperature is below the set point, the mass flow must be reduced.
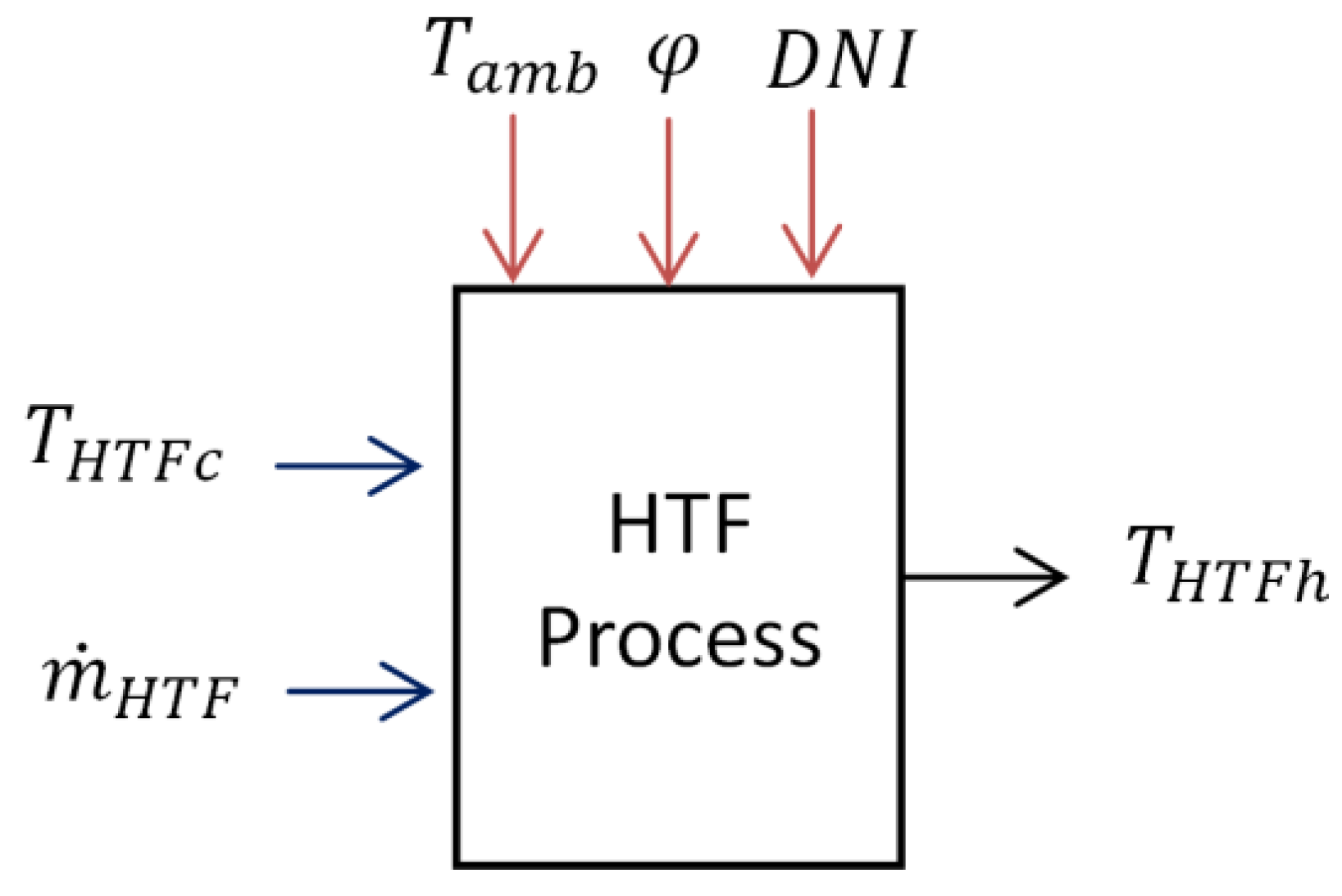
Table 1 and
Table 2 show all the variables (perturbations, input, output and control variables) involved in the HTF-heating process:
Table 1.
Input, output and control variables of the HTF-heating process.
Table 1.
Input, output and control variables of the HTF-heating process.
| Variable | Acronym | Description |
|---|
| Input | THTFc | Heat transfer fluid (HTF) temperature at the input of the solar field (SF) (°C) |
| Output | THTFh | HTF temperature at the output of the SF (°C) |
| Control | | HTF mass flow (kg/s) |
Table 2.
Perturbations of the HTF-heating process.
Table 2.
Perturbations of the HTF-heating process.
| Perturbations | Description |
|---|
| Direct solar irradiation (DNI) | Direct normal irradiation (W/m2) |
| φ | Angle of incidence (°) |
| Tamb | Ambient temperature (°C) |
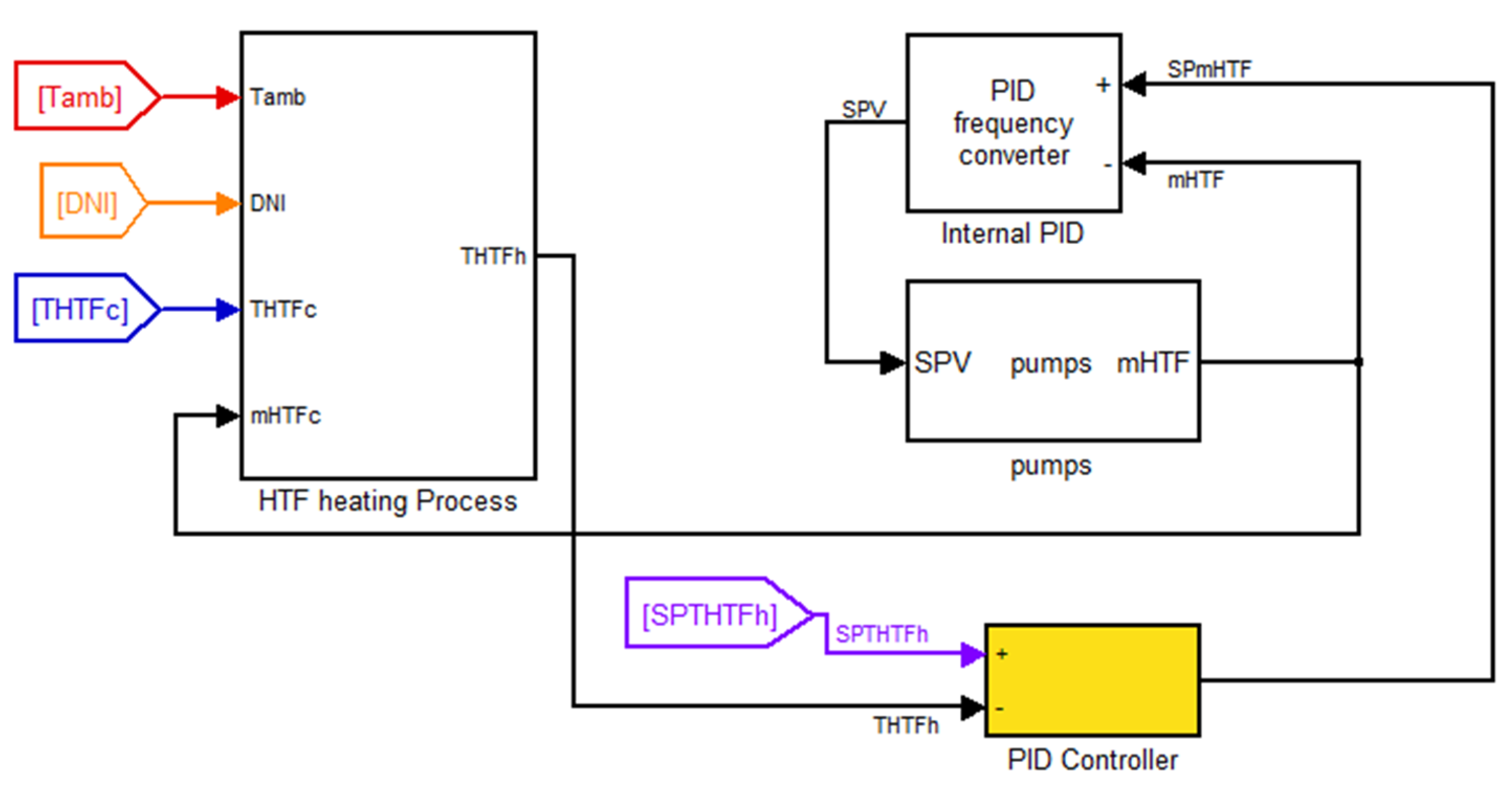
Figure 7 shows the block diagram that represents the process described above.
Figure 7.
Heat transfer fluid (HTF)-heating process model.
Figure 7.
Heat transfer fluid (HTF)-heating process model.
The goal of this work is to obtain a simple, accurate and dynamic model that allows designers to optimize the control of this process.
2.3. Modeling of the HTF-Heating Process
Several models of different parts of the PTC thermoelectric plants have been developed in the last years. In [
15], a mathematical model is described that compares the quasi-dynamic test (QDT) and the steady-state test (SST) in five different types of collectors. In [
16], the authors present a dynamic model for the collector field and a steady-state model for the power plant; this paper is based on a real PTC solar plant and the whole plant has been mathematically modeled. In [
17] models for different geometries and insulation materials with different thicknesses have been carried out in order to select the best one for high temperature processes; in this paper, all the models are numerically compared and, hence, absolute values are not provided. A paper written by one of the main manufacturers of solar absorber pipes [
18] explains all the thermal exchanges between the different parts or elements that form a pipe; this paper is a good starting point to develop the dynamic model of the HTF-heating process. In reference [
19], the authors established a computational fluid dynamics (CFD) model to calculate the temperature profile on the wall of the absorber tubes of DSG plants. The authors of [
20] compare three different models of absorber pipes: a one- and a two-dimensional analytical model and a three-dimensional one using finite-element techniques.
It must be said that most of these references model the absorber pipes in order to determine the gradient of temperature between their elements, but they are not used as a dynamic model susceptible of being used in the control of the HTF-heating process.
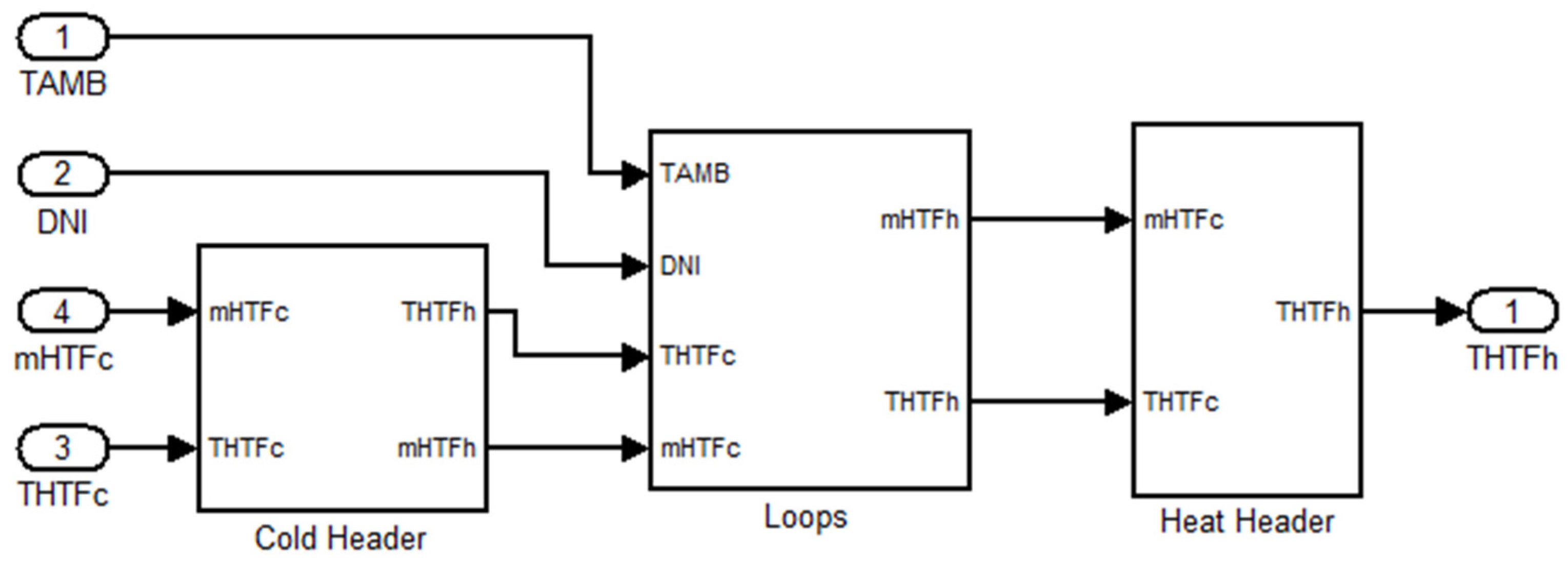
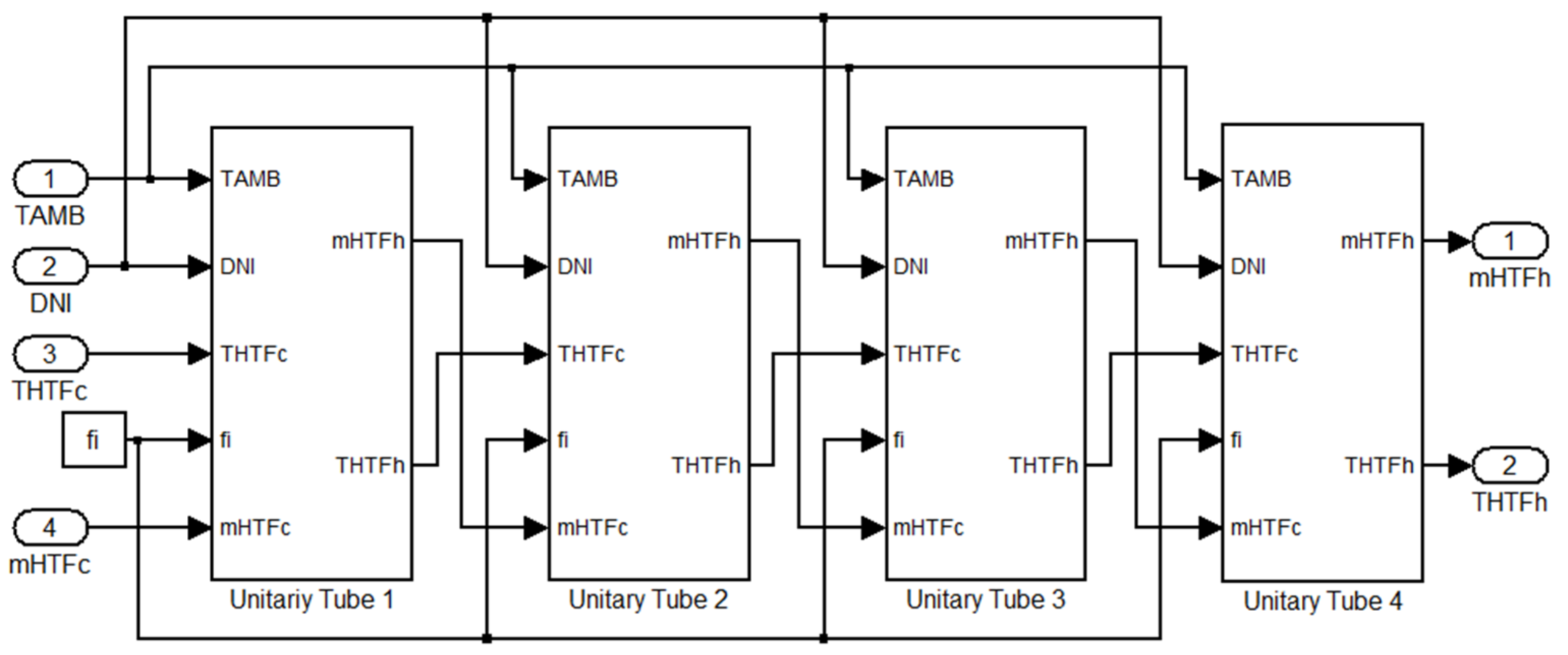
To model the HTF-heating process, some simplifications of the SF must be carried out, namely, the 168 loops have been modeled as four serial-connected unitary blocks. Each unitary block contains 168 parallel-connected SCAs. This configuration is shown in
Figure 8.
Figure 8.
Loop simplification.
Figure 8.
Loop simplification.
Similarly, the headers are modeled as four serial-connected blocks, each containing a quarter of the total amount of HTF.
Figure 9 shows the block diagram of the SF to be used in the modeling of the HTF-heating process, and
Figure 10 shows the blocks used to model the loops described above.
Figure 9.
Solar field (SF) model.
Figure 9.
Solar field (SF) model.
These Simulink blocks can be easily used for modeling larger or smaller SFs by respectively adding or removing unitary tubes.
Energy transfer from solar radiation to the fluid takes place inside the unitary tubes as well as inside the headers. For that reason, all the equations related to mass and energy conservation principles should be included in those blocks.
The conservation energy principle provides the following equations:
Energy can be transferred as work, heat and mass:
where
is the absorbed or released heat,
is the work done by the HTF and e is the energy transported per unit mass of a moving fluid, whose expression is given by Equation (3):
Finally, assuming that in the absorber pipes kinetic and gravitational energies are negligible and that, due to the mass conservation principle in the control volume considered in the process, input and output mass flows are similar, Equation (2) is simplified as indicated in Equation (4):
where
is the heat that the HTF absorbs from the solar radiation once all the losses due to thermal transfer from the fluid to the environment have been taken into account.
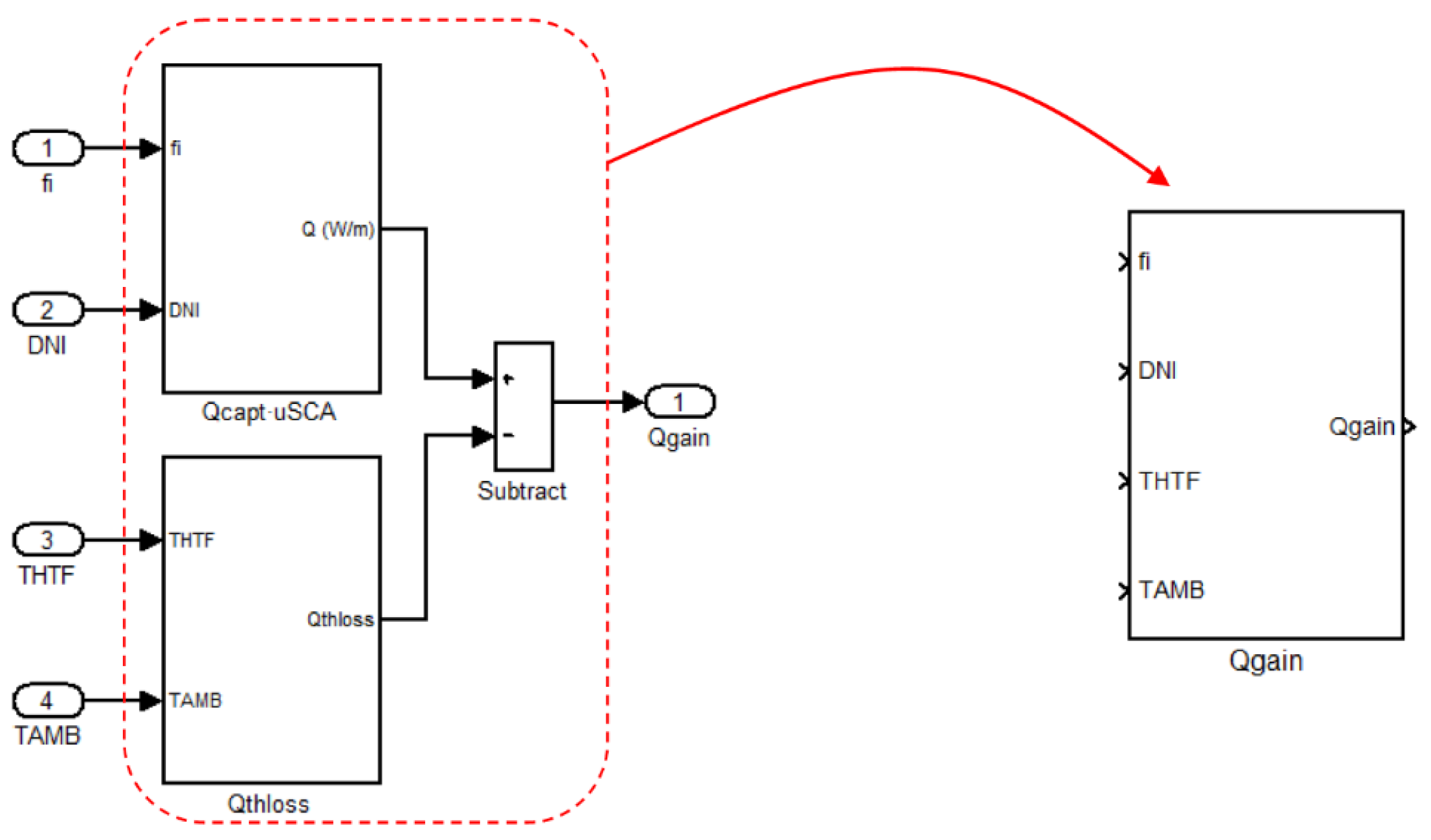
The net heat transferred from the HTF to other subsystems of the solar plant is the result of the total heat absorbed by the fluid minus the thermal losses due to radiation, convection and conduction from the fluid to the air around it.
The heat absorbed by the fluid depends on geometric, optical and thermal factors. Firstly, not all the solar radiation that reaches the mirrors (
) is reflected over the absorber tubes and then absorbed by the fluid, due to phenomena such as shadows, angle of incidence far from the optimal 90°, dirty mirrors, non-optimal reflectivity and transmissivity, etc. This results in the heat that reaches the fluid being reduced by the efficiency of the SCA (
). Additionally, of all the heat reaching the fluid, some is lost in unwanted thermal transfers (
):
All these phenomena have been modeled in a Simulink block (
Figure 11) called
.
Figure 11.
Simulink block model to calculate .
Figure 11.
Simulink block model to calculate .
Figure 12 shows all the thermal exchanges involved in the different parts of the SCE (mirrors, absorber tube, HTF) with the environment. Some of those losses are negligible when compared to others [
15,
16,
17]. This is the case of conduction and convection losses between the outer wall of the metallic tube and the inner wall of the glass cover (thanks to the vacuum created between them), or of conduction thermal losses produced in the walls of the tubes to mention a few.
Figure 12.
Thermal exchanges between solar collector elements (SCE) and surround ambient.
Figure 12.
Thermal exchanges between solar collector elements (SCE) and surround ambient.
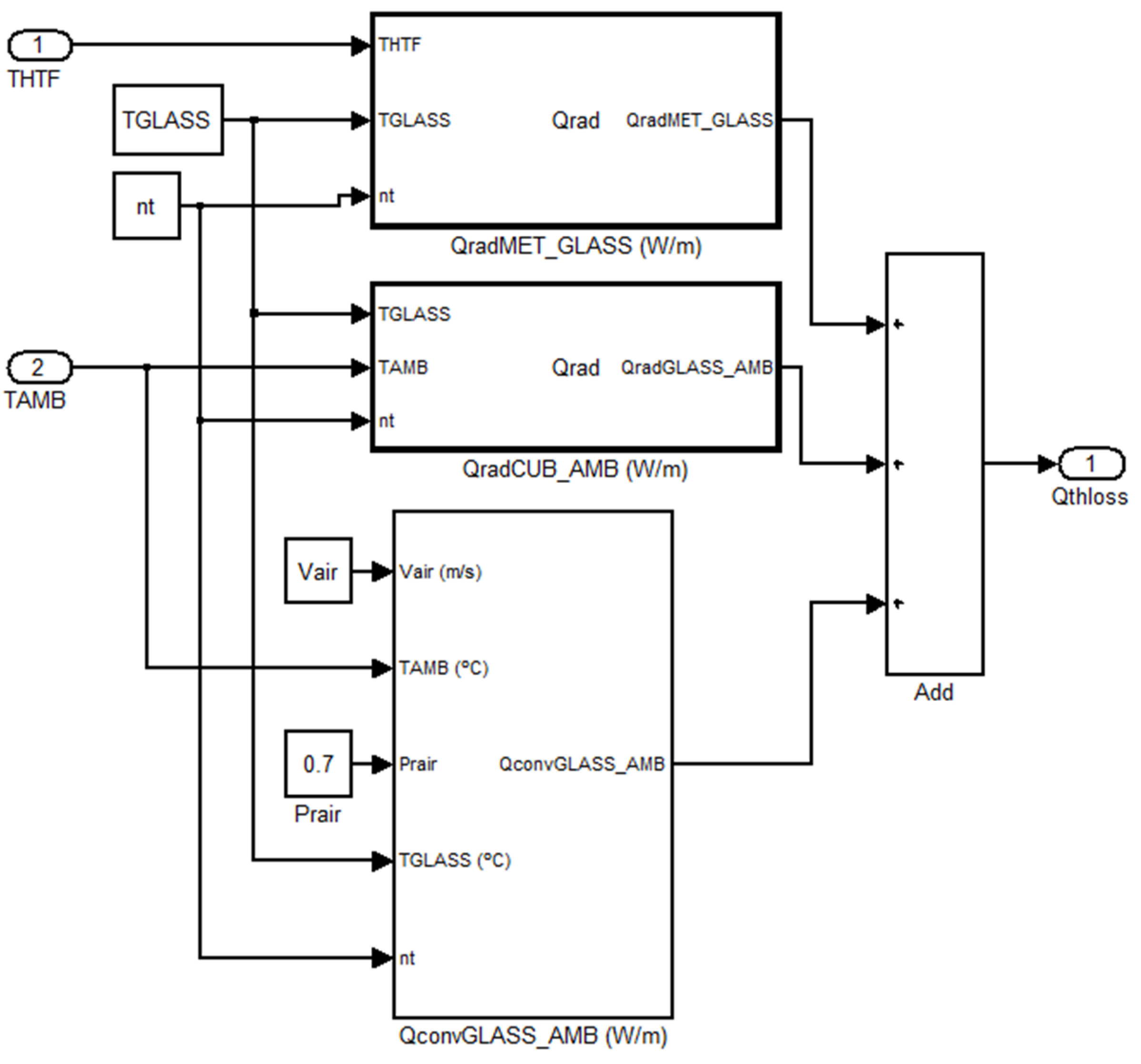
Figure 13 shows the Simulink blocks used to model all those thermal losses, which are included in the
block of
Figure 11.
Several equations are included in these blocks:
where
represents the radiation thermal losses per meter (W/m) from the outer wall of the absorber pipe glass cover to the environment,
is the emissivity coefficient of the external surface of the glass cover,
is the Stefan-Boltzmann constant (W/m
2·C
4),
is the external surface of the absorber pipe glass cover per unit length (m
2/m) and
and
are, respectively, the glass cover and the ambient temperatures (°C):
where
represents the convection thermal losses per meter (W/m) from the outer wall of the absorber pipe glass cover to the surround ambientand
is the convection coefficient between the external surface of the glass cover and the surround ambient. This coefficient is highly dependent on wind speed and can be calculated as:
In Equation (8), is the dimensionless Nusselt number, is the outer diameter of the glass cover and is the thermal conductivity of the air.
To calculate the Nusselt number, Hilpert equation for forced convection flow is used:
where
Re is the dimensionless Reynolds number and parameters,
C and
m depend on the value of the Reynolds number.
is the dimensionless Prandtl number of the air, the value of which is around 0.7.
Finally, the dimensionless Reynolds number of the air over the outer wall of the glass cover is calculated from Equation (10):
where
are the air speed, density and dynamic viscosity respectively.
Equation (11) is used to calculate thermal radiation transference from the outer surface of the metallic pipe to the inner wall of the glass cover
:
where
is the external surface of the metalic pipe per unit length (m
2/m) and
and
are, respectively, the metallic pipe and the glass cover temperatures (°C).
Figure 13.
Thermal losses blocks.
Figure 13.
Thermal losses blocks.
Once all the blocks have been defined and all the equations have been included, the dynamic model of the HTF heating process is obtained.
Figure 14 shows the Simulink diagram that includes all the blocks and equations described above. Inside that block there are the four unitary tubes that contain the time-dependent Equation (4) as well as the block
described in
Figure 11. In this way, the fluid temperature varies along the path as do all the temperature-dependent variables (enthalpy, fluid density,
etc.).
Figure 14.
HTF heating process.
Figure 14.
HTF heating process.