Bi-Level Optimization for Available Transfer Capability Evaluation in Deregulated Electricity Market
Abstract
:1. Introduction
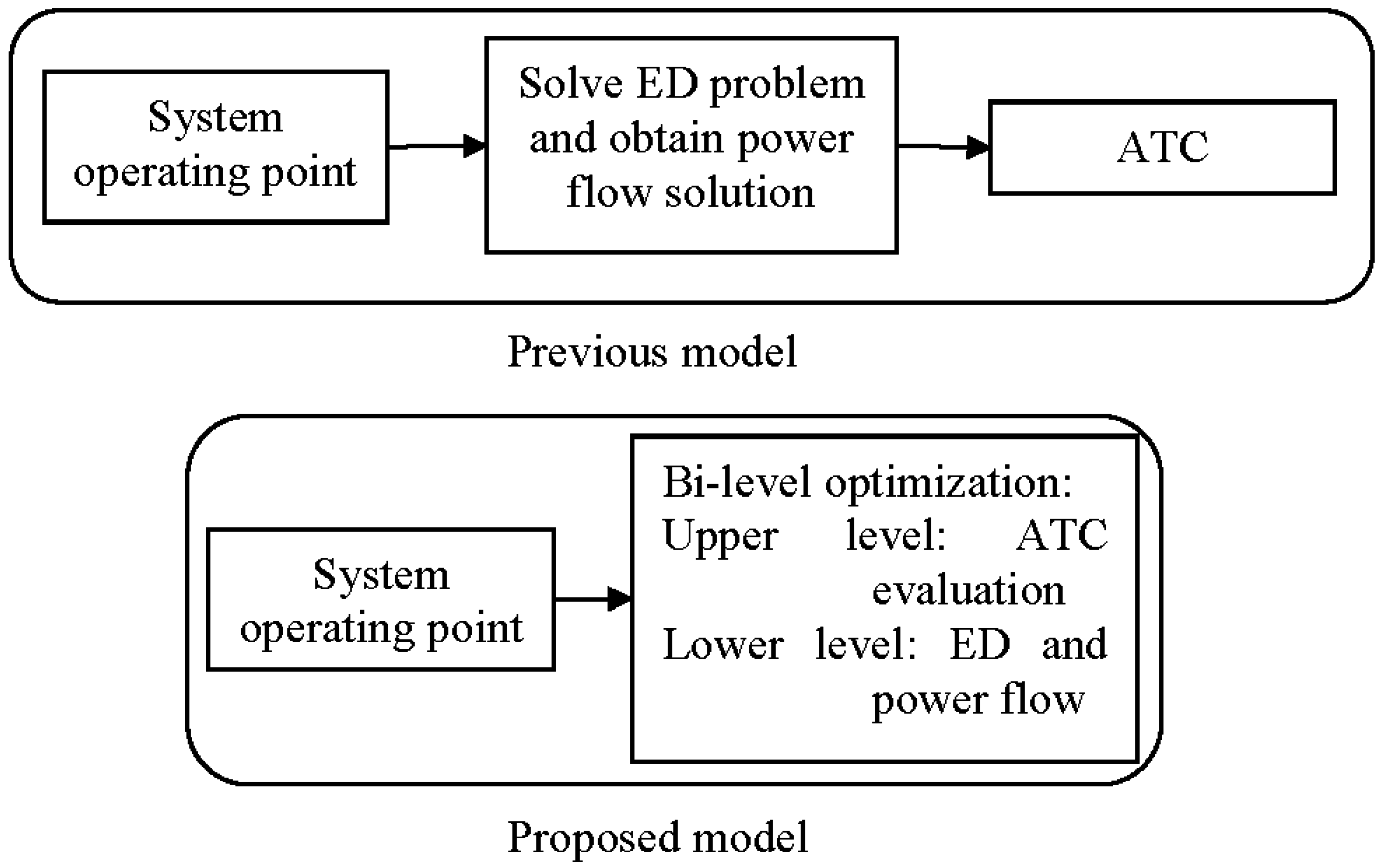
2. Bi-Level Optimization for ATC Evaluation
2.1. ISO’s Economic Dispatch
2.2. Bi-Level Optimization Model for ATC Evaluation
2.3. MPEC Formulation of Bi-Level Optimization Model
2.4. MILP Transformation
3. Case Studies
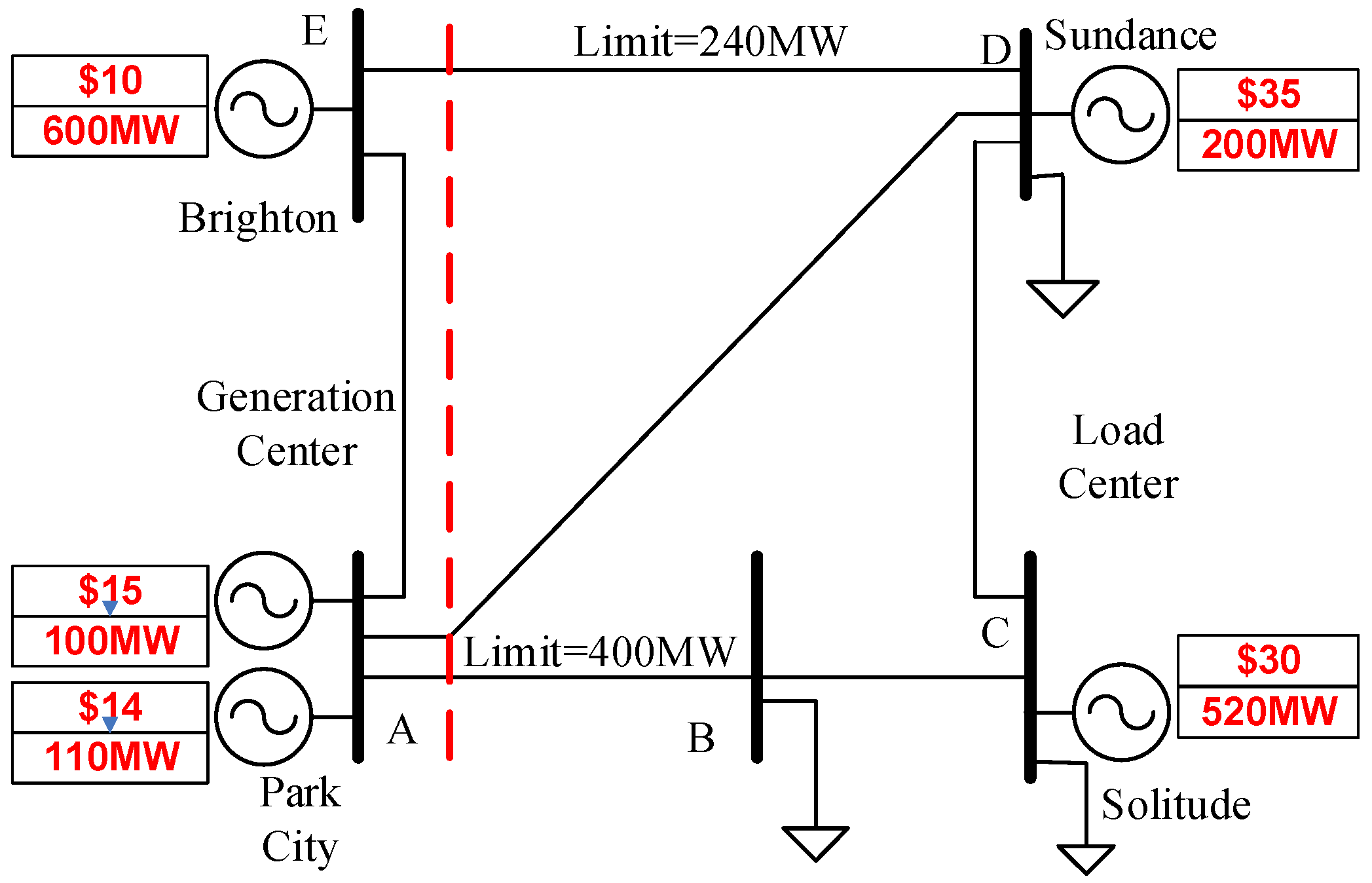
3.1. PJM 5-Bus System
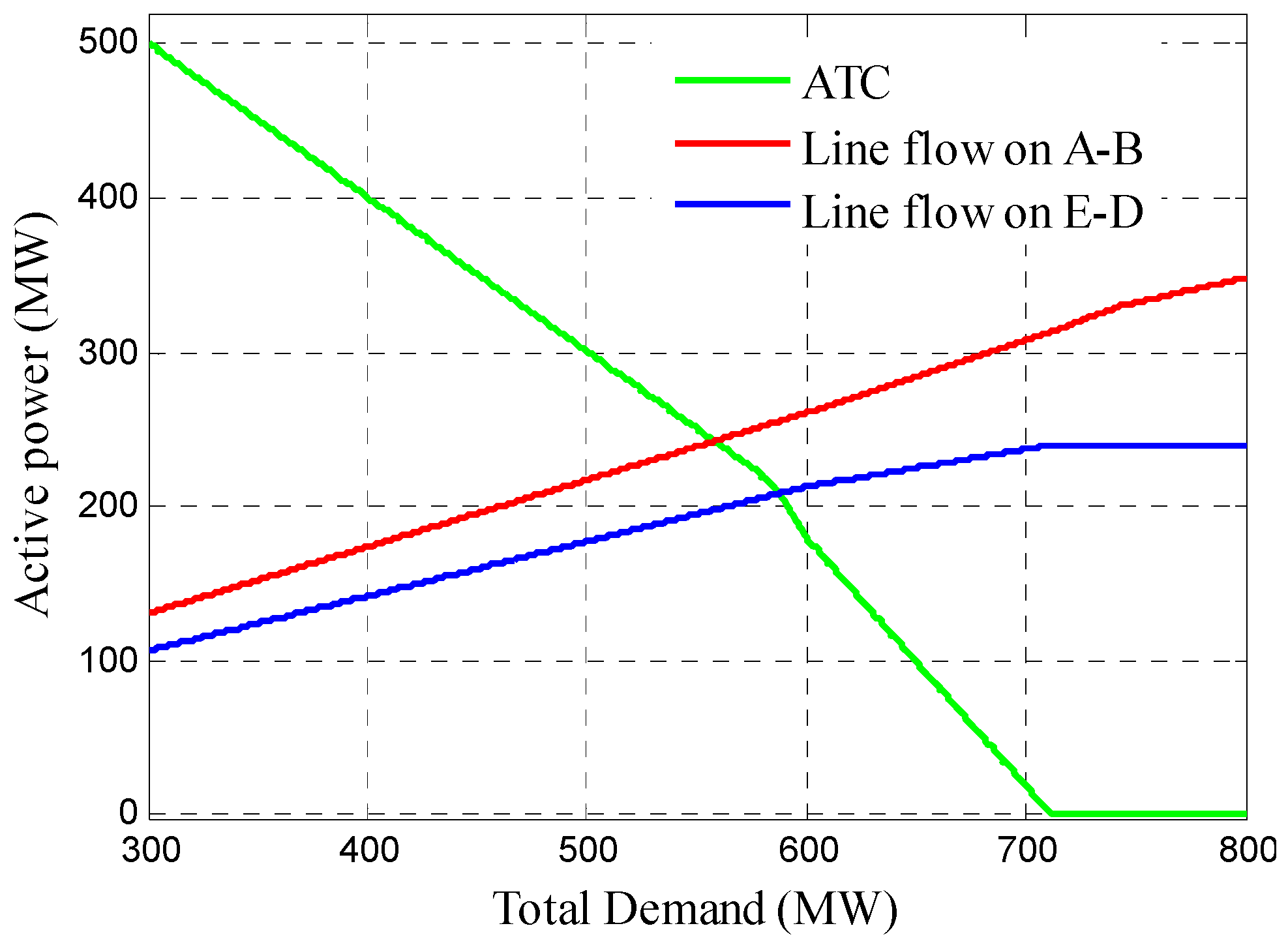
| Total Demand Level (MW) | |||||
|---|---|---|---|---|---|
| 400 | 500 | 600 | 700 | 800 | |
| ATC (MW) | 400.7 | 300.7 | 179.8 | 19.0 | 0 |
| Cost ($) | 4000 | 500 | 6000 | 7400 | 9996 |
| G1 | 0 | 0 | 0 | 100 | 110 |
| G2 | 0 | 0 | 0 | 0 | 100 |
| G3 | 0 | 0 | 0 | 0 | 0 |
| G4 | 0 | 0 | 0 | 0 | 42.24 |
| G5 | 400 | 500 | 600 | 600 | 547.76 |
| A–B | 173.8 | 217.2 | 260.7 | 307.59 | 348.1 |
| E–D | 141.9 | 177.4 | 212.9 | 237.13 | 240 |
| Tie-Line Outage | ||||
|---|---|---|---|---|
| No outage | E–D | A–B | A–D | |
| ATC (MW) | 18.975 | 63.736 | 0 | 0 |
| Cost ($) | 7400 | 7400 | 12,326.346 | 10,664.084 |
| G1 | 100 | 100 | 0 | 0 |
| G2 | 0 | 0 | 0 | 0 |
| G3 | 0 | 0 | 266.317 | 0 |
| G4 | 0 | 0 | 0 | 146.563 |
| G5 | 600 | 600 | 433.683 | 553.437 |
| A–B | 307.567 | 380.427 | – | 313.437 |
| E–D | 237.137 | -- | 240 | 240 |
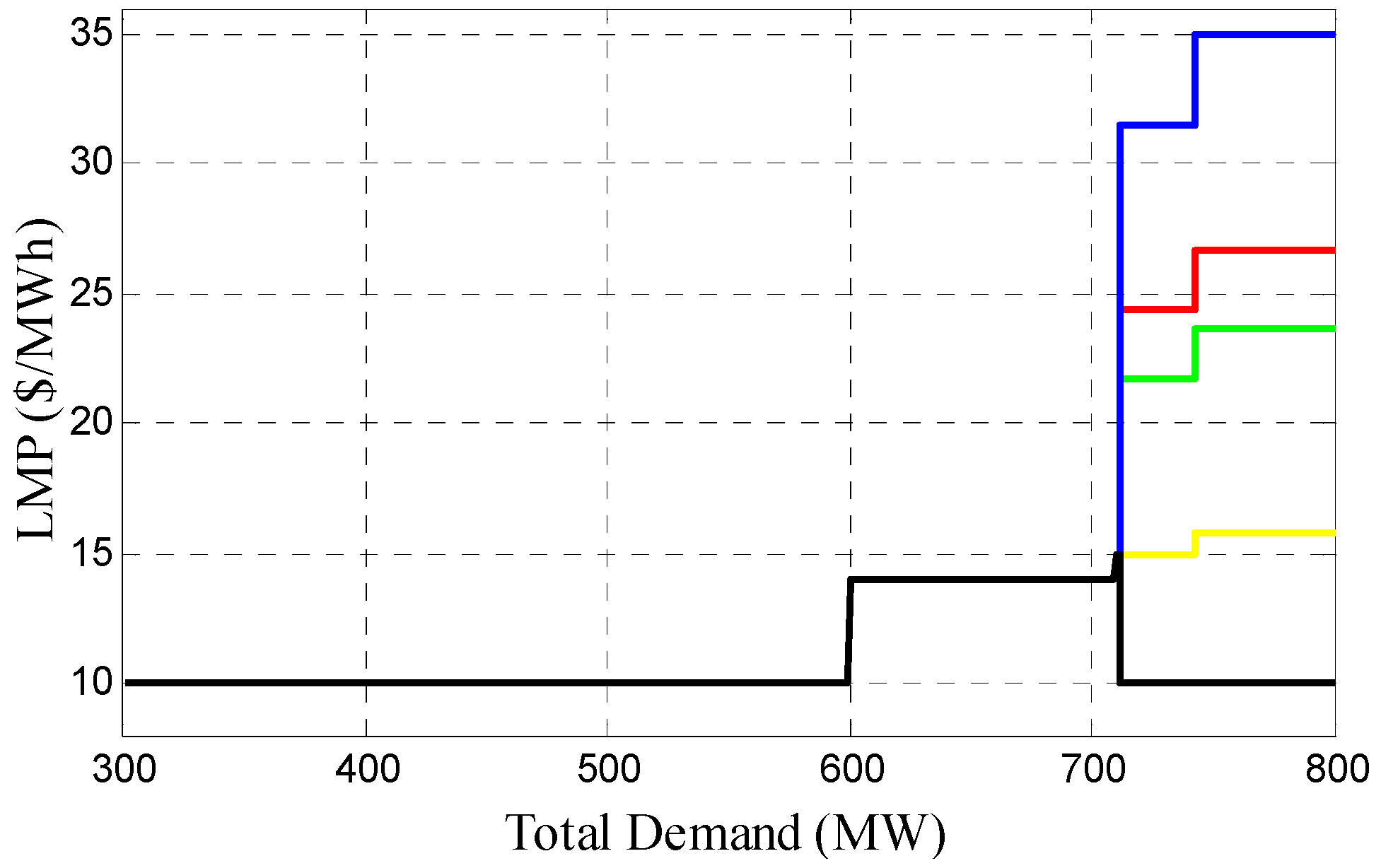
| Tie-Line Outage | Bus LMP ($/MWh) | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| No outage | 14 | 14 | 14 | 14 | 14 |
| E–D | 14 | 14 | 14 | 14 | 14 |
| A–B | 13.477 | 30 | 30 | 30 | 10 |
| A–D | 12.132 | 21.5 | 25.102 | 35 | 10 |
3.2. IEEE 30-Bus System
| Gen. Unit | Bus | Cost bid ($/MWh) | Pmax (MW) |
|---|---|---|---|
| 1 | 1 | 10 | 200 |
| 2 | 2 | 15 | 100 |
| 3 | 22 | 30 | 50 |
| 4 | 27 | 35 | 55 |
| 5 | 23 | 40 | 30 |
| 6 | 13 | 45 | 40 |
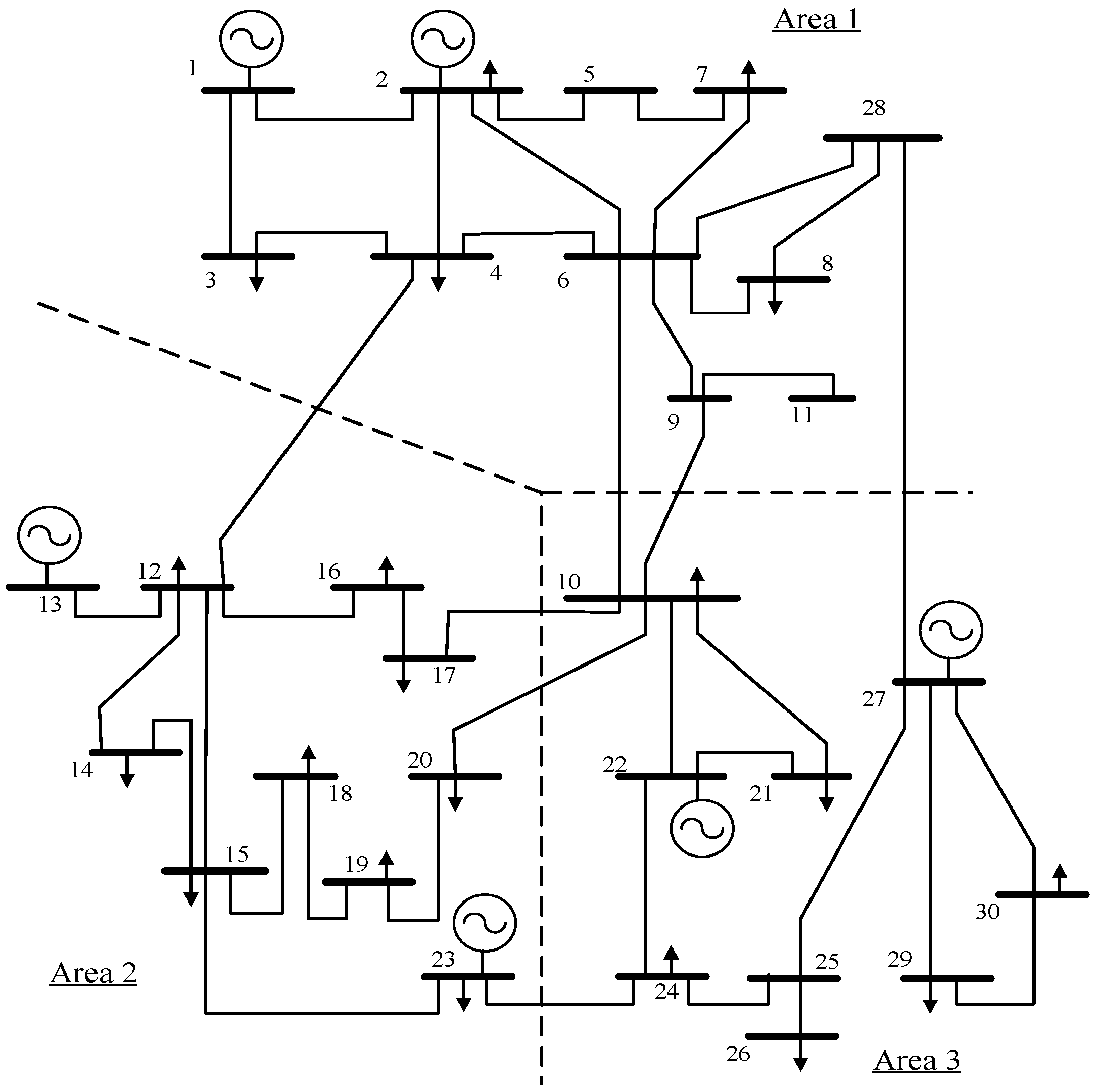
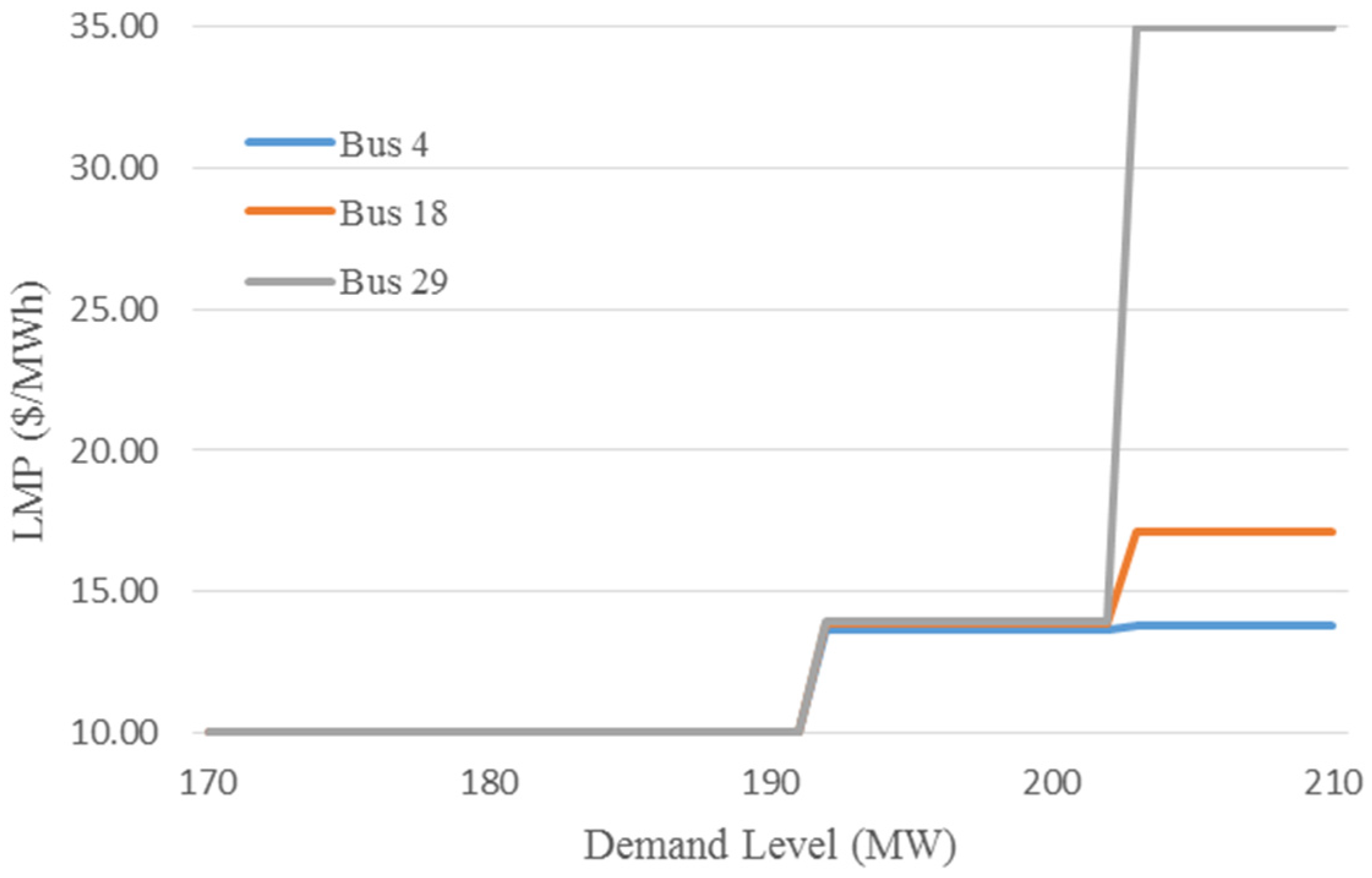
| Total Demand Level (MW) | ||||
|---|---|---|---|---|
| 180 | 189.2 | 200 | 210 | |
| Cost ($) | 1800 | 1892 | 2033.45 | 2367.26 |
| G1 | 180 | 189.2 | 193.31 | 193.286 |
| G2 | 0 | 0 | 6.69 | 7.529 |
| G3 | 0 | 0 | 0 | 0 |
| G4 | 0 | 0 | 0 | 9.185 |
| G5 | 0 | 0 | 0 | 0 |
| G6 | 0 | 0 | 0 | 0 |
| Bus 6-10 | 15.75 | 16.56 | 17.51 | 17.73 |
| Bus 9-10 | 27.57 | 28.98 | 30.65 | 31.03 |
| Bus 4-12 | 37.76 | 39.69 | 41.93 | 42.56 |
| Bus 10-20 | 9.30 | 9.78 | 10.34 | 10.89 |
| Bus 10-17 | 6.77 | 7.12 | 7.54 | 8.22 |
| Bus 23-24 | 0.37 | 0.39 | 0.40 | −0.71 |
| Bus 28-27 | 18.52 | 19.47 | 20.59 | 15.71 |
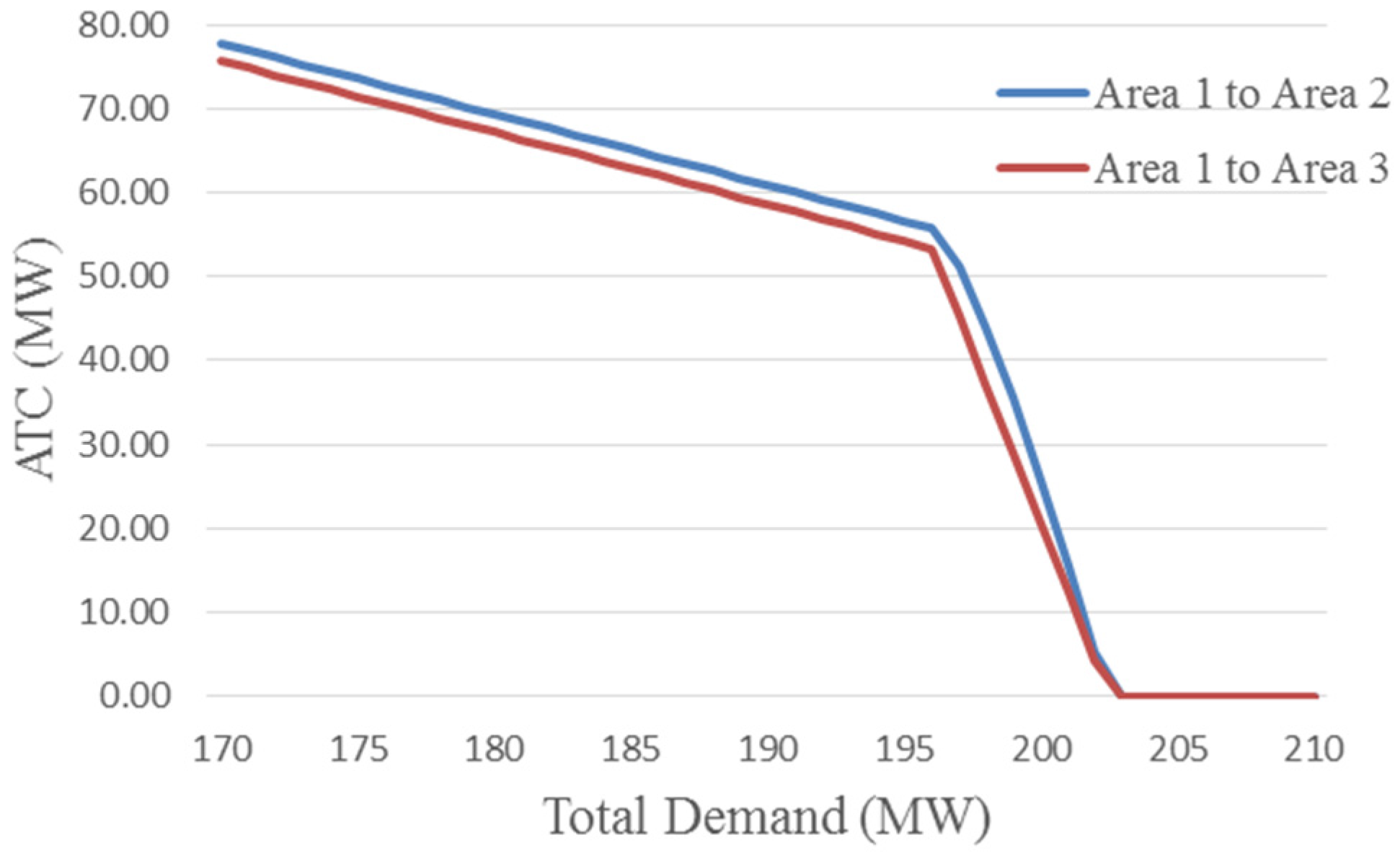
| ATC From Area 1 to Area 3 | ||||
| ATC (MW) | 67.19 | 59.38 | 20.67 | 0 |
| ATC From Area 1 to Area 2 | ||||
| ATC | 69.35 | 61.57 | 25.61 | 0 |
| Tie-line outage | |||||
|---|---|---|---|---|---|
| No outage | 4–12 | 6–10 | 9–10 | 28–27 | |
| Cost ($) | 1892 | 1911.773 | 1892 | 1892 | 1985.937 |
| G1 | 189.2 | 188.549 | 189.2 | 189.2 | 185.443 |
| G2 | 0 | 0.1 | 0 | 0 | 0 |
| G3 | 0 | 0 | 0 | 0 | 0 |
| G4 | 0 | 0 | 0 | 0 | 3.757 |
| G5 | 0 | 0 | 0 | 0 | 0 |
| G6 | 0 | 0.551 | 0 | 0 | 0 |
| Bus 6-10 | 16.56 | 28.08 | – | 28.35 | 20.248 |
| Bus 9-10 | 28.98 | 49.141 | 38.012 | – | 35.434 |
| Bus 4-12 | 39.69 | – | 45.008 | 51.833 | 45.261 |
| Bus 10-20 | 9.78 | 19.694 | 8.068 | 5.877 | 10.001 |
| Bus 10-17 | 7.12 | 25 | 4.294 | 0.667 | 6.38 |
| Bus 23-24 | 0.39 | −10.955 | 1.171 | 2.177 | 5.443 |
| Bus 28-27 | 19.47 | 26.929 | 31.68 | 24.518 | – |
| ATC From Area 1 to Area 3 | |||||
| ATC (MW) | 59.38 | 13.85 | 53.97 | 14.64 | 47.66 |
| ATC From Area 1 to Area 2 | |||||
| ATC | 61.57 | 12.85 | 49.87 | 17.78 | 52.06 |
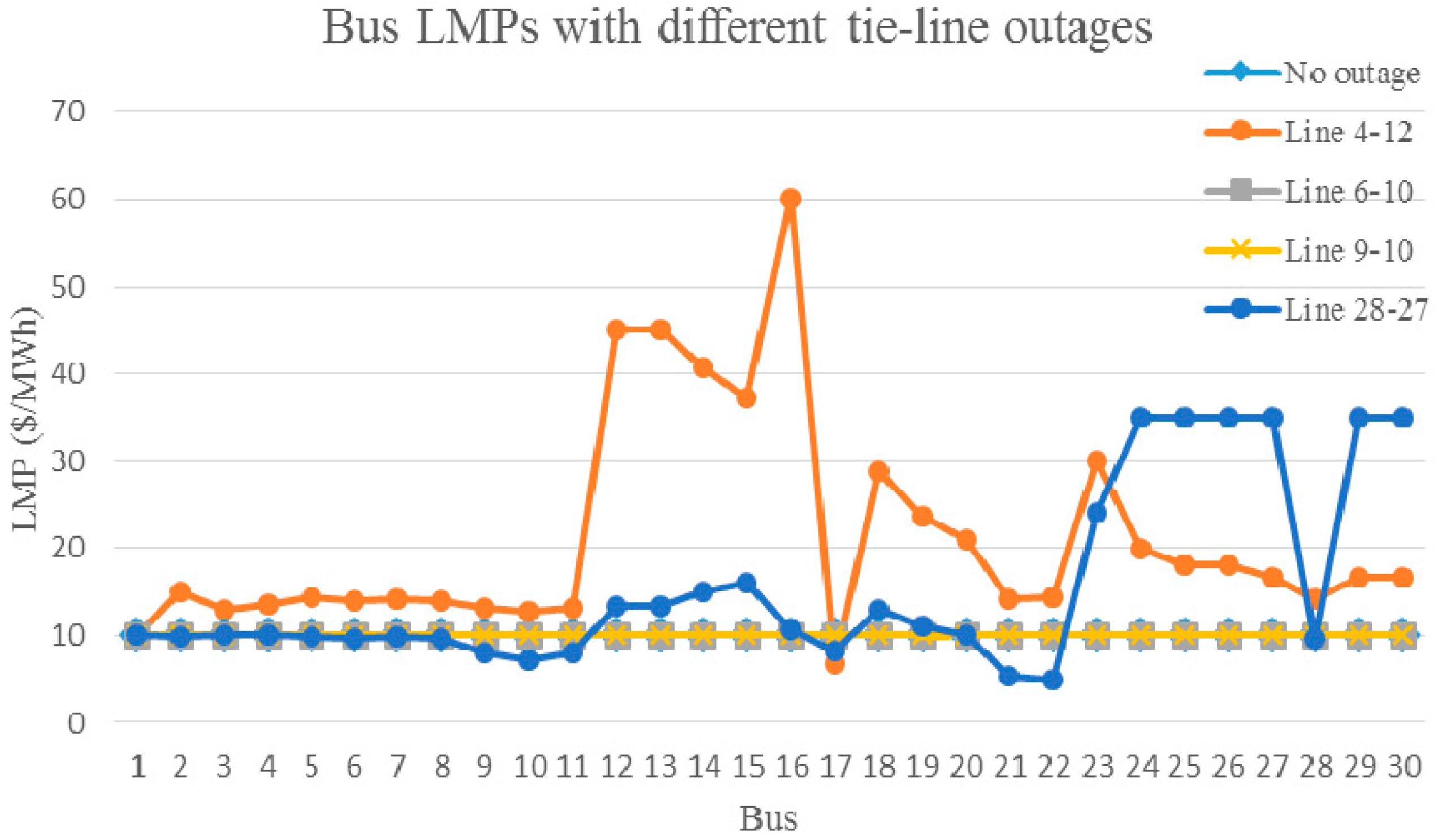
3.3. IEEE 118-Bus System
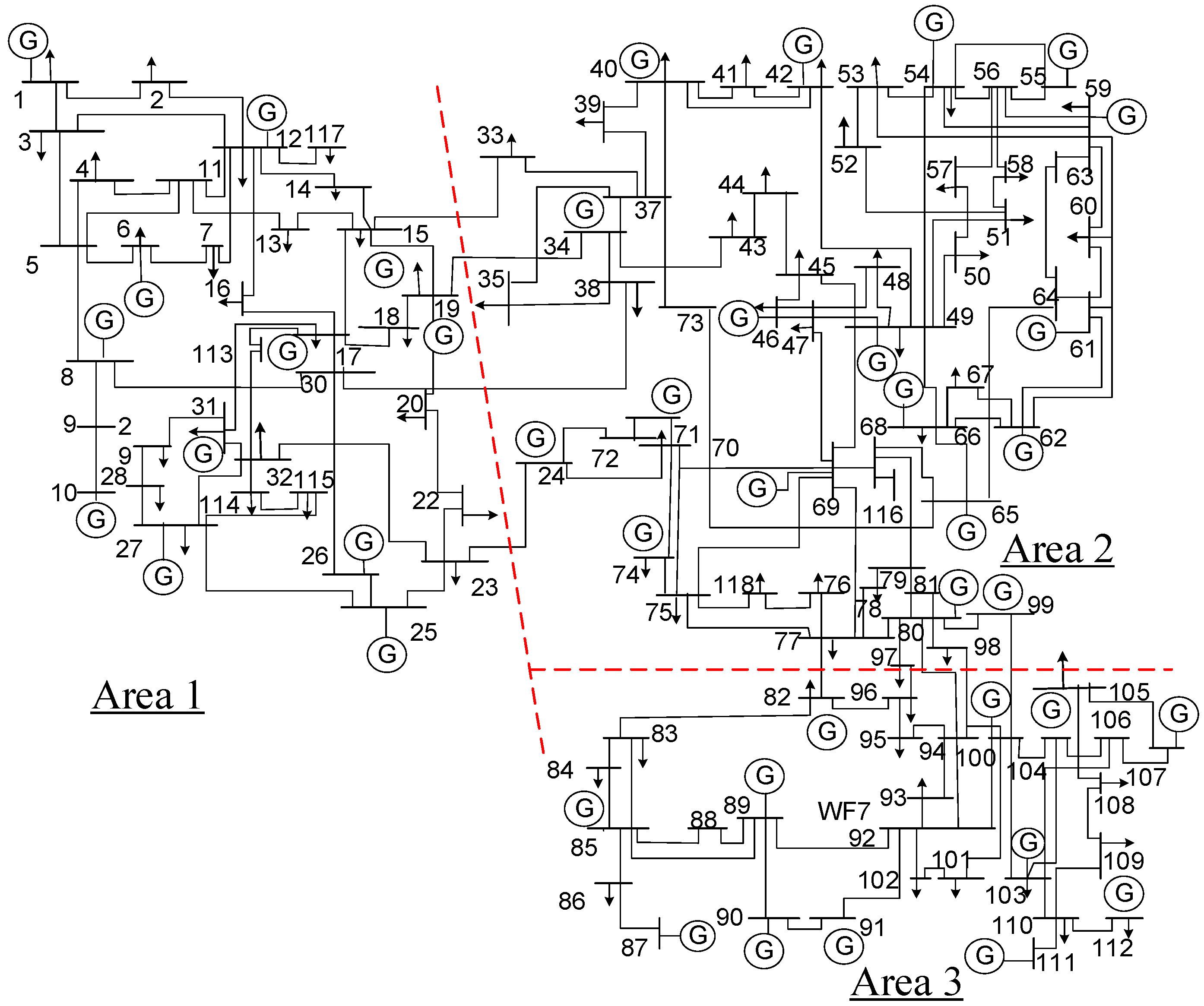
| Gen | Disp. Power | Gen | Disp. Power | Gen | Disp. Power |
|---|---|---|---|---|---|
| 1 | 128.981 | 19 | 100 | 37 | 0 |
| 2 | 200 | 20 | 119 | 38 | 0 |
| 3 | 0 | 21 | 304 | 39 | 0 |
| 4 | 100 | 22 | 148 | 40 | 0 |
| 5 | 550 | 23 | 100 | 41 | 0 |
| 6 | 0 | 24 | 100 | 42 | 0 |
| 7 | 100 | 25 | 255 | 43 | 0 |
| 8 | 100 | 26 | 260 | 44 | 0 |
| 9 | 100 | 27 | 100 | 45 | 0 |
| 10 | 100 | 28 | 491 | 46 | 0 |
| 11 | 38.04 | 29 | 133.979 | 47 | 0 |
| 12 | 414 | 30 | 0 | 48 | 0 |
| 13 | 0 | 31 | 0 | 49 | 0 |
| 14 | 0 | 32 | 0 | 50 | 0 |
| 15 | 0 | 33 | 0 | 51 | 0 |
| 16 | 100 | 34 | 0 | 52 | 0 |
| 17 | 100 | 35 | 0 | 53 | 0 |
| 18 | 100 | 36 | 0 | 54 | 0 |
| Tie-Line Power Flow (MW) | |||||
| 23–24 | 0.907 | 30–38 | 150 | 80–96 | −50.546 |
| 15–33 | 150 | 77–82 | 98.545 | 98–100 | 64.542 |
| 19–34 | 46.85 | 97–96 | 58.216 | 99–100 | 47.141 |
| Gen. Cost ($) | 98084.119 | ||||
| ATC Area 1 to 2 (MW) | 0 | ||||
| ATC Area 2 to 1 (MW) | 965.5066 | ||||
| ATC Area 2 to 3 (MW) | 1052.2074 | ||||
| ATC Area 3 to 2 (MW) | 2333.093 | ||||
| Gen | Disp. Power | Gen | Disp. Power | Gen | Disp. Power |
|---|---|---|---|---|---|
| 1 | 220 | 19 | 100 | 37 | 0 |
| 2 | 200 | 20 | 119 | 38 | 0 |
| 3 | 250 | 21 | 304 | 39 | 0 |
| 4 | 100 | 22 | 148 | 40 | 0 |
| 5 | 550 | 23 | 100 | 41 | 0 |
| 6 | 185 | 24 | 100 | 42 | 0 |
| 7 | 100 | 25 | 255 | 43 | 0 |
| 8 | 100 | 26 | 260 | 44 | 0 |
| 9 | 100 | 27 | 100 | 45 | 0 |
| 10 | 52.503 | 28 | 491 | 46 | 0 |
| 11 | 0 | 29 | 107.497 | 47 | 0 |
| 12 | 0 | 30 | 0 | 48 | 0 |
| 13 | 0 | 31 | 0 | 49 | 0 |
| 14 | 0 | 32 | 0 | 50 | 0 |
| 15 | 0 | 33 | 0 | 51 | 0 |
| 16 | 100 | 34 | 0 | 52 | 0 |
| 17 | 100 | 35 | 0 | 53 | 0 |
| 18 | 100 | 36 | 0 | 54 | 0 |
| Tie-Line Power flow (MW) | |||||
| 23–24 | 146.971 | 30–38 | 150 | 80–96 | −50.857 |
| 15–33 | -- | 77–82 | 97.777 | 98–100 | 64.696 |
| 19–34 | 140.853 | 97–96 | 58.527 | 99–100 | 47.294 |
| Gen. Cost ($) | 95374.176 | ||||
| ATC Area 1 to 2 (MW) | 14.4699 | ||||
| ATC Area 2 to 1 (MW) | 831.282 | ||||
| ATC Area 2 to 3 (MW) | 1561.9466 | ||||
| ATC Area 3 to 2 (MW) | 2328.8769 | ||||
| Gen | Disp. Power | Gen | Disp. Power | Gen | Disp. Power |
|---|---|---|---|---|---|
| 1 | 129.167 | 19 | 100 | 37 | 0 |
| 2 | 200 | 20 | 119 | 38 | 0 |
| 3 | 0 | 21 | 304 | 39 | 0 |
| 4 | 100 | 22 | 148 | 40 | 0 |
| 5 | 550 | 23 | 100 | 41 | 0 |
| 6 | 0 | 24 | 100 | 42 | 0 |
| 7 | 100 | 25 | 255 | 43 | 0 |
| 8 | 100 | 26 | 260 | 44 | 0 |
| 9 | 100 | 27 | 100 | 45 | 0 |
| 10 | 100 | 28 | 491 | 46 | 0 |
| 11 | 36.528 | 29 | 135.305 | 47 | 0 |
| 12 | 414 | 30 | 0 | 48 | 0 |
| 13 | 0 | 31 | 0 | 49 | 0 |
| 14 | 0 | 32 | 0 | 50 | 0 |
| 15 | 0 | 33 | 0 | 51 | 0 |
| 16 | 100 | 34 | 0 | 52 | 0 |
| 17 | 100 | 35 | 0 | 53 | 0 |
| 18 | 100 | 36 | 0 | 54 | 0 |
| Tie-Line Power Flow (MW) | |||||
| 23–24 | 0.675 | 30–38 | 150 | 80–96 | −69.585 |
| 15–33 | 150 | 77–82 | -- | 98–100 | 69.118 |
| 19–34 | 46.851 | 97–96 | 77.245 | 99–100 | 51.712 |
| Gen. Cost ($) | 98113.686 | ||||
| ATC Area 1 to 2 (MW) | 0 | ||||
| ATC Area 2 to 1 (MW) | 965.771 | ||||
| ATC Area 2 to 3 (MW) | 1129.7202 | ||||
| ATC Area 3 to 2 (MW) | 2309.0415 | ||||
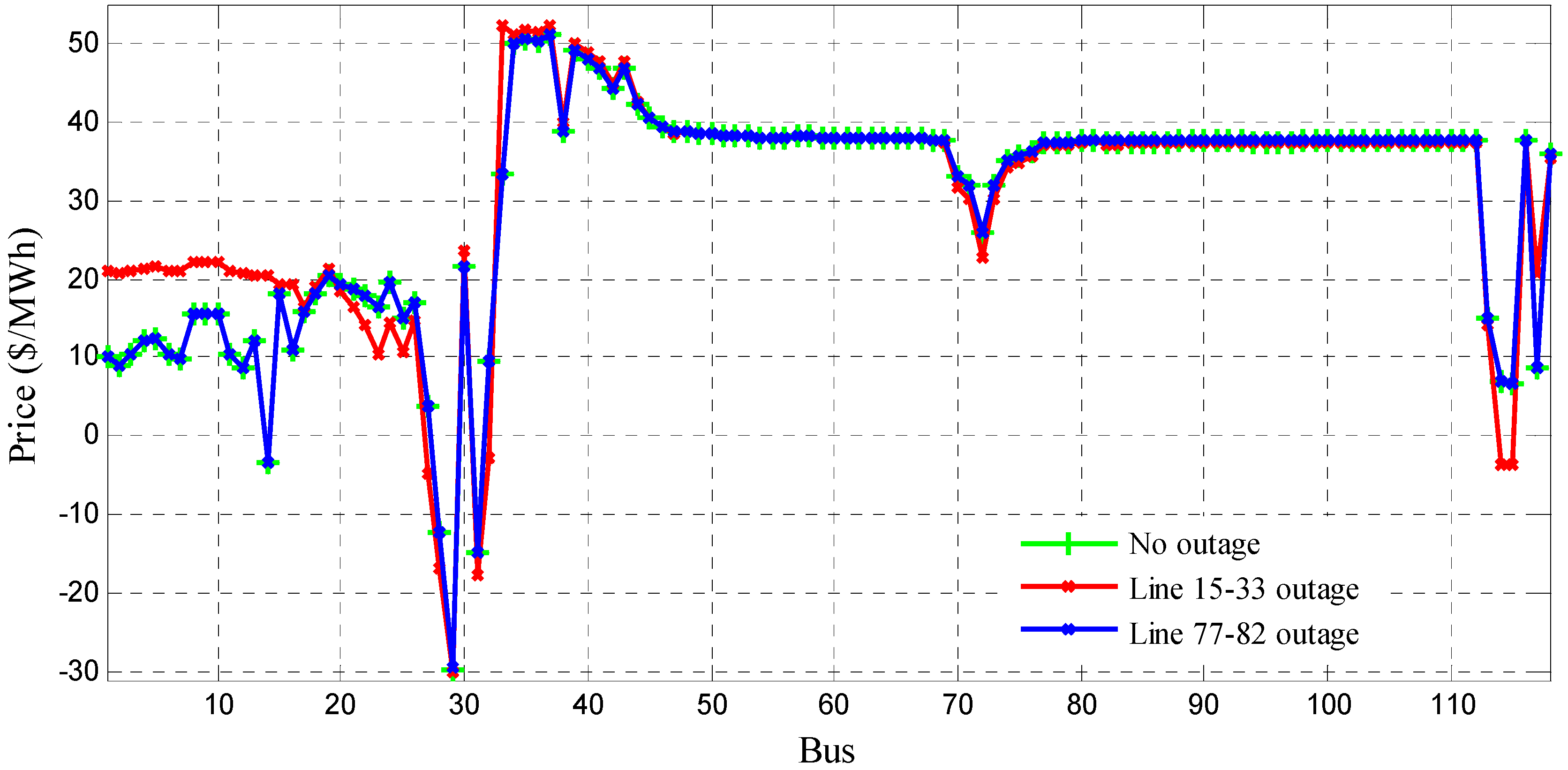
4. Conclusions
- (1)
- A bi-level optimization model for ATC evaluation in the deregulated electricity market is proposed in which the system uncertainty such as demand variation and N-1 transmission contingencies can be considered in the ATC evaluation and ED endogenously, and the ATC results can be obtained simultaneously with the ISO’s market economic dispatch (ED) results.
- (2)
- The proposed bi-level optimization model is formulated as a mathematic program with equilibrium constraints (MPEC) by recasting the lower level problem as its Karush-Kuhn-Tucker (KKT) optimality conditions. Then this MPEC is transformed to a mixed-integer linear programming (MILP) problem, which is solved by available software.
- (3)
- The case studies performed in PJM 5-bus, IEEE 30-bus, and IEEE 118-bus systems under different system demand levels and system topologies validate the proposed method. The simulation results demonstrate that ATC decreases with the system load level due to remain generation capacity and tie-line capacity reduction.
- (4)
- The change of the system topology has a different impact on the economic dispatch and ATC. Under some conditions, line outage can increase ATC without increasing the generation operating cost. Therefore, there is a tradeoff between the economic and reliability concerns in the system topology optimization.
Acknowledgments
Conflicts of Interest
Abbreviations
| ATC | Available Transfer Capability |
| TTC | Total Transfer Capability |
| ETC | Existing Transfer Capability |
| CBM | capacity benefit margin |
| TRM | transmission reliability margin |
| ED | economic dispatch |
| OASIS | Open Access Same-time Information System |
| NERC | North American Electric Reliability Corporation |
| ISO | Independent System Operator |
| RPF | repeated power flow |
| CPF | continuation power flow |
| OPF | optimal power flow |
| MPEC | mathematic program with equilibrium constraints |
| KKT | Karush-Kuhn-Tucher |
| MILP | mixed-integer linear programming |
References
- Force, T.T.C.T. Available Transfer Capability Definitions and Determination; North American Electric Reliability Council: Princeton, NJ, USA, 1996. [Google Scholar]
- Zheng, Y.; Yang, J.; Hu, Z.G.; Zhou, M.; Li, G.Y. Credibility theory-based available transfer capability assessment. Energies 2015, 8, 6059–6078. [Google Scholar] [CrossRef]
- Li, G.Q.; Chen, H.H. Study of probabilistic available transfer capability by improved particle swarm optimization. Proc. CSEE 2006, 26, 18–23. [Google Scholar]
- Hamoud, G. Assessment of available transfer capability of transmission systems. IEEE Trans. Power Syst. 2000, 15, 27–32. [Google Scholar] [CrossRef]
- Ilic, M.D.; Yoon, Y.Y.; Zobian, A. Available transfer capability (ATC) and its value under open access. IEEE Trans. Power Syst. 1997, 12, 636–645. [Google Scholar] [CrossRef]
- Nallan, H.C.; Rastgoufard, P. Computational voltage stability assessment of large-scale power systems. Electr. Power Syst. Res. 1996, 38, 177–181. [Google Scholar] [CrossRef]
- Ejebe, G.C.; Tong, J.; Waight, G.G.; Frame, J.G.; Wang, X.; Tinney, W.F. Available transfer capability calculations. IEEE Trans. Power Syst. 1998, 13, 1521–1527. [Google Scholar] [CrossRef]
- Ou, Y.; Singh, C. Assessment of available transfer capability and margins. IEEE Trans. Power Syst. 2002, 17, 463–468. [Google Scholar] [CrossRef]
- Sawhney, H.; Jeyasurya, B. Application of unified power flow controller for available transfer capability enhancement. Electr. Power Syst. Res. 2004, 69, 155–160. [Google Scholar] [CrossRef]
- Fang, X.; Li, F.; Gao, N.; Guo, Q. Available transfer capability of photovoltaic generation incorporated system. In Proceedings of the IEEE PES General Meeting 2014, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5.
- Pan, X.; Xu, G.Y. Available transfer capability calculation considering voltage stability margin. Electr. Power Syst. Res. 2005, 76, 52–57. [Google Scholar] [CrossRef]
- Min, L.; Abur, A.; Zhao, L. Two-level multi-area TTC calculation by updating power transfer distribution factors. In Proceedings of the Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; pp. 491–496.
- Shin, D.; Kim, J.; Kim, K.; Singh, C. Probabilistic approach to available transfer capability calculation. Electr. Power Syst. Res. 2007, 77, 813–820. [Google Scholar] [CrossRef]
- Rodrigues, A.B.; Da Silva, M.G. Probabilistic assessment of available transfer capability based on Monte Carlo method with sequential simulation. IEEE Trans. Power Syst. 2007, 22, 484–492. [Google Scholar] [CrossRef]
- Cui, Y.L.; Bie, Z.H.; Wang, X.F. Study on calculation of probability available transfer capability. In Proceedings of the 2002 International Conference on Power System Technology (PowerCon 2002), Kunming, China, 13–17 October 2002; pp. 2052–2056.
- Fang, X.; Li, F.X.; Gao, N.C. Probabilistic available transfer capability evaluation for power systems with high-penetration wind power. In Proceedings of the 13th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014; pp. 1–6.
- Ou, Y.; Singh, C. Calculation of risk and statistical indices associated with available transfer capability. IEE Proc. Gener. 2003, 150, 239–244. [Google Scholar] [CrossRef]
- Othman, M.M.; Mohamed, A.; Hussain, A. Fast evaluation of available transfer capability using cubic spline interpolation technique. Electr. Power Syst. Res. 2005, 73, 335–342. [Google Scholar] [CrossRef]
- Tuglie, E.D.; Dicorato, M.; Scala, M.L.; Scarpellini, P. A static optimization approach to assess dynamic available transfer capability. IEEE Trans. Power Syst. 2000, 15, 1069–1076. [Google Scholar] [CrossRef]
- Li, W.Y.; Vaahedi, E.; Lin, Z.H. BC Hydro’s transmission reliability margin assessment in total transfer capability calculations. IEEE Trans. Power Syst. 2013, 28, 4796–4802. [Google Scholar] [CrossRef]
- Ramezani, M.; Haghifam, M.; Singh, C.; Seifi, H.; Moghaddam, M.P. Determination of capacity benefit margin in multi-area power systems using particle swarm optimization. IEEE Trans. Power Syst. 2009, 24, 631–641. [Google Scholar] [CrossRef]
- Sun, R.; Song, Y.; Sun, Y. Capacity benefit margin assessment based on multi-area generation reliability exponential analytic model. IET Gener. Transm. Distrib. 2008, 2, 610–620. [Google Scholar] [CrossRef]
- Salim, N.A.; Othman, M.M.; Serwan, M.S.; Fotuhi-Firuzabad, M.; Safdarian, A.; Musirin, I. Determination of available transfer capability with implication of cascading collapse uncertainty. IET Gener. Transm. Distrib. 2014, 8, 705–715. [Google Scholar] [CrossRef]
- Li, F.; Bo, R. DCOPF-based LMP simulation: Algorithm, comparison with acopf, and sensitivity. IEEE Trans. Power Syst. 2007, 22, 1475–1485. [Google Scholar] [CrossRef]
- Fang, X.; Hu, Q.R.; Li, F.X.; Wang, B.B.; Li, Y. Coupon-based demand response considering wind power uncertainty: A strategic bidding model for load serving entities. IEEE Trans. Power Syst. 2015, in press. [Google Scholar] [CrossRef]
- Wogrin, S.; Centeno, E.; Barquin, J. Generation capacity expansion in liberalized electricity markets: A stochastic MPEC approach. IEEE Trans. Power Syst. 2011, 26, 2526–2532. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Conejo, A.J.; Fuller, J.D.; Hobbs, B.F.; Ruiz, C. Complementarity Modeling in Energy Markets; Springer: New York, NY, USA, 2012. [Google Scholar]
- Fang, X.; Li, F.X.; Hu, Q.R.; Gao, N.C. The impact of FTR on LSE’s strategic bidding considering coupon based demand response. In Proceedings of the IEEE Power and Energy Society General Meeting 2015, Denver, CO, USA, 26–30 July 2015.
- Fang, X.; Wei, Y.; Li, F.X. Evaluation of Lmp intervals considering wind uncertainty. IEEE Trans. Power Syst. 2015, in press. [Google Scholar] [CrossRef]
- Pieper, H. Algorithms for Mathematical Programs with Equilibrium Constraints with Applications to Deregulated Electricity Markets. Ph.D. Thesis, Department of Management Science and Engineering, Stanford University, Stanford, CA, USA, Junuary 2001. [Google Scholar]
- Taha, A.F.; Panchal, J.H. Multilevel decision-making in decentralized energy systems with multiple technologies and uncertainty. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 894–907. [Google Scholar] [CrossRef]
- Christie, R.; Wollenberg, B.; Wangensteen, I. Transmission management in the deregulated environment. Proc. IEEE 2000, 88, 170–195. [Google Scholar] [CrossRef]
- Amat, J.F.; McCarl, B. A representation and economic interpretation of a two-level programming problem. J. Oper. Res. Soc. 1981, 32, 783–792. [Google Scholar] [CrossRef]
- Li, F.X.; Bo, R. Small test systems for power system economic studies. In Proceedings of the IEEE Power and Energy Society General Meeting 2010, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–4.
- Fang, X.; Li, F.X.; Wei, Y.L.; Azim, R.; Xu, Y. Reactive power planning under high penetration of wind energy using benders decomposition. IET Gener. Trans. Distrib. 2015, in press. [Google Scholar] [CrossRef]
- GAMS Manual. Available online: http://www.gams.com/ (accessed on 1 November 2015).
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS: A User’s Guide; GAMS Development Corporation: Washington, DC, USA, 1998. [Google Scholar]
- Wei, Y.; Li, F.; Tomsovic, K. Measuring the volatility of wholesale electricity prices caused by the wind power uncertainty with a correlation model. IET Renew. Power Gener. 2012, 6, 315–323. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Fang, X.; Zhao, X.; Chen, H. Bi-Level Optimization for Available Transfer Capability Evaluation in Deregulated Electricity Market. Energies 2015, 8, 13344-13360. https://doi.org/10.3390/en81212370
Wang B, Fang X, Zhao X, Chen H. Bi-Level Optimization for Available Transfer Capability Evaluation in Deregulated Electricity Market. Energies. 2015; 8(12):13344-13360. https://doi.org/10.3390/en81212370
Chicago/Turabian StyleWang, Beibei, Xin Fang, Xiayang Zhao, and Houhe Chen. 2015. "Bi-Level Optimization for Available Transfer Capability Evaluation in Deregulated Electricity Market" Energies 8, no. 12: 13344-13360. https://doi.org/10.3390/en81212370
APA StyleWang, B., Fang, X., Zhao, X., & Chen, H. (2015). Bi-Level Optimization for Available Transfer Capability Evaluation in Deregulated Electricity Market. Energies, 8(12), 13344-13360. https://doi.org/10.3390/en81212370





