Forecasting China’s Annual Biofuel Production Using an Improved Grey Model
Abstract
:1. Introduction
2. Literature Review
2.1. Predicting Biofuel Production
2.2. Problems with Predicting Production
3. Building the Dynamic Grey Fuzzy Markov Prediction Model
3.1. Conventional Grey Model
3.1.1. GM (1,1) Model Building Process
- Accumulated generating operation (AGO)
- Grey modeling
- Inverse accumulated generating operation (IAGO)
3.1.2. Accuracy Considerations
| Index | C | P | |
|---|---|---|---|
| Accuracy grade | Excellent | ≤0.35 | ≥95% |
| Well | ≤0.50 | ≥80% | |
| Conformity | ≤0.65 | ≥70% | |
| Non-conformity | ≥0.80 | ≤60% | |
3.2. Dynamic Grey Model
3.3. Dynamic Grey Fuzzy Markov Prediction Model
3.3.1. Fuzzy Classifications
3.3.2. Determination of the State Transition Matrix
3.3.3. Fuzzy Markov Residual Error Correction
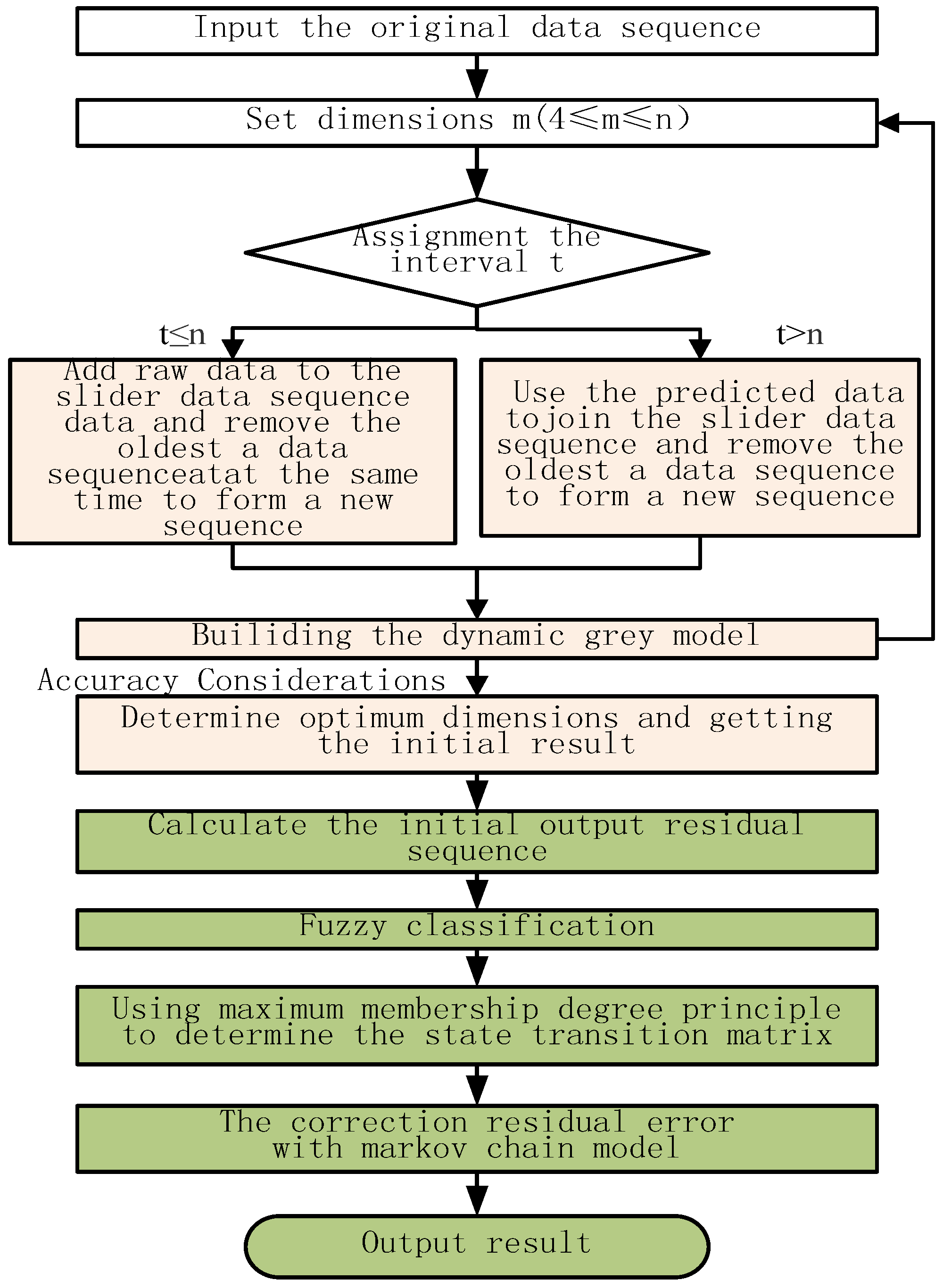
4. Feasibility Analysis of the Grey Fuzzy Markov Prediction Model
4.1. Data Source
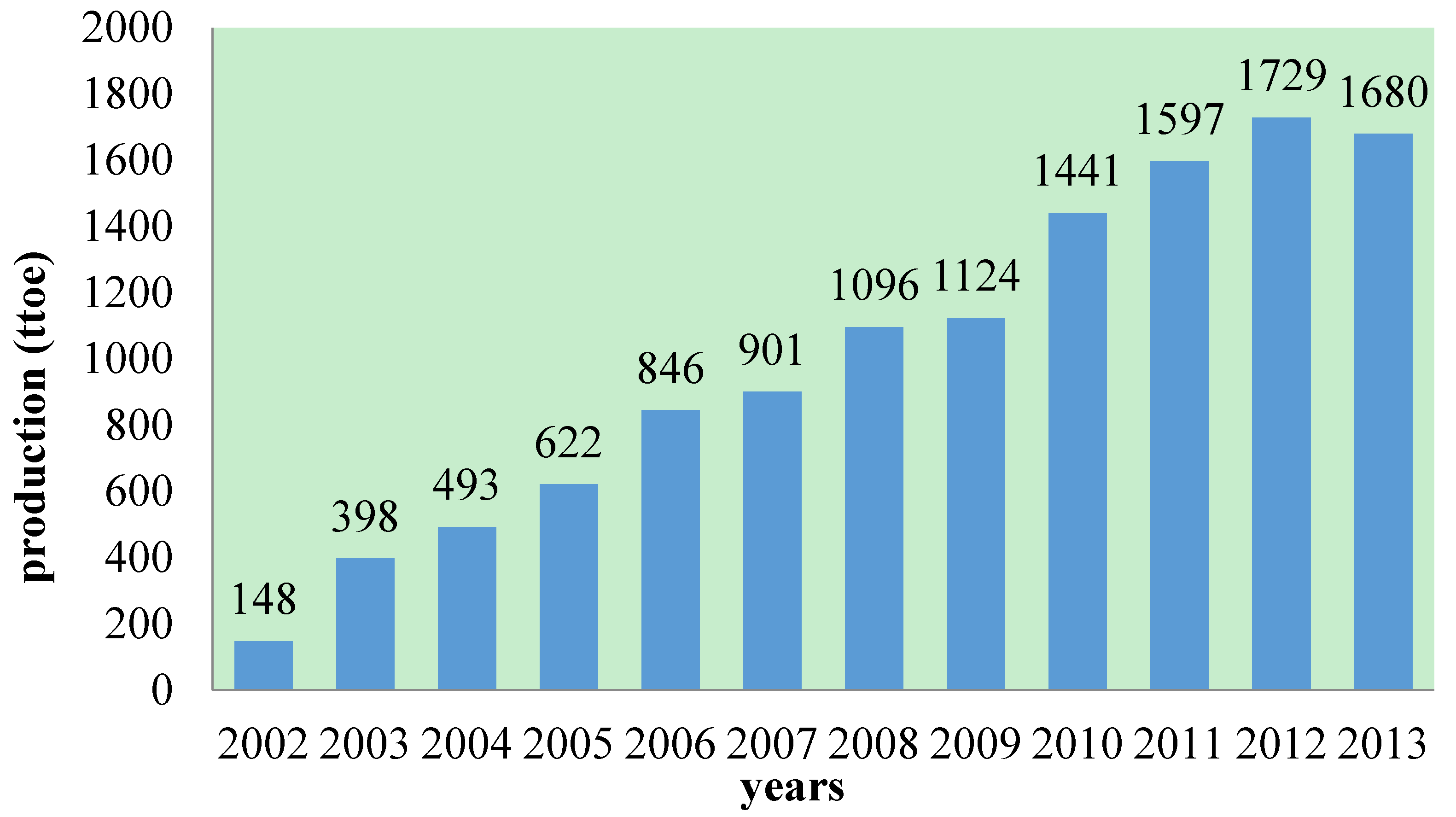
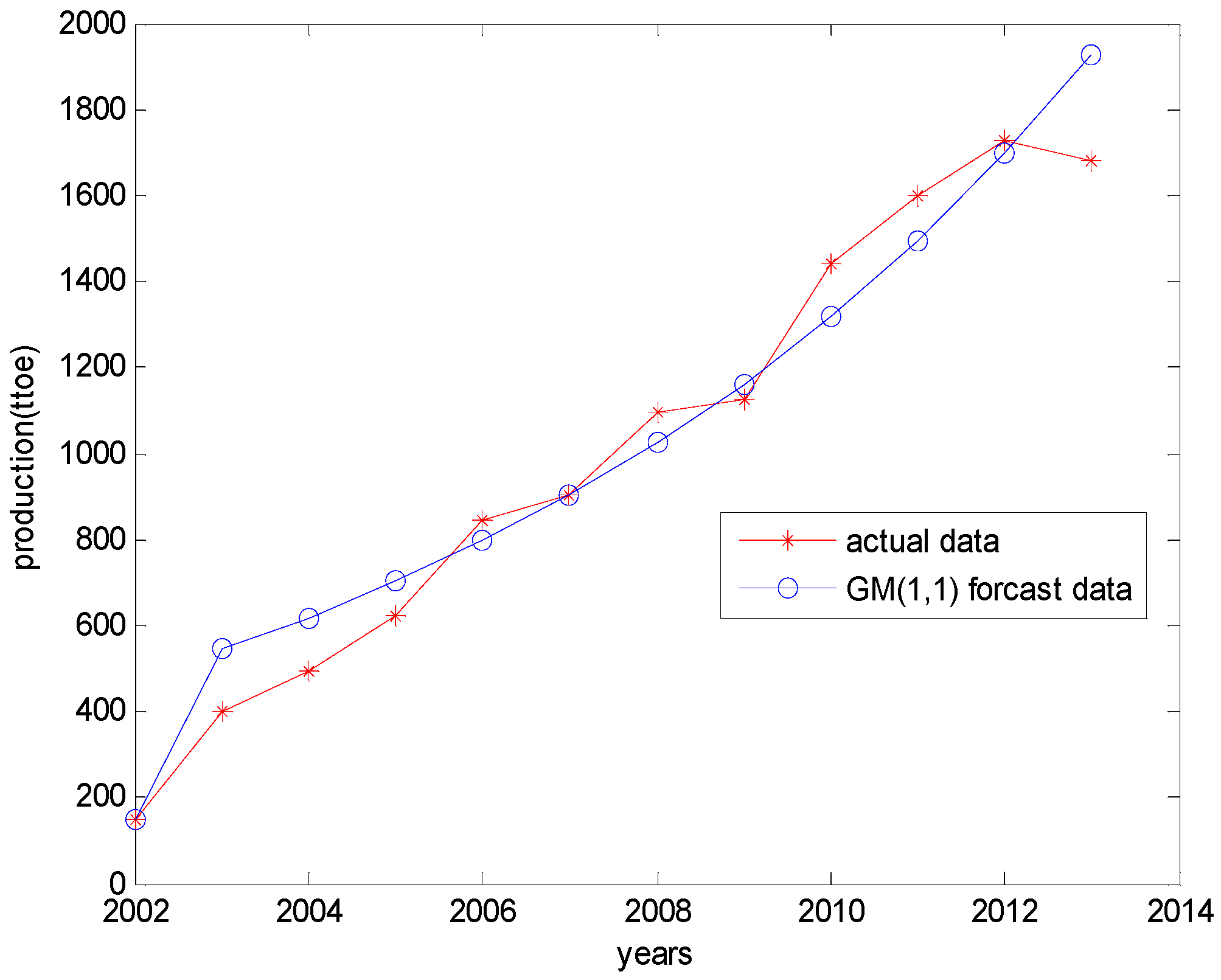
4.2. Results of the GM (1,1) Model
| Years | Raw Data | GM (1,1) Data | Residual | Correctly Predicted Percentage |
|---|---|---|---|---|
| 2002 | 148.00 | 148.00 | 0 | 100 |
| 2003 | 398.00 | 545.29 | 147.29 | 62.9925 |
| 2004 | 493.00 | 618.65 | 125.65 | 74.5132 |
| 2005 | 622.00 | 701.88 | 79.88 | 87.1576 |
| 2006 | 846.00 | 796.31 | –49.69 | 94.1265 |
| 2007 | 901.00 | 903.44 | 2.44 | 99.7292 |
| 2008 | 1096.00 | 1025.00 | –71.00 | 93.5219 |
| 2009 | 1124.00 | 1162.90 | 38.90 | 96.5392 |
| 2010 | 1441.00 | 1319.30 | –121.70 | 91.5545 |
| 2011 | 1597.00 | 1496.80 | –100.20 | 93.7257 |
| 2012 | 1729.00 | 1698.20 | –30.80 | 98.2186 |
| 2013 | 1680.00 | 1926.70 | 246.7 | 85.3155 |
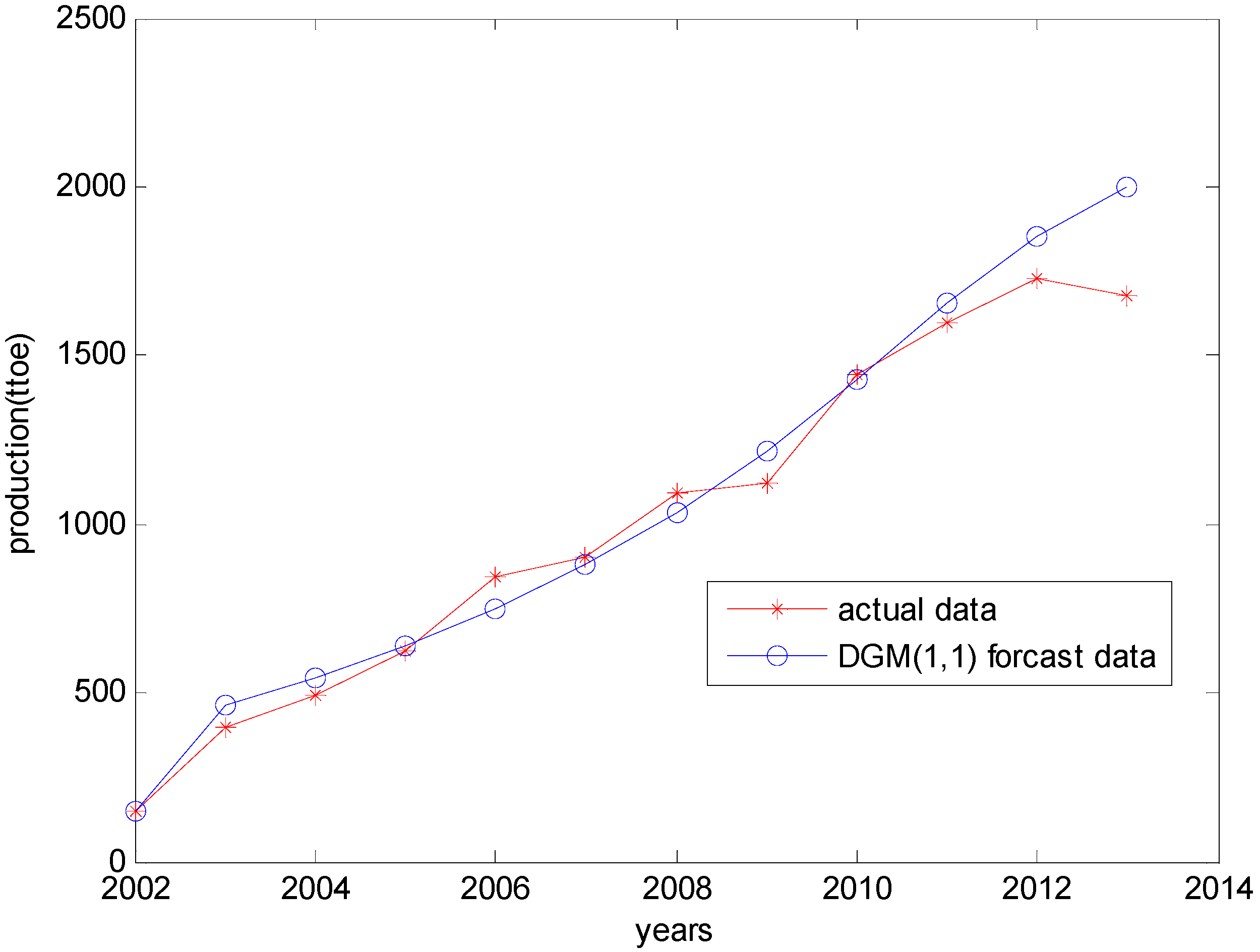
4.3. Results of the Dynamic Grey Prediction Model
| Dimension | 4 | 5 | 6 | 7 | 8 |
| C | 0.2162 | 0.2394 | 0.2193 | 0.2209 | 0.2036 |
| Dimension | 9 | 10 | 11 | 12 | - |
| C | 0.2245 | 0.2493 | 0.2633 | 0.2079 | - |
| Years | Raw Data | DGM (1,1) Data | Residual | Relative Error | Correctly Predicted Percentage |
|---|---|---|---|---|---|
| 2002 | 148.00 | 148.00 | 0 | 0 | 100 |
| 2003 | 398.00 | 462.58 | −64.58 | −0.1396 | 86.0392 |
| 2004 | 493.00 | 543.28 | −50.28 | −0.0926 | 90.7451 |
| 2005 | 622.00 | 638.07 | −16.07 | −0.0252 | 97.4815 |
| 2006 | 846.00 | 749.39 | 96.61 | 0.1289 | 87.1082 |
| 2007 | 901.00 | 880.13 | 20.87 | 0.0237 | 97.6288 |
| 2008 | 1096.00 | 1033.70 | 62.30 | 0.0603 | 93.9731 |
| 2009 | 1124.00 | 1214.00 | −90.00 | −0.0741 | 92.5865 |
| 2010 | 1441.00 | 1425.80 | 15.20 | 0.0107 | 98.9339 |
| 2011 | 1597.00 | 1658.90 | −61.90 | −0.0373 | 96.2686 |
| 2012 | 1729.00 | 1852.00 | −123.00 | −0.0664 | 93.3585 |
| 2013 | 1680.00 | 2002.40 | −322.40 | −0.1610 | 83.8993 |
4.4. Results of the Dynamic Grey Fuzzy Markov Prediction Model
| Years | Raw Data | DGM (1,1) Data | Residual | Relative Error | State |
|---|---|---|---|---|---|
| 2002 | 148.00 | 148.00 | 0 | 0 | 2 |
| 2003 | 398.00 | 462.58 | −64.58 | −0.1396 | 1 |
| 2004 | 493.00 | 543.28 | −50.28 | −0.0926 | 1 |
| 2005 | 622.00 | 638.07 | −16.07 | −0.0252 | 2 |
| 2006 | 846.00 | 749.39 | 96.61 | 0.1289 | 3 |
| 2007 | 901.00 | 880.13 | 20.87 | 0.0237 | 2 |
| 2008 | 1096.00 | 1033.70 | 62.30 | 0.0603 | 3 |
| 2009 | 1124.00 | 1214.00 | −90.00 | −0.0741 | 1 |
| State | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|
| 1 | 0.4383 | 0.4475 | 0.4429 | 0.4452 |
| 2 | 0.3150 | 0.3425 | 0.3287 | 0.3356 |
| 3 | 0.2002 | 0.2100 | 0.2283 | 0.2192 |
| Years | DGM (1,1) Data | Improved Result | Upper Limit | Lower Limit | Mid Value | Probability |
|---|---|---|---|---|---|---|
| 2010 | 1425.80 | 1400.13 | 1226.19 | 1368.77 | 1297.48 | 0.44 |
| 1425.80 | - | 1368.77 | 1482.83 | 1425.80 | 0.32 | |
| 1425.80 | - | 1482.83 | 1625.41 | 1554.12 | 0.25 | |
| 2011 | 1658.90 | 1623.44 | 1426.65 | 1592.54 | 1509.60 | 0.45 |
| 1658.90 | - | 1592.54 | 1725.26 | 1658.90 | 0.34 | |
| 1658.90 | - | 1725.26 | 1891.15 | 1808.20 | 0.21 | |
| 2012 | 1852.00 | 1816.05 | 1592.72 | 1777.92 | 1685.32 | 0.44 |
| 1852.00 | - | 1777.92 | 1926.08 | 1852.00 | 0.33 | |
| 1852.00 | - | 1926.08 | 2111.28 | 2018.68 | 0.23 | |
| 2013 | 2002.40 | 1861.67 | 1722.06 | 1922.30 | 1822.18 | 0.45 |
| 2002.40 | - | 1922.30 | 2082.50 | 2002.40 | 0.34 | |
| 2002.40 | - | 2082.50 | 2282.74 | 2182.62 | 0.22 |
| Years | Raw Data | DGFM (1,1) Data | Residual | Relative Error |
|---|---|---|---|---|
| 2002 | 148.00 | 148 | 0 | 0.0000 |
| 2003 | 398.00 | 462.58 | −64.58 | −0.1396 |
| 2004 | 493.00 | 543.28 | −50.28 | −0.0926 |
| 2005 | 622.00 | 638.07 | −16.07 | −0.0252 |
| 2006 | 846.00 | 749.39 | 96.61 | 0.1289 |
| 2007 | 901.00 | 880.13 | 20.87 | 0.0237 |
| 2008 | 1096.00 | 1033.7 | 62.3 | 0.0603 |
| 2009 | 1124.00 | 1214 | −90 | −0.0741 |
| 2010 | 1441.00 | 1400.13 | 40.87 | 0.0292 |
| 2011 | 1597.00 | 1623.44 | −26.44 | −0.0163 |
| 2012 | 1729.00 | 1816.05 | −87.05 | −0.0479 |
| 2013 | 1680.00 | 1861.67 | −181.67 | −0.0976 |

5. Comparison of the Three Methods
5.1. Comparison in Terms of Prediction Data
| Years | Raw Data | GM (1,1) | DGM (1,1) | DGFM (1,1) |
|---|---|---|---|---|
| 2010 | 1441.00 | 1319.30 | 1425.80 | 1400.13 |
| 2011 | 1597.00 | 1496.80 | 1658.90 | 1623.44 |
| 2012 | 1729.00 | 1698.20 | 1852.00 | 1816.05 |
| 2013 | 1680.00 | 1926.70 | 2002.40 | 1861.67 |
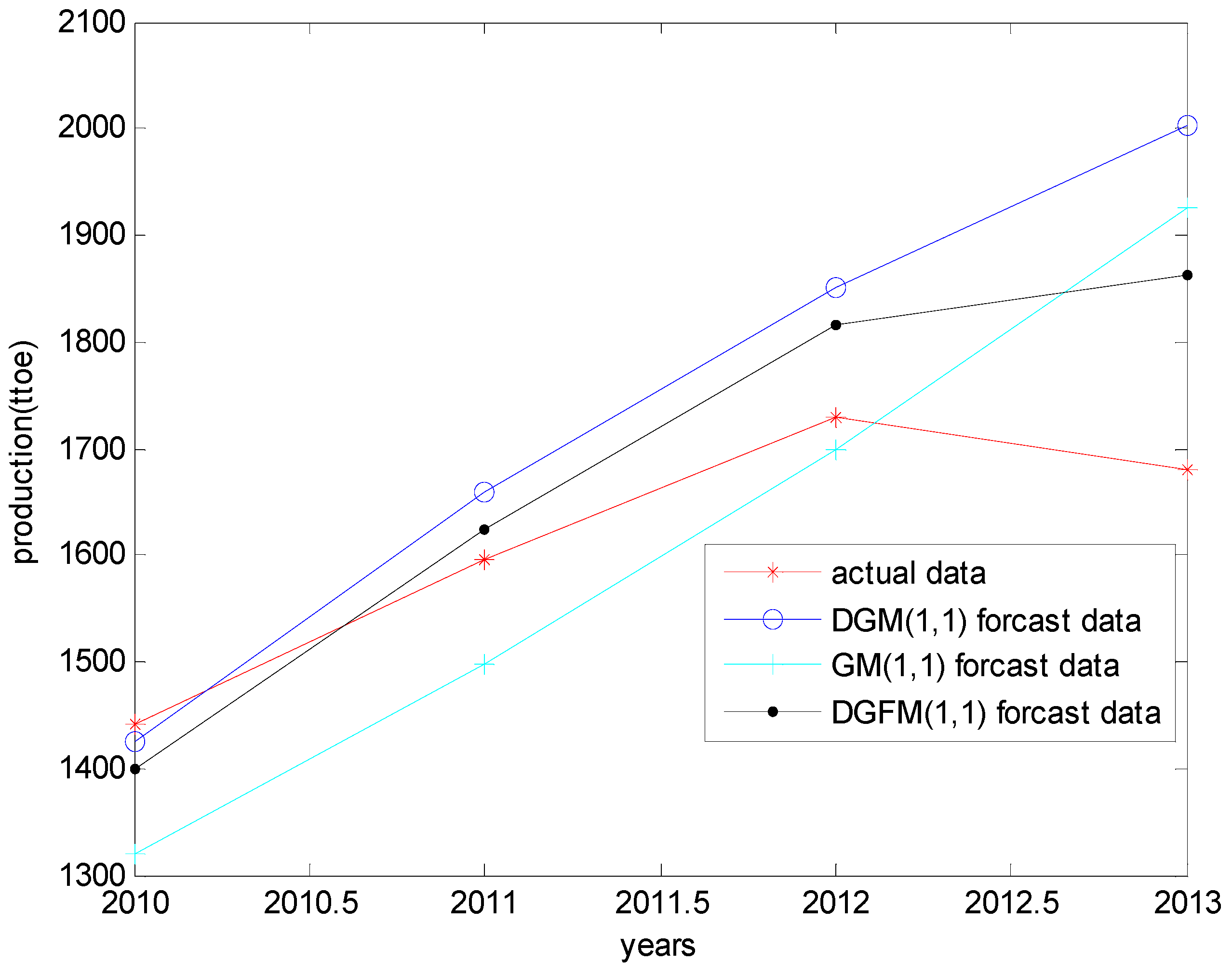
5.2. Comparison in Terms of Prediction Accuracy
| Prediction Accuracies | GM (1,1) | DGM (1,1) | DGFM (1,1) |
|---|---|---|---|
| Correctly predicted percentage | 92.20% | 93.11% | 94.91% |
| C-value | 0.2079 | 0.2036 | 0.1443 |
| p-value | 83.30% | 91.60% | 91.60% |
6. Forecasting China’s Biofuel Production from 2015 to 2020 Using the DGFM (1,1) Model
6.1. Forecasting Process
| Years | Forcasting Data | Years | Forcasting Data |
|---|---|---|---|
| 2015 | 2203.40 | 2018 | 2835.80 |
| 2016 | 2413.10 | 2019 | 3115.70 |
| 2017 | 2595.90 | 2020 | 3436.10 |
| Years | Raw Data | DGM Data | Relative Error | State |
|---|---|---|---|---|
| 2002 | 148.00 | 148.00 | 0.0000 | 2 |
| 2003 | 398.00 | 462.58 | −0.1396 | 1 |
| 2004 | 493.00 | 543.28 | −0.0926 | 1 |
| 2005 | 622.00 | 638.07 | −0.0252 | 2 |
| 2006 | 846.00 | 749.39 | 0.1289 | 3 |
| 2007 | 901.00 | 880.13 | 0.0237 | 2 |
| 2008 | 1096.00 | 1033.70 | 0.0603 | 3 |
| 2009 | 1124.00 | 1214.00 | −0.0741 | 1 |
| 2010 | 1441.00 | 1425.80 | 0.0107 | 2 |
| 2011 | 1597.00 | 1658.90 | −0.0373 | 2 |
| 2012 | 1729.00 | 1852.00 | −0.0664 | 1 |
| 2013 | 1680.00 | 2002.40 | −0.1610 | 1 |
| Years | Forcasting Data | Years | Forcasting Data |
|---|---|---|---|
| 2015 | 2153.11 | 2018 | 2771.07 |
| 2016 | 2358.02 | 2019 | 3044.58 |
| 2017 | 2536.65 | 2020 | 3357.67 |
6.2. Analysis of the Results
7. Conclusions
- (1)
- The grey dynamic fuzzy Markov prediction model can blend in new information in a timely and effective manner. Simultaneously, it can discard outdated information, that is, information declines caused by time lapses. Moreover, compared to the conventional model, the results of the grey dynamic fuzzy Markov prediction model closely mirror the actual data.
- (2)
- The grey dynamic fuzzy Markov prediction model is based on the conventional GM (1,1) prediction model. The proposed model is simple and easy to understand. It has strong applicability and shows high precision as a linear prediction model. Thus, it has important practical significance, as shown in this study, for biofuel production prediction.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Annual Energy Outlook 2014; U.S. Energy Information Administration (EIA): Washington, DC, USA, 2014.
- Domestic and International Oil and Gas Industry Development Report 2014; China National Petroleum Corporation (CNPC) Research Institute of Economics and Technology: Beijing, China, 2014. (In Chinese)
- Odgaard, O.; Delman, J. China’s energy security and its challenges towards 2035. Energy Policy 2014, 71, 107–117. [Google Scholar] [CrossRef]
- Research on China’s Medium and Long Term Energy Development Strategy; State Council Development Research Center: Beijing, China, 2011. (In Chinese)
- Doku, A.; Di Falco, S. Biofuels in developing countries: Are comparative advantages enough? Energy Policy 2012, 44, 101–117. [Google Scholar] [CrossRef]
- Charles, M.B.; Ryan, R.; Ryan, N.; Oloruntoba, R. Public policy and biofuels: The way forward? Energy Policy 2007, 35, 5737–5746. [Google Scholar] [CrossRef]
- Wiesenthal, T.; Leduc, G.; Christidis, P.; Schade, B.; Pelkmans, L.; Govaerts, L.; Georgopoulos, P. Biofuel support policies in Europe: Lessons learnt for the long way ahead. Renew. Sustain. Energy Rev. 2009, 13, 789–800. [Google Scholar] [CrossRef]
- Gregg, J.S.; Andres, R.J.; Marland, G. China: Emissions pattern of the world Leader in CO2 emissions from fossil fuel consumption and cement production. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Zhou, A.; Thomson, E. The development of biofuels in Asia. Appl. Energy 2009, 86, S11–S20. [Google Scholar] [CrossRef]
- Environmental Protection Bureau (EPB). Available online: http://tech.sina.com.cn/d/2014-10-31/14329750274.shtml (accessed 31 October 2014). (In Chinese)
- Wang, C.; Cai, W.J.; Lu, X.D.; Chen, J.N. CO2 mitigation scenarios in China’s road transport sector. Energy Convers. Manag. 2007, 48, 2110–2118. [Google Scholar] [CrossRef]
- China’s Medium-Term and Long-Term Plan for Renewable Energy Development; National Development and Reform Commission: Beijing, China, 2007. (In Chinese)
- Chang, S.Y.; Zhao, L.L.; Govinda, R.T.; Zhang, X.L. Biofuels development in China: Technology options and policies needed to meet the 2020 target. Energy Policy 2012, 51, 64–79. [Google Scholar] [CrossRef]
- Qiu, H.G.; Huang, J.K.; Keyzer, M. Biofuel development, food security and the use of marginal land in China. J. Environ. Qual. 2011, 40, 1058–1067. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.S.; Zhao, L.X.; Meng, H.B.; Sun, L.Y.; Yan, J.Y. Estimation of un-used land potential for biofuels development in (the) People’s Republic of China. Appl. Energy 2009, 86, S77–S85. [Google Scholar] [CrossRef]
- Wu, Y.M. Research on Fiscal Policy Support for Fuel Ethanol Industry in China Using CGE Model. Ph.D. Thesis, University of Geosciences, Beijing, China, 2014. [Google Scholar]
- Amirnekooei, K.; Ardehali, M.M.; Sadri, A. Integrated resource planning for Iran: Development of reference energy system, forecast, and long-term energy-environment plan. Energy 2012, 46, 374–385. [Google Scholar] [CrossRef]
- Bennett, C.J.; Stewart, R.A.; Lu, J.W. Forecasting low voltage distribution network demand profiles using a pattern recognition based expert system. Energy 2014, 67, 200–212. [Google Scholar]
- Tunckaya, Y.; Koklukaya, E. Comparative prediction analysis of 600 MWe coal-fired power plant production rate using statistical and neural-based models. J. Energy Inst. 2015, 88, 11–18. [Google Scholar] [CrossRef]
- Carpinone, A.; Giorgio, M.; Langella, R.; Testa, A. Markov chain modeling for very-short-term wind power forecasting. Electr. Power Syst. Res. 2015, 122, 152–158. [Google Scholar] [CrossRef]
- Urasawa, S. Real-time GDP forecasting for Japan: A dynamic factor model approach. J. Jpn. Int. Econ. 2014, 34, 116–134. [Google Scholar] [CrossRef]
- Deng, J.L. Basis of Gray Theory; Huazhong University of Science and Technology Press: Wuhan, China, 1987. (In Chinese) [Google Scholar]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Liu, S.F.; Deng, J.L. The range suitable for GM(1,1). Syst. Eng. Theory Pract. 2000, 20, 121–124. [Google Scholar]
- Xiong, P.P.; Dang, Y.G.; Yao, T.X.; Wang, Z.X. Optimal modeling and forecasting of the energy consumption and production in China. Energy 2014, 77, 623–634. [Google Scholar] [CrossRef]
- Hamzacebi, C.; Es, H.A. Forecasting the annual electricity consumption of Turkey using an optimized grey model. Energy 2014, 70, 165–171. [Google Scholar] [CrossRef]
- Soldo, B. Forecasting natural gas consumption. Appl. Energy 2012, 92, 26–37. [Google Scholar] [CrossRef]
- Wu, L.F.; Liu, S.F.; Liu, D.L.; Fang, Z.G.; Xu, H.Y. Modeling and forecasting CO2 emissions in the BRICS (Brazil, Russia, India, China, and South Africa) countries using a novel multi-variable grey model. Energy 2015, 79, 489–495. [Google Scholar] [CrossRef]
- Wang, J.Z.; Dong, Y.; Wu, J.; Mu, R.; Jiang, H. Coal production forecast and low carbon policies in China. Energy Policy 2011, 39, 5970–5979. [Google Scholar] [CrossRef]
- Lin, C.T.; Yang, S.Y. Forecast of the output value of Taiwan’s opto-electronics industry using the Grey forecasting model. Technol. Forecast. Soc. Change 2003, 70, 177–186. [Google Scholar] [CrossRef]
- Truong, D.Q.; Ahn, K.K. Wave prediction based on a modified grey model MGM(1,1) for real time control of wave energy converters in irregular waves. Renew. Energy 2012, 43, 242–255. [Google Scholar] [CrossRef]
- Liu, X.Y.; Peng, H.Q.; Bai, Y.; Zhu, Y.J.; Liao, L.L. Tourism Flows Prediction based on an Improved Grey GM(1,1) model. Soc. Behav. Sci. 2014, 138, 767–775. [Google Scholar] [CrossRef]
- Xie, N.M.; Liu, S.F. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2009, 33, 1173–1186. [Google Scholar] [CrossRef]
- Tien, T.L. A new grey prediction model FGM(1, 1). Math. Comput. Model. 2009, 49, 1416–1426. [Google Scholar] [CrossRef]
- Li, D.C.; Yeh, C.W.; Chang, C.J. An improved grey-based approach for early manufacturing data forecasting. Comput. Ind. Eng. 2009, 57, 1161–1167. [Google Scholar] [CrossRef]
- Ou, S.L. Forecasting agricultural output with an improved grey forecasting model based on the genetic algorithm. Comput. Electron. Agric. 2012, 85, 33–39. [Google Scholar] [CrossRef]
- Evans, M. An alternative approach to estimating the parameters of a generalized Grey Verhulst model: An application to steel intensity of use in the UK. Expert Syst. Appl. 2014, 41, 1236–1244. [Google Scholar] [CrossRef]
- Oztaysi, B. A decision model for information technology selection using AHP integrated Topsis-Grey: The case of content management systems. Knowl. Based Syst. 2014, 70, 44–54. [Google Scholar] [CrossRef]
- Bahrami, S.; Hooshmand, R.; Parastegari, M. Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm. Energy 2014, 72, 434–442. [Google Scholar] [CrossRef]
- Wang, H.Y.; Ma, F. A study of information renewal GM(1,1) model for predicting urban medium and long-term water demand. Eng. J. Wuhan Univ. 2004, 37, 32–36. [Google Scholar]
- Zhou, Z.L.; Yin, C.W. Application of Grey metabolic Model in the prediction of the Cotton Output in China. Asian Agric. Res. 2011, 3, 1–6. [Google Scholar]
- BP Statistical Review of World Energy 2014. Available online: http://www.bp.com/zh_cn/china/reports-and-publications/bp_2014.html (accessed on 1 June 2014).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, N.; Zhang, Y.; Sun, Y.; Jiang, Y.; Chen, D. Forecasting China’s Annual Biofuel Production Using an Improved Grey Model. Energies 2015, 8, 12080-12099. https://doi.org/10.3390/en81012080
Geng N, Zhang Y, Sun Y, Jiang Y, Chen D. Forecasting China’s Annual Biofuel Production Using an Improved Grey Model. Energies. 2015; 8(10):12080-12099. https://doi.org/10.3390/en81012080
Chicago/Turabian StyleGeng, Nana, Yong Zhang, Yixiang Sun, Yunjian Jiang, and Dandan Chen. 2015. "Forecasting China’s Annual Biofuel Production Using an Improved Grey Model" Energies 8, no. 10: 12080-12099. https://doi.org/10.3390/en81012080
APA StyleGeng, N., Zhang, Y., Sun, Y., Jiang, Y., & Chen, D. (2015). Forecasting China’s Annual Biofuel Production Using an Improved Grey Model. Energies, 8(10), 12080-12099. https://doi.org/10.3390/en81012080





