Miniaturized Air-Driven Planar Magnetic Generators
Abstract
:1. Introduction
2. Design of the Two Generators
2.1. Overall Design

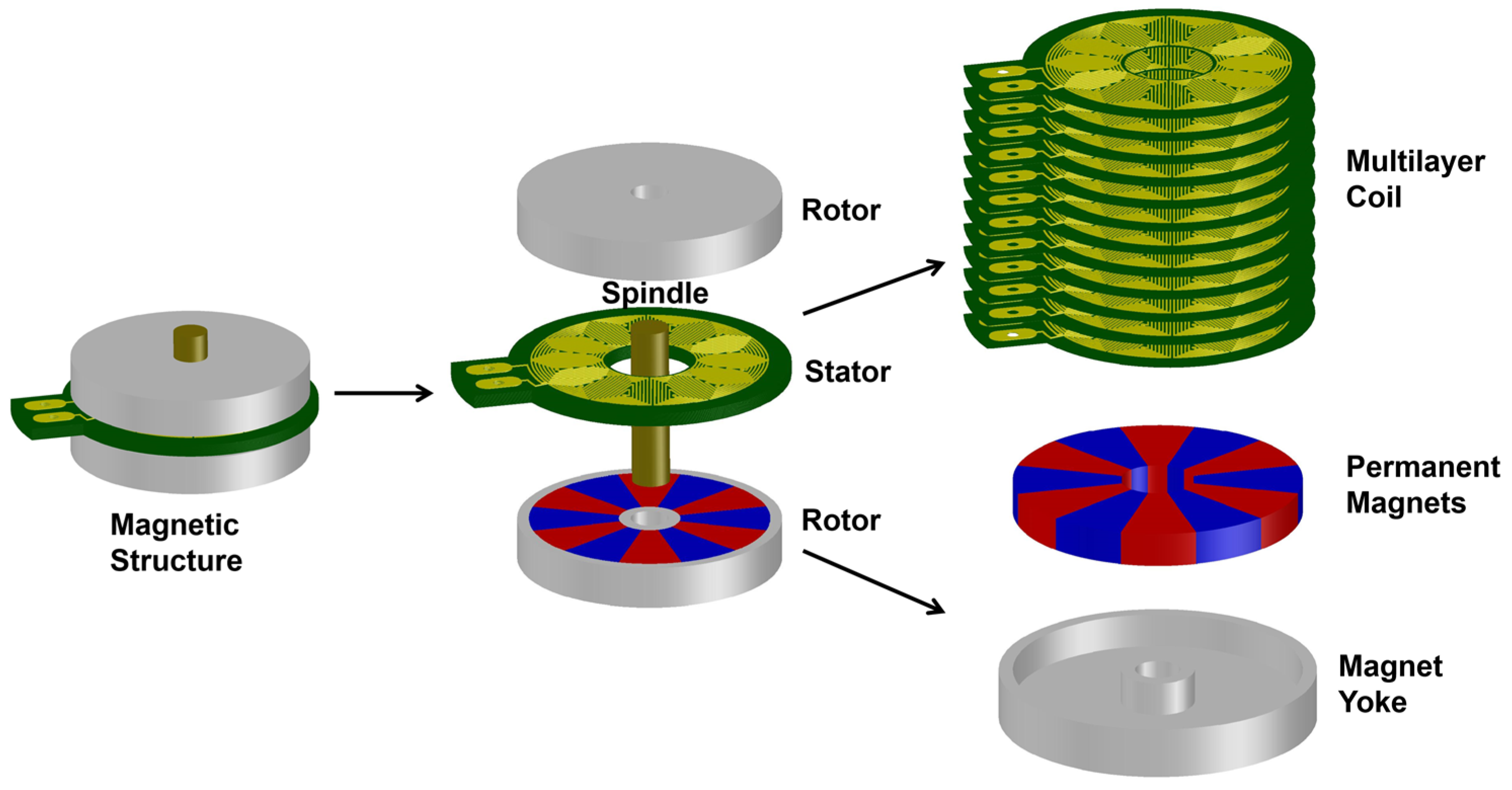
| Parameter | Description | Value in Generator 1 | Value in Generator 2 |
|---|---|---|---|
| Rci | Inner radius of sector coil | 2 mm | 2 mm |
| Rco | Outer radius of sector coil | 5 mm | 5.1 mm |
| Rmi | Inner radius of sector magnet | 1.3 mm | 1.6 mm |
| Rmo | Outer radius of sector magnet | 5.1 mm | 6.5 mm |
| hm | Magnet thickness | 1.2 mm | 1.2 mm |
| he | Yoke thickness | 0.6 mm | 1.3 mm |
| hc | Multilayer coil thickness | 0.3 mm (6 layers) 0.6 mm (12 layers) | 0.3 mm (4 layers) 0.9 mm (12 layers) |
| hδ | Air-gap thickness | 1 mm | 1.2 mm |
| p | Number of pole pairs | 6 | 6 |
| q | Linewidth and spacing of microcoil | 75 μm | 75 μm |
| θ | Pole angle | 30° | 30° |
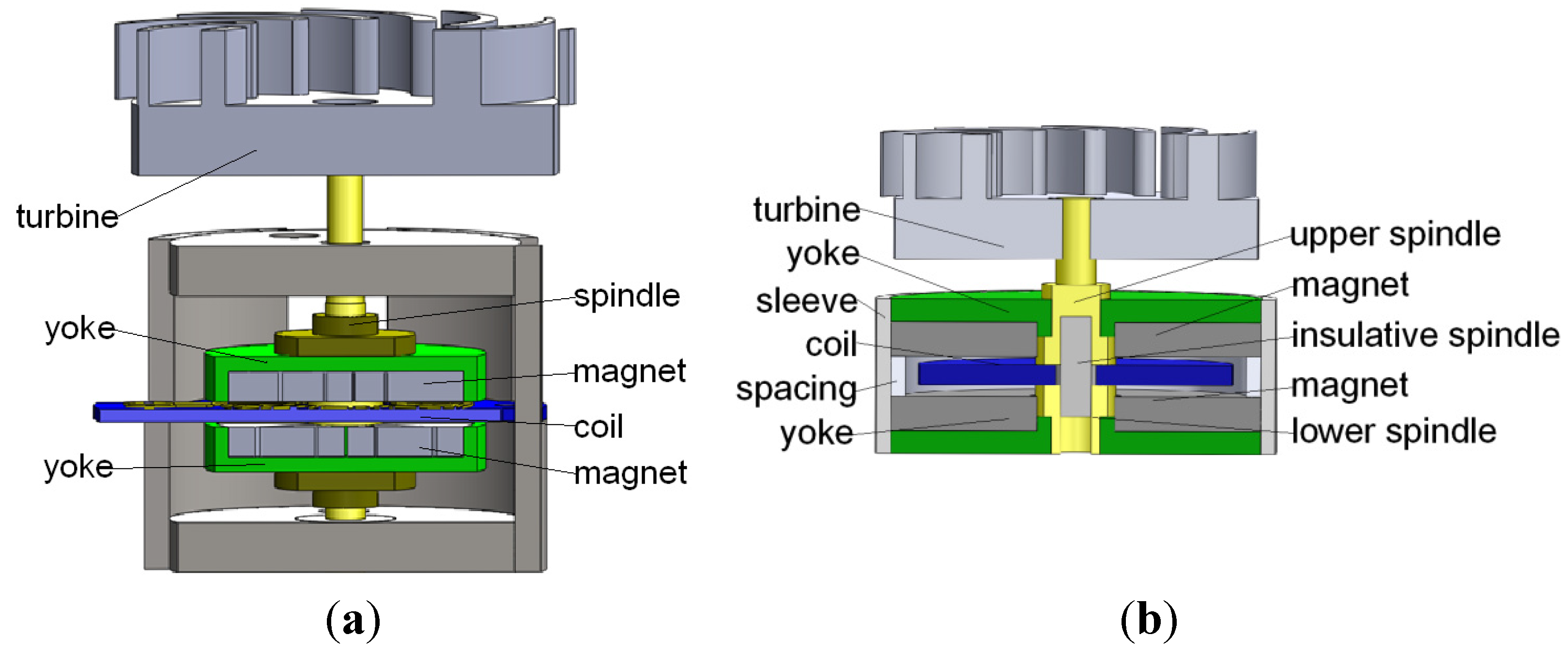
2.2. Magnetic Material Selection
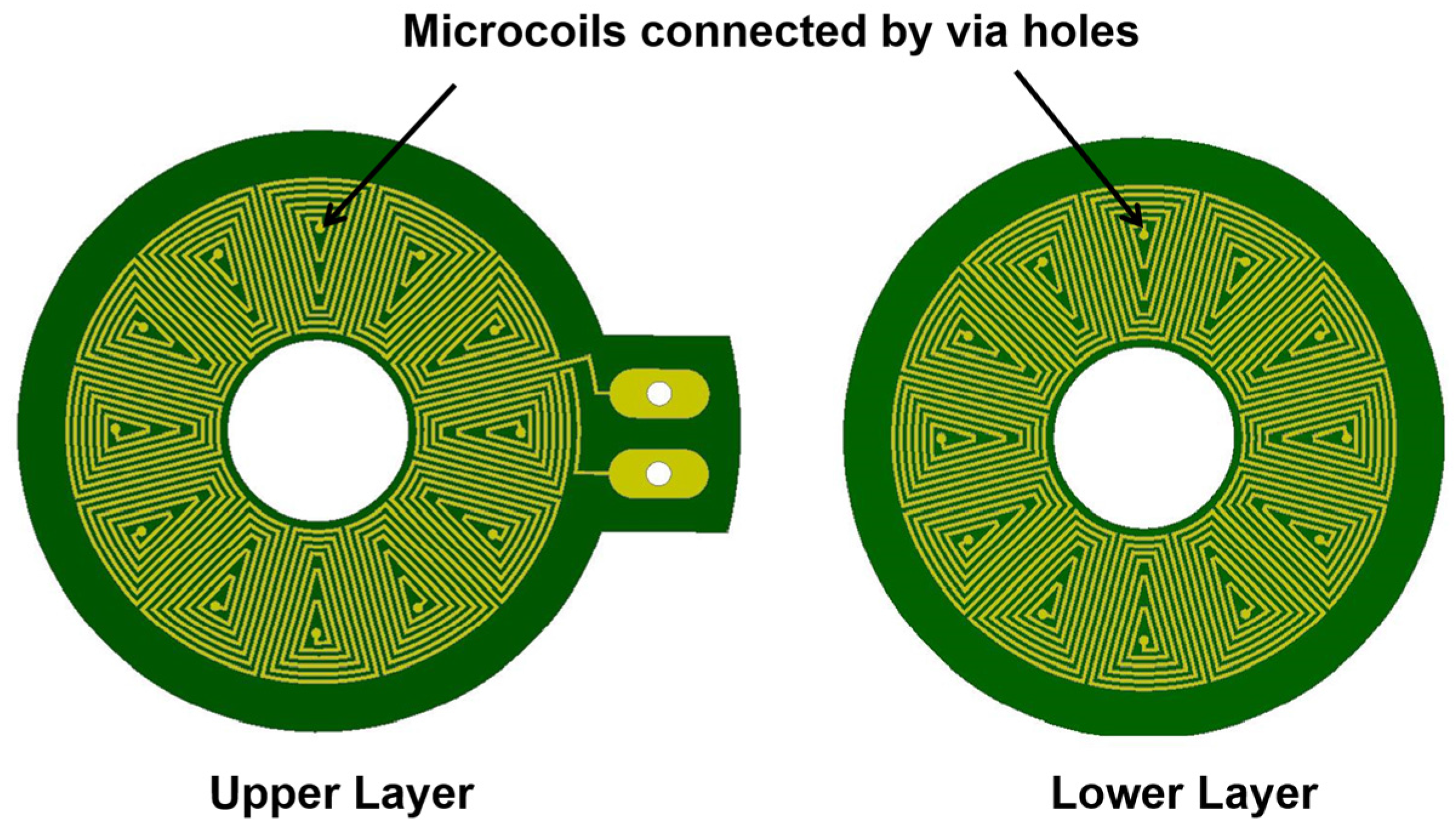
2.3. Coil Design
2.3.1. Coil Design of Coil-Fixing Generator (Generator 1)
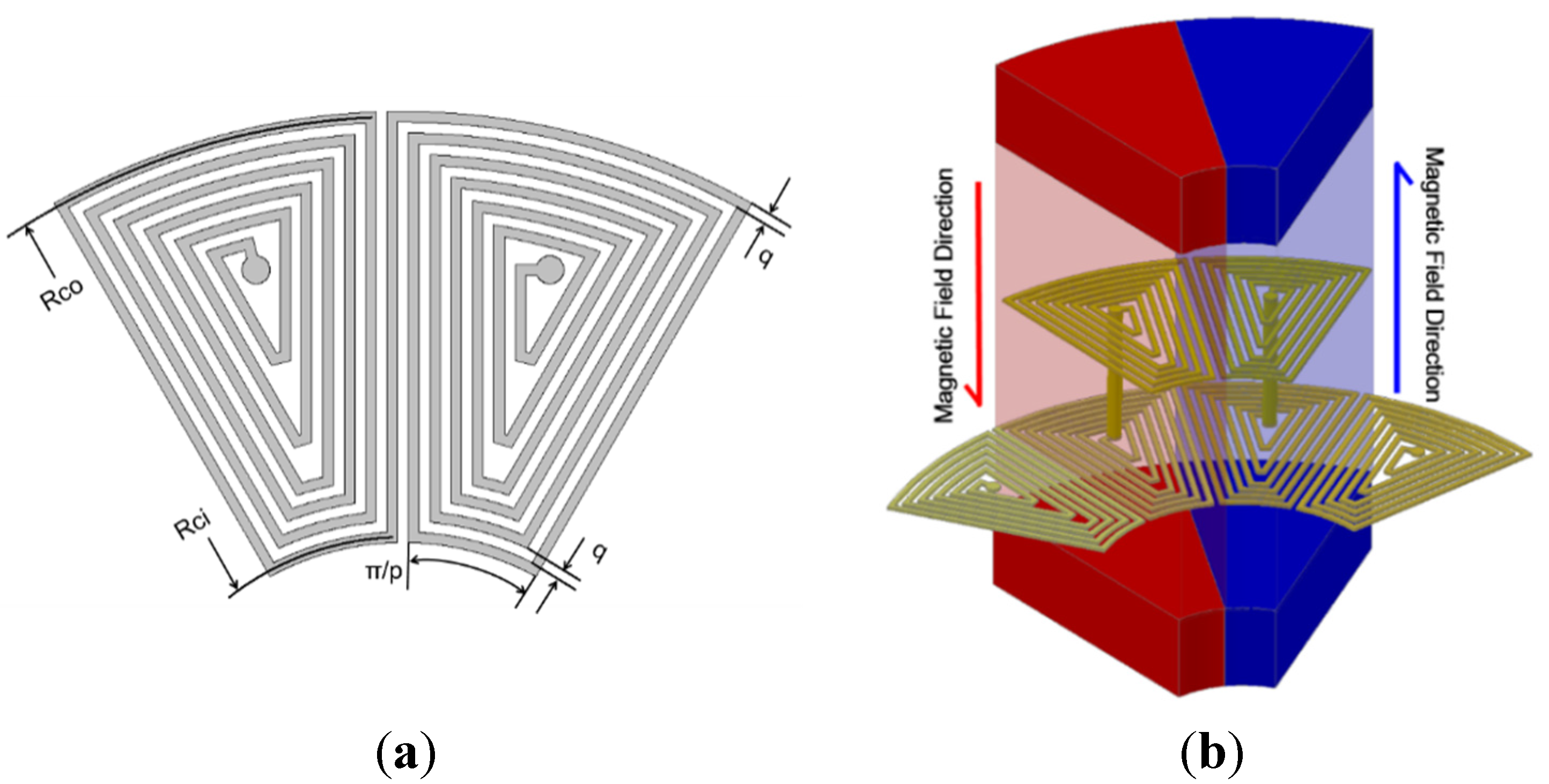
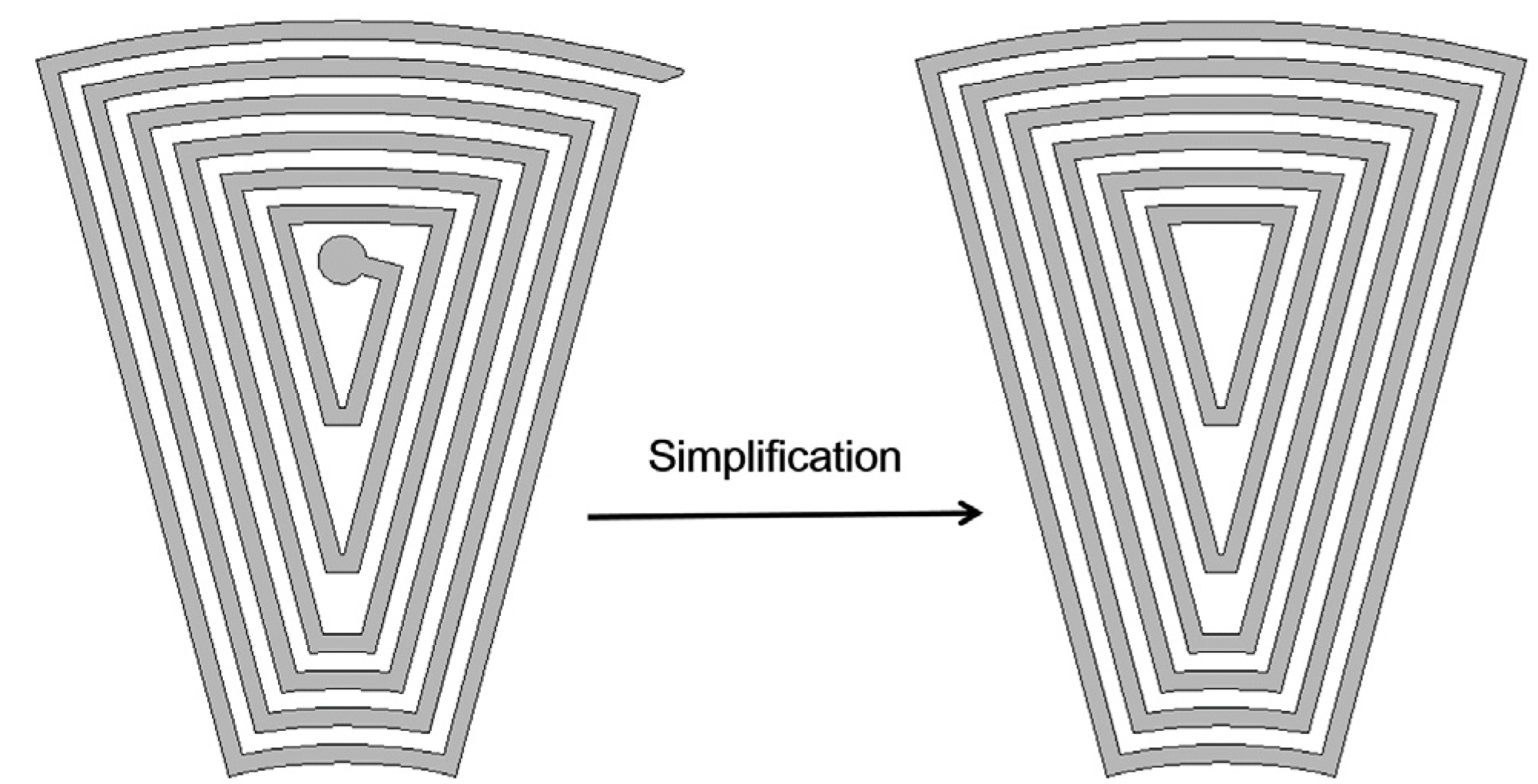
2.3.2. Coil Design of Magnets-Fixing Generator (Generator 2)
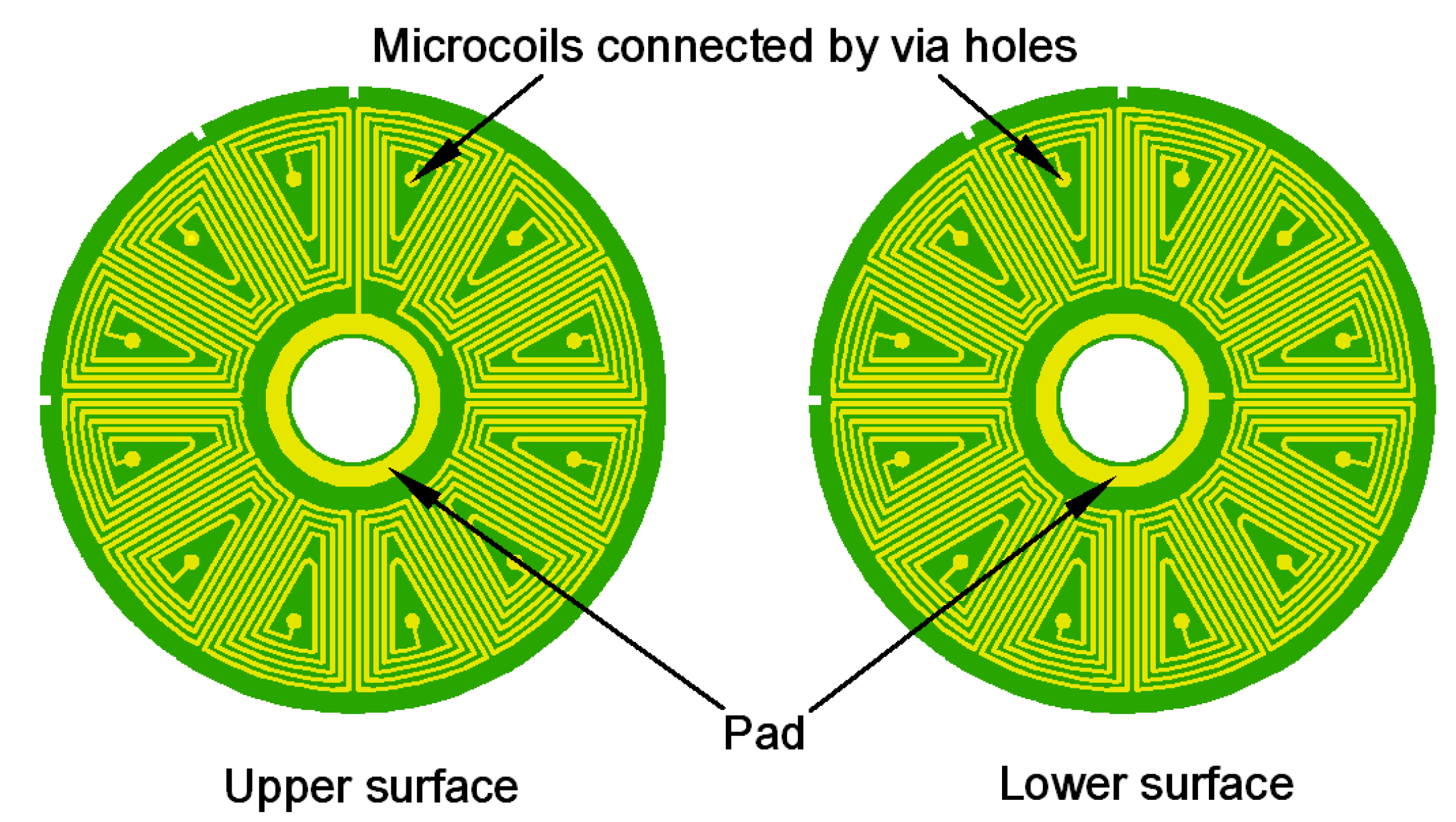
2.4. Magnetic Structure Design
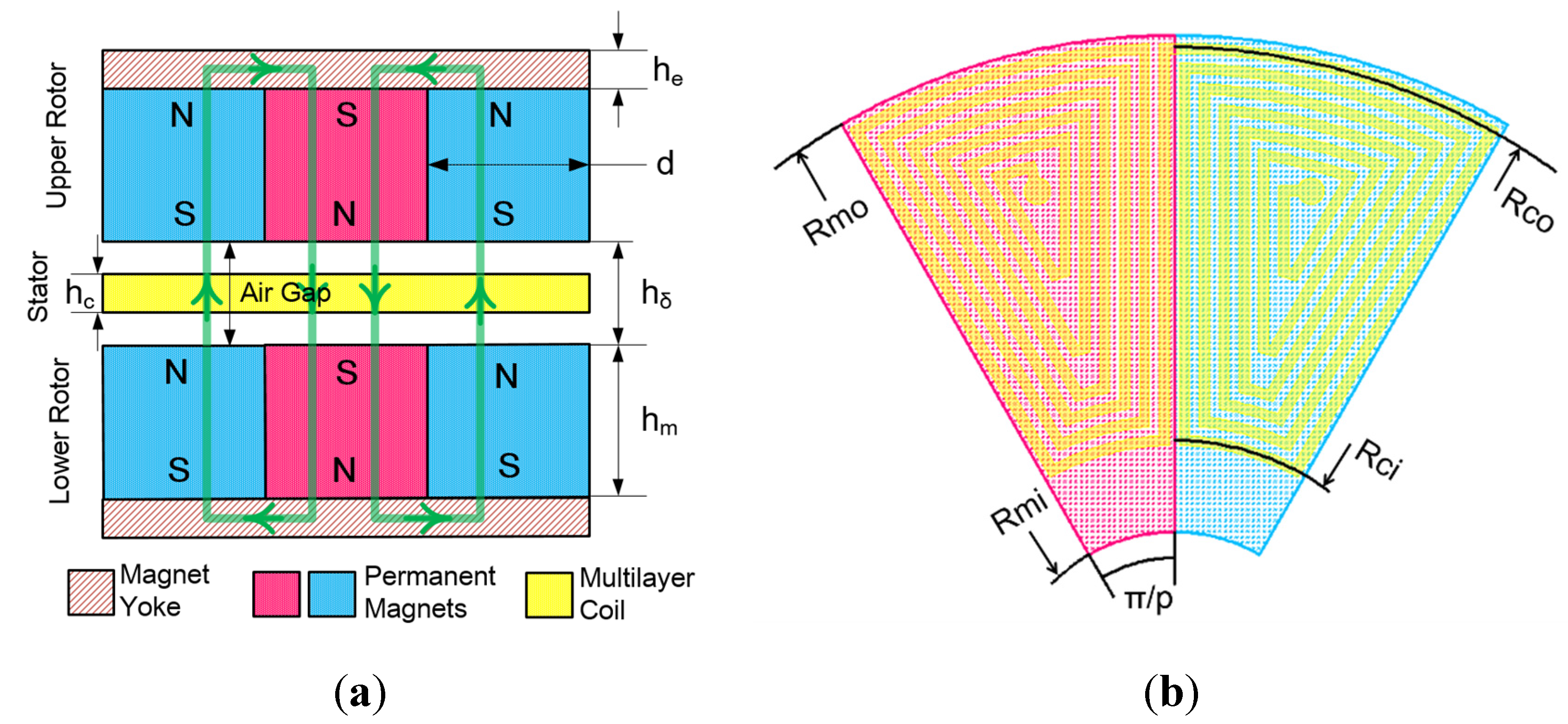
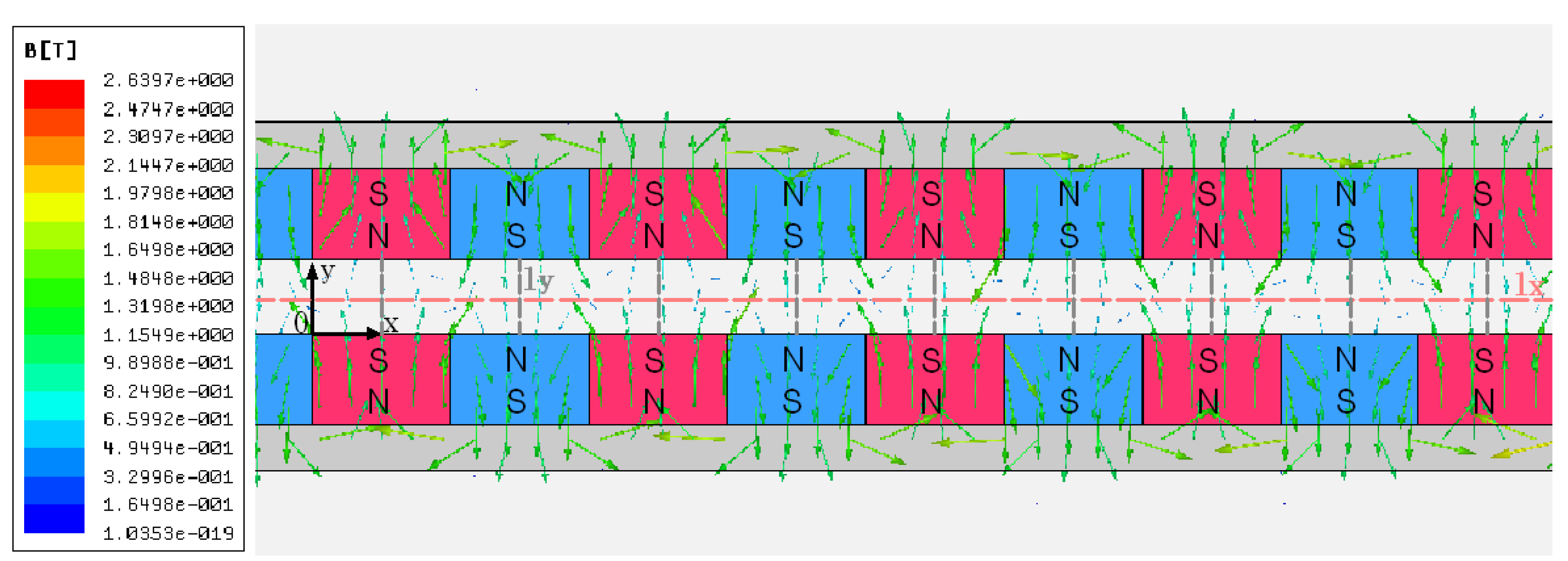
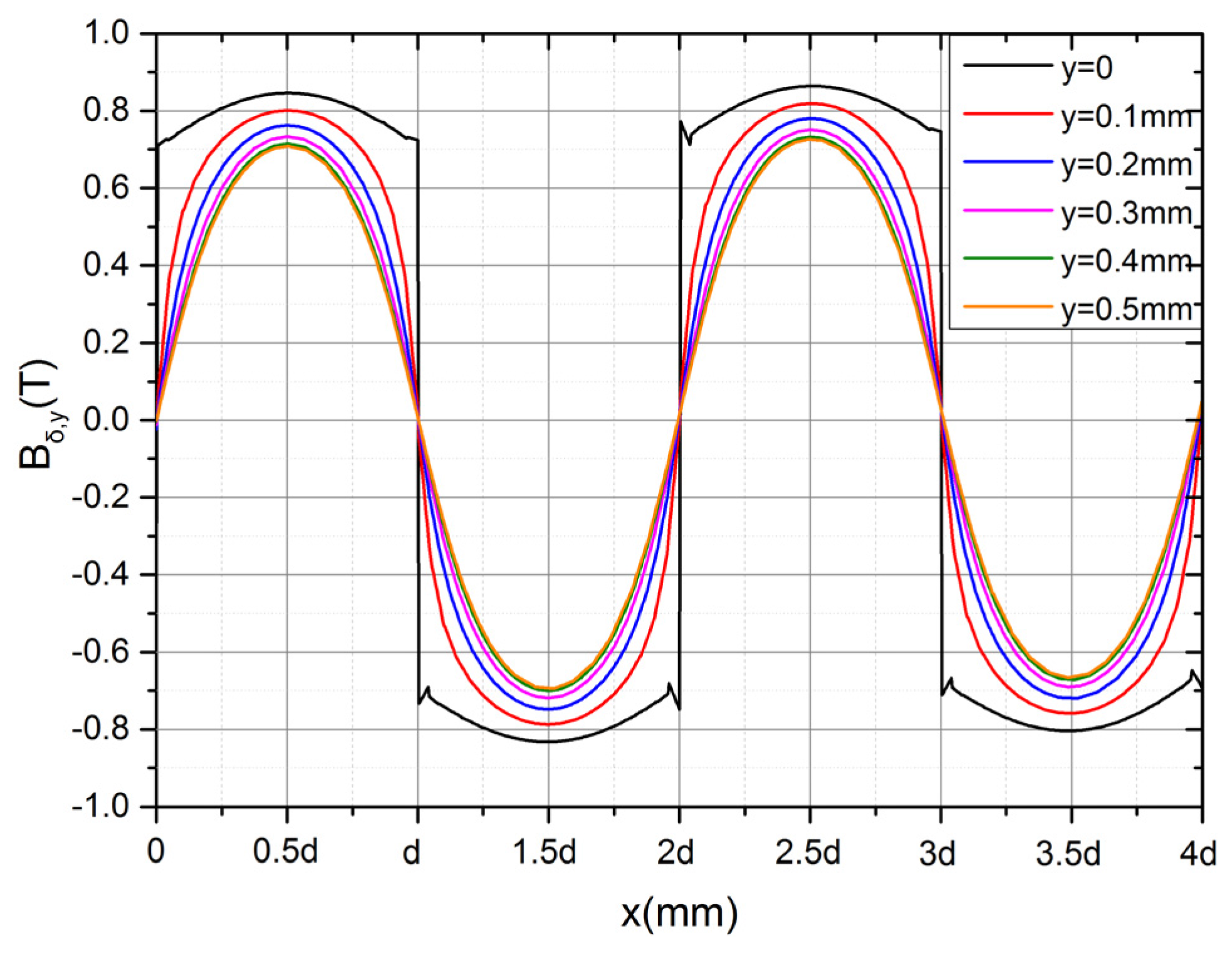

3. Fabrication

4. Experiments and Results
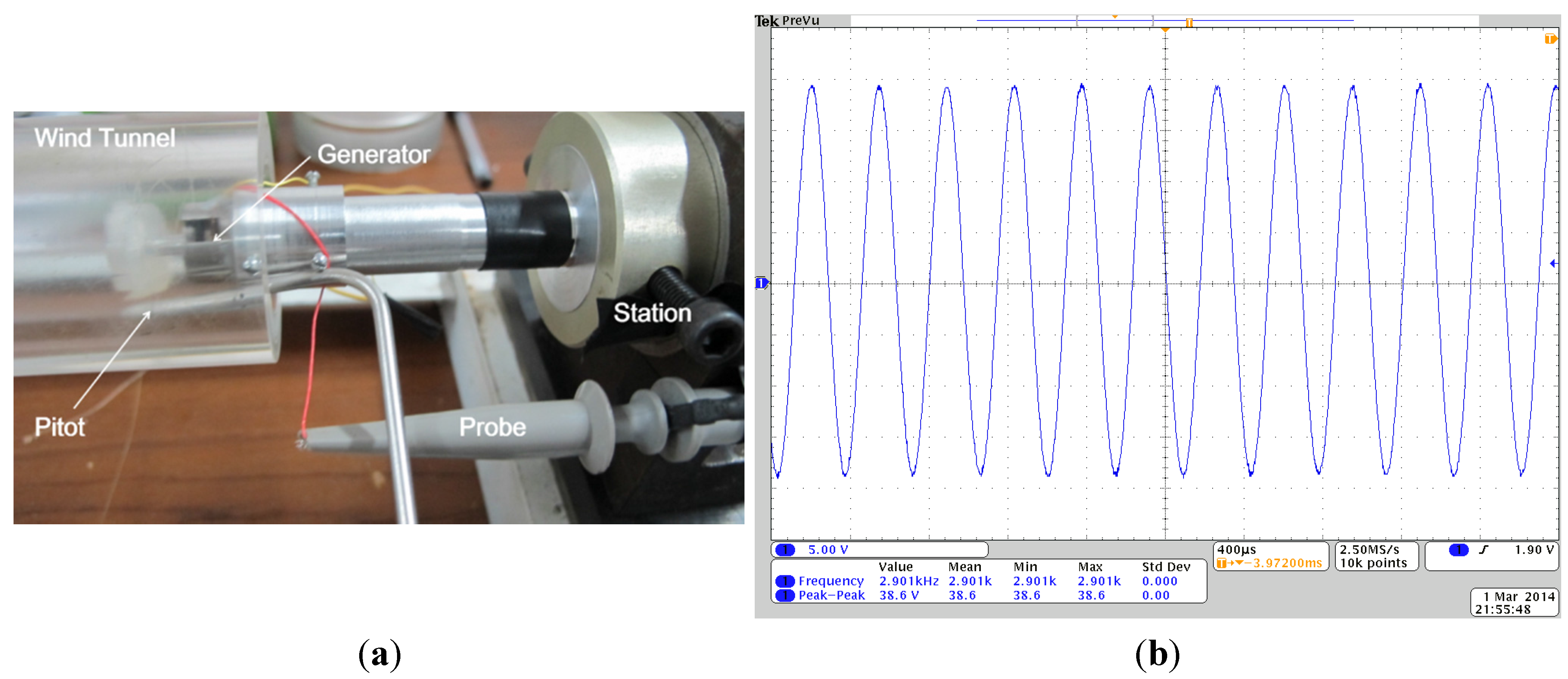
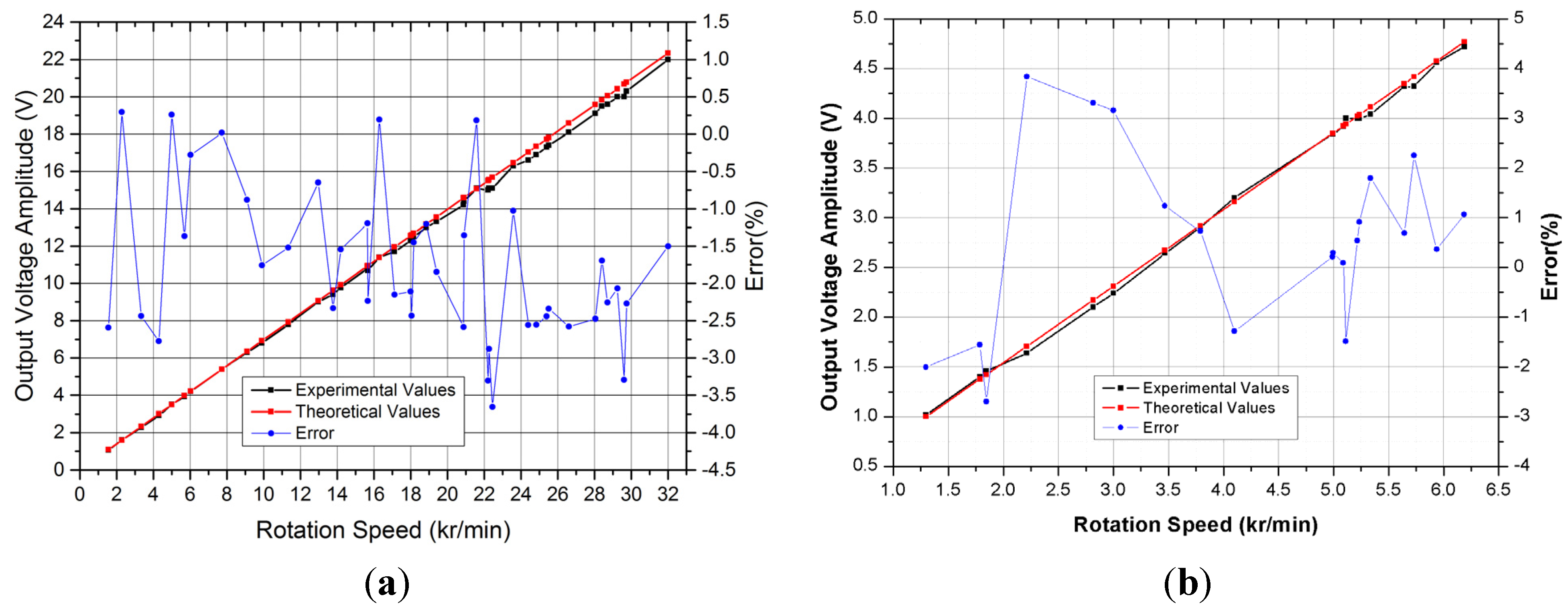
5. Discussion
| Reference | Volume (cm3) | Rotation Speed (krpm) | No-Load Vrms (V) | Normalized Voltage (mV·krpm−1) | Internal Resistance (Ω) | Max. Power (Wrms) | Power Density (W·cm−3) |
|---|---|---|---|---|---|---|---|
| Generator 1 | 0.38 | 32 | 15.55 | 485 | 116 | 0.521 | 1.37 |
| Generator 2 | 0.823 | 6.2 | 3.337 | 538 | 70.5 | 0.0395 | 0.048 |
| [3] | 0.05 | 2.2 | 0.111 | 50 | 4.1 × 10−4 | 8.2 × 10−3 | |
| [8] | 0.761 | 13.3 | 0.218 | 16.39 | |||
| [4] | 3.4 × 10−3 | 392 | 0.12 | 0.31 | 1.8 | 6.6 × 10−3 | 1.95 |
| [5] | 0.11 | 200 | 0.464 | 2.32 | 0.32 | 1.05 | 9.5 |
| [6] | 0.077 | 10 | 9.26 × 10−3 | 0.926 | 0.23 | 3.6 × 10−4 | 4.6 × 10−3 |
| [7] | 1.253 | 4 | 3.2 | 800 | 5.8 × 10−3 | 4.63 × 10−3 | |
| [9] | 0.041 | 30 | 0.42 | 14 | 45 | 0.0011 | 0.027 |
| [10] | 0.023 | 380 | 4.18 | 11 | 5.0 | 220 | |
| [11] | 0.146 | 120 | 0.50 | 4.2 | 1.3 | 8.9 | |
| [12] | 0.136 | 305 | 1.60 | 5.24 | 8.0 | 59 |
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Tang, R.; Yuan, D. Modern Permanent Magnet Machines-Theory and Design; Machine Press: Beijing, China, 1997; Volume 4, pp. 329–330. [Google Scholar]
- Arnold, D.P. Review of microscale magnetic power generation. Magn. IEEE Trans. 2007, 43, 3940–3951. [Google Scholar] [CrossRef]
- Pan, C.T.; Wu, T.T. Development of a rotary electromagnetic microgenerator. J. Micromech. Microeng. 2007, 17, 120–128. [Google Scholar] [CrossRef]
- Herrault, F.; Ji, C.H.; Allen, M.G.; Toulouse, E.D. Ultraminiaturized High-Speed Permanent-Magnet Generators for Milliwatt-Level Power Generation. J. Microelectromech. Syst. 2008, 17, 1376–1387. [Google Scholar] [CrossRef]
- Herrault, F.; Yen, B.C.; Chang-Hyeon, J.; Spakovszky, Z.S.; Lang, J.H.; Allen, M.G. Fabrication and Performance of Silicon-Embedded Permanent-Magnet Microgenerators. J. Microelectromech. Syst. 2010, 19, 4–13. [Google Scholar] [CrossRef]
- Sun, S.C.; Shi, G.C. Design and fabrication of micro rotational generators. Opt. Precis. Eng. 2011, 6, 1306–1312. [Google Scholar]
- Cordero, R.; Rivera, A.; Neuman, M.; Warrington, R.; Romero, E. Micro-Rotational Electromagnetic Generator for High Speed Applications. In Proceedings of the 25th International Conference on Micro Electro Mechanical Systems (MEMS), Paris, France, 19 January–2 February 2012; pp. 1257–1260.
- Chen, Y.J.; Pan, C.T.; Liu, Z.H. Analysis of an in-plane micro-generator with various microcoil shapes. Microsyst. Technol. 2013, 19, 43–52. [Google Scholar] [CrossRef]
- Holmes, A.S.; Hong, G.; Pullen, K.R. Axial-flux permanent magnet machines for micropower generation. Microelectromech. Syst. J. 2005, 14, 54–62. [Google Scholar] [CrossRef]
- Raisigel, H.; Cugat, O.; Delamare, J. Permanent magnet planar micro-generators. Sens. Actuators A Phys. 2006, 130–131, 438–444. [Google Scholar] [CrossRef]
- Arnold, D.P.; Das, S.; Park, J.W.; Lulica, Z.; Jeffrey, H.L.; Allen, M.G. Microfabricated high-speed axial-flux multiwatt permanent-magnet generators-part II: Design, fabrication, and testing. J. Microelectromech. Syst. 2006, 15, 1351–1363. [Google Scholar] [CrossRef]
- Arnold, D.P.; Herrault, F.; Zana, I.; Galle, P.; Park, J.; Das, S.; Lang, J.H.; Allen, M.G. Design optimization of an 8-Watt, microscale, axial-flux, permanent-magnet generator. J. Micromech. Microeng. 2006, 16, 290–296. [Google Scholar] [CrossRef]
- Gieras, J.F.; Wang, R.J.; Kamper, M.J. Axial Flux Permanent Magnet Brushless Machines; Springer: New York, NY, USA, 2008; Volume 1, p. 7. [Google Scholar]
- Howey, D.A.; Bansal, A.; Holmes, A.S. Design and performance of a centimetre-scale shrouded wind turbine for energy harvesting. Smart Mater. Struct. 2011, 20, 085021. [Google Scholar] [CrossRef]
- Zhao, J.; Shi, G.; Du, L. Design method of magnetic circuit in planar permanent magnetic micro-generator. Acta Armamentarii 2014, 35, 1144–1151. [Google Scholar]
- Das, S.; Arnold, D.P.; Zana, I.; Jin-Woo, P.; Allen, M.G.; Lang, J.H. Microfabricated high-speed axial-flux multiwatt permanent-magnet generators—Part I: Modeling. J. Microelectromech. Syst. 2006, 15, 1330–1350. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Shi, G.; Du, L. Miniaturized Air-Driven Planar Magnetic Generators. Energies 2015, 8, 11755-11769. https://doi.org/10.3390/en81011755
Zhao J, Shi G, Du L. Miniaturized Air-Driven Planar Magnetic Generators. Energies. 2015; 8(10):11755-11769. https://doi.org/10.3390/en81011755
Chicago/Turabian StyleZhao, Jingjing, Gengchen Shi, and Lin Du. 2015. "Miniaturized Air-Driven Planar Magnetic Generators" Energies 8, no. 10: 11755-11769. https://doi.org/10.3390/en81011755
APA StyleZhao, J., Shi, G., & Du, L. (2015). Miniaturized Air-Driven Planar Magnetic Generators. Energies, 8(10), 11755-11769. https://doi.org/10.3390/en81011755





