A Dynamic Economic Dispatch Model Incorporating Wind Power Based on Chance Constrained Programming
Abstract
:1. Introduction
2. DED Problem Formulation
2.1. Objective Function
- is the total generation cost over the whole time horizon;
- is the number of periods;
- is the number of thermal units;
- is the power output (MW) of the th unit corresponding to time period ;
- is the generation cost of the th unit corresponding to time period ;
- is the valve point loading effect of the th unit corresponding to time period ;
2.2. System and Unit Constraints
2.2.1. Power Balance Constraints
2.2.2. Generation Limits of Thermal Units and Wind Farm
2.2.3. Chance Constraint on Wind Power
2.2.4. Ramp Rate Limits of Thermal Units
2.2.5. Spinning Reserve Constraints
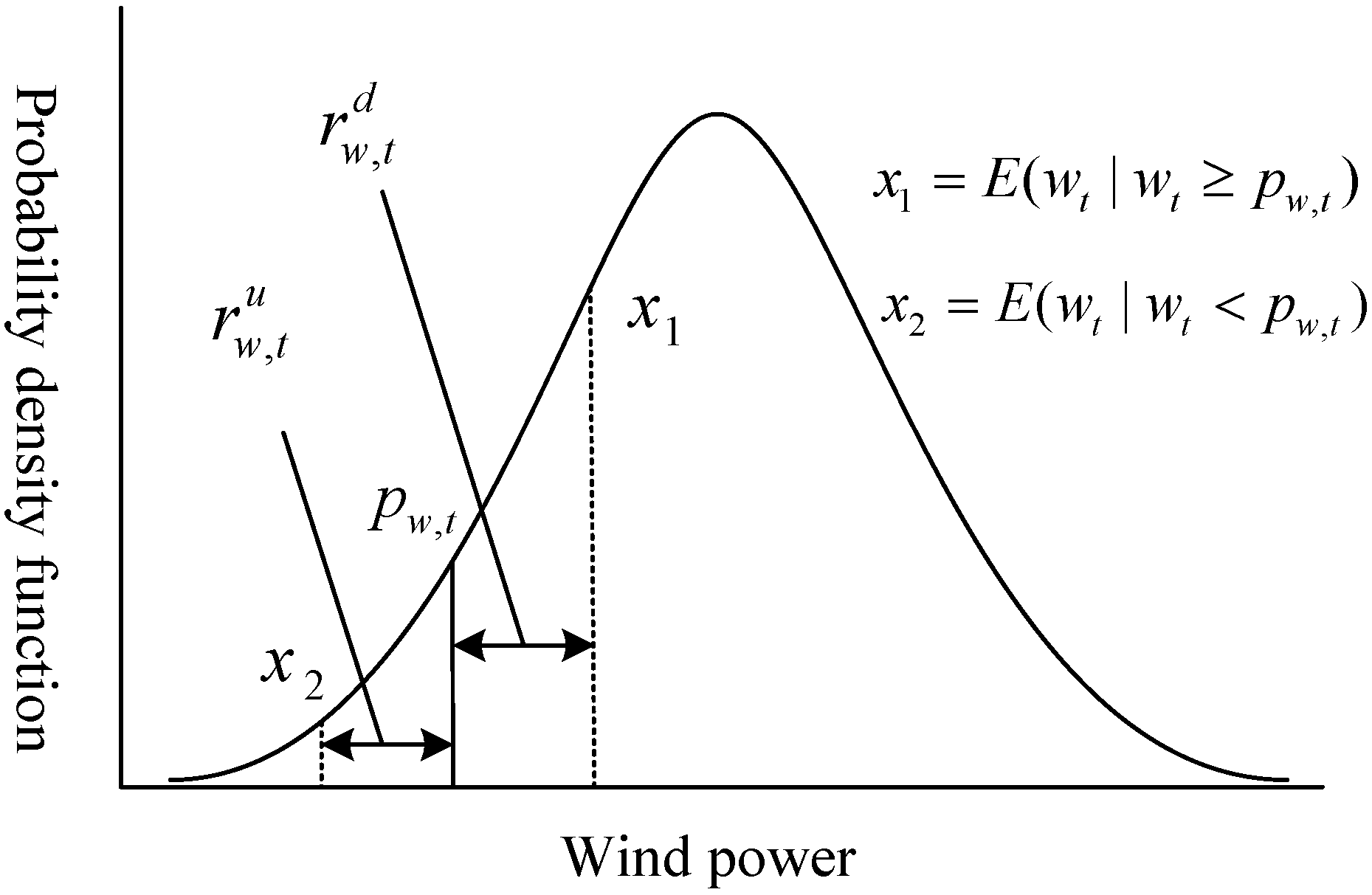
3. Equivalent Transformation of the DED Model
3.1. Beta Distribution of Wind Power
3.2. Equivalent Transformation
4. Improved PSO Approach
- J is the population size;
- is the dynamic inertia weight factor, and can be dynamically set with the following equation [6]:
4.1. Feasible Region Adjustment Strategy
4.2. Hill Climbing Search Operation
4.3. DED Constraints Handling Using PSO-HCSO
4.4. The Procedure of Improved PSO Approach
5. Simulation Results and Discussions
| Period | Expected Value (MW) | Standard Deviation (MW) | α | β | Period | Expected Value (MW) | Standard Deviation (MW) | α | β |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 70.4 | 17.25 | 10.38 | 18.81 | 13 | 133.24 | 33.25 | 4.58 | 2.23 |
| 2 | 55.50 | 13.87 | 11.24 | 28.87 | 14 | 129.50 | 32.37 | 4.88 | 2.58 |
| 3 | 34.50 | 9.63 | 10.43 | 49.45 | 15 | 147.15 | 36.75 | 3.37 | 1.17 |
| 4 | 28.3 | 10.23 | 6.42 | 38.47 | 16 | 140.7 | 35.40 | 3.86 | 1.57 |
| 5 | 42.1 | 10.54 | 12.35 | 45.73 | 17 | 133.4 | 33.25 | 4.58 | 2.22 |
| 6 | 59.50 | 14.87 | 10.90 | 25.37 | 18 | 108.5 | 27.13 | 6.68 | 5.51 |
| 7 | 70.56 | 17.17 | 10.51 | 18.99 | 19 | 84.7 | 21.06 | 8.83 | 11.81 |
| 8 | 80.50 | 20.12 | 9.09 | 13.27 | 20 | 77.3 | 19.25 | 9.44 | 14.74 |
| 9 | 94.50 | 23.62 | 7.89 | 8.64 | 21 | 66.5 | 16.62 | 10.30 | 20.36 |
| 10 | 112.4 | 28.84 | 5.99 | 4.57 | 22 | 42.2 | 10.5 | 12.50 | 46.14 |
| 11 | 126.7 | 31.53 | 5.17 | 2.91 | 23 | 35.3 | 8.75 | 13.20 | 60.82 |
| 12 | 130.5 | 32.62 | 4.80 | 2.48 | 24 | 63.8 | 15.75 | 10.80 | 22.72 |
| J | K | H | hcount | ε |
|---|---|---|---|---|
| 40 | 200 | 200 | 4 | h/(H+0.00001) |
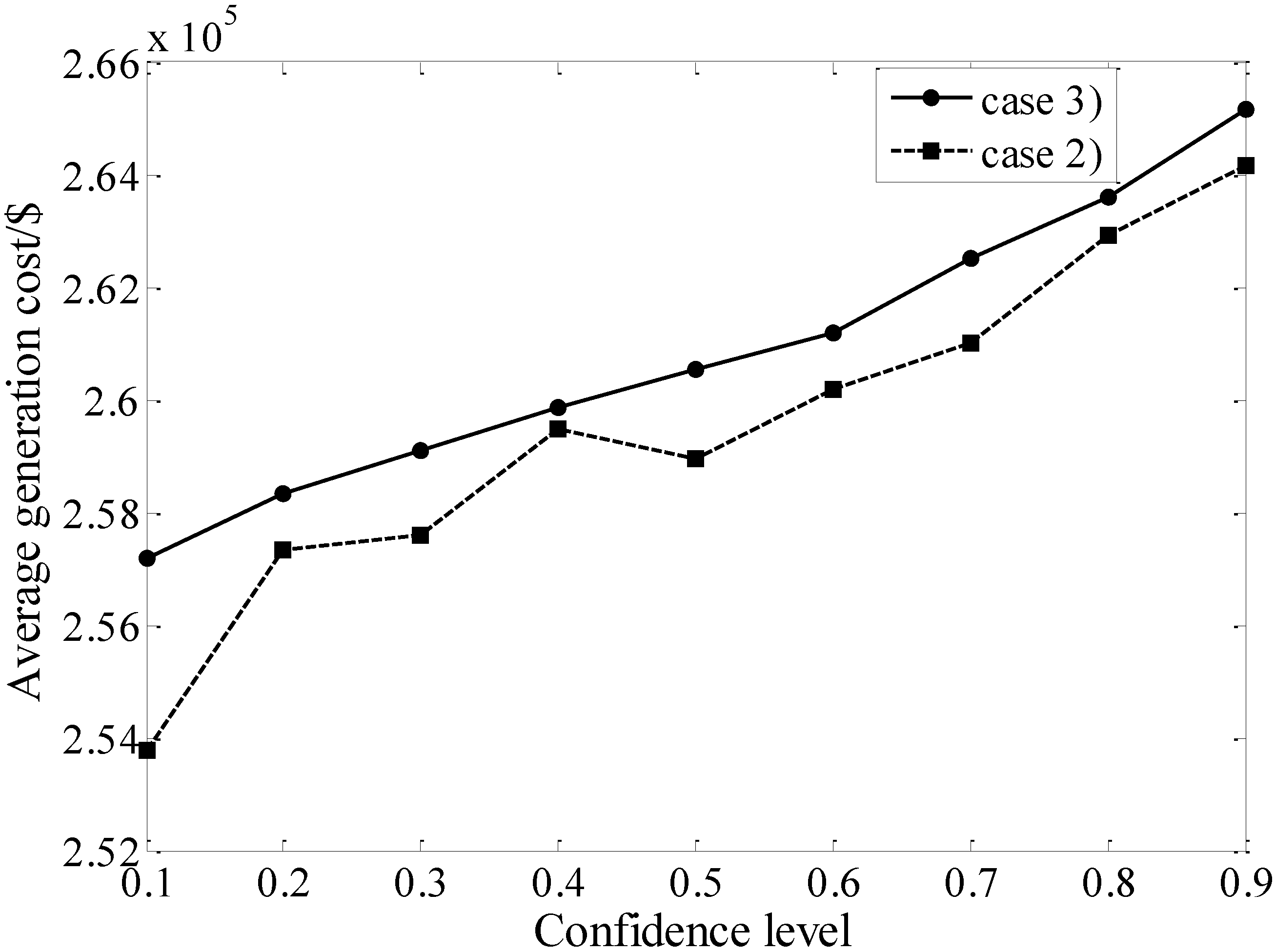
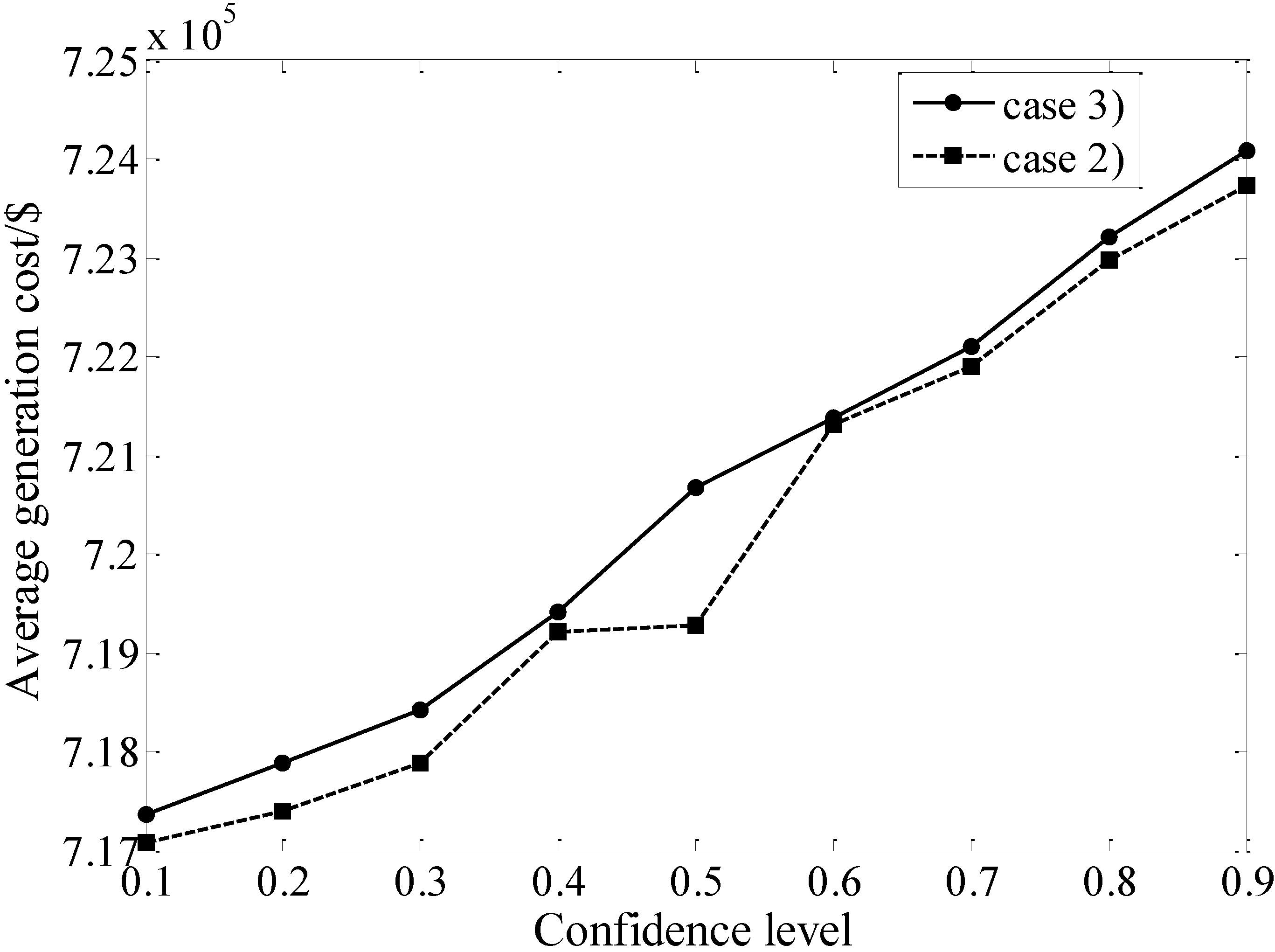
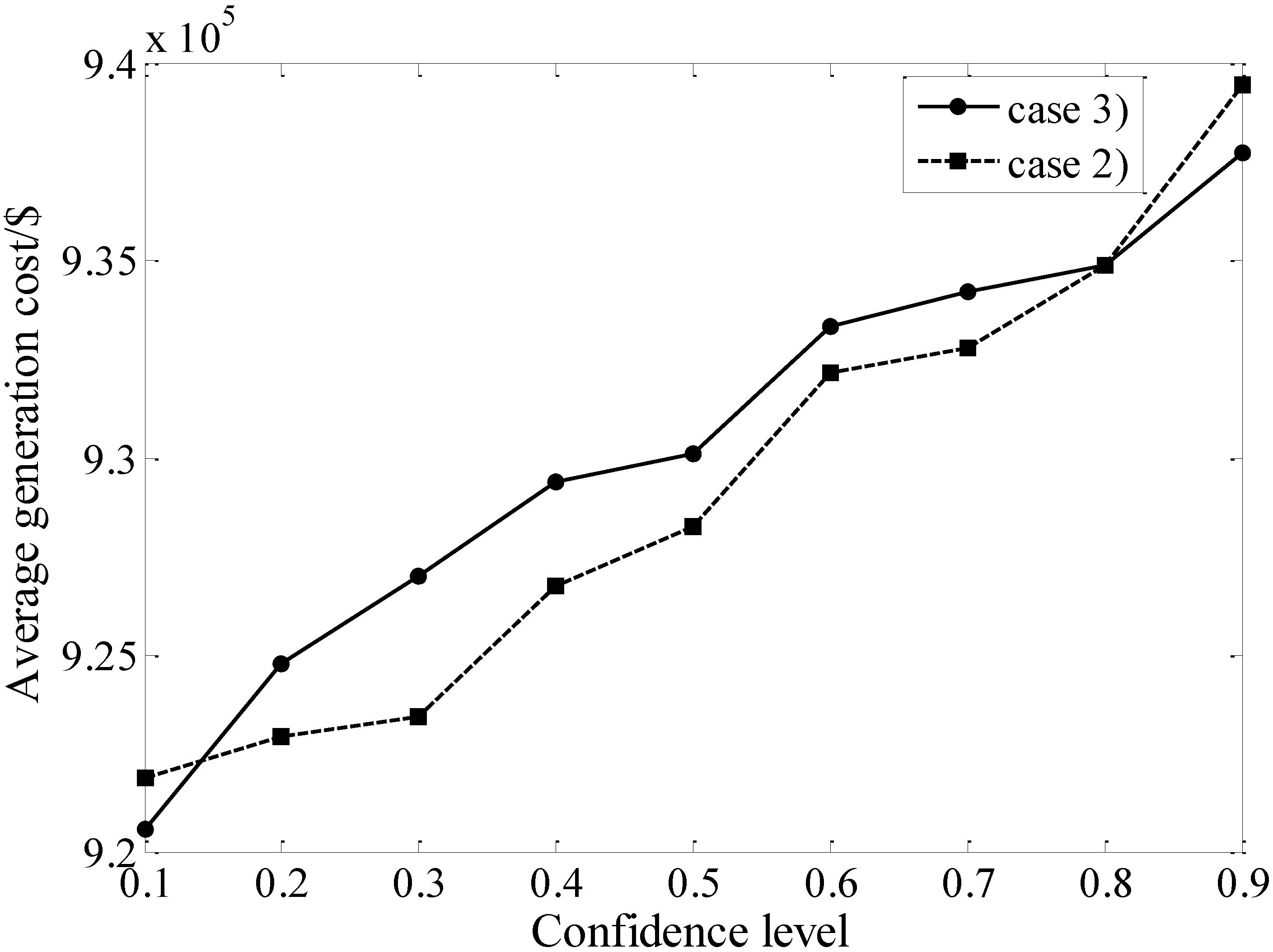
5.1. Comparisons Among the Three Cases of the DED Model
- Case (1): the DED model without considering wind power;
- Case (2): the DED model without considering wind effect in the reserve constraint;
- Case (3): the proposed DED model in this paper.
| Cases | Confidence Level | Average Generation Cost ($) | ||
|---|---|---|---|---|
| System 1 | System 2 | System 3 | ||
| Case (1) | 1 | 278,903.3311 | 736,673.0726 | 952,079.3252 |
| Case (2) | 0.9 | 264,895.0451 | 723,729.9923 | 939,455.4055 |
| 0.5 | 258,950.8628 | 719,280.7467 | 928,252.2498 | |
| 0.1 | 253,792.2061 | 717,075.4436 | 921,874.4037 | |
| Case (3) | 0.9 | 265,158.6006 | 724,077.6842 | 937,747.6542 |
| 0.5 | 260,537.2281 | 720,665.7621 | 930,092.0212 | |
| 0.1 | 257,194.5871 | 717,358.1034 | 920,580.2708 | |
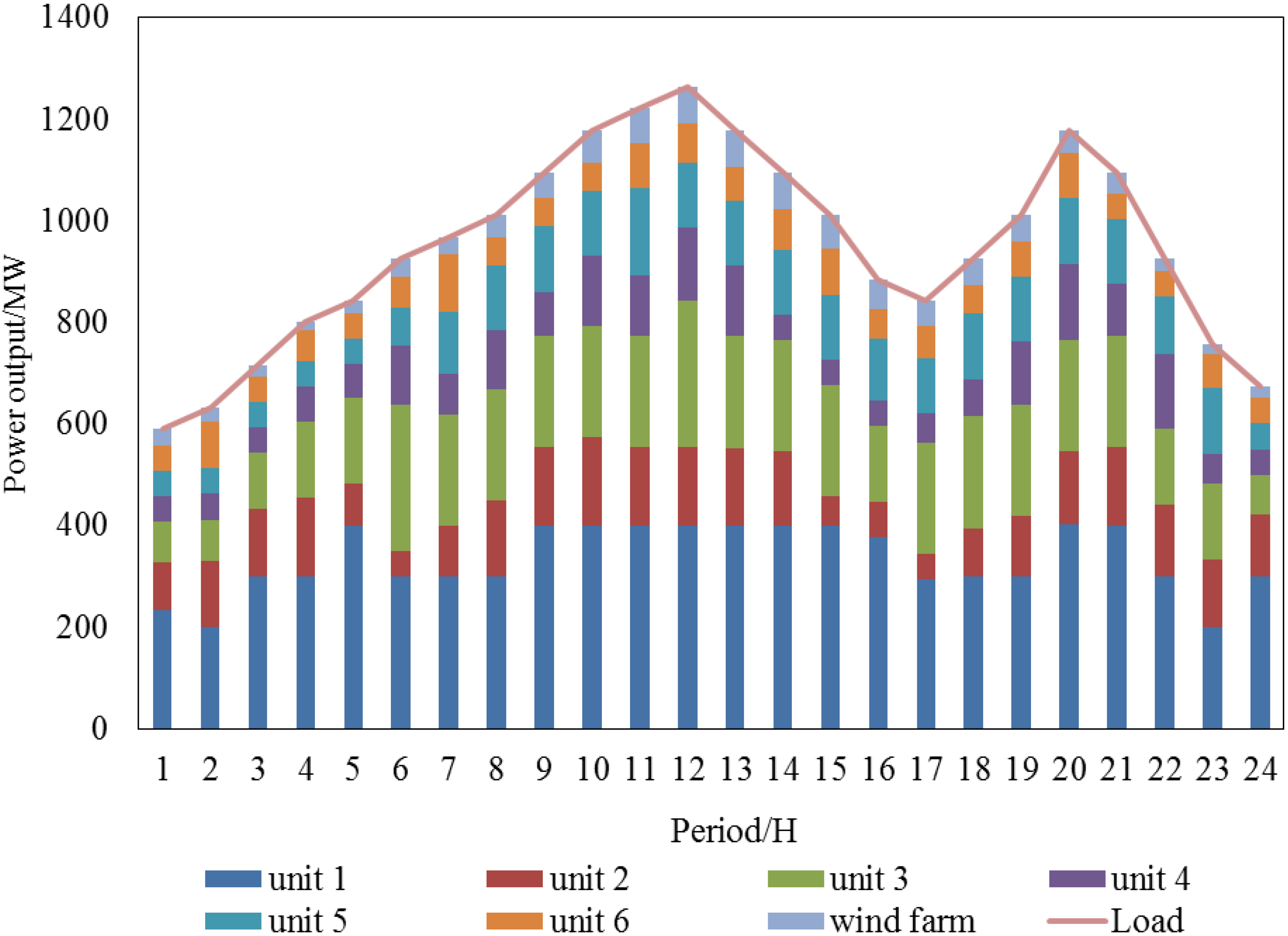
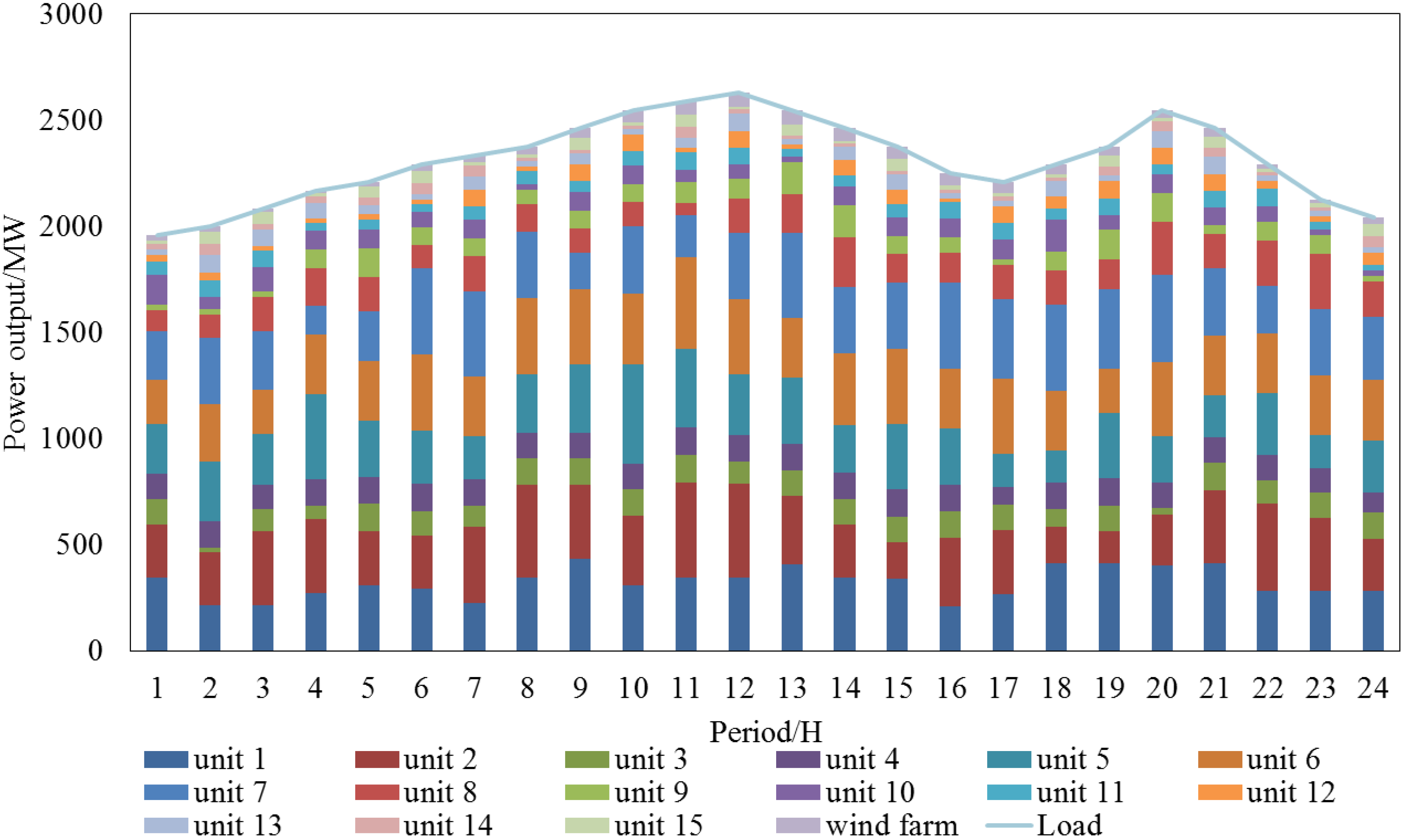
| Unit Index | Output/MW (t = 1) | Output/MW (t = 5) | Output/MW (t = 9) | Output/MW (t = 13) | Output/MW (t = 17) | Output/MW (t = 21) |
|---|---|---|---|---|---|---|
| 1 | 6.3027 | 2.4145 | 3.8440 | 3.1906 | 7.1055 | 6.0383 |
| 2 | 2.4001 | 3.8585 | 3.0919 | 3.8967 | 4.2176 | 4.7125 |
| 3 | 5.0852 | 2.4041 | 2.4051 | 5.3315 | 6.9680 | 5.5158 |
| 4 | 2.4005 | 2.4001 | 3.7132 | 2.4245 | 9.1081 | 5.4245 |
| 5 | 2.4008 | 2.4000 | 2.4001 | 7.7075 | 2.7151 | 2.4124 |
| 6 | 4.0328 | 9.1759 | 4.0017 | 7.5375 | 14.5461 | 7.5095 |
| 7 | 7.0616 | 4.0334 | 13.6143 | 8.2265 | 16.3442 | 6.4664 |
| 8 | 11.4758 | 4.0024 | 15.0108 | 13.5385 | 4.1028 | 8.2579 |
| 9 | 4.0005 | 4.0094 | 4.0025 | 13.9355 | 14.7954 | 4.0497 |
| 10 | 19.2252 | 47.0962 | 75.9820 | 75.9848 | 75.9389 | 52.5536 |
| 11 | 18.3423 | 55.2031 | 61.0610 | 53.5547 | 75.6070 | 31.5227 |
| 12 | 75.8896 | 15.4675 | 73.2103 | 75.9948 | 75.6298 | 53.2694 |
| 13 | 44.3981 | 62.5945 | 21.5289 | 40.1115 | 62.9386 | 75.9777 |
| 14 | 29.0682 | 78.5853 | 67.5916 | 75.0436 | 93.0661 | 91.2458 |
| 15 | 25.1687 | 25.0787 | 99.7008 | 58.6896 | 80.7636 | 69.7929 |
| 16 | 66.9136 | 25.1137 | 90.0044 | 60.3383 | 78.6772 | 97.6501 |
| 17 | 111.8911 | 54.4301 | 150.9160 | 129.1319 | 151.3966 | 102.5665 |
| 18 | 127.2128 | 91.5275 | 119.8840 | 105.7696 | 155.0000 | 148.3436 |
| 19 | 82.4911 | 81.7769 | 142.5084 | 101.8499 | 149.4214 | 104.2932 |
| 20 | 103.2164 | 84.7880 | 154.9953 | 152.8019 | 136.8211 | 102.9801 |
| 21 | 149.4256 | 79.7549 | 94.8661 | 176.8049 | 163.8401 | 167.1249 |
| 22 | 131.0308 | 142.1999 | 108.1115 | 171.1631 | 182.4127 | 84.5785 |
| 23 | 127.8570 | 125.8213 | 135.2337 | 154.7178 | 163.3203 | 153.6023 |
| 24 | 276.5693 | 158.4972 | 306.4523 | 290.2500 | 284.4019 | 287.2902 |
| 25 | 239.6986 | 270.5251 | 379.2529 | 328.7933 | 398.3654 | 331.9537 |
| 26 | 359.0842 | 372.9581 | 320.0320 | 329.1593 | 378.8603 | 275.4983 |
| WF | 19.3572 | 19.3837 | 54.5853 | 62.0524 | 63.6360 | 27.8695 |
5.2. Wind Penetration as a Function of the Confidence Level Under Two Systems
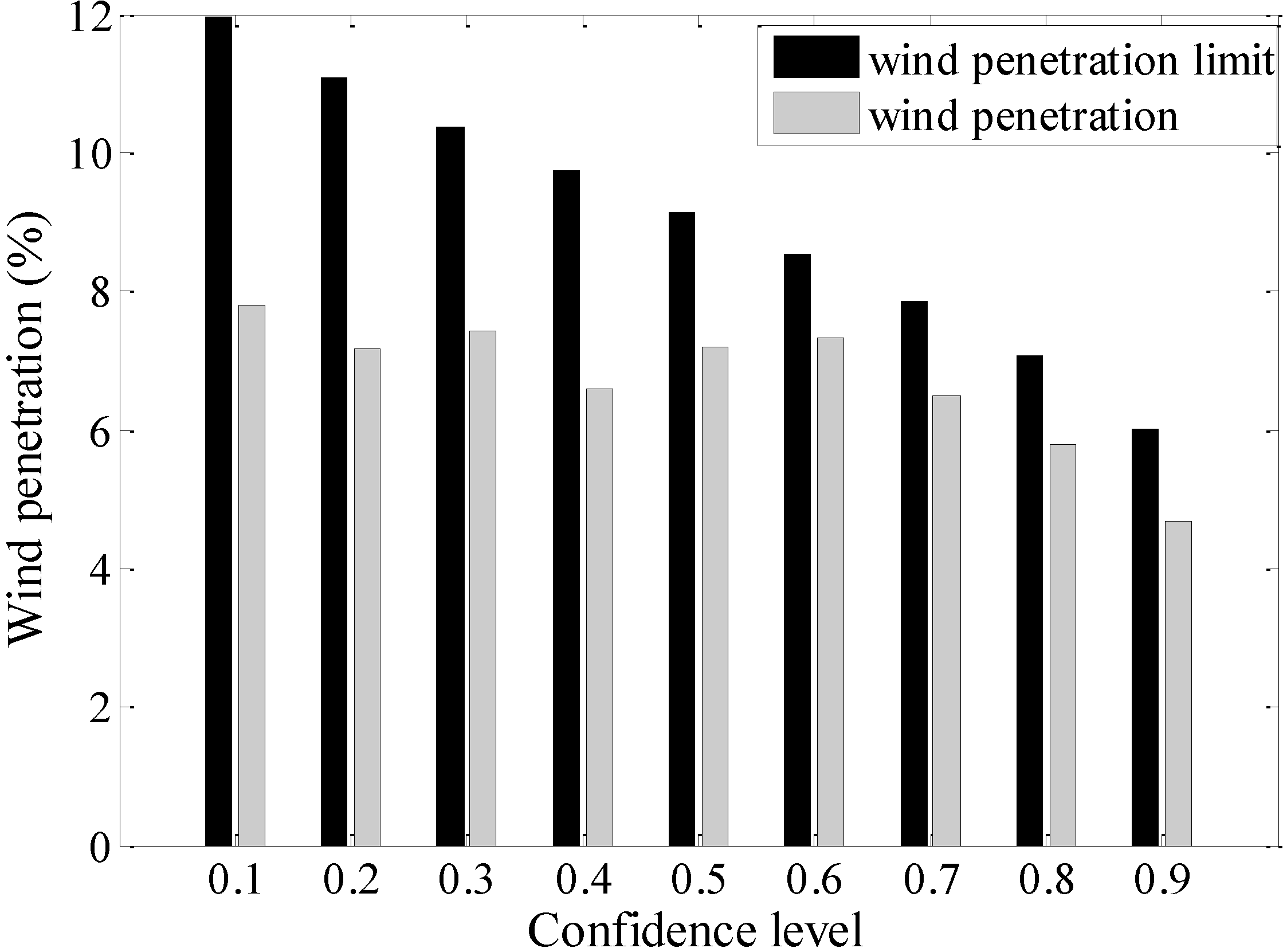
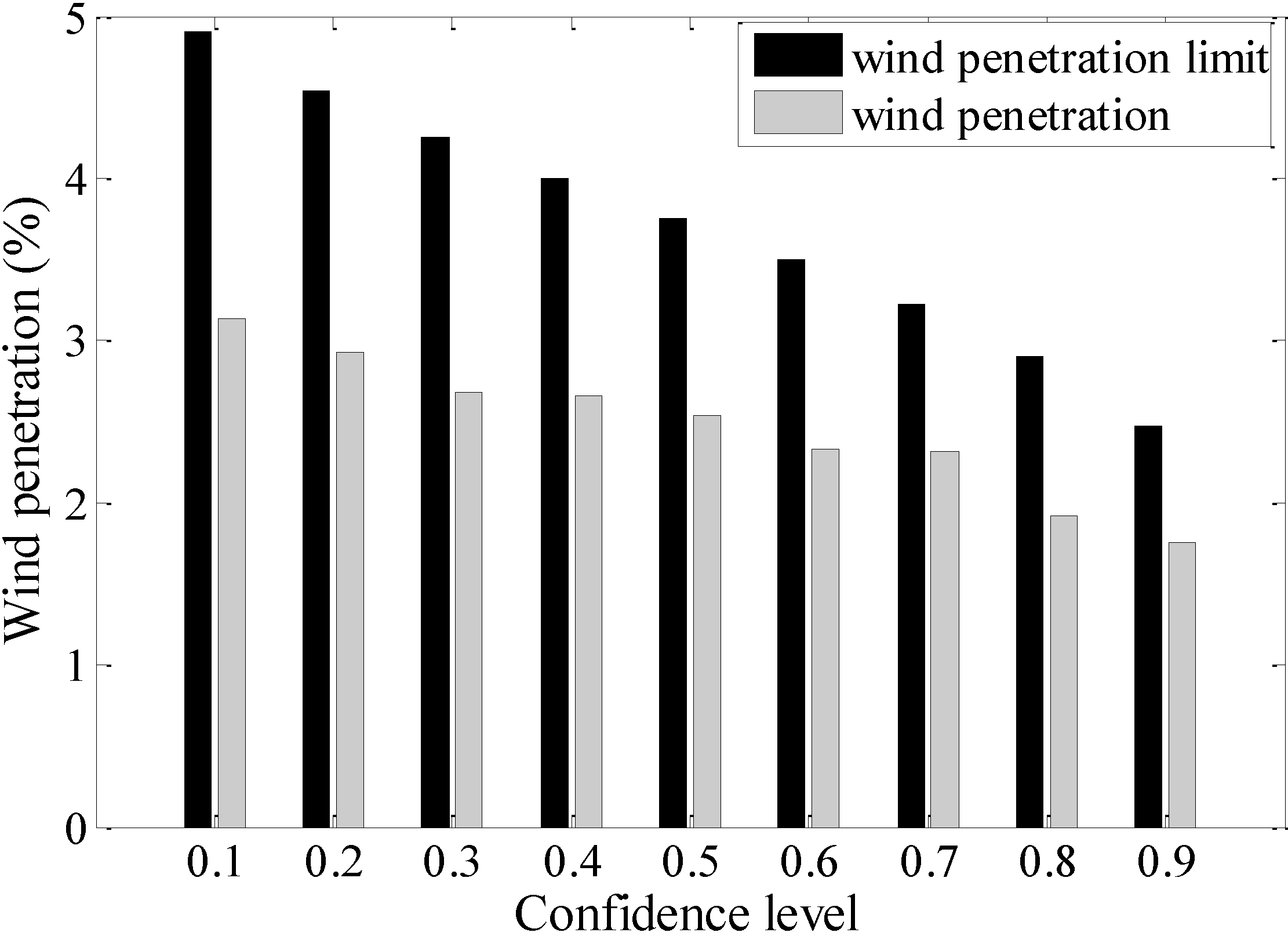
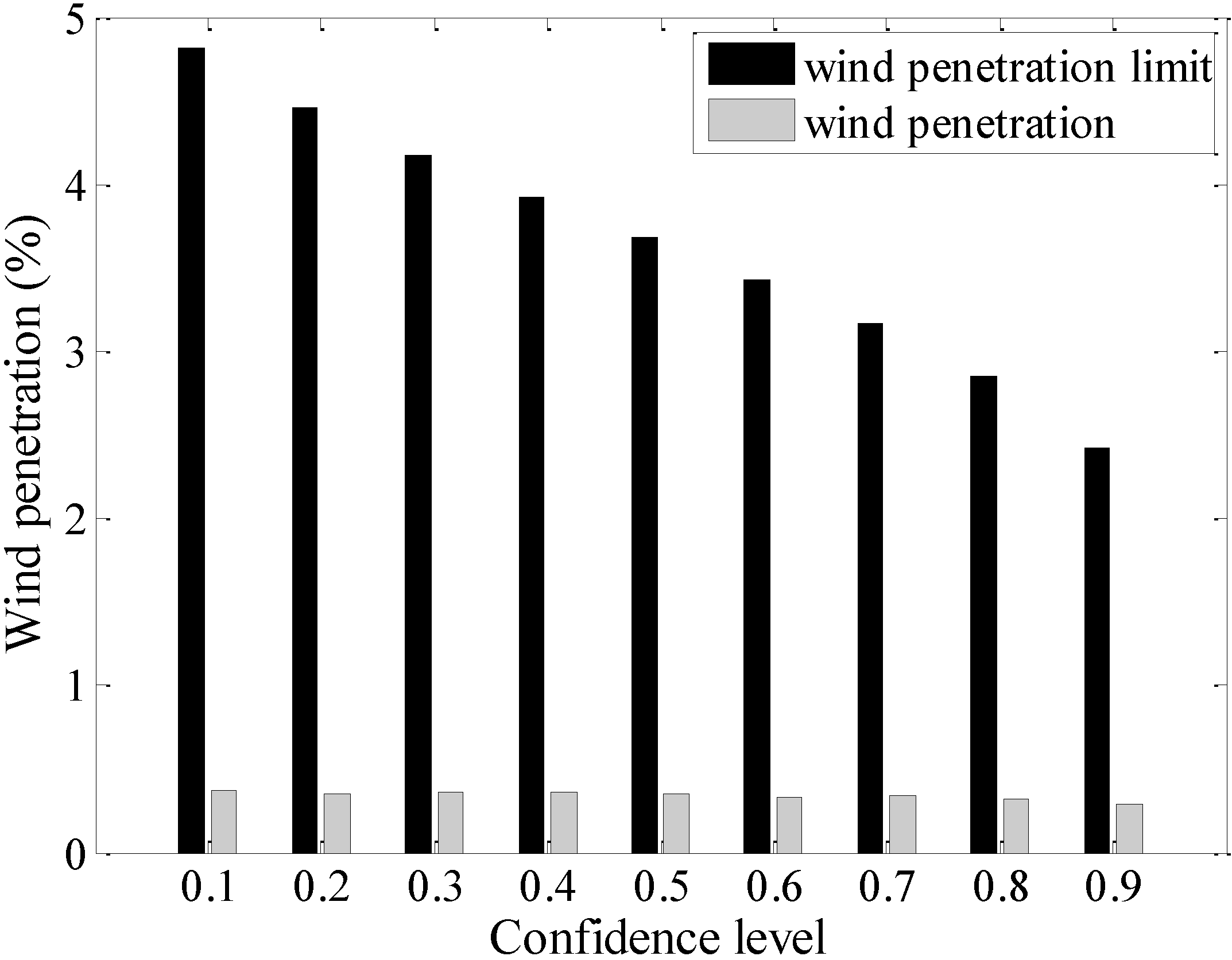
5.3. Discussion about the Optimal Reserve Allocation
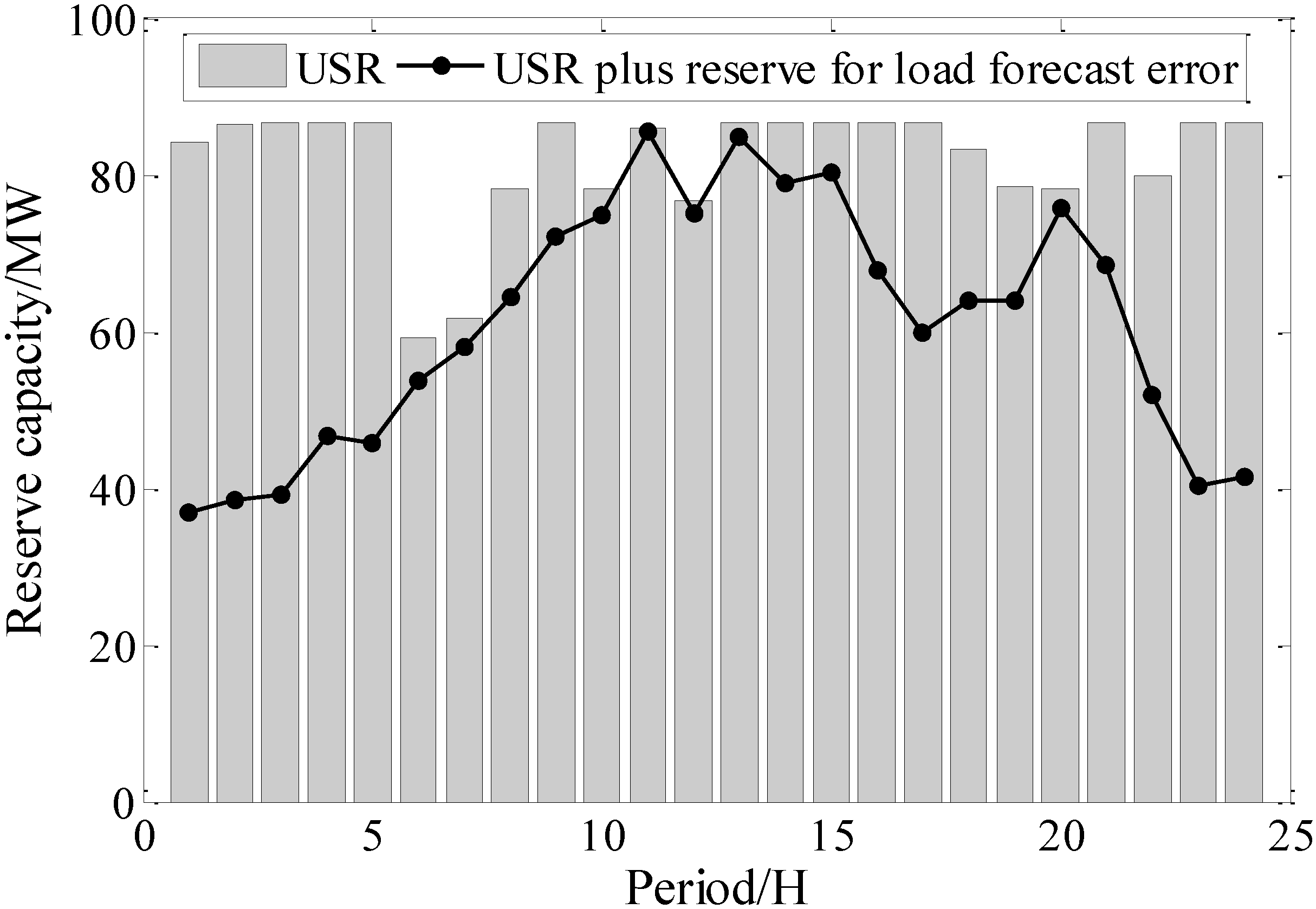
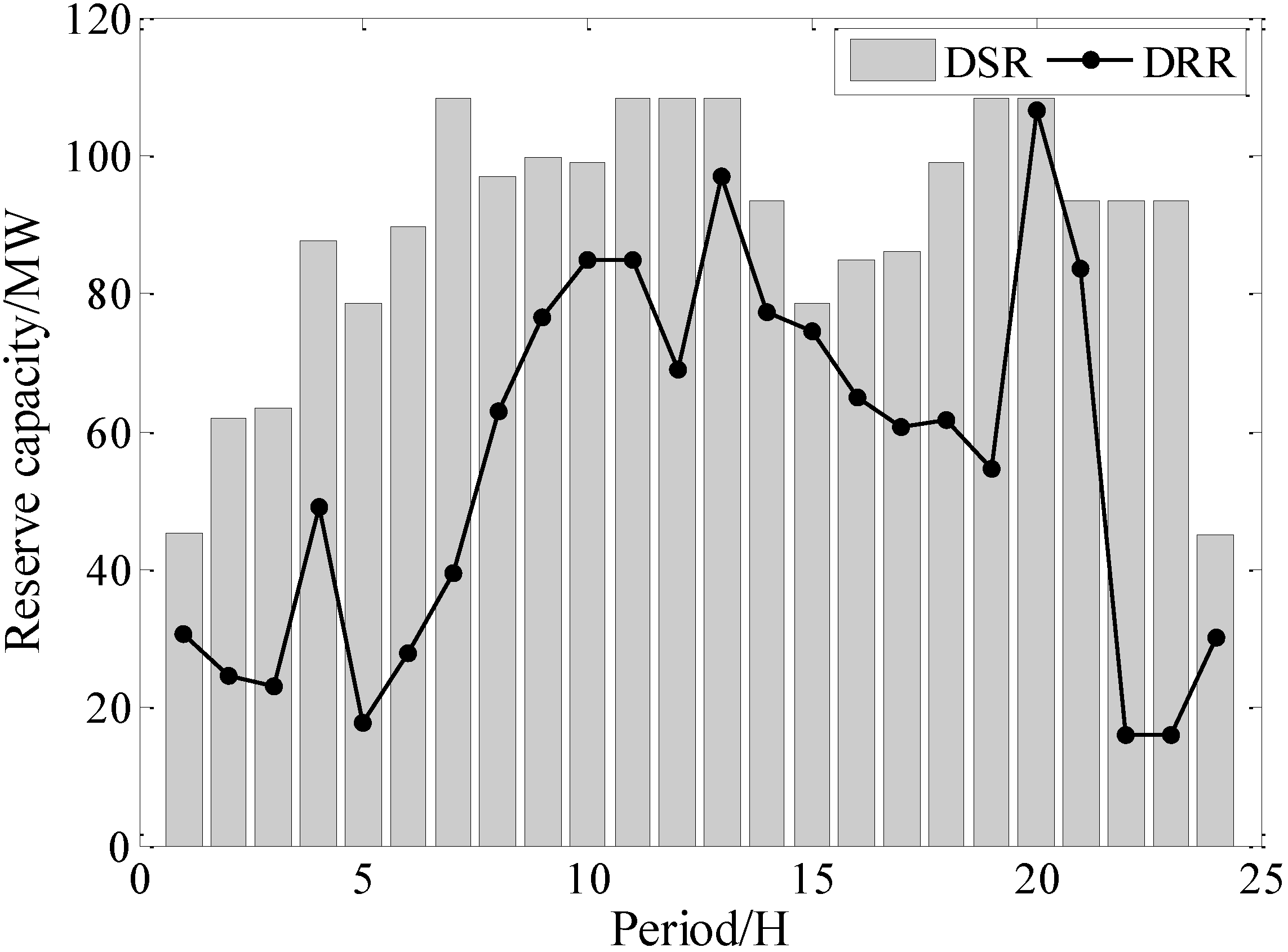
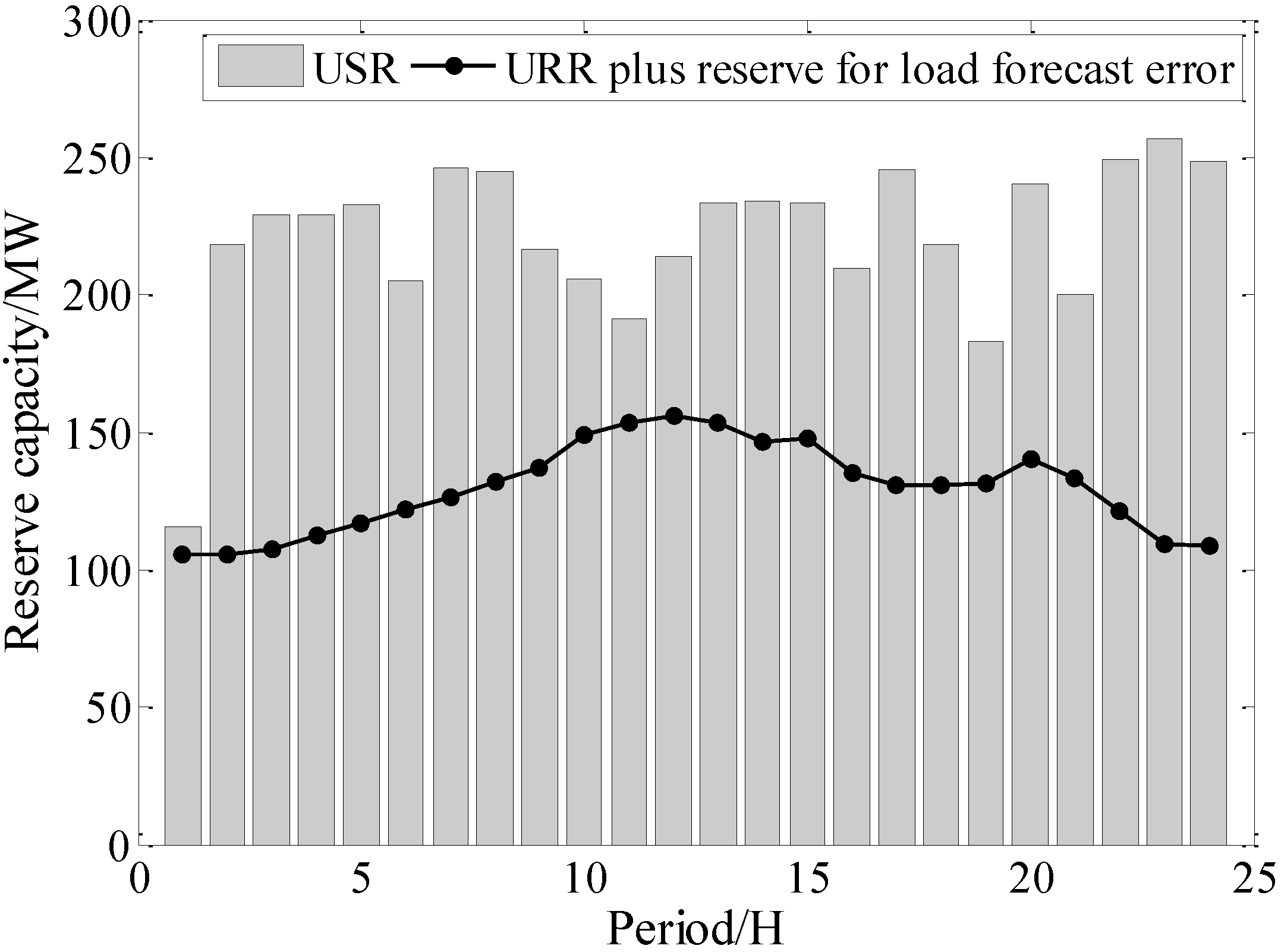
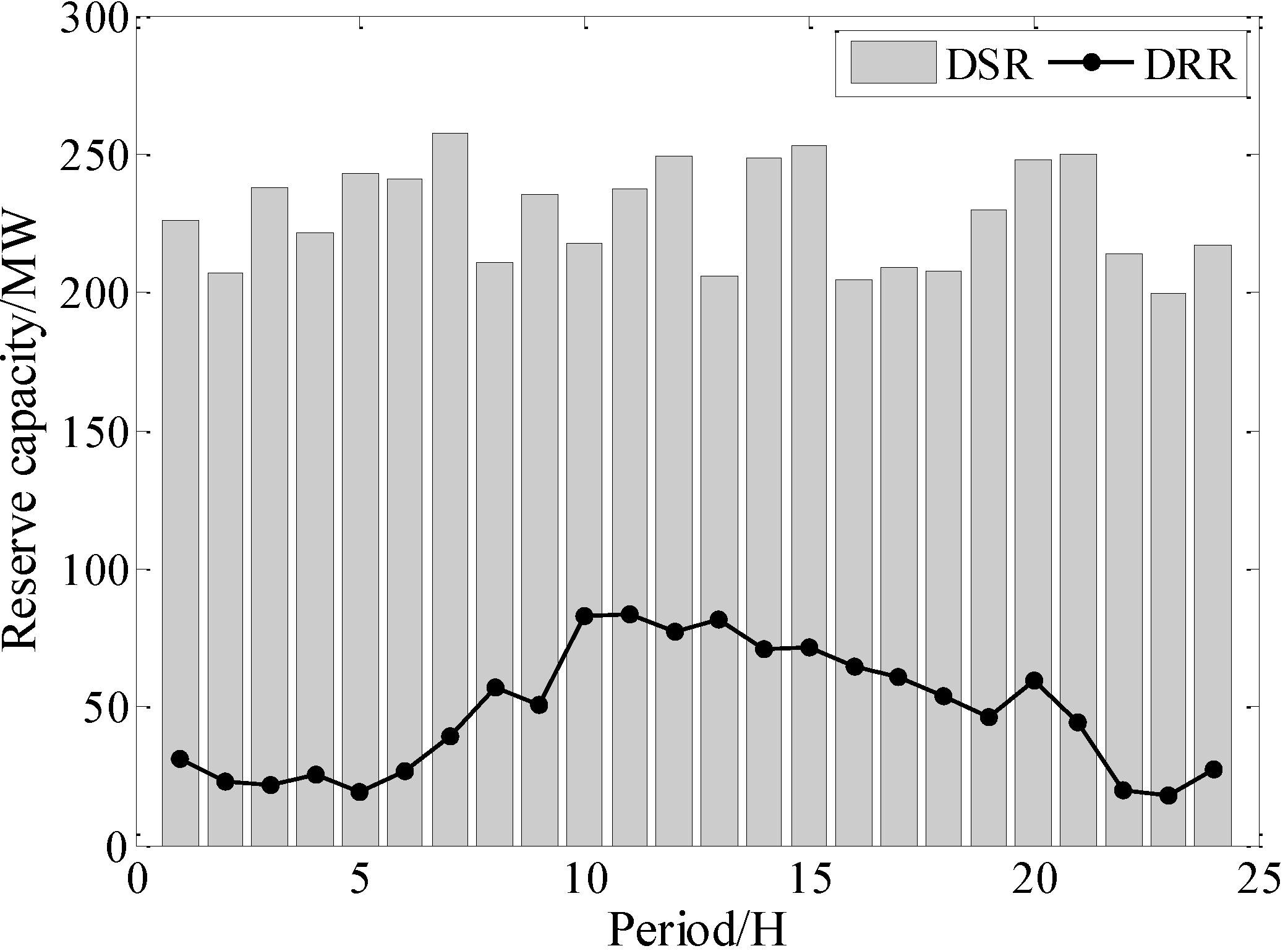
5.4. Comparisons between the PSO-HCSO and PSO without HCSO
| H | Average Generation Cost ($) | Average Time (s) |
|---|---|---|
| 100 | 269,280.7296 | 328.2577 |
| 200 | 265,158.6006 | 386.8114 |
| 300 | 262,533.7753 | 436.2356 |
| 400 | 261,153.0924 | 538.3722 |
| Approach | Confidence Level | Average Generation Cost ($) | Average Time (s) | ||
|---|---|---|---|---|---|
| PSO-HCSO | PSO without HCSO | PSO-HCSO | PSO without HCSO | ||
| System 1 | 0.9 | 265,158.6006 | 273,039.6325 | 386.8114 | 336.6071 |
| 0.5 | 260,537.2281 | 263,514.4852 | 359.3236 | 308.3647 | |
| 0.1 | 257,194.5871 | 262,368.0024 | 373.6618 | 317.1135 | |
| System 2 | 0.9 | 724,077.6842 | 731,239.0336 | 418.3461 | 409.6045 |
| 0.5 | 720,665.7621 | 727,088.0353 | 402.1863 | 386.9233 | |
| 0.1 | 717,358.1034 | 720,196.5471 | 447.1164 | 422.8967 | |
| System 3 | 0.9 | 937,747.6542 | 945,013.2889 | 456.7289 | 420.0858 |
| 0.5 | 930,092.0212 | 938,816.0995 | 428.3801 | 416.1260 | |
| 0.1 | 920,580.2708 | 929,187.2603 | 470.2236 | 436.2757 | |
6. Conclusions
Acknowledgments
Author Contributions
List of Abbreviations and Symbols
Abbreviations
| ED | Economic dispatch |
| DED | Dynamic economic dispatch |
| USR | Up spinning reserve |
| DSR | Down spinning reserve |
| URR | Up reserve requirement |
| DRR | Down reserve requirement |
| PSO | Particle swarm optimization |
| HCSO | Hill climbing search operation |
| PSO-HCSO | Particle swarm optimization with hill climbing search operation |
Probability density function | |
| CDF | Cumulative density function |
| FRA | Feasible region adjustment |
Symbols
| T | Number of Periods |
| I | Number of thermal units |
| t | Index of time period,
|
| i | Index of thermal unit,
|
Total generation cost | |
Power output of thermal unit i at time t | |
Scheduled wind power of wind farm at time t | |
Load demand at time t | |
Generation cost of thermal unit i at time t | |
| , , | Cost coefficients of thermal unit i |
Valve point loading effect of thermal unit i at time t | |
| , | Coefficients related to valve point effect of thermal unit i |
| , | Minimum and Maximum generation limits of thermal unit i |
Actual wind generation, a random variable | |
Installed capacity of wind farm | |
| ρ | Confidence level |
| , | Upper and lower ramp rate limits of thermal unit
|
| T10, T60 | 10 min and 1 h respectively |
URFW at time
| |
DRRW at time
| |
| α, β | Parameters of the beta function |
| , | Mean value and the standard deviation |
| , | PDF and CDF of actual wind generation at time t |
| , | PDF and CDF of normalized actual wind generation at time t |
| D | Dimension of the particle |
| k, K | Current number and maximum number of iteration |
| , | Velocity and position of the jth particle at generation k |
Dynamic inertia weight factor | |
| , | Acceleration coefficients corresponding to cognitive and social behavior |
Personal best position of jth particle at generation k | |
Global best position at generation k in the whole population | |
| λ | Penalty factor |
Penalty functions | |
| H | Maximum number of the HCSO |
The number of times that does not change continuously |
Conflicts of Interest
References
- Ren, B.Q.; Jiang, C.W. A review on the economic dispatch and risk management considering wind power in power market. Renew. Sustain. Energy Rev. 2009, 13, 2169–2174. [Google Scholar] [CrossRef]
- Xia, X.; Elaiw, A. Optimal dynamic economic dispatch of generation: A review. Electr. Power Syst. Res. 2010, 80, 975–986. [Google Scholar] [CrossRef]
- Guo, C.X.; Zhan, J.P.; Wu, Q.H. Dynamic economic emission dispatch based on group search optimizer with multiple producers. Electr. Power Syst. Res. 2012, 86, 8–16. [Google Scholar] [CrossRef]
- Chen, C.L. Optimal wind-thermal generating unit commitment. IEEE Trans. Energy Convers. 2008, 23, 273–280. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, Y.; Sun, H.; Wei, Q.H. Dynamic economic dispatch in wind power integrated system. Proc. CSEE 2009, 29, 3–18. [Google Scholar]
- Jiang, W.; Yan, Z.; Hu, Z. A novel improved particle swarm optimization approach for dynamic economic dispatch incorporating wind power. Electr. Power Compon. Syst. 2010, 39, 461–477. [Google Scholar] [CrossRef]
- Hetzer, J.; Yu, C.D.; Bhattarai, K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers. 2008, 23, 603–611. [Google Scholar] [CrossRef]
- Zhou, W.; Sun, H.; Peng, Y. Risk reserve constrained economic dispatch model with wind power penetration. Energies 2010, 3, 1880–1894. [Google Scholar] [CrossRef]
- Bofinger, S.; Luig, A.; Beyer, H.G. Qualification of wind power forecasts. In Proceedings of the Global Wind Power Conference, Paris, France, 2–5 April 2002; pp. 2–5.
- Bludszuweit, H.; Dominguez-Navarro, J.A.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Fabbri, A.; Roman, T.G.S.; Abbad, J.R.; Quezada, V.H.M. Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market. IEEE Trans. Power Syst. 2005, 20, 1440–1446. [Google Scholar] [CrossRef]
- Wu, D.L.; Wang, Y.; Guo, C.X.; Liu, Y. An economic dispatching model considering wind power forecast errors in electricity market environment. Autom. Electr. Power Syst. 2012, 36, 23–28. [Google Scholar]
- Liu, X. Impact of beta-distributed wind power on economic load dispatch. Electr. Power Compon. Syst. 2011, 39, 768–779. [Google Scholar] [CrossRef]
- Miranda, V.; Hang, P.S. Economic dispatch model with fuzzy wind constraints and attitudes of dispatchers. IEEE Trans. Power Syst. 2005, 20, 2143–2145. [Google Scholar] [CrossRef]
- Pappala, V.S.; Erlich, I.; Rohrig, K.; Dobschinski, J. A stochastic model for the optimal operation of a wind-thermal power system. IEEE Trans. Power Syst. 2009, 24, 940–950. [Google Scholar]
- Bouffard, F.; Galiana, F.D. Stochastic security for operations planning with significant wind power generation. IEEE Trans. Power Syst. 2008, 23, 306–316. [Google Scholar] [CrossRef]
- Yang, N.; Wen, F. A chance constrained programming approach to transmission system expansion planning. Electr. Power Syst. Res. 2005, 75, 171–177. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Zhang, J.H. A chance constrained transmission network expansion planning method with consideration of load and wind farm uncertainties. IEEE Trans. Power Syst. 2009, 24, 1568–1576. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Walters, D.C.; Sheble, G.B. Genetic algorithm solution of economic dispatch with valve point loading. IEEE Trans. Power Syst. 1993, 8, 1325–1332. [Google Scholar] [CrossRef]
- Chiang, C.L. Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels. IEEE Trans. Power Syst. 2005, 20, 1690–1699. [Google Scholar]
- Coelho, L.S.; Mariani, V.C. Combining of chaotic difference evolution and quadratic programming for economic dispatch optimization with valve-point effect. IEEE Trans. Power Syst. 2006, 22, 1273–1282. [Google Scholar]
- Victoire, T.A.A.; Jeyakumar, A.E. Reserve constrained dynamic dispatch of units with valve-point effects. IEEE Trans. Power Syst. 2005, 22, 1273–1282. [Google Scholar] [CrossRef]
- Chakraborty, S.; Senjyu, T.; Yona, A.; Saber, A.Y. Solving economic load dispatch problem with valve-point effects using a hybrid quantum mechanics inspired particle swarm optimization. IET Gener. Trans. Distrib. 2011, 5, 1042–1052. [Google Scholar]
- Nidul, S.; Chakrabarti, R.; Chattopadhyay, P.K. Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 2003, 7, 83–94. [Google Scholar] [CrossRef]
- Attaviriyanupap, P.; Kita, H.; Tanaka, E. A hybrid EP and SQP for dynamic economic dispatch with nonsmoooth fuel cost function. IEEE Trans. Power Syst. 2002, 17, 411–416. [Google Scholar] [CrossRef]
- Gaing, Z.L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Lee, T.Y. Optimal spinning reserve for a wind-thermal power system using PSO. IEEE Trans. Power Syst. 2007, 22, 1612–1621. [Google Scholar] [CrossRef]
- Park, J.B.; Lee, K.S.; Shin, J.R.; Lee, K.Y. A particle swarm optimization for economic dispatch with non-smooth cost functions. IEEE Trans. Power Syst. 2005, 20, 34–42. [Google Scholar] [CrossRef]
- Li, X.H.; Jiang, C.W. Short-term operation model and risk management for wind power penetrated system in electricity market. IEEE Trans. Power Syst. 2011, 26, 932–939. [Google Scholar] [CrossRef]
- Panigrahi, B.K.; Pandi, V.R.; Das, S. Adaptive particle swarm optimization approach for static and dynamic economic load dispatch. Energy Convers. Manag. 2008, 49, 1407–1415. [Google Scholar] [CrossRef]
- Park, J.B.; Jeong, Y.W.; Shin, J.R.; Lee, K.Y. An improved particle swarm optimization for nonconvex economic dispatch problems. IEEE Trans. Power Syst. 2010, 25, 156–166. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Zhang, H. A Dynamic Economic Dispatch Model Incorporating Wind Power Based on Chance Constrained Programming. Energies 2015, 8, 233-256. https://doi.org/10.3390/en8010233
Cheng W, Zhang H. A Dynamic Economic Dispatch Model Incorporating Wind Power Based on Chance Constrained Programming. Energies. 2015; 8(1):233-256. https://doi.org/10.3390/en8010233
Chicago/Turabian StyleCheng, Wushan, and Haifeng Zhang. 2015. "A Dynamic Economic Dispatch Model Incorporating Wind Power Based on Chance Constrained Programming" Energies 8, no. 1: 233-256. https://doi.org/10.3390/en8010233
APA StyleCheng, W., & Zhang, H. (2015). A Dynamic Economic Dispatch Model Incorporating Wind Power Based on Chance Constrained Programming. Energies, 8(1), 233-256. https://doi.org/10.3390/en8010233