A Neural Network Combined Inverse Controller for a Two-Rear-Wheel Independently Driven Electric Vehicle
Abstract
:1. Introduction
2. Two-Rear-Wheel Independently Driven EV
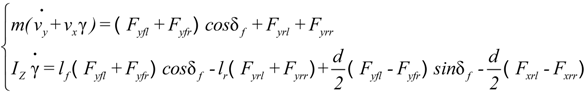
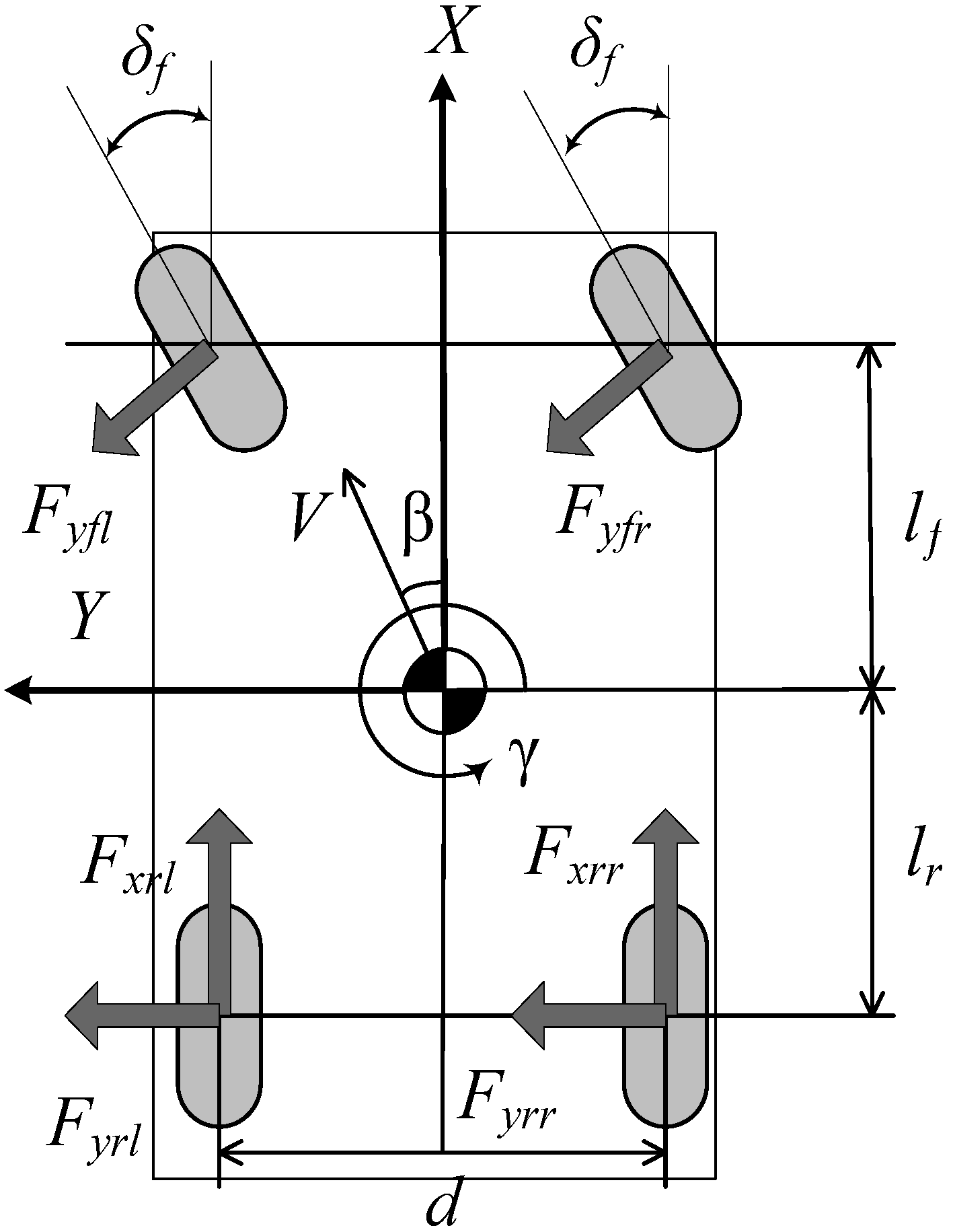
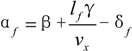
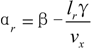
3. Neural Network Combined Inverse Control
3.1. Neural Network Right Inversion Controller
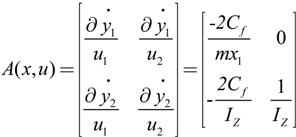
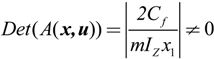
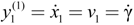 and
and 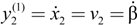 , the inverse system Φ can be described as:
, the inverse system Φ can be described as:
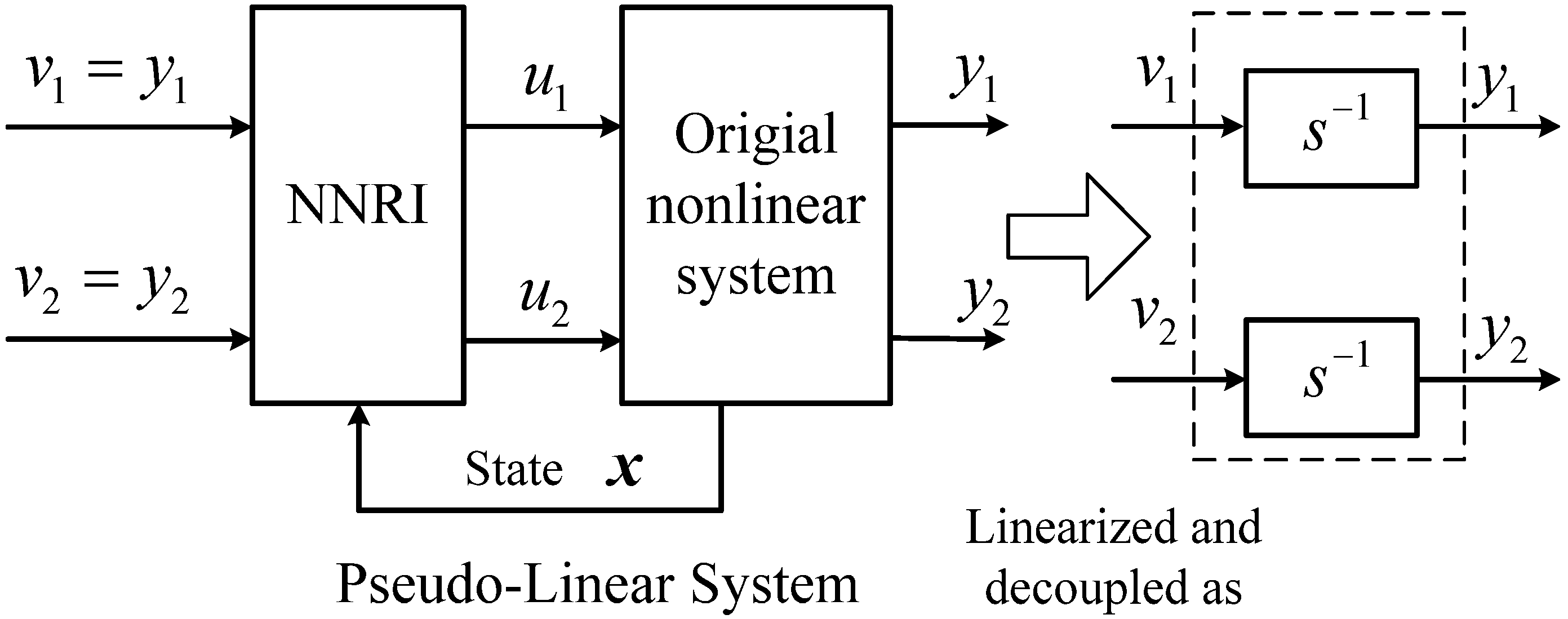
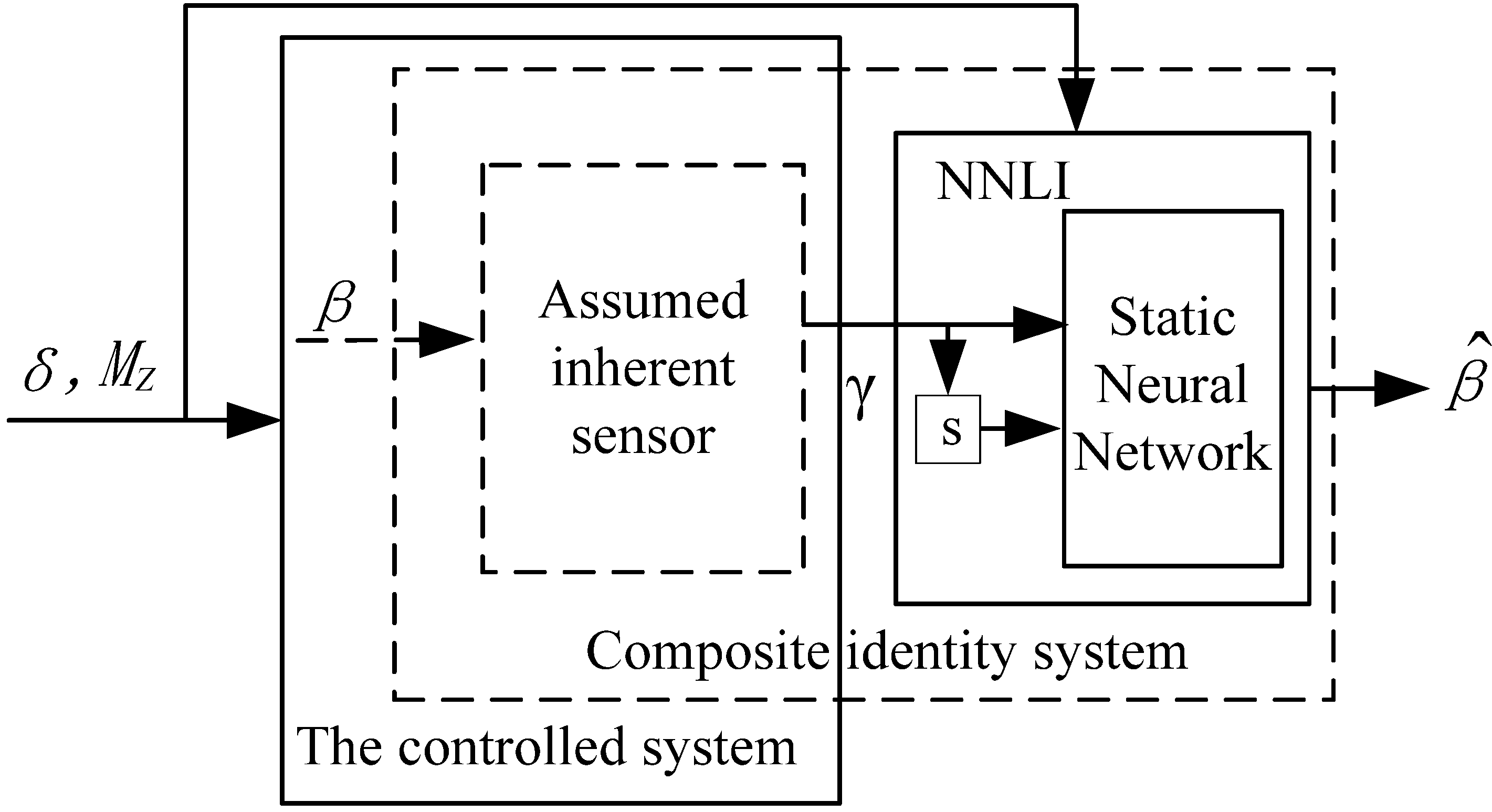
3.2. Neural Network Left Inversion Sideslip Angle Soft-Sensor
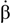 and
and 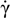 . In other words, to construct the NNRI controller, it is essential to obtain the state variables. As mentioned above, the soft-sensor to estimate the sideslip angle is needed for some reasons such as system cost.
. In other words, to construct the NNRI controller, it is essential to obtain the state variables. As mentioned above, the soft-sensor to estimate the sideslip angle is needed for some reasons such as system cost.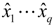 (can be estimated) are the inputs of the subsystem, while the variables xq+1⋯xi which can be measured directly are the outputs. The variables ui are the input variables of the controlled system. If a left inversion of the “assumed inherent sensor” can be constructed and cascaded behind the assumed inherent sensor, a so-called composite identity system is obtained, whose outputs would be the identity mapping of its inputs. It means that the outputs of the “assumed inherent sensor” inversion will reproduce completely the inputs of the “assumed inherent sensor”. Therefore, the non-directly measured variables
(can be estimated) are the inputs of the subsystem, while the variables xq+1⋯xi which can be measured directly are the outputs. The variables ui are the input variables of the controlled system. If a left inversion of the “assumed inherent sensor” can be constructed and cascaded behind the assumed inherent sensor, a so-called composite identity system is obtained, whose outputs would be the identity mapping of its inputs. It means that the outputs of the “assumed inherent sensor” inversion will reproduce completely the inputs of the “assumed inherent sensor”. Therefore, the non-directly measured variables 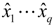 of the controlled system can be estimated from the variables xq+1⋯xi, which can be measured directly.
of the controlled system can be estimated from the variables xq+1⋯xi, which can be measured directly.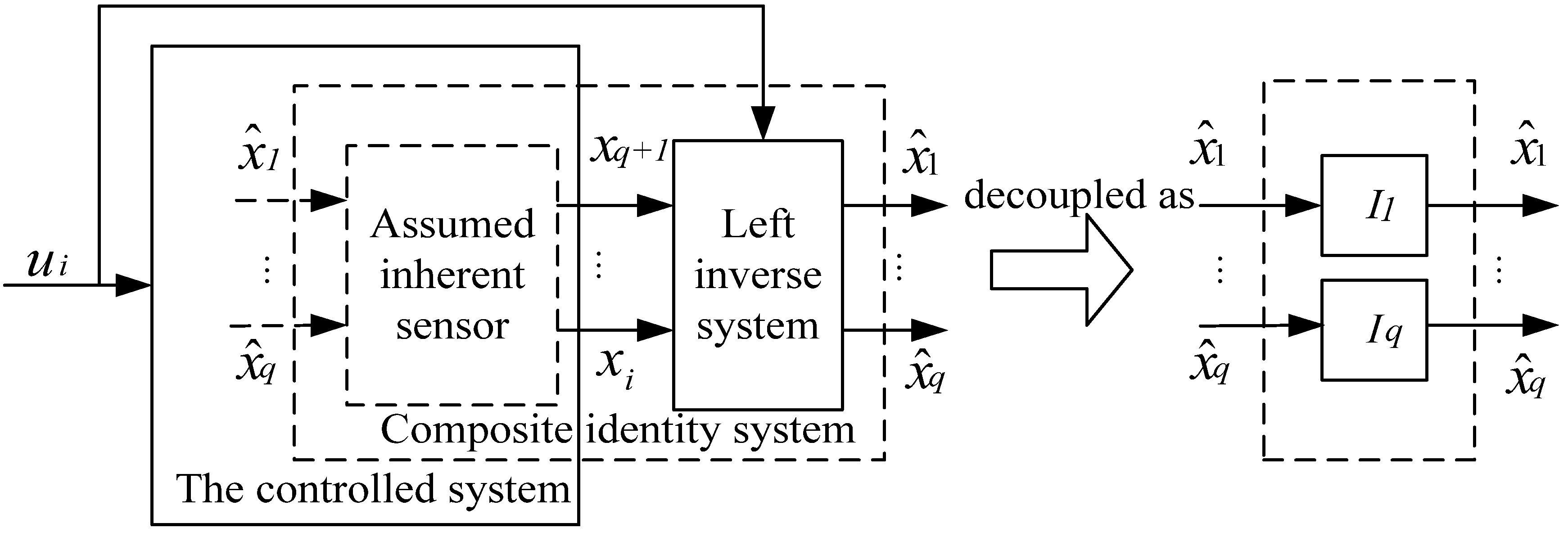
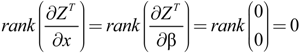

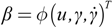
3.3. Neural Network Combined Inverse Controller
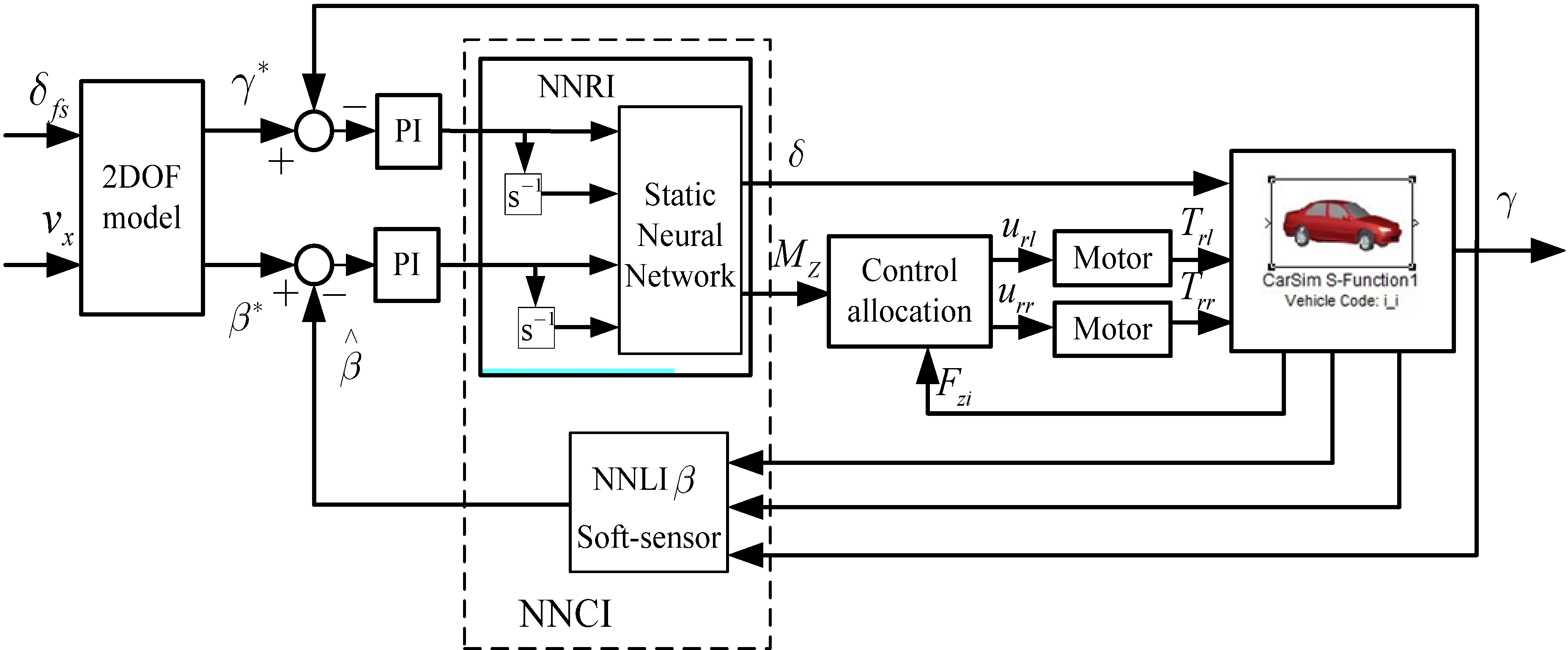
4. Verification
4.1. Ramp Steering Maneuver
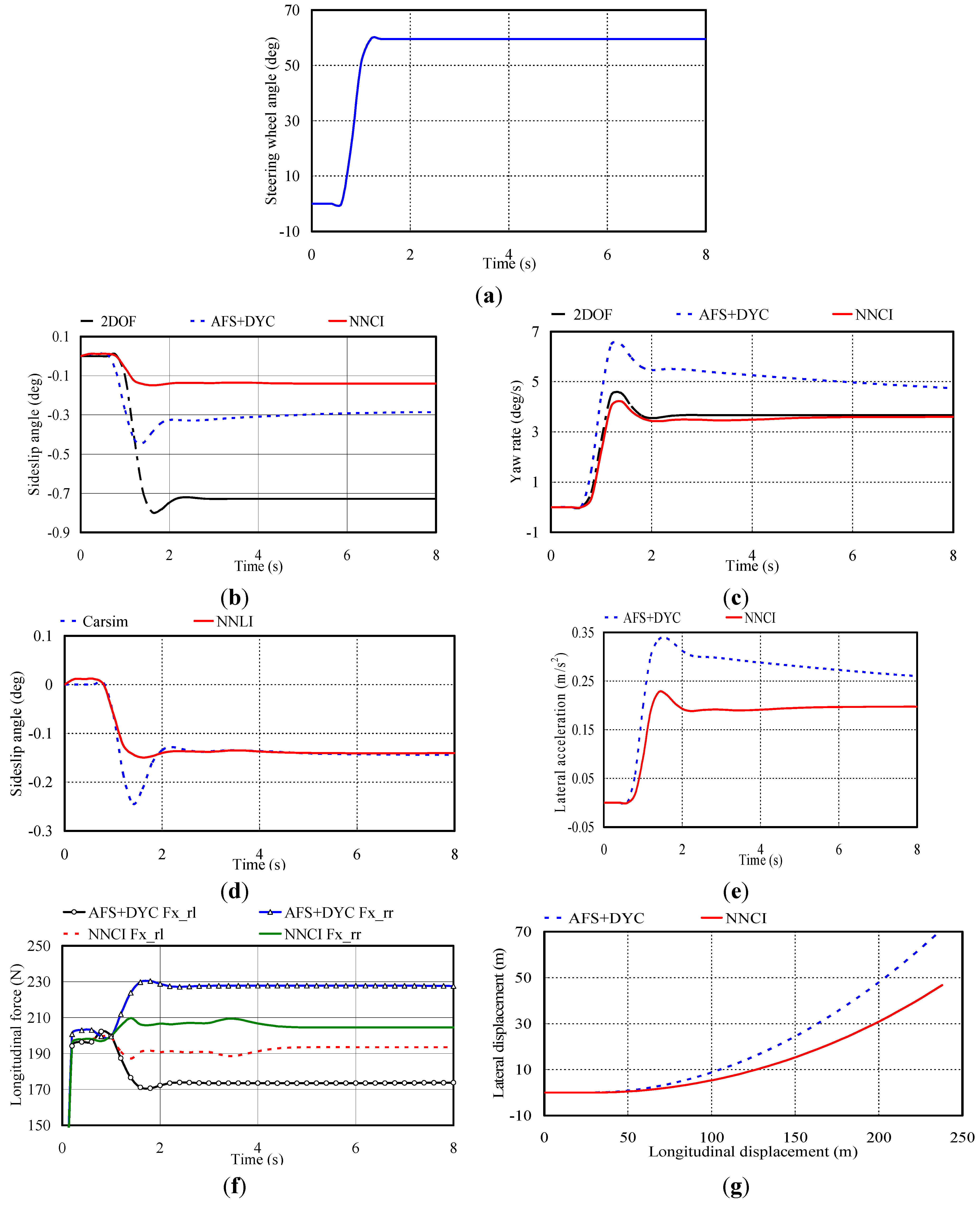
4.2. Single Lane Change Steering Maneuver
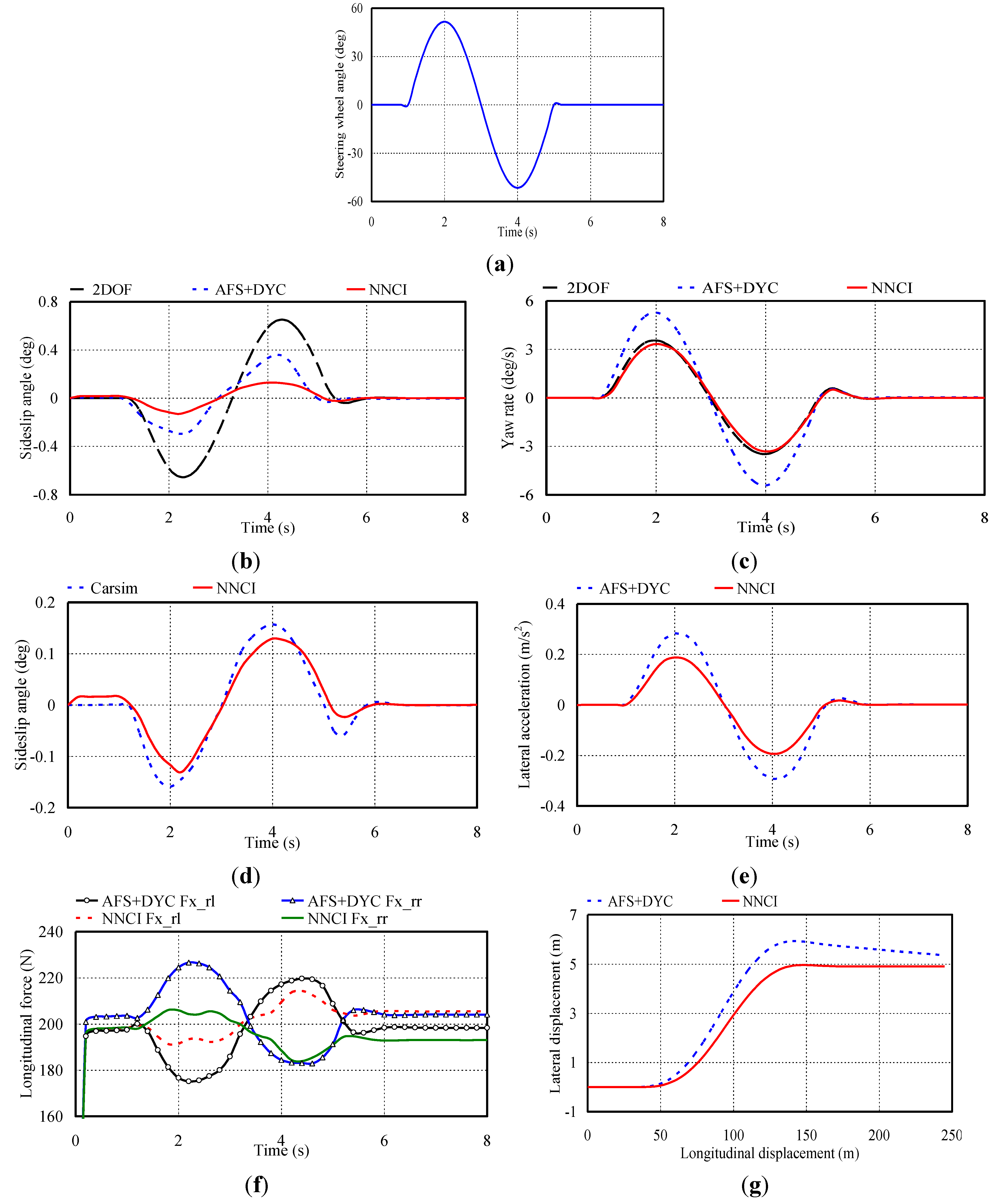
4.3. Double Lane Changing Maneuver
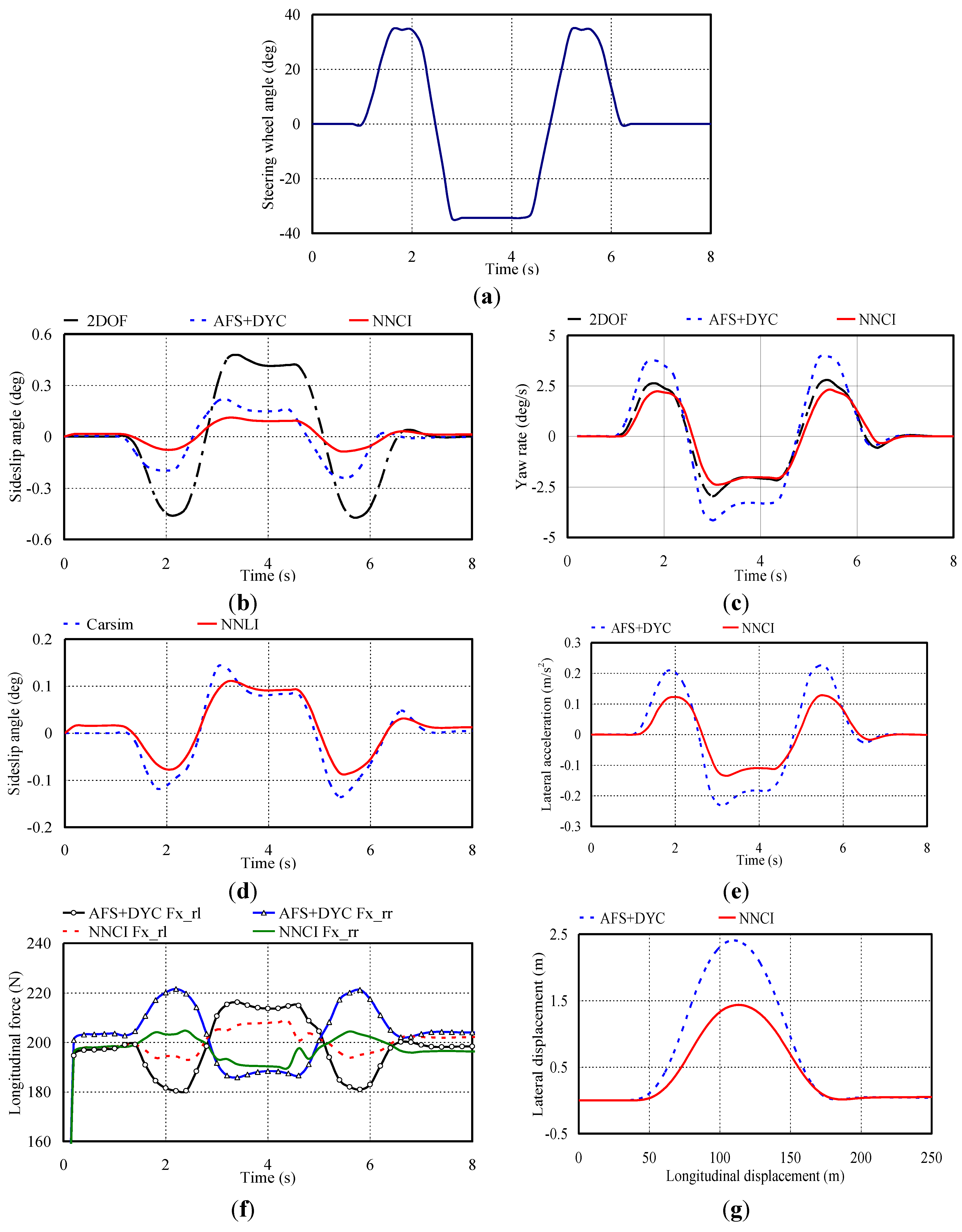
5. Conclusions and Future Works

Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hori, Y. Future vehicle driven by electricity and control-research on four-wheel-motored “UOT March II”. IEEE Trans. Ind. Electron. 2004, 51, 954–962. [Google Scholar] [CrossRef]
- Wang, R.; Chen, Y.; Feng, D.; Huang, X.; Wang, J. Development and performance characterization of an electric ground vehicle with independently actuated in-wheel motors. J. Power Sources 2011, 196, 3962–3971. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of permanent magnet brushless drives for electric and hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef] [Green Version]
- Magallan, G.A.; Angelo, C.H.D.; García, G.O. Maximization of the traction forces in a 2WD electric vehicle. IEEE Trans. Veh. Technol. 2011, 60, 369–380. [Google Scholar] [CrossRef]
- Long, B.; Lim, S.T.; Ryu, J.H.; Chong, K.T. Energy-regenerative braking control of electric vehicles using three-phase brushless direct-current motors. Energies 2014, 7, 99–114. [Google Scholar]
- Xu, G.; Li, W.; Xu, K.; Song, Z. An Intelligent regenerative braking strategy for electric vehicles. Energies 2011, 4, 1461–1477. [Google Scholar] [CrossRef]
- Shuai, Z.; Zhang, H.; Wang, J.; Li, J.; Ouyang, M. Lateral motion control for four-wheel-independent-drive electric vehicles using optimal torque allocation and dynamic message priority scheduling. Control Eng. Pract. 2014, 24, 55–66. [Google Scholar] [CrossRef]
- Kang, J.; Yoo, J.; Yi, K. Driving control algorithm for maneuverability, lateral stability, and rollover prevention of 4WD electric vehicles with independently driven front and rear wheels. IEEE Trans. Veh. Technol. 2011, 60, 2987–3001. [Google Scholar] [CrossRef]
- Mirzaei, M. A new strategy for minimum usage of external yaw moment in vehicle dynamic control system. Transp. Res. Part C Emerg. Technol. 2010, 18, 213–224. [Google Scholar] [CrossRef]
- Lim, E.H.M.; Hedrick, J.K. Lateral and longitudinal vehicle control coupling for automated vehicle operation. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999; pp. 3676–3680.
- Mrino, R.; Cinili, F. Input-output decoupling control by measurement feedback in four wheel steering vehicles. IEEE Trans. Control Syst. Technol. 2009, 17, 1163–1172. [Google Scholar] [CrossRef]
- Jia, Y. Robust control with decoupling performance for steering and traction of 4WS vehicles under velocity-varying motion. IEEE Trans. Control Syst. Technol. 2000, 8, 554–569. [Google Scholar] [CrossRef]
- Kumarawadu, S.; Lee, T. Neuroadaptive output tracking of fully autonomous road vehicles with an observer. IEEE Trans. Intell. Transp. Syst. 2009, 10, 335–345. [Google Scholar] [CrossRef]
- Fernando, W.U.N.; Kumarawadu, S. Discrete-time neuroadaptive control using dynamic state feedback with application to vehicle motion control for intelligent vehicle highway systems. IET Control Theory Appl. 2010, 4, 1465–1477. [Google Scholar] [CrossRef]
- Zhang, Z.; Chau, K.T.; Wang, Z. Analysis and stabilization of chaos in the electric-vehicle steering system. Trans. Veh. Technol. 2013, 62, 118–126. [Google Scholar] [CrossRef] [Green Version]
- Bevly, D.M.; Ryu, J.; Gerdes, J.C. Integrating INS sensors with GPS measurements for continuous estimation of vehicle sideslip, roll, and tire cornering stiffness. IEEE Trans. Intell. Transp. Syst. 2006, 7, 483–493. [Google Scholar] [CrossRef]
- Nam, K.; Oh, S.; Fujimoto, H. Estimation of sideslip and roll angles of electric vehicles using lateral tire force sensors through RLS and kalman filter approaches. IEEE Trans. Ind. Electron. 2013, 60, 988–1000. [Google Scholar] [CrossRef]
- Wenzel, T.A.; Burnham, K.J.; Blundell, M.V.; Williams, R.A. Dual extended kalman filter for vehicle state and parameter estimation. Veh. Syst. Dyn. 2006, 44, 153–171. [Google Scholar] [CrossRef]
- Doumiati, M.; Victorino, A.C.; Charara, A.; Lechner, D. On board real-time estimation of vehicle lateral tire-road forces and sideslip angle. IEEE ASME. Trans. Mechatron. 2011, 16, 601–614. [Google Scholar] [CrossRef]
- Ding, N.; Taheri, S. Application of recursive least square algorithm on estimation of vehicle sideslip angle and road friction. Math. Probl. Eng. 2010. [Google Scholar] [CrossRef]
- You, S.; Hahn, J.; Lee, H. New adaptive approaches to real-time estimation of vehicle sideslip angle. Control Eng. Pract. 2009, 17, 1367–1379. [Google Scholar] [CrossRef]
- Gao, X.; Yu, Z.; Neubeck, J.; Wiedemann, J. Sideslip angle estimation based on input-output linearization with tire-road friction adaptation. Veh. Syst. Dyn. 2010, 48, 217–234. [Google Scholar] [CrossRef]
- Solmaz, S. Simultaneous estimation of road friction and sideslip angle based on switched multiple non-linear observers. IET Control Theory Appl. 2012, 6, 2235–2247. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar] [CrossRef]
- Piyabongkarn, D.; Rajamani, R.; Grogg, J.; Lew, J. Development and experimental evaluation of a slip angle estimator for vehicle stability control. IEEE Trans. Control Syst. Technol. 2009, 17, 78–88. [Google Scholar] [CrossRef]
- Melzi, S.; Sabbioni, E. On the vehicle sideslip angle estimation through neural networks: Numerical and experimental results. Mech. Syst. Signal Process. 2011, 25, 2005–2019. [Google Scholar] [CrossRef]
- Subudhi, B.; Ge, S.S. Sliding-mode-observer-based adaptive slip ratio control for electric and hybrid vehicles. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1617–1626. [Google Scholar] [CrossRef]
- Dai, X.; Wang, W.; Ding, Y. “Assumed inherent sensor” inversion based ANN dynamic soft-sensing method and its application in erythromycin fermentation process. Comput. Chem. Eng. 2006, 30, 1203–1225. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, G.; Dai, X. Soft-sensing method based on modified ANN inversion and its application in erythromycin fermentation. In Proceedings of the IEEE International conference on Information and Automation, Shenyang, China, 6–8 June 2012; pp. 900–905.
- Liu, G.; Yu, K.; Zhao, W. Neural network based internal model decoupling control of three-motor drive system. Electr. Power Comp. Syst. 2012, 40, 1621–1638. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, D.; Liu, G.; Zhao, W.; Miao, P.; Jiang, Y.; Zhou, H. A Neural Network Combined Inverse Controller for a Two-Rear-Wheel Independently Driven Electric Vehicle. Energies 2014, 7, 4614-4628. https://doi.org/10.3390/en7074614
Zhang D, Liu G, Zhao W, Miao P, Jiang Y, Zhou H. A Neural Network Combined Inverse Controller for a Two-Rear-Wheel Independently Driven Electric Vehicle. Energies. 2014; 7(7):4614-4628. https://doi.org/10.3390/en7074614
Chicago/Turabian StyleZhang, Duo, Guohai Liu, Wenxiang Zhao, Penghu Miao, Yan Jiang, and Huawei Zhou. 2014. "A Neural Network Combined Inverse Controller for a Two-Rear-Wheel Independently Driven Electric Vehicle" Energies 7, no. 7: 4614-4628. https://doi.org/10.3390/en7074614



