Energy Substitution, Technical Change and Rebound Effects

Abstract

This paper investigates the relationships between energy efficiency improvements by producers, the ease of substitution between energy and other inputs and the size of the resulting “rebound effects”. Fundamentally, easier substitution leads to larger rebounds. Focusing upon conceptual and methodological issues, the paper highlights the challenges of estimating and modeling rebound effects with the help of production and cost functions and questions the robustness of the evidence base in this area. It argues that the multiple definitions of “elasticities of substitution” are a source of confusion, the most commonly estimated elasticity is of little practical value, the empirical literature is contradictory, prone to bias and difficult to use and there are only tenuous links between this literature and the assumptions used within energy-economic models. While “energy-augmenting technical change” provides the natural choice of independent variable for an estimate of rebound effects, most empirical studies do not estimate this form of technical change, many modeling studies do not simulate it and others simulate it in such a way as to underestimate rebound effects. As a result, the paper argues that current econometric and modeling studies do not provide reliable guidance on the magnitude of rebound effects in different industrial sectors.

1. Introduction

The “rebound effect” is an umbrella term for a variety of economic mechanisms that reduce the “energy savings” from improved energy efficiency [1]. For producers, cost-effective energy efficiency improvements encourage increased consumption of energy services, boost productivity, increase output and potentially impact energy use throughout the economy. The rebound effect is commonly defined as the percentage of potential energy savings that are offset by these different mechanisms. For producers, the potential energy savings are typically estimated by engineering models that assume no economic responses to improved energy efficiency, while “actual” savings are estimated by energy-economic models that simulate those responses with the help of econometrically estimated production or cost functions [1–4].

Energy efficiency or energy productivity may generally be defined as the ratio of useful outputs to energy inputs for a specified system. Inputs and outputs may be defined in thermodynamic, physical or economic terms [5] and different definitions and measures, as well as different choices of system boundary, may lead to different conclusions regarding the nature, source, magnitude and sign of energy productivity improvements, as well as of the energy savings that result. But neoclassical production theory narrows the range of choices for these variables: defining energy productivity solely in economic terms and focusing upon only two sources of energy productivity improvements: namely the substitution of energy by other inputs and technical change. The latter provides a common choice of independent variable for studies of rebound effects in industrial production [3,6].

In a widely cited paper, Saunders [7] uses neoclassical production theory to argue that: “… the ease with which fuel can substitute for other factors of production (such as capital and labour) has a strong influence on how much rebound will be experienced … the greater this ease of substitution, the greater will be the rebound”. Saunders [2,8–11] had extended this analysis in subsequent works, but consistently concludes that rebound effects will be larger when “…the greater is the flexibility of the economy to adapt to energy efficiency gains via substitution” [10]. Saunders' results therefore imply that empirical studies of the “ease of substitution” between energy and other inputs should allow the likely magnitude of rebound effects in different sectors to be explored [7].

This paper investigates the relationships between energy productivity improvements for producers, the ease of substitution between energy and other inputs and the size of the resulting rebound effects. It assesses the meaning and applicability of the above statement by Saunders [7], the challenge of estimating and modeling rebound effects with production and cost functions and the robustness of the evidence base in this area. The paper focuses on conceptual and methodological issues, partly with the aim of clarifying these issues for non-specialists.

The paper begins by outlining how different types of energy productivity improvement are represented in neoclassical production theory, how these may lead to rebound effects and how energy substitution contributes to those effects. The following three sections examine how the “ease of substitution” between energy and other inputs is defined and measured and how these estimates are commonly used. The paper highlights the challenges in estimating “elasticities of substitution”, the difficulties in interpreting the available literature, the contradictions in the empirical results and the tenuous link between these results and the assumptions used in energy-economic models. Section 8 compares the different ways of estimating and modeling technical change and highlights the limitations of commonly used measures when applied to the estimation of rebound effects. On the basis of these arguments, the paper argues that current econometric and modeling studies do not provide reliable guidance on the magnitude of rebound effects in different sectors. The paper concludes by indicating the requirements for providing more realistic guidance.

2. Key Concepts from Production Theory

Neoclassical production functions indicate the maximum possible economic output (Y) obtainable from capital (K), labor (L) and intermediate inputs to a firm or sector given the technology available at a particular time (t) [12]. Intermediates are commonly disaggregated into energy (E) and materials (M) (while consistent with the structure of input-output tables, the treatment of capital and labor as primary inputs and energy as a secondary or intermediate input is problematic from the perspective of the natural sciences):

$$Y=f(K,L,E,M,t)$$

(1)

Production functions are normally assumed to be positive, twice differentiable and quasi-concave with constant returns to scale. Under standard assumptions a dual cost function can be defined which indicates the minimum possible cost (C) of producing output Y, given the prices of each input (p_i) and the current state of technology (t):

$$C=g(p_K,p_L,p_E,p_M,Y,t)$$

(2)

Dividing through by output gives a unit cost function (c = C/Y):

$$c=h(p_K,p_L,p_E,p_M,t)$$

(3)

Cost functions are preferred to production functions in empirical studies since the independent variables (input prices) are more likely to be exogenous.

Assuming perfect competition and profit maximization, the marginal product of each input should be equal to the input price (p_i) and the elasticity of cost with respect to this price should be equal to the “value share” (s_i):

$$\frac{\partial Y}{\partial X_i}=p_i$$

(4)

$$\frac{\partial lnC}{\partial ln{p}_i}=s_i$$

(5)

where:

$$s_i=\frac{p_i{X}_i}{C}$$

(6)

The output produced from a given quantity of inputs typically increases over time as technology improves. The rate of change of total factor productivity (ε_ft) is then given by:

$${\mathit{\varepsilon }}_{\text{ft}}=\frac{\partial lnY}{\partial t}$$

(7)

The equivalent cost function definition is:

$${\mathit{\varepsilon }}_{\text{gt}}=\frac{\partial lnC}{\partial t}$$

(8)

With constant returns to scale: ε_ft = ε_gt.

Energy productivity (θ_E) is defined as the ratio of economic output to energy inputs:

$${\mathrm{\theta }}_E=\frac{Y}{E}=\frac{f(K,L,E,M,t)}{E}$$

(9)

Aggregate energy productivity therefore depends upon the level of each input, the current state of technology and the level of output, as well as upon how individual inputs are measured and aggregated (e.g., how different types of energy carrier are combined). The inverse of energy productivity (energy intensity) can be derived from the unit cost function using Shephard's Lemma:

$$\frac{\partial c}{\partial p_E}=\frac{E}{Y}=\frac{1}{{\mathrm{\theta }}_E}$$

(10)

Increases in energy prices encourage the substitution of other inputs for energy, thereby improving aggregate energy productivity but since costs have increased output may fall. In contrast, technical change is assumed to improve energy productivity independently of changes in relative prices and without reducing output. Total factor productivity measures the net impact of technical change on all inputs. Technical change has frequently been assumed to be time-dependent, exogenous and neutral (N), with the productivity of all inputs increasing at the same constant rate (ε_ft = λ_N ≥ 0). In this form, technical change may be represented as a time-dependent multiplier on the production function:

$$Y={\tau }_{N}f(K,L,E,M)$$

(11)

where:

$${\tau }_N(t)=e^{{\lambda }_{N}t}$$

(12)

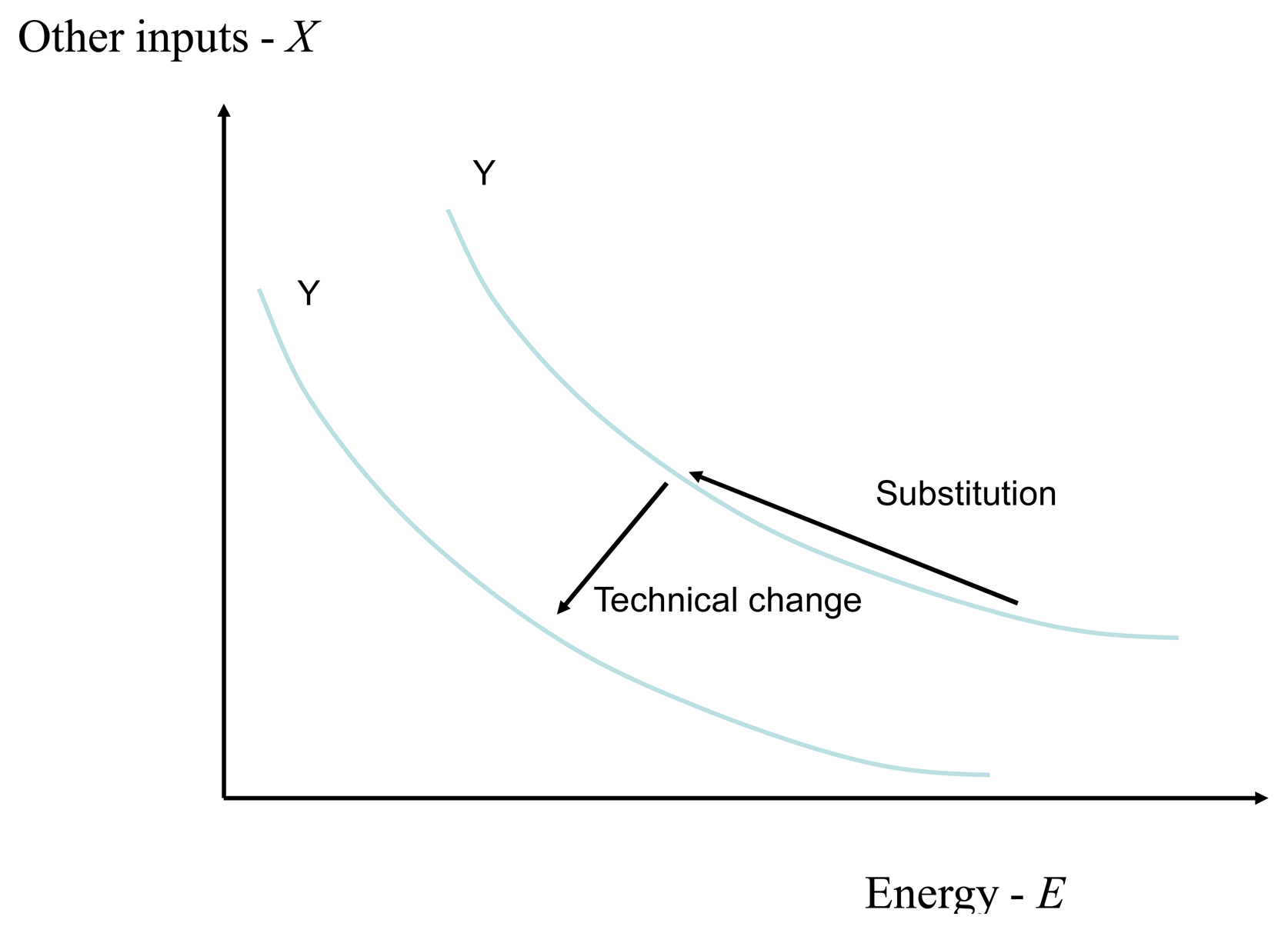
Substitution is conventionally represented as movement along an isoquant of a production or cost function and technical change as a shift of the isoquants (Figure 1). However, the distinction between the two is less clear from an engineering perspective and both may reflect a complex mix of investment, operational changes and shifts in the composition of output [13].

In practice, technical change is frequently biased in that the productivity of some inputs increases more rapidly than others [12]. In empirical studies, this is commonly measured by the rate of change in the value share of each input, independent of changes in relative prices:

$${\mathrm{\psi }}_i=\frac{\partial s_i}{\partial t}$$

(13)

Technical change is said to be “input saving” if the value share of that input falls over time (ψ_i < 0) and “input using” if it increases (ψ_i > 0) [14,15]. Note that $\sum _i{\mathrm{\psi }}_i=1$.

In modeling studies, biases in technical change are commonly simulated by including “augmenting multipliers” (τ_i(t) = e^λit where λ_i > 0) on one or more inputs to the production function:

$$Y=f({\tau }_{K}K,{\tau }_{L}L,{\tau }_{E}E,{\tau }_{M}M)$$

(14)

Letting X̃i = τ_iX_i, this can be expressed as:

$$Y=\tilde{f}(\tilde{K},\tilde{L},\tilde{E},\tilde{M})$$

(15)

Letting p_ĩ = p_i/τ_i, the equivalent effective cost function is:

$$C=\tilde{g}(p_{\tilde{K}},p_{\tilde{L}},p_{\tilde{E}},p_{\tilde{M}})$$

(16)

The “effective production function” (f̃) indicates the maximum output obtainable from the effective (X̃_i) rather than real inputs. “Input-augmenting technical change” is defined as ∂Y/∂τ_i > 0; implying that the marginal productivity of input X_i increases over time and its “effective price” (p_ĩ) falls. The energy-augmenting multiplier (τ_E) converts energy inputs (E) to “effective energy” (Ẽ). Although the latter is sometimes referred to as “energy services”, it is different from the engineering interpretation of that term.

A key point relevant to the estimation of rebound effects is that “energy-augmenting” technical change is not the same as “energy saving” technical change. As described below, the former may not lead to the latter owing to substitution between inputs. Also, the direction of technical change is likely to be influenced by relative prices.

3. Technical Change, Energy Substitution and Rebound Effects

Saunders [7] defined rebound effects in relation to energy-augmenting technical change (τ_E). This represents a “pure” energy productivity improvement that does not affect the productivity of other inputs or negatively affect economic output. But as described below, empirical studies may not directly estimate this form of technical change, energy-economic models may not simulate it (or may simulate it in different ways) and studies of rebound effects may make a different choice for the independent variable. Also, isolating energy-augmenting technical change in this way is somewhat artificial as new technologies frequently improve the productivity of multiple inputs simultaneously.

In general, energy-augmenting technical change will not lead to a proportionate improvement in aggregate energy productivity (θ_E) because:

• lower price effective energy will stimulate the substitution of (effective) energy for other (effective) inputs; and

• lower input costs will stimulate an increase in output which in turn will “drag up” energy consumption.

In combination, these substitution and output effects will increase energy consumption above what it would have been in the absence of these responses. The sum of the two is the direct rebound effect for producers. In addition, there will also be various indirect and economy-wide rebound effects. For example, if the relevant product forms an intermediate input to other sectors (e.g., steel in car production), reductions in product prices may stimulate increased output from those sectors and hence further increase economy-wide energy consumption. But this paper is concerned solely with direct rebound effects.

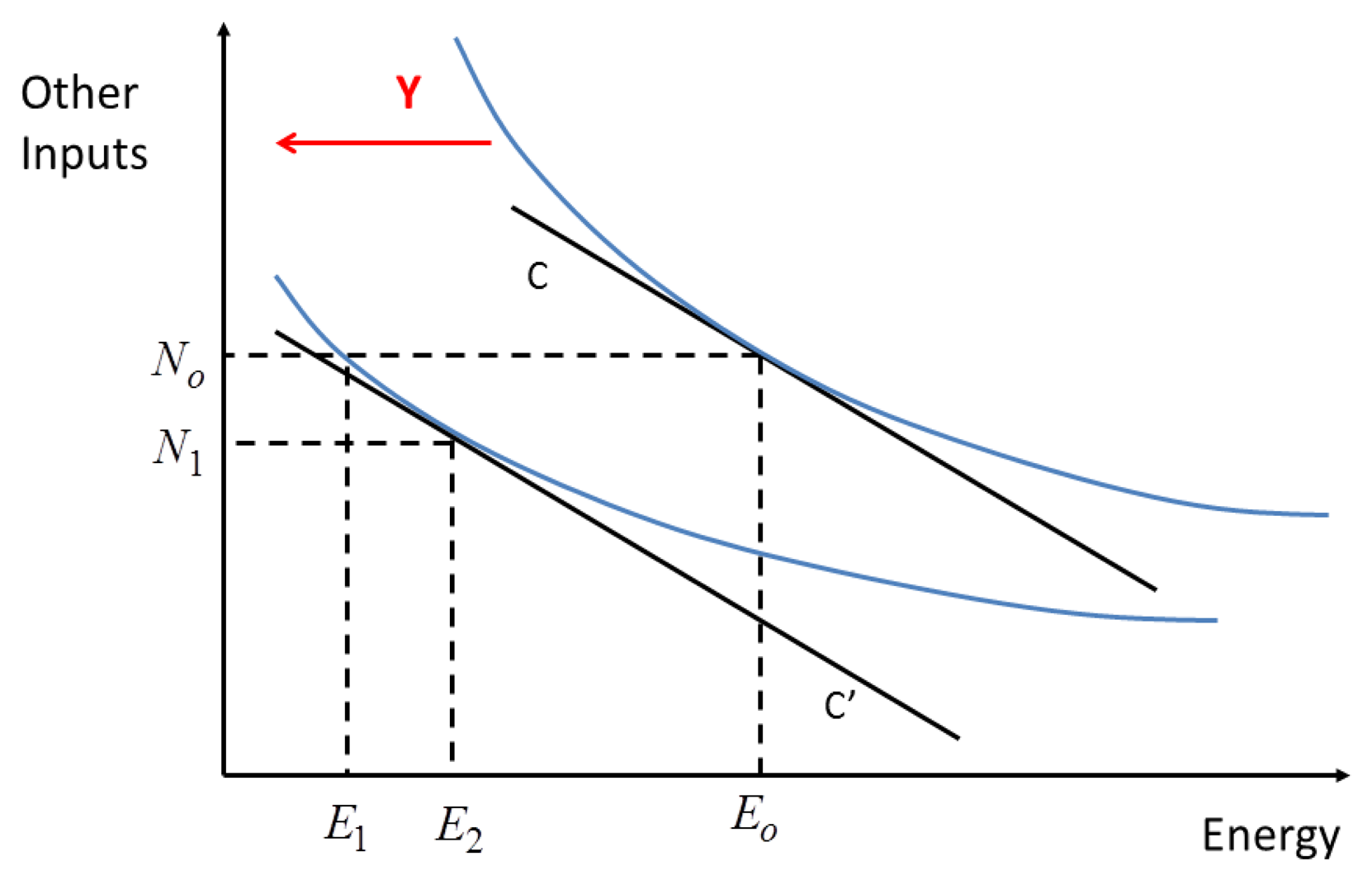
The contribution of substitution to the direct rebound effect may be illustrated graphically. For simplicity, we assume that non-energy inputs are “separable” from energy inputs and can therefore be grouped together, or “nested”. The meaning and implications of this assumption are described further below. Figure 2 shows a two-input conventional production function, where the optimal mix of energy (E) and a “nest” of other inputs (N) to produce output Y for an expenditure of C is given by the intersection of the isoquants with the iso-cost line (N₀, E₀). Energy-saving technical change shifts the isoquants to the left and changes their slope. If other inputs remain unchanged, the potential energy savings are E₀ − E₁. However, over time producers will shift to a new, lower cost input mix (N₁, E₂), leading to actual energy savings of E₀ − E₂ which are less than the potential savings. The size of the rebound effect ((E₂ − E₁)/(E₀ − E₁)) depends upon the ease of substitution between energy and other inputs—indicated by the curvature of the isoquant.

Technical change may also increase output (not shown) since: first, a higher level of output can be produced for a given expenditure on inputs; and second, reductions in product prices may increase aggregate supply and hence output. This increase in output will further increase energy use. The total direct rebound effect is the sum of these substitution and output effects. In what follows, we focus on the substitution effect—which Saunders [11] found to be more important.

4. Rebound Effects with a Constant Elasticity of Substitution (CES) Production Function

These examples illustrate the importance of substitution for rebound effects and suggest that these effects will be larger when the scope of substitution between energy and other inputs is easier. Saunders [10] demonstrates this formally, using the following definition of the direct rebound effect (R):

$$R=1+{\mathrm{\eta }}_{{\tau }_E}(E)$$

(17)

where η_τE(E) is the elasticity of energy consumption with respect to energy-augmenting technical change:

$${\mathrm{\eta }}_{{\tau }_E}(E)=\frac{\partial lnE}{\partial ln{\tau }_E}$$

(18)

We expect 0 ≥ η_τE and hence 0 ≤ R ≤ 1. But the direct rebound effect could theoretically exceed unity (“backfire”) or be negative (“super conservation”). Since E = Y/θ_E, Equation (18) can be decomposed:

$${\mathrm{\eta }}_{{\tau }_E}(E)={\mathrm{\eta }}_{{\tau }_E}(Y)-{\mathrm{\eta }}_{{\tau }_E}({\theta }_E)$$

(19)

If, η_τE (θ_E) ≤ 1, there is a substitution effect; and if η_τE (Y) ≥ 0, there is an output effect. Saunders [9] derived these elasticities for a variety of production and cost functions, but his original analysis [7] employed a CES production function similar to that used in the majority of energy-economic models. The particular formulation rests upon the assumption that capital and labor are separable from energy and may therefore be grouped together:

$$Y={\upsilon }_N{\left\{a{\left[{\left(K\right)}^{\gamma }{\left(L\right)}^{1-\gamma }\right]}^{\rho }+b{\left({\tau }_{E}E\right)}^{\rho }\right\}}^{\frac{1}{\rho }}$$

(20)

As shown in [9], the substitution, output and rebound effects are (Appendix 1 derives the substitution effect):

$${\mathrm{\eta }}_{{\tau }_E}(\mathrm{\theta })=1-\sigma$$

(21)

$${\mathrm{\eta }}_{{\tau }_E}(Y)=\frac{\sigma }{1-s_E}$$

(22)

$$R=\frac{\sigma }{1-s_E}$$

(23)

where σ = 1/(1 − ρ) is the Hicks elasticity of substitution (HES) between the capital-labour composite and effective energy—a standard measure of the ease of substitution. If σ = 0, there is no rebound effect; while if σ > 1, energy-augmenting technical change reduces aggregate energy productivity (Δθ < 1) and increases energy consumption (ΔE > 1). This appears unlikely, since it implies that energy is a non-essential input. But Saunders [7] demonstrates that alternative “nesting structures” of the same function (i.e., (KE)L and (LE)K) always lead to rebound effects greater than 100%, regardless of the HES between the nests. Hence, the estimated magnitude of rebound effects appears sensitive to the particular choice of nesting structure and functional form.

This discussion suggests that sectors where substitution towards energy is easier (i.e., σ is larger) will be more vulnerable to rebound effects. Hogan and Manne [16] used analogous arguments to suggest that sectors where substitution away from energy is easier will be less vulnerable to rising energy prices. Both conclusions have important policy implications and highlight the importance of accurately estimating both the ease of substitution and the rate of energy-augmenting technical change in different sectors.

So does the existing evidence base allow the ease of substitution and rate of energy-augmenting technical change within different sectors to be accurately identified? How well do energy-economic models reflect this evidence base? And can the available empirical and modeling studies provide reliable guidance on the magnitude of rebound effects in different sectors? The remainder of the paper addresses these questions by examining: first, the definition and estimation of energy substitution (Sections 5 and 6); second, the use of those estimates within energy-economic models (Section 7); and third, the estimation and representation of energy-augmenting technical change (Section 8).

5. Defining Substitution–the Choice of Measure

We first look more closely at how the “ease of substitution” is defined. The previous discussion used the Hicks elasticity of substitution (σ or HES) which measures the ease with which a decrease in one input (i) can be compensated by an increase in another (j) while holding output fixed [17]. It is defined as:

$$HE{S}_{ij}=-\frac{\partial ln(X_i/X_j)}{\partial ln({\pi }_i/{\pi }_j)}$$

(24)

where π_i is the marginal productivity of input X_i (∂Y/∂X_i). This definition refers to movement along an isoquant of a production function and is a scale-free measure of the curvature of this isoquant: the less the curvature the easier it is to substitute between two inputs and the larger the HES (HES_ij ≥ 0). The extremes are: a linear production function (HES_ij = ∞) and a Leontief (fixed proportions) production function (HES_ij = 0). For a Cobb Douglas production function HES = 1, while for a CES production function, HES is constant (as the name suggests) between 0 and infinity. If HES_ij > 1, each input can fully substitute for the other (i.e., the isoquants cross the axes). Assuming profit maximization and perfect competition, the HES can also be defined in relation to a change in relative prices:

$$HE{S}_{ij}=\frac{\partial ln(X_i/X_j)}{\partial ln(p_j/p_i)}$$

(25)

The HES was originally defined for a two-input production function (capital and labor). When applied to multi-input production functions it is sometimes termed the Hicks Allen elasticity of substitution (HAES), but this extension creates difficulties since the ease of substitution between i and j may depend upon the level or price of other inputs. This may not be the case if i and j are separable from other inputs but, as discussed below, this assumption often does not hold. Also, the value of the HAES depends upon the particular price changes being considered. For this reason, most empirical studies define substitution in relation to changes in a single input price, with the most common measures being the Cross price elasticity (CPE_ij), the Allen-Uzawa elasticity of substitution (AES_ij) and the Morishima elasticity of substitution (MES_ij). The relevant definitions are given in

Table 1. Comparing common definitions of substitution elasticities. Source: Broadstock et al. [18].

Definition	Output	Other inputs Xk ≠ Xi,j	Other input prices pk ≠ pi, j	Type	Substitutes (complements)	Input shares$\frac{\ge }{\le }1$	Symmetric
$\begin{array}{l}HE{S}_{ij}=-\frac{\partial ln(X_i/X_j)}{\partial ln({\pi }_j/{\pi }_i)}\\ HE{S}_{ij}=-\frac{\partial ln(X_i/X_j)}{\partial ln(p_j/p_i)}\end{array}$	Fixed	Fixed	Fixed	Two input, two price	HESij > 0	$\frac{\partial (s_i/s_j)}{\partial (X_i/X_j)}\frac{\ge }{\le }0$	Yes
$\mathit{\text{HAE}}{S}_{ij}=-\frac{\partial ln(X_i/X_j)}{\partial ln(p_j/p_i)}$	Fixed	Variable	Fixed	Two input, two price	HAESij > 0 (<0)	$\frac{\partial (s_i/s_j)}{\partial (X_i/X_j)}\frac{\ge }{\le }0$	No
$CP{E}_{ij}=\frac{\partial ln{X}_i}{\partial ln{p}_j}$	Fixed	Variable	Fixed	One input, one price	CPEij > 0 (<0)	$\frac{\partial ln{s}_i}{\partial ln{p}_j}\frac{\ge }{\le }0$	No
$AE{S}_{ij}=-\frac{1}{s_j}\frac{\partial ln{X}_i}{\partial ln{p}_j}$	Fixed	Variable	Fixed	One input, one price	AESij > 0 (<0)	$\frac{\partial ln{s}_i}{\partial ln{p}_j}\frac{\ge }{\le }0$	Yes
$ME{S}_{ij}=\frac{\partial ln(X_i/X_j)}{\partial ln(p_j)}$	Fixed	Variable	Fixed	Two input, one price	MESij > 0 (<0)	$\frac{\partial ln(s_i/s_j)}{\partial ln{p}_j}\frac{\ge }{\le }0$	No

Note: X_i = level of input i; p_i = unit price of input i; π_i = marginal productivity of input i (∂f/∂x_i); and s_i = share of i in input costs (s_i = X_ip_i/C). Under perfect competition, s_i is equal to the share of i in the value of output.

and Box 1. Substitution between two inputs is easier when these measures are larger and their sign is commonly used to define inputs as either substitutes (+ve) or complements (−ve). However, whether two inputs may be described as substitutes or complements depends upon the particular elasticity that is being used. This, together with inconsistent terminology, complicates the interpretation of the empirical literature.

Box 1. Relationships among common substitution elasticities

$$\begin{array}{c}AE{S}_{ij}=\frac{CP{E}_{ij}}{s_j}\\ ME{S}_{ij}=CP{E}_{ij}-CP{E}_{jj}\\ \mathit{\text{HAE}}{S}_{ij}=ME{S}_{ij}\left[\frac{\partial ln{p}_j}{\partial ln\left(\frac{p_j}{p_i}\right)}\right]-ME{S}_{ij}\left[\frac{\partial ln{p}_i}{\partial ln\left(\frac{p_j}{p_i}\right)}\right]\\ \frac{\partial ln{s}_i}{\partial ln{p}_j}=s_j(AE{S}_{ij}-1)\\ \frac{\partial ln(s_i/s_j)}{\partial ln{p}_j}=(ME{S}_{ij}-1)\end{array}$$

Source: Broadstock et al. [18], Frondel [19,20], Sato and Koizumi [21]. If only p_j changes and p_i is fixed, then HAES_ij = MES_ij, while if only p_i changes and p_j is fixed, then HAES_ij = MES_ji.

The great majority of empirical studies estimates the AES and uses its sign to classify input pairs as either substitutes or complements. This reflects the most common understanding of these terms, which is the effect of a change in the price of one input on the demand for another. However, exactly the same information is provided by the CPE—the AES just divides the CPE by the value share of one of the inputs (Box 1). This is not very helpful since it implies that quantitative estimates of the AES lack meaning and are difficult to compare since they depends upon value shares [19]. The AES is also symmetric (AES_ij = AES_ji) which is equally unhelpful since the impacts of interest usually depend upon which price is changing (p_i or p_j). Hence, in most circumstances, it seems preferable to estimate the CPE, since this is asymmetric (CPE_ij ≠ CPE_ji) and measures the change in demand for a single input following a price change, rather than the change in a ratio of inputs [19].

The MES is closer to the original Hicks definition since it measures the percentage change in a ratio of inputs and indicates the curvature of an isoquant. Like the CPE, it is also asymmetric. However, the sign of the MES is of little value for defining substitutes or complements since the MES should generally be positive. A negative estimate of MES_ij is likely to indicate problems with the specification, since it implies substitution away (towards) from an input despite a fall (increase) in its relative price. This also follows from Equation (2) in Box 1, since we expect CPE_jj < 0 and |CPE_jj|>|CPE_ij|.

6. Measuring Substitution—The Energy-Capital Debate

With the CES production function of Equation (20), the magnitude of rebound effects from energy-augmenting technical change depends upon the magnitude of the HES between effective energy and the capital-labor composite. Many energy-economic models use a similar functional form, implying that their estimates of rebound effects will be sensitive to the assumed value of the HES between energy and other inputs. But most empirical studies do not use the CES functional form owing to the constraints it imposes on the potential for substitution. Instead, they use more flexible functional forms such as the translog and derive the CPE, the AES or MES from the estimated parameter values. Translog production and cost functions were originally introduced by Christensen et al. [22], and are widely used for empirical work because they do not impose any restrictions on input substitutability. Estimation usually involves applying Shepard's Lemma to derive linear cost share equations and imposing various restrictions on the parameter values.

These differences create considerable difficulties in using the empirical literature to infer appropriate values for the HES to use within energy-economic models. Moreover, these difficulties are greatly exacerbated by the fact that the empirical literature is itself confusing, contradictory and difficult to interpret. To illustrate these difficulties, we take the long-standing debate over energy-capital substitution as an example.

Engineering studies have long indicated significant potential for cost-effectively improving energy efficiency through various forms of capital investment—which could be interpreted as substituting physical capital for energy. This potential is reproduced in the assumptions used for many energy-economic models. But beginning with Berndt and Wood [23], a large number of econometric studies have suggested that energy and capital are AES and CPE complements, implying that an increase in energy prices will reduce the rate of capital investment [18]. Such a result implies that energy and capital are closely linked in economic production and that increases in energy prices could reduce output growth.

Berndt and Wood [23] estimated a four-input (KLEM) translog cost function for US manufacturing over the period of 1947–1971, and found all input pairs to be substitutes apart from capital and energy (CPE_KE = −0.16; CPE_EK = −0.17). Since then, more than one hundred studies have estimated different types of substitution elasticity between capital and energy in different countries and sectors and time periods, but have failed to reach a consensus on whether these inputs may “generally” be regarded as substitutes or complements. In a review of over 50 studies providing elasticity estimates, Broadstock et al. [19] found that ∼40% of estimates suggested that energy and capital were complements (CPE_KE < 0) and ∼55% suggested they were substitutes (CPE_KE > 0) with widely differing values. In a meta-analysis of ∼40 studies, Koetse et al. [24] found energy and capital to be substitutes, with a “base case”. CPE_KE estimate of +0.17 for time series data and +0.52 for cross-sectional data. Following earlier authors, e.g., [25], Koetse et al. [24] interpret the former as representing short-run adjustments and the latter long-run, hence suggesting greater scope for substitution as the capital stock rotates. However, Frondel and Schmidt [26] demonstrate that alternative explanations for this finding are equally plausible. Specifically, when a static translog cost function is estimated, the cost share of energy strongly influences the magnitude of the estimated CPE_KE [26]. When material inputs are included in the specification, the cost shares of capital and energy becomes smaller, together with the estimated CPE_KE. Since studies using time-series data are more likely to include material inputs, they are more likely to find energy-capital complementarity.

Broadstock et al. [18] showed how different studies have analyzed different countries, sectors and time periods using different specifications, data sets and methods of estimation and come to quite different conclusions on energy-capital substitutability. While this may be expected if the degree of substitutability depends upon the sector, level of aggregation and time period, it is notable that many studies reach different conclusions for the same sector and time period, or for the same sector in different countries. For example, Raj and Veall [27] found that studies using the original Berndt and Wood dataset have produced 38 estimates of AES_KE, ranging from −3.94 to +10.84. Studies cite a range of possible causes for the variation in results, including differences in data type, level of sectoral aggregation, measurement and aggregation of inputs, functional form, relative value share of each input and assumptions about homogeneity and seperability (see below) [18]. However, different studies cite different causes, and there appears to be no consensus on either the relative importance of each cause or their likely direction of influence.

This ongoing debate illustrates how the estimation of substitution elasticities raises a variety of theoretical and methodological issues that collectively make it very difficult to interpret the results and draw useful conclusions [18]. Of particular importance to the present discussion are the explicit or implicit assumptions about the separability of inputs. Separability implies that the HES between two inputs is unaffected by the level or price of the other inputs. These two conditions are only equivalent when relative input shares are independent of the level of output. In addition, if two inputs (i,j) are separable from a third (k), then the ease of substitution between i and k (as measured by the CPE, AES or MES) is equal to that between j and k (e.g., CPE_ik = CPE_jk) [28].

Separability assumptions are commonly used to justify either the omission of inputs for which data is unavailable (notably materials) or the grouping, or nesting, of different inputs. Nesting implies that producers engage in a two-stage decision process: first optimizing the combination of inputs within each nest, and then optimizing the combination of nests required to produce the final output. Two inputs may only be legitimately grouped within a nest if they are separable from inputs outside of the nest. For example, Saunders' (KL)E nesting structure requires that capital and labor are separable from energy [7]. One of the contributions of Berndt and Wood [23] was to show that capital and labor was not separable from either energy or materials within their dataset.

But even when two inputs (e.g., i and j) within a nest are separable from a third (e.g., k), this does not mean that measures of the CPE, AES or MES between i and j are unaffected by the price of k. As Frondel and Schmidt [29] have shown, even if capital and labor were separable from energy under the standard definition (as in Equation (20)), the ease of substitution between capital and labor (as measured by the CPE, AES or MES) may still be affected by the price of energy. Frondel and Schmidt [29] define a stricter condition of empirical dual separability, in which the value of CPE_ij is unaffected by the price of k. Stability of AES_ij requires the additional condition that the value shares are unaffected, which seems unlikely. Hence, the empirical measures of substitution between i and j are likely to depend upon the price of other inputs, even when i and j are separable from those inputs.

This suggests that estimates of substitution elasticities are likely to be biased if separability is assumed where not supported by the data, or if measures of any input are omitted. The latter situation is common, particularly with regard to the omission of materials. In practice, studies that exclude materials more often indicate capital-energy substitutability, while those that include materials indicate complementarity [18,23,26].

In sum, the multiple definitions of substitution elasticities, the range of factors influencing empirical estimates and the sensitivity of results to those factors make the evidence base in this area confusing, contradictory, prone to bias and difficult to use. At a minimum, statements about substitutability need to be qualified by the countries, sectors and time periods to which they apply the manner in which inputs are disaggregated and measured and the specific assumptions that are made—with the latter being supported, where possible, by statistical tests. But the resulting estimates may still not be useful for particular applications, including the parameterization of energy-economic models. To illustrate this, the next section examines how substitution elasticities are used in energy-economic models and highlights the limited basis for the assumptions made.

7. Assuming Substitution—Energy-Economic Modeling

Energy-economic models based upon computable general equilibrium (CGE) techniques are widely used for exploring policy-relevant questions including the estimation of rebound effects. Such models almost invariably use CES production functions and assume that some inputs are separable from others. Parameterisation requires assumptions about the HES between input groups [30,31] and these can have a major influence on results [4,32,33]. For example, Grepperud and Rasmussen [4] estimate the rebound effects from energy-augmenting technical change to be substantially higher in the Norwegian primary metals sector than in the fisheries sector, owing to the (assumed) greater opportunities for energy substitution in the former [4].

For such results to be robust, the assumed parameter values should be firmly based upon empirical research. Unfortunately, it is common practice to assume these values with only limited reference to the empirical literature. Moreover, even when such references are made, there are considerable difficulties in using empirical studies to infer values of the HES for CGE models. This is because most of these models:

▪

differ from the cited empirical studies in the manner in which individual inputs are aggregated and in the level of sectoral aggregation;

▪

assume values for HES parameters within CES production functions, while most empirical studies use flexible cost functions to estimate the AES, CPE and/or MES;

▪

impose separability between groups (nests) of inputs while most empirical studies do not; and

▪

require estimates of the HES between those groups, while most empirical studies provide estimates of the AES, CPE and/or MES between individual pairs of inputs.

These points are briefly elaborated below.

Blackorby and Russell [34] showed that the AES, MES and HES are identical if (and only if) there are only two inputs to the production function, or the production function has a Cobb Douglas or non-nested CES structure (e.g., Y = (a_KK^−ρ + a_LL^−ρ + a_EE^−ρ + a_MM^−ρ)^−1/ρ). But the two-input case is of limited interest, the Cobb-Douglas structure is excessively restrictive and the non-nested CES requires the HES between all inputs to be identical [35]—which appears unlikely. In order to provide greater flexibility in substitution possibilities, most CGE models impose separability assumptions to create a nested CES functional form [36] in which inputs are grouped in pairs—such as the (KL)E structure of Equation (20). A more general nested CES is:

$$Y={\left[a{\left(K*\right)}^{\rho }+(1-a){\left(E*\right)}^{\rho }\right]}^{\frac{1}{\rho }}$$

(26)

where both the capital-labor composite (K*) and the energy-materials composite (E*) are CES functions as well:

$$K^{*}={\left(b{K}^{\alpha }+(1-b)L^{\alpha }\right)}^{\frac{1}{a}}$$

(27)

$$E^{*}={\left(c{E}^{\beta }+(1-c)M^{\beta }\right)}^{\frac{1}{\beta }}$$

(28)

The structure of this “two-level” nested CES, in which capital K and labour L are nested as well as energy E and materials M, rests on the assumption that K* is separable from E*. Saunder's functional form (Equation (20)) follows the same structure, but omits materials and uses a simpler (Cobb Douglas) form for the KL nest [7]. Alternative nesting schemes (such as (KE)(LM) or (EL)(KM)) are widely used, but the appropriate choice is rarely tested [37,38]. If a distinction is made (as it should) between different types of capital, labour or energy inputs (e.g., electricity and non-electricity), a multilevel CES can be formed, with more than one function nested within the original one. Lecca et al. [39] demonstrate the sensitivity of model results to these assumptions and criticize the arbitrary choice of both nesting structure and parameter values in the majority of energy-economic models. But such a structure is difficult to either estimate directly or to parameterize from the results of existing research. Sanstad et al. [40] observe that: “… There appears to be no published econometric estimation of a nested CES model with general factor-augmenting technical change, even in a degree of complexity less than is common in integrated assessment and energy simulation models …”. To illustrate, we take a closer look at the implied values of the HES, AES and CPE within such a structure.

With a nested CES, the AES between a pair of inputs belonging to different nests is equal to the HES between the nests [28]. For example, the (KL)(EM) nesting structure implies that: AES_KE = AES_KM = AES_LE = AES_LM. = HES_K*E*. But the AES between a pair of inputs belonging to the same nest is not equal to HES between those inputs. Indeed, while two inputs within an individual nest are necessarily HES substitutes, they may at the same time be AES (and CPE) complements (i.e., AES < 0). The AES between these two inputs is only equal to the HES if the output of the nest is held constant [36]. Taking labor and capital as an example in Equation (26):

$$AE{S}_{LK}=HE{S}_{K^{*}{E}^{*}}+\frac{1}{a}(HE{S}_{LK}-HE{S}_{K^{*}{E}^{*}})$$

(29)

Hence, it is possible for AES_LK to be negative, provided HES_K*E* > HES_LK. In other words, the scope for substitution between the capital-labor composite (K*) and the energy-materials composite (E*) is greater than the scope for substitution between capital and labour in the production of K*.

Hence, estimates of the AES, CPE or MES between two inputs provide little guidance in choosing the appropriate values of the HES between those inputs that are required for the nested CES functions used in CGE models. If the separability assumptions were valid, a particular nested CES could be parameterised if the function was estimated directly. But the majority of empirical studies estimate flexible functional forms such as the translog and do not impose separability restrictions. Moreover even if separability restrictions were to be imposed, this would not ensure that estimates of the AES or CPE between two inputs were invariant to the price of other (possibly omitted) inputs since this would require the stricter conditions described by Frondel and Schmidt [26,29]. Furthermore, even if the stricter condition were to hold, the implied nesting structure may not correspond to that used within a particular energy-economic model.

Table 2. Nesting structures and assumed values of the Hicks elasticity of substitution (HES) in a selection of contemporary CGE models. Source: based on van der Werf [38].

Authors	Nesting structure	Assumed HES
Bosetti et al. [41]	(KL)E	HESK,L = 1.0; HESKL,E = 0.5
Burniaux et al. [42]	(KE)L	HESK,E = 0 or 0.8; HESKE,L = 0 or 1.0
Edenhofer et al. [43]	KLE	HESK,L,E = 0.4
Gerlagh and van der Zwaan [44]	(KL)E	HESK,L = 1.0; HESKL,E = 0.4
Goulder and Schneider [45]	KLEM	HESK,L,E,M = 1.0
Kemfert [46]	(KLM)E	HESKLM,E = 0.5
Manne et al. [47]	(KL)E	HESKL = 1.0; HESKL,E = 0.4
Popp [48]	KLE	HESK,L,E = 1.0
Sue Wing [49]	(KL)(EM)	HESK,L = 0.68–0.94; HESE.M = 0.7; HESKL,EM = 0.7

compares the nesting structures and assumed values of HES in a number of contemporary CGE models. Over half of these models exclude material inputs, so therefore implicitly assume that these are separable from other inputs. These models further vary in how they disaggregate and nest individual inputs (e.g., fuel and electricity) and how they model technical change. The basis for the assumed values for the HES between different inputs and nests of inputs is rarely made clear, sensitivity tests are uncommon and the values chosen vary widely between different models.

In sum, the assumptions made for production structures and substitution elasticities within most CGE models appear to be only weakly linked to an empirical literature that is itself contradictory and inconclusive. This suggests that the results of such models, including their estimates of rebound effects, should be treated with considerable caution. Unless more flexible functional forms can be adopted, e.g., [50], sensitivity analysis of nesting structures and parameter values should be employed.

8. Representing Technical Change—Competing Approaches

Sections 2 and 3 argued that the magnitude of rebound effects from energy-augmenting technical change should be proportional to the flexibility of producers to adapt to those efficiency gains via substitution [7,10]. But Sections 4–7 highlighted the difficulties in both estimating this flexibility and in using these results to parameterize energy-economic models. The multiple definitions of substitution elasticities are a source of confusion, the most commonly estimated elasticity is of little practical value, the empirical literature is contradictory, prone to bias and difficult to use, and there are only tenuous links between this literature and the assumptions used within energy-economic models. While simply assuming values for substitution elasticities “… is tantamount assuming the answer …” [10], it appears to be very common.

Further challenges are created by the use of energy-augmenting technical change as the independent variable for an estimate of rebound effects. This is because most empirical studies do not directly estimate this form of technical change and many energy-economic models do not simulate it. To illustrate, we summarize the most common approaches to estimating and modeling technical change and highlight the implications of using two different approaches within a CES production function.

As noted, empirical studies typically employ flexible cost functions such as the translog and use Shepards Lemma to derive equations for the value share of each input. With a suitable functional form, this allows the “energy price bias” to be estimated:

$${\mathrm{\psi }}_E=\frac{\partial s_E}{\partial t}$$

(30)

where ψ_E ≤ 0 (ψ_E ≥ 0) indicates energy saving (using) technical change. But energy-saving technical change is not equivalent to energy-augmenting technical change because capital, labor and materials augmenting technical change, as well as substitution between inputs, also affect the energy value share (s_E). While τ_i represents technical change for a single input before input shares adjust, ψ_i represents the net effect of technical change on all inputs after input shares adjust. Substitution towards energy may limit the reduction in the energy value share brought about by energy-augmenting technical change—and in some circumstances may even increase the energy value share. Hence, in principle, it is possible for energy-augmenting technical change (τ_E ≥ 0) to coexist with energy-using technical change (ψ_E ≥ 0).

In a widely cited study, Hogan and Jorgenson [51] find energy-using technical change in US industry over the period 1958–1979. Saunders [10] argues that this result suggests rebound effects greater than unity in US industry—implying that efficiency improvements increased aggregate energy consumption. However, since Hogan and Jorgenson measure energy-using rather than energy-augmenting technical change, their results do not allow the magnitude of the rebound effect (as defined by Equation (17)) to be directly estimated. While they find an increasing value share of energy, this may have derived from a number of sources and is not necessarily indicative of backfire following energy augmenting technical change.

Modeling studies typically employ CES production functions. While some model energy-augmenting technical change in a similar manner to Saunders [7] (Equation (20)), others incorporate an “autonomous energy efficiency index” (AEEI) to indicate the rate of growth of aggregate energy productivity [40,52,53]:

$$\mathit{\text{AEEI}}=\frac{\partial ln{\mathrm{\theta }}_E}{\partial t}$$

(31)

But again, the AEEI is not equivalent to energy-augmenting technical change (τ_E), since labor, capital and materials augmenting technical change, as well as input substitution, will also affect aggregate energy productivity (θ_E). Hogan and Jorgensen [51] derive the following relationship between the AEEI and the energy price bias (ψ_E):

$${\mathrm{\psi }}_E=s_E({\mathit{\varepsilon }}_{\text{gt}}-\mathit{\text{AEEI}})$$

(32)

In other words, the energy price bias is the “share weighted” deviation of the autonomous energy efficiency trend from the trend in total factor productivity (ε_gt). Positive values for ε_gt imply improvements in total factor productivity (declining costs per unit of output), while positive values for AEEI imply improvements in energy productivity (declining energy intensity) over time. If aggregate energy productivity is improving at the same rate as total factor productivity (ε_gt = AEEI, then the energy price bias is zero. If energy productivity is improving faster (slower) than total factor productivity, then the energy price bias is negative (positive) and technical change is energy-saving (energy-using). Normally, we would expect the AEEI and the energy price bias to be opposite in sign (e.g., if AEEI > 0, we expect ψ_E < 0). But energy-saving technical change may also result from falling total factor productivity (ε_gt < 0), even if energy productivity is improving (AEEI > 0) provided |ε_gt| > |AEEI| [40]. Sanstad et al. [40] find evidence of this within developing countries.

Different models use different CES formulations and nesting structures and implement either the AEEI or energy-augmenting technical change (τ_E) in different ways [38]. For example, the version used by Manne and Richels [52] nests a Cobb-Douglas function for “value added” (capital and labor) within a CES and simulates “autonomous energy efficiency improvements” by a negative growth rate of the “distribution parameter” b (b = e^−δt where δ ≥ 0):

$$Y={\left[a{\left(K^{\gamma }{L}^{1-\gamma }\right)}^{\rho }+b{\left(E\right)}^{\rho }\right]}^{\frac{1}{\rho }}$$

(33)

In contrast, Saunders' version of this function simulates energy-augmenting technical change by a positive growth rate for parameter τ_E (τ_E(t) = e^λEt where λ_E ≥ 0) [7]:

$$Y={\left[a{\left(K^{\gamma }{L}^{1-\gamma }\right)}^{\rho }+b{\left({\tau }_{E}E\right)}^{\rho }\right]}^{\frac{1}{\rho }}$$

(34)

These two approaches to representing technical change are not equivalent. Combining both approaches, Appendix 2, shows that with this functional form:

$$\mathit{\text{AEEI}}=\sigma \delta +(1-\sigma ){\lambda }_E$$

(35)

The Manne Richels approach has λ_E = 0, therefore, AEEI = σδ. Since σ ≥ 0 and δ ≥ 0, a negative growth rate for parameter b always leads to a positive AEEI. Hence, with this approach technical change for energy inputs always leads to a proportionate reduction in aggregate energy productivity. As a result, this approach is incapable of simulating any substitution response to this technical change and hence of simulating the substitution component of the direct rebound effect. The model may still allow the output component of the direct rebound effect to be simulated. A likely outcome is that the energy savings from improved energy efficiency will be overestimated.

In contrast, the Saunders' approach has δ = 0 [7], therefore, AEEI = (1 − σ)δλ_E. Since λ_E ≥ 0, the impact of energy-augmenting technical change on aggregate energy productivity depends upon the elasticity of substitution between energy and value-added. As shown in Section 3, this form of technical change only leads to a positive AEEI when σ ≤ 1. In other words, substitution contributes to a rebound effect that reduces energy savings. Consistent with this, we find that models that depict energy-saving technical progress invariably assume a value for the HES between energy and other inputs that is less than unity [54–59].

In sum, the estimation of direct rebound effects for producers requires specification of the magnitude and direction of energy-augmenting technical change. Most empirical studies do not estimate this form of technical change, many energy-economic models do not simulate it and others simulate it in a manner that precludes the accurate modeling of rebound effects. As a result, the available evidence provides insufficient guidance on the magnitude of rebound effects within different industrial sectors. When combined with the difficulties in specifying substitution elasticities discussed earlier, the result is considerable uncertainty over the magnitude of rebound effects in industrial production.

9. Summary

This paper has explored the relationships between energy productivity improvements for producers, the “ease of substitution” between energy and other inputs and the size of the resulting rebound effects. It has shown how easier substitution drives larger rebounds, but the relevant mechanisms are not straightforward and are difficult to capture empirically. There are three main findings.

First, the multiple definitions of substitution elasticities are a source of confusion, the most commonly estimated elasticity is of little practical value and the empirical literature is contradictory, prone to bias and difficult to use. For example, engineering studies suggest a large potential for improving energy efficiency by substituting capital for energy, but three decades of econometric research has achieved no consensus on whether these inputs are best described as substitutes or complements, and no consensus on how different factors influence empirical results.

Second, there are only tenuous links between the empirical literature on substitution elasticities and the assumptions used within energy-economic models. Most models employ nested CES production functions and make assumptions about the HES between these nests, while most empirical studies use translog cost functions and estimate the AES, CPE or MES between input pairs. Using the latter to parameterize the former is problematic. In addition: the process of compiling parameter values is rarely transparent; sensitivity tests are uncommon; the empirical studies (when cited) frequently apply to different sectors, time periods and levels of aggregation to those represented by the models; and different models use widely different assumptions. All these observations suggest that the results of CGE models, including the estimates of rebound effects, should be treated with caution and that sensitivity tests should be more extensively employed.

Third, while energy-augmenting technical change provides the natural choice of independent variable for an estimate of rebound effects, most empirical studies do not estimate this form of technical change, many modeling studies do not simulate it and others simulate in a manner that precludes the accurate modeling of rebound effects. As a result, the available evidence base provides only limited guidance on the magnitude of direct rebound effects for producers and widely used modeling tools may overestimate the future energy savings from improved energy efficiency.

These conclusions provide pointers to how future studies may more adequately capture direct rebound effects. For empirical studies, the most important requirement is the explicit estimation of input-augmenting technical change, such as achieved recently by Saunders [11] for the US and Stern and Kander [60] for Sweden. Interestingly, both studies suggest substantial direct rebound effects (e.g., 60% or more) from energy augmenting technical change [10]. In practice, simultaneous improvements in the productivity of other inputs may amplify these effects.

For modeling studies, the requirements include (where possible) greater use of flexible functional forms, abandonment of the AEEI in favor of input-augmenting technical change, the inclusion of materials inputs, much more careful attention to the empirical basis for elasticity assumptions and extensive sensitivity tests of parameter values and nesting structures. These recommendations could be challenging to implement. But in their absence, our knowledge of rebound effects in industrial production is likely to remain limited and our confidence in future energy savings may be misplaced.