Optimization of the Interconnect Ribs for a Cathode-Supported Solid Oxide Fuel Cell
Abstract
: A comprehensive mathematical model of the performance of the cathode-supported solid oxide fuel cell (SOFC) with syngas fuel is presented. The model couples the intricate interdependency between the ionic conduction, electronic conduction, gas transport, the electrochemical reaction processes in the functional layers and on the electrode/electrolyte interfaces, methane steam reforming (MSR) and the water gas shift reaction (WGSR). The validity of the mathematical model is demonstrated by the excellent agreement between the numerical and experimental I-V curves. The effect of anode rib width and cathode rib width on gas diffusion and cell performance is examined. The results show conclusively that the cell performance is strongly influenced by the rib width. Furthermore, the anode optimal rib width is smaller than that for cathode, which is contrary to anode-supported SOFC. Finally, the formulae for the anode and cathode optimal rib width are given, which provide an easy to use guidance for the broad SOFC engineering community.1. Introduction
Solid oxide fuel cell (SOFC) is considered to be one of the more promising new energy technologies [1–3]. In the last decade, there has been a great deal of research aiming to increase the performance of a single SOFC by looking for new electrodes and electrolyte materials, optimizing electrode microstructure or improving electrode and electrolyte preparation techniques [4–10] and so on. Currently, a single SOFC may produce a power density of 2.45 W·cm−2 at 800 °C and 0.7 V [11]. However, when multiple cells are connected by an interconnector (bipolar plates) to form a SOFC stack, the performance of SOFC at the stack level decreases by 50% or more compared to a single level SOFC [12,13]. There are many factors limiting the performance of SOFC as part of a stack. One of the primary factors is the additional losses caused by the interconnector geometry. Herein, additional losses are created by two main aspects: (i) the interconnector used in a stack can cause a significant contact resistance between the electrode and the interconnector; (ii) the interconnector limits gas diffusion in electrode.
Small grooves in interconnectors are defined as channels, which are commonly used to carry the fuel and air gas flow. The ribs, which separate and define the channels, make direct contact with the electrodes. In designing the layer architecture, there is a tradeoff that must be considered between the rib and channel sizes. On one hand, wider ribs and ribs covering a bigger fraction of the cell area may reduce the interface resistance to current flow by increasing the electrode-interconnect contact area and reducing the current path through the possibly high resistance electrode material. Hence, such ribs will give a better conduction of the electrical current and reduce ohmic losses. On the other hand, the chemical species do not diffuse as well underneath wide ribs. Narrow ribs are needed to facilitate more uniform distribution of reactive gases across the area of the electrolyte surface and thus to promote electrochemical performance. The implications of the tradeoff to the cell performance can be very significant. It was reported that the power density was only 0.76 W·cm−2 at 0.7 V operating voltage for the combination of 2.6 mm channels and 2.4 mm ribs at the cathode side, while that for 4 mm channels and 1 mm ribs was 1.03 W·cm−2 [12]. Clearly, optimizing rib and channel sizes are of the utmost importance to realize the full potential of SOFCs.
Several authors have investigated the impact of the rib size on SOFC performance. Tanner and Virkar [14] proposed a simplified model to examine the effect of the interconnect design on the effective ohmic resistance of the membrane-electrode assembly in an SOFC stack. Lin et al. [15] provided a phenomenological model and analytical expressions to estimate the rib effects on the concentration and ohimc polarizations of anode-supported SOFC stacks. Ji et al. [16] showed that the terminal output of a SOFC stack depended strongly on the contact resistance. Jeon et al. [17] proposed a detailed microstructural model and examined systematically the influence of the rib width, pitch width and the contact area specific resistance (ASRcontact) on the stack-cell performance. Noh et al. [18] showed that by modifying the current collection configuration, cell performance was improved by more than 30%. Based on systematic examination of the stack cell performance as a function of various influencing factors, Liu et al. [19] proposed a simple expression for the optimal rib width as a function of the pitch width and ASRcontact that was independent of the porosity, layer thickness and conductivity of the electrode and easy for SOFC engineers to use.
Unfortunately, the existing numerical studies on the rib design optimization have been carried out with two assumptions: (i) equal ASRcontact for the anode-interconnect and cathode-interconnect interfaces and (ii) equal width of the optimal anode and cathode rib widths. However, as demonstrated experimentally by Kornely et al. [12] and Dey et al. [20], ASRcontact for the anode-interconnect and cathode-interconnect interfaces can be very different. Therefore, the optimal anode rib width isn't equivalent to the optimal cathode rib width as the optimal rib width depends on ASRcontact [19,21]. Even if ASRcontact for the anode-interconnect and cathode-interconnect interfaces are equal, the optimal rib widths for anode and cathode should be different. Previous studies have already shown very different effects of the cathode and anode ribs on the mass transport in the electrodes. For anode-supported SOFC, the anode gas transport was only mildly affected by the anode rib, which is benefit from thick anode, while an oxygen depletion zone of 0.46 mm was found with a cathode rib width of only 0.8 mm due to thin cathode thickness limiting the oxygen diffusion to the area under rib [19]. On the contrary, for cathode-supported SOFCs, the anode rib has an important influence on the anode gas transport; the minimum hydrogen concentration under anode rib is only about one third of that under anode channel [22]. The existing experimental and theoretical findings indicate clearly that the optimal design of the stack cell should use different widths for the anode and the cathode ribs.
We have developed a comprehensive two dimensional model for an anode-supported SOFC with hydrogen as fuel and optimized the anode and cathode rib widths without the above two assumptions [21]. The numerical results show that the output current density depends strongly on the rib widths and the optimal rib widths for the anode and the cathode are quite different. Moreover, the optimal widths for both the anode and cathode ribs are found to be only sensitive to the contact resistance and the pitch width. Finally, the formulae for optimal rib width are given. However, these formulae are only valid for an anode-supported SOFC. The effects of the cathode and anode ribs on the mass transport for cathode-supported SOFC are different to that for anode-supported SOFC, which are demonstrated by references [19,22].
On one hand, from the aspect of anode concentration loss, the effect of anode rib width on the anode concentration loss is rather limited for anode-supported SOFCs due to the thick anode providing a wide alleyway allowing fuel to penetrate under the ribs. However, it is a quite different situation for a cathode-supported SOFC. The anode rib width has a serious influence on anode concentration loss since thin anode of cathode-supported SOFC limits fuel diffusion to the area under rib. Consequently, the optimal anode rib width for cathode-supported SOFC should be relatively small in comparison with that for anode-supported SOFC in order to reduce anode concentration loss. On the other hand, from aspect of cathode concentration loss, the thin cathode of anode-supported SOFC limits the oxygen diffusion to the area under rib and increases cathode concentration loss, while a thick cathode in a cathode-supported SOFC promotes oxygen diffusion to the area under rib. Therefore, the optimal cathode rib width of an anode-supported SOFC should be smaller than that of cathode-supported SOFC. As a result, the formulae for optimal rib widths of anode-supported SOFC given in our previous paper [21] can't be applied to a cathode-supported SOFC. There is an urgent need to investigate the optimal rib width for cathode-supported SOFCs. Due to such a research need, the objective of this work is to study the optimal rib width of cathode-supported SOFCs to provide guidelines for cathode-supported SOFC fabrication.
Compared with cathode-supported SOFCs, anode-supported SOFCs have attracted more attention. However, cathode-supported SOFCs show various advantages over anode-supported SOFCs. One is the low cost of cathode supporting materials such as strontium-doped lanthanum manganese. Moreover, when operating on hydrocarbon fuels with low steam-to-carbon ratio, a relatively thin anode would prevent it from depositing carbon. In addition, a thin anode layer would also provide benefits in terms of tolerance to volume contraction/expansion resulting from the accidental anode redox cycles.
In this paper, the previously developed model [21] is modified to investigate the performance of a cathode-supported SOFC. Different from the previous study with hydrogen as fuel, syngas is used, which consists of methane (CH4), steam (H2O), carbon monoxide (CO), hydrogen (H2) and carbon dioxide (CO2). The methane steam reforming and water gas shift reaction are taken into account in this model. The optimal anode and cathode rib widths for different ASRcontact are obtained and formulized to provide an easy-to-use guidance for designing the rib-channel layout.
2. Model
2.1. Geometric Model
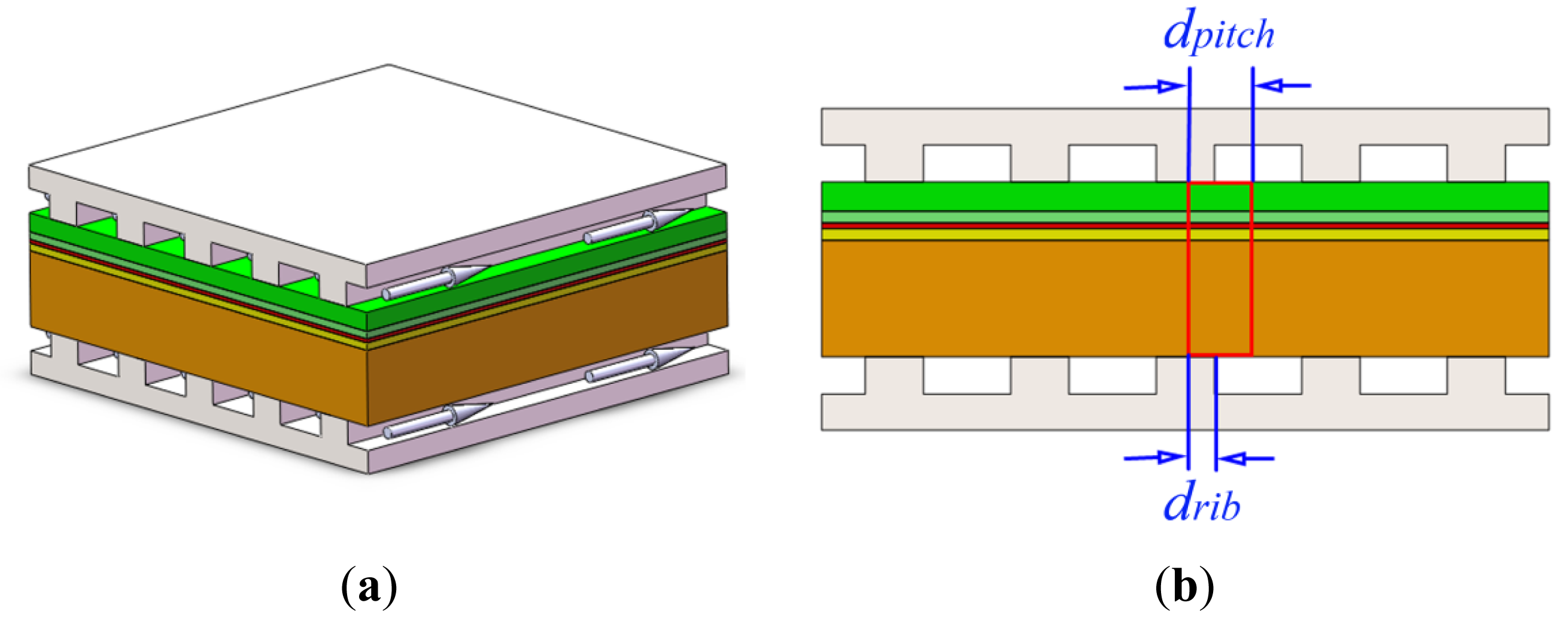
Figure 1a shows a repeating cell unit of a cathode-supported cell stack. As demonstrated before [19,23], a 2D model is equivalent to a 3D model when discussing the effects of rib widths on the fuel cell performance as they provide essentially the same results. Therefore, a 2D model (Figure 1b) is used here. Due to symmetry, we select half of the repeating unit of stack as our computational domain, which is shown by the red line in Figure 1b. The computational domain consists of five layers: (1) an anode current collector layer (ACCL) with relatively large Ni- and YSZ-particles and high porosity to decrease gases transport resistance; (2) an anode functional layer (AFL) with fine Ni- and YSZ-particles and low porosity to reduce the active losses by affording abundant three phase boundaries (TPBs); (3) an electrolyte layer; (4) a cathode functional layer (CFL) with fine LSM- and YSZ-particles and low porosity and (5) a cathode support layer (CSL) with relatively large LSM-particles and high porosity. In Figure 1b, drib is one half of the interconnect rib width and dpitch is the pitch width (the sum of one half of the rib width, drib, and one half of the channel width, dchannel).
2.2. Modeling Mass Transport
The gases transport in SOFC porous electrodes is complex and includes three distinct mass-transfer mechanisms: Knudsen diffusion, molecular diffusion, as well as viscous flow. Thus, the dusty gas model (DGM) is required to estimate accurately the transport of gases in SOFC porous electrodes. However, the fluxes of different species are coupled with one another in the DGM and further coupling of the DGM with the mass conservation equations and the bulk chemical reactions is cumbersome to perform. In our previous study [24], the DGM in the form of an Fick's model (DGMFM) was derived from the DGM, which can give an explicit analytical expression for the flux of each species. Thus, DGMFM is adopted to describe the gases transport in SOFC porous electrodes. The molar mass conservation equation of species i is given by:
Permeability coefficient k and the viscosity coefficient of fluid μ can be calculated by the following expressions [25]:
and can be evaluated by the following equations [26–28]:
In this study, the fuel consists of methane (CH4), steam (H2O), carbon monoxide (CO), hydrogen (H2) and carbon dioxide (CO2). MSR and WGSR are taken into account in porous anode, described respectively as:
The rate of MSR occurring on the surface of the catalyst particle can be estimated by following formula [29–31]:
The shift reaction occurs wherever the gas is present, which is considered to be at equilibrium in the porous anode due to the high working temperatures. On the basis of experimental data, a shift reaction rate expression can be formulated as [29–31]:
2.3. Modeling Electrical Conduction
The electronic charge transfer in the electrodes (ACCL, AFL, CFL and CSL) is governed by:
Scurrent may be calculated by the equation below:
itrans is the local charge transfer current density and can be calculated as according to the empirical Butler-Volmer equation.
For Ni/YSZ AFL TPBs, itrans is derived as [32,33]:
For LSM/YSZ CFL TPBs, itrans is derived as [32,33]:
The volume-specific TPB length λTPB can be written as [21,34]:
The area-specific TPB length λTPB can be written as [21,34]:
The effective electronic and ionic conductivities of composite electrode are strong relied on microstructures like particles size, porosity, volume fractions. The coordination number theory based percolation micro-model reveals the relationship between the effective electrode properties and the microstructure parameters [36–39]. Considering a binary system with random packing of spheres, corresponding to the electrode-particles (denoted as el) and electrolyte-particles (denoted as io), The effective electric conductivity of k-phase is estimated as [40]:
for Ni, LSM and YSZ may be estimated as [17,43]:
2.4. Boundary Conditions (BCs)
Proper settings of the boundary conditions are required to solve these coupled partial differential equations correctly. The boundary settings for the mass transport equations are shown in Table 1. The boundary settings for the electronic and ionic charge transfer equations are shown in Table 2. The molar concentrations at the ACCL/channel interface or CSL/channel interface, C0, are related to the molar fractions by the ideal gas equation of state. The total gas pressure at the electrode/channel interface is set at 1 atm. The contact resistance is set on the interface between the interconnect ribs and the electrodes. That is, local current densities cross the rib/anode (irib→ACCL) and the cathode/rib (iCSL→rib) interfaces are determined by:
2.5. Numerical Solution
The finite element commercial software COMSOL MULTIPHSICS® (COMSOL, Inc., Burlington, MA, USA) was used in the present study to solve the required partial differential equations (PDEs) of the gas transport equation, ionic conduction equation and electronic conduction equation. The discretized PDEs were solved by using the direct solver with a relative convergence tolerance of 1 × 10−6. Structured mesh elements were used and consisted of 720 rectangles with 10,474 degrees of freedom.
2.6. Numerical Validation
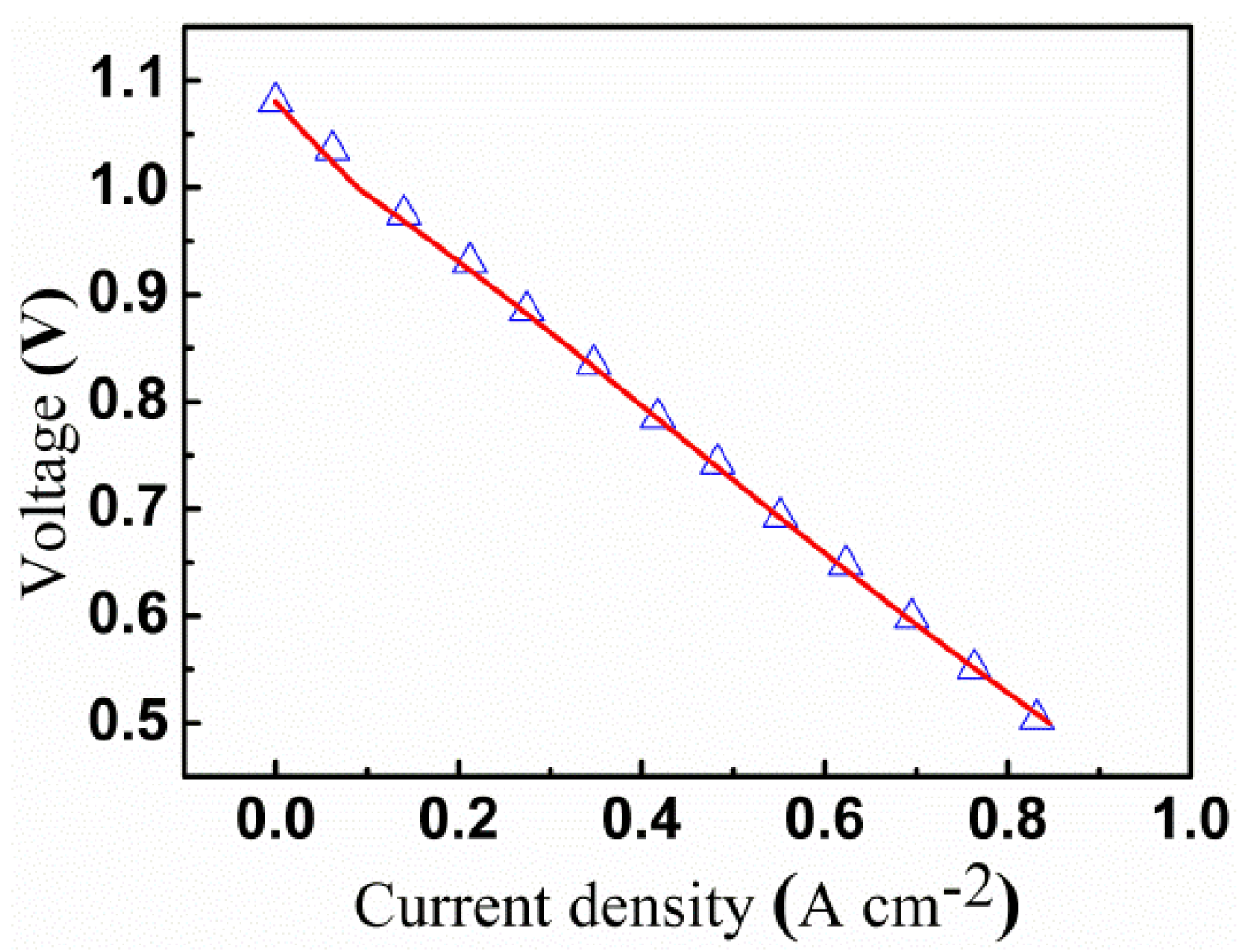
Nickel or silver meshes are the typical current collectors used for single cell testing. The meshes may be regarded as interconnect ribs with small pitch widths. A pitch width of 0.2 mm and a rib width of 0.05 mm corresponding to the experimental description were used here for the numerical model validation. Model parameters are listed in Tables 3–5.The simulated I-V relations are compared with the experimental results of Wang et al. [44] in Figure 2. As shown in Figure 2, the theoretical results agree with the experimental measurements very well. Hence, the numerical model is used in the following to optimize interconnect rib. Moreover, except for those specified explicitly for each testing case, the model parameters listed in Tables 3–5 are used throughout the paper.
3. Results and Discussion
3.1. The Effect of Rib Width on the Cell Performance
In order to investigate the influence of the rib width on the cell performance, four models were established with the same settings as described above except the size of interconnector geometry structure. The pitch width (dpitch), the anode rib width and the cathode rib width for four models are listed in Table 6.
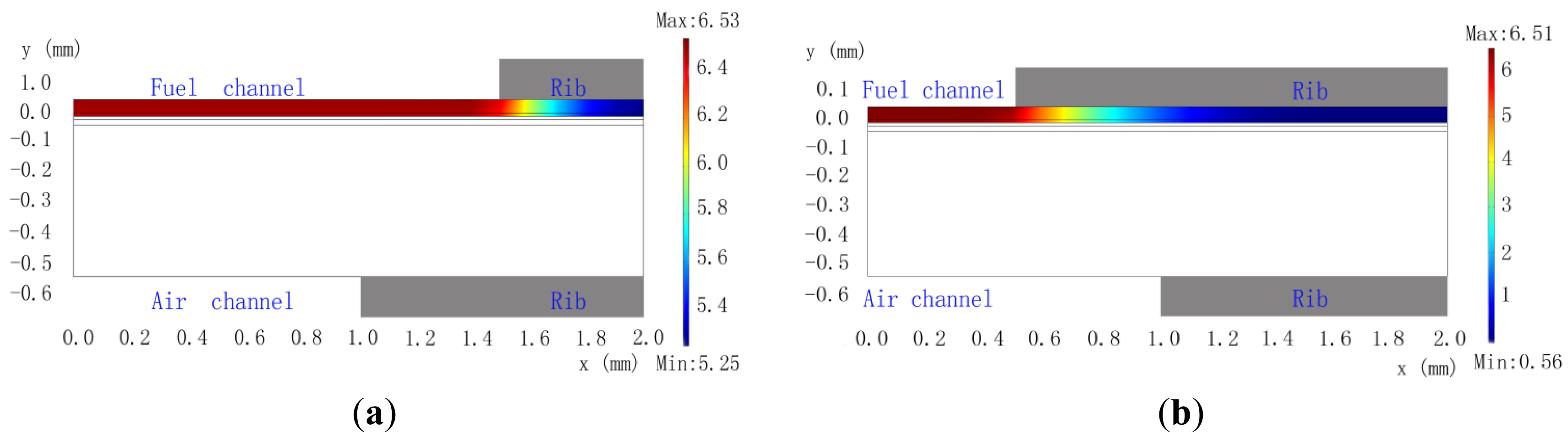
Figure 3 shows the H2 concentration distribution in the anode of a cathode-supported SOFC. It is obvious that the H2 concentration gradients in the vertical direction are small, which is beneficial for a thin anode. However, the H2 concentration gradient in the horizontal direction is quite large. This is because the anode thickness is very thin which limits the H2 diffusion to the area under rib. Comparing Figure 3a with Figure 3b, it isn't difficult to find that the smallest H2 concentration is only 0.56 mol m3 for the Cell-B, which is only about one tenth of that for the Cell-A. Thus, the anode rib width has a significant impact on the fuel diffusion for cathode-supported SOFC, which is quite different to that for anode-supported SOFC [21]. For Cell-B, the output current densities for Vop of 0.7, 0.6 and 0.5 V are respectively 0.4166, 0.5099 and 0.5992 A·cm−2, as shown in Table 7. However, the output current densities of Cell-A are 35.1%, 36.2% and 37.5% more than that of Cell-B for Vop of 0.7,0.6 and 0.5 V, respectively. Clearly, the anode rib width has a significant impact on the cell performance.
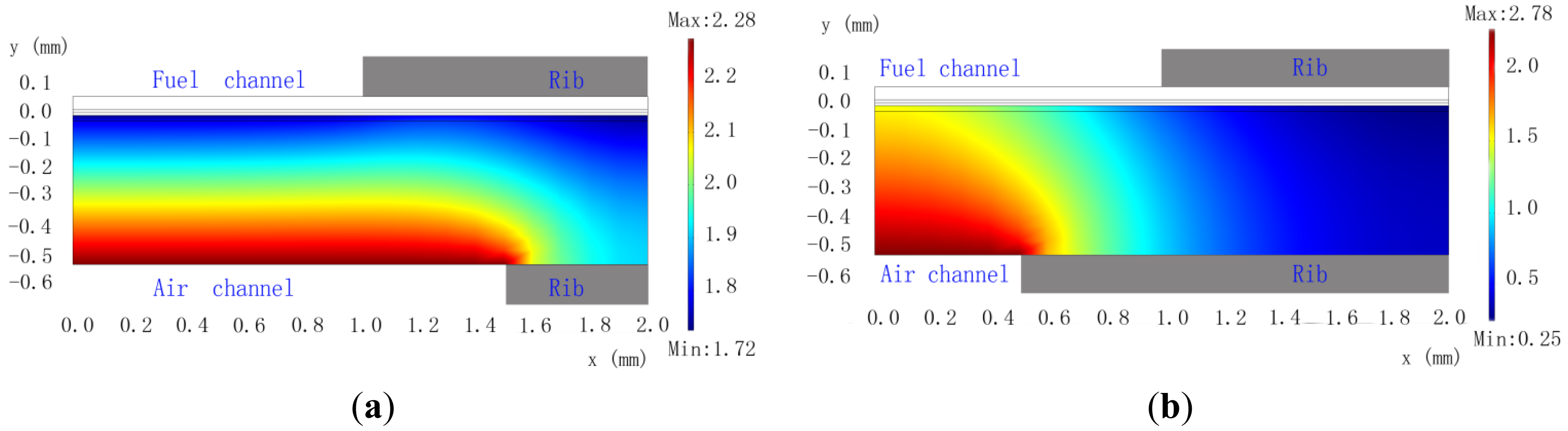
As shown in Figure 4a, although there is the change of O2 concentration in the vertical direction for Cell-C, the distributions of O2 concentration is reasonably uniform near the cathode/electrolyte interface. Figure 4b, however, shows a quite different situation for Cell-D. The change of O2 concentration near the cathode/electrolyte interface of Cell-D is quite large, decreasing from 1.5 mol·m−3 under the channel to 0.25 mol·m−3 under the rib, as can be seen in Figure 4b. Similarly to anode rib, the O2 diffusion is strongly influenced by the cathode rib. For Cell-D, the output current densities for Vop of 0.7, 0.6 and 0.5 V are respectively 0.4722, 0.5575 and 0.6290 A·cm−2, as given in Table 7. However, the output current densities of Cell-C are 10.5%, 18.1% and 26.7% more than that of Cell-D for Vop of 0.7, 0.6 and 0.5 V, respectively. Obviously, it is very necessary to optimize the cathode rib width for increasing cell performance.
3.2. Expressions for the Optimal Rib Widths
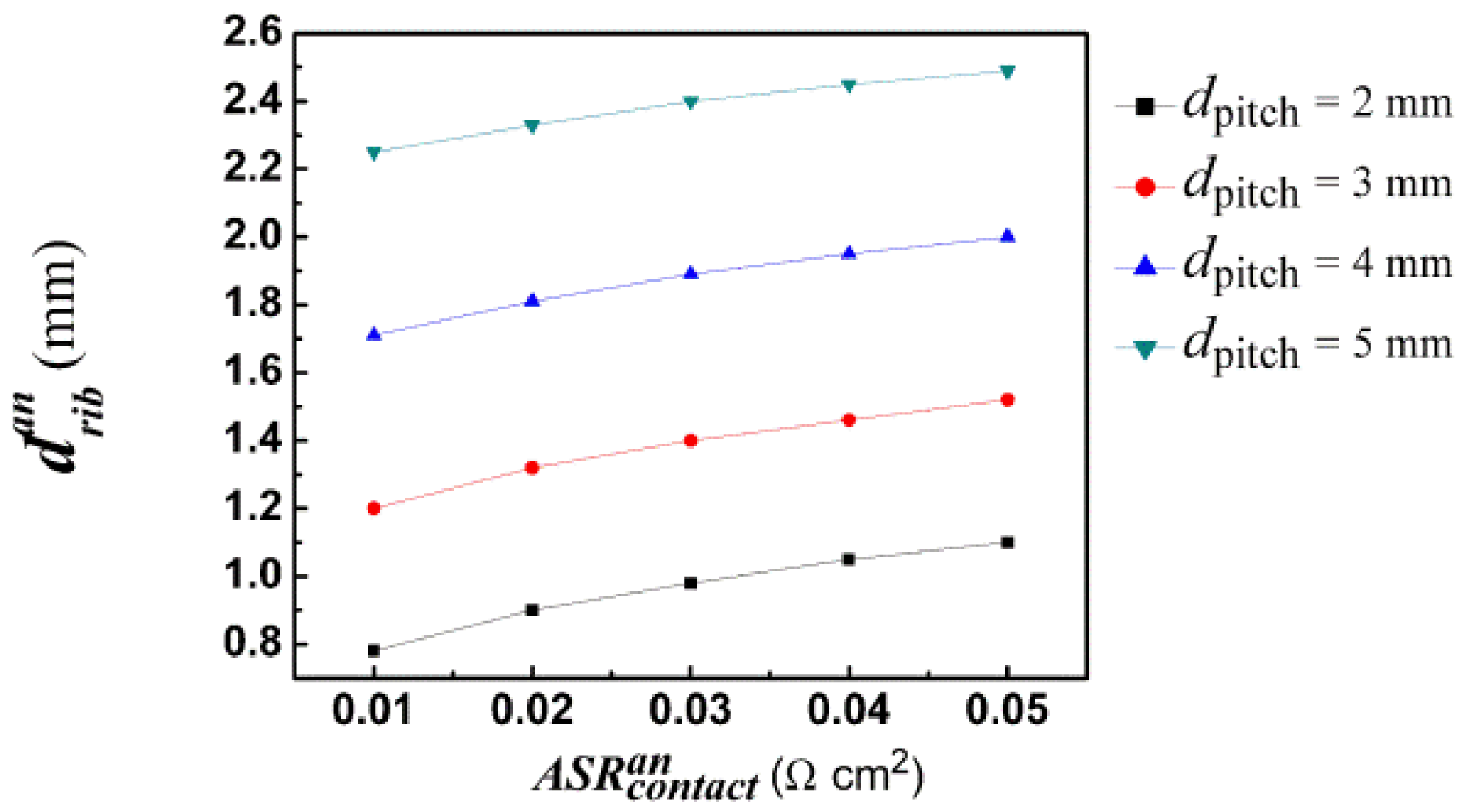
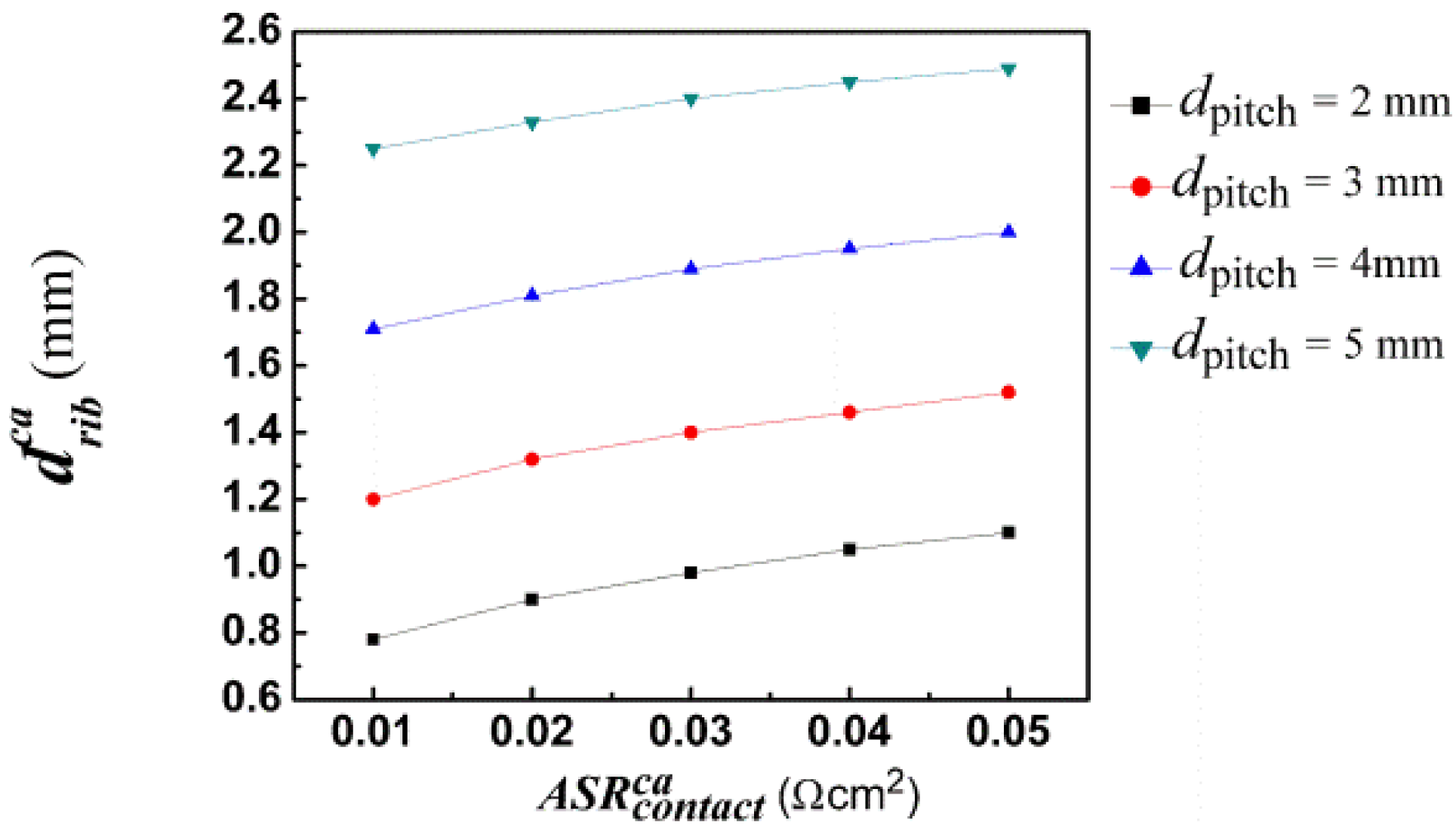
As described above, the cell performance depends strongly on the rib width and a suitable choice of the rib width is very important for high cell performance. An optimal rib width is obtained for a given pitch width by changing rib width to achieve the maximum cell current density [47]. Our previous study demonstrated that the optimal rib width is only sensitive to the rib-electrode contact resistance and pitch width [19,21]. Therefore we only discuss the relationship between the optimal rib width and rib-electrode contact resistance and pitch width in the following section.
By comparing Figure 5 with Figure 6, it has been observed that the optimal anode rib width is smaller than the optimal cathode rib width for the same pitch width and contact resistance, which is contrary to the anode-supported situation. The reason is that cathode thickness is about 8 times the anode thickness for a cathode-supported SOFC. Thus, the influence of ribs on gas diffusion at the anode side is more serious than that at the cathode side for a fixed rib width. In order to reduce the concentration losses, the anode rib width should be relatively smaller than the cathode rib width.
For a given pitch width, the optimal rib width is found to be dependent approximately linearly on the contact resistance, such as shown in Figures 5 and 6. The relationship between the contact resistance and the optimal rib widths can be formulized as:
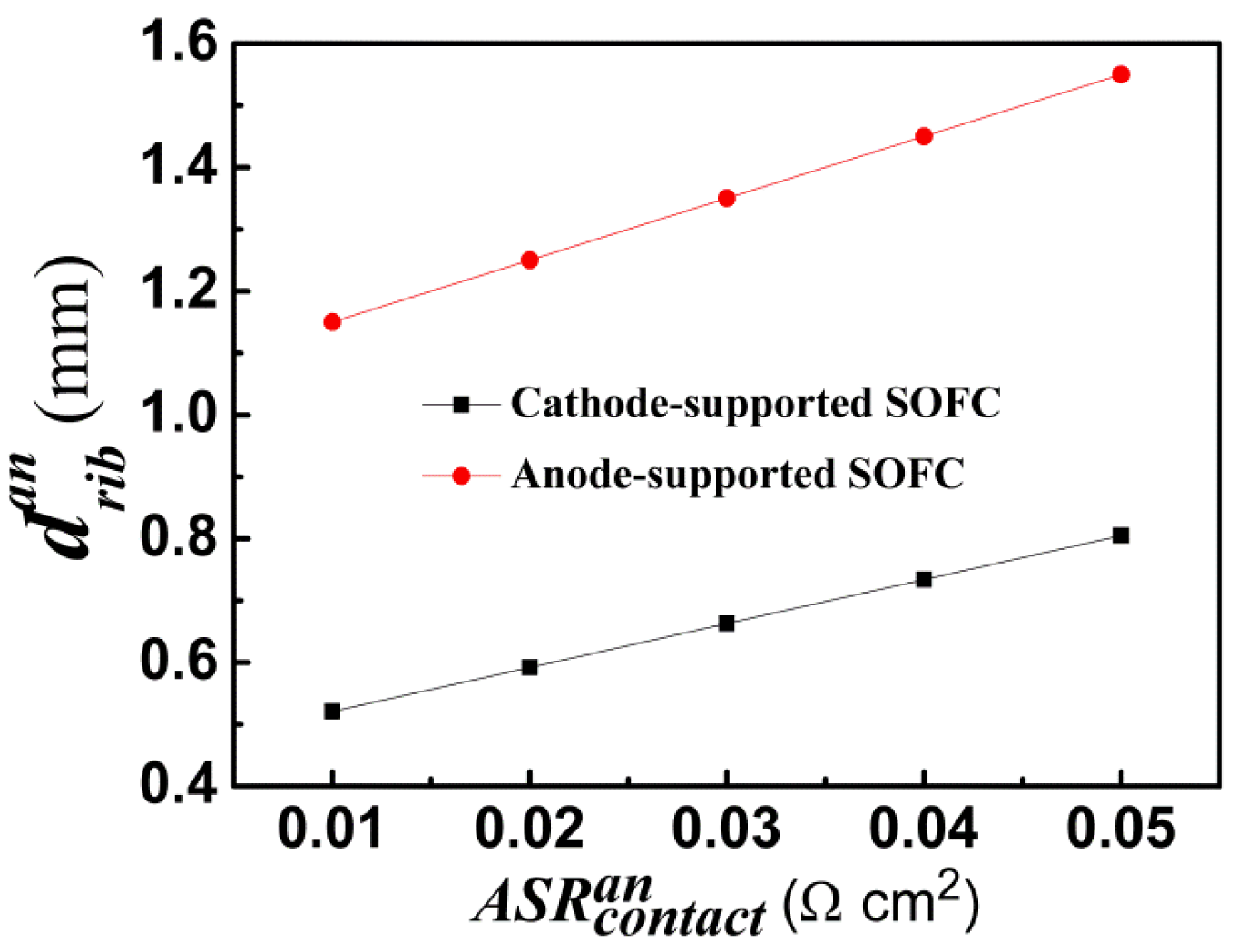
Figures 7 and 8 show the optimal anode and cathode rib widths of anode- and cathode-supported SOFCs, respectively, with the pitch width as 2 mm. Obviously, the optimal anode rib width of the anode-supported SOFC is about twice as large as that of the cathode-supported SOFC. However, the optimal cathode rib width of anode-supported SOFC is only about one half of that of cathode-supported SOFC. It can be safely concluded that the formulae of optimal rib widths for anode-supported SOFC can't be applied to cathode-supported SOFC. This is just the problem that this work solves. The above analysis also reveals the importance and necessity of this study.
4. Conclusions
We have described a comprehensive mathematical model for the performance of a cathode-supported SOFC with syngas fuel. The model takes into account the contact resistance between the electrode and rib and the dependence of the effective electrode properties on the microstructure parameters of the porous electrode. The impact of anode rib width and cathode rib width are studied. The numerical results show conclusively that the output current density depends strongly on the rib width and the rib design optimization is of high engineering importance. Systematic optimization of the anode rib width and cathode rib width for the maximum output current have been carried out. The formulae for the anode and cathode optimal rib width are given, which provides an easy to use guidance for the broad SOFC engineering community.
Acknowledgments
We gratefully acknowledge the financial support of Jiangsu Province Colleges and Universities Natural Science Projects (13KJB480003), the Jiangsu University of Science and Technology (35321101) and the National Science Foundation of China (21106058).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Razbani, O.; Assadi, M.; Andersson, M. Three dimensional cfd modeling and experimental validation of an electrolyte supported solid oxide fuel cell fed with methane-free biogas. Int. J. Hydrog. Energy 2013, 38, 10068–10080. [Google Scholar]
- Chen, D.; Zeng, Q.; Su, S.; Bi, W.; Ren, Z. Geometric optimization of a 10-cell modular planar solid oxide fuel cell stack manifold. Appl. Energy 2013, 121, 1100–1107. [Google Scholar]
- Shirazi, A.; Aminyavari, M.; Najafi, B.; Rinaldi, F.; Razaghi, M. Thermal-economic-environmental analysis and multi-objective optimization of an internal-reforming solid oxide fuel cell-gas turbine hybrid system. Int. J. Hydrog. Energy 2012, 37, 19111–19124. [Google Scholar]
- Liu, Q.; Dong, X.; Xiao, G.; Zhao, F.; Chen, F. A novel electrode material for symmetrical SOFCs. Adv. Mater. 2010, 22, 5478–5482. [Google Scholar]
- Suzuki, T.; Hasan, Z.; Funahashi, Y.; Yamaguchi, T.; Fujishiro, Y.; Awano, M. Impact of anode microstructure on solid oxide fuel cells. Science 2009, 325, 852–855. [Google Scholar]
- Yang, L.; Liu, Z.; Wang, S.; Choi, Y.; Zuo, C.; Liu, M. A mixed proton, oxygen ion, and electron conducting cathode for sofcs based on oxide proton conductors. J. Power Sources 2010, 195, 471–474. [Google Scholar]
- Huang, J.; Xie, F.; Wang, C.; Mao, Z. Development of solid oxide fuel cell materials for intermediate-to-low temperature operation. Int. J. Hydrog. Energy 2012, 37, 877–883. [Google Scholar]
- Chen, G.; You, H.-X.; Kasai, Y.; Sato, H.; Abudula, A. Characterization of planer cathode-supported sofc prepared by a dual dry pressing method. J. Alloys Compd. 2011, 509, 5159–5162. [Google Scholar]
- Liu, M.; Dong, D.; Zhao, F.; Gao, J.; Ding, D.; Liu, X.; Meng, G. High-performance cathode-supported sofcs prepared by a single-step co-firing process. J. Power Sources 2008, 182, 585–588. [Google Scholar]
- Wang, B.; Lai, Z. Finger-like voids induced by viscous fingering during phase inversion of alumina/pes/nmp suspensions. J. Membr. Sci. 2012, 405, 275–283. [Google Scholar]
- Mukhopadhyay, M.; Mukhopadhyay, J.; Das Sharma, A.; Basu, R.N. Engineered anode structure for enhanced electrochemical performance of anode-supported planar solid oxide fuel cell. Int. J. Hydrog. Energy 2012, 37, 2524–2534. [Google Scholar]
- Kornely, M.; Leonide, A.; Weber, A.; Ivers-Tiffée, E. Performance limiting factors in anode-supported cells originating from metallic interconnector design. J. Power Sources 2011, 196, 7209–7216. [Google Scholar]
- Blum, L.; Meulenberg, W.A.; Nabielek, H.; Steinberger-Wilckens, R. Worldwide sofc technology overview and benchmark. Int. J. Appl. Ceram. Technol. 2005, 2, 482–492. [Google Scholar]
- Tanner, C.W.; Virkar, A.V. A simple model for interconnect design of planar solid oxide fuel cells. J. Power Sources 2003, 113, 44–56. [Google Scholar]
- Lin, Z.; Stevenson, J.W.; Khaleel, M.A. The effect of interconnect rib size on the fuel cell concentration polarization in planar sofcs. J. Power Sources 2003, 117, 92–97. [Google Scholar]
- Ji, Y.; Yuan, K.; Chung, J.; Chen, Y. Effects of transport scale on heat/mass transfer and performance optimization for solid oxide fuel cells. J. Power Sources 2006, 161, 380–391. [Google Scholar]
- Jeon, D.H.; Nam, J.H.; Kim, C.J. Microstructural optimization of anode-supported solid oxide fuel cells by a comprehensive microscale model. J. Electrochem. Soc. 2006, 153, A406–A417. [Google Scholar]
- Noh, H.-S.; Hwang, J.; Yoon, K.; Kim, B.-K.; Lee, H.-W.; Lee, J.-H.; Son, J.-W. Optimization of current collection to reduce the lateral conduction loss of thin-film-processed cathodes. J. Power Sources 2012, 230, 109–114. [Google Scholar]
- Liu, S.; Song, C.; Lin, Z. The effects of the interconnect rib contact resistance on the performance of planar solid oxide fuel cell stack and the rib design optimization. J. Power Sources 2008, 183, 214–225. [Google Scholar]
- Dey, T.; Singdeo, D.; Bose, M.; Basu, R.N.; Ghosh, P.C. Study of contact resistance at the electrode-interconnect interfaces in planar type solid oxide fuel cells. J. Power Sources 2013, 233, 290–298. [Google Scholar]
- Kong, W.; Li, J.; Liu, S.; Lin, Z. The influence of interconnect ribs on the performance of planar solid oxide fuel cell and formulae for optimal rib sizes. J. Power Sources 2012, 204, 106–115. [Google Scholar]
- Kong, W.; Su, S.C.; Gao, X.; Zhang, D.H.; Yu, Z.D. Optimization of the anode current collector layer thickness for the cathode-supported solid oxide fuel cell. Adv. Mater. Res. 2013, 712, 1325–1329. [Google Scholar]
- Liu, S.; Kong, W.; Lin, Z. Three-dimensional modeling of planar solid oxide fuel cells and the rib design optimization. J. Power Sources 2009, 194, 854–863. [Google Scholar]
- Kong, W.; Zhu, H.; Fei, Z.; Lin, Z. A modified dusty gas model in the form of a fick's model for the prediction of multicomponent mass transport in a solid oxide fuel cell anode. J. Power Sources 2012, 206, 171–178. [Google Scholar]
- Li, J.; Kong, W.; Lin, Z. Theoretical studies on the electrochemical and mechanical properties and microstructure optimization of micro-tubular solid oxide fuel cells. J. Power Sources 2013, 232, 106–122. [Google Scholar]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. New method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar]
- Veldsink, J.W.; Versteeg, G.F.; van Swaaij, W.P.M.; van Damme, R.M.J. The use of the dusty-gas model for the description of mass transport with chemical reaction in porous media. Chem. Eng. J. Biochem. Eng. J. 1995, 57, 115–125. [Google Scholar]
- Todd, B.; Young, J.B. Thermodynamic and transport properties of gases for use in solid oxide fuel cell modelling. J. Power Sources 2002, 110, 186–200. [Google Scholar]
- Lehnert, W.; Meusinger, J.; Thom, F. Modelling of gas transport phenomena in sofc anodes. J. Power Sources 2000, 87, 57–63. [Google Scholar]
- Klein, J.; Bultel, Y.; Georges, S.; Pons, M. Modeling of a sofc fuelled by methane: From direct internal reforming to gradual internal reforming. Chem. Eng. Sci. 2007, 62, 1636–1649. [Google Scholar]
- Hou, K.; Hughes, R. The kinetics of methane steam reforming over a Ni/α-Al2O catalyst. Chem. Eng. J. 2001, 82, 311–328. [Google Scholar]
- Costamagna, P.; Honegger, K. Modeling of solid oxide heat exchanger integrated stacks and simulation at high fuel utilization. J. Electrochem. Soc. 1998, 145, 3995–4007. [Google Scholar]
- Zhu, H.Y.; Kee, R.J. Modeling distributed charge-transfer processes in sofc membrane electrode assemblies. J. Electrochem. Soc. 2008, 155, B715–B729. [Google Scholar]
- Liu, S.; Kong, W.; Lin, Z. A microscale modeling tool for the design and optimization of solid oxide fuel cells. Energies 2009, 2, 427–444. [Google Scholar]
- Costamagna, P.; Costa, P.; Antonucci, V. Micro-modelling of solid oxide fuel cell electrodes. Electrochim. Acta 1998, 43, 375–394. [Google Scholar]
- Ali, A.; Wen, X.; Nandakumar, K.; Luo, B.J.; Chuang, K.T. Geometrical modeling of microstructure of solid oxide fuel cell composite electrodes. J. Power Sources 2008, 185, 961–966. [Google Scholar]
- Janardhanan, V.M.; Heuveline, V.; Deutschmann, O. Three-phase boundary length in solid-oxide fuel cells: A mathematical model. J. Power Sources 2008, 178, 368–372. [Google Scholar]
- Chen, D.; He, H.; Zhang, D.; Wang, H.; Ni, M. Percolation theory in solid oxide fuel cell composite electrodes with a mixed electronic and ionic conductor. Energies 2013, 6, 1632–1656. [Google Scholar]
- Chen, X.J.; Chan, S.H.; Khor, K.A. Simulation of a composite cathode in solid oxide fuel cells. Electrochim. Acta 2004, 49, 1851–1861. [Google Scholar]
- Wu, J.J.; McLachlan, D.S. Percolation exponents and thresholds obtained from the nearly ideal continuum percolation system graphite-boron nitride. Phys. Rev. B 1997, 56, 1236–1248. [Google Scholar]
- Suzuki, M.; Oshima, T. Co-ordination number of a multi-component randomly packed bed of spheres with size distribution. Powder Technol. 1985, 44, 213–218. [Google Scholar]
- Bouvard, D.; Lange, F.F. Relation between percolation and particle coordination in binary powder mixtures. Acta Metall. Mater. 1991, 39, 3083–3090. [Google Scholar]
- Shi, Y.X.; Cai, N.S.; Li, C. Numerical modeling of an anode-supported sofc button cell considering anodic surface diffusion. J. Power Sources 2007, 164, 639–648. [Google Scholar]
- Chen, T.; Li, T.; Miao, H.; Wang, W.G.; Wu, Y. Operation of Ni-YSZ anode supported solid oxide fuel cell on different simulated syngas. ECS Trans. 2009, 25, 1905–1910. [Google Scholar]
- Chen, D.; Bi, W.; Kong, W.; Lin, Z. Combined micro-scale and macro-scale modeling of the composite electrode of a solid oxide fuel cell. J. Power Sources 2010, 195, 6598–6610. [Google Scholar]
- Zhao, F.; Virkar, A.V. Dependence of polarization in anode-supported solid oxide fuel cells on various cell parameters. J. Power Sources 2005, 141, 79–95. [Google Scholar]
- Selleri, T.; Najafi, B.; Rinaldi, F.; Colombo, G. Mathematical modeling and multi-objective optimization of a mini-channel heat exchanger via genetic algorithm. J. Therm. Sci. Eng. Appl. 2013, 5. [Google Scholar] [CrossRef]

| Equations | Boundary | ACCL/channel interface | AFL/electrolyte interface | All others | ||
|---|---|---|---|---|---|---|
| Fuel transfer | BC type | gas molar concentration | (H2) inward molar flux | (H2O) inward molar flux | insulation | |
| BC | - | |||||
| Equations | Boundary | CSL/channel interface | CFL/electrolyte interface | All others | ||
| Air transfer | BC type | (O2) molar concentration | (N2) molar concentration | (O2) inward molar flux | (N2) inward molar flux | insulation |
| BC | 0 | - | ||||
| Equations | Boundary | Rib/CSL interface | Rib/ACCL interface | CFL/Electrolyte interface | AFL/Electrolyte interface | All others |
|---|---|---|---|---|---|---|
| Electronic transfer | BC Type | (φe,rib/CSL) Reference potential | (φe,rib/ACCL) Reference potential | Inward current flow | Inward current flow | Electric insulation |
| BC | Vop | E0 = 1.08 V | - | |||
| Ionic transfer | BC Type | - | - | Interior current source | Interior current source | Electric insulation |
| BC | - | - | - |
| Parameter | Value | Parameter | Value | |
|---|---|---|---|---|
| Temperature, T (°C) | 850 | Reaction symmetric factor for cathode, | 0.2, 0.8 | |
| Operation voltage, Vop (V) | 0.7 | Exchange transfer current density of cathode | 7 × 10−5 | |
| Tortuosity factor, τ | 4 | Activation energies for the anode, EH2(J mol−1) | 120 × 103 | |
| Fuel composition (molar fraction) at the anode/channel interface | CH4(%) | 10 | Reaction symmetric factor for anode, | 1, 0.5 |
| CO(%) | 8 | Exchange transfer current density of anode, | 8.0 × 10−4 | |
| CO2 (%) | 17 | The volumetric active surface area of Ni particles in AFL, (m2·m−3) | 1.05 × 106 | |
| H2O (%) | 5 | The volumetric active surface area of Ni particles in ACCL, ( m2·m−3) | 4.13 × 105 | |
| H2 (%) | 60 | Area specific contact resistance at the rib-anode interface, (Ω·cm2) | 0.01 | |
| Activation energies for the cathode, EO2 (J mol−1) | 130 × 103 | Area specific contact resistance at the rib-cathode interface, (Ω·cm2) | 0.01 | |
| Layer | rel(m) | ϕel | ε | Thickness (μm) | γ |
|---|---|---|---|---|---|
| ACCL | 1 ×10−6 | 0.5 | 0.45 | 45 | 1 |
| AFL | 0.5 × 10−6 | 0.5 | 0.3 | 10 | 1 |
| Electrolyte | - | - | - | 10 | 1 |
| CFL | 0.5 × 10−6 | 0.5 | 0.3 | 20 | 1 |
| CCCL | 1 × 10−6 | 1 | 0.45 | 500 | 1 |
| Title | νi ( m3 mol−1)[28] | μref ×106 (Pa·s) | Tref (K) | cref |
|---|---|---|---|---|
| H2 | 6.12 × 10−6 | 8.404 | 273 | 71 |
| H2O | 13.1 × 10−6 | 8.933 | 273 | 961 |
| CH4 | 2.514 × 10−5 | 10.198 | 273 | 164 |
| CO | 1.8 × 10−5 | 16.807 | 273 | 100 |
| CO2 | 2.67 × 10−5 | 13.807 | 273 | 254 |
| O2 | 16.3 × 10−6 | 19.20 | 273 | 125 |
| N2 | 18.5 × 10−6 | 16.606 | 273 | 104 |
| Model | dpitch (mm) | (mm) | (mm) |
|---|---|---|---|
| Cell-A | 2 | 0.5 | 1.0 |
| Cell-B | 2 | 1.5 | 1.0 |
| Cell-C | 2 | 1.0 | 0.5 |
| Cell-D | 2 | 1.0 | 1.5 |
| Vop (V) | 0.7 | 0.6 | 0.5 |
|---|---|---|---|
| The output current density of Cell-A (A·cm−2) | 0.5629 | 0.6944 | 0.8242 |
| The output current density of Cell-B (A·cm−2) | 0.4166 | 0.5099 | 0.5992 |
| The output current density of Cell-C (A·cm−2) | 0.5216 | 0.6585 | 0.7975 |
| The output current density of Cell-D (A·cm−2) | 0.4722 | 0.5575 | 0.6290 |
| Position | Pitch (mm) | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Anode side | Aan (mm) | 0.45 | 0.74 | 1.26 | 1.78 |
| Ban (mm·Ω−1·cm−2) | 7.1 | 7.6 | 4.8 | 3.9 | |
| Cathode side | Aca (mm) | 0.73 | 1.15 | 1.66 | 2.2 |
| Bca (mm·Ω−1·cm−2) | 7.9 | 7.8 | 7.2 | 6 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kong, W.; Gao, X.; Liu, S.; Su, S.; Chen, D. Optimization of the Interconnect Ribs for a Cathode-Supported Solid Oxide Fuel Cell. Energies 2014, 7, 295-313. https://doi.org/10.3390/en7010295
Kong W, Gao X, Liu S, Su S, Chen D. Optimization of the Interconnect Ribs for a Cathode-Supported Solid Oxide Fuel Cell. Energies. 2014; 7(1):295-313. https://doi.org/10.3390/en7010295
Chicago/Turabian StyleKong, Wei, Xiang Gao, Shixue Liu, Shichuan Su, and Daifen Chen. 2014. "Optimization of the Interconnect Ribs for a Cathode-Supported Solid Oxide Fuel Cell" Energies 7, no. 1: 295-313. https://doi.org/10.3390/en7010295
APA StyleKong, W., Gao, X., Liu, S., Su, S., & Chen, D. (2014). Optimization of the Interconnect Ribs for a Cathode-Supported Solid Oxide Fuel Cell. Energies, 7(1), 295-313. https://doi.org/10.3390/en7010295




