General and Simple Decision Method for DG Penetration Level in View of Voltage Regulation at Distribution Substation Transformers
Abstract
:1. Introduction
2. Impact of Distributed Generation (DG) on On-Load Tap Changer (OLTC) Operations
2.1. Representation of the Line Drop Compensation (LDC) Method of OLTC Transformer
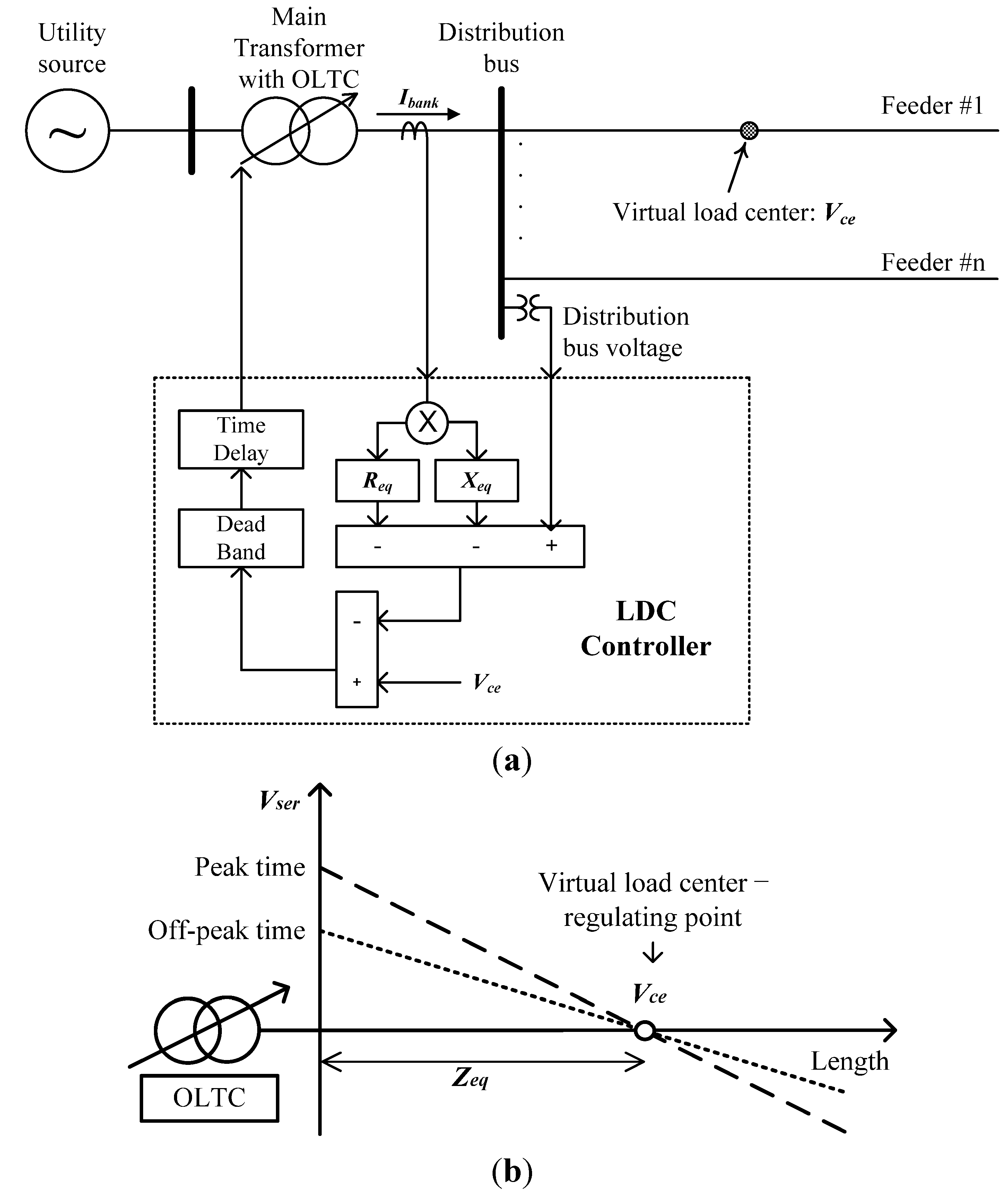
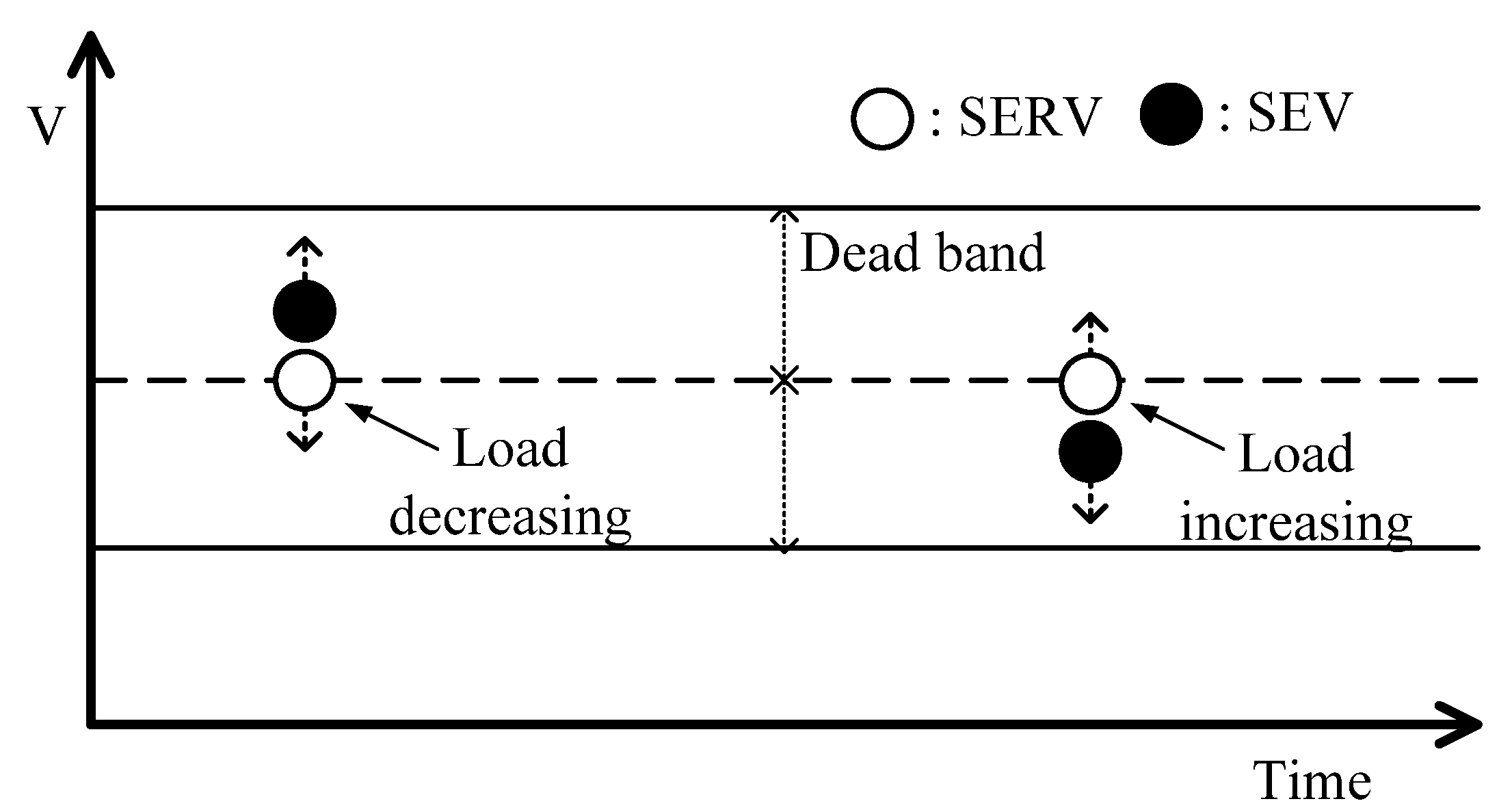
2.2. Impact of DG on LDC Control Method
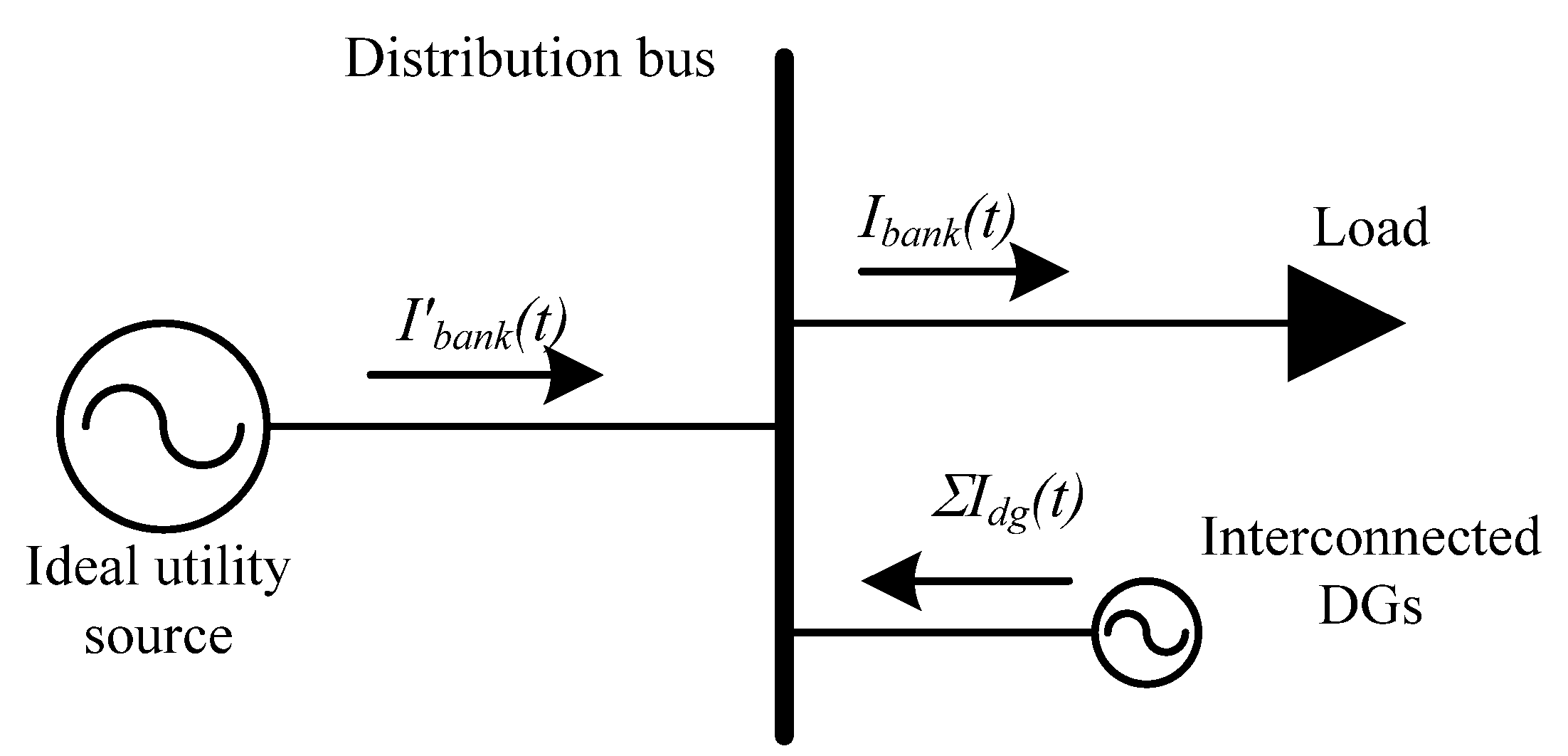
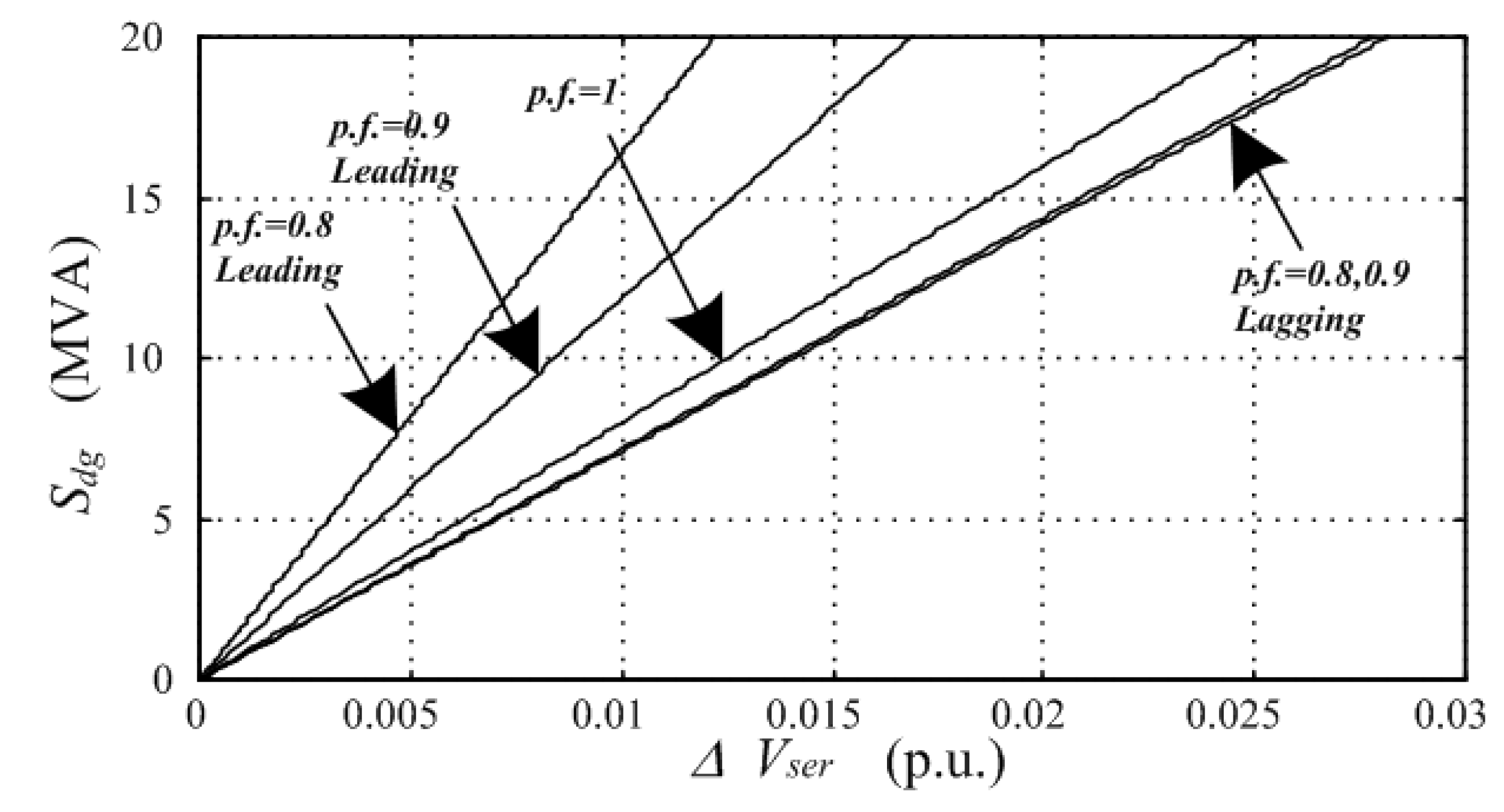
3. DG Penetration Limits in View of Voltage Regulation at Distribution Substation Transformer Level
3.1. Generalized Formulation
3.2. Further Simplification for Simplified Interconnection Process
4. Simple Rule in View of Voltage Regulation at Distribution Substation Transformer Level
4.1. General Approach
| Cases | Dead band (db) | % Rule |
|---|---|---|
| Case I | 1.00% | 20.0% |
| 1.25% | 25.0% | |
| 1.50% | 30.0% | |
| Case II | 1.00% | 27.3% |
| 1.25% | 34.1% | |
| 1.50% | 40.9% | |
| Case III | 1.00% | 28.6% |
| 1.25% | 35.7% | |
| 1.50% | 42.9% |
4.2. Simple Approach
4.3. Simplified Interconnection Process at Distribution Substation Transformer Level
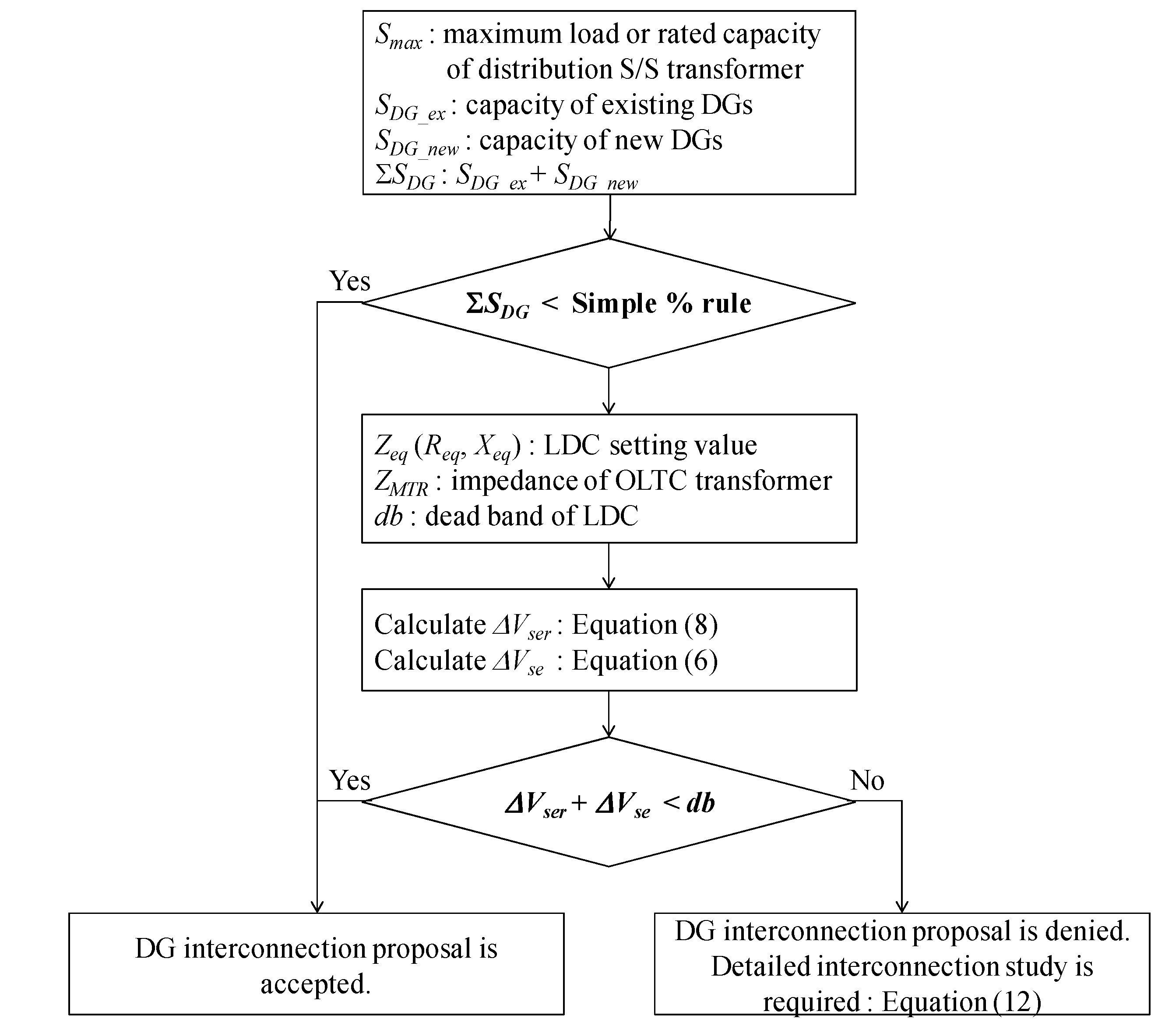
5. Conclusions
Conflicts of Interest
References
- Institute of Electrical and Electronics Engineers (IEEE). IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems; IEEE Press: New York, NY, USA, 2003. [Google Scholar]
- Kim, T.-E.; Kim, J.-E. A Method for Determining the Introduction Limit of Distributed Generation System in Distribution System. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Vancouver, BC, Canada, 15–19 July 2001; pp. 456–461.
- Bhowmik, A.; Maitra, A.; Halpin, S.M.; Schatz, J.E. Determination of allowable penetration levels of distributed generation resources based on harmonic limit considerations. IEEE Trans. Power Deliv. 2003, 18, 619–624. [Google Scholar] [CrossRef]
- Morren, J.; de Hann, S.W.H. Maximum Penetration Level of Distributed Generation without Voltage Limits. In Proceedings of the 20th International Conference and Exhibition on Electricity Distribution (CIRED 2009), Prague, Czech Republic, 8–11 June 2009.
- Thong, V.V.; Dommelen, D.V.; Belmans, R. Penetration Level of Distributed Energy Resources with Anti-Islanding Criteria and Secure Operation of Power System. In Proceedings of the IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006.
- Miller, N.; Ye, Z. Report on Distributed Generation Penetration Study; National Renewable Energy Laboratory: Golden, CO, USA, 2003.
- Ayres, H.M.; Freitas, W.; de Almeida, M.C.; da Silva, L.C.P. Method for determining the maximum allowable penetration level of distributed generation without steady-state voltage violations. IET Gener. Transm. Distrib. 2010, 4, 495–508. [Google Scholar] [CrossRef]
- California Energy Commission Rule 21 Working Group. California Electric Rule 21 Supplemental Review Guideline, California Distributed Energy Resource Guide; California Energy Commission: Sacramento, CA, USA, 2005.
- Federal Energy Regulatory Commission (FERC). Small Generator Interconnection Procedures (SGIP) and Small Generator Interconnection Agreement (SGIA); FERC: Washington, DC, USA, 2006.
- Interstate Renewable Energy Council (IREC). The Model Interconnection Standards and Procedures for Small Generator Facilities (IREC Procedures); IREC: Latham, NY, USA, 2006. [Google Scholar]
- National Association of Regulatory Utility Commissioners (NARUC). Small Generation Resource Interconnection Procedures (NARUC Procedures); NARUC: Washington, DC, USA, 2008. [Google Scholar]
- Bundesverband der Energie- und Wasserwirtschaft (BDEW). Generating Plants Connected to the Medium-Voltage Network; BDEW: Berlin, Germany, 2008. [Google Scholar]
- Katiraei, F.; Agüero, J.R. Solar PV integration challenges. IEEE Power Energy Mag. 2011, 9, 62–71. [Google Scholar] [CrossRef]
- Calovic, M.-S. Modeling and analysis of under load tap changing transformer control system. IEEE Trans. Power Appar. Syst. 1984, 107, 1909–1915. [Google Scholar] [CrossRef]
- Choi, J.-H.; Kim, J.-C. Advanced voltage regulation method of power distribution systems interconnected with dispersed storage and generation systems. IEEE Trans. Power Deliv. 2001, 16, 329–334. [Google Scholar] [CrossRef]
- Choi, J.-H.; Moon, S.-I. The dead band control of LTC transformer at distribution substation. IEEE Trans. Power Syst. 2009, 24, 319–326. [Google Scholar] [CrossRef]
- Choi, J.-H. Operation and Integration Strategies of Dispersed Generations in Power Distribution System. Ph.D. Thesis, Soongsil University, Seoul, Korea, 2001. [Google Scholar]
- Korea Electric Power Company. A Study on the New Technical Guidelines for Interconnection Capacity of Distributed Generations in Distribution System (Korean); Korea Electric Power Research Institute (KEPRI): Deajeon, Korea, 2011. [Google Scholar]
- Choi, J.-H.; Kim, J.-C. The online voltage control of ULTC transformer for distribution voltage regulation. Int. J. Electr. Power Energy Syst. 2001, 23, 91–98. [Google Scholar] [CrossRef]
- Choi, J.-H.; Jung, W.-W.; Song, I.-K. Interconnection Guidelines and Control Coordination Reactive Power Support Functions of Distributed Energy Resources. In Proceedings of the 21th International Conference on Electricity Distribution (CIRED), Frankfurt, Germany, 6–9 June 2011.
- Zhang, B.S.; Lam, A.Y.S.; Dominguez-Garcia, A.; Tse, D. Optimal Distributed Voltage Regulation in Power Distribution Networks. Cornell University Library Web Page. Available online: http://arxiv.org/abs/1204.5226v1 (accessed on 23 April 2012).
- Tedesco, F.; Casavola, A. A Distributed Command Governor Approach for Voltage Regulation in Medium Voltage Power Grids with Distributed Generation. In Proceedings of the 2013 American Control Conference (ACC), Washington, DC, USA, 17–19 June 2013.
- Choi, J.-H.; Ahn, S.-J.; Jung, W.-W.; Chu, C.-M.; Song, I.-K. Technical Solution/Recommendations for Large Penetration of DGs in KEPCO Distribution Network. In Proceedings of the International Conference on Electricity Distribution (CIRED), Lisbon, Portugal, 29–30 May 2012.
- Calderaro, V.; Galdi, V.; Piccolo, A.; Massa, G. Optimal Fuzzy Controller for Voltage Control in Distribution Systems. In Proceedings of the 11th International Conference on Intelligent Systems Design and Applications (ISDA), Cordoba, Argentina, 22–24 November 2011; pp. 1282–1287.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Song, I.-K.; Jung, W.-W.; Chu, C.-M.; Cho, S.-S.; Kang, H.-K.; Choi, J.-H. General and Simple Decision Method for DG Penetration Level in View of Voltage Regulation at Distribution Substation Transformers. Energies 2013, 6, 4786-4798. https://doi.org/10.3390/en6094786
Song I-K, Jung W-W, Chu C-M, Cho S-S, Kang H-K, Choi J-H. General and Simple Decision Method for DG Penetration Level in View of Voltage Regulation at Distribution Substation Transformers. Energies. 2013; 6(9):4786-4798. https://doi.org/10.3390/en6094786
Chicago/Turabian StyleSong, Il-Keun, Won-Wook Jung, Chul-Min Chu, Seong-Soo Cho, Hyun-Koo Kang, and Joon-Ho Choi. 2013. "General and Simple Decision Method for DG Penetration Level in View of Voltage Regulation at Distribution Substation Transformers" Energies 6, no. 9: 4786-4798. https://doi.org/10.3390/en6094786
APA StyleSong, I.-K., Jung, W.-W., Chu, C.-M., Cho, S.-S., Kang, H.-K., & Choi, J.-H. (2013). General and Simple Decision Method for DG Penetration Level in View of Voltage Regulation at Distribution Substation Transformers. Energies, 6(9), 4786-4798. https://doi.org/10.3390/en6094786





