An Insight into the Effect of Advanced Injection Strategies on Pollutant Emissions of a Heavy-Duty Diesel Engine
Abstract
:1. Introduction

2. The Numerical Model
2.1. The Engine Specification and the Computing Mesh
| Engine type | Units | Caterpillar 3406 |
|---|---|---|
| Bore × Stroke | mm | 137.2 × 165.1 |
| Compression ratio | - | 15.1:1 |
| Displacement | l | 2.44 |
| Connecting rod length | mm | 261.62 |
| Squish clearance | mm | 4.16 |
| IVO/IVC | - | −32° ATDC/−147° After top dead center (ATDC) |
| EVO/EVC | - | 128° ATDC/29° ATDC |
| Intake manifold air pressure—IMAP | kPa/rpm | 184/1600 |
| Intake manifold air temperature—IMAT | K | 310 |
| Engine speed | rpm | 1600 |
| Peak torque | Nm/rpm | 1972/1200 |
| Peak power | kW/rpm | 265/1700 |
| Piston shape (Bowl in piston) | - | Mexican hat style |
| Fuel fed | Units | Common rail |
|---|---|---|
| Injection pressure | MPa | Up to 120 MPa |
| Number of nozzle holes | - | 6 |
| Nozzle hole diameter | mm | 0.259 |
| Start of injection | - | 9 Before top dead center (BTDC) |
| Injection duration | - | 21.5 crank angle (CA) |
| Fuel injected | g/cycle | 0.1622 (at full load) |
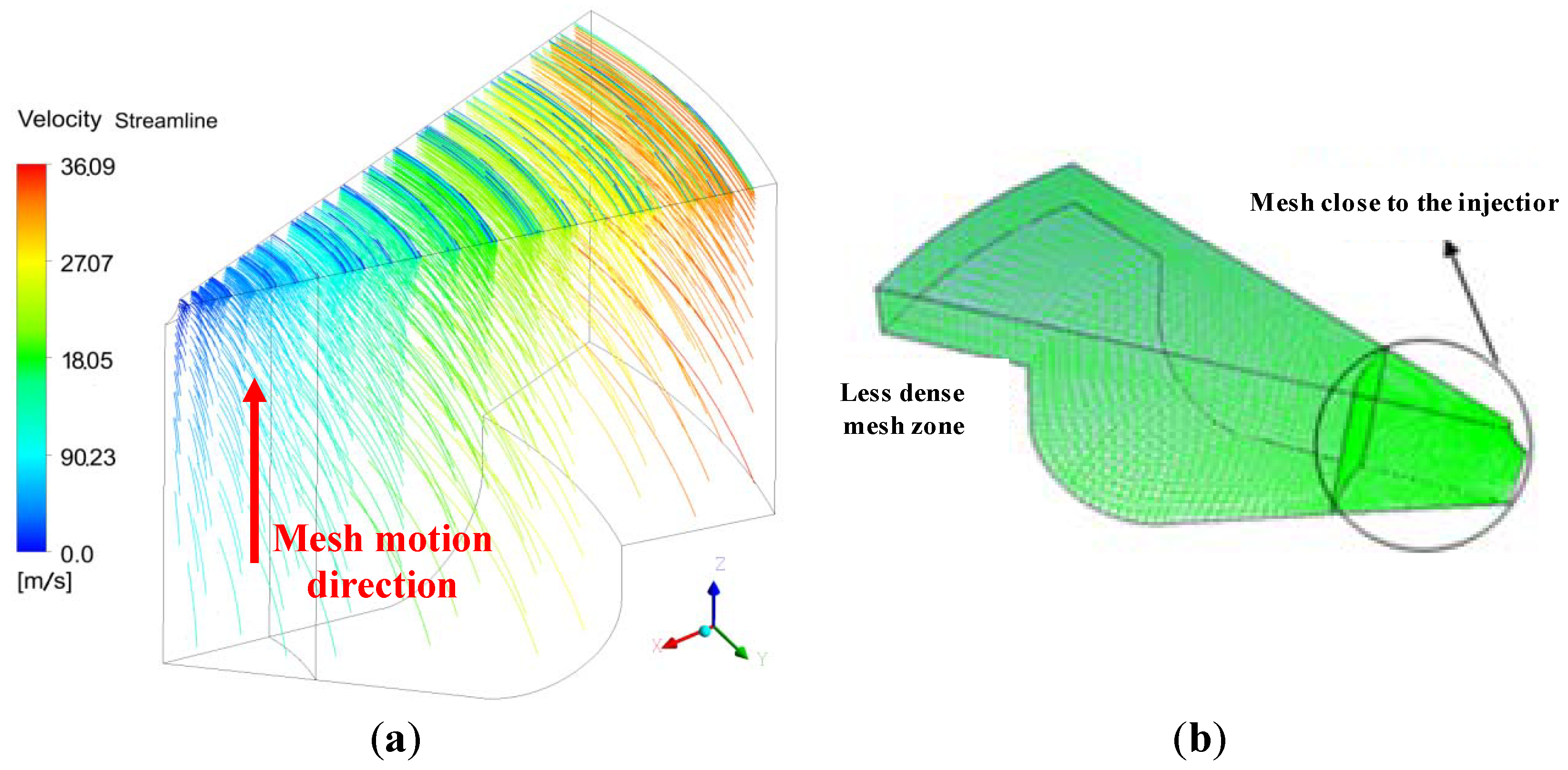
2.2. The Turbulent Combustion Model
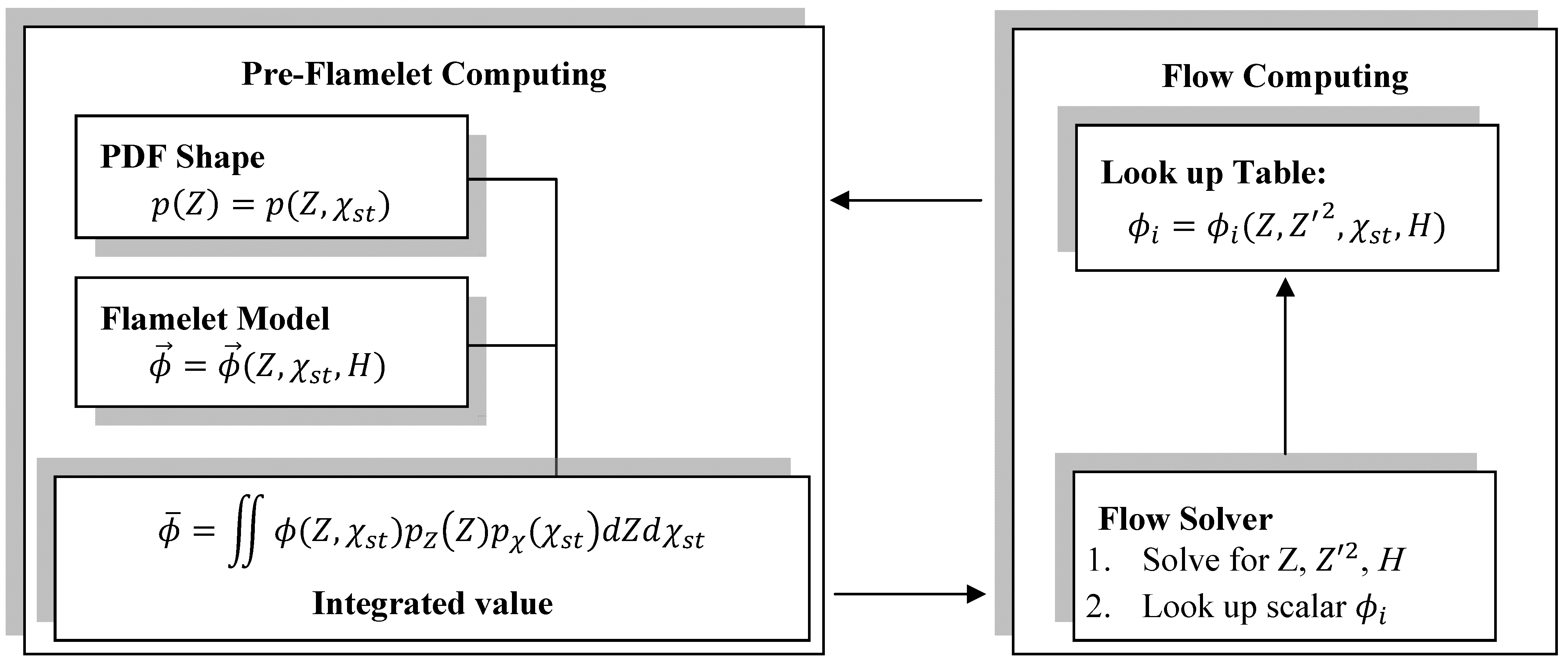
2.3. The Spray Model
2.4. The Pollutant Emission Models
| Constant | Values | Function |
|---|---|---|
| 54 s−1 | Model constant for soot inception rate | |
| 21.000 K | Activation temperature of soot inception | |
| 1 | Model constant for coagulation rate | |
| 11.700 kg m kmol−1 s−1 | Surface growth rate scaling factor | |
| 12.100 K | Activation temperature of surface growth rate | |
| 105.812 kg m kmol−1 s−1 K−1/2 | Oxidation model constant | |
| 0.04 | Collisional efficiency parameter | |
| 0.015 | Oxidation rate scaling parameter |
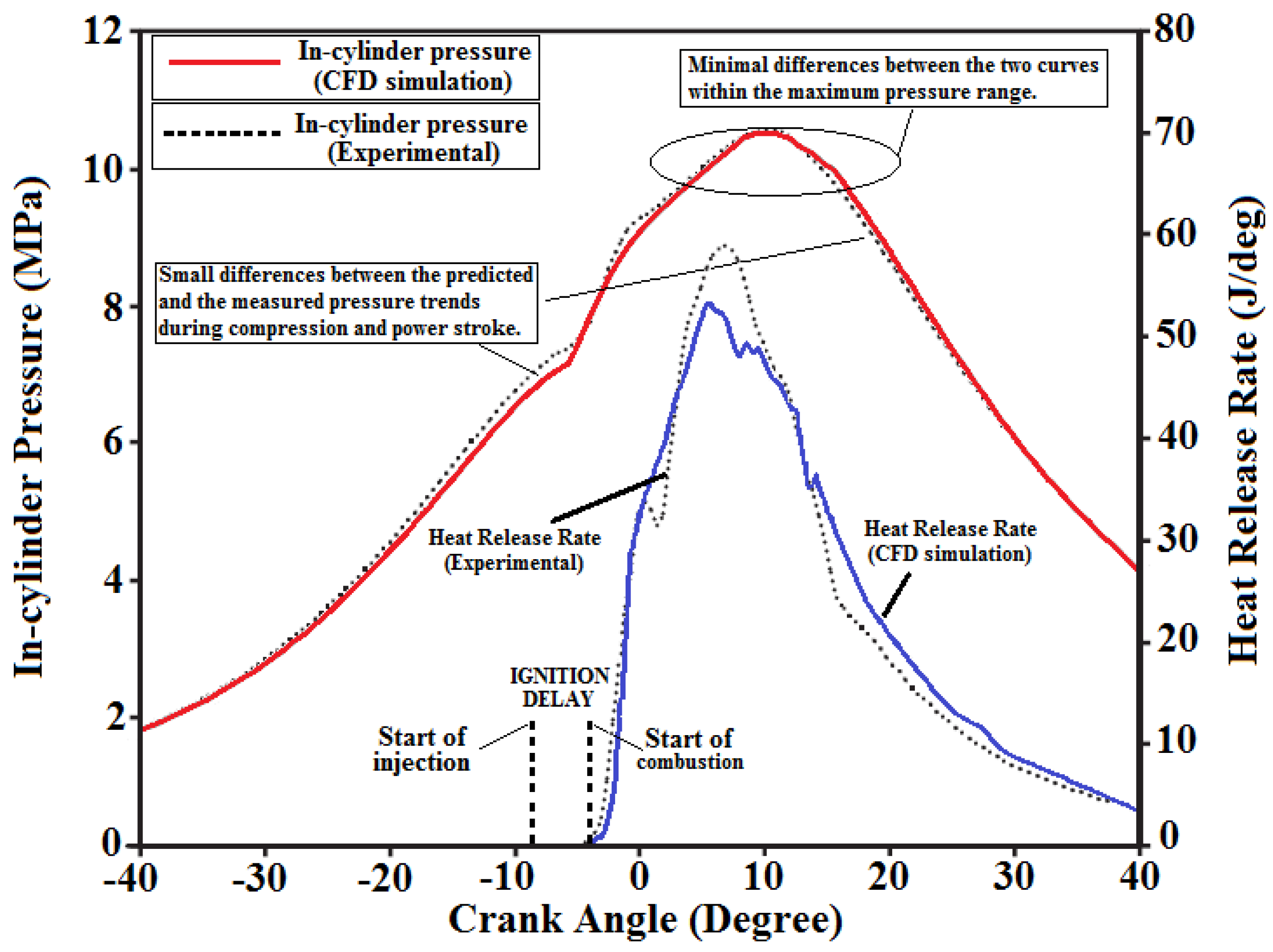
3. The Numerical Validation: The Single Injection Case

4. The Investigated Cases for Multiple Injection Strategies

| - | First strategy: main split into 2 injections | |||
| - | Scheme 1 | Scheme 2 | Scheme 3 | |
| n. of simulations | 4 | 4 | 4 | |
| - | Second strategy: main split into 3 injections | |||
| - | Scheme 1 | Scheme 2 | Scheme 3 | |
| n. of simulations | 4 | 4 | 4 | |
| - | EGR (%) | |||
| - | 10 | 20 | ||
| - | Total number of cases: 48 | |||
5. Results and Discussions
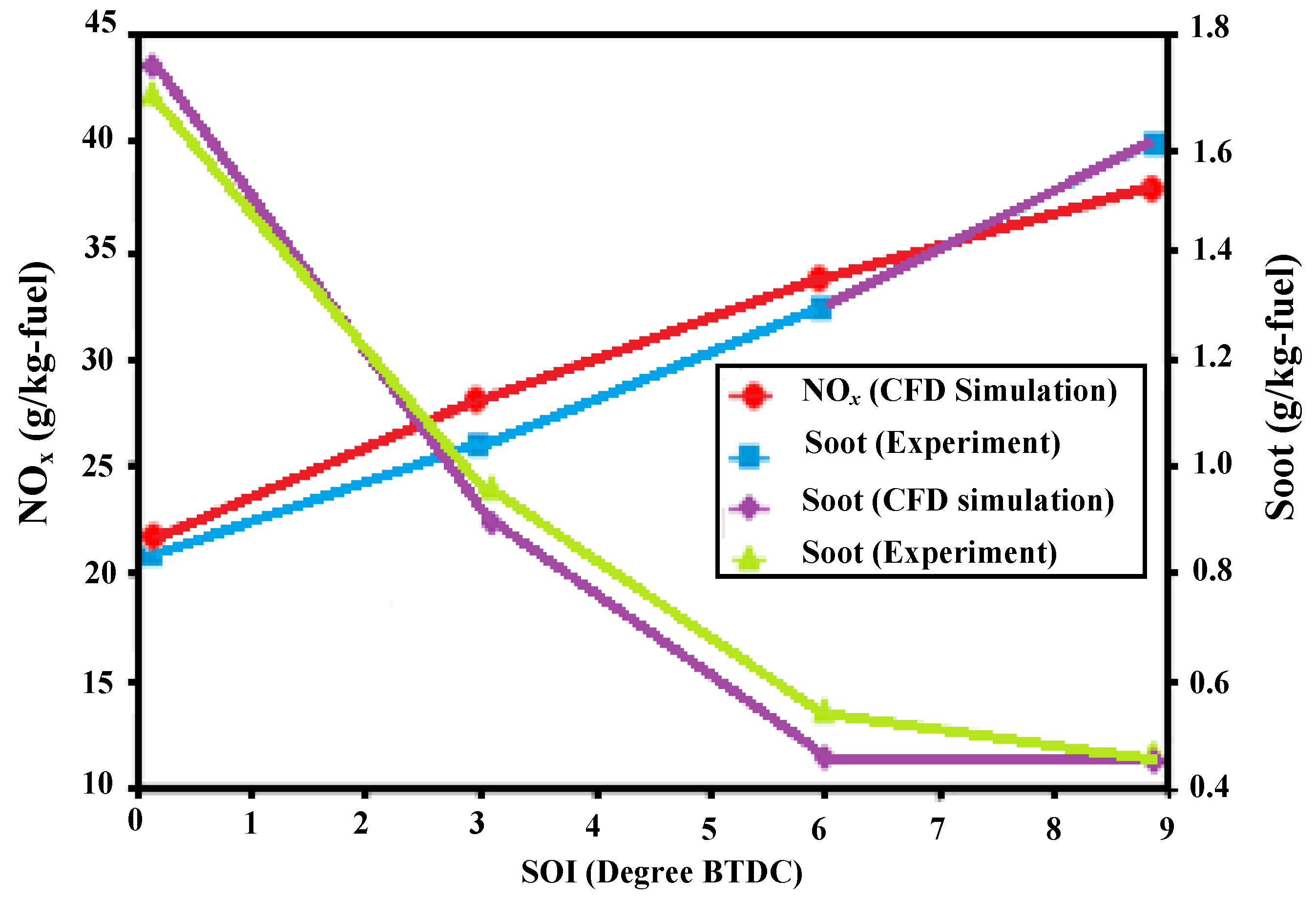
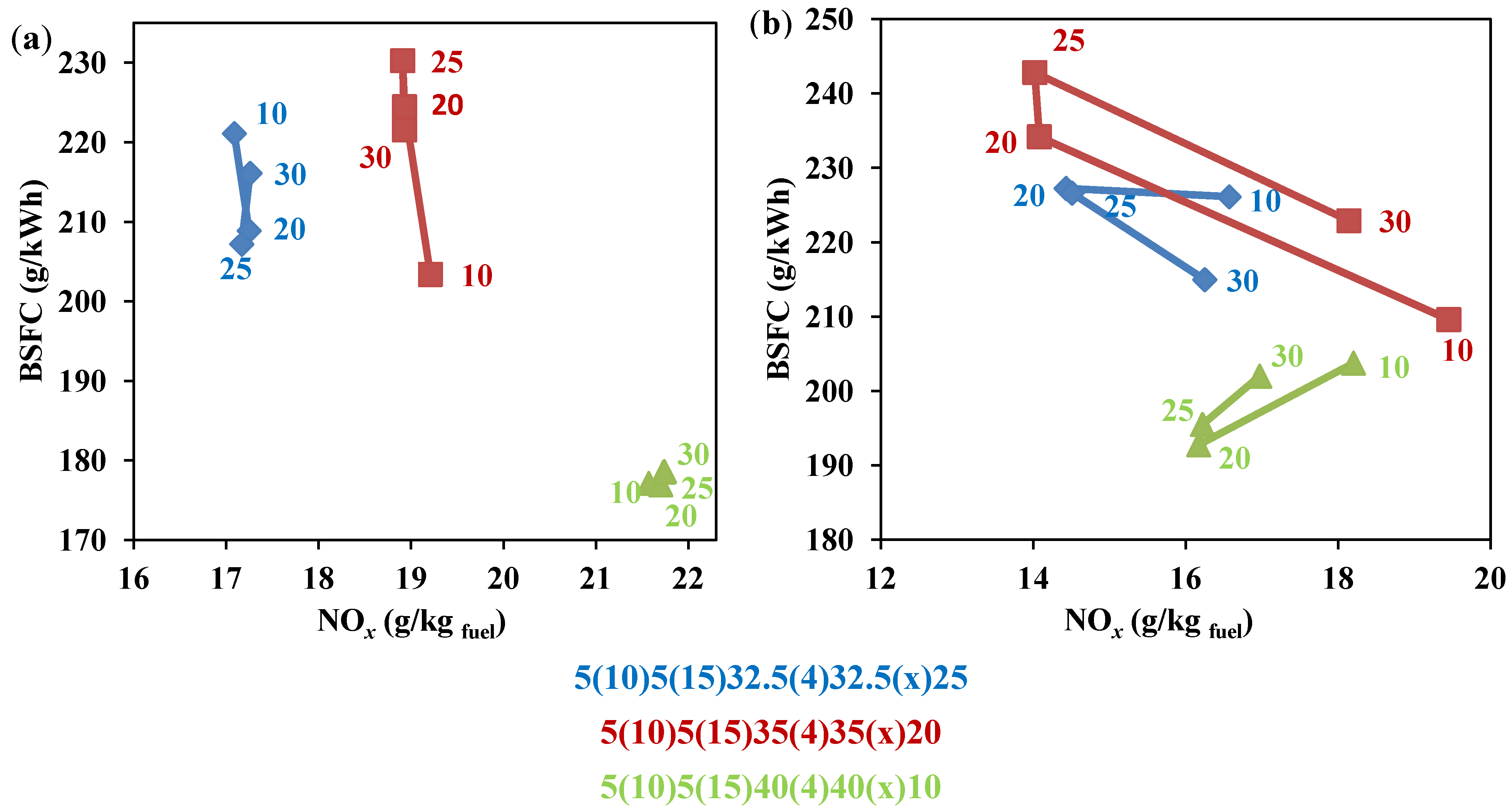
5.1. The First Multiple Injection Strategy: Splitting the Main into Two Injections


- NOx abatement for EGR increasing;
- minimal impact of the main combustion on soot production;
- maximization of the soot oxidation due to the combustion of an optimized percentage of fuel during the power stroke.
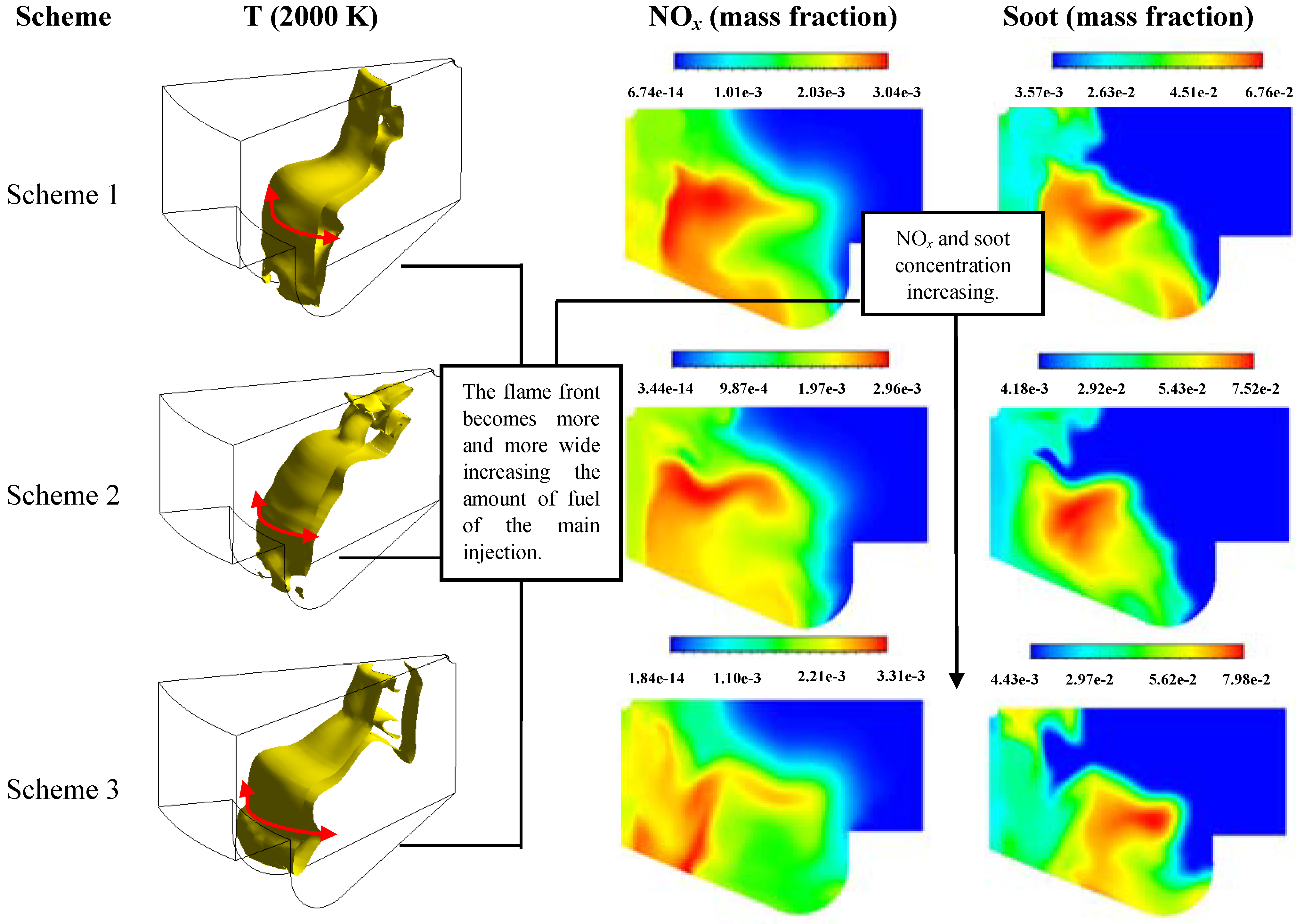
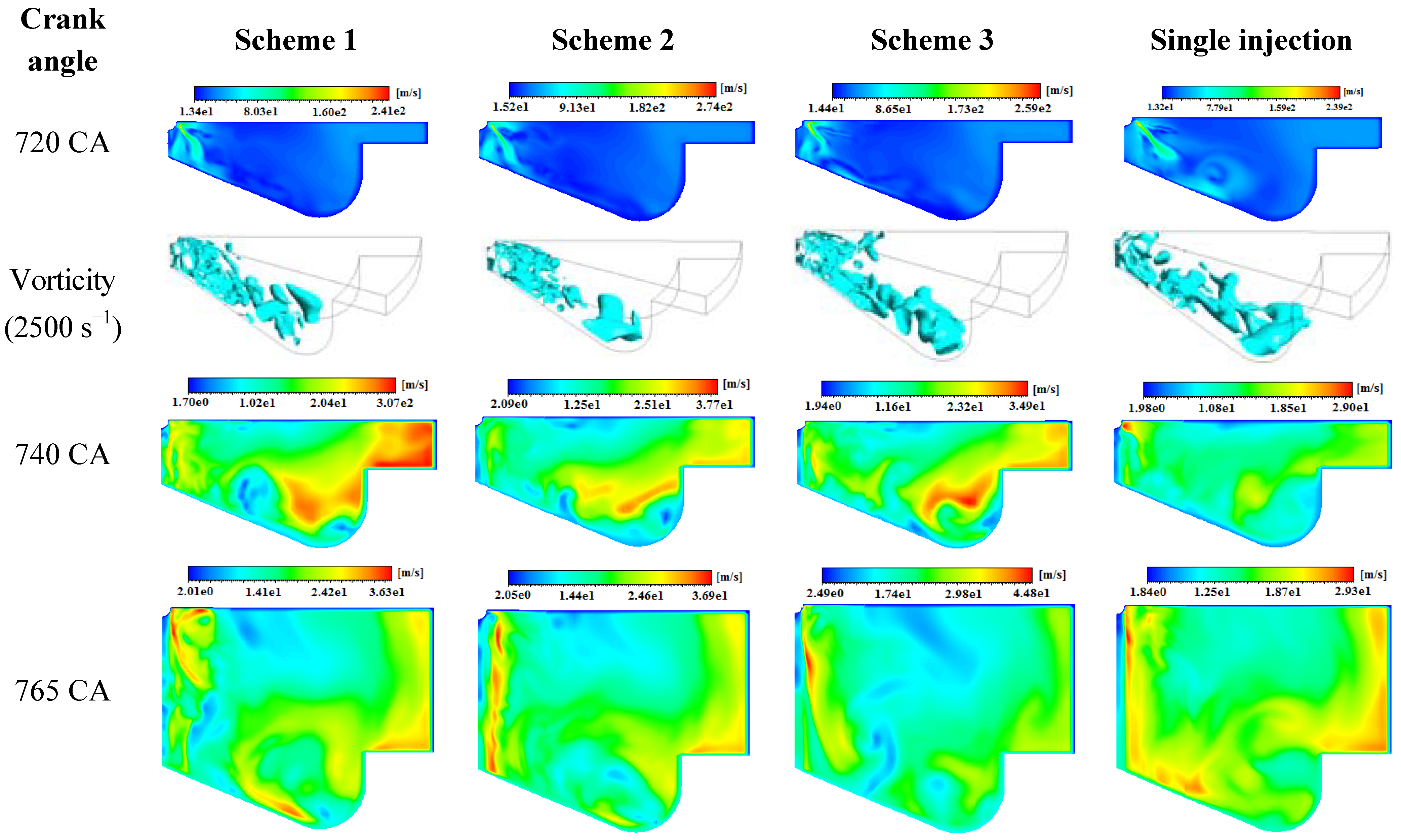
A Fluid Dynamic Overview
5.2. The Second Multiple Injection Strategy: Splitting the Main into Three Injections

| Pollutant emission | 5(10)5(15)21.6(4)21.6(4)21.6(10)25 | 5(10)5(15)23.3(4)23.3(4)23.3(10)20 | Single Injection |
|---|---|---|---|
| % EGR | 20 | 20 | 10 |
| NOx (g/kgfuel) | 14.78 | 15.29 | 21.30 |
| NOx reduction (%) | −30.61% | −28.21% | - |
| Soot (g/kgfuel) | 0.27 | 0.29 | 0.93 |
| Soot reduction (%) | −70.96% | −68.81% | - |
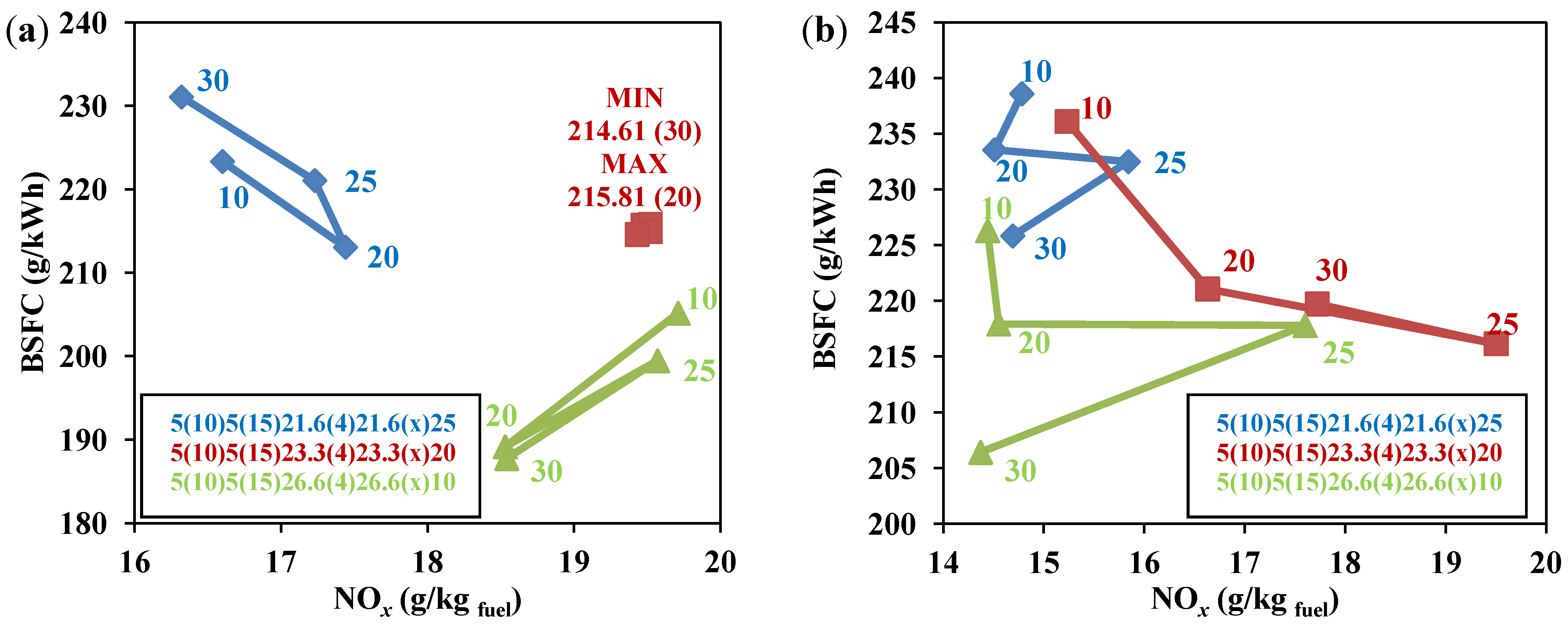
An Insight about Post Injection Pulse
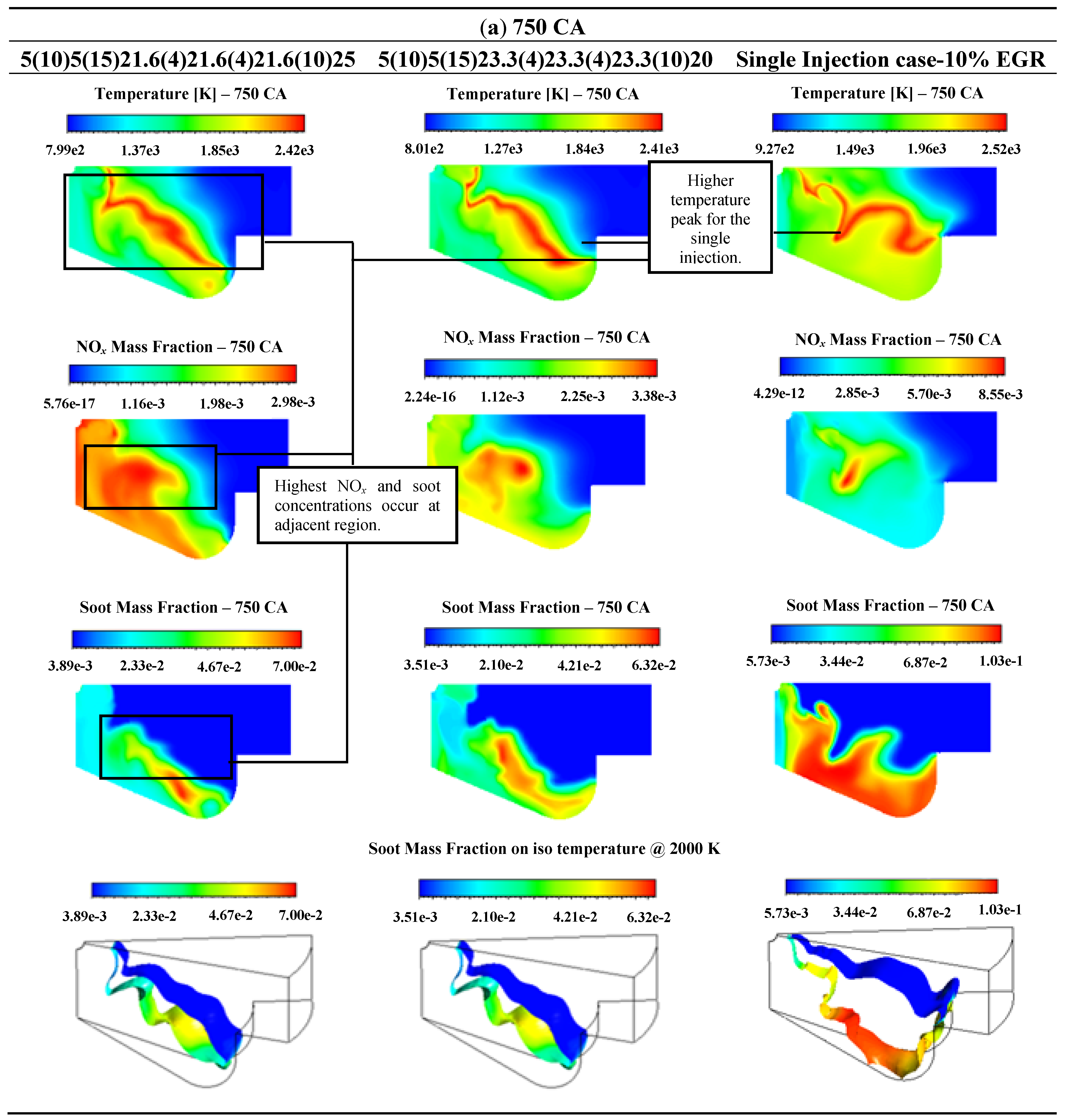
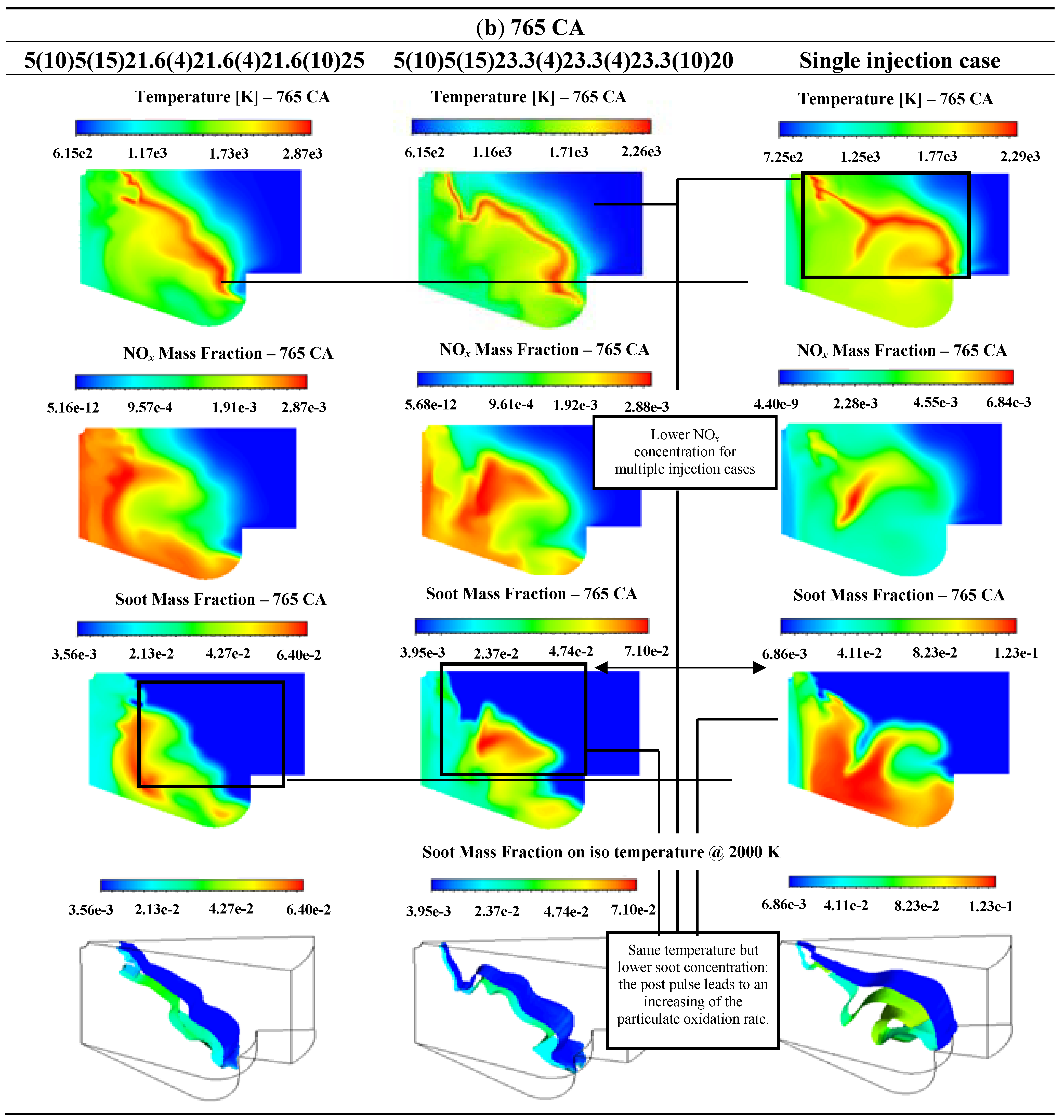
6. Conclusions
Acknowledgment
References
- Ferrari, G. Motori a Combustione Interna; [in Italian]; Il Capitello: Rome, Italy, 2008; pp. 482–532. [Google Scholar]
- Brijesh, P.; Sreedhara, S. Exhaust emissions and its control methods in compression ignition engines: A review. Int. J. Automot. Technol. 2013, 14, 195–206. [Google Scholar] [CrossRef]
- Mendez, S.; Thirouard, B. Using multiple injection strategies in diesel combustion: Potential to improve emissions, noise and fuel economy trade-off in low CR engines. SAE Int. J. Fuels Lubr. 2009, 1, 662–674. [Google Scholar]
- Gan, S.; Ng, H.K.; Pang, K.M. Homogeneous charge compression ignition (HCCI) combustion: Implementation and effects on pollutants in direct injection diesel engines. Appl. Energy 2011, 88, 559–567. [Google Scholar] [CrossRef]
- Tree, D.R.; Svensson, K.I. Soot processes in compression ignition engines. Prog. Energy Combust. Sci. 2007, 33, 272–309. [Google Scholar] [CrossRef]
- Shundoh, S.; Komori, M.; Tsujimura, K.; Kobayashi, S. NOx reduction from diesel combustion using pilot injection with high pressure fuel injection. SAE Spec. Publ. 1992, 895, 25–36. [Google Scholar]
- Takeda, Y.; Keiichi, N.; Keiichi, N. Emission Characteristics of Premixed Lean Diesel Combustion with Extremely Early Staged Fuel Injection. In Proceedings of International Fuels & Lubricants Meeting & Exposition, Dearborn, MI, USA, 6–8 May 1996.
- Choi, W.; Choi, B.C.; Park, H.K.; Joo, K.J.; Lee, J.H. In-Cylinder Flow Field Analysis of a Single Cylinder DI Diesel Engine Using PIV and CFD; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Arcoumanis, C.; Bicen, A.F.; Whitelaw, J.H. Squish and swirl-squish interaction in motored model engines. J. Fluids Eng. 1983, 105, 105–112. [Google Scholar] [CrossRef]
- Baritaud, T. Multi-Dimensional Simulation of Engine Internal Flow, 1st ed.; Editions Technip: Rueil-Malmaison, France, 1998; pp. 234–237. [Google Scholar]
- Xi, J.; Zhong, B.J. Reduced kinetic mechanism of n-heptane oxidation in modeling polycyclic aromatic hydrocarbon formation in diesel combustion. Chem. Eng. Technol. 2006, 29, 1461–1468. [Google Scholar] [CrossRef]
- Kong, S.C.; Han, Z.Y.; Reitz, R.D. The development and application of a diesel ignition and combustion model for multidimensional engine simulation. SAE Trans. 1995, 104, 502–508. [Google Scholar]
- Reitz, R.D. Mechanism of atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the Effect of Drop Drag and Breakup on Fuel Sprays; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1993. [Google Scholar]
- Cipolat, D. Analysis of energy release and NOx emissions of a CI engine fuelled on diesel and DME. Appl. Therm. Eng. 2007, 27, 2095–2103. [Google Scholar] [CrossRef]
- Jafarmadar, S.; Hosenzadeh, M.B. Improvement of emissions and performance by using of air jet, EGR and insulation methods in a DI diesel engine. Therm. Sci. 2013, 17, 57–70. [Google Scholar] [CrossRef]
- Ansys Fluent 12.0 Theory Guide. 2009. Available online: https://www.sharcnet.ca/Software/Fluent12/html/ug/node676.htm (accessed on 16 January 2013).
- Mobasheri, R.; Peng, Z.; Mirsalim, S.M. Analysis the effect of advanced injection strategies on engine performance and pollutant emissions in a heavy duty DI-diesel engine by CFD modeling. Int. J. Heat Fluid Flow 2012, 33, 59–69. [Google Scholar] [CrossRef]
- Hentschel, W.; Ritcher, J. Time-Resolved Analysis of Soot Formation and Oxidation in a Directed-Injection Diesel Engine for Different EGR Rates by an Extinction Method; SAE Technical Papers; SAE International: Warrendale, PA, USA, 1995. [Google Scholar]
- Zheng, M.; Reader, G.T.; Hawley, J.G. Diesel engine exhaust gas recirculation—A review on advanced and novel concept. Energy Convers. Manag. 2004, 45, 883–900. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Meloni, R.; Naso, V. An Insight into the Effect of Advanced Injection Strategies on Pollutant Emissions of a Heavy-Duty Diesel Engine. Energies 2013, 6, 4331-4351. https://doi.org/10.3390/en6094331
Meloni R, Naso V. An Insight into the Effect of Advanced Injection Strategies on Pollutant Emissions of a Heavy-Duty Diesel Engine. Energies. 2013; 6(9):4331-4351. https://doi.org/10.3390/en6094331
Chicago/Turabian StyleMeloni, Roberto, and Vincenzo Naso. 2013. "An Insight into the Effect of Advanced Injection Strategies on Pollutant Emissions of a Heavy-Duty Diesel Engine" Energies 6, no. 9: 4331-4351. https://doi.org/10.3390/en6094331
APA StyleMeloni, R., & Naso, V. (2013). An Insight into the Effect of Advanced Injection Strategies on Pollutant Emissions of a Heavy-Duty Diesel Engine. Energies, 6(9), 4331-4351. https://doi.org/10.3390/en6094331




