PSO was inspired by the social behavior of biological organisms, especially the ability of the groups of some species of animals to work as a whole in locating desirable positions in a given area, e.g., birds flocking to a food source. In PSO, such social behavior is modeled as an optimization algorithm that guides a population of particles moving towards the most promising area of the search space. These particles are called the swarm. Unlike in the other evolutionary computation techniques, each particle in PSO is also associated with a velocity that is dynamically adjusted according to the historical behaviors of the particle. Hence, the particle’s position is changed according to its own behavior and that of its neighbors. Therefore, the particles have a tendency to move towards a suitable search area over the course of the search process.
Particle Swarm Optimization for Constrained Engineering Design Problems
The particle swarm algorithm was first introduced by Eberhart and Kennedy [
17]. The motivation behind the algorithm was the intelligent collective behavior of organisms in a swarm (e.g., a flock of migrating birds) because the behavior of a single organism in the swarm may be totally inefficient. PSO was first designed to simulate birds seeking food, which is defined as a “cornfield vector”. Similar to other evolutionary algorithms, PSO can solve a variety of hard optimization problems but with a faster convergence rate [
26]. Another advantage is that it requires only a few parameters to be tuned, making it attractive from an implementation viewpoint. Standard PSO is usually applied to solve unconstrained optimization problems. In this paper, the standard PSO algorithm is extended to solve constrained mechanical design optimization problems using methods that preserve a feasible population. PSO algorithms have also been applied to constrained optimization problems. For example, a bird finds food through social cooperation with other birds around it (within its neighborhood). PSO was then expanded to a multidimensional search. If the search space is
d dimensional, the
ith particle of the swarm can be represented by a
d dimensional vector
x. The velocity of this particle can be represesented by another
d dimensional vector
v. The original PSO algorithm is described below:
where the index
i represents the number of particles in the population and the index
d represents the dimension of the solution;
xi and
vi are the current position and velocity of the
ith particle, respectively;
c1 and
c2 are learning factors and are the social and cognitive components, respectively; and
R1 and
R2 are two random numbers between [0,1];
w is the inertial weight factor, and shows the effect of previous velocity vector on the new vector. Equation (1) calculates a new velocity
(vi+1) for each particle based on its previous velocity, the best location it has achieved (p
best) so far, and the global best location (g
best) the population has achieved. Equation (2) provides the particle’s updated position in the search space.
Many researchers have expanded on the original idea with alterations ranging from minor parameter adjustments to complete a reworking of the algorithm. Others have used PSO to compare other global optimization algorithms, including genetic algorithms and differential evolution.
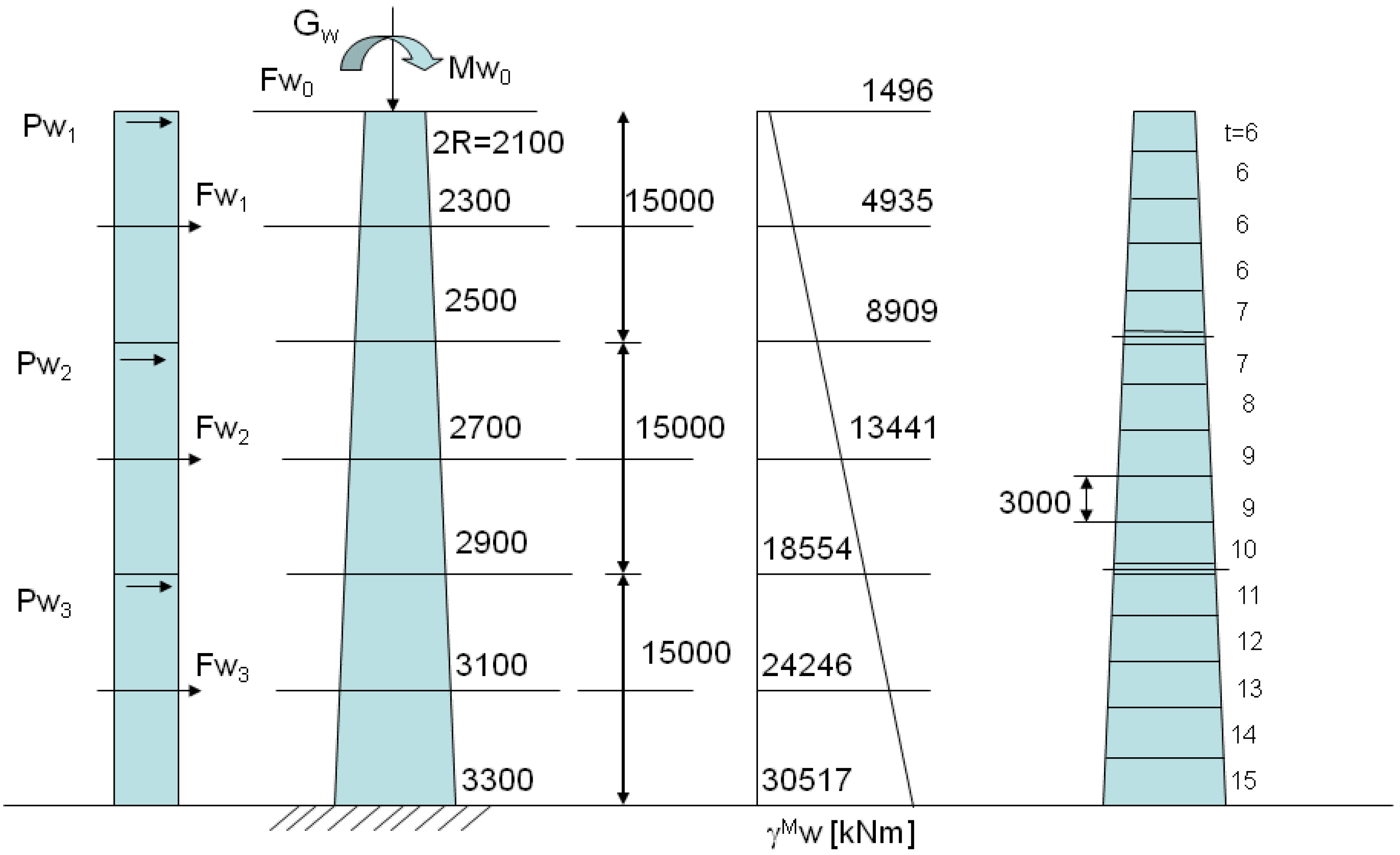
In the last few decades, great attention has been paid to structural optimization because raw material consumption is one of the most important factors that influence building construction. Material cost increases are offset entirely by the reduction of the use of that material due to the material being stronger and therefore less of the material being required. Additionally, as structures become larger such as wind turbine tower, production, transportation and installation costs will also rise. Because of the increasing demand for high-performance and low-cost structures, designers prefer to minimize the volume or the weight of the structure by optimization.
Many researchers have been working to find a technique to maintain a feasible population. There are a number of techniques proposed to handle constrained optimization problems. One of them is a technique called “fly back mechanism” and is proposed by He
et al. [
26]. This technique maintains a feasible population by incorporating a well-known basic PSO algorithm for solving structural optimization problems. PSO algorithms based on this technique are more reliable when compared with other algorithms based on penalty functions. According to this technique, the particles are initialized in a feasible search space. When the particles fly in feasible space to search for the solution, if any particle passes into infeasible space, it returns to a previous feasible position by flying back. Thus, a solution in feasible space will be guaranteed. Because the particle is most likely close to the boundary, the particle swarm optimization algorithm, improved by using a fly-back mechanism, has the important advantage of finding the global minimum faster than other algorithms for constrained structural optimization problems.
According to He
et al. [
26], regarding the proposed constraint handling technique, the improved particle swarm optimization with fly-back mechanism requires a feasible initial population to guarantee that the solution of successive generations are feasible. To generate a feasible initial population, an extra loop at the beginning of the algorithm is required to keep randomly re-initializing infeasible particles to ensure that they stay inside the feasible search space. General experience indicates that this is simple method is sufficiently good most mechanical and structural design problems since their feasible search spaces are usually large and feasible particles can be easily generated. Small size populations are preferred to minimize the time to find a feasible initial population. When examining all results presented in [
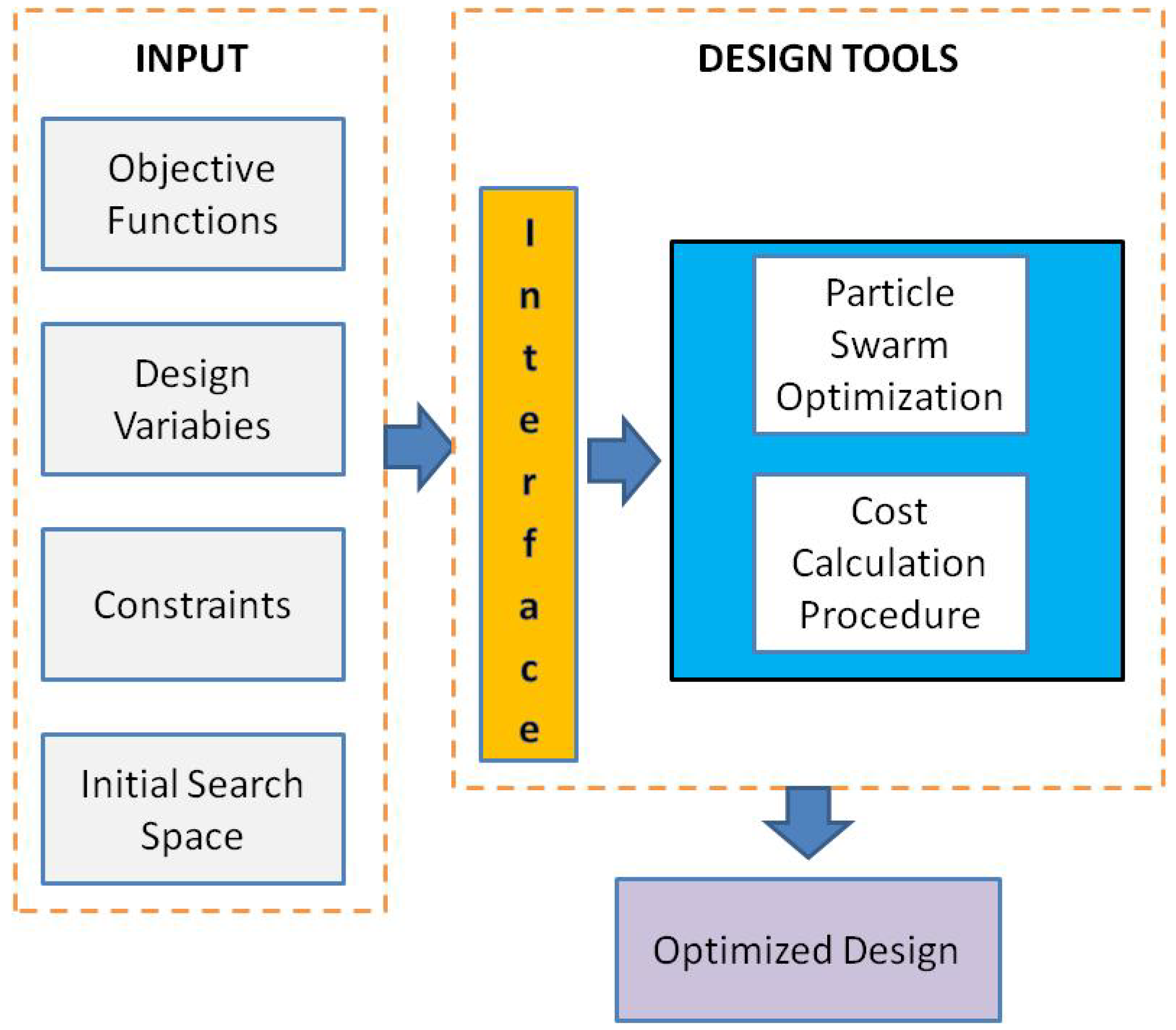
26] it can be seen that the optimization results by the particle swarm optimization algorithm with fly-back mechanism are better or equal to other existing methods such as Genetic algorithm, Genetic search technique, Runarsson stochastic ranking method. However, a more important drawback of this technique is the requirement of an all-feasible initial population. This may be a disadvantage when dealing with problems with a very small feasible region. The “fly-back” mechanism keeps particles from flying out of the feasible region by discarding those flights which generate infeasible solutions. Since a large number of the particles' flying behaviors are wasted, due to searching outside the boundary in the complex structure optimization problem, iteration number may rise and time cost may increase. In this study, the particle swarm optimization algorithm with fly-back mechanism is used for the cost minimization of wind turbine towers. The particle swarm optimization algorithm can be described using the general flowchart given in
Figure 1.
Figure 1.
The flowchart of the particle swarm optimization.
Figure 1.
The flowchart of the particle swarm optimization.