EMS-Data-Based Load Modeling to Evaluate the Effect of Conservation Voltage Reduction at a National Level
Abstract
:1. Introduction
2. Linearized Load Modeling Based on EMS Data
- ;
- : Active power consumption of the load before the kth conservation voltage reduction;
- : Active power consumption of the load after the kth conservation voltage reduction;
- : Terminal voltage before the kth conservation voltage reduction;
- : Terminal voltage after the kth conservation voltage reduction;
- : Constant impedance fraction of the active power consumption;
- : Constant current fraction of the active power consumption;
- : Constant power fraction of the active power consumption.
- ;
- : Reactive power consumption of the load before the kth conservation voltage reduction;
- : Reactive power consumption of the load after the kth conservation voltage reduction;
- : Constant impedance fraction of the reactive power consumption;
- : Constant current fraction of the reactive power consumption;
- : Constant power fraction of the reactive power consumption.
- : Normalized active power consumption;
- : Normalized reactive power consumption;
- : Normalized terminal voltage.
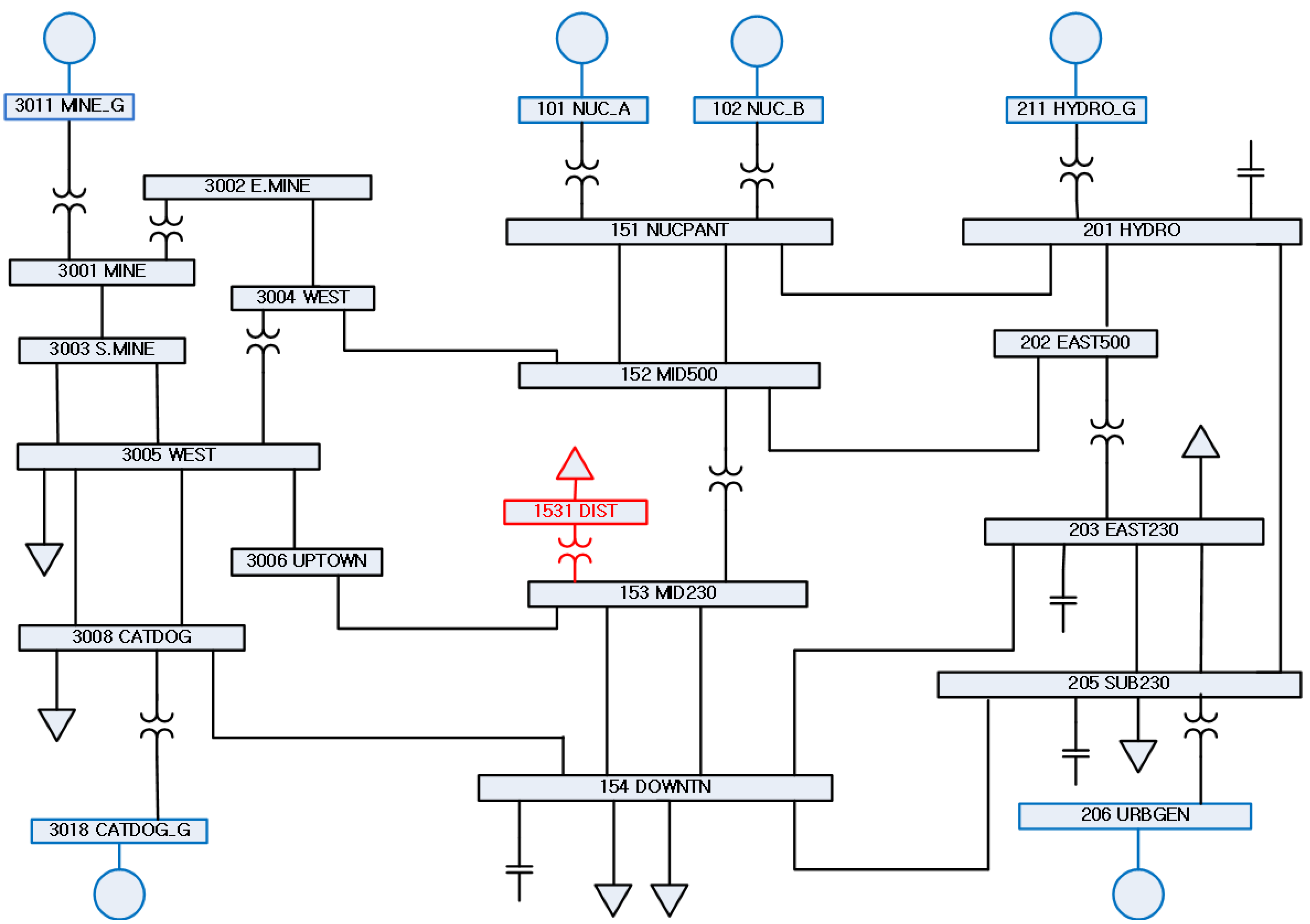
3. Verification of the Linearized Load Model Using PSS/E Simulations
| Model type | Case | ZIP parameter | Linearizing parameter | Voltage reduction (%) | ||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 2.5 | 5.0 | ||||||
| pZ | pI | pP | pC | Active power (MW) | ||||
| ZIP Model | KEPCO | 0.350 | 0.130 | 0.520 | 0.830 | 200.0 | 195.9 | 192.0 |
| Linearized Load Model | 0.000 | 0.830 | 0.170 | 0.830 | 200.0 | 195.9 | 191.8 | |
| 0.415 | 0.000 | 0.585 | 0.830 | 200.0 | 195.9 | 192.0 | ||
| Model type | Case | ZIP parameter | Linearizing parameter | Voltage reduction (%) | ||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 2.5 | 5.0 | ||||||
| qZ | qI | qP | qC | Reactive power (MVAR) | ||||
| ZIP Model | KEPCO | 0.560 | 0.080 | 0.360 | 1.200 | 100.0 | 97.10 | 94.20 |
| Linearized Load Model | 0.200 | 0.800 | 0.000 | 1.200 | 100.0 | 97.00 | 94.10 | |
| 0.600 | 0.000 | 0.400 | 1.200 | 100.0 | 97.10 | 94.20 | ||
4. Modeling Aggregated Loads Based on EMS Data
4.1. Case I: 344th Transformer Bank
| Variation number | Voltage (kV) | Active power (MW) | Reactive power (MVAR) | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| 1 | 23.925 | 23.525 | 23.856 | 23.300 | 6.6667 | 6.4755 |
| 2 | 23.869 | 23.449 | 22.551 | 22.340 | 5.4362 | 5.3044 |
| 3 | 23.948 | 23.578 | 22.345 | 22.123 | 4.2452 | 4.0826 |
| 4 | 24.052 | 23.633 | 21.611 | 21.380 | 3.6168 | 3.5685 |
| 5 | 23.885 | 23.288 | 24.498 | 24.267 | 2.4412 | 2.3731 |
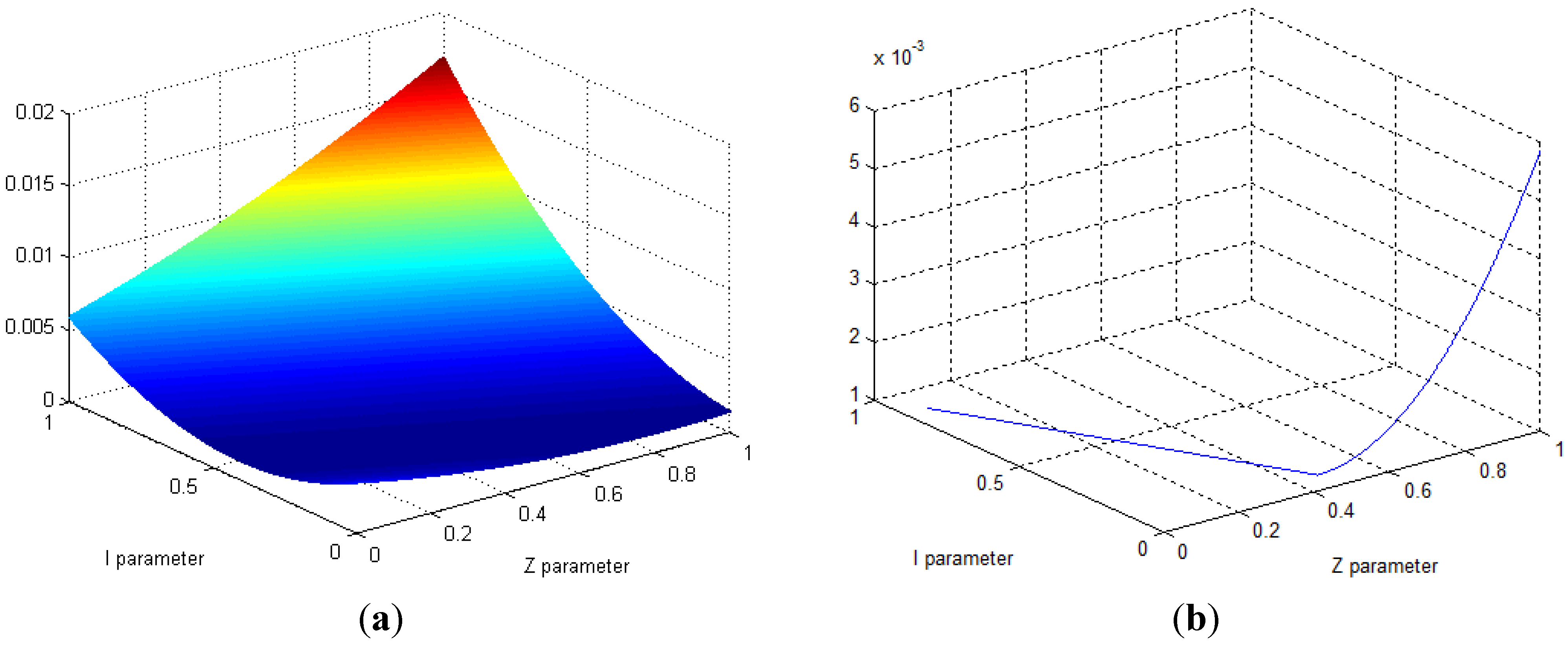
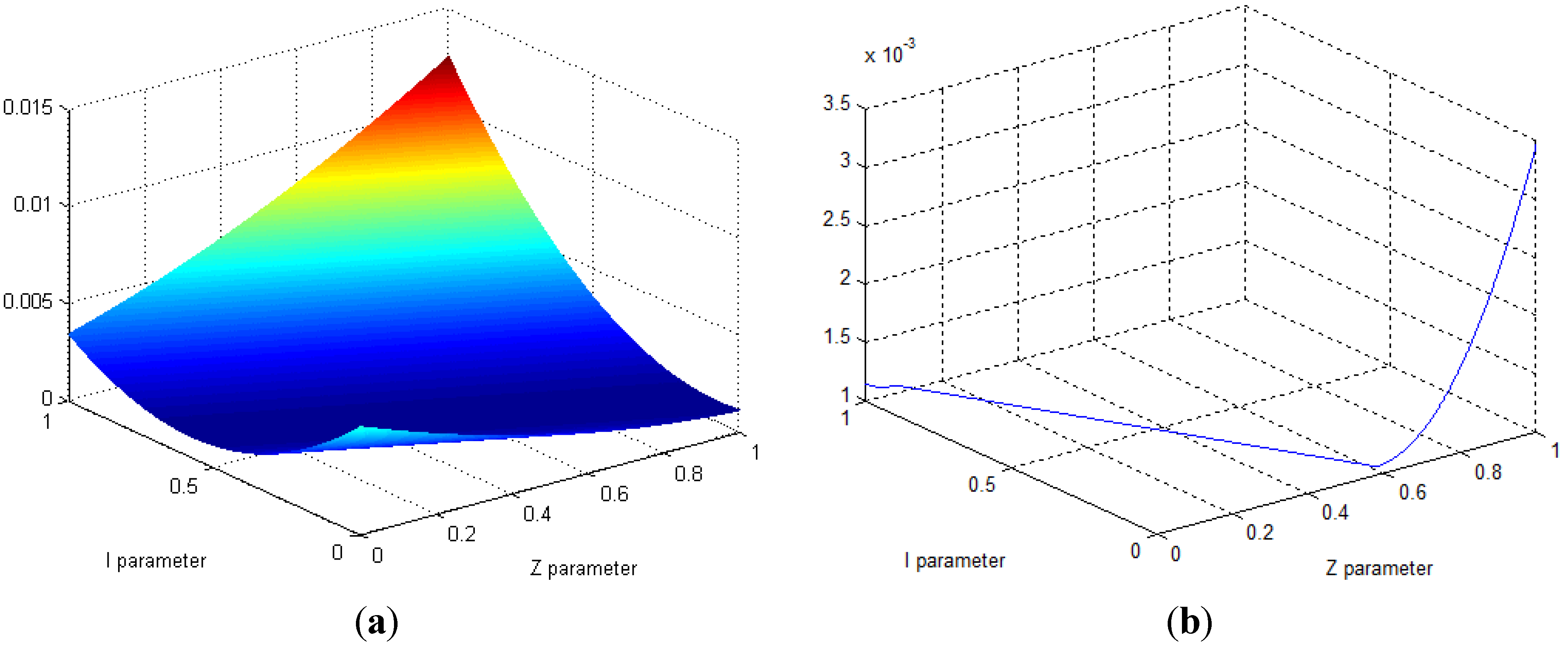
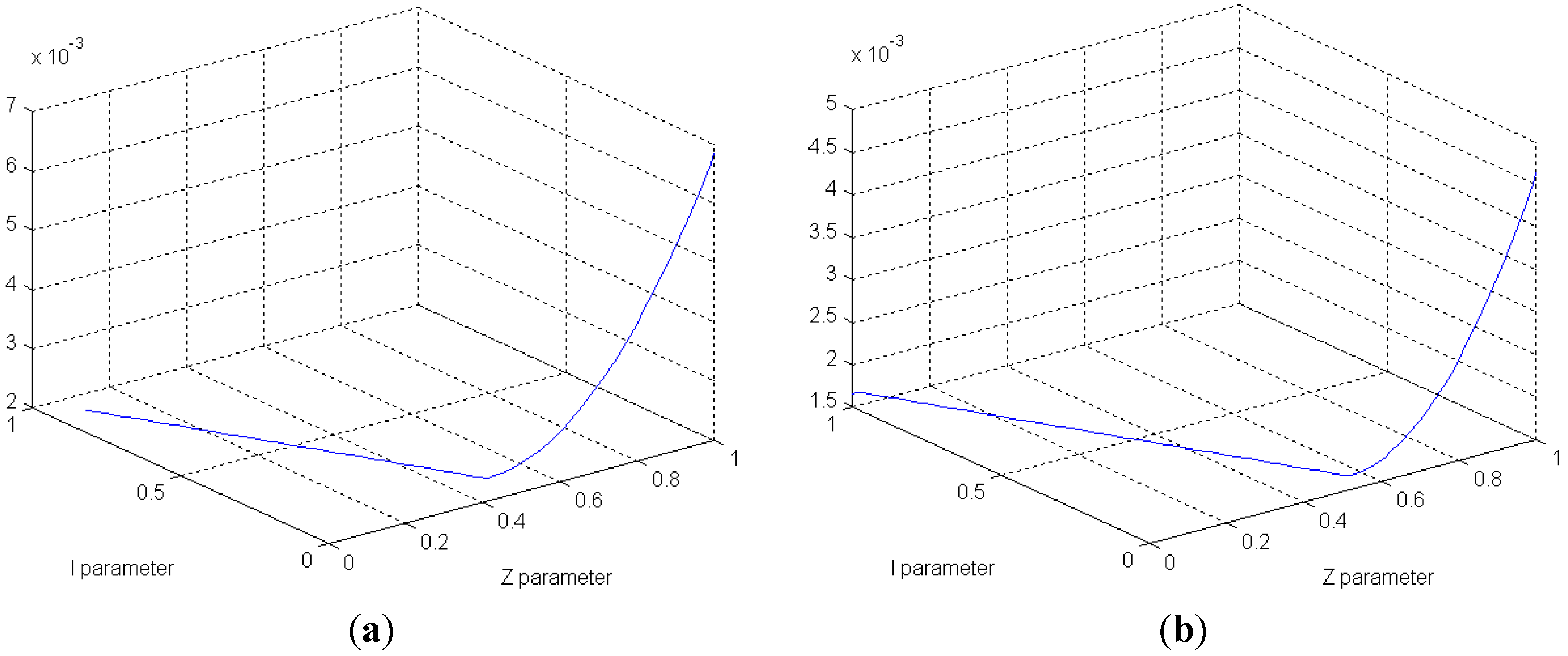
4.2. Case II: 1509th Transformer Bank
| Variation number | Voltage (kV) | Active power (MW) | Reactive power (MVAR) | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| 1 | 24.085 | 23.669 | 28.503 | 28.389 | 6.7556 | 6.6122 |
| 2 | 23.662 | 23.215 | 19.472 | 19.384 | 4.8135 | 4.7296 |
| 3 | 24.085 | 23.639 | 37.74 | 37.662 | 6.3672 | 6.2591 |
| 4 | 23.662 | 23.180 | 19.269 | 19.203 | 2.0635 | 2.0415 |
| 5 | 24.088 | 23.675 | 33.897 | 32.390 | 7.9982 | 7.9739 |
4.3. Case III: 346th Transformer Bank
| Variation number | Voltage (kV) | Active power (MW) | Reactive power (MVAR) | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| 1 | 23.761 | 23.347 | 15.146 | 15.030 | 3.5245 | 3.5201 |
| 2 | 23.533 | 23.175 | 16.669 | 16.643 | 5.4516 | 5.3461 |
| 3 | 23.462 | 23.037 | 17.495 | 17.458 | 5.5834 | 5.4823 |
| 4 | 23.575 | 23.099 | 17.500 | 17.344 | 5.5351 | 5.3153 |
| 5 | 23.887 | 23.519 | 17.330 | 17.280 | 4.9352 | 4.9110 |
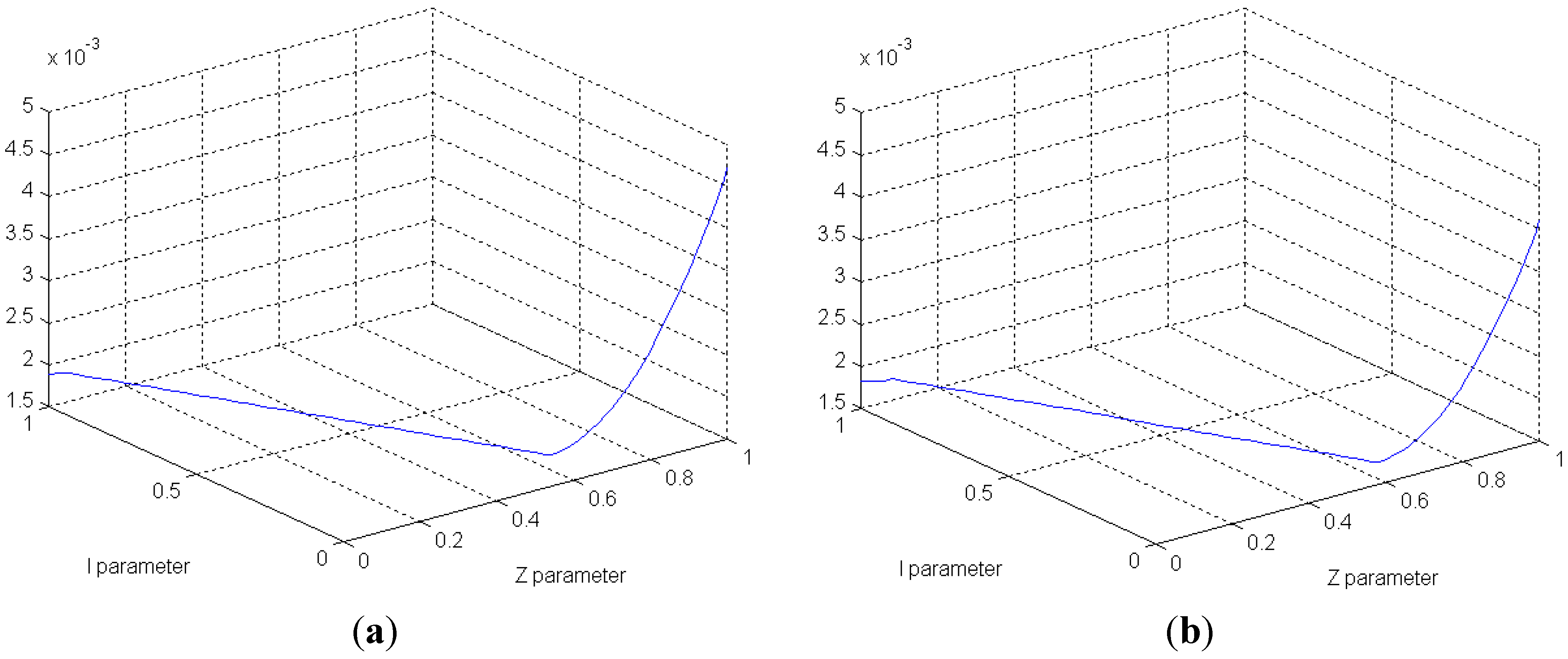
4.4. Case IV: 673th Transformer Bank
| Variation number | Voltage (kV) | Active power (MW) | Reactive power (MVAR) | |||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| 1 | 23.444 | 23.091 | 5.8985 | 5.7845 | 181.83 | 180.37 |
| 2 | 23.398 | 23.751 | 1.0472 | 1.0551 | 200.83 | 201.88 |
| 3 | 24.105 | 23.740 | 0.9336 | 0.9183 | 179.30 | 175.19 |
| 4 | 23.205 | 22.856 | 3.1273 | 3.1125 | 205.57 | 196.50 |
| 5 | 23.419 | 23.046 | 3.2868 | 3.2719 | 182.35 | 174.01 |
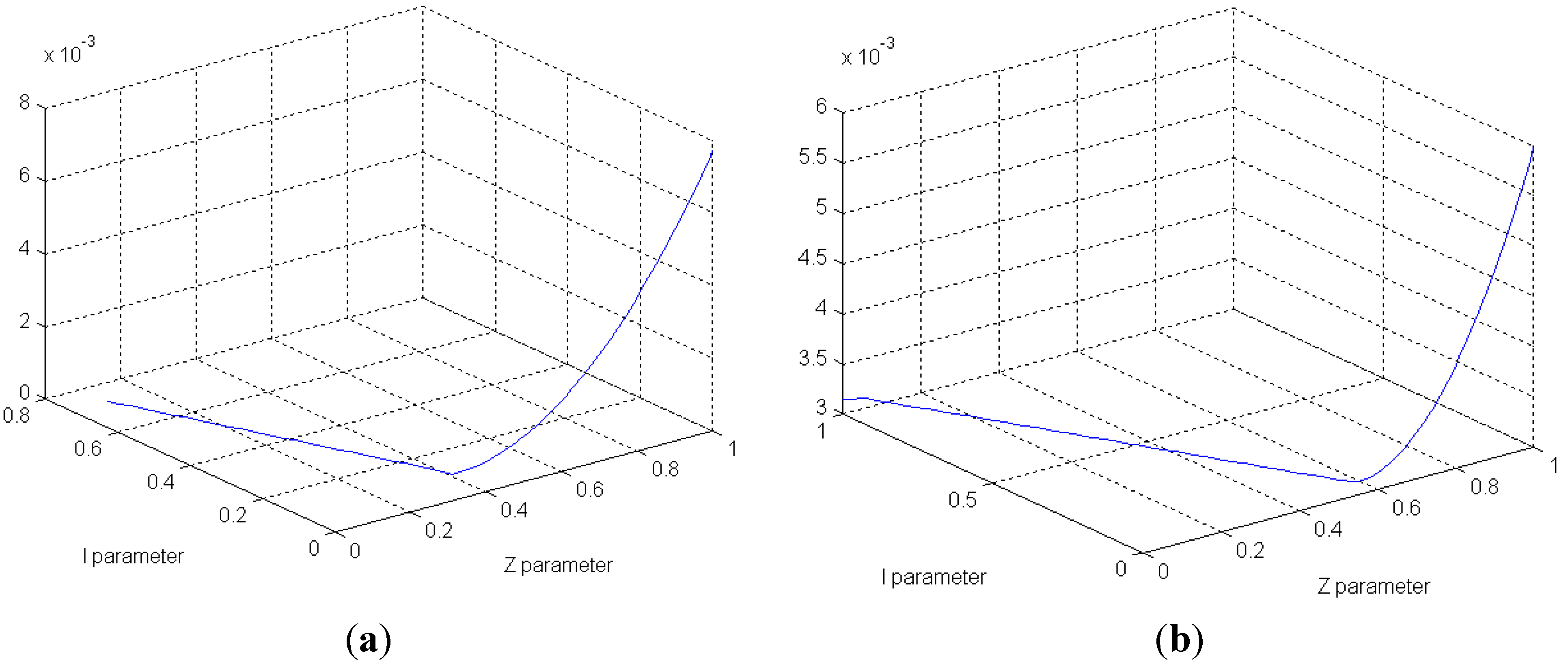
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Amin, S.M.; Gellings, C.W. The North American power delivery system: Balancing market restructuring and environmental economics with infrastructure security. Energy 2006, 31, 967–999. [Google Scholar] [CrossRef]
- Dong, C.; Huang, G.H.; Cai, Y.P.; Xu, Y. An interval-parameter minimax regret programming approach for power management systems planning under uncertainty. Appl. Energy 2011, 88, 2835–2845. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Tan, Q.; Yang, Z.F. An integrated approach for climate-change impact analysis and adaptation planning under multi-level uncertainties—Part I: Methodology. Renew. Sustain. Energy Rev. 2011, 15, 2779–2790. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, Y.P.; Huang, G.H.; Dai, J. A review on optimization modeling of energy systems planning and GHG emission mitigation under uncertainty. Energies 2011, 4, 1624–1656. [Google Scholar] [CrossRef]
- De Steese, J.G.; Merrick, S.B.; Kennedy, B.W. Estimating methodology for a large regional application of conservation voltage reduction. IEEE Trans. Power Syst. 1990, 5, 862–870. [Google Scholar]
- Belvin, R.C.; Short, T.A. Voltage Reduction Results on a 24-kV Circuit. In Proceedings of IEEE PES Transmission and Distribution Conference and Exposition (T&D), Orlando, FL, USA, 7–10 May 2012; pp. 1–4.
- Chen, C.S.; Wu, T.H.; Lee, C.C.; TzengJoseph, Y.M. The application of load models of electric appliances to distribution system analysis. IEEE Trans. Power Syst. 1995, 10, 1376–1382. [Google Scholar] [CrossRef]
- Price, W.W.; Wirgau, K.A.; Murdoch, A.; Mitsche, J.V.; Vaahedi, E.; El-Kady, M. Load modeling for power flow and transient stability computer studies. IEEE Trans. Power Syst. 1988, 3, 180–187. [Google Scholar] [CrossRef]
- Kim, J.; Shim, K.B.; Kim, J.H. Load modeling of electric locomotive using parameter identification. J. Electr. Eng. Technol. 2007, 2, 145–151. [Google Scholar] [CrossRef]
- Chang, H.H. Non-intrusive demand monitoring and load identification for energy management systems based on transient feature analyses. Energies 2012, 5, 4569–4589. [Google Scholar] [CrossRef]
- Ahmed, Z.; Alexander, G.; Muhammad, A.I.; Sutharshan, R. Non-intrusive load monitoring approaches for disaggregated energy sensing: A survey. Sensors 2012, 12, 16838–16866. [Google Scholar] [CrossRef] [PubMed]
- Dias, L.G.; El-Hawary, M.E. Nonlinear parameter estimation experiments for static load modelling in electric power systems. IEEE Proc. C Gener. Trans. Distrib. 1989, 136, 68–77. [Google Scholar] [CrossRef]
- Li, Y.; Chiang, H.D.; Choi, B.K.; Chen, Y.T.; Huang, D.H.; Lauby, M.G. Representative static load models for transient stability analysis: Development and examination. IEEE Proc. C Gener. Trans. Distrib. 2007, 1, 422–431. [Google Scholar] [CrossRef]
- Lee, S.H.; Son, S.E.; Lee, S.M.; Cho, J.M.; Song, K.B.; Park, J.W. Kalman-filter based static load modeling of real power system using K-EMS data. J. Electr. Eng. Technol. 2012, 7, 304–311. [Google Scholar] [CrossRef]
- Hiskens, I.A. Nonlinear dynamic model evaluation from disturbance measurements. IEEE Trans. Power Syst. 2001, 16, 702–710. [Google Scholar] [CrossRef]
- Pereira, L.; Kosterev, D.; Mackin, P.; Davies, D.; Undrill, J.; Zhu, W. An interim dynamic induction motor model for stability studies in the WSCC. IEEE Trans. Power Syst. 2002, 17, 1108–1115. [Google Scholar] [CrossRef]
- Knyazkin, V.; Canizares, C.A.; Soder, L.H. On the parameter estimation and modeling of aggregate power system loads. IEEE Trans. Power Syst. 2004, 19, 1023–1031. [Google Scholar] [CrossRef]
- Renmu, H.; Jin, M.; Hill, D.J. Composite load modeling via measurement approach. IEEE Trans. Power Syst. 2006, 21, 663–672. [Google Scholar] [CrossRef]
- Choi, B.K.; Chiang, H.D.; Li, Y.; Li, H.; Chen, Y.T.; Huang, D.H.; Lauby, M.G. Measurement-based dynamic load models: Derivation, comparison, and validation. IEEE Trans. Power Syst. 2006, 21, 1276–1283. [Google Scholar] [CrossRef]
- Jin, M.; Dong, H.; He, R.M.; Dong, Z.Y.; Hill, D.J. Reducing identified parameters of measurement-based composite load model. IEEE Trans. Power Syst. 2008, 23, 76–83. [Google Scholar] [CrossRef]
- Choi, B.K.; Chiang, H.D. Multiple solutions and plateau phenomenon in measurement-based load model development: Issues and suggestions. IEEE Trans. Power Syst. 2009, 24, 824–831. [Google Scholar] [CrossRef]
- Bai, H.; Zhang, P.; Ajjarapu, V. A novel parameter identification approach via hybrid learning for aggregate load modeling. IEEE Trans. Power Syst. 2009, 24, 1145–1154. [Google Scholar] [CrossRef]
- Chen, Q.; Jua, P.; Shi, K.Q.; Tang, Y.; Shao, Z.Y.; Yang, W.Y. Parameter estimation and comparison of the load models with considering distribution network directly or indirectly. Int. J. Electr. Power Energy Syst. 2010, 32, 965–968. [Google Scholar] [CrossRef]
- Liang, X.; Xu, W.; Chung, C.Y.; Freitas, W.; Xiong, K. Dynamic load models for industrial facilities. IEEE Trans. Power Syst. 2012, 27, 69–80. [Google Scholar] [CrossRef]
- Independent Electricity System Operator (IESO). Voltage Reduction Test Report; IESO: Ontario, Canada, 2010; pp. 5–6. [Google Scholar]
- System Operations Division. Emergency Operations Manual; PJM: Valley Forge, PA, USA, 2011; pp. 32–33. [Google Scholar]
- Electricity Regulatory Commission. Korean Electricity Market Rule; Korea Power Exchange: Seoul, Korea, 2013; pp. 46–48. [Google Scholar]
- Siemens Power Technologies International. PSS/E Program Operation Manual; Siemens Industry: Schenectady, NY, USA, 2010; pp. 1339–1345. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nam, S.-R.; Kang, S.-H.; Lee, J.-H.; Choi, E.-J.; Ahn, S.-J.; Choi, J.-H. EMS-Data-Based Load Modeling to Evaluate the Effect of Conservation Voltage Reduction at a National Level. Energies 2013, 6, 3692-3705. https://doi.org/10.3390/en6083692
Nam S-R, Kang S-H, Lee J-H, Choi E-J, Ahn S-J, Choi J-H. EMS-Data-Based Load Modeling to Evaluate the Effect of Conservation Voltage Reduction at a National Level. Energies. 2013; 6(8):3692-3705. https://doi.org/10.3390/en6083692
Chicago/Turabian StyleNam, Soon-Ryul, Sang-Hee Kang, Joo-Ho Lee, Eun-Jae Choi, Seon-Ju Ahn, and Joon-Ho Choi. 2013. "EMS-Data-Based Load Modeling to Evaluate the Effect of Conservation Voltage Reduction at a National Level" Energies 6, no. 8: 3692-3705. https://doi.org/10.3390/en6083692
APA StyleNam, S.-R., Kang, S.-H., Lee, J.-H., Choi, E.-J., Ahn, S.-J., & Choi, J.-H. (2013). EMS-Data-Based Load Modeling to Evaluate the Effect of Conservation Voltage Reduction at a National Level. Energies, 6(8), 3692-3705. https://doi.org/10.3390/en6083692







