Next Article in Journal
Massively-Parallel Molecular Dynamics Simulation of Clathrate Hydrates on Blue Gene Platforms
Next Article in Special Issue
The Analysis of the Aerodynamic Character and Structural Response of Large-Scale Wind Turbine Blades
Previous Article in Journal
Modeling of a Point Absorber for Energy Conversion in Italian Seas
Previous Article in Special Issue
Mitigation Techniques to Reduce the Impact of Wind Turbines on Radar Services
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 6
Issue 6
10.3390/en6063052
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Using Atmospheric Pressure Tendency to Optimise Battery Charging in Off-Grid Hybrid Wind-Diesel Systems for Telecoms

by
Shane Phelan
*,
Paula Meehan
and
Stephen Daniels
School of Electronic Engineering, Dublin City University, Dublin 9, Ireland
*
Author to whom correspondence should be addressed.
Energies 2013, 6(6), 3052-3071; https://doi.org/10.3390/en6063052
Submission received: 25 March 2013 / Revised: 31 March 2013 / Accepted: 13 June 2013 / Published: 20 June 2013
(This article belongs to the Special Issue Wind Turbines 2013)
Browse Figures
Versions Notes

Abstract

:
Off grid telecom base stations in developing nations are powered by diesel generators. They are typically oversized and run at a fraction of their rated load for most of their operating lifetime. Running generators at partial load is inefficient and, over time, physically damages the engine. A hybrid configuration uses a battery bank, which powers the telecoms’ load for a portion of the time. The generator only operates when the battery bank needs to be charged. Adding a wind turbine further reduces the generator run hours and saves fuel. The generator is oblivious to the current wind conditions, which leads to simultaneous generator-wind power production. As the batteries become charged by the generator, the wind turbine controller is forced to dump surplus power as heat through a resistive load. This paper details how the relationship between barometric pressure and wind speed can be used to add intelligence to the battery charger. A Simulink model of the system is developed to test the different battery charging configurations. This paper demonstrates that if the battery charger is aware of upcoming wind conditions, it will provide modest fuel savings and reduce generator run hours in small-scale hybrid energy systems.

1. Introduction

There are over 600,000 off-grid telecoms base stations distributed throughout the world [1], with 118,000 in India alone [2]. Each base station houses at least one set of base transceiver station (BTS) equipment, which contains the power systems, cooling, radio frequency (RF) conversion and signal processing equipment required to transmit. This equipment can consume up to 5 kW of power, depending on the location and importance of the site in the network [3]. Virtually all of these base stations are being powered by a pair of AC diesel generators running alternately at partial load 24 h a day. Partial load operation is a consequence of over-dimensioning of diesel generators, which is a persistent problem for powering telecom sites. This occurs where generators are sized to cope with the peak power of a site, which will generally occur a small number of times in a given year [4]. The remainder of the time, the generator will run at partial load, which is highly inefficient ([5], p. 34), as the generator is optimised to run at its rated load. The fuel consumption of these sites costs mobile phone operators hundreds of millions of dollars every year [1], and with the number of sites continuously increasing and the price of diesel on an upward trend, these costs will only increase. A hybrid energy system (HES) can be seen as one type of configuration that provides a fuel saving alternative to a diesel generator running continuously.
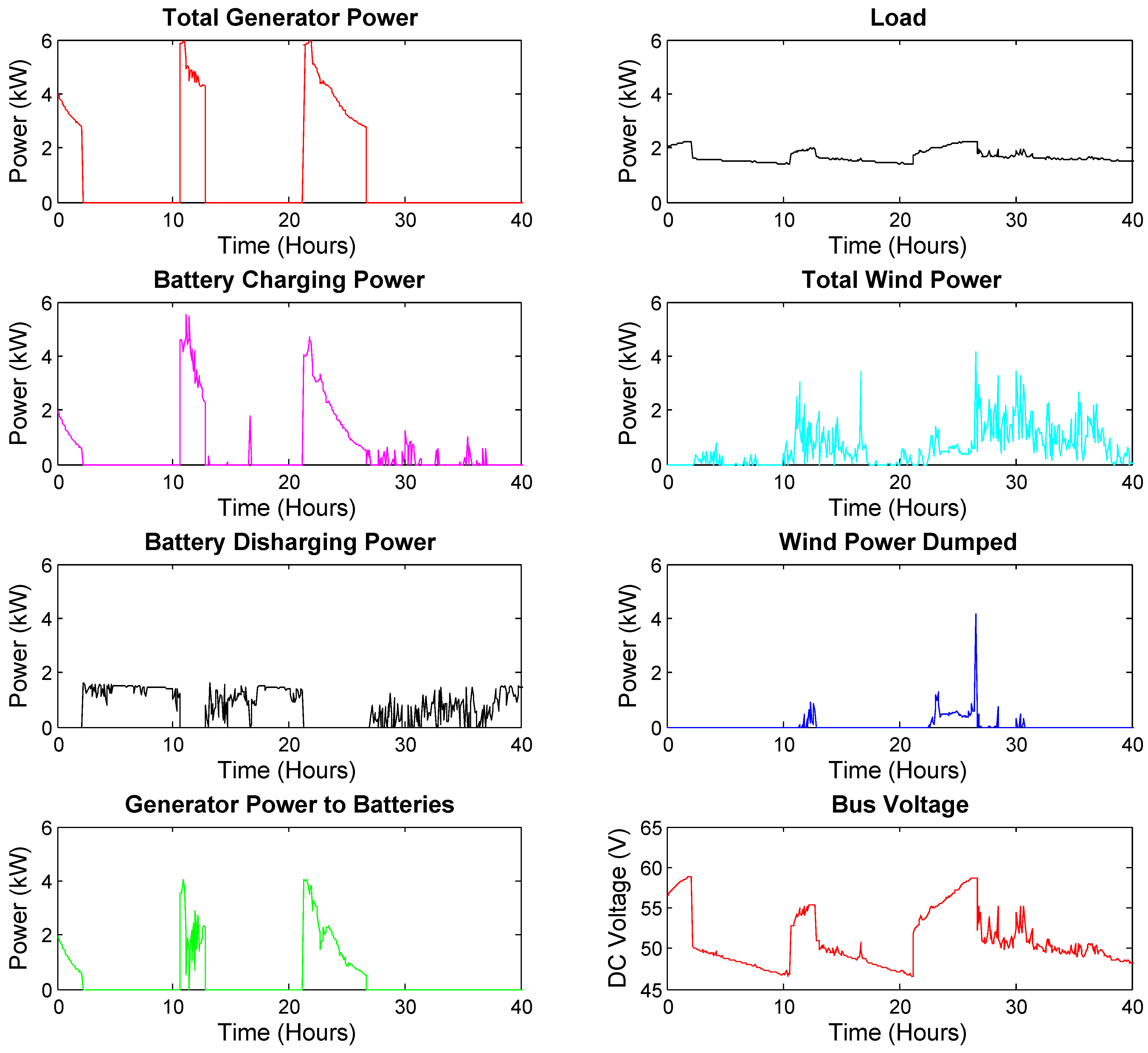
In this context, it can be described as an uninterruptible power supply (UPS) with two or more sources of power, as demonstrated in Figure 1. In its simplest form, a diesel generator, a battery bank and the load are connected together in parallel. The diesel generator only operates when the batteries need to be charged, reducing the number of hours the generator is running. This process saves fuel, as the generator is more heavily loaded [6] when charging the batteries and providing power to the load, therefore increasing the efficiency. This is in contrast to the traditional case [1], where the generator is powering the load only. The fuel consumption of a hybrid system in its “simple form” can be reduced further [7,8,9] with the addition of a wind turbine or solar photovoltaic (PV) panels. It has been suggested [10] that defining this type of configuration as a hybrid system with renewable energy sources (HSRES) is more appropriate for this type of application. Depending on the location, the use of PV or wind must be selected and sized [11,12,13] correctly to account for seasonal lulls [14] in power production.
Energies 06 03052 g001 1024
Figure 1. Off-grid hybrid energy system (HES) with current transducer (CT) measurement points.
Figure 1. Off-grid hybrid energy system (HES) with current transducer (CT) measurement points.
Energies 06 03052 g001
Designing a hybrid PV-diesel can be approached from several perspectives in terms of peak power, panel area, cell efficiency and the number of days of energy storage that the system can provide without sunlight. Often, a compromise in features is the most financially attractive option, with a portion of the power being supplied by PV and a backup time ranging from a few hours to as much as a day [10] or more [15]. The use of a diesel generator in conjunction with a PV array can be used to the reduce the upfront costs, while taking care to choose the optimal tilt angle for the installation [16]. The diesel generator is also useful for supplementing the lower power contributions from the panels as a result of seasonal variations in the climate [17]. Wind turbines are also prone to seasonal change, but to less of an extent than solar-based systems.
Hybrid wind-diesel systems come in several forms, which vary as a result of the type of load or weather patterns imposed on the equipment. Larger deployments are often based on synchronous hybrid configurations with an AC bus, but without a battery bank [18]. These applications tend to provide power to remote villages [19] or islands [20], which have no access to the grid. With synchronous systems, the battery bank is not there to act as a “buffer” to smooth out variations in the load and wind. As a result, there are significant gains to be made from control system optimisations [21], which anticipate [22] variations in both the wind supply and the load. The complementary nature [17] of wind and solar has encouraged the addition of solar PV as a supplemental power source for many systems [7,8,9,10]. The use of hydrogen as a supplemental [23] and, eventually, primary [24] power source for HSRES applications has seen a surge in research activity [25,26,27]. A physical hybrid wind-diesel test platform [28] was used to gather system performance data on a telecoms base station in Ireland. Throughout the testing period, data was acquired, describing current flows, fuel usage, temperatures, voltages, power dumped and cumulative power for all of the components in the structure. These measurements allowed a clear picture of the internal operation of the HSRES to be established.

2. Hybrid System with Renewable Energy Sources

The HSRES (Figure 1, pictured in [28]) consists of a 5.8 kW Fortis Montana wind turbine, 6 kW DC diesel generator, 400 Ah battery bank and DC load (2 kW temporary test load), which is all connected together on a common 48 VDC bus. The wind turbine was mounted on top of a 35 meter lattice telecom tower. The diesel generator, equipped with a DC alternator, charges the battery bank when the voltage falls below a specific set-point. The wind turbine and generator are both connected in parallel to the DC bus, so when the generator is running, the wind turbine will also simultaneously contribute power to the battery bank.

2.1. Generator

The generator is mounted on top of a 600 L bunded double skin fuel tank with two fuel connections for the input and return lines. The graph in Figure 2, highlighting the amount of power dumped, power flow from the generator and wind turbine demonstrates the flow of wind power when the generator is charging the batteries. During the act of charging the battery bank, the generator engages at a low “cut in” voltage and disengages at a higher “cut out” voltage, which is referred to as a generator cycle. During a cycle, the generator operates in two modes; the first mode is constant current (CC) mode. CC mode charges the battery bank with the highest current that the generator can provide until a specified voltage is reached. This can be seen in the “Total Generator Power” graph within Figure 2 at times 11 h and 22 h, where the power is maintained at 6 kW for a period of time. The generator then switches to constant voltage (CV) mode, where it maintains a fixed voltage until the battery bank reaches the cut out voltage.
Energies 06 03052 g002 1024
Figure 2. Energy flow in the test hybrid system with renewable energy sources (HSRES).
Figure 2. Energy flow in the test hybrid system with renewable energy sources (HSRES).
Energies 06 03052 g002
As the battery bank voltage rises, the power flowing into it, from the generator, will trail off over time. The generator controller is configured to charge the battery bank using two-stage charging, as the three-stage configuration is not economical in a cycling environment [29]. Additionally, its ability to accept charge becomes diminished [29], which causes the voltage to rise and forces the wind turbine controller to dump power. This power diversion is evident in the “Wind Power Dumped” graph within Figure 2 during the generator charge cycles. Throughout the charge cycle, the voltage of the battery bank is rising as the power is stored. This is evident in the first generator cycle in Figure 2, where power is dumped towards the end of the generator cycle, where the bus voltage is highest. The second cycle occurs during a much windier period, and so, the voltage rises faster, causing more energy to be dumped.
The aim of this work is to reduce the number of occurrences where power is being dumped. A Simulink model of the HSRES will be utilised to test the type of component configurations that are required to avoid power loss from excess wind production. This model will simulate the performance of each major component in the HSRES and how they interact together. Their performance characteristics are described in the subsequent subsections, while their model profiles are discussed in the dedicated Simulink section.

2.2. Battery Bank

The battery bank contains absorbed glass mat (AGM) batteries, which are favourable to flooded lead acid batteries for this application, as their maintenance needs and storage requirements are much lower. Their price also compares favourably against lithium ion-based battery banks. Throughout this work, a partial-state-of-charge (PSoC) cycling regime is used, which keeps the battery bank between 40% and 80% state-of-charge (SoC). PSoC cycling is a new term used to describe the type of conditions that battery banks in hybrid electric cars experience throughout their operating life [29]. This SoC range prolongs battery life compared to a battery bank that is fully discharged on a frequent basis. PSoC cycling requires occasional equalisation charges to reduce sulfation on the battery plates [29]; discussions with the manufacturer [30] indicated that that this process should occur at least once a month. Despite these charging criteria, the battery bank would not be expected to last longer than five years, due to the intensity of the cycling they are subjected to.

2.3. Telecoms Load

The telecom load, which this system is designed to power, is a single operator configuration consisting of three 120 ∘ antennas, a single small diameter parabolic point-to-point antenna and internal base transceiver station (BTS) equipment. As described in [28], an average demand profile was taken for this load over a period of 30 days. This load varies between 0.8 kW and 1.4 kW throughout the day as demand changes, with an average daily load of 1.2 kW.

2.4. Wind Turbine

The wind turbine used during testing was a Fortis Montana 5.8 kW [31]. It provides three-phase “wild” AC power to the turbine controller, which then rectifies the power into DC to charge the 48 V battery bank. The controller is configured to charge the battery bank to a maximum of 56.4 V, which corresponds to ∼2.35 V for each cell in the battery bank (24 in total). This value is in the conservative range of cut off voltages for a battery bank undergoing active cycles, which is recommended to prevent gassing in AGM battery banks [30]. Gassing is common in lead acid batteries when charging at high voltages, which are typically experienced towards the end of a charging cycle or equalisation charge. Generally, this gas recombines into the battery electrolyte, but if pressure builds up, a valve releases the gas. This loss of gas is replaced in flooded lead acid batteries by topping them up with distilled water every three months [29]. The electrolyte in AGM batteries is stored in glass fibre mats and, hence, cannot be topped up as they are sealed. They are fitted with an emergency valve that opens when excess gas builds up inside. When this gas vents, it cannot be replaced, leading to the cell eventually drying out. As a result, care is taken with AGM batteries to avoid the higher voltages that cause gassing.
As the voltage of the battery bank approaches 56.4 V, the controller will begin to dump power through its resistor banks to dissipate the excess power. It achieves this diversion using pulse width modulation (PWM) switching, where a duty cycle of 0% allows all the power to the battery bank up to a level of 100%, where all of the power is being dumped into the resistor bank and dissipated as heat.

3. Simulink Model

This information acquired from the physical HSRES test system formed the basis of a Simulink-based model, which was used to simulate different HSRES configuration settings. The model uses the individual performance profiles derived from the data acquired from the remote monitoring equipment installed on the physical test system. Modelling different HSRES configurations is the quickest and most cost effective method of testing different components and evaluating how they operate together. There are numerous different methods for modelling hybrid systems with configurations based on Simulink [19], the Hybrid Optimization Model for Electric Renewables (HOMER) [32] being the most popular method in this area in the last five years.
HOMER is a feature-rich modelling environment with pre-existing component models for generators of an array of sizes, solar panels, wind turbines, fuel cells, hydro, utility grid, a wide range of different loads and storage methods [33]. This software allows a user to get a system model running quickly with a high degree of accuracy, but it does not allow the low level control system modifications and accommodation of real-time wind data into the model, as is described in this work. It is very accessible software in that it does not require the user to have in-depth knowledge of the low level operations of the systems that they are simulating.
Simulink is a powerful modelling tool, which can be coded in block diagrams. It requires a deeper understanding of the system than is the case with HOMER. This allows a more tailored model to be built specifically for the problem. It is more flexible in terms of the types of calculations that can be performed and how it can integrate easily with dynamic data sources, which would be changing in real-time. It is particularly popular in the area of hydrogen fuel cell research, where fuel cells and electrolyzers are being integrated into hybrid systems [34].

3.1. Battery Bank Model

The Simulink model described in this work is designed around a common DC bus. Similar to the system described in [28], the performance and behaviour of each component is affected by the status of the battery bank. The voltage of the battery bank is supplied to each component in the system, and this voltage dictates the currents flowing out of the other elements of the model. The battery bank is represented using the generic battery module from Mathworks [35]. This model has been used in other hybrid Simulink systems, such as [19] and, also, [32], to simulate hybrid energy systems.

3.2. Generator Fuel Consumption Model

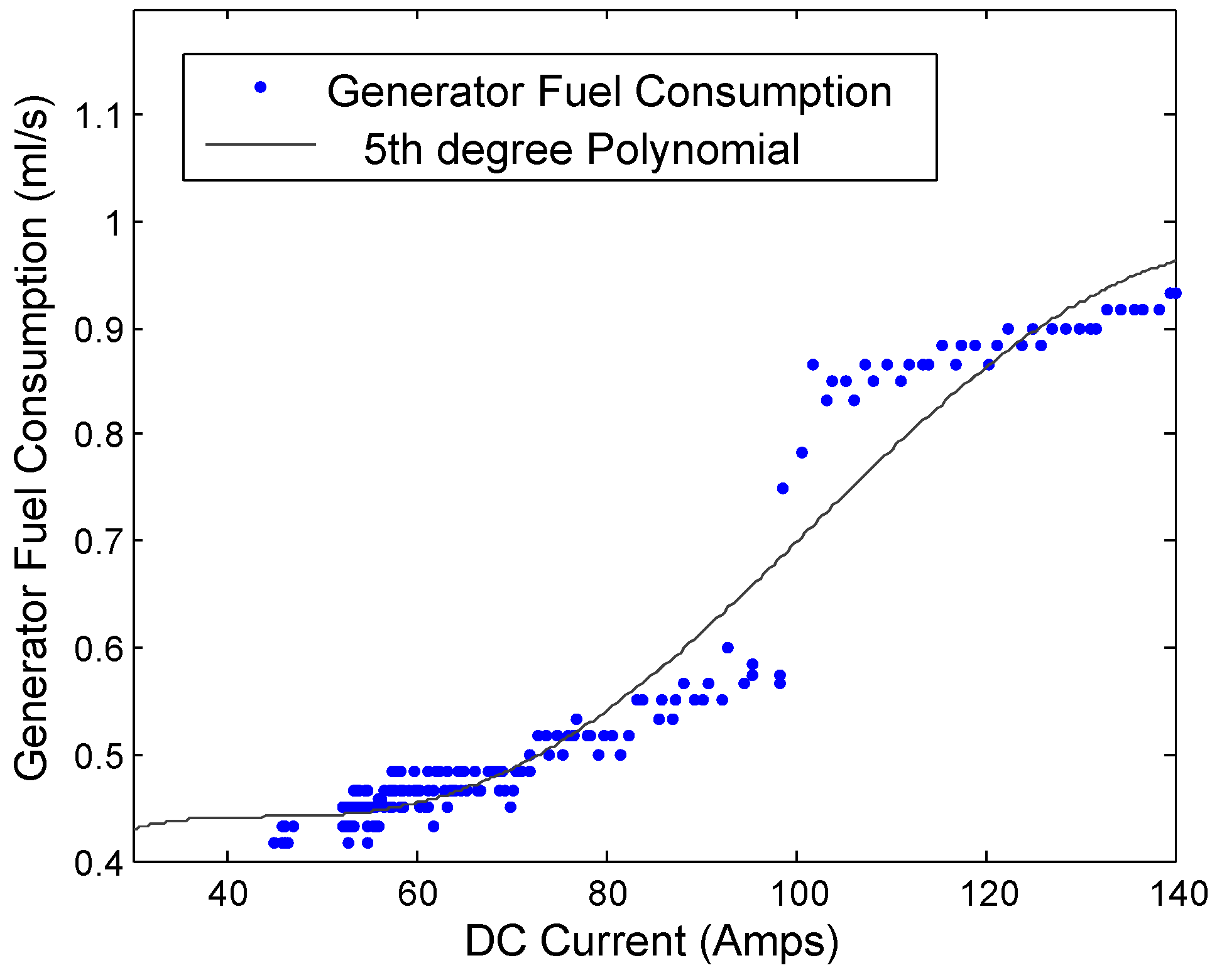
The fuel consumption was measured using a differential (between input/return) in-line flow meter, which was polled every minute to obtain cumulative mL/minute values. The fuel consumption was measured over a full battery charging cycle to give a complete picture for the fuel consumption against DC current.
The fuel consumption equation for the fuel profile was found by fitting a curve to the cumulative fuel and DC current data that was acquired during the fuel consumption testing of the generator. This equation is used in the Simulink model to represent how the fuel consumption changes in proportion to the load over time; see Figure 3. The fuel consumption can be found by substituting in the DC current for “i” in Equation (1):
Energies 06 03052 g003 1024
Figure 3. DC generator fuel consumption profile.
Figure 3. DC generator fuel consumption profile.
Energies 06 03052 g003
F u e l ( m L / s ) = 1.5 × 10 − 10 i 5 − 7.7 × 10 − 8 i 4 + 1.4 × 10 − 5 i 3 − 0.0011 × i 2 + 0.037 × i − 0.037
This equation is valid from 20 A to 200 A, outside of which the polynomial approximation diverges from the fuel profile. The current will not drop below 25 A during this work, as the lowest load the generator will encounter is 20 A from the load and 5 A from the battery bank when it is charged to 80% SoC.

3.3. Telecoms Load Model

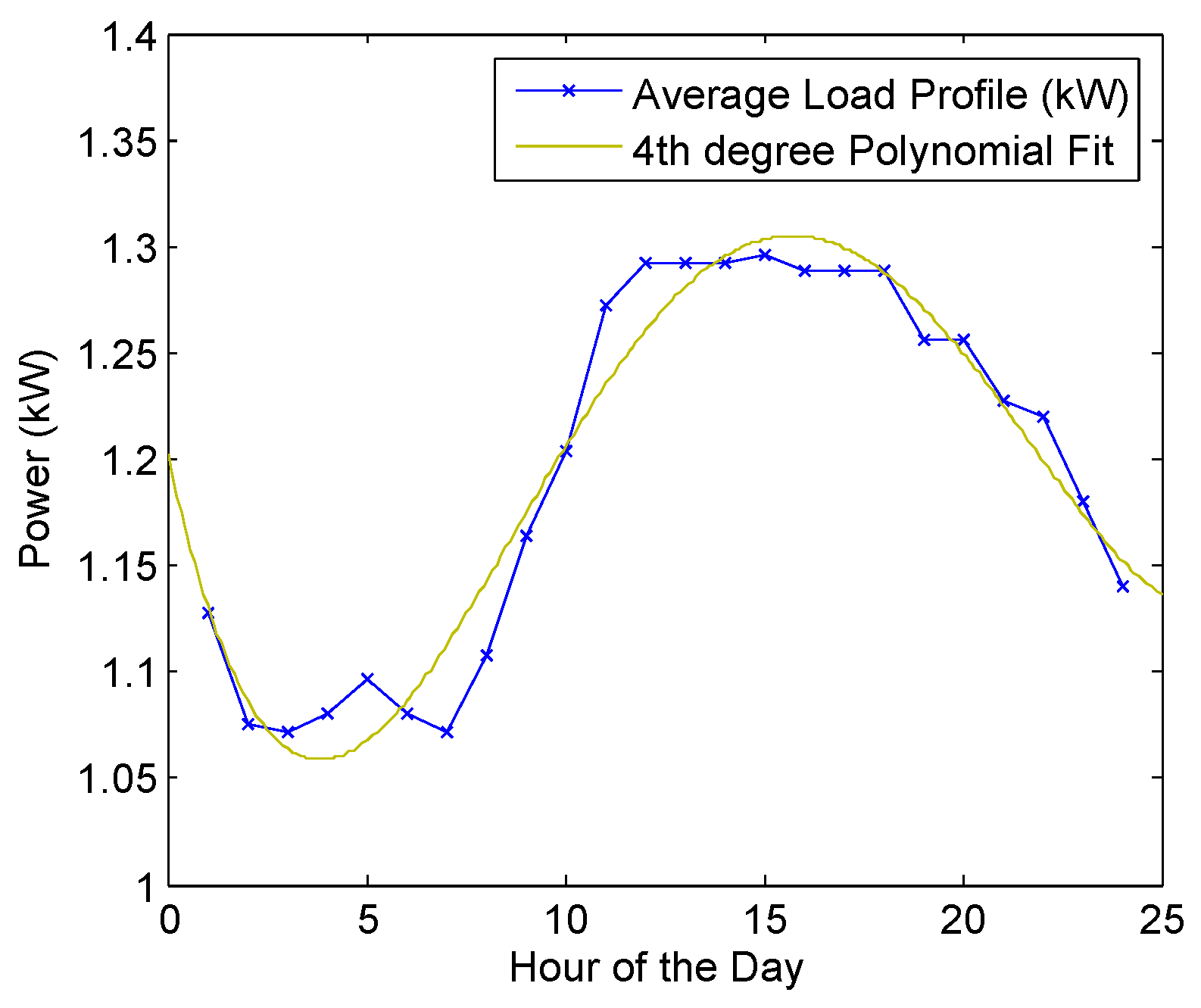
This load profile can be seen in Figure 4, where the variation over a 24 h period is clear. The following equation has been derived from this profile and used in the simulated model of the HSRES:
L o a d ( k W ) = 1.346 × 10 − 5 u 4 − 0.00082126 × u 3 + 0.015426 × u 2 − 0.085309 × u + 1.2024
This equation accepts a time value, “u”, which is an integer hour value ranging from 1.0 h to 24.0 h. The output is a varying kW value, which is representative of a single telecom operator.
Energies 06 03052 g004 1024
Figure 4. Telecom load profile with fourth degree polynomial approximation.
Figure 4. Telecom load profile with fourth degree polynomial approximation.
Energies 06 03052 g004

3.4. Wind Turbine Model

As discussed earlier, the wind turbine diverts power to a resistive load as the battery bank becomes charged. It achieves this diversion using PWM switching, where a duty cycle of 0% allows all the power to the battery bank up to a level of 100%, where all of the power is being dumped into the resistor bank and dissipated as heat. The point of transition where the duty cycle changes can be seen in Figure 5.
Energies 06 03052 g005 1024
Figure 5. pulse width modulation (PWM) diversion, PWM 1 ⇒ Dump all power, PWM 0 ⇒ Store all power.
Figure 5. pulse width modulation (PWM) diversion, PWM 1 ⇒ Dump all power, PWM 0 ⇒ Store all power.
Energies 06 03052 g005
In Figure 5, the PWM controller is given a fixed sequence to emulate the stages before, during and after the wind controller dumps power. This emulates the scenario where the batteries are undergoing a charging cycle from the diesel generator and the voltage is slowly rising towards the final voltage of 58 V limited by the generator. As stated previously, the wind controller will dump all power with a bus voltage above 56.4 V, and this can be seen to occur approximately one third of the way through the charging cycle. Beyond this voltage, the duty cycle stays at 100% until the charging cycle ends. Once it ends, the voltage of the battery bank drops immediately as it is loaded. This causes the PWM signal to revert back to 0% duty cycle, and all available power is sent to the battery bank. The aim of this work is to try to ensure that the wind power is not dumped during times of high wind levels, as significant amounts of potential power would be lost. The power dumped/stored is measured cumulatively, and Simulink operates fast enough to avoid any measurement problems [36] that can occur when measuring PWM signals with physical sensors. Data from the test HSRES demonstrates that the amount of power dumped is in excess of 5% during periods of moderate to high wind speeds.
In the simulated model, the input to the wind turbine model is anemometer data acquired by the highest performing sensor on the Dublin City University (DCU) campus, as described earlier. This data is captured by the remote anemometers at 1 s intervals and averaged into 12 s data points before transmission, as the HSRES model operates on a 1 s simulation interval and the wind data is up-sampled to every 1 s to match the resolution that the model operates at. The wind speed is in m/s and is then converted to power in kW using a seventh order function, which is a close polynomial fit of the manufacturers wind turbine curve [31]. The equation for this curve can be seen in Equation (3), where “u” is the wind speed:
P o w e r ( k W ) = − 8.4083 × 10 − 8 u 7 + 7.8915 × 10 − 6 u 6 − 0.00027472 u 5 + 0.0044283 u 4 − 0.035937 u 3 + 0.18246 u 2 − 0.38095 u + 0.24257
The constructed model can be seen in Figure 6, with the external inputs from the wind speed and barometric pressure data.
Energies 06 03052 g006 1024
Figure 6. Overview of HSRES in Simulink.
Figure 6. Overview of HSRES in Simulink.
Energies 06 03052 g006

4. Battery Charging and Wind Prediction Methodology

The objective of this methodology is to modify the behaviour of the generator based on impending wind conditions. The method will impede the generator from turning on and consuming fuel when a spell of wind is forecast. In this method, the rate of change of barometric pressure is being used to estimate short-term wind conditions.
Temperature differences over 1000 km areas manifest as regions of different barometric pressures. A pressure difference between two regions will cause wind to flow between these regions. The Coriolis effect affects the earth’s wind flow as a result of its rotation. This causes rotational wind movement in these areas of differing pressure and in the case of low pressure regions, known as cyclones. As depressions move from one region to another, the barometric pressure changes, within a certain range (generally 950–1030 mb), when measured at fixed points. Isobars [placed at four millibar (mB) intervals] connect regions with the same pressure, and the closer these lines are together, the higher the pressure gradient and larger subsequent wind speeds [37].
The growing install-capacity of commercial wind power has led to an increased focus on forecasting techniques, which increase the reliability of integrating intermittent power into the grid. The variable nature of wind means that its power can fluctuate significantly over relatively short time scales. This behaviour requires a certain amount of spinning reserve on the grid, where thermal generators can immediately begin supplying power to the grid during sudden lulls in wind power. Accurate forecasting reduces the amount of spinning reserve required to accommodate the wind onto the grid, which reduces costs and allows a greater penetration overall [38]. The time scale for wind forecasting is divided into four levels [39] and is an explanation of their uses in commercial wind forecasting:
  • Very short-term: from a few seconds to 30 min ahead;
  • Short-term: from 30 min to 6 h ahead;
  • Medium-term: from 6 h to one day ahead;
  • Long-term: from 1 d to one week ahead.
Each of the time-scales facilitate the decision making process of the day ahead electricity markets. This allows operators to commit to generating a certain amount of power, while incurring penalties or increased spot market prices if they fail to meet their targets. In the case of off-grid hybrid systems, the time scale is limited by the number of hours of backup offered by the battery bank. While a backup period of 24 h is recommended [10] as the optimal cost/storage level for an off-grid HSRES, operators may choose lower storage levels to reduce upfront costs. This reduces the time available for predicting wind power before the generator is forced to initialise charging.
Persistence forecasting is a method based on the principle that the wind speed now is going to be very similar in the future. If the average wind speed now is 7 m/s, then in 30 min, it is likely to be close to 7 m/s. As the time period increases, the accuracy decreases and, hence, why this method is limited to short-term forecasting [39]. Persistence forecasting would not be suitable for the wind prediction methodology that we hope to implement. The system needs to know if there is going to be an increase in the wind speed, rather than no change.
The physical approach to predicting wind speed and weather patterns in general using numeric weather predictors (NWP) is the standard tool used by meteorological departments. This technique uses large sets of meteorological data, which are fed into sophisticated weather models to make a prediction. The processing of this data requires vast computing power and despite the utilisation of a supercomputer, a “run” typically takes up to 6 h. This restricts this type of prediction to medium- to long-term predictions. Typically, this type of prediction is relatively accurate up to 5 d in advance. This type of weather prediction is useful for commercial wind farms, who can use the information to enhance dispatch control decisions [40]. This type of information would enhance the control decisions in this system, but issues, such as the resolution of the predictions (typically larger than 15 km 2 ), local terrain and cost of accessing the data, would need to be resolved.
Statistical forecasting requires the use of historical weather patterns as training data for creating algorithms. The amount of training data required can range from as little as 24 h using neural networks to as high as 28 months, in some cases, using Markov models [41]. Artificial neural networks (ANN) are seen as highly accurate forecasting tools, especially when combined (hybrid structures) with some of the new techniques, such as fuzzy logic [39]. An ANN-based forecasting system would potentially offer a suitable platform to enhance the control system algorithm. The main issues with ANN processing are that it is seen as a “black box” approach, where interactions between neurons are difficult to quantify. Many implementations are continuously retraining themselves with new data, and this could be seen as a liability by customers who prioritise reliability over price.
Our proposed method keeps track of this pressure gradient using a barometric sensor as the pressure systems of the region move above it. Pressure gradients have been used recently to predict [42] wind speed using hidden Markov models (HMMs) to identify cross dependencies between barometric pressure and wind speed. Barometric pressure has also been found to be the most important variable when predicting step ahead wind speed using data mining methods with NPTree as the prediction model [43]. Their motivations are analogous to those in this work in that they are striving to provide a solution to users who were frustrated with the use of black-box-like expressions that do not explain the relationship between input and output. The relationship between the data input and output in this work is intended to be much clearer than black-box type methods. Using a differential over a three hour period, the pressure gradient is monitored and applied to a common marine meteorological scale [44], as seen in Table 1. An example of this would be if a barometric pressure gradient of 3 mb in 3 h was measured, then the likelihood of wind with speeds in excess of 10 m/s occurring in the short-term is very high. This was observed to be the case at the measurement location used in this study.
Table
Table 1. Marine forecasting terminology for barometric pressure tendency [44].
Table 1. Marine forecasting terminology for barometric pressure tendency [44].
Pressure tendency over 3 h (mb)Marine forecast termApproaching weather
<0.1 mbSteadyCalm
0.1–1.5 mbRising (or falling) slowlyLight breeze
1.6–3.5 mbRising (or falling)Strong breeze
3.6–6 mbRising (or falling) quicklyGale
>6 mbRising (or falling) rapidlyStorm
Depending on the application, wind speeds need to be predicted to an appropriate degree of accuracy, as the implications of any errors may have financial repercussions, as is the case in wind generation scheduling. This happens when a wind farm commits to producing a specific amount of energy over a given time-frame. If the wind farm fails to produce this power, then extra power plants need to be dispatched to make up for the short fall. These power stations, known as peaking plants, are one of the most expensive type of electricity sources. In some cases, the cost of errors in power prediction for wind farms can be as high as 10% [45] of the total income in wind sites with forecast horizons of up to 48 h. In this situation, it is only necessary to know three levels of wind to make a fuel saving. The pressure differentials have been focused into three categories, as demonstrated in Table 2. Pressure changes are generally small, and the majority of changes, over a 3 h period, are less than 2 mb, as can be seen in the pressure gradient instances element of Figure 7. As can be seen in the wind recorded 6 h after pressure changes section of Figure 7, small changes in pressure result in low wind speeds. It can also be observed that pressure changes between 2 and 3 mb demonstrate relatively higher wind speeds between 5 and 9 m/s. Pressure changes of 3 mb and higher show comparatively higher wind speeds between 9 and 14 m/s, which is the region that produces significant amounts of wind power. While the wind speed distribution beyond 9 m/s appears low, it must be remembered that every time the wind speed doubles, the power increases by a factor of eight ([46], p. 31).
Table
Table 2. Table describing relationship between expected wind speed and charging signal. CC, constant current.
Table 2. Table describing relationship between expected wind speed and charging signal. CC, constant current.
Tendency 3 hWind levelsWind speed anticipatedSuitability for 1.2 kW loadCharger responseSignal
<2 mbInsufficient<5 m/sCannot sustain loadCharge3
≥ 2 <3 mbSufficient5 m/s–10 m/sCan sustain load and periodically charge battery bankCC mode only2
≥3 mbSignificant>10 m/sCan sustain load and charge battery bankInhibit charging1
Energies 06 03052 g007 1024
Figure 7. Normalised wind speeds recorded after pressure changes and how many of these changes that occur in a three month period.
Figure 7. Normalised wind speeds recorded after pressure changes and how many of these changes that occur in a three month period.
Energies 06 03052 g007
The decisions in Table 2 are made for an average load level and wind turbine power profile. Larger or more efficient wind turbines/lower loads would allow for more aggressive charging signals. The wind speed and barometric pressure data was acquired on the east coast of Ireland in Dublin City University (DCU), as described in [47]. These sensors were installed, for several different projects, to allow unrestricted and unlimited access to real-time wind or barometric pressure data. Prior to the sensor deployment, data access required a payment to the Meteorological Office when a request is made for information on their servers [48]. The data can also be acquired with simple weather stations that have an anemometer and barometric pressure sensor. In the simplest form, a working system could be deployed using a low cost micro-controller and pressure sensor; the anemometer is only needed for verification of wind increases following changes in pressure. If a location is to be analysed for prospective deployment of this system, historical meteorological data from a weather station (within 500 miles) is an excellent first step for establishing the location’s viability. An extract from the sensor data can be seen in Figure 8. This figure shows the wind speed, barometric pressure and output from the charging algorithm for the generator. It can be seen that during instances of rapidly decreasing pressure, e.g., at t = 14 × 10 5 , there is a subsequent rapid increase in wind speed; see Figure 8, sub-plot 1. The signal sent to the generator control system can then be seen in Figure 8, sub-plot 3. In this case, the generator has been signalled to immediately shut down, due to the wind forecast.
Energies 06 03052 g008 1024
Figure 8. The effect of barometric pressure on the charging signal.
Figure 8. The effect of barometric pressure on the charging signal.
Energies 06 03052 g008
Equation for three=hour differential of barometric pressure; Δt is 3 h:
y ( k ) = 1 Δ t ( u ( k ) − u ( k − 1 ) )
This equation represents the internal operation of the du/dt block in the Simulink model. It calculates the difference between the current value, u(k), and the previous value, u(k−1), with respect to the time step, Δt. The simulation time step is one second, so the differential calculation was delayed to run every 10,800 s (3 h) to correspond with the pressure tendency measurements in Table 1.
This is the method in operation; as pressure decreases, the battery charger settings change. Increases in pressure have been ignored, as they have been observed to offer little consistency in terms of rapid changes followed by increases in wind speed. High pressure is generally associated with clear and calm weather, with only moderate wind at best [37].

5. Results

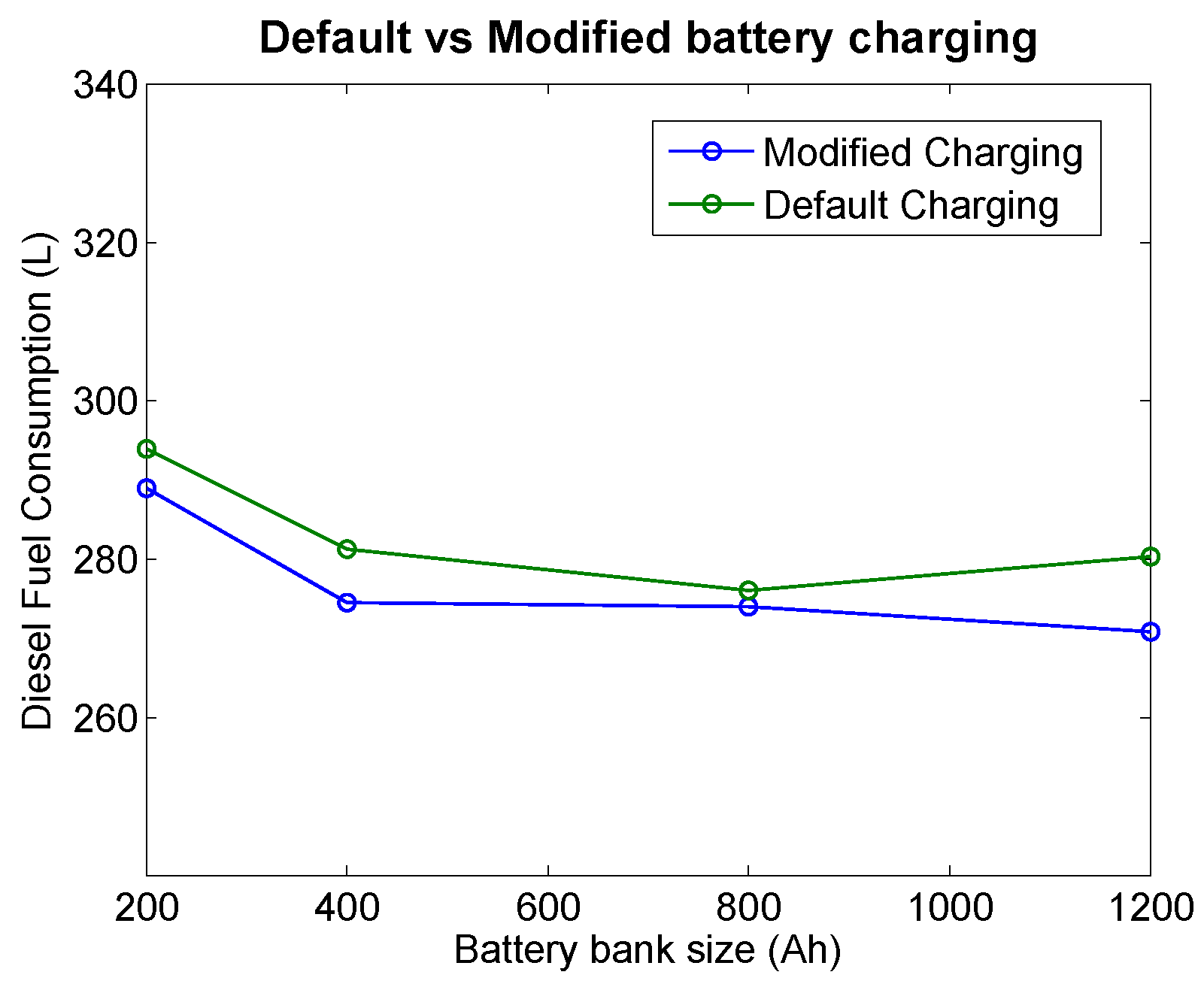
By adopting the algorithm described in section 3, fuel savings are between 1% and 2 % in moderate wind conditions, where the average wind speed at a height of 10 m is between 4 m/s and 6 m/s. The system model was run for two different scenarios, with the results of each illustrated in Figure 9. Both scenarios adopt a lower SoC boundary of 40% and a higher SoC boundary of approximately 85%. Scenario 1, the default charging setting, is a charging regime chosen for optimal operation for a hybrid system undergoing continuous cycling with an absorbed glass mat (AGM) battery bank. This regime is optimal for two reasons. Firstly, a lower state-of-charge (SoC) of 40% was chosen as a compromise between hours of battery operation and battery lifetime. An upper SoC of 85% was selected, as the power the batteries can absorb decreases approaching and beyond this point, resulting in the generator operating inefficiently. As the batteries are not being charged correctly with the 85% SoC limit, they must undergo a full charge to 100% SoC at least once every four weeks [30]. The second scenario uses the same charging regime as Scenario 1, but the algorithm has extra “awareness” of the potential future power contribution from the wind turbine. Using the control system modification described earlier, during periods of decreasing barometric pressure above a certain rate, the generator will hold off on charging the battery bank. It can be seen in Figure 9 that Scenario 2 (modified charging) has a lower fuel consumption than Scenario 1.
Energies 06 03052 g009 1024
Figure 9. Fuel savings with and without the charging algorithm.
Figure 9. Fuel savings with and without the charging algorithm.
Energies 06 03052 g009
Focusing on a single battery bank size, 400 Ah was used as the basis for a batch of testing in the Simulink model; the HSRES was tested for four different groupings of equipment. The combinations included a DC generator, battery bank and wind turbine, with a control system modification being the final combination. This run was simulated for a 500 hour operational time-frame using wind speed and barometric pressure as data inputs, as seen in Figure 8. The total fuel consumed by the equipment over this period was recorded in Table 3. The use of a battery bank immediately results in substantial fuel savings over a continuously operating generator. This type of saving is similar in magnitude to other commercial trials [49].
Table
Table 3. Relative fuel cost of different energy configurations in 500 h model run.
Table 3. Relative fuel cost of different energy configurations in 500 h model run.
Equipment combinationFuel consumption (litres of diesel)Run hours
Generator698 L500 h
Generator & battery bank352 L186 h
Generator & battery bank & wind281 L148 h
Generator & battery bank & wind & algorithm274 L143 h
Using the costing data from [49] as a template, the savings made by adopting a hybrid charging strategy are not limited to fuel savings only. A diesel generator has a service interval of 250 h of operation. This involves personnel physically visiting the generator to perform routine maintenance, such as changing filters, oil and any other issues that need addressing. A cost of $250 was attributed to each visit, so the control methodology used in this paper saves both fuel consumption and the amount of maintenance needed over the long term. The area of wind-diesel-battery systems is widely researched and well understood, so the prospects for improving energy efficiency within the constraints of existing technology are finite. While this algorithm can attain 2 to 3% fuel savings, the total (maximum saving) power dumped is as high as 7% for small battery banks, decreasing to as low as 1% for large battery banks. Based on conservative settings to preserve battery health, the maximum savings cannot always be achieved. Sustained periods of windy conditions will eventually cause the battery bank to reach capacity, despite being predicted correctly, leading to unavoidable portions of dumped power. New battery technologies, which are less sensitive to undercharging/over-charging, will facilitate double-digit gains in efficiency, as the algorithm can be more aggressive with its cut off limits. The cost of implementing such a prediction system is very low, with the only requirements being a micro-controller and a pressure sensor. These costs would be quickly offset with the fuel and maintenance savings. The cumulative knock-on savings in a multitude of different areas as a result of saving fuel is as follows:
  • Reduced fuel consumption;
  • Lower run hours;
  • Less frequent physical maintenance ;
  • Lower CO 2 emissions;
  • Extension of generator engine lifetime;
  • Lower instances of noise emissions into adjacent villages.
These results are based on Simulink simulations of a HSRES; the next steps are to develop a physical electromechanical model of the HSRES. It should be developed in a controlled lab environment for testing before deployment to a physical environment, to allow closer examination of the effects of the algorithm on battery health.

6. Conclusions

The data from the wind-diesel test site reveals that power is lost when the generator and wind turbine operate concurrently. This happens particularly towards the final stages of a charging cycle, when the battery bank is unable to accept much more charge. A portion of this (normally wasted) power can be saved with more effective generator scheduling. The optimal situation is that the generator is not running when there is enough wind to supply the load, but this is not always avoidable.
It has been shown that with the adoption of a charging algorithm based on changing barometric pressure, fuel and run hour savings can be made. These savings reduce the amount of maintenance required for the generator and, also, the number of fuel deliveries to a remote location. These savings are more significant when applied to telecom operators with broad portfolios of diesel powered off-grid base stations.
The proposed method works effectively for geographical regions of continuously changing barometric pressure and frequently developing weather systems. It is no coincidence that these areas will have higher average wind speeds than regions where there is a dominant pressure pattern, such as the Mediterranean [50].

Acknowledgments

The authors would like to thank the Irish Research Council for Science, Engineering and Technology (IRCSET) and Cinergy Ltd for their assistance in funding this research and providing access to their power generation equipment for data acquisition. Furthermore, thanks to the Energy and Design lab for providing a platform to perform this research.

Conflict of Interest

The author wishes to highlight that his PhD funding is part of an enterprise partnership scheme part funded by IRCSET and Cinergy Ltd.

References

  1. Mobile for Development. Green Power for Mobile Interactive Replication Guide; Technical Report; GSMA: London, UK, 2011; pp. 1–41. [Google Scholar]
  2. Ombra, M.; Di Noto, F.; Jaffrain, J.; Lansburg, S.; Brunarie, J. Hybrid Power Systems Deliver Efficient Energy Management for Off-Grid BTS Sites. In Proceedings of the IEEE 34th International Telecommunications Energy Conference, Scottsdale, AZ, USA, 30 September–4 October 2012; pp. 1–7.
  3. Roy, S.N. Energy Logic: A Road Map to Reducing Energy Consumption in Telecom Munications Networks. In Proceedings of the IEEE 30th International Telecommunications Energy Conference, San Diego, CA, USA, 14–18 September 2008; pp. 1–9.
  4. Nordin, H.; Lindemark, B. System Reliability, Dimensioning and Environmental Impact of Diesel Engine Generator Sets Used in Telecom Applications. In Proceedings of the IEEE 21st International Telecommunications Energy Conference, Copenhagen, Denmark, 9 June 1999; Volume 8528, p. 377.
  5. Mahon, L. Diesel Generator Handbook; Butterworth-Heinemann: Burlington, MA, USA, 1992; pp. 3–621. [Google Scholar]
  6. Edwards, R.; Mahieu, V.; Griesemann, J. Well-to-Wheels Analysis of Future Automotive Fuels and Powertrains in the European Context; Technical Report; Society of Automotive Engineers: New York, NY, USA, 2004; pp. 1072–1084. [Google Scholar]
  7. Saheb-Koussa, D.; Haddadi, M.; Belhamel, M. Economic and technical study of a hybrid system (wind-photovoltaic-diesel) for rural electrification in Algeria. Appl. Energy 2009, 86, 1024–1030. [Google Scholar] [CrossRef]
  8. Nema, P.; Rangnekar, S.; Nema, R.K. Pre-Feasibility Study of PV-Solar/Wind Hybrid Energy System for GSM Type Mobile Telephony Base Station in Central India. In Proceedings of The 2nd International Conference of Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; Volume 5, pp. 152–156.
  9. Nejad, M.; Radzi, M. Hybrid Renewable Energy Systems in Remote Areas of Equatorial Countries. In Proceedings of IEEE Student Conference on Research and Development (SCOReD), Penang, Malaysia, 5–6 December 2012; pp. 11–16.
  10. Notton, G.; Lazarov, V.; Zarkov, Z.; Stoyanov, L. Optimization of Hybrid Systems with Renewable Energy Sources: Trends for Research. In Proceedings of First IEEE International Symposium on Environment Identities and Mediterranean Area, Corse-Ajaccio, France, 10–13 July 2006; pp. 144–149.
  11. Li, J.; Wei, W.; Xiang, J. A simple sizing algorithm for stand-alone PV/wind/battery hybrid microgrids. Energies 2012, 5, 5307–5323. [Google Scholar] [CrossRef]
  12. Erdinc, O.; Uzunoglu, M. A new perspective in optimum sizing of hybrid renewable energy systems: Consideration of component performance degradation issue. Int. J. Hydrog. Energy 2012, 16, 1412–1425. [Google Scholar] [CrossRef]
  13. Lujano-Rojas, J.M.; Dufo-López, R.; Bernal-Agustín, J.L. Optimal sizing of small wind/battery systems considering the DC bus voltage stability effect on energy capture, wind speed variability, and load uncertainty. Appl. Energy 2012, 93, 404–412. [Google Scholar] [CrossRef]
  14. Wu, Y.K.; Hong, J.S. A Literature Review of Wind Forecasting Technology in the World. In Proceedings of IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 504–509.
  15. Muselli, M.; Notton, G.; Louche, A. Design of hybrid-photovoltaic power generator, with optimization of energy management. Sol. Energy 1999, 65, 143–157. [Google Scholar] [CrossRef]
  16. Kaldellis, J. Optimum hybrid photovoltaic-based solution for remote telecommunication stations. Renew. Energy 2010, 35, 2307–2315. [Google Scholar] [CrossRef]
  17. Takle, E.S.; Shaw, R.H. Complimentary nature of wind and solar energy at a continental mid-latitude station. Int. J. Energy Res. 1979, 3, 103–112. [Google Scholar] [CrossRef]
  18. Panickar, P.S.; Rahman, S.; Islam, S.M.; Pryor, T.L. Adaptive Control Strategies in Wind-Diesel Hybrid Systems; Murdoch University Energy Research Institute: Perth, Australia, 2000. [Google Scholar]
  19. Kathirvel, C.; Porkumaran, K. Analysis and Design of Hybrid Wind/Diesel System with Energy Storage for Rural Application. In Proceedings of International Power Engineering Conference (IPEC), Singapore, 27–29 October 2010; Volume 2, pp. 250–255.
  20. McKenna, E.; Olsen, T.L. Performance and Economics of a Wind-Diesel Hybrid Energy System: Naval Air Landing Field, San Clemente Island, California; Citeseer: Denver, CO, USA, 1999; pp. 1–108. [Google Scholar]
  21. Hu, Y.; Solana, P. Optimization of a hybrid diesel-wind generation plant with operational options. Renew. Energy 2013, 51, 364–372. [Google Scholar] [CrossRef]
  22. Sharma, H.; Islam, S.; Pryor, T. Dynamic Modelling and Simulation of a Hybrid Wind Diesel Remote Area Power System. Int. J. Renew. Energy Eng. 2000, 2, 123–128. [Google Scholar]
  23. Dufo-López, R.; Bernal-Agustín, J.L. Multi-objective design of PV wind diesel hydrogen battery systems. Renew. Energy 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
  24. Ahmed, N.A.; Miyatake, M.; Al-Othman, A.K. Power fluctuations suppression of stand-alone hybrid generation combining solar photovoltaic/wind turbine and fuel cell systems. Energy Convers. Manag. 2008, 49, 2711–2719. [Google Scholar] [CrossRef]
  25. Nehrir, M.H.; Wang, C.; Strunz, K.; Aki, H.; Ramakumar, R.; Bing, J.; Miao, Z.; Salameh, Z. A review of hybrid renewable alternative energy systems for electric power generation. IEEE Trans. Sustain. Energy 2011, 2, 392–403. [Google Scholar] [CrossRef]
  26. Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
  27. Zhou, L. Progress and problems in hydrogen storage methods. Renewable and Sustainable Energy Reviews 2005, 9, 395–408. [Google Scholar] [CrossRef]
  28. Phelan, S.; Meehan, P.; Krishnamurthy, S.; Daniels, S. Smart Energy Management for Off-Grid Hybrid Sites in Telecoms. In Proceedings of Symposium on ICT and Energy Efficiency and Workshop on Information Theory and Security (CIICT 2012), Dublin, Ireland, 4–5 July 2012; pp. 15–21.
  29. Linden, D.; Reddy, T. Handbook of Batteries; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
  30. Vision Battery Specification CL400 2V 400Ah(10hr); Shenzhen Center Power Tech. Co. Ltd.: Shenzhen, China, 2011.
  31. Montana Wind Turbine; Fortis: Hoogkerk, The Netherlands, 2012. Available online: http://www.fortiswindenergy.com/products/wind-turbines/montana (accessed on 2 September 2012).
  32. Nair, N.K.K.C.; Garimella, N. Battery energy storage systems: Assessment for small-scale renewable energy integration. Energy Build. 2010, 42, 2124–2130. [Google Scholar] [CrossRef]
  33. Lilienthal, P.; Flowers, L.; Rossmann, C. The Hybrid Optimization Model for Electric Renewables; HOMER Energy: Boulder, CO, USA, 1995. [Google Scholar]
  34. Panahandeh, B.; Bard, J.; Outzourhit, A.; Zejli, D. Simulation of PVWind-hybrid systems combined with hydrogen storage for rural electrification. Int. J. Hydrog. Energy 2011, 36, 4185–4197. [Google Scholar] [CrossRef]
  35. Implement Generic Battery Model—Simulink; MathWorks: Stavanger, Norway, 2012.
  36. Williams, N.J.; Dyk, E.E.V.; Vorster, F.J. Monitoring solar home systems with pulse width modulation charge control. J. Sol. Energy Eng. 2011, 133, 021006:1–021006:7. [Google Scholar] [CrossRef]
  37. Stull, R.B.; Ahrens, C.D. Meteorology for Scientists and Engineers; Earth Science Series; Brooks/Cole: Belmont, CA, USA, 2000. [Google Scholar]
  38. Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef] [Green Version]
  39. Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A Review of Wind Power and Wind Speed Forecasting Methods with Different Time Horizons. In Proceedings of IEEE North American Power Symposium, Arlington, TX, USA, 26–28 September 2010; Volume 4, pp. 1–8.
  40. Tanabe, T.; Sato, T.; Tanikawa, R.; Aoki, I.; Funabashi, T.; Yokoyama, R. Generation Scheduling for Wind Power Generation by Storage Battery System and Meteorological Forecast. In Proceedings of IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7.
  41. Colak, I.; Sagiroglu, S.; Yesilbudak, M. Data mining and wind power prediction: A literature review. Renew. Energy 2012, 46, 241–247. [Google Scholar] [CrossRef]
  42. Hocaolu, F.O.; Gerek, O.N.; Kurban, M. A novel wind speed modeling approach using atmospheric pressure observations and hidden Markov models. J. Wind Eng. Ind. Aerodyn. 2010, 98, 472–481. [Google Scholar] [CrossRef]
  43. Mori, H.; Umezawa, Y. Application of NBTree to Selection of Meteorological Variables in Wind Speed Prediction. In Proceedings of IEEE Transmission & Distribution Conference & Exposition: Asia and Pacific, Seoul, South Korea, 26–30 October 2009; Number 2. pp. 1–4.
  44. Marine Forecasts Glossary; Met Office: Devon, UK, 2012. Available online: http://www.metoffice.gov.uk/weather/marine/guide/glossary.html (accessed on: 27 February 2013).
  45. Fabbri, A.; Roman, T.G.S.; Abbad, J.R.; Quezada, V.H.M. Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market. IEEE Trans. Power Syst. 2005, 20, 1440–1446. [Google Scholar] [CrossRef]
  46. Manwell, J.; McGowan, J.; Rogers, A. Wind Energy Explained: Theory, Design and Application; John Wiley&Sons Ltd.: Sussex, UK, 2002; p. 577. [Google Scholar]
  47. Yang, J.; Phelan, S.; Meehan, P.; Daniels, S. A Distributed Real Time Sensor Network for Enhancing Energy Efficiency Through ICT. In Proceedings of Symposium on ICT and Energy Efficiency and Workshop on Information Theory and Security (CIICT 2012), Dublin, Ireland, 4–5 July 2012; pp. 8–14.
  48. Climate Data & Products; Met Eireann: Dublin, Ireland, 2013. Available online: http://www.met.ie/climate/climate-data-information.asp (accessed on 27 May 2013).
  49. Brunarie, J. Fuel savings make a powerful case for hybrid diesel generator systems. Power Eng. Int. 2011, 19, 32–36. [Google Scholar]
  50. Slonosky, V.; Jones, P.; Davies, T. Variability of the surface atmospheric circulation over Europe, 1774 to 1995. Int. J. Climatol. 2000, 20, 1875–1897. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Phelan, S.; Meehan, P.; Daniels, S. Using Atmospheric Pressure Tendency to Optimise Battery Charging in Off-Grid Hybrid Wind-Diesel Systems for Telecoms. Energies 2013, 6, 3052-3071. https://doi.org/10.3390/en6063052

AMA Style

Phelan S, Meehan P, Daniels S. Using Atmospheric Pressure Tendency to Optimise Battery Charging in Off-Grid Hybrid Wind-Diesel Systems for Telecoms. Energies. 2013; 6(6):3052-3071. https://doi.org/10.3390/en6063052

Chicago/Turabian Style

Phelan, Shane, Paula Meehan, and Stephen Daniels. 2013. "Using Atmospheric Pressure Tendency to Optimise Battery Charging in Off-Grid Hybrid Wind-Diesel Systems for Telecoms" Energies 6, no. 6: 3052-3071. https://doi.org/10.3390/en6063052

Article Metrics

Back to TopTop