1. Introduction
The expansion of power plants based on renewable energy sources has experienced an important boost in recent years. Increases in prices of traditional energy sources, the threat of climate change, and policies implemented by national governments have propelled expansions of this kind of power plants. Renewable energies with greater integration in electric power systems are wind energy and solar photovoltaic energy, and they are increasing their integration with time: in 2050, wind energy is expected to provide 12% of the global electricity consumption [
1], while PV energy is expected to provide 11% [
2]. The integration of the electric energy generated by these power plants into electric power networks is not exempt from problems, which are mainly due to the variability and volatility of renewable resources. Accurate forecasts of power production at wind farms or at PV plants have direct implications on the economic operation of power systems [
3,
4] and on the economic results of the plants whose generated energy is sold in electricity markets [
5]. These economic reasons have driven the development of short-term power forecasting models for wind farms or for relatively large grid-connected PV plants.
The development of numerical weather predictions (NWP) tools has helped in the advance of new power forecasting models for electric plants based on renewable resources, providing new input variables. These NWP tools have the objective, from a set of initial conditions, to supply information regarding the state of the atmosphere for a given time horizon. Models underlying NWP tools can be classified into global models and regional/mesoscale models. Global models simulate the behavior of the atmosphere to a global (worldwide) scale, and regional/mesoscale models simulate the behavior of the atmosphere for more limited areas such as continents, countries or regions. The use of weather forecasted variables, mainly radiation and temperature, can help to improve short-term power forecasting models for PV plants.
PV systems are the most direct way to convert solar radiation into electric power. Traditionally, small PV systems have been used to produce electricity for low power applications in isolated areas (isolated from electric power networks). Installation cost reductions, subsidies, and attractive feed-in tariffs, have propelled constructions of relatively large PV plants connected to electric grids. PV plants, connected to medium (or high) voltage electric networks, can have capacity of tens (or, in some cases, even a few hundred) of MW.
In countries with an operative day-ahead electricity market, large power plants based on renewable energies can act, as any other electricity producer, providing power generation sale offers to electricity markets. Obviously, producers corresponding to power plants based on variable renewable resources, such as wind or solar radiation, use forecasts of hourly energy generation to prepare energy sale offers. The use of these forecasts presents a risk: in electricity markets, when power producers are not following their schedule (that presented to the Market Operator), they are penalized with retributions lower than those established in markets for those hours with deviation between the energy actually produced and that presented in offers, so for a PV power producer, high quality forecasting systems are needed for reducing penalties in electricity markets, and for optimizing profits.
In the last decade, tens of short-term wind power forecasting models have been described in the international literature. Nevertheless, despite the fact that future contributions of PV plants to the global electricity consumption will be comparable to that corresponding to wind farms, short-term forecasting models for PV plants are in their early stages. Most of the published works corresponding to short-term forecasting models for PV plants are oriented to solar radiation predictions [
6,
7,
8,
9], while only a few works describe models aimed at directly forecasting the hourly power production in PV plants [
10,
11,
12,
13,
14,
15,
16,
17]. Most of these published models are based on artificial neural networks (ANNs). A hybrid approach with the combination of a data filtering technique based on wavelet transformation and ANNs is presented in [
10] and used to obtain one-hour-ahead power output forecasts. Several forecasting techniques are evaluated and compared in [
11] for predicting the power output of a PV plant with forecasting horizons of 1 and 2 h ahead; the best results are obtained with models based on ANNs optimized with Genetic Algorithm (GA). A model based on recurrent neural networks to forecast hourly insolation and temperature for the next 24 h is described in [
12]; both forecasts are used to calculate the hourly power generation in the PV plant. Support vector machines are used in [
13] and [
14] to forecast directly the hourly power generation for the next 24 h. In [
15] a multilayer perceptron ANN optimized with GAs is used to provide hourly power generation in a PV installation for the 24 h of the next day. In all these works describing forecasting models with horizons covering 24 h, some forecasted weather variables (such as global solar radiation, temperature, relative humidity or cloudiness, obtained from a NWP tool), are used as inputs in the forecasting model. Even these forecasted weather values are used in [
16] to forecast the hourly power production for all PV plants in a local or regional scale. Genetic programming of evolution of fuzzy rules has been proposed in [
17] to estimate the output of a PV plant, allowing the selection of the best forecasting model.
But in all the referenced works, the proposed forecasting models only provide the electric power point (spot) forecasts. They do not supply any additional information that enables the evaluation of the risk associated with the use of such forecasted values. Although several wind power forecasting models published recently deal with this evaluation, none have been applied to PV plants.
This paper presents a new short-term power forecasting model for PV plants, named HIstorical SImilar Mining (HISIMI) model, which provides the user with useful dimensions of electric power forecast. Thus, this forecasting model, based on transitions (in the past time) between different power intervals of electric generation in the PV plant, is able to achieve the point forecast, and also the uncertainty associated with that value. HISIMI model uses a database comprised of historical values of weather variables forecasted by a mesoscale NWP tool and the corresponding historical real power production in the PV plant. Spot (point) forecasts obtained with the HISIMI model have been compared with those obtained from a multilayer perceptron based model, and the “persistence” model, with the same input database: the HISIMI model has shown lower forecasting errors. Furthermore, this model also provides the uncertainty associated with the point forecast, increasing the value of the forecasting information. This uncertainty is provided by the HISIMI model in the form of the probability value that the PV power production is included in each one of the above mentioned power intervals.
The paper is structured as follows:
Section 2 presents the structure of the proposed power forecasting model (HISIMI);
Section 3 describes the methodology followed in the development of the HISIMI model, which structure is optimized with a genetic algorithm;
Section 4 shows the results obtained with the HISIMI model in the forecast of PV power production (point or spot forecast) in a grid-connected PV plant;
Section 5 analyses the additional and useful forecasting information supplied by this new model in the form of uncertainty representation; lastly,
Section 6 presents the conclusions.
2. PV Power Forecasting Model
In this paper, the PV power forecasting model uses historical data collected from the PV plant under study; this model performs a “kind of search” of this historical database aimed at utilizing similar historical cases regarding electric power transitions in order to forecast the electric power generation. The proposed search mechanism is based on data mining techniques. Thus, the model was named HIstorical SImilar MIning (HISIMI).
The data, that comprises the model’s historical database, are forecasted values for weather variables obtained with a mesoscale NWP tool and the corresponding electric power generation measures obtained from the PV plant using a Supervisory Control and Data Acquisition (SCADA) system. In order to extract information regarding electric power transitions between consecutive past time instants, the historical similar mining mechanism is applied to the cases in the historical database. Thus, good power forecast results require the use of a database with historical cases of good quality, with a high volume of reliable information, which also implies the need to find mechanisms to deal with such information, capable of searching the most relevant historical cases of power transitions to forecast the electric power corresponding to the current case. After obtaining the power transition information, an array called Probability Matrix (PMt+k) is created, which contains power transition probabilities between the future instants t+k−1 and t+k, where t is the instant when the forecast is generated -present instant-; and k is the number of time steps of the forecast (forecasting horizon). Thus, the HISIMI model provides valuable forecast information, using probability values: prediction of uncertainties, associated with electric power forecasted values, and electric power forecasts (point or spot forecasts). The following subsections contain more detailed explanations regarding the HISIMI model.
2.1. Database of the Forecasting Model
The model uses a database that contains records with the historical values of variables corresponding to the PV plant. Thus, a record constitutes a historical case which contains values forecasted by a NWP tool, for several weather variables (two values for each variable, which correspond to instants c−1 and c); the value of the solar hour for both instants; and also the two corresponding real PV power production values (Pc−1 and Pc) of the PV plant. The pairs of past instants c−1 and c are necessary to model power transitions. The index c ranges from 2 to present instant t and it is expressed in hours. At this point, notice that the size of the records depend on the number of forecasted weather variables and the number of the remaining variables related to the short-term forecast of power generation in the PV plant.
2.2. Mechanism Based on Data Mining (MDM)
This mechanism used to process electric power transitions information plays a key role in the success of the developed model. The purpose of the MDM is to examine historical cases, and to assign different weight values to such cases according to similarity between them and the current case. This allows selecting—via weights—only information concerning historical cases relevant to the current case.
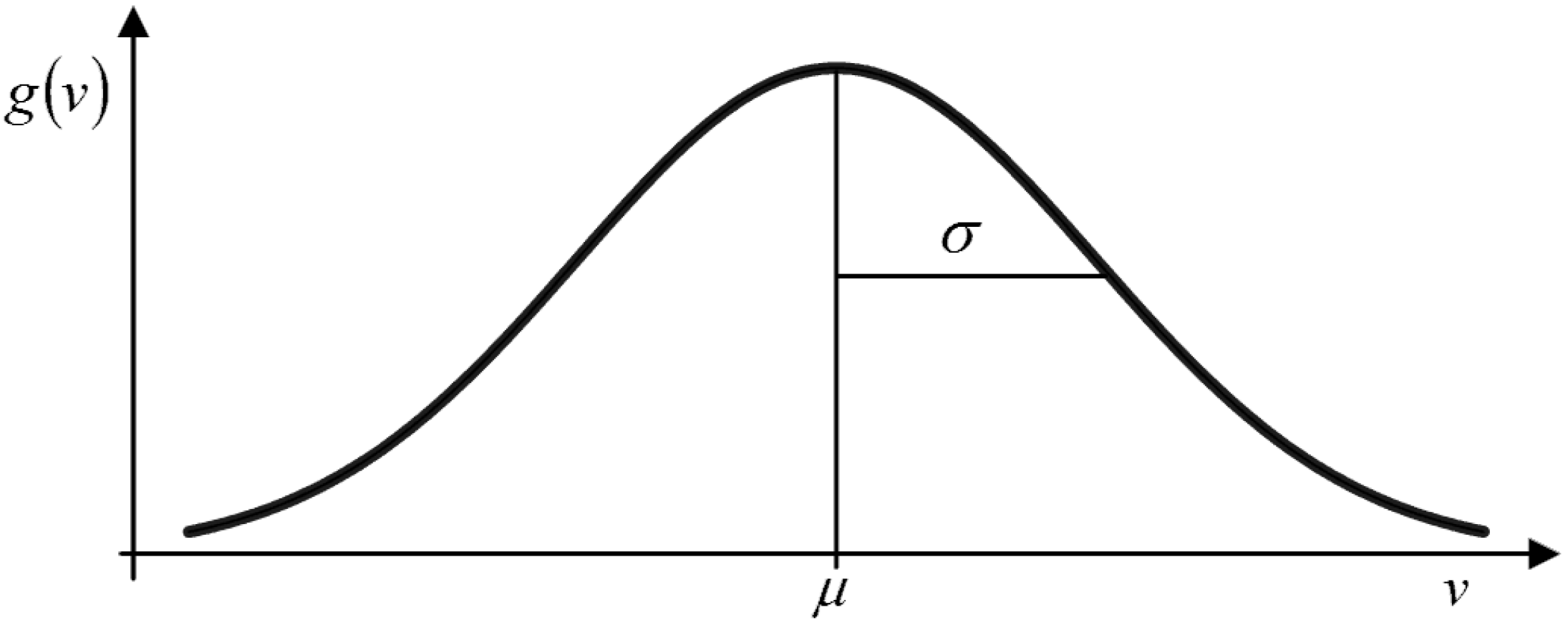
The proposed MDM is based on a local Gaussian function (
Figure 1) that is expressed in Equation (1):
where
v represents the prospection variable;
µ represents the “mean or central” value assigned to the prospection variable;
σ represents the “standard deviation” assigned to the prospection variable, that defines a width of the range of exploration; and
g represents the weight function corresponding to a value of the prospection variable
v.
Figure 1.
Graphical representation of local Gaussian function.
Figure 1.
Graphical representation of local Gaussian function.
Note that, in
Figure 1, the proposed local Gaussian function allows the selection of the central or mean value (
μ) and the standard deviation value,
σ. The selected central values for the Gaussian functions correspond to the current case values, and the standard deviation values can be chosen by an optimization process, as explained later. With these two parameters (
μ and
σ), which determine the Gaussian function, the weight values can be obtained according to the neighborhood or similarity between the historical cases and the current case. Thus, the MDM identifies historical cases with the highest similarity to the case for which it is intended to provide the electric power forecast, that is, the MDM determines higher weight values for a series of cases of electric power transitions that will be used to provide the forecast information.
Because an optimization process (to be explained later) can select the best inputs (variables from records) to be used by the model, assuming a HISIMI model that uses
l variables, the associated value that defines the “similarity” with the current case,
FHc, is defined in Equation (2):
where
gi,c represents the weight value associated with the local Gaussian function corresponding to the input variable
i.
2.3. Power Intervals
The objective of the model is to achieve a representation of power transitions that occurred in the past with similar input variable values. Even with a reduced database, there could be a large set of different power transitions. Thus, transitions between specific electric power values are not considered, but transitions between intervals of electric power values (power intervals) of the PV plant are considered.
This aspect requires defining a set of power intervals that allows transforming the electric power continuous variable into a discrete variable. So, a total of
n non-overlapped power intervals with the same width, covering all possible values for the electric power generation in the PV plant, are defined. Each interval is defined by its minimum and maximum power values (in kW),
a and
b, respectively. The average value of the interval
m is defined in Equation (3), where
am and
bm correspond to the minimum and maximum values of that interval:
With the average values of all the power intervals, the average power values vector, [
AP], is created, as shown in Equation (4), where
I1<
I2<…<
In:
This technique groups power values in a neighborhood that will be represented by the average power value of the corresponding interval.
2.4. Probability Matrix (PM)
We define two discrete random variables:
X associated with the interval corresponding to electric power value at future instant
t+k−1, and
Y associated with the interval corresponding to electric power value at future instant
t+k. Thus, the electric power interval
x ∈
X varies (and also the interval
y ∈
Y) from 1 to
n. Probabilities of transition of the power interval from instant
t+k−1 to the next one,
t+k, can be expressed by a square matrix with
n rows and
n columns applying the mechanism MDM. This matrix, named as the pseudo-probabilities matrix for hour
t+k,
PPMt+k, is shown in
Table 1. Each element in this matrix represents the pseudo-probability of a power transition from one power interval in instant
t+k−1 (interval
x, that is, row
x in the matrix) to another power interval in instant
t+k (interval
y, that is, column
y in the matrix). The element
PPMt+k (
x,
y), corresponding to row
x and column
y, is calculated using the sum of values
FHc from Equation (2) considering all cases in the database.
The “normalization” of values of the matrix of
Table 1 to values between 0 and 1, leads to the matrix
PMt+k, which contains the bivariate distribution of power transitions, from one power interval
x (associated with instant
t+k−1) to another power interval
y (associated with instant
t+k). Note that results are obtained after applying the mechanism MDM, which defines the space of global events of power transitions.
The elements of the
PMt+k matrix can be associated with a joint probability distribution
fXY (
x,
y) (
Table 2), that satisfies Equation (5):
where
fXY (
x,
y) represents the probability that the interval of the electric power variable is
x in a given instant, and
y in the following one,
i.e.,
P(
X =
x,
Y =
y).
Table 1.
Representation of a pseudo-probabilities matrix for n power intervals.
Table 1.
Representation of a pseudo-probabilities matrix for n power intervals.
| Pseudo-probabilities | Power interval in t+k |
| 1 | 2 | … | n |
| Power interval in t+k−1 | 1 | … | … | … | … |
| 2 | … | … | … | … |
| … | … | … | … | … |
| n | … | … | … | … |
Table 2.
Power transition probability matrix.
Table 2.
Power transition probability matrix.
| fXY (x, y) | y |
|---|
| 1 | 2 | … | n |
|---|
| x | 1 | fXY (1, 1) | fXY (1, 2) | … | fXY (1, n) |
| 2 | fXY (2, 1) | fXY (2, 2) | … | fXY (2, n) |
| … | … | … | … | … |
| n | fXY (n, 1) | fXY (n, 2) | … | fXY (n, n) |
Then, two marginal probability functions
fm1 and
fm2 can be defined, for each transition in
t+k, by Equations (6) and (7) respectively:
where
Rx denotes the set of all
fXY (
x,
y) for which
X =
x:
where
Ry denotes the set of all
fXY (
x,
y) for which
Y =
y.
Note that for each new forecast (for future time instant t+k), a probability matrix is created and therefore also a bivariate distribution.
2.5. Model Outputs
2.5.1. Uncertainty Prediction
Some of the main outputs of the HISIMI model are the probability values of power transitions for each future instant t+k (transition from instant t+k−1 to the instant t+k). This information can be processed in order to obtain different types of useful predictions. In order to obtain predictions of forecast uncertainty, a new discrete probability distribution for each instant can be obtained as the product of two discrete distributions, fm1 and fm2, obtained for two consecutive forecasting instant, t+k−1 and t+k, denoted as fm1;t+k−1 and fm2;t+k.
We define an “uncertainty vector” for instant
t+k, [
u]
t+k, for the uncertainty prediction, as the product of the values of the marginal probability functions defined in Equations (6) and (7), as is given in Equation (8).
Afterwards, the values of the vector [u]t+k, defined in Equation (8), are normalized (to values between 0 and 1), leading to a new vector, [un]t+k, in which each element of this new vector, corresponding to a power interval, is associated with the probability that the forecasted electric power value belongs to that interval; thus, this vector gives a measure of uncertainty associated with electric power forecasts.
2.5.2. Point Forecast
The point forecast
PFt+k (in kW) can be obtained by computing the expected power value for a future instant
t+k as seen in Equation (9):
where
AP(
y) is the element of the vector [
AP] corresponding to the power interval
y, and
un,t+k (
y) is the element of the vector [
un]
t+k corresponding to the power interval
y.
3. Optimization of the PV Power Forecasting Model
The proposed HISIMI model includes a set of parameters whose values can be optimized. These parameters correspond to the number of power intervals, and the standard deviation of the Gaussian functions used for the prospection variables. In order to optimize the values of these parameters, an optimization process ruled by a genetic algorithm (GA) [
18] was developed. In this process, the selection of the best input (prospection) variables, among those available ones, was also included. All available input variables must be normalized in the range 0 to 1. This normalization allows using the same range in the standard deviation of all the prospection variables.
Binary encoding with 1 and 0 is used to store the value of these parameters in the chromosome that defines the solution stored in each individual. The structure chosen for the chromosome used by the GA is shown in
Figure 2. The chromosome is composed of three or more genes, each one with a fixed size. First
p bits, which compose the first gene, correspond to the inputs (prospection) variables used by the HISIMI model among those available (we suppose a total of
p available variables in the historical database), that is, an “1” value in the bit
bij means that the input
j is used by the model as prospection variable, while a “0” value means that the input
j is not used by the model. At least one of these first
p bits must be activated (value “1”) because the model represented by the individual needs one or more inputs (prospection variables). The second gene, with a 6 bits size, corresponds to the number of intervals minus two, expressed in binary, used by the model: a value “000000” means 2 intervals, while a value “111111” means 65 intervals. The third gene corresponds to the standard deviation of the Gaussian function for the first input (prospection) variable,
σ1 (the first variable selected as input); it is composed of 16 bits, and its value is equal to the binary number contained in the 16 bits plus one and divided by 32,768. So, the standard deviation can take values from 2
−15 to 2 (remember that input variables are normalized). The fourth gene, if available, corresponds to the standard deviation of the Gaussian function of the second (prospection) variable selected as input, and so on for the following genes. In
Figure 2, the standard deviation of the Gaussian function for the last input variable selected is
σl, assuming that
l inputs have been selected in the first gene. The maximum number of genes is equal to the number of available input variables plus the two first genes.
Figure 2.
Structure of the chromosome used in the optimization of the HISIMI model.
Figure 2.
Structure of the chromosome used in the optimization of the HISIMI model.
As a first step in the optimization process, an initial population is created randomly: the value of each bit in each individual is randomly assigned. After creating the two first genes, the remaining genes that compose the individual are completed according to the number of variables selected (as inputs of the HISIMI) in the first gene.
The fitness function for the GA optimization was the inverse of the RMS error with the data set used in the construction of the HISIMI model. RMS (root mean square) error is defined in Equation (10), where
N represents the number of data evaluated,
Pi the real power generation value and
the value obtained (forecasted) with the model, and the index
i covers all instants corresponding to the data set which error is evaluated:
So, individuals that represented better forecasting models would achieve greater fitness values. In the creation of a new population, roulette wheel selection, elitism (only the best individual), two-point crossover and mutation were used. After a sufficient number of generations, the parameters of the best HISIMI model were obtained, that is, the optimization process selected the inputs used for the best model, among those available inputs, the number of power intervals for the electric power generated by the PV plant, and the values of the standard deviations of the Gaussian functions used in the MDM mechanism.
In order to prevent over-fit of the HISIMI model to the data used to build the model, we used 5-fold cross-validation [
19]: The data set used to develop the model was divided into 5 subsets of approximately equal size. The evaluation of the model is carried out in five stages; in each stage, one subset is taken as the cross-validation data set, while the other four subsets are used to build the model. The RMS error of the studied model is the average of the RMS errors with the cross-validation data sets in the five stages.
4. Model Testing
The methodology described in the previous two sections was applied to develop a short-term forecasting model for a grid-connected PV plant. The plant, with ground mounted fixed panels and a capacity of 2.8 MWp, is located in Spain. The data available to develop the model include the hourly power generation in the PV plant for a whole year. The data show high intra-hour variability of the power output of the PV plant.
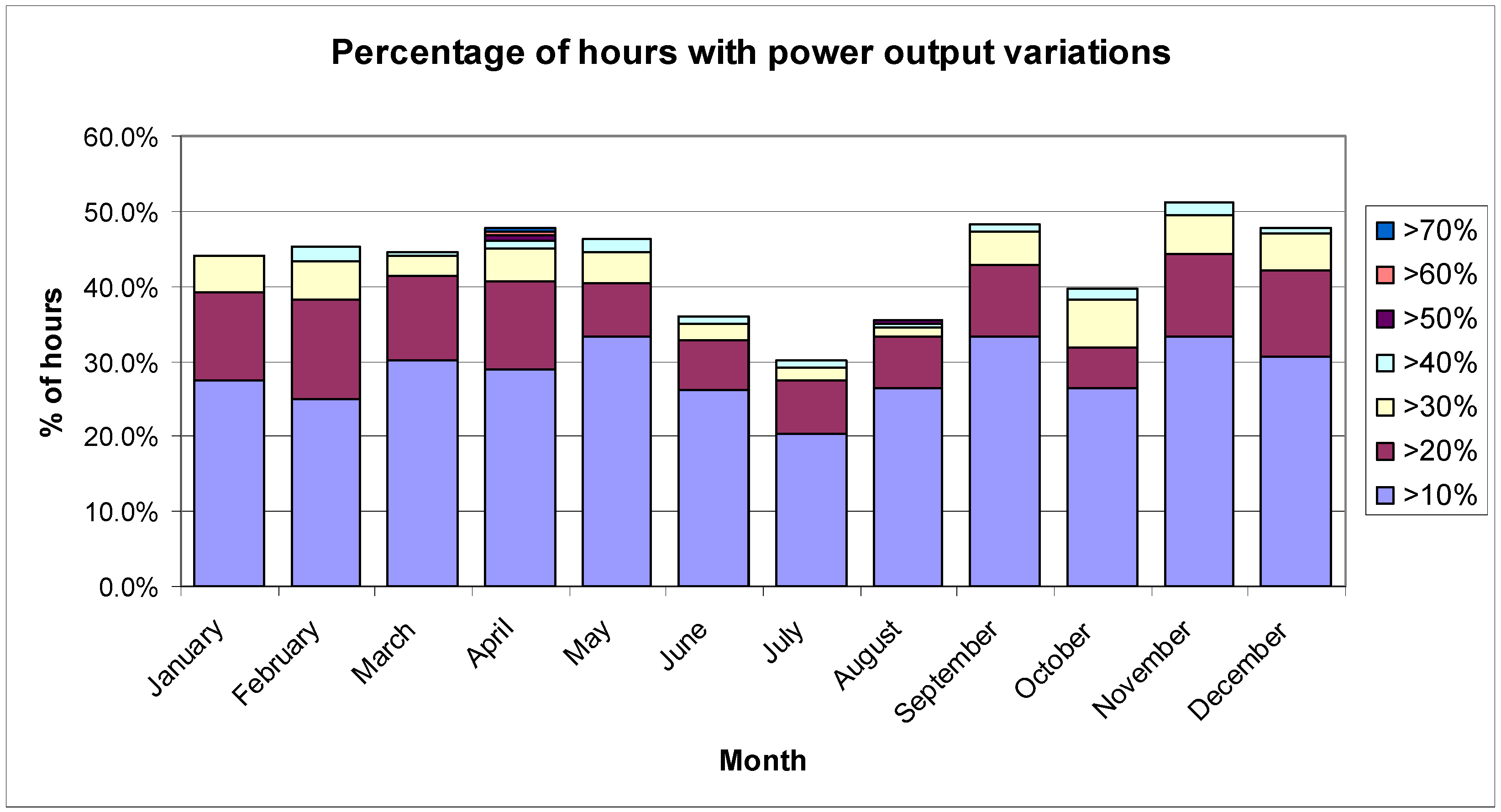
Figure 3 illustrates the percentage of hours with power output variations of more than 10%, 20%,
etc., with respect to power rating of the PV plant, in a monthly basis, for the period between 09:00 to 14:00 (solar hour). In that figure, the vertical axis represents the percentage of hours, in which the absolute difference (variation) for the power output of the PV plant, from one hour to the following one, is greater than 10%, 20%,
etc., of the power rating. Notice that at least 30% of hours presents variability over 10% (280 kW) of power rating (2.8 MW) for all the months. Furthermore, for the data of the whole year, 43% of hours in the considered period presents variability over 10% of the power rating.
Figure 3.
Percentage of hours with power output variations with respect to power rating of the PV plant.
Figure 3.
Percentage of hours with power output variations with respect to power rating of the PV plant.
The available data also include forecasted values for the hourly average surface shortwave radiation (
v1) and temperature (
v2) obtained with an NWP tool. This tool was the Weather Research and Forecasting (WRF) model [
20], a mesoscale NWP model that can simulate atmospheric dynamics and provide numerical predictions for a wide set of weather variables in a selected geographic zone. The hourly average surface shortwave radiation and temperature values correspond to those forecasted (with the NWP tool) with the data assimilation (moment when real weather measures were supplied to the model to predict the future values) of the hour 00:00. The forecasted hourly average values include all the values for the next 24 h, making that forecasting horizons for the HISIMI model range from 1 to 24 h. Obviously, the maximum forecasting horizon with the HISIMI model coincides with that of the weather variables forecasted with the NWP tool (24 h in our case).
Because the production in a PV plant is very dependent on the solar hour, we included two variables in the historical database to represent it (named
v3 and
v4). These two variables are expressed in Equation (11), where
h corresponds to the solar hour for the location of the PV plant for the corresponding instant:
So, a record in the database contains ten values: two values for the forecasted hourly surface shortwave radiation, two values for the hourly average surface temperature, two values for variable v3, two values for variable v4, and two values for the hourly power production in the PV plant. The two values of each variable correspond to two consecutive instants, c−1 and c.
The database with the historical cases was divided into two sets: 80% of the records were used as the training set, while the remaining 20% of the records were used as the testing set. Only the training set was used to build the HISIMI forecasting model, while the testing set was only used for comparative purposes with other forecasting models.
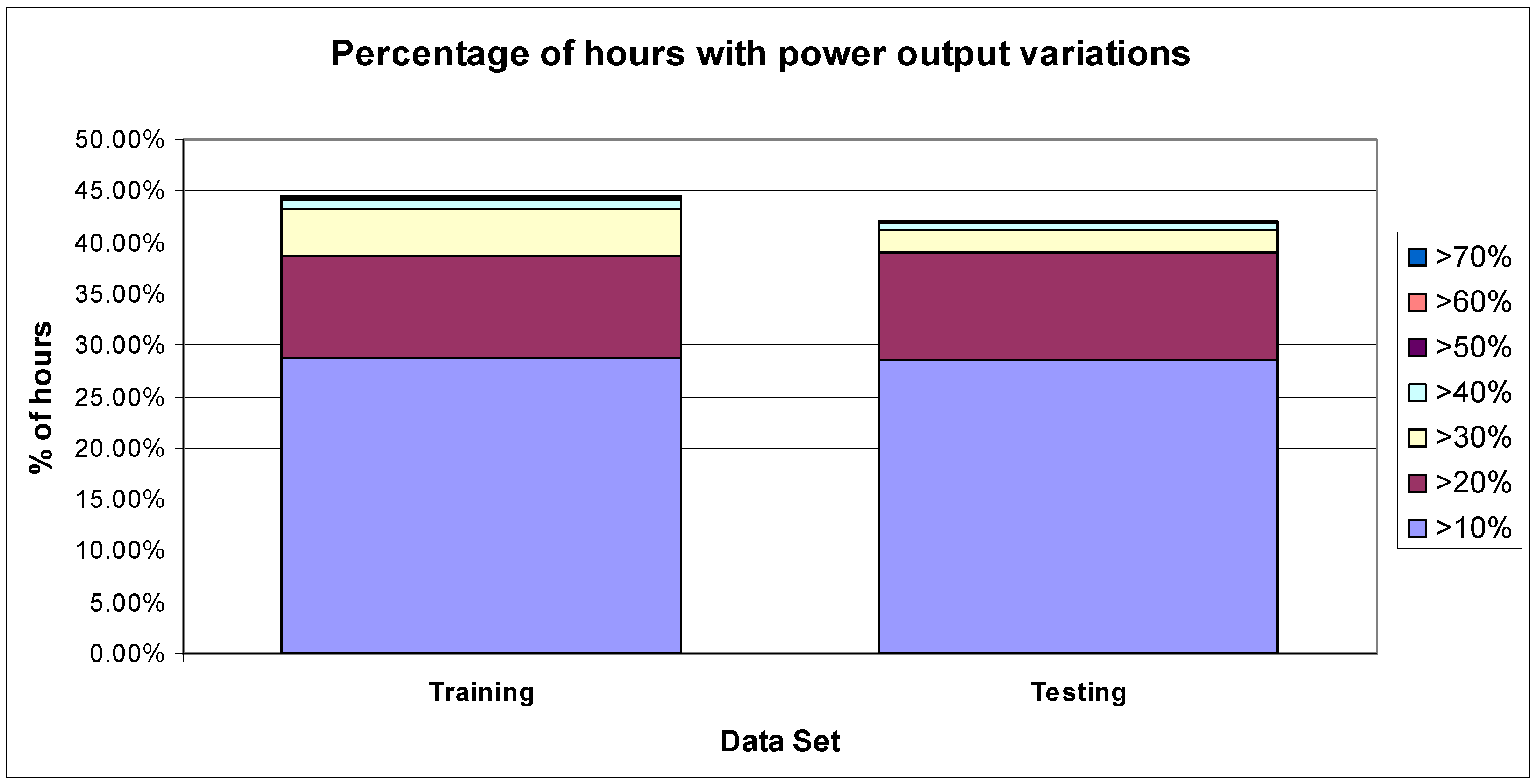
Figure 4 shows the variations in the power output of the PV plant during the diurnal period of 9:00–14:00 (solar hour) for both data sets of training and testing. The percentages of hours with variations over 10% of the power rating are quite similar for such data sets.
Figure 4.
Percentage of hours with power output variations with respect to power rating of the PV plant, for the data sets of training and testing.
Figure 4.
Percentage of hours with power output variations with respect to power rating of the PV plant, for the data sets of training and testing.
The structure of the HISIMI model was optimized with a genetic algorithm (described in
Section 3). The population size was 50 individuals and the number of generations 50. The crossover rate was 90% and the mutation rate 2%. Elitism was applied copying the best individual from one generation to the following one. The fitness function was the inverse of the RMS error with the data of the training set using 5-fold cross-validation. The model obtained after the optimization process used the input variables
v1 (forecasted hourly average surface shortwave radiation),
v2 (forecasted hourly average surface temperature), and
v4. The number of power intervals was 9 and the range of any interval was 314 kW. The two extremes of the last interval (ninth) were centered on the maximum value of the power output of the PV plant for the training data set (2512 kW in our case) and the ones of first interval were centered on the minimum power output,
i.e., they were centered in 0 kW. Thus the first interval spanned from −157 to 157 kW, the second from 157 to 471 kW, and so on until the ninth interval from 2355 to 2669 kW. The standard deviations for the three used inputs of the HISIMI model were 0.314453125 (for
v1), 0.193359375 (for
v2) and 0.076171875 (for
v4).
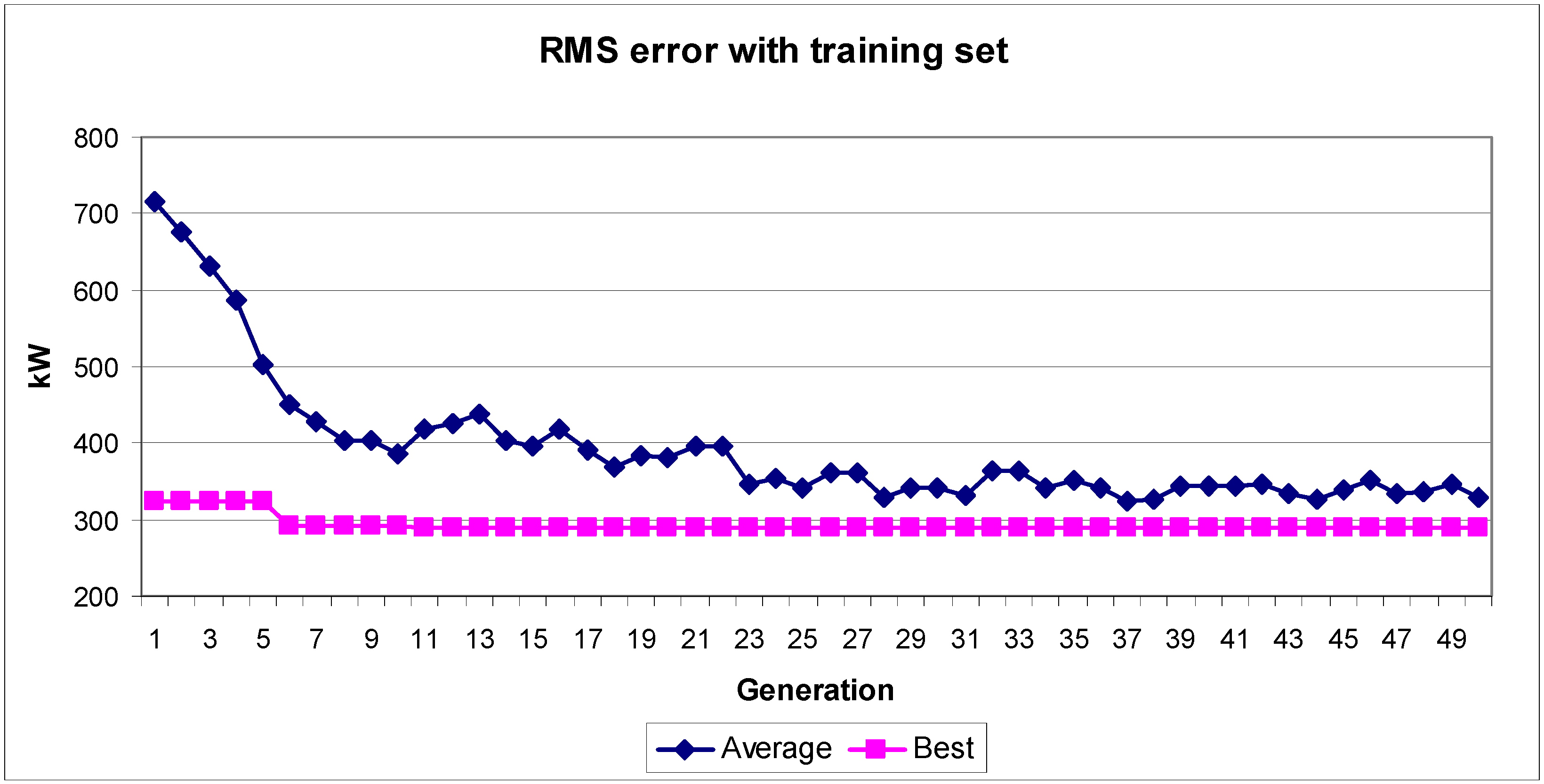
Figure 5 plots the RMS error with the data of the training set, using the 5-fold cross-validation, throughout the optimization process for the best individual in each generation and the average value of RMS error for all the individuals in each generation.
Figure 5.
RMS error of the best individual and average RMS error of all the individuals in each generation.
Figure 5.
RMS error of the best individual and average RMS error of all the individuals in each generation.
Lastly, the obtained HISIMI model was applied to the testing set. The RMS error for all the data in the testing set (forecasting horizons from 1 to 24 h) was 283.89 kW, just 10.14% with respect to the total capacity of the PV plant.
In order to evaluate the HISIMI model performance, two other forecasting models were built for comparative purposes. The first one was a variation of the persistence model. The classical persistence model offers, as forecast for any horizon, the last known value,
i.e., the average power generation value in the last hour. In our case, we have modified the persistence model so that it offers the power generation in the PV plant in the previous day at the same hour as that corresponding to the forecasting horizon; this variation of the persistence model was used in [
15] for comparative purposes. The second model was an artificial neural network based model: a multilayer perceptron neural network, MLP, with one hidden layer, which could use any of the available variables as inputs, and offered only one output: the hourly average power production in the PV plant. 75% of the cases in the training data set was used to train the network, while the remaining 25% of the cases was used as the cross-validation set. The structure of the MLP based model was also optimized with a genetic algorithm. The transfer function for the neurons in the hidden layer was the hyperbolic tangent and a linear hyperbolic tangent function was used for the output neuron. In the optimization process, the number of neurons in the hidden layer, the inputs used by the network, and the parameters of the back-propagation training algorithm (learning factor and momentum) were selected. The population size was 50 individuals and 50 generations were completed. The final MLP neural network obtained after the optimization process had 15 neurons in the hidden layer.
Table 3 summarizes the main parameters of the optimization of the HISIMI and MLP models.
Table 3.
Main parameters of the optimization of the HISIMI and MLP models.
Table 3.
Main parameters of the optimization of the HISIMI and MLP models.
| Model | HISIMI | MLP |
|---|
| Population size | 50 | 50 |
| Number of generations | 50 | 50 |
| Crossover rate | 90% | 90% |
| Mutation rate | 2% | 1% |
| Inputs selected | v1, v2, v4 | v1, v3, v4 |
| Power Intervals | 9 | - |
| Neurons in hidden layer | - | 15 |
Once these comparative models were built, they were applied to forecast the PV plant’s hourly power generation for the data of the testing data set. RMS errors were 286.11 kW for the MLP based model, and 445.48 kW for the persistence model. Therefore, the optimized HISIMI model obtained better results than the other two models (since the HISIMI model achieved the aforementioned 283.89 kW). The improvement in RMS error with respect to the results obtained with another model is calculated by Equation (12), where
RMSreference corresponds to the RMS error obtained with the model used as reference, and
RMSmodel corresponds to the RMS error of the compared model. The RMS forecasting error for the HISIMI model was 0.8% better than that obtained with the MLP model, and 36.3% better than that obtained with the persistence model.
Table 4 summarizes the forecasting results obtained with the three models:
Table 4.
Summary of forecasting results.
Table 4.
Summary of forecasting results.
| Forecasting Results | HISIMI | MLP | Persistence |
|---|
| RMS error (kW) | 283.89 | 286.11 | 445.48 |
| Normalized RMS (%) | 10.14 | 10.22 | 15.91 |
| Improvement with respect to Persistence (%) | 36.3 | 35.8 | - |
| Improvement with respect to MLP (%) | 0.8 | - | - |
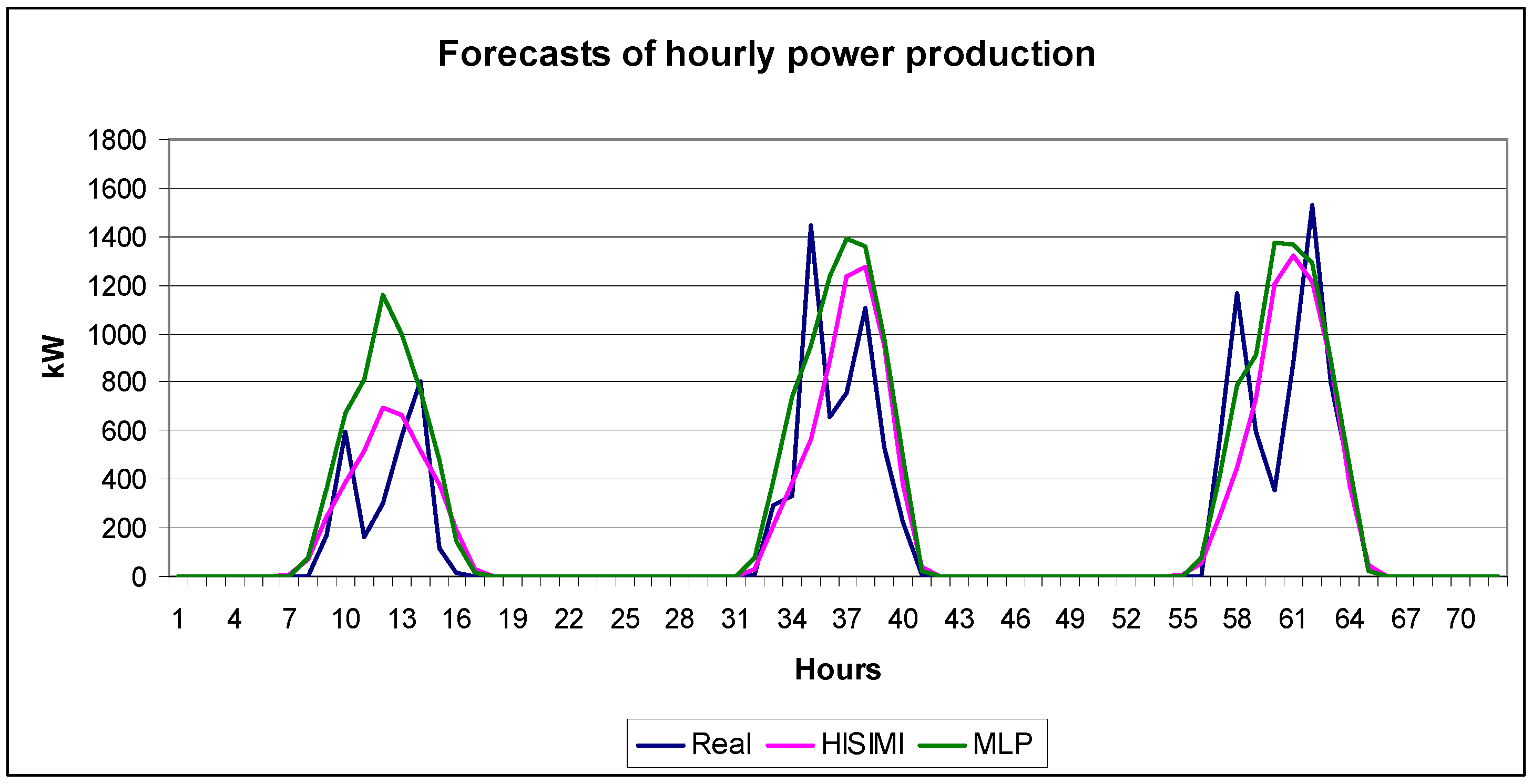
Figure 6 shows real power production and the corresponding hourly PV power spot forecast obtained with the HISIMI and MLP models for three consecutive days (in the testing data set), which are cloudy and rainy days. Power forecasts, from the studied models, were carried out in the first hour in the morning, covering all hours of the day.
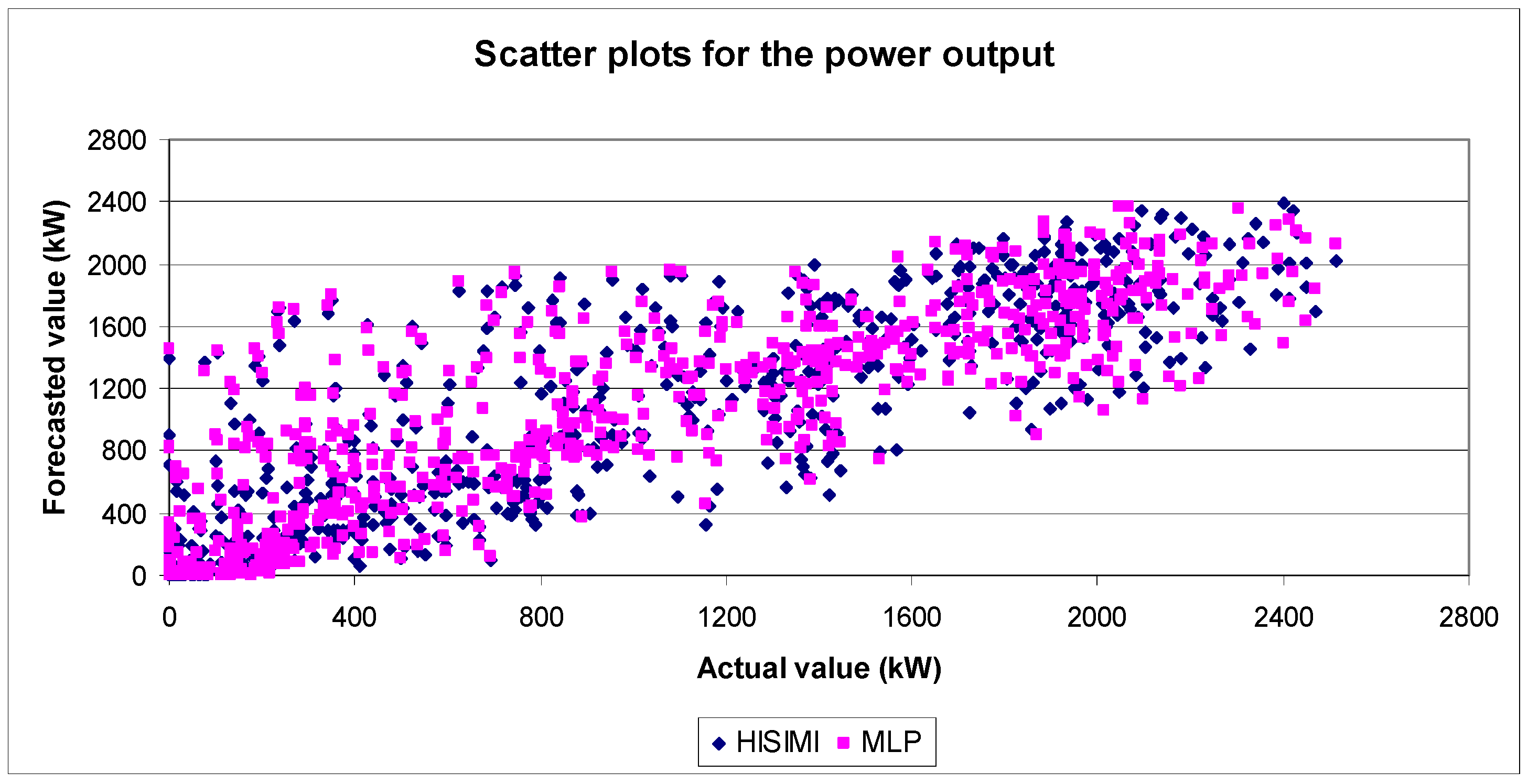
Figure 7 represents the scatters plots of forecasted values
versus actual values of power output for HISIMI and MLP models.
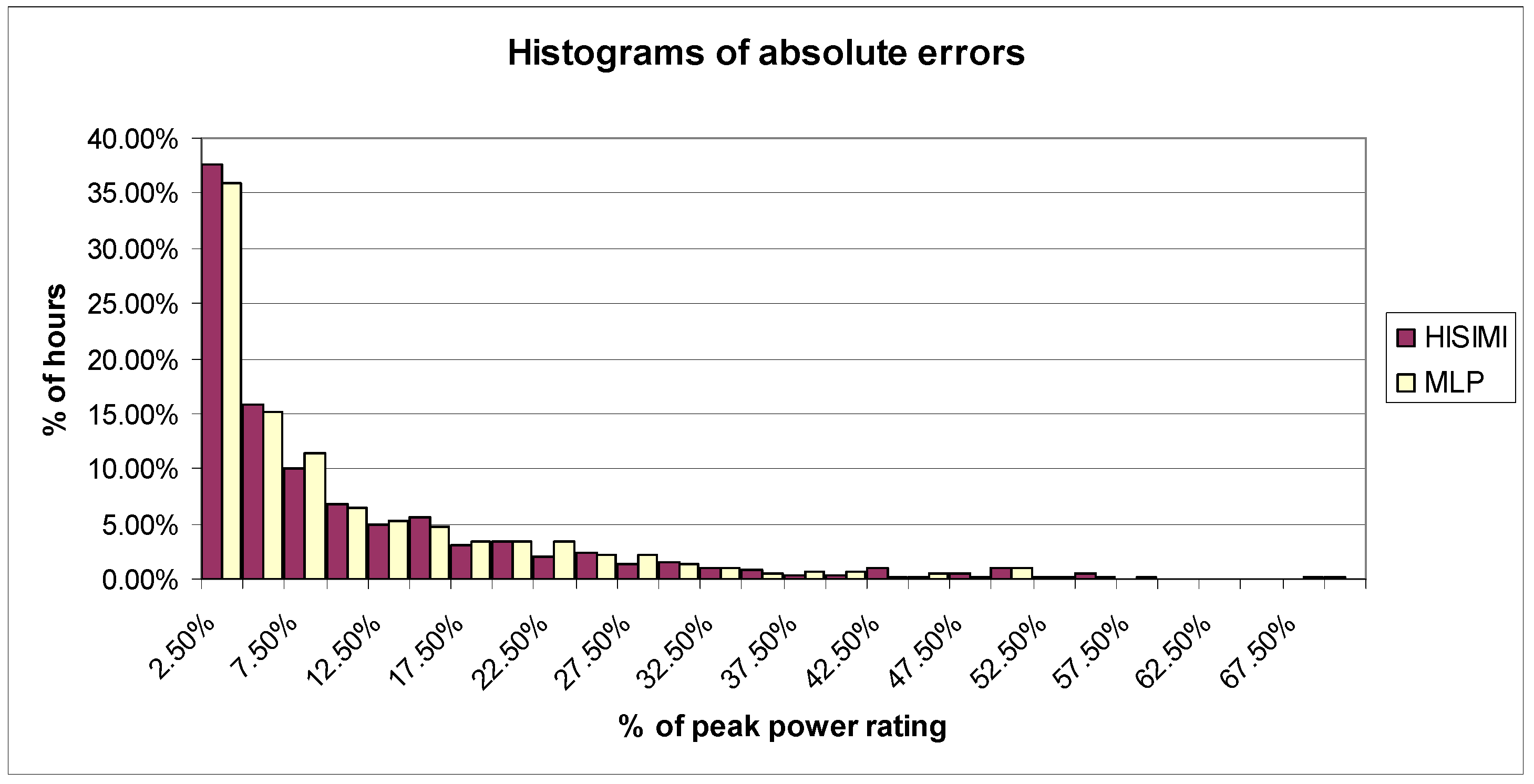
Figure 8 shows the histograms of the absolute forecasting errors, for both models (HISIMI and MLP), for all diurnal hours in the testing data set. Absolute errors are expressed, in the horizontal axis of
Figure 8, in percentage with respect to the power rating of the PV plant. The vertical axis represents the percentage of diurnal hours in the testing data set. Absolute errors for both models are quite similar, although the HISIMI model presents more hours with lower errors. For example, in 37.65% of the hours, the absolute forecasting error of the HISIMI model remains under 2.5% of the power rating, while for the MLP model this percentage of hours is 36%.
Figure 6.
Forecasts of the hourly power production for three cloudy and rainy days in the testing set.
Figure 6.
Forecasts of the hourly power production for three cloudy and rainy days in the testing set.
Figure 7.
Scatter plots of forecasted values versus actual values of power output for HISIMI and MLP models.
Figure 7.
Scatter plots of forecasted values versus actual values of power output for HISIMI and MLP models.
Figure 8.
Histograms of absolute errors for the HISIMI and MLP models in the testing data set.
Figure 8.
Histograms of absolute errors for the HISIMI and MLP models in the testing data set.
Thus, spot forecasting results obtained by HISIMI model are better than those obtained with the other two models (MLP model and persistence model); furthermore, a key advantage of the HISIMI model is the uncertainty prediction (probabilities) associated with the numerical point (spot) forecasting value (analyzed in the following
Section 5). The two other forecasting models are not capable of providing such useful forecasting information (probabilities).
5. Analysis of Information Provided by the PV Power Forecasting Model
Most of forecasting models described in the literature only provide spot power forecasts (point forecasts), while the HISIMI model provides more complete information based on power transitions for each forecasting time: spot forecasts and uncertainty predictions are computed using discrete probability functions.
In our case of a real-life grid-connected photovoltaic plant, the daily PV power production forecast was carried out with the data of 00:00, with forecasting steps of one hour. The uncertainty associated with each point forecast can easily be calculated using the primary output of the HISIMI model, that is, the discrete probability distribution associated with the electric power transition for each step in the forecasting horizon, i.e., for each one of the hour periods from 00:00 to 23:00.
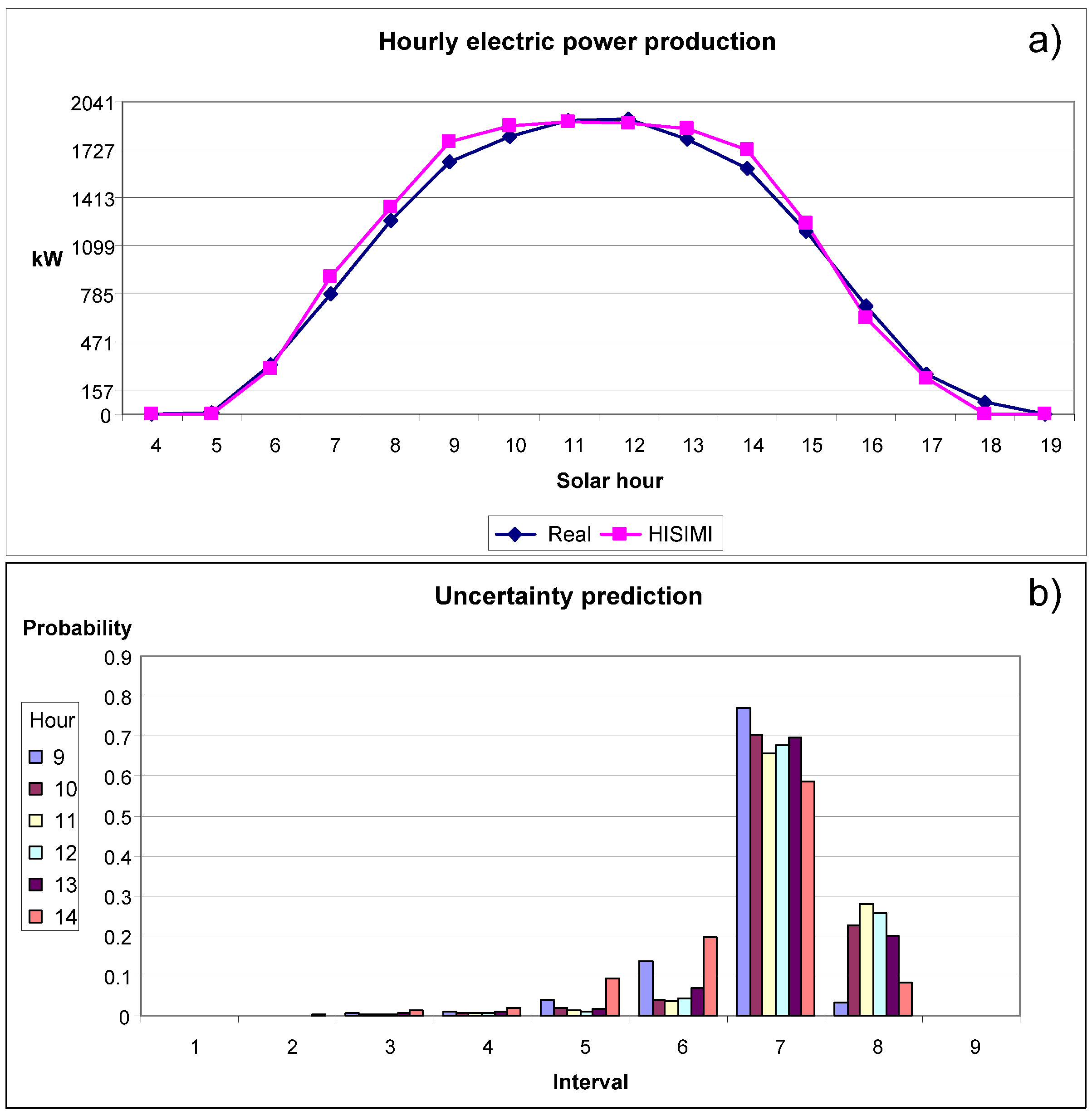
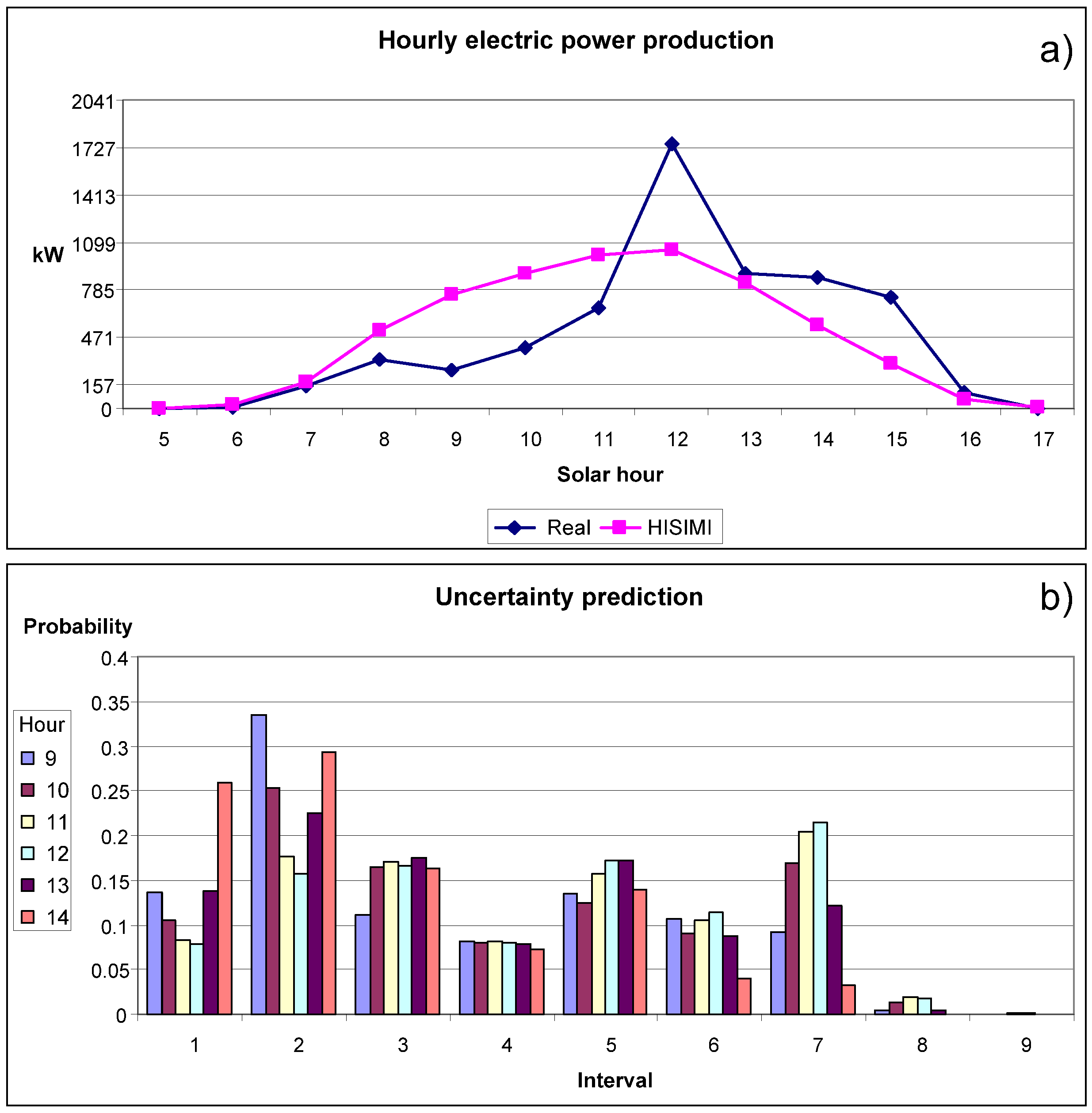
Figure 9a plots the real hourly PV power production values as well as the spot forecasted values of electric power from the HISIMI model, for a sunny day belonging to the testing data set. The vertical axis shows limits of the power intervals for the HISIMI model: the first interval corresponds to values between −157 and 157 kW (in
Figure 9a only the positive half of the interval is represented); the second interval corresponds to power output values between 157 and 451 kW; and so on.
Figure 9b gives the probability distributions, corresponding to the uncertainty of the point forecast, for central hours of the day (from 9:00 to 14:00). The horizontal axis of
Figure 9b shows the power intervals, while the corresponding probability values are represented in the vertical axis. Thus, for example, the hour 9 (period between 9:00 and 10:00) presents two intervals with significant probabilities: the sixth and the seventh. Notice that for a solar hour containing only two consecutive power intervals with significant probabilities (above the value 0.1), the uncertainty is relatively low (with respect to solar hours containing three o more power intervals with significant probabilities), because the point forecast should correspond mainly to a weighted average value of the powers represented by both intervals. For the day represented in
Figure 9a, the uncertainty about the spot forecasts of electric power is very low, because there are few power intervals with significant probabilities in each hour (only one or two consecutive power intervals).
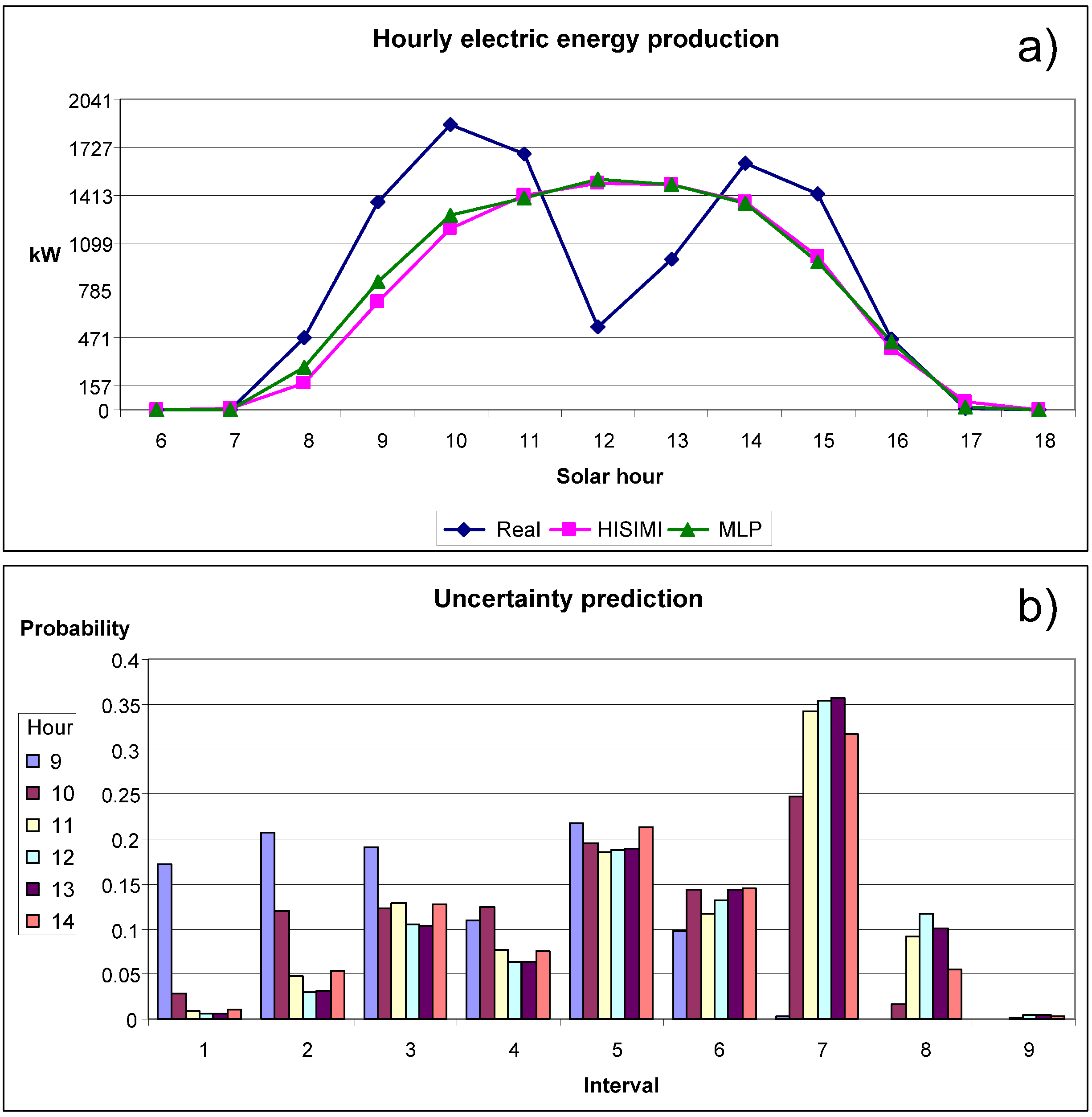
Figure 10a plots the real hourly PV power production values and the forecasted ones of the HISIMI model for a partly cloudy day belonging to the testing data set. In this case, the forecasts differ from the actual values of power output, especially in hours from 7:00 to 10:00, and in hours from 12:00 to 15:00.
Figure 10b shows the uncertainty associated with the spot forecasts for those hours: only for the hour from 12:00 to 13:00 there are two power intervals with significant probabilities. The other five hours present at least three power intervals with significant probabilities.
Figure 11a plots the values of the real hourly PV power production and the forecasted ones of the HISIMI model for a rainy day (most of the hours with rain) belonging to the testing data set. Spot forecasts present significant errors.
Figure 11b shows the uncertainty associated with the spot forecasts for the hours between 9:00 and 14:00. All hours in the represented period have at least three power intervals with significant probability. For example, there are five power intervals with probability over 10% for hour 9:00; this also occurs for the four selected hours between 9:00 and 13:00; and four power intervals can be identified in the selected last hour (from 13:00 to 14:00). The uncertainty (associated with the spot forecasts) provided by the HISIMI model is notably high for the day represented in
Figure 11a.
Figure 12a shows the values of forecasted and real hourly power output for a cloudy and rainy day (cloudy day with showers). In that figure the spot forecasts obtained with HISIMI model are represented, as well as the spot forecasts obtained with the MLP model. Both models provide quite similar spot forecasts, with significant errors with respect to the actual power output value.
Figure 12b represents the uncertainty prediction for six central hours of that day, obtained with HISIMI model. There are at least three power intervals with significant probability for six hours represented in the figure, denoting a high uncertainty. So, although the HISIMI model and the MLP model provide very similar spot forecasts, the HISIMI also provides information to help in the evaluation of the risk assumed using those values of spot forecasts.
Analyzing the information produced by HISIMI model we highlight the differences between the results provided by our model and those offered by common short-term power point (spot) forecasting systems. With the model described in this paper, the user has access to more comprehensive information, including that related to predictions of uncertainty. The modeling of the uncertainty in the spot forecast, in the form of probability distributions, provide the possibility of analyzing the associated risk when the spot forecasted values are used to prepare energy sale offers for electricity markets.
Figure 9.
Forecasted hourly power production (a) and uncertainty prediction for six central hours; (b) (from 9:00 to 14:00) on a sunny day.
Figure 9.
Forecasted hourly power production (a) and uncertainty prediction for six central hours; (b) (from 9:00 to 14:00) on a sunny day.
Figure 10.
Forecasted production of hourly power (a) and uncertainty prediction for six hours; (b) on a partly cloudy day.
Figure 10.
Forecasted production of hourly power (a) and uncertainty prediction for six hours; (b) on a partly cloudy day.
Figure 11.
Forecasted hourly power production (a) and uncertainty prediction for six central hours; (b) (from 9:00 to 14:00) on a rainy day.
Figure 11.
Forecasted hourly power production (a) and uncertainty prediction for six central hours; (b) (from 9:00 to 14:00) on a rainy day.
Figure 12.
Forecasted hourly power production (a) and uncertainty prediction for six central hours; (b) (from 9:00 to 14:00) on a cloudy and rainy day.
Figure 12.
Forecasted hourly power production (a) and uncertainty prediction for six central hours; (b) (from 9:00 to 14:00) on a cloudy and rainy day.
6. Conclusions
A new short-term power forecasting model for PV plants, HISIMI, has been described in the paper. This model presents an innovative set of characteristics, which are:
The HISIMI model allows a stochastic modeling based on similarity between input values in a database of historical cases. This similarity focuses mainly on variables forecasted by NWP tools.
A database with a significant number of historical cases is used to model stochastic forecast, by creating discrete probability distribution functions.
A genetic algorithm optimizes the structure of the HISIMI model, allowing the selection of the best inputs (variables) to be used by the model as well as the optimal values of basic parameters that define the model.
The stochastic modeling of electric power transitions allows for the estimation of uncertainties in point (spot) forecasts of electric power. Uncertainty results obtained from HISIMI provide the probability distributions associated with the spot values.
Spot forecasts are calculated using such discrete probability distributions.
Another useful characteristic of the HISIMI model is its ability to easily update the database used by this model. As soon as new past values are available, they can be included in the database. If window techniques are used, i.e., the database is limited to the last period defined by a time window (for example, last six months), even the HISIMI model could be easily be adapted to a new NWP tool that would provide the prospection variables.
The forecasting model of this paper has been tested using real-life data which show high intra-hour variability of the power output of a photovoltaic plant. This model has improved spot forecasting results with respect to the ones from the persistence model and the MLP model (non-stochastic models).
The new model presented in this paper overcomes common short-term forecasting models: besides the value for spot forecasts, provided by conventional forecasting models, the proposed model achieves uncertainty values of the spot forecasts. This new forecasting result (i.e., uncertainty) allows for integration of the HISIMI model into applications where there is a risk associated with forecasting errors. This risk is evident in electricity markets where forecasting errors, and the consequent deviations between values of real power generation and offered (forecasted) power, can lead to economic penalties: in the case of these penalties, the information regarding the uncertainty is very useful to advance an expected value of penalty, so the market agent can plan to cover the risk.