Single Switched Capacitor Battery Balancing System Enhancements
Abstract
:1. Introduction
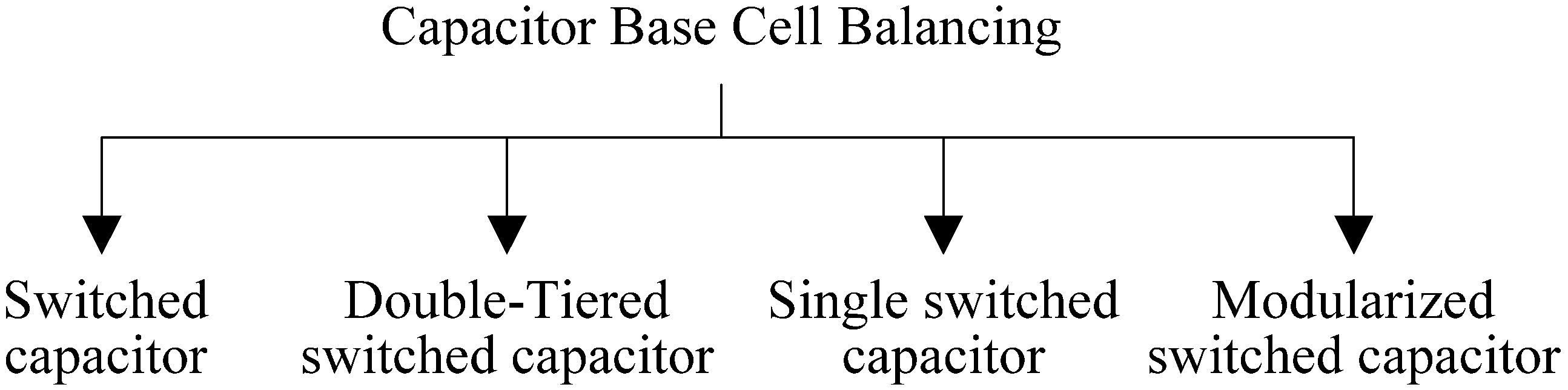
2. Shuttling Capacitor Cell Balancing Topologies
2.1. Switched Capacitor
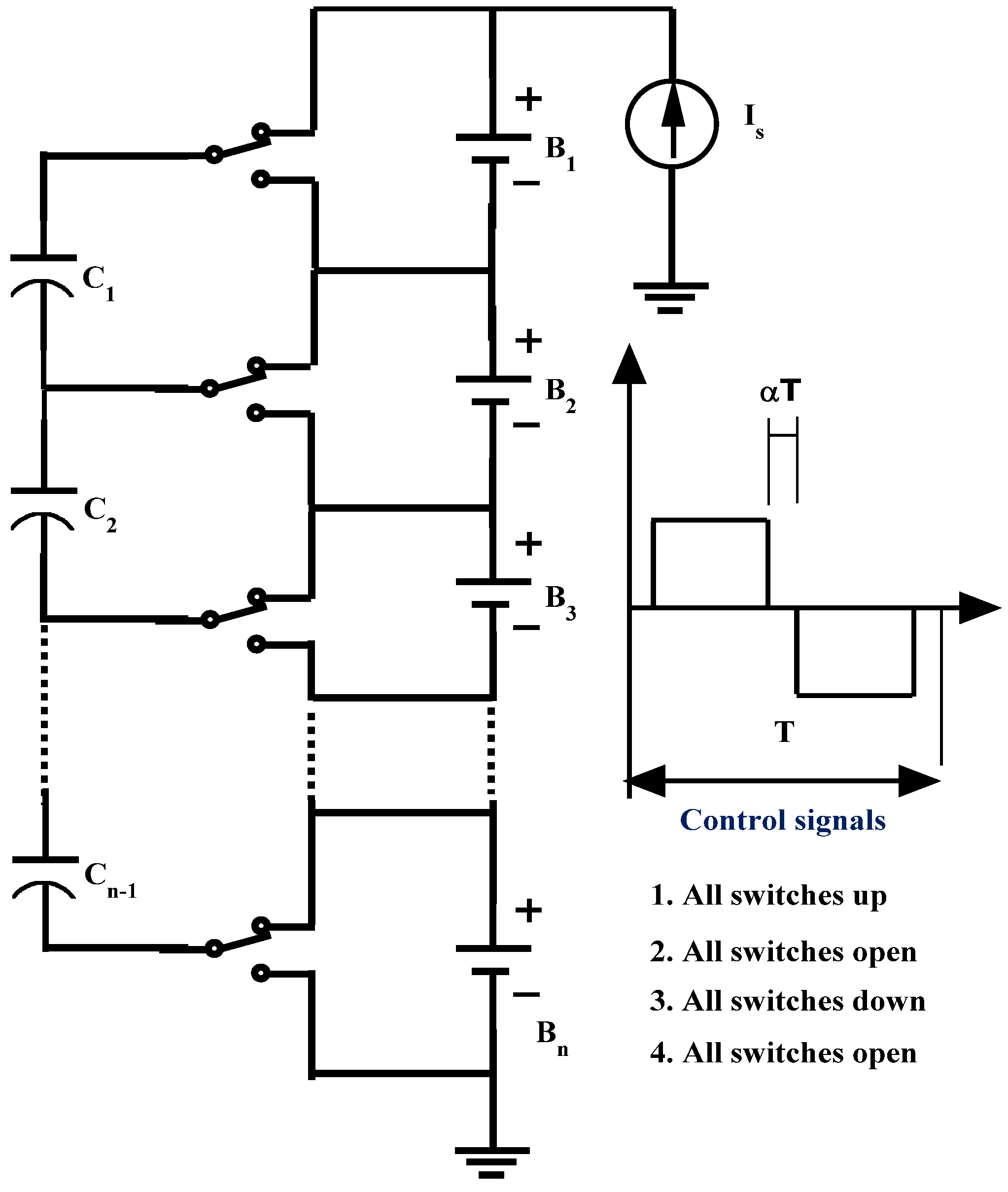
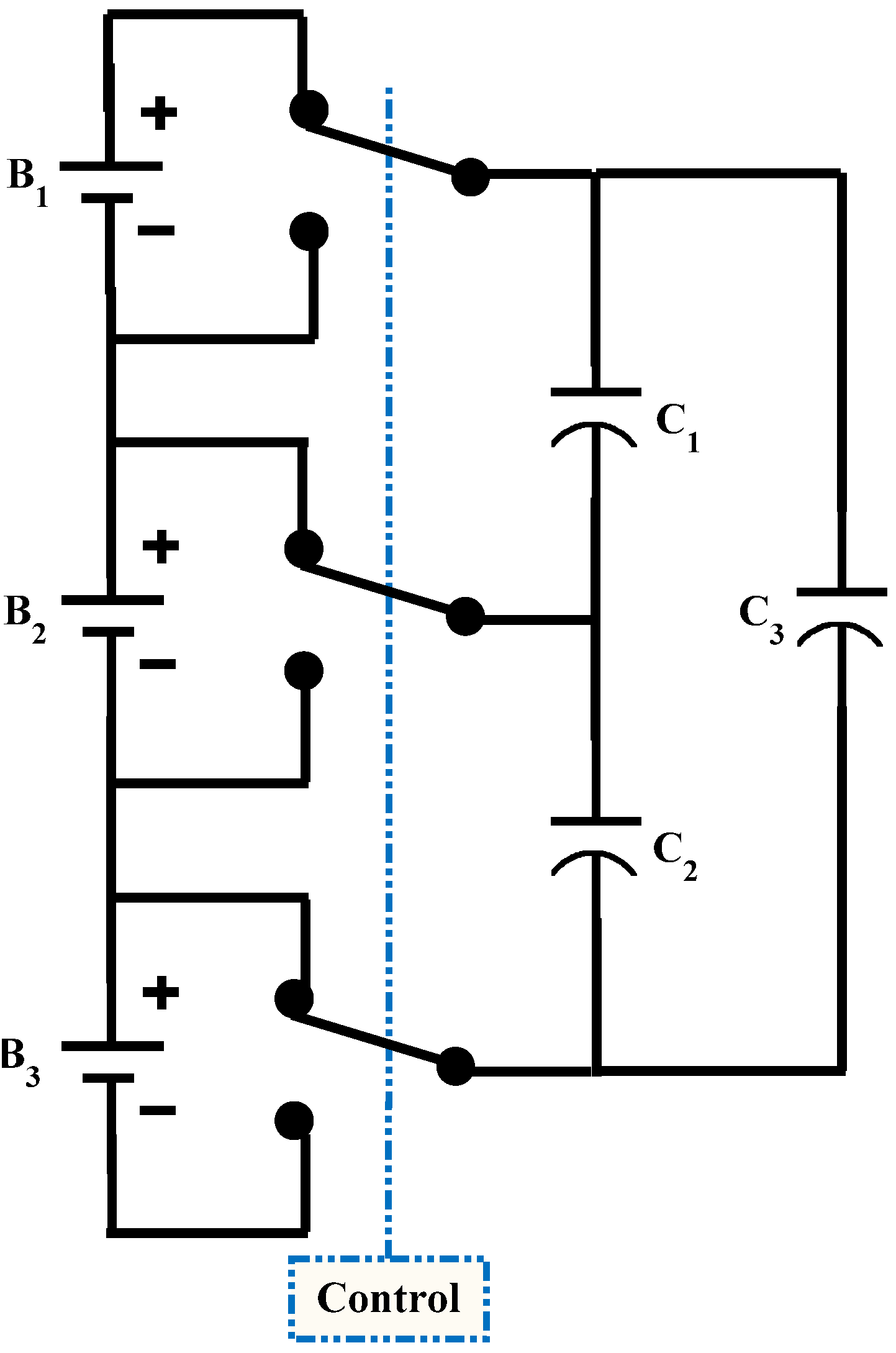
2.2. Double-Tiered Switched Capacitor
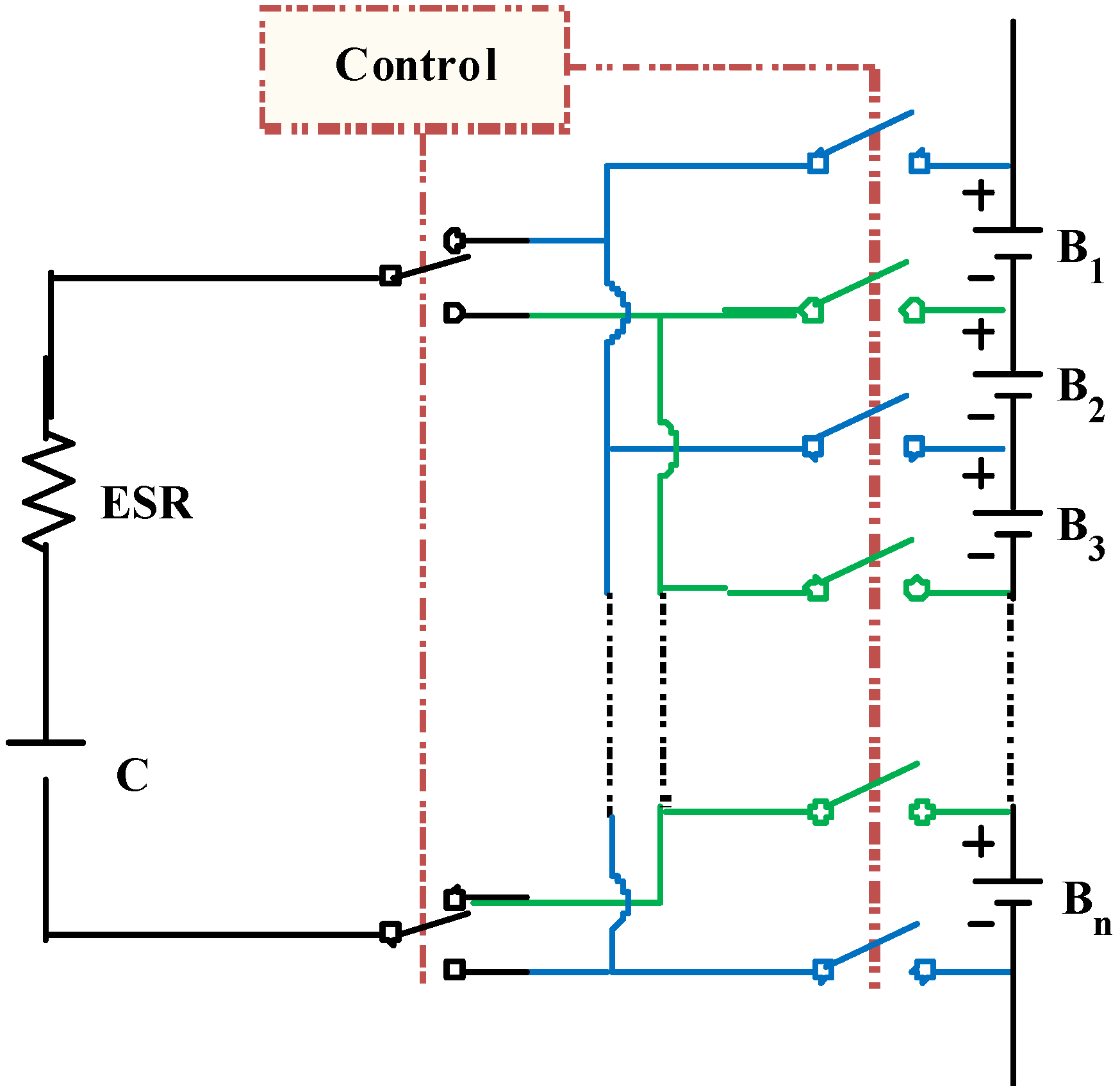
2.3. Single Switched Capacitor
| No. of cells | SC switches (2n) | SSC Switches (n + 5) |
|---|---|---|
| 2 | 4 | 7 |
| 3 | 6 | 8 |
| 4 | 8 | 9 |
| 5 | 10 | 10 |
| 6 | 12 | 11 |
| 8 | 16 | 13 |
| 16 | 32 | 21 |
2.4. Modularized Switched Capacitor
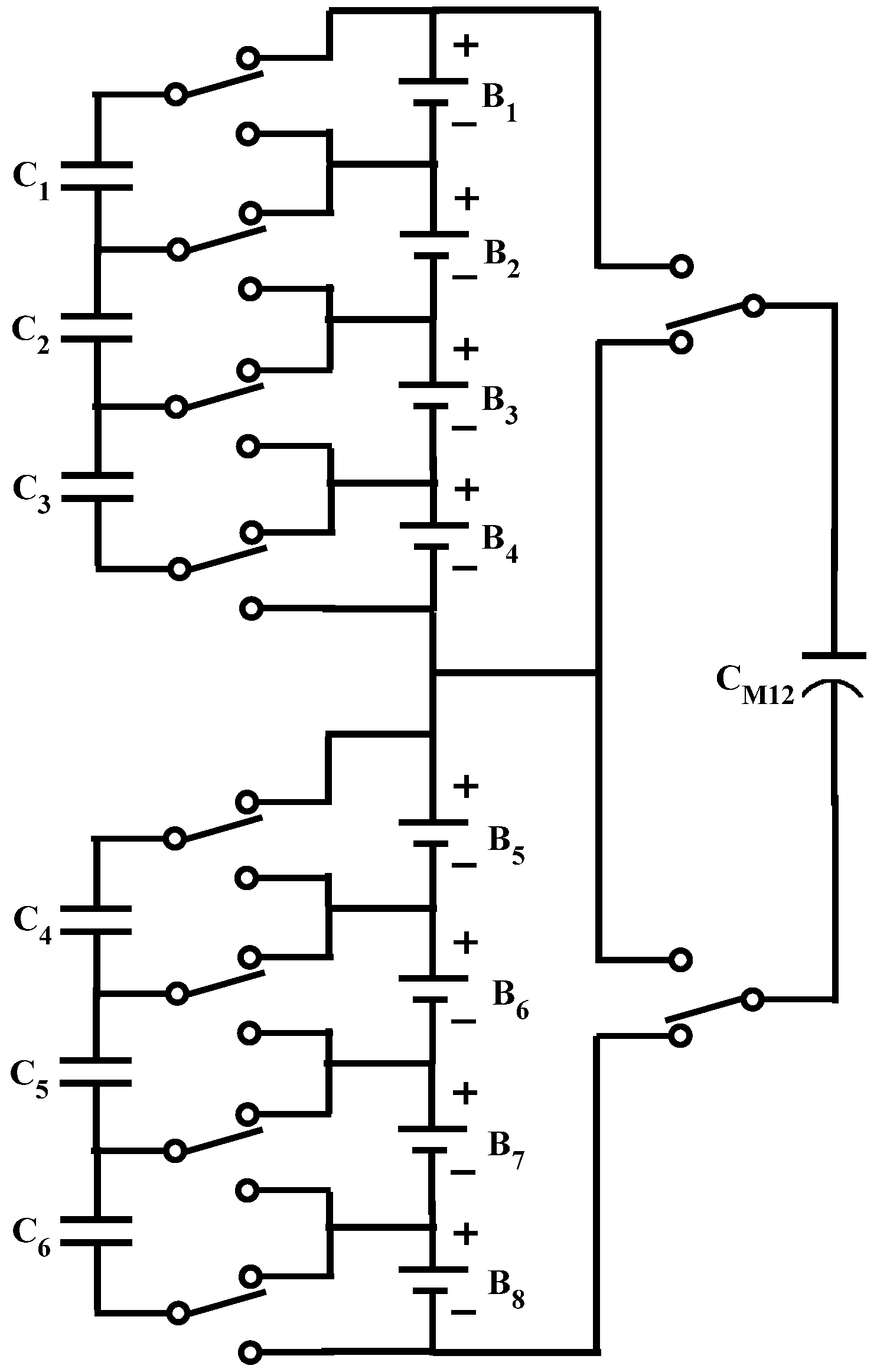
3. Shuttling Capacitors Balancing Topologies Simulation
- The SSC has only one capacitor and less switches while the MSC balancing method utilizes more capacitors and switches than the traditional SC and DTSC balancing methods.
- Both SC and DTSC have a straightforward control strategy, on the contrary, the SSC and MSC need a relatively complex control.
- The SC and DTSC methods with a simple control strategy have a long final balancing time and have a great problem that, when the SoC difference between the cells is small, as well as, the voltage difference, the equalization current becomes smaller. That will increase the equalization time significantly.
- Compared to the SC method, the DTSC has one more capacitor, however it decreases the balancing speed up to 42%, some times more, of the normal SC.

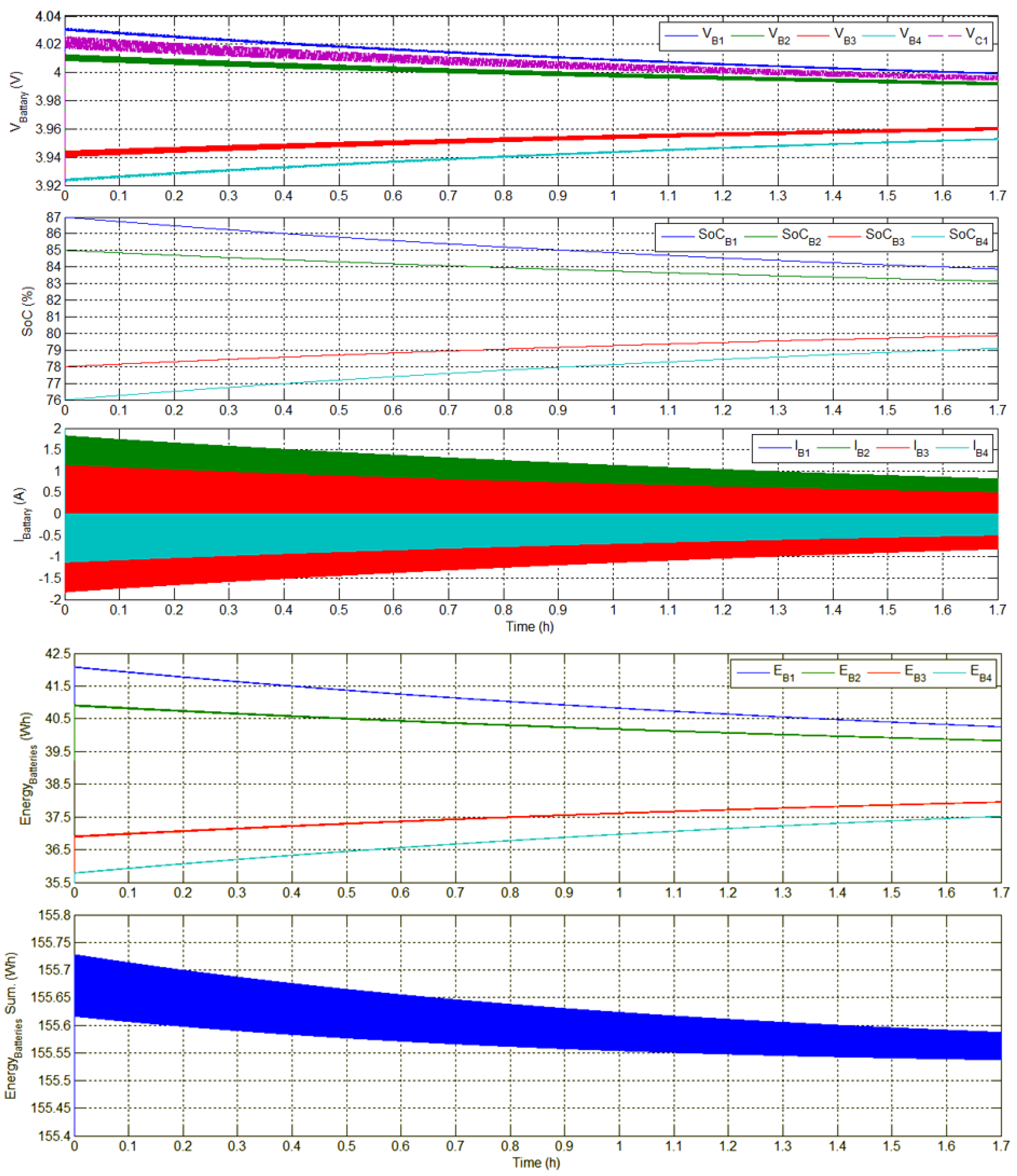
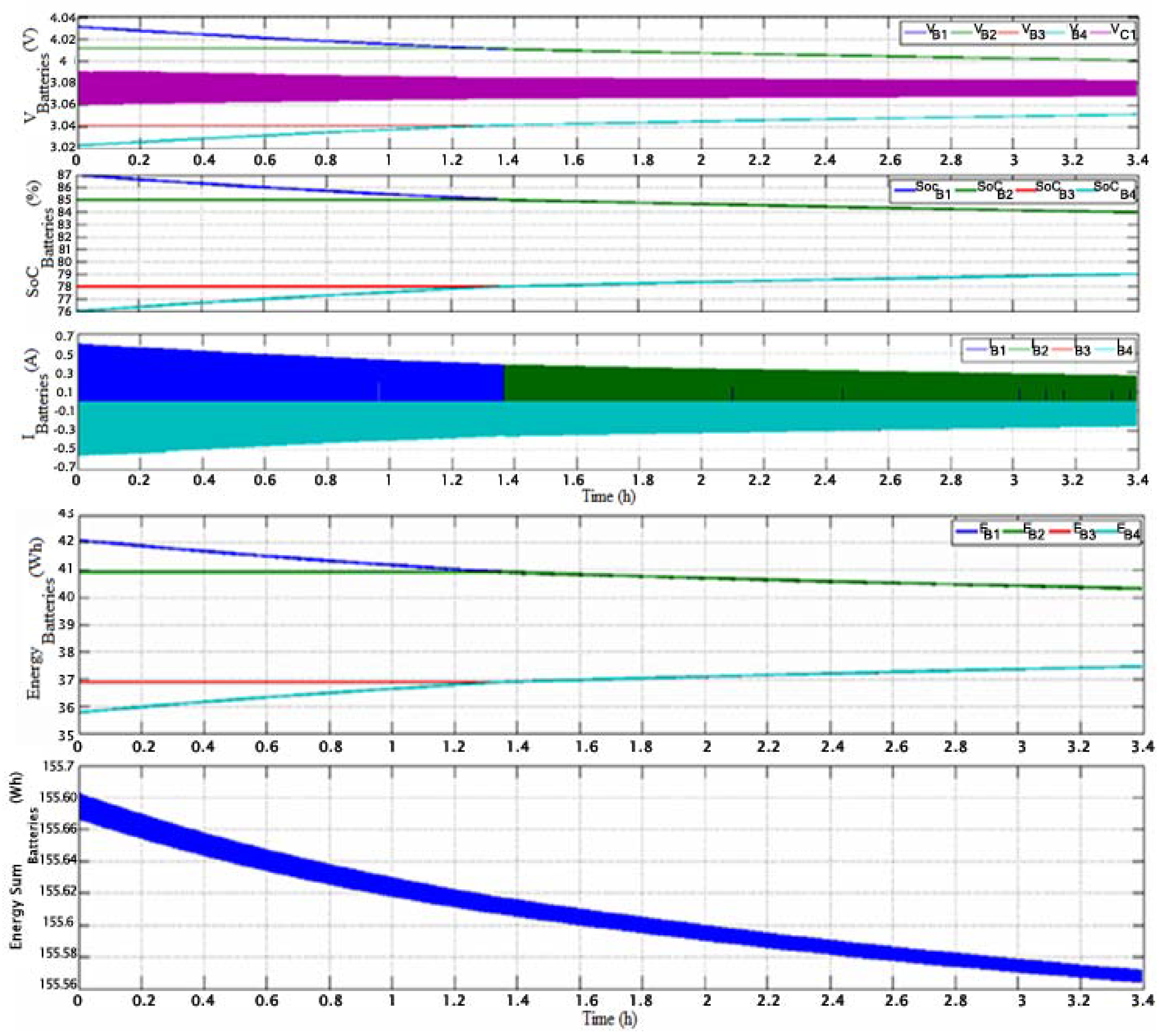
4. Single Switched Capacitor Control Strategy
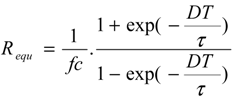
4.1. SSC Proposed Control Strategy
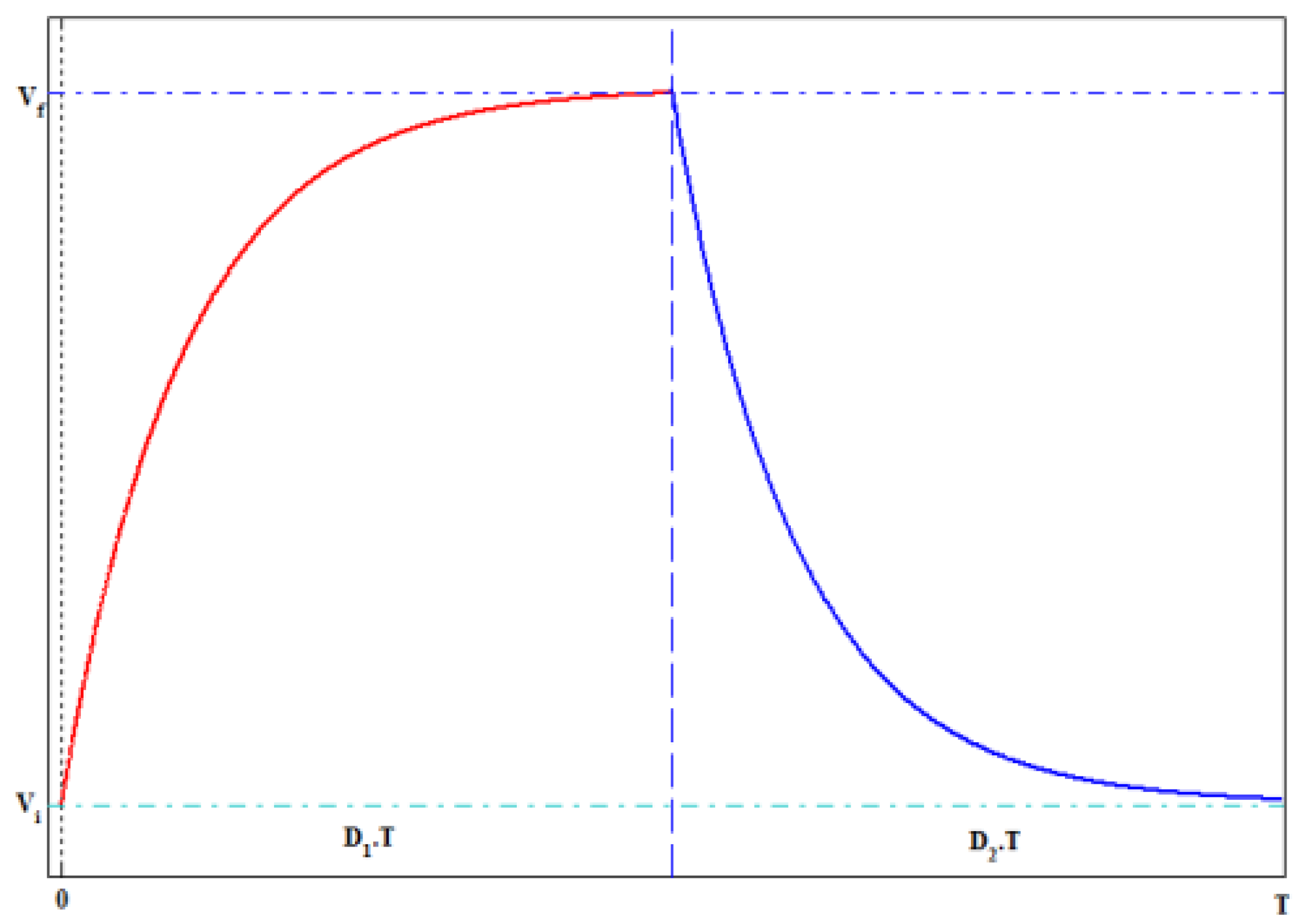
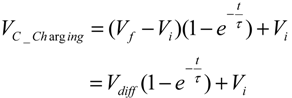
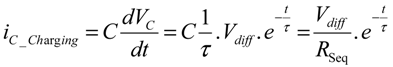




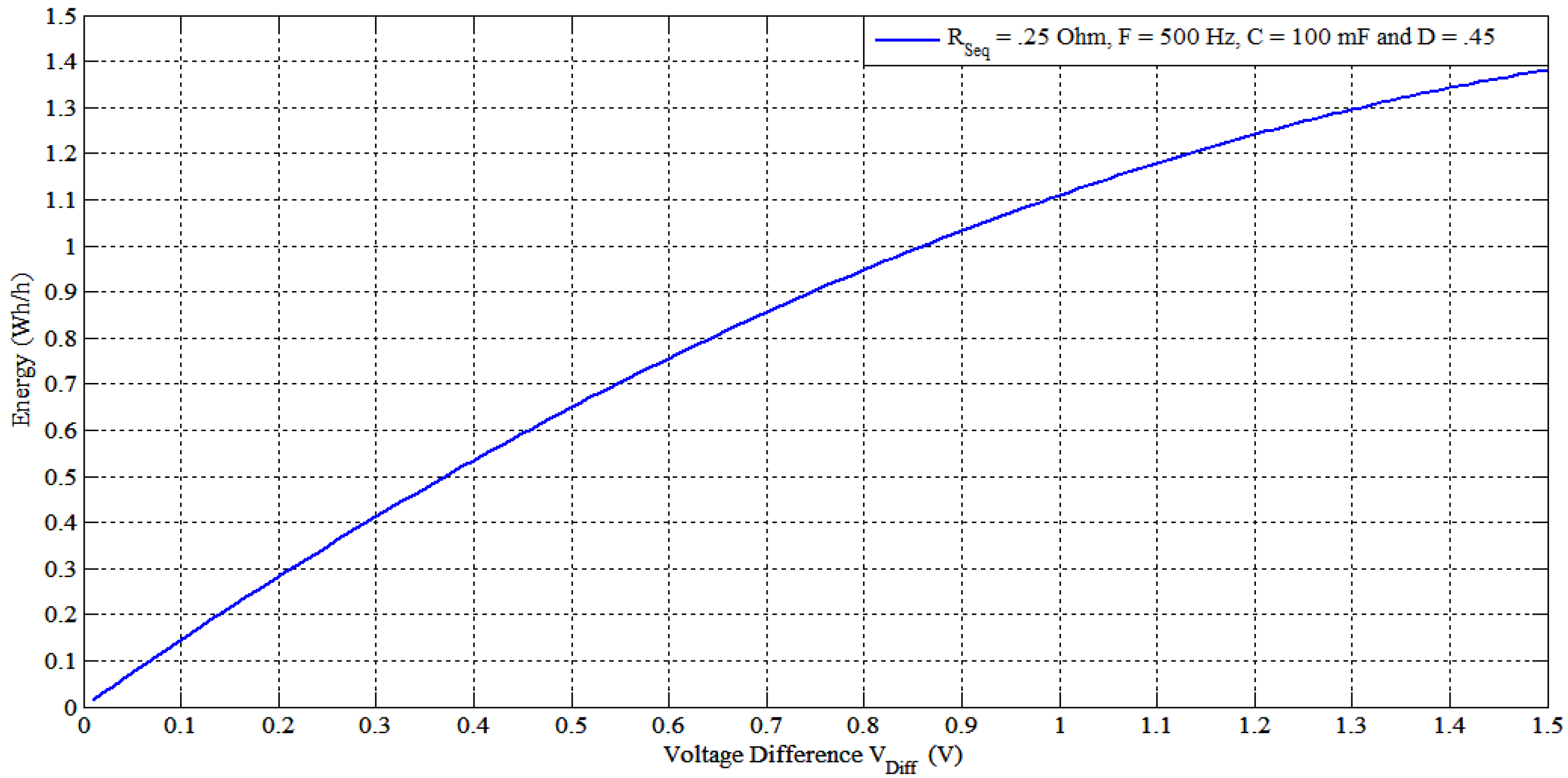
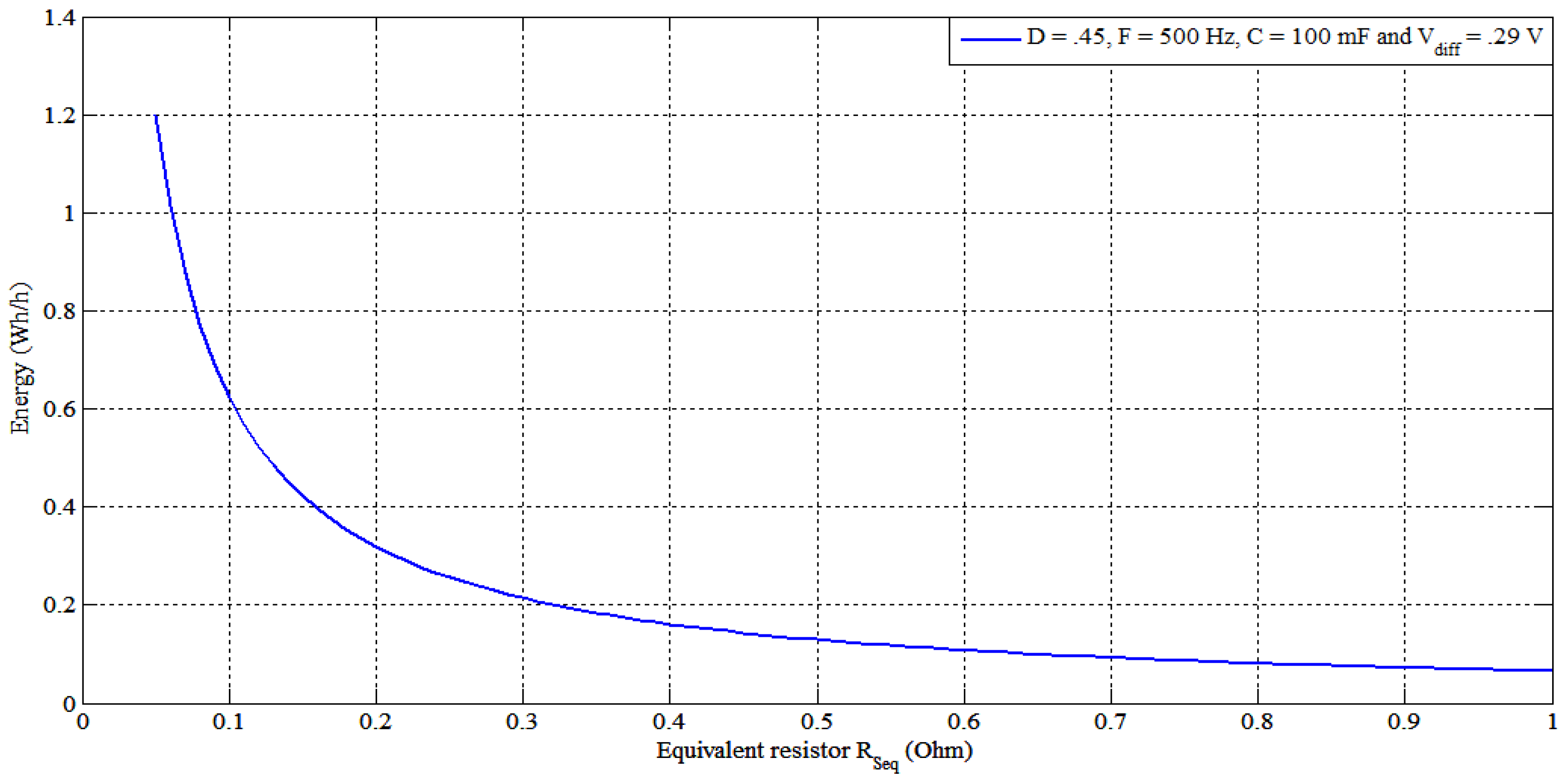
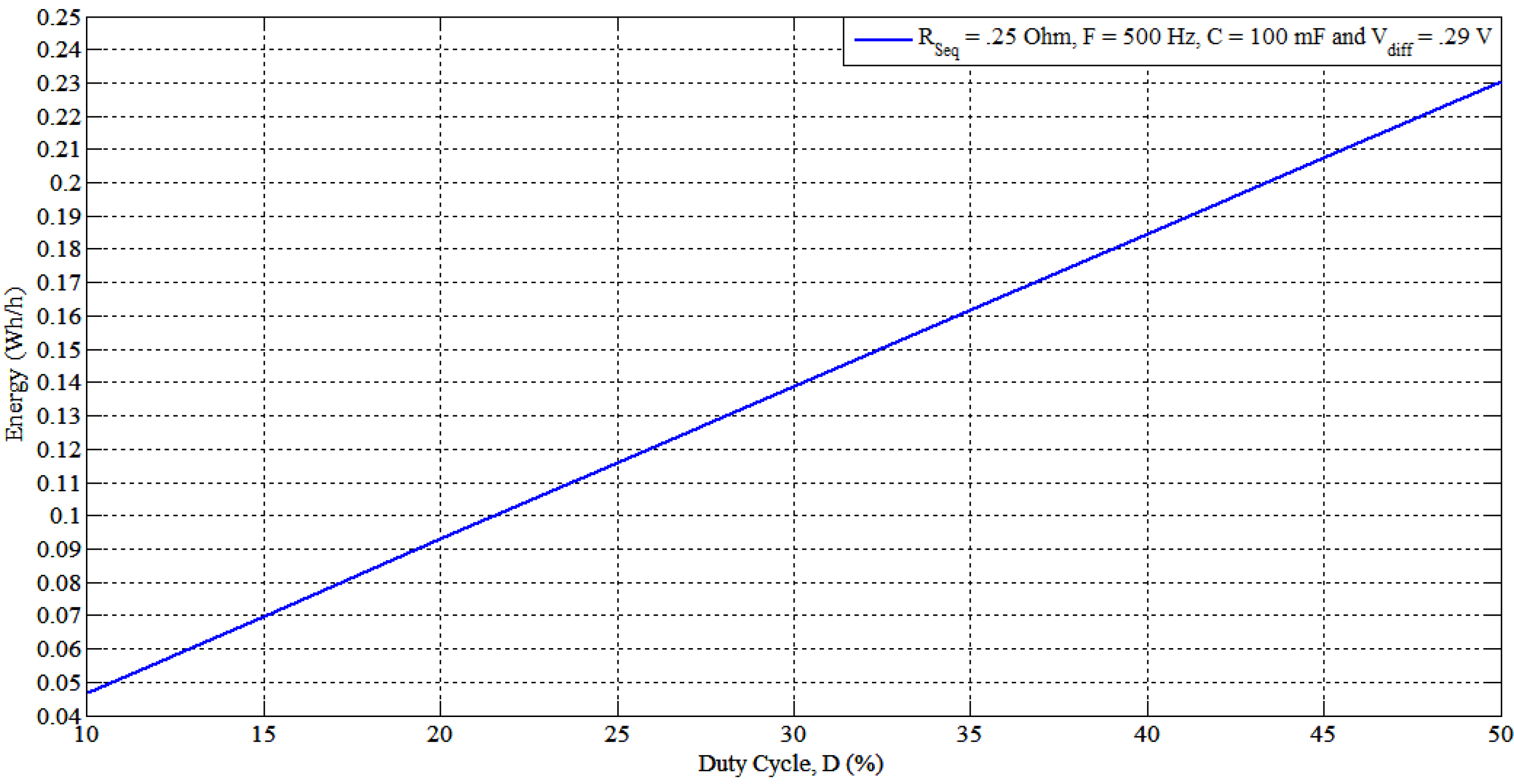
4.2. SSC Strategy Proceeding
- Extracting the function of the transferred energy between the cells and the capacitor [see Equation (5)]. This function can be easily maximized for transferred energy, but has to take into account the five premonition variables (C, F, Vdiff, RSeq and D).
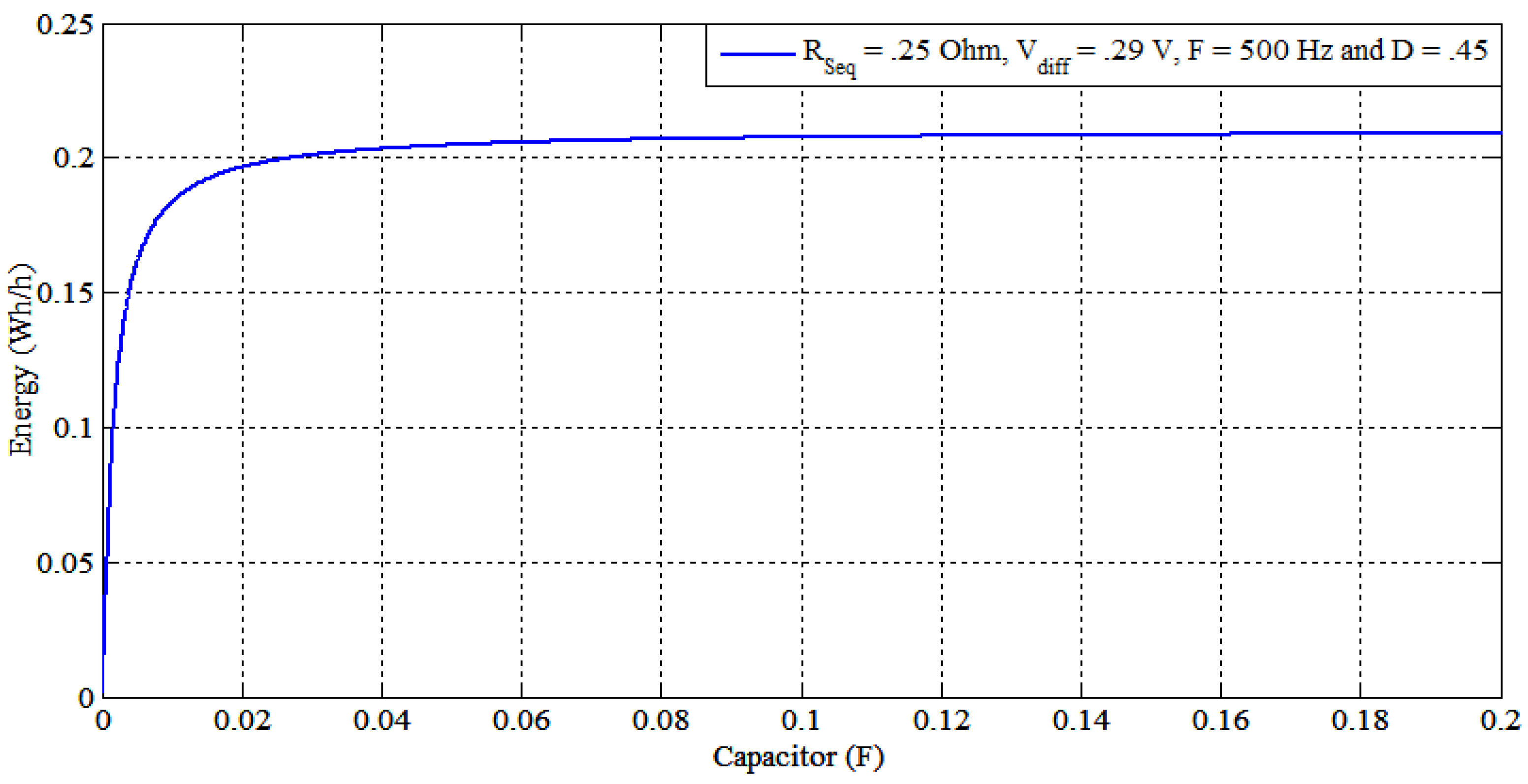
- Selecting the optimal capacitor value (minimum) by maximizing the energy function with respect to the capacitor value at different switching frequencies. The transferred energy will be a function of (C, F), with any arbitrary Vdiff and D because the latter two parameters will vary during balancing periods.
- After select the capacitor value with the given ESR, maximizing the energy transfer with the calculated C and RSeq values as a function of (F, D) at different values of Vdiff.
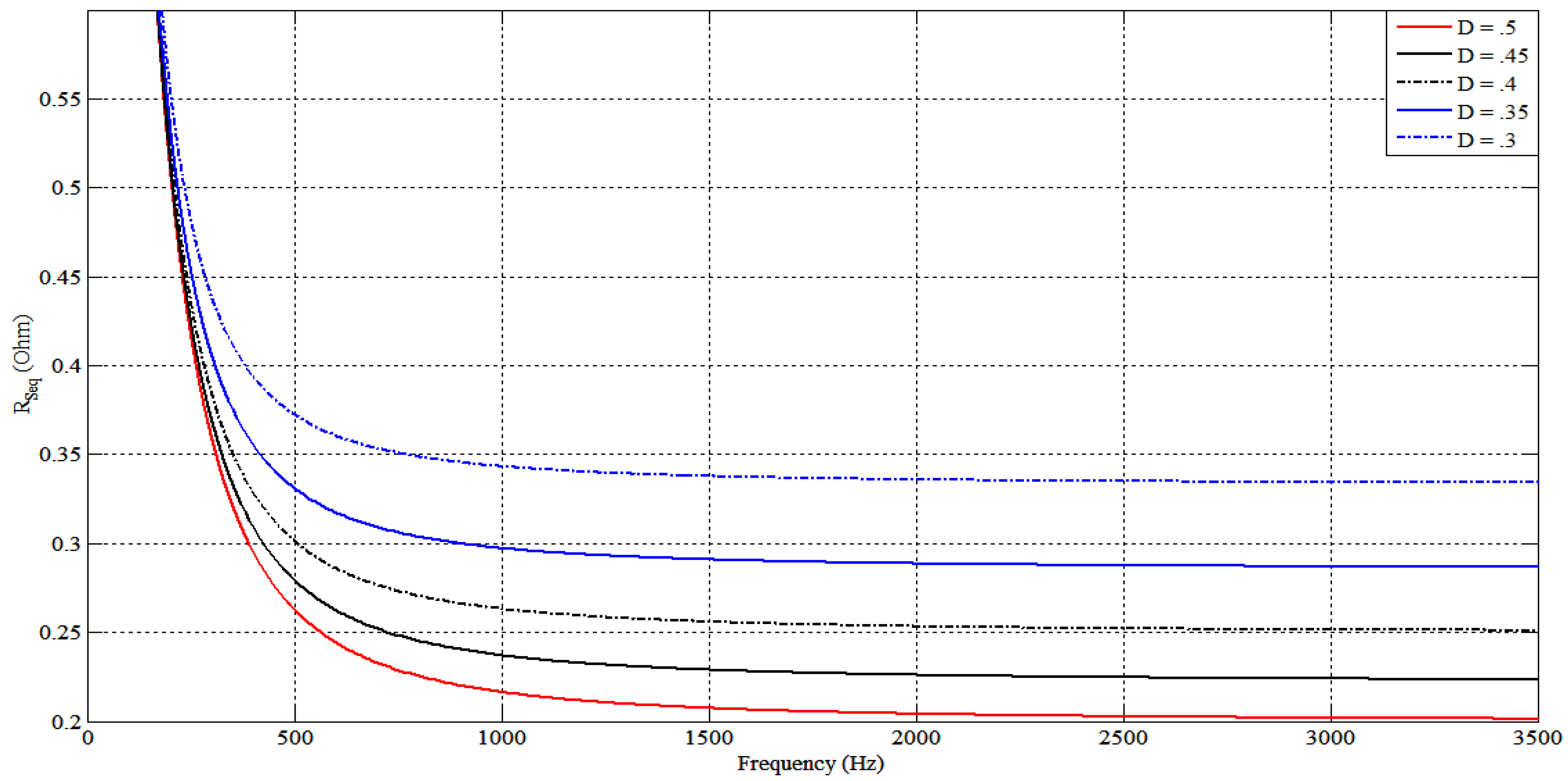
- Dividing the balancing period into zones according to voltage difference Vdiff, and decide the required maximum current allowed through the capacitor and the corresponding equivalent resistor RSeq value. This resistor value allows to select a D value and the allowable switching frequency range as illustrated in Figure 15.
- By knowing the higher and lower cell voltage, applying the corresponding F and D along the balancing time according to the cell voltages to get the maximum energy transfer.
- 6.
- The big challenge of using the shuttling capacitor topologies with Li-ion batteries is their nearly flat voltage during the discharge curves shown in Figure 16. This is particularly the case for lithium iron phosphate batteries. A 10 mV difference is nearly equal 10% SoC in the flat region for the Li-ion batteries compared with 20 mV per 10% SoC for the lead-acid batteries. In addition, one has to consider the voltage drops in the switches, so the capacitor balancing will have difficulties to equalize the cells with a very small voltage difference.

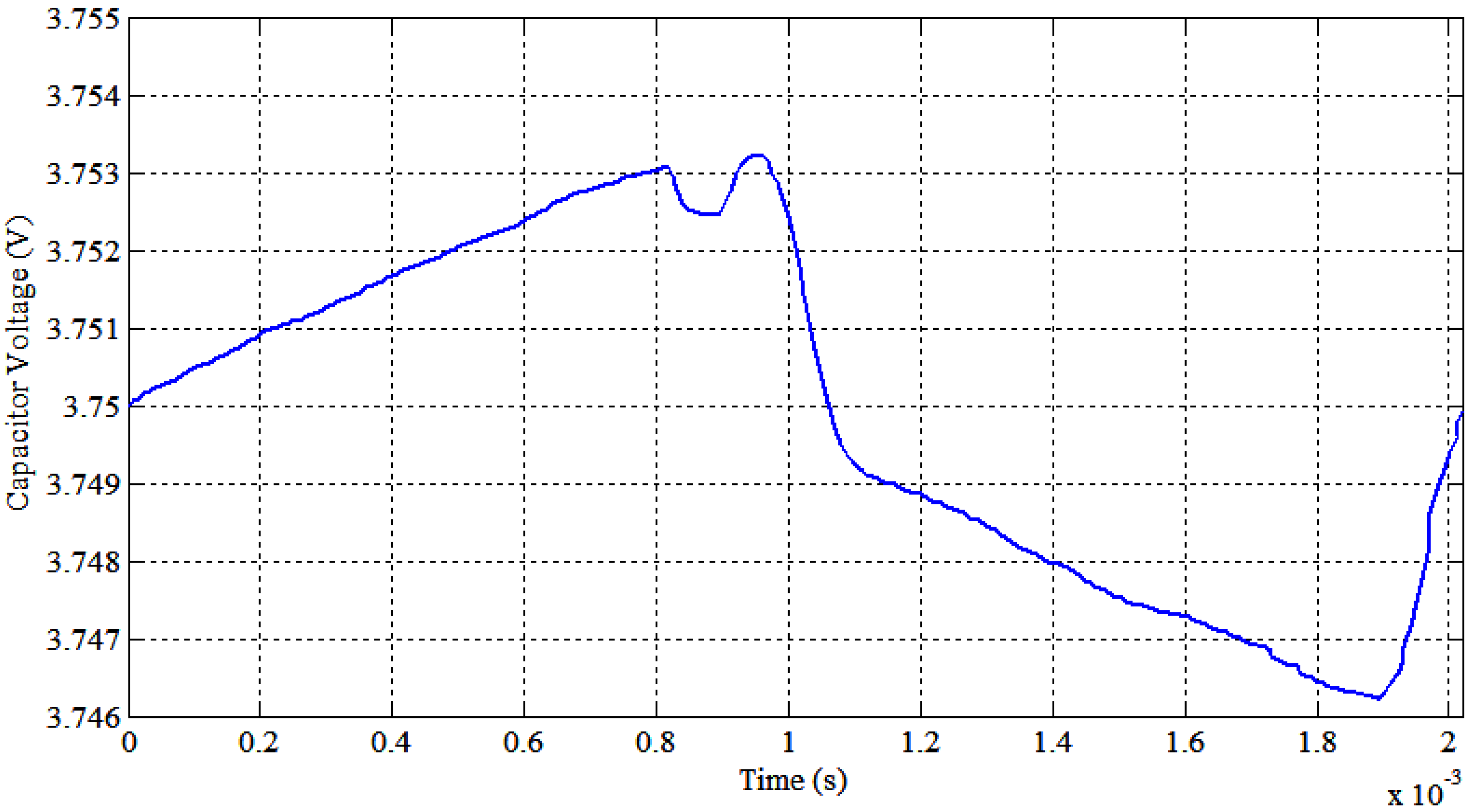
- 7.
- Some protective steps are necessary for experimental prototype implementation:
- When the balancing starts, and if the capacitor voltage is lower than the low charge cell voltage, the capacitor must be switched first to the lower voltage cell in order to prevent high capacitor charging current. Another solution to avoid high balancing current can be done by controlling the duty cycle, which can easily control the switched capacitor balancing current, as shown in Figure 15.
- The other limitation is the upper limit of the switching frequency, for reasons such as the manufacturer-recommended maximum operating frequency or the response time of the battery [27,28]. In other words, how many milliseconds are needed for the battery to reach its final voltage when applying a step current pulse. In addition the cells impedance will be increased at high frequency, leading to more losses and voltage drops.
4.3. Proposed SSC Balancing Simulation
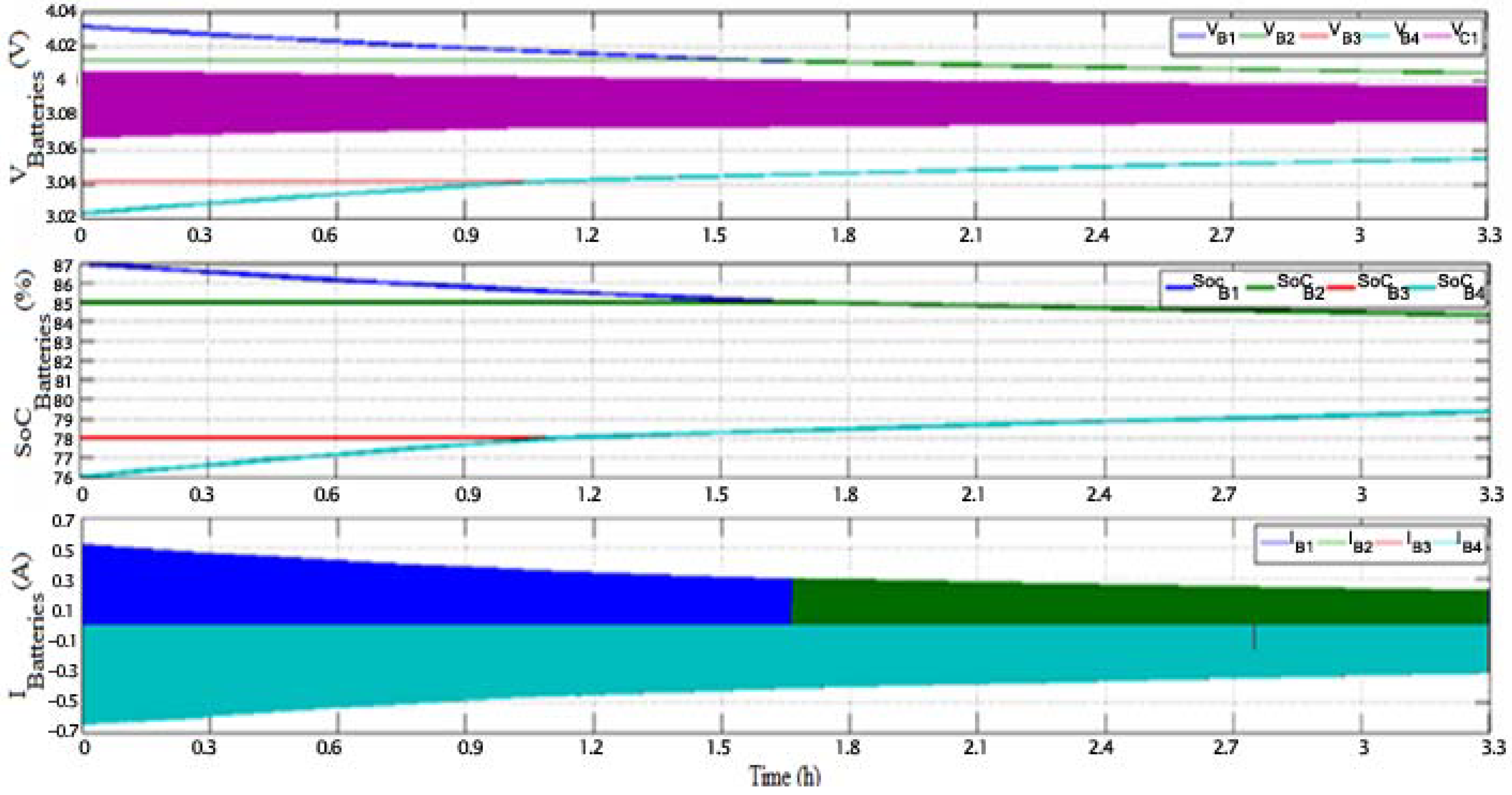
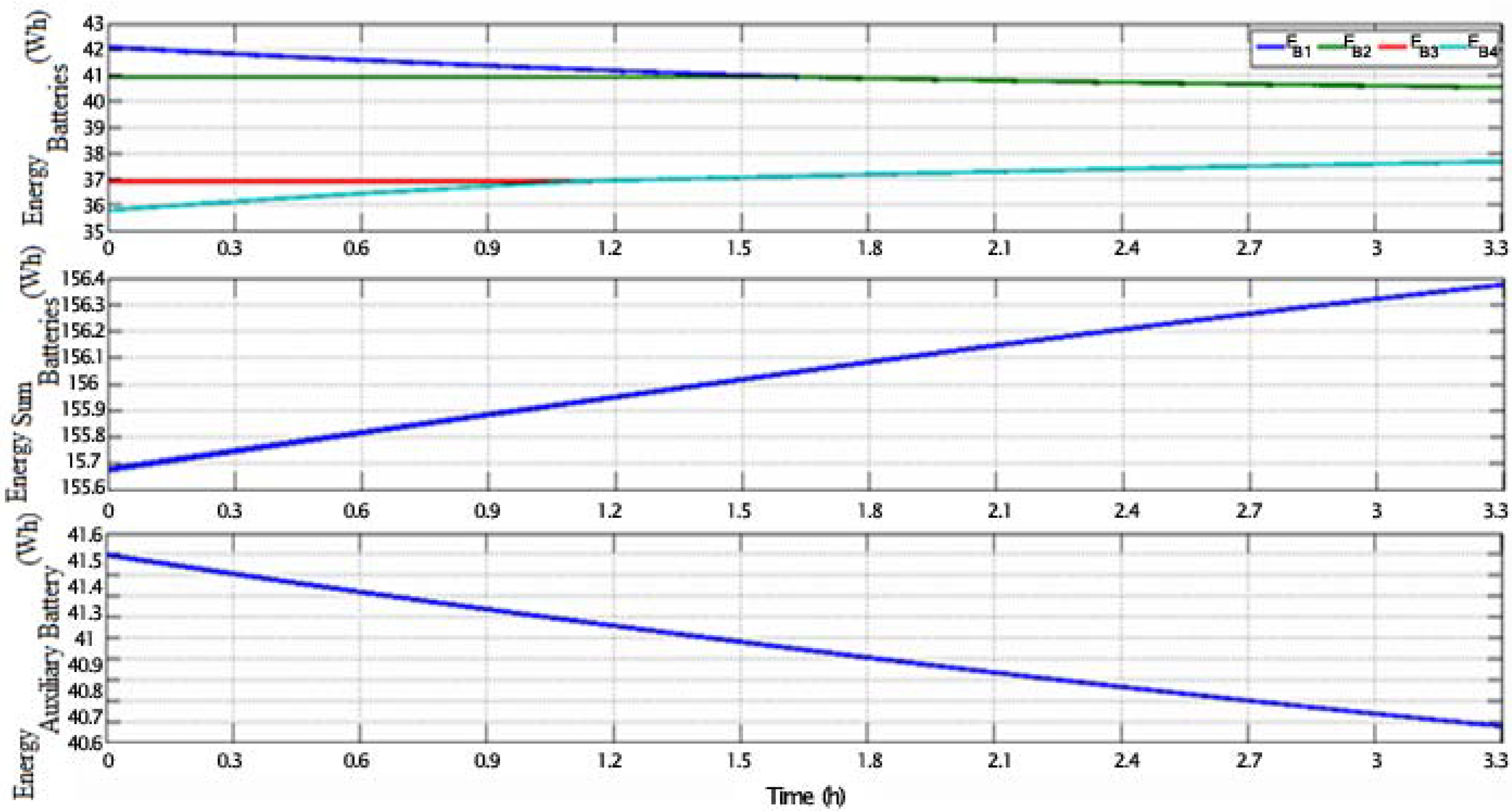
5. Experimental Prototype and Experimental Results
5.1. Experimental Prototype
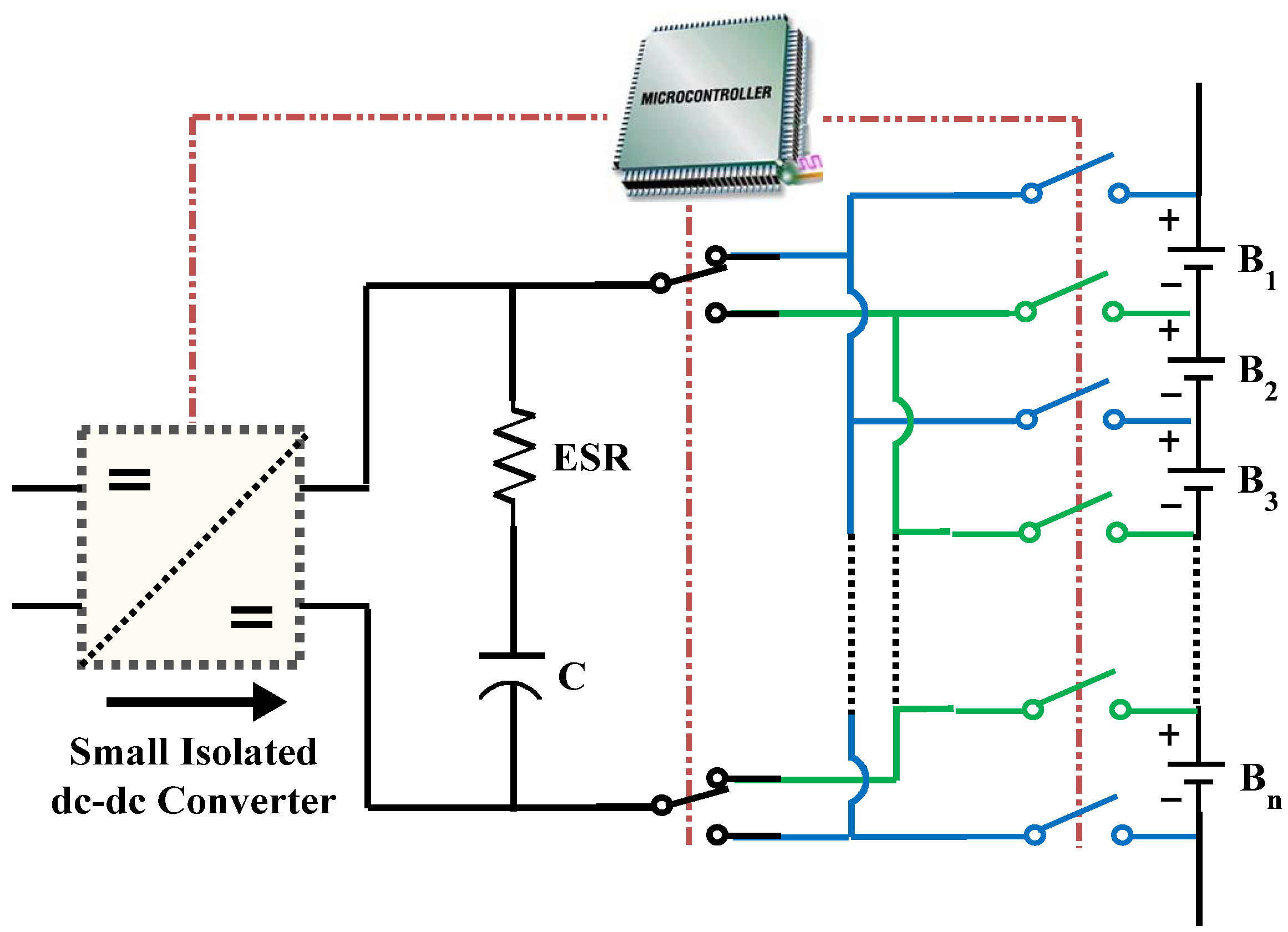
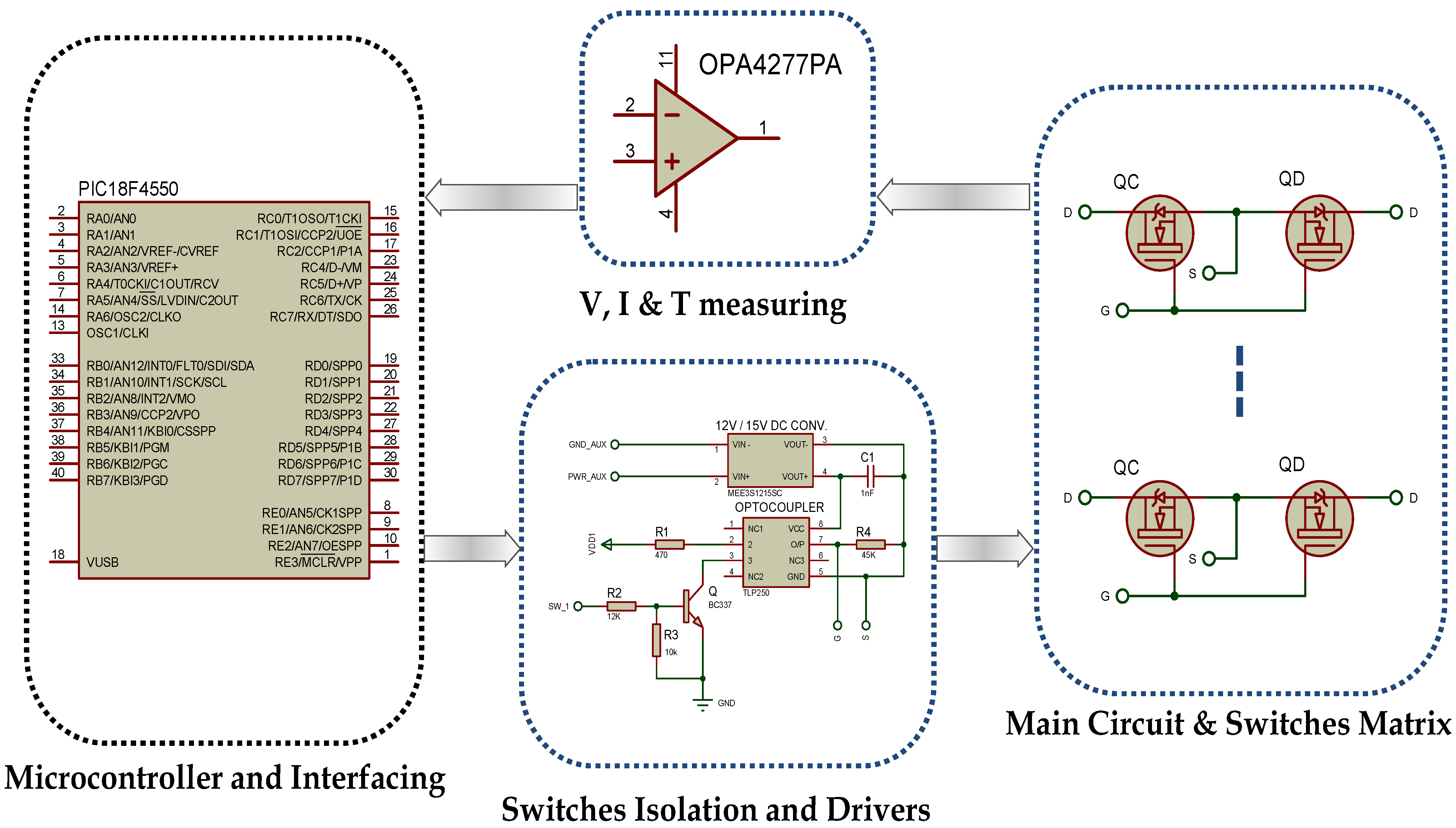
- The SSC main circuit including the cells connectors, the switches matrix, the capacitor and the boosting circuit.
- The first part of the SSC circuits contains the balancing capacitor series with current sensing resistor, main switches, protection fuses and the module’s cells’ connectors (see Figure 17).
- The bidirectional switches are implemented by using two anti-series “IRFB3806PBF” MOSFETs.
- The experimental tests are performed with 22 mF with maximum ESRs of 65 mΩ.
- The isolated boosting dc/dc converter “MEE3S1205SC” has an input/output voltage rating of 12/5 V and 0.6 A output current (3W).
- The switches isolation optocouplers and driving circuit.
- This circuit provides the isolation between the control circuit (microcontroller) and the power circuits (switches). The implementation of the switches isolation driver-circuit is performed by using TLP250 optocoupler, having a turn-on time of 0.5 μs.
- One converter for each bidirectional switch is implemented to insure the full isolation between the power circuit elements.
- Power supply circuit, sensors (such as current, voltage temperature sensors).
- The power circuit is supplied from the auxiliary battery through a 7812 voltage regulator. Then two MEE3S1215SC (12/15V, 3W) isolated converters are implemented to have ±15 V sources.
- The SSC balancing current is measured through of 10 mΩ resistor serially connected to the capacitor.
- The cells’ voltages are measured by using a differential method. A high precision operational amplifier “OPA4277PA”, with four op-amps inside, is used for this purpose and its outputs are connected directly to microcontroller’s ADC.
- Temperature sensor is illustrated using the thermometer “LM35DT”. They are four connectors to measure the four cells’ temperatures in the circuit.
- The fan power supply utilizes a 12 V (7812) voltage regulator. The fan speed is controlled by PWM output from the microcontroller.
- The microcontroller circuit
- The microcontroller “PIC18F4550”, which is used for controlling purpose technique with 20 MHz crystal.
- An additional high speed analog multiplexer/demultiplexer “74HC4051”, is used for future analog reading.
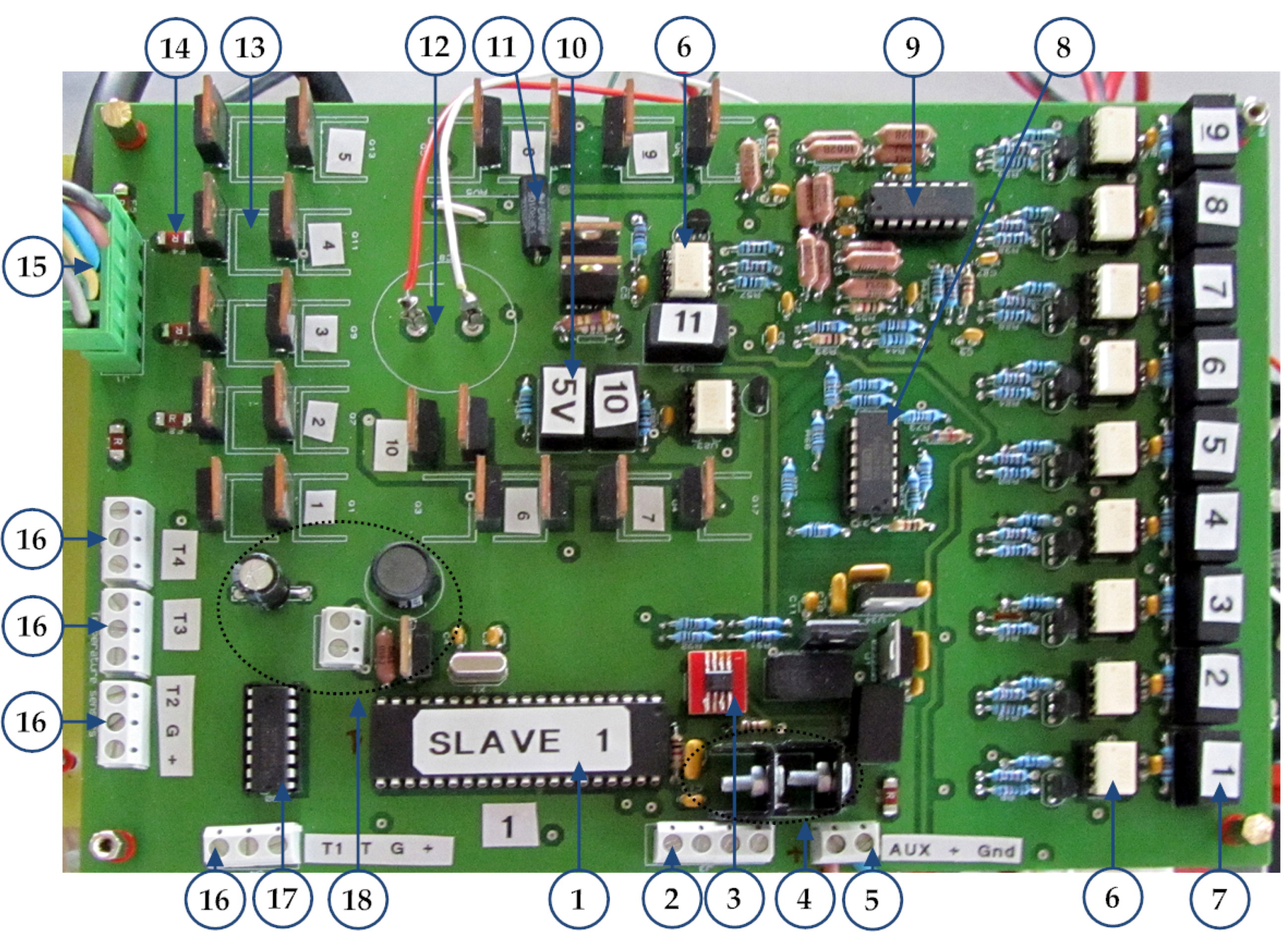
- Microcontroller “PIC18F4550”;
- I2C interfacing connector;
- I2C interfacing isolation “ADUM1251”;
- Module power supply regulators “7812” circuit;
- Auxiliary battery input;
- Switches’ driver optocoupler isolation matrix “TLP250”;
- Switches’ driver isolated converter matrix “MEE3S1215SC”;
- Current sensing op-amps “LM324AN”;
- Voltage sensing op-amps “OPA4277PA”;
- Boosting converter “MEE3S1205SC”;
- Balancing current sensing resistor (10 mΩ);
- Capacitor connection points;
- Switches matrix;
- Protection fuses;
- Module’s cells’ connectors;
- Cells temperature sensors connectors;
- Analog multiplexer/demultiplexer “74HC4051”;
- Cooling fan control circuit and its connectors.
5.2. Experimental Results
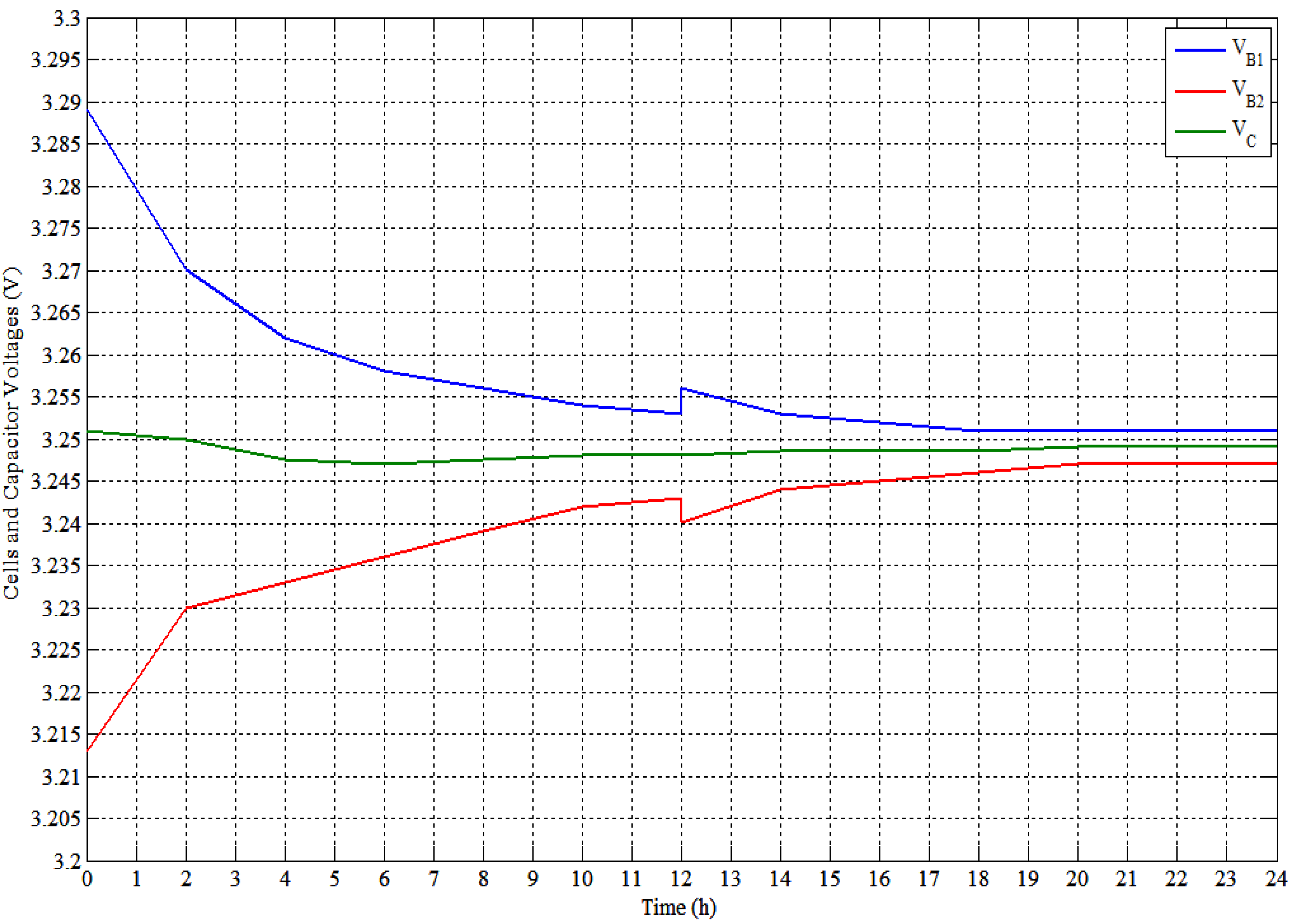
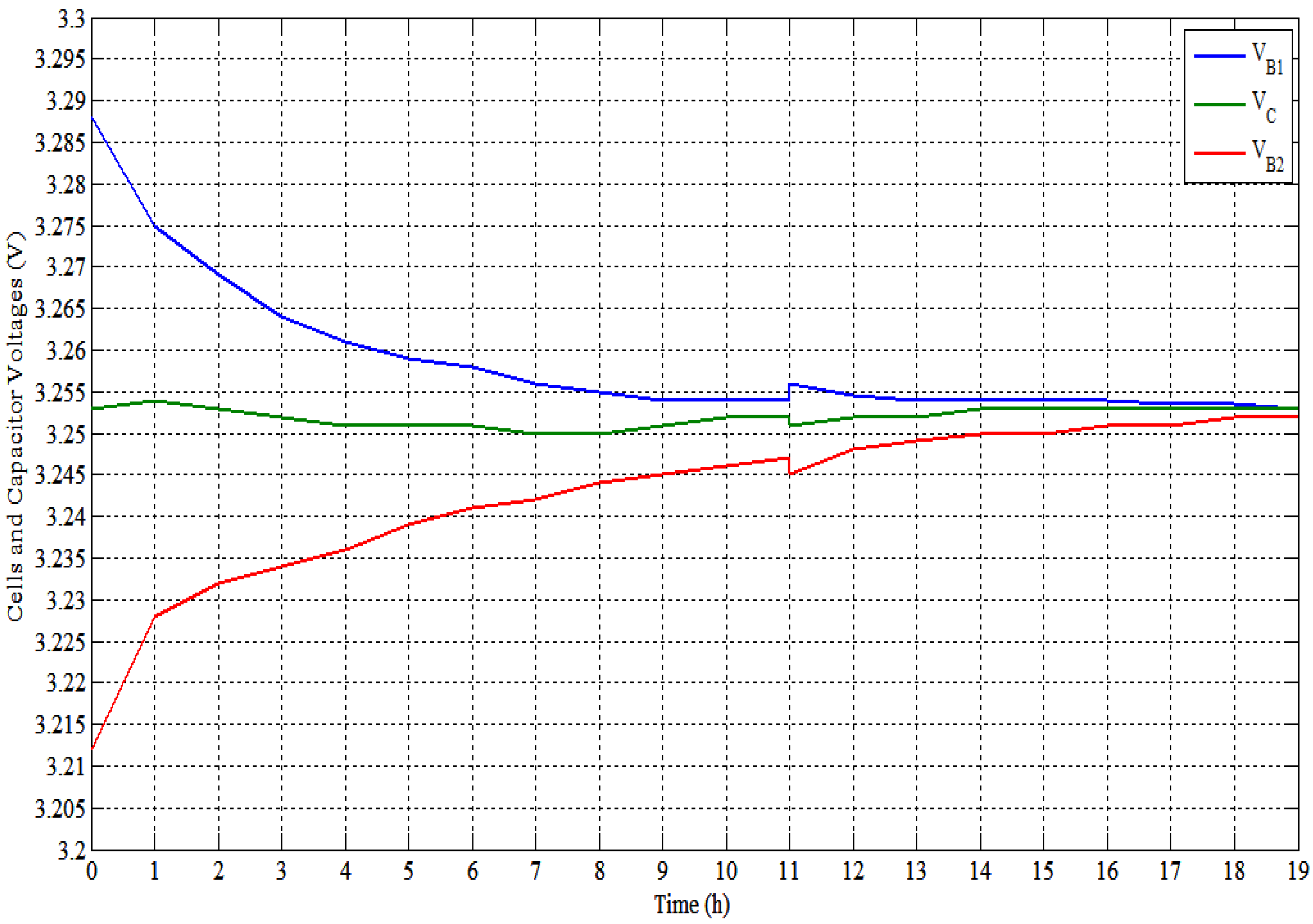
- Two tests have been performed on these cells. The two cells started with voltages of 3.288 and 3.212 V (Vdiff. = 76 mV). The initial SoCs of these cells are around 35% and 11.3%, respectively (SoC difference is around 23.7% or 545 mAh);
- The two tests are performed with 22 mF (maximum ESRs of 65 mΩ) at switching frequency of 588 Hz (T = 1.7 ms);
- The cells and the capacitor voltages are measured by using Fluke “177” digital multimeter with an accuracy of ±0.09%;
- These tests are performed by using open-loop control. It means that the controller did not measure the cells’ voltages, it is directly shuttling the energy between the two cells;
- The time of tests is around 24 hours for the balancing between cells, where there is a rest of nearly 12 hours after the first 12 hours of balancing;
- First test (no. 1) is carried out without using the proposed balancing technique;
- Second test (no. 2) is carried out with using the proposed balancing technique. The test has fixed boosting pulses of 40 μs;
| Test No. | C (mF) | F (Hz) | Balancing time (h) | OCV @ balance | SoC @ balance | Notes | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cell1 (V) | Cell2 (V) | Diff. (mV) | Cell1 (%) | Cell2 (%) | Diff. (%) | Sum. (%) | |||||
| 1 | 22 | 588 | 20 | 3.251 | 3.247 | 4 | 22.5 | 21.3 | 1.2 | 43.8 | 4 mV till 24 h |
| 2 | 22 | 588 | 19 | 3.253 | 3.252 | 1 | 23.2 | 22.9 | 0.3 | 46.1 | 4 mV @ 14 h |
- As can be seen in test no. 1: the minimum voltage difference, which can be obtained is 4 mV. This voltage is obtained after 20 hours and still constant (4 mV) and remains constant till 24 hours of test. In addition, this Li-ion flat voltage region gives SoC difference around 8% according to the voltage difference (4 mV).
- The proposed SSC’s control topology test no. 2: give the smallest voltage difference (1 mV) between the cells with the smallest balancing time (19 hours). This small voltage difference can overcome lithium iron phosphate batteries’ flat voltage balancing problems. The cells reach a voltage difference of 4 mV at 14 hours.
- Comparing the two tests with the same capacitor value and the switching frequency. For the same final voltage differences (4 mV) the proposed SSC balancing system (second test) reach it after 14 hours and the normal SSC balancing (first test) reach it after 20 hours. That means the proposed SSC balancing reduces the balancing time by 30%.
6. Conclusions
Abbreviations
| BMS | Battery management systems |
| DTSC | Double-tiered switched capacitor balancing |
| EV | Electric vehicle |
| EPNGV | Extended Partnership for a New Generation of Vehicles |
| Li-ion | Lithium-Ion |
| Li-Po | Lithium-Polymer |
| MSC | Modularized switched capacitor balancing |
| PWM | Pulse width modulation |
| RUL | Remaining useful life |
| SC | Switched capacitor balancing |
| SoC | State of charge (%) |
| SoH | State of health (%) |
| SSC | Single Switched Capacitor balancing |
References
- Daowd, M.; Omar, N.; van den Bossche, P.; van Mierlo, J. A review of passive and active battery balancing based on MATLAB/Simulink. J. Int. Rev. Electr. Eng. 2011, 6, 2974–2989. [Google Scholar]
- Daowd, M.; Omar, N.; van den Bossche, P.; van Mierlo, J. Passive and Active Battery Balancing Comparison based on MATLAB Simulation. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), West Chicago, IL, USA, 6–9 September 2011; pp. 1–7.
- Jian, C.; Schofield, N.; Emadi, A. Battery Balancing Methods: A Comprehensive Review. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC ’08), Harbin, China, 3–5 September 2008; pp. 1–6.
- Kong, Z.-G.; Zhu, C.-B.; Lu, R.-G.; Cheng, S.-K. Comparison and Evaluation of Charge Equalization Technique for Series Connected Batteries. In Proceedings of the 37th IEEE Power Electronics Specialists Conference (PESC ’06), Jeju, South Korea, 18–22 June 2006; pp. 1–6.
- Moore, S.W.; Schneider, P.J. A Review of Cell Equalization Methods for Lithium Ion and Lithium Polymer Battery Systems. In Proceedings of the SAE 2001 World Congress, Detroit, MI, USA, 5–8 March 2001.
- Isaacson, M.J.; Hollandsworth, R.P.; Giampaoli, P.J.; Linkowsky, F.A.; Salim, A.; Teofilo, V.L. Advanced Lithium Ion Battery Charger. In Proceedings of the Fifteenth Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 11–14 January 2000; pp. 193–198.
- Kutkut, N.H.; Divan, D.M. Dynamic Equalization Techniques for Series Battery Stacks. In Proceedings of the 18th International Telecommunications Energy Conference (INTELEC ’96), Boston, MA, USA, 6–10 October 1996; pp. 514–521.
- Lindemark, B. Individual Cell Voltage Equalizers (ICE) for Reliable Battery Performance. In Proceedings of the 13th International Telecommunications Energy Conference (INTELEC ’91), Kyoto, Japan, 5–8 November 1991; pp. 196–201.
- Stuart, T.A.; Wei, Z. Fast equalization for large lithium ion batteries. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 27–31. [Google Scholar] [CrossRef]
- Kimball, J.W.; Kuhn, B.T.; Krein, P.T. Increased Performance of Battery Packs by Active Equalization. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC ’07), Arlington, TX, USA, 9–12 September 2007; pp. 323–327.
- Kobzev, G.A. Switched-capacitor Systems for Battery Equalization. In Proceedings of Modern Techniques and Technology, MTT 2000, 6th International Scientific and Practical Conference of Students, Post-graduates and Young Scientists, Tomsk, Russia, 28 February–3 March 2000; pp. 57–59.
- West, S.; Krein, P.T. Equalization of Valve-regulated Lead-acid Batteries: Issues and Life Test Results. In Proceedings of the Twenty-second International Telecommunications Energy Conference (INTELEC ’00), Dresden, Germany, 7–10 May 2000; pp. 439–446.
- Pascual, C.; Krein, P.T. Switched Capacitor System for Automatic Series Battery Equalization. In Proceedings of the Twelfth Annual Applied Power Electronics Conference and Exposition (APEC ’97), Atlanta, Georgia, 23–27 February 1997; Volume 842, pp. 848–854.
- Baughman, A.C.; Ferdowsi, M. Double-tiered switched-capacitor battery charge equalization technique. IEEE Trans. Ind. Electron. 2008, 55, 2277–2285. [Google Scholar] [CrossRef]
- Baughman, A.; Ferdowsi, M. Analysis of the Double-Tiered Three-Battery Switched Capacitor Battery Balancing System. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC ’06), Windsor, UK, 6–8 September 2006; pp. 1–6.
- Baughman, A.; Ferdowsi, M. Double-tiered Capacitive Shuttling Method for Balancing Series-connected Batteries. In Proceedings of the 2005 IEEE Conference on Vehicle Power and Propulsion, Chicago, IL, USA, 7–9 September 2005; pp. 109–113.
- Speltino, C.; Stefanopoulou, A.; Fiengo, G. Cell Equalization in Battery Stacks through State of Charge Estimation Polling. In Proceedings of the American Control Conference (ACC’10), Baltimore, MD, USA, 30 June–2 July 2010; pp. 5050–5055.
- Daowd, M.; Omar, N.; van den Bossche, P.; van Mierlo, J. Capacitor Based Battery Balancing System. In Proceedings of the 26th Hybrid and Fuel Cell Electric Vehicle Symposium (EVS-26), Los Angeles, CA, USA, 6–9 May 2012; pp. 1–9.
- Park, H.S.; Kim, C.H.; Park, K.B.; Moon, G.W.; Lee, J.H. Design of a charge equalizer based on battery modularization. IEEE Trans. Veh. Technol. 2009, 58, 3216–3223. [Google Scholar] [CrossRef]
- Al Sakka, M.; Gualous, H.; van Mierlo, J.; Culcu, H. Thermal modeling and heat management of supercapacitor modules for vehicle applications. J. Power Sources 2009, 194, 581–587. [Google Scholar]
- Yonghua, C.; Joeri, V.M.; Lataire, P.; Buechel, M.; Knorr, R.; Gallay, R. Method of Identifying Voltage Difference of Super Capacitors and Principle of Voltage Balancing. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10.
- Daowd, M.; Omar, N.; van den Bossche, P.; van Mierlo, J. A comparative study of battery models parameter estimation. J. Int. Rev. Electr. Eng. 2012, 7, 4915–4924. [Google Scholar]
- Daowd, M.; Omar, N.; Verbrugge, B.; van den Bossche, P.; van Mierlo, J. Battery Models Parameter Estimation based on MATLAB/Simulink. In Proceedings of the 25th Electric Vehicle Symposium (EVS-25), Shenzhen, China, 5–9 November 2010.
- Daowd, M.; Omar, N.; van den Bossche, P.; van Mierlo, J. Extended PNGV battery model for electric and hybrid vehicles. J. Int. Rev. Electr. Eng. 2011, 6, 1264–1278. [Google Scholar]
- Kimball, J.W.; Krein, P.T. Analysis and Design of Switched Capacitor Converters. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition (APEC’05), Austin, TX, USA, 6–10 March 2005; Volume 1473, pp. 1473–1477.
- Ben-Yaakov, S.; Evzelman, M. Generic and unified model of Switched Capacitor Converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE’09), San Jose, CA, USA, 20–24 September 2009; pp. 3501–3508.
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Ke, Z.; Nawrocki, S.; Renxiang, W.; Jin, W. High Current Battery Impedance Testing for Power Electronics Circuit Design. In Proceedings of the Vehicle Power and Propulsion Conference, (VPPC ’09), Dearborn, MI, USA, 7–10 September 2009; pp. 531–535.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Daowd, M.; Antoine, M.; Omar, N.; Van den Bossche, P.; Van Mierlo, J. Single Switched Capacitor Battery Balancing System Enhancements. Energies 2013, 6, 2149-2174. https://doi.org/10.3390/en6042149
Daowd M, Antoine M, Omar N, Van den Bossche P, Van Mierlo J. Single Switched Capacitor Battery Balancing System Enhancements. Energies. 2013; 6(4):2149-2174. https://doi.org/10.3390/en6042149
Chicago/Turabian StyleDaowd, Mohamed, Mailier Antoine, Noshin Omar, Peter Van den Bossche, and Joeri Van Mierlo. 2013. "Single Switched Capacitor Battery Balancing System Enhancements" Energies 6, no. 4: 2149-2174. https://doi.org/10.3390/en6042149
APA StyleDaowd, M., Antoine, M., Omar, N., Van den Bossche, P., & Van Mierlo, J. (2013). Single Switched Capacitor Battery Balancing System Enhancements. Energies, 6(4), 2149-2174. https://doi.org/10.3390/en6042149





