Biomass Fuel and Combustion Conditions Selection in a Fixed Bed Combustor
Abstract
:1. Introduction
2. Experimental Section and Methodology
2.1. Experimental Plant
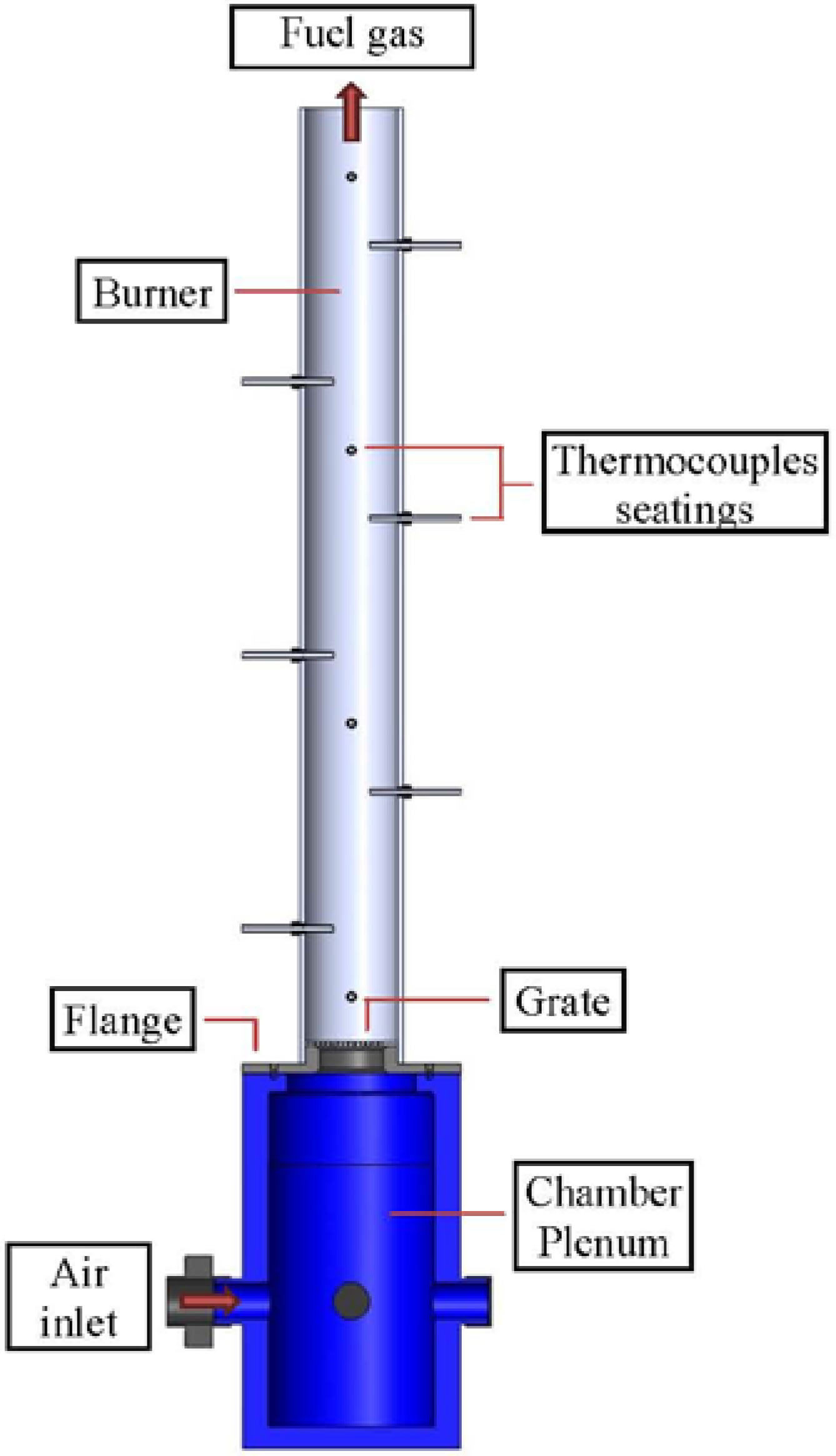

2.2. Ignition Front Propagation in a Fixed Bed

2.3. Variable Selection
2.4. Fuels

| Fuel type | Formula dry basis ash free | Lower heating value (MJ kg−1) | Water (immediate analysis as received. Wet basis with ash) (%) |
|---|---|---|---|
| Brassica pellet (bp) | CH1.41O0.78 | 13.1 | 9 |
| Wood pellet (wp) | CH1.48O0.71 | 16.3 | 6.2 |
| Olive stone (os) | CH1.50O0.64 | 15.3 | 13 |
Granulometry

- µ
- characteristic mass of the distribution (kg);
- MT
- total mass of the distribution (kg);
- k
- form factor that was used to fit the distribution (-).
- λ
- characteristic length of the distribution (m).
- Svol
- sphere volume (m3).
- Vp
- volume of the characteristic particle (m3);
- Ap
- surface area of the characteristic particle (m2).
| Fuel type | Radius of the equivalent sphere (Er) (mm) | Sphericity (ψ) |
|---|---|---|
| Brassica pellet (bp) | 4.1 | 0.86 |
| Wood pellet (wp) | 3.8 | 0.87 |
| Olive stone (os) | 4.2 | 0.98 |
2.5. Grey Relational Grade Error (GRGe)
2.5.1. GRA
- If the highest value is the optimal value (as in the case of the ignition mass flow rate variable):
- If the lowest value is the optimal value (as in the case of the maximum temperature variable):where yi represents the variables as a function of the J factors.
2.5.2. GRGe
3. Results and Discussion
| Fuel | AMF | IMF | IMFU | IMFU (%) | MT | MTU | MTU (%) | AE | GRG | GRGe |
|---|---|---|---|---|---|---|---|---|---|---|
| Brassica pellet (bp) | 0.08 | 0.04 | 1.74 × 10−3 | 4.69 | 740 | 2.40 | 0.32 | 0.39 | 6.67 × 10−1 | 0.00 |
| 0.15 | 0.05 | 2.40 × 10−3 | 4.89 | 910 | 3.20 | 0.35 | 0.49 | 5.44 × 10−1 | 2.17 × 10−2 | |
| 0.18 | 0.06 | 2.75 × 10−3 | 4.50 | 1240 | 9.00 | 0.73 | 0.55 | 5.68 × 10−1 | 9.38 × 10−2 | |
| 0.23 | 0.06 | 2.93 × 10−3 | 4.88 | 1300 | 9.00 | 0.69 | 0.72 | 5.35 × 10−1 | 8.64 × 10−2 | |
| 0.35 | 0.07 | 4.08 × 10−3 | 6.27 | 1290 | 9.00 | 0.70 | 0.97 | 6.69 × 10−1 | 2.56 × 10−3 | |
| 0.38 | 0.05 | 2.69 × 10−3 | 5.18 | 1040 | 4.00 | 0.38 | 1.38 | 5.01 × 10−1 | 3.20 × 10−2 | |
| Olive stone (os) | 0.13 | 0.05 | 2.46 × 10−3 | 5.13 | 880 | 3.20 | 0.36 | 0.42 | 6.67 × 10−1 | 0.00 |
| 0.15 | 0.05 | 3.10 × 10−3 | 5.96 | 930 | 3.20 | 0.34 | 0.54 | 5.94 × 10−1 | 1.27 × 10−1 | |
| 0.23 | 0.06 | 2.65 × 10−3 | 4.81 | 1010 | 0.00 | 0.00 | 0.66 | 6.29 × 10−1 | 3.21 × 10−1 | |
| 0.28 | 0.05 | 2.34 × 10−3 | 4.59 | 1100 | 4.00 | 0.36 | 0.87 | 3.89 × 10−1 | 8.11 × 10−2 | |
| 0.35 | 0.06 | 4.58 × 10−3 | 8.17 | 960 | 3.20 | 0.33 | 0.85 | 7.89 × 10−1 | 6.19 × 10−3 | |
| Wood pellet (wp) | 0.15 | 0.05 | 4.21 × 10−3 | 8.42 | 890 | 3.20 | 0.36 | 0.43 | 6.67 × 10−1 | 0.00 |
| 0.33 | 0.07 | 4.18 × 10−3 | 6.06 | 1020 | 4.00 | 0.39 | 0.81 | 7.23 × 10−1 | 4.62 × 10−3 | |
| 0.35 | 0.07 | 6.12 × 10−3 | 9.14 | 990 | 3.20 | 0.32 | 0.98 | 6.69 × 10−1 | 2.58 × 10−1 | |
| 0.43 | 0.06 | 6.31 × 10−3 | 10.35 | 1040 | 4.00 | 0.38 | 1.21 | 4.77 × 10−1 | 1.08 × 10−1 | |
| 0.48 | 0.05 | 4.30 × 10−3 | 8.43 | 1100 | 4.00 | 0.36 | 1.63 | 3.39 × 10−1 | 3.69 × 10−2 |

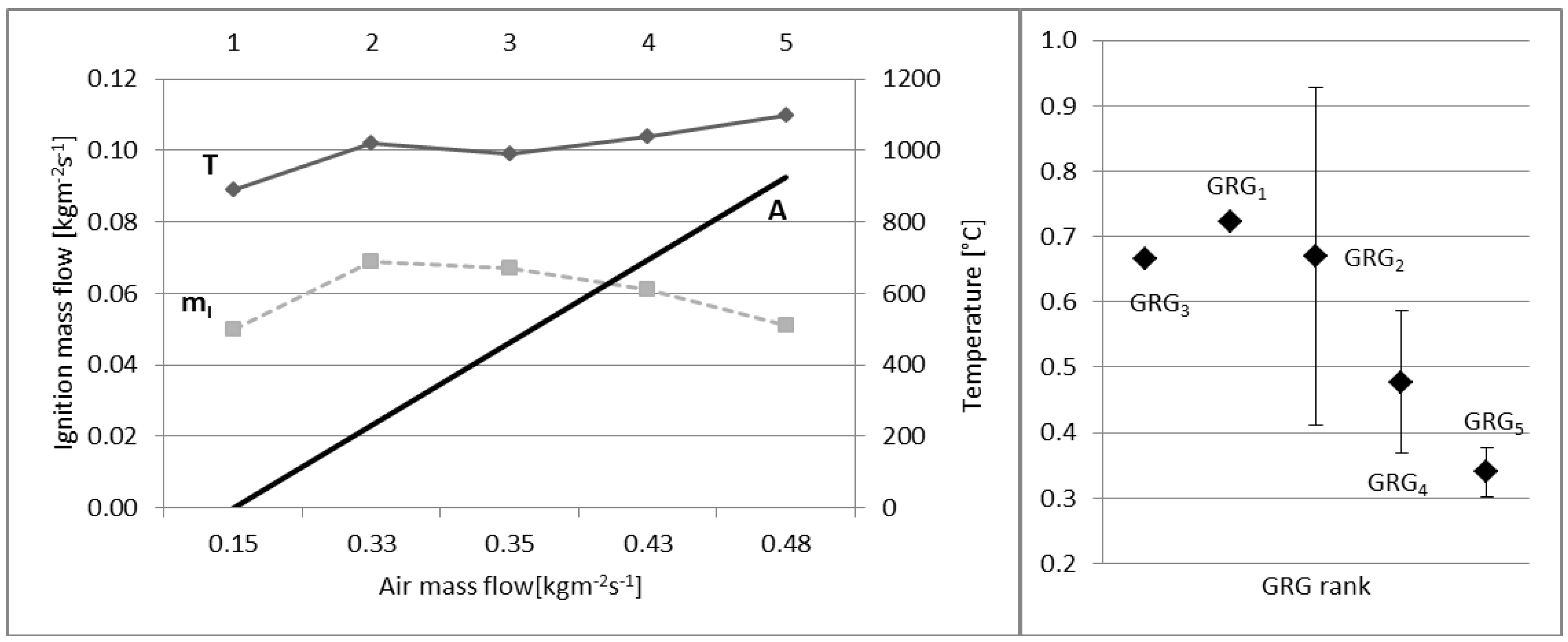
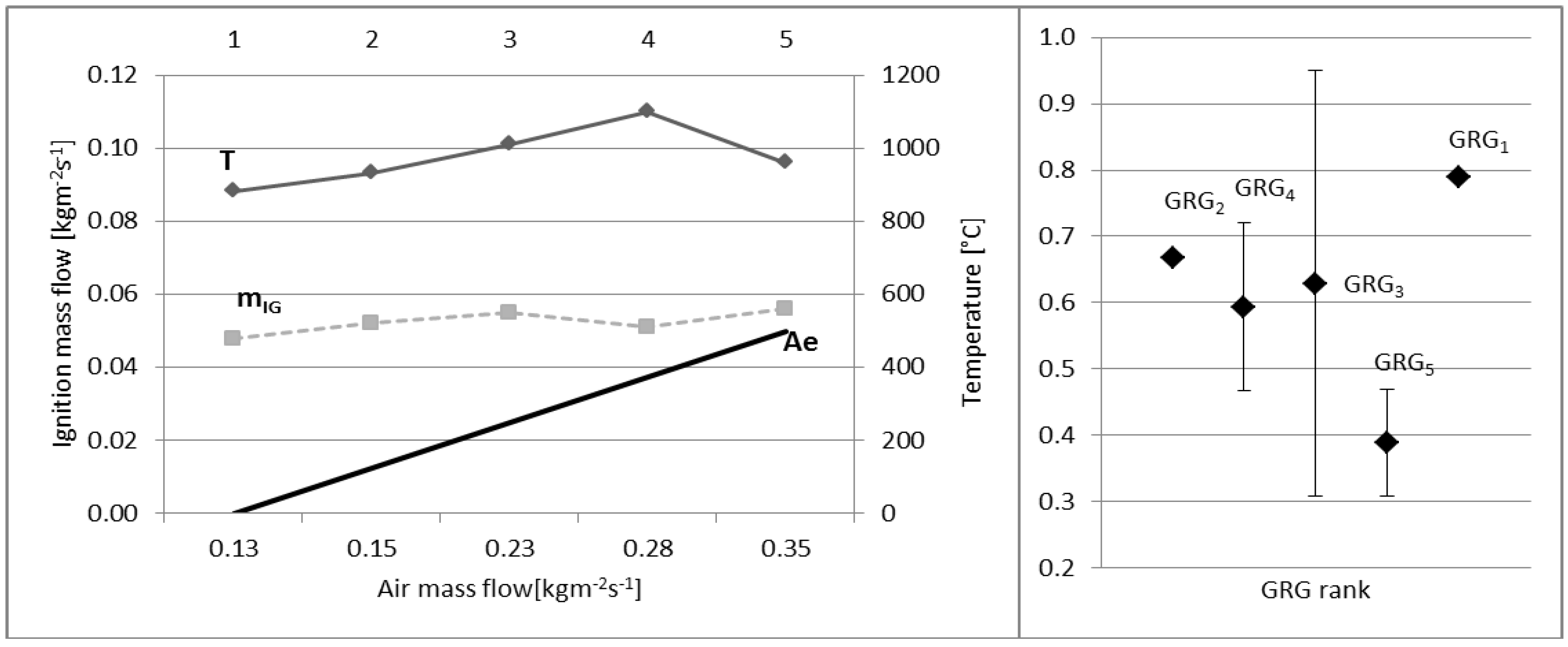
4. Conclusions
Acknowledgments
Conflicts of Interest
Nomenclature
| AE | air excess |
| AMF | air mass flow (kg m−2 s−1) |
| Ap | surface area of the characteristic particle (m2) |
| bp | brassica pellet |
| Er | radius of the equivalent sphere |
| EPT | error propagation theory |
| GRA | grey relational analysis |
| GRC | grey relational coefficient (ξ) |
| GRG | grey relational grade (γ) |
| GRGe | grey relational grade error (∆(γ)) |
| IMF | ignition mass flux (kg m−2 s−1) |
| IMFU | ignition mass flux uncertainty (kg m−2 s−1) |
| k | form factor of the Rosin-Ramler distribution (-) |
| LHV | lower heating value in water basis with ash (as received) (kJ kg−1) |
| M | mass (kg) |
ignition mass flux (kg m−2 s−1) | |
| MT | maximum temperature (°C) |
| MT | Total mass of the distribution (kg) |
| MTU | maximum temperature uncertainty (°C) |
| os | olive stone |
| Svol | sphere volume (m3) |
| Vp | volume of the characteristic particle (m3) |
| wp | wood pellet |
| ζ | distinguish coefficient |
| λ | characteristic length of the distribution (m) |
| µ | characteristic length of the distribution (kg) |
| ψ | sphericity |
References
- The Spanish Ministry of Industry, Energy and Tourism. Instituto para la Diversificación y Ahorro de la Energía (IDEA). Plan de Acción de Ahorro y Eficiencia Energética 2011–2020 (in Spanish). Available online: http://www.idae.es/index.php/mod.documentos/mem.descarga?file=/documentos_11905_PAEE_2011_2020._A2011_A_a1e6383b.pdf (accessed on 13 September 2013).
- Directorate General for Energy. EU Energy Trends to 2030. Available online: http://ec.europa.eu/energy/observatory/trends_2030/doc/trends_to_2030_update_2009.pdf (accessed on 13 September 2013).
- Nussbaumer, T. Combustion and co-combustion of biomass: Fundamentals, technologies, and primary measures for emission reduction. Energy Fuels 2003, 17, 1510–1521. [Google Scholar] [CrossRef]
- Senneca, O. Kinetics of pyrolysis, combustion and gasification of three biomass fuels. Fuel Process. Technol. 2007, 88, 87–97. [Google Scholar] [CrossRef]
- Chaney, J.; Liu, H.; Li, J. An overview of CFD modelling of small-scale fixed-bed biomass pellet boilers with preliminary results from a simplified approach. Energy Convers. Manag. 2012, 63, 149–156. [Google Scholar] [CrossRef]
- Collazo, J.; Pazo, J.A.; Granada, E.; Saavedra, A.; Eguia, P. Determination of the specific heat of biomass materials and the combustion energy of coke by DSC analysis. Energy 2012, 45, 746–752. [Google Scholar] [CrossRef]
- Mehrabian, R.; Scharler, R.; Obernberger, I. Effects of pyrolysis conditions on the heating rate in biomass particles and applicability of TGA kinetic parameters in particle thermal conversion modelling. Fuel 2012, 93, 567–575. [Google Scholar] [CrossRef]
- Wang, T.; Yang, H.; Wu, Y.; Liu, Q.; Lv, J.; Zhang, H. Experimental study on the effects of chemical and mineral components on the attrition characteristics of coal ashes for fluidized bed boilers. Energy Fuels 2012, 26, 990–994. [Google Scholar] [CrossRef]
- Anca-Couce, A.; Zobel, N.; Jakobsen, H.A. Multi-scale modeling of fixed-bed thermo-chemical processes of biomass with the representative particle model: Application to pyrolysis. Fuel 2013, 103, 773–782. [Google Scholar] [CrossRef]
- Houshfar, E.; Lovas, T.; Skreiberg, O. Experimental investigation on NOx reduction by primary measures in biomass combustion: Straw, peat, sewage sludge, forest residues and wood pellets. Energies 2012, 5, 270–290. [Google Scholar] [CrossRef]
- Morissette, R.; Savoie, P.; Villeneuve, J. Combustion of corn stover bales in a small 146-kW boiler. Energies 2011, 4, 1102–1111. [Google Scholar] [CrossRef]
- Perez, J.F.; Melgar, A.; Benjumea, P.N. Effect of operating and design parameters on the gasification/combustion process of waste biomass in fixed bed downdraft reactors: An experimental study. Fuel 2012, 96, 487–496. [Google Scholar] [CrossRef]
- Horttanainen, M.; Saastamoinen, J.; Sarkomaa, P. Operational limits of ignition front propagation against airflow in packed beds of different wood fuels. Energy Fuels 2002, 16, 676–686. [Google Scholar] [CrossRef]
- Johansson, R.; Thunman, H.; Leckner, B. Sensitivity analysis of a fixed bed combustion model. Energy Fuels 2007, 21, 1493–1503. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Y. Grey Systems: Theory and Applications; Springer-Verlag: Berlin, Germany, 2010. [Google Scholar]
- Wang, H.; Jiang, X.; Liu, J.; Lin, W. Experiment and grey relational analysis of CWS spheres combustion in a fluidized bed. Energy Fuels 2007, 21, 1924–1930. [Google Scholar] [CrossRef]
- Asian, N.; Shahrivar, A.A.; Abdollahi, H. Multi-objective optimization of some process parameters of a lab-scale thickener using grey relational analysis. Sep. Purif. Technol. 2012, 90, 189–195. [Google Scholar] [CrossRef]
- Kuo, Y.; Yang, T.; Huang, G. The use of grey relational analysis in solving multiple attribute decision-making problems. Comput. Ind. Eng. 2008, 55, 80–93. [Google Scholar] [CrossRef]
- Yin, C.; Rosendahl, L.; Clausen, S.; Hvid, S.L. Characterizing and modeling of an 88 MW grate-fired boiler burning wheat straw: Experience and lessons. Energy 2012, 41, 473–482. [Google Scholar] [CrossRef]
- Saavedra, A.; Arce, E.; Miguez, J.L.; Granada, E. Potential effect of uncertainty on the GRG interpretation. Grey Syst. Theory Appl. 2013, 3, 121–128. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology (JCGM). International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM). 2012. Available online: http://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf (accessed on 13 September 2013).
- Porteiro, J.; Patiño, D.; Collazo, J.; Granada, E.; Moran, J.; Miguez, J.L. Experimental analysis of the ignition front propagation of several biomass fuels in a fixed-bed combustor. Fuel 2010, 89, 26–35. [Google Scholar] [CrossRef]
- Patino, D. Análisis Experimental de Combustión de Biomasa en un Quemador de Lecho Fijo (in Spanish). Ph.D. Thesis, University of Vigo, Vigo, Spain, 2009. [Google Scholar]
- Shin, D.; Choi, S. The combustion of simulated waste particles in a fixed bed. Combust. Flame 2000, 121, 167–180. [Google Scholar] [CrossRef]
- Hermansson, S.; Thunman, H. Measures to reduce grate material wear in fixed-bed combustion. Energy Fuels 2011, 25, 1387–1395. [Google Scholar] [CrossRef]
- Thunman, H.; Leckner, B. Co-current and counter-current fixed bed combustion of biofuel—A comparison. Fuel 2003, 82, 275–283. [Google Scholar] [CrossRef]
- Porteiro, J.; Patiño, D.; Miguez, J.L.; Granada, E.; Moran, J.; Collazo, J. Study of the reaction front thickness in a counter-current fixed-bed combustor of a pelletised biomass. Combust. Flame 2012, 159, 1296–1302. [Google Scholar] [CrossRef]
- Buczynski, R.; Weber, R.; Szlek, A.; Nosek, R. Time-dependent combustion of solid fuels in a fixed-bed: Measurements and mathematical modeling. Energy Fuels 2012, 26, 4767–4774. [Google Scholar] [CrossRef]
- Bidabadi, M.; Abedinejad, M.S.; Fereidooni, J. Modeling of the propagation of a reaction front in fixed bed combustion of wood particles. J. Mech. 2011, 27, 453–459. [Google Scholar] [CrossRef]
- Bitra, V.S.P.; Womac, A.R.; Yang, Y.T.; Igathinathane, C.; Miu, P.I.; Chevanan, N.; Sokhansanj, S. Knife mill operating factors effect on switchgrass particle size distributions. Bioresour. Technol. 2009, 100, 5176–5188. [Google Scholar] [CrossRef] [PubMed]
- Liao, K.; Yao, Q.; Wu, X.; Jia, W. A numerical corrosion rate prediction method for direct assessment of wet gas gathering pipelines internal corrosion. Energies 2012, 5, 3892–3907. [Google Scholar] [CrossRef]
- Moran, J.; Granada, E.; Míguez, J.L.; Porteiro, J. Use of grey relational analysis to assess and optimize small biomass boilers. Fuel Process. Technol. 2006, 87, 123–127. [Google Scholar] [CrossRef]
- Subbaya, K.M.; Suresha, B.; Rajendra, N.; Varadarajan, Y.S. Grey-based Taguchi approach for wear assessment of SiC filled carbon-epoxy composites. Mater. Des. 2012, 41, 124–130. [Google Scholar] [CrossRef]
- Deng, J. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Chang, A.Y. Prioritising the types of manufacturing flexibility in an uncertain environment. Int. J. Prod. Res. 2012, 50, 2133–2149. [Google Scholar] [CrossRef]
- Li, H.Z.; Tao, W.; Gao, T.; Li, H.; Lu, Y.H.; Su, Z.M. Improving the accuracy of density functional theory (DFT) calculation for homolysis bond dissociation energies of Y-NO bond: Generalized regression neural network based on grey relational analysis and principal component analysis. Int. J. Mol. Sci. 2011, 12, 2242–2261. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Lin, Y. Evaluating and ranking energy performance of office buildings using grey relational analysis. Energy 2011, 36, 2551–2556. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology (JCGM). Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. September 2008. Available online: http://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 13 September 2013).
- Hughes, I.G.; Hase, T.P.A. Measurements and Their Uncertainties: A Practical Guide to Modern Error Analysis; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Pazo, J.A.; Granada, E.; Saavedra, A.; Patino, D.; Collazo, J. Heterogenic solid biofuel sampling methodology and uncertainty associated with prompt analysis. Int. J. Mol. Sci. 2010, 11, 2118–2133. [Google Scholar] [CrossRef] [PubMed]
- Ryu, C.; Yang, Y.B.; Khor, A.; Yates, N.E.; Sharifi, V.N.; Switenbank, J. Effect of fuel properties on biomass combustion: Part I. Experiments—Fuel type equivalence ratio and particle size. Fuel 2006, 85, 1039–1046. [Google Scholar] [CrossRef]
- Saastamoinen, J.J.; Taipale, R.; Horttanainen, M.; Sarkomaa, P. Propagation of the ignition front in beds of wood particles. Combust. Flame 2000, 123, 214–226. [Google Scholar] [CrossRef]
- Liang, L.; Sun, R.; Fei, J.; Wu, S.; Liu, X.; Dai, K.; Yao, N. Experimental study on effects of moisture content on combustion characteristics of simulated municipal solid wastes in a fixed bed. Bioresour. Technol. 2008, 99, 7238–7246. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Li, Z.; Zhao, G.; Zhang, F.; Zhu, Q. Effect of air preheating and fuel moisture on combustion characteristics of corn straw in a fixed bed. Energy Convers. Manag. 2008, 49, 3560–3565. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Arce, M.E.; Saavedra, Á.; Míguez, J.L.; Granada, E.; Cacabelos, A. Biomass Fuel and Combustion Conditions Selection in a Fixed Bed Combustor. Energies 2013, 6, 5973-5989. https://doi.org/10.3390/en6115973
Arce ME, Saavedra Á, Míguez JL, Granada E, Cacabelos A. Biomass Fuel and Combustion Conditions Selection in a Fixed Bed Combustor. Energies. 2013; 6(11):5973-5989. https://doi.org/10.3390/en6115973
Chicago/Turabian StyleArce, María E., Ángeles Saavedra, José L. Míguez, Enrique Granada, and Antón Cacabelos. 2013. "Biomass Fuel and Combustion Conditions Selection in a Fixed Bed Combustor" Energies 6, no. 11: 5973-5989. https://doi.org/10.3390/en6115973
APA StyleArce, M. E., Saavedra, Á., Míguez, J. L., Granada, E., & Cacabelos, A. (2013). Biomass Fuel and Combustion Conditions Selection in a Fixed Bed Combustor. Energies, 6(11), 5973-5989. https://doi.org/10.3390/en6115973





