PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation
Abstract
:1. Introduction
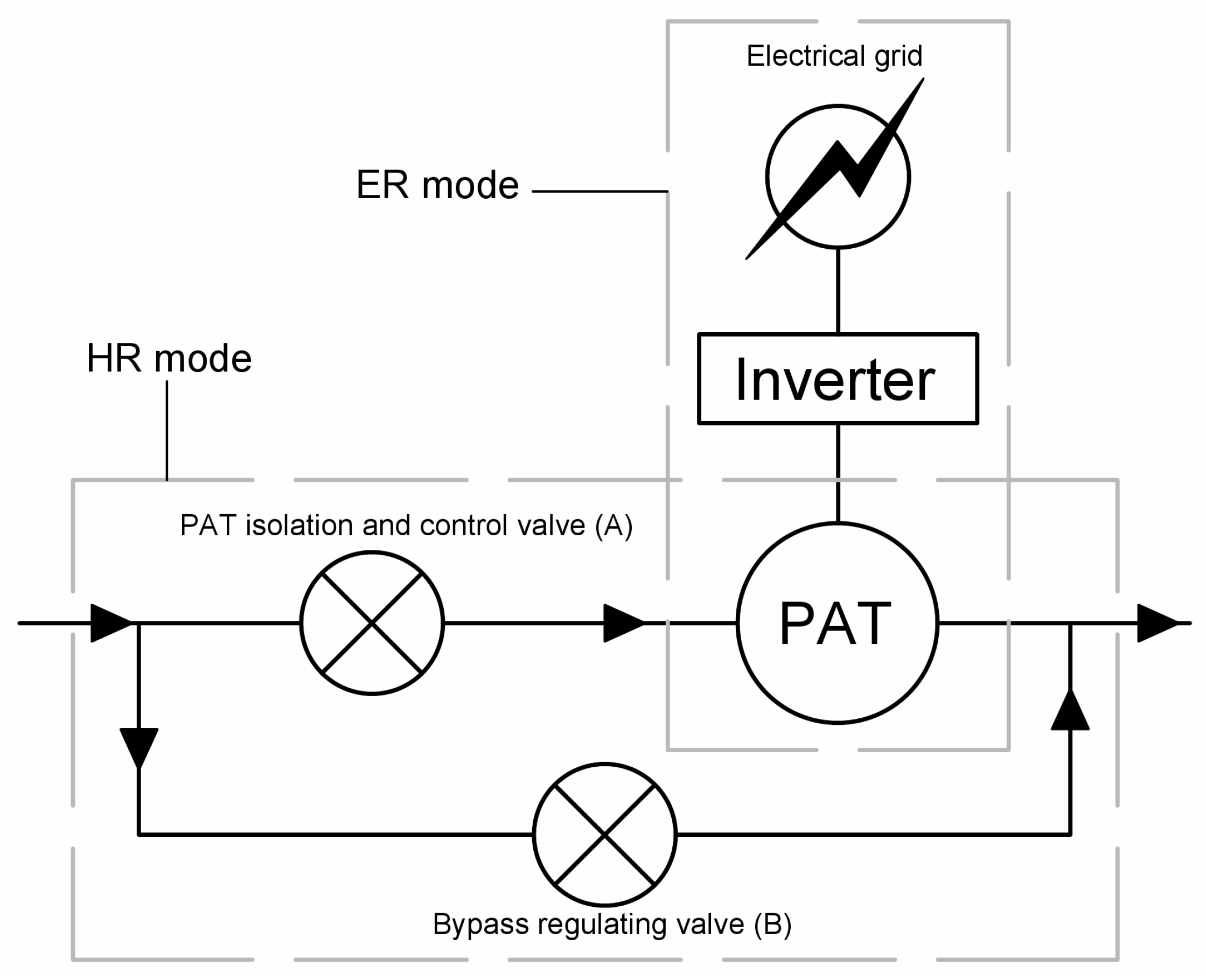

2. Energy Recovery in Water Supply Systems
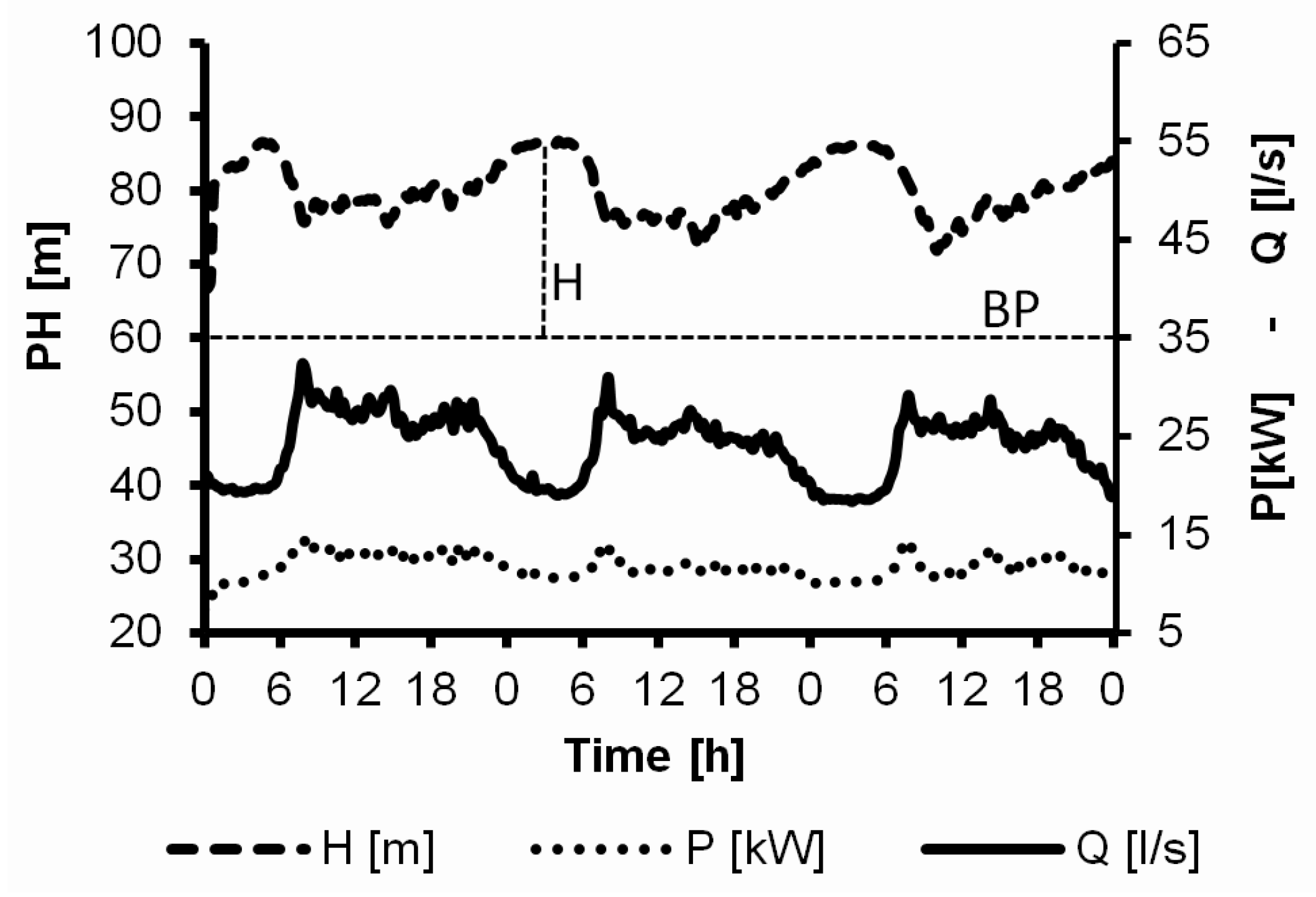
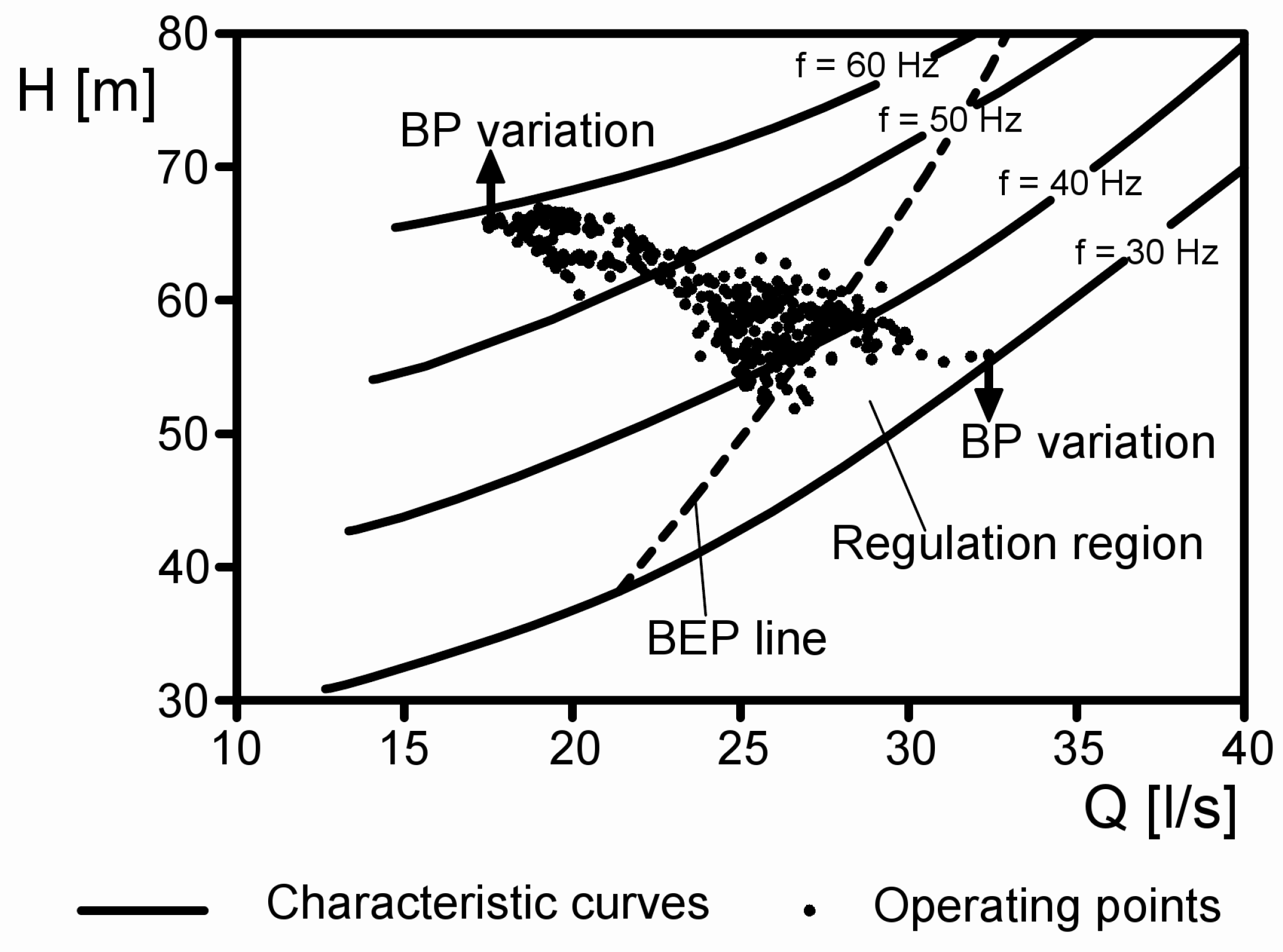
3. Variable Operating Strategy in ER Mode
- a measured pattern of flow-rate and pressure-head conditions is assigned and the available head is determined based on the required backpressure (), as in Figure 3;
- a PAT type is considered (e.g., centrifugal, semi-axial);
- a wide set of PAT characteristic curves is considered in the PAT operating region, by changing the number of stages and impeller diameter;
- for each PAT the rotation speed is changed within the limits of the allowed frequency range;
- for each PAT the overall plant efficiency is calculated by Equation (2);where is the time interval, n the number of points in the operating region and the efficiency is dependent on the induction frequency f, which can be set for each point of the operating region in order to obtain the desired head-drop discharge coordinate;
- the PAT that maximizes the produced energy, i.e., the PAT having the largest , is considered the optimal design solution;
- the near-optimal machine is selected from the market and its turbine mode curves are calculated in order to verify the actual efficiency.

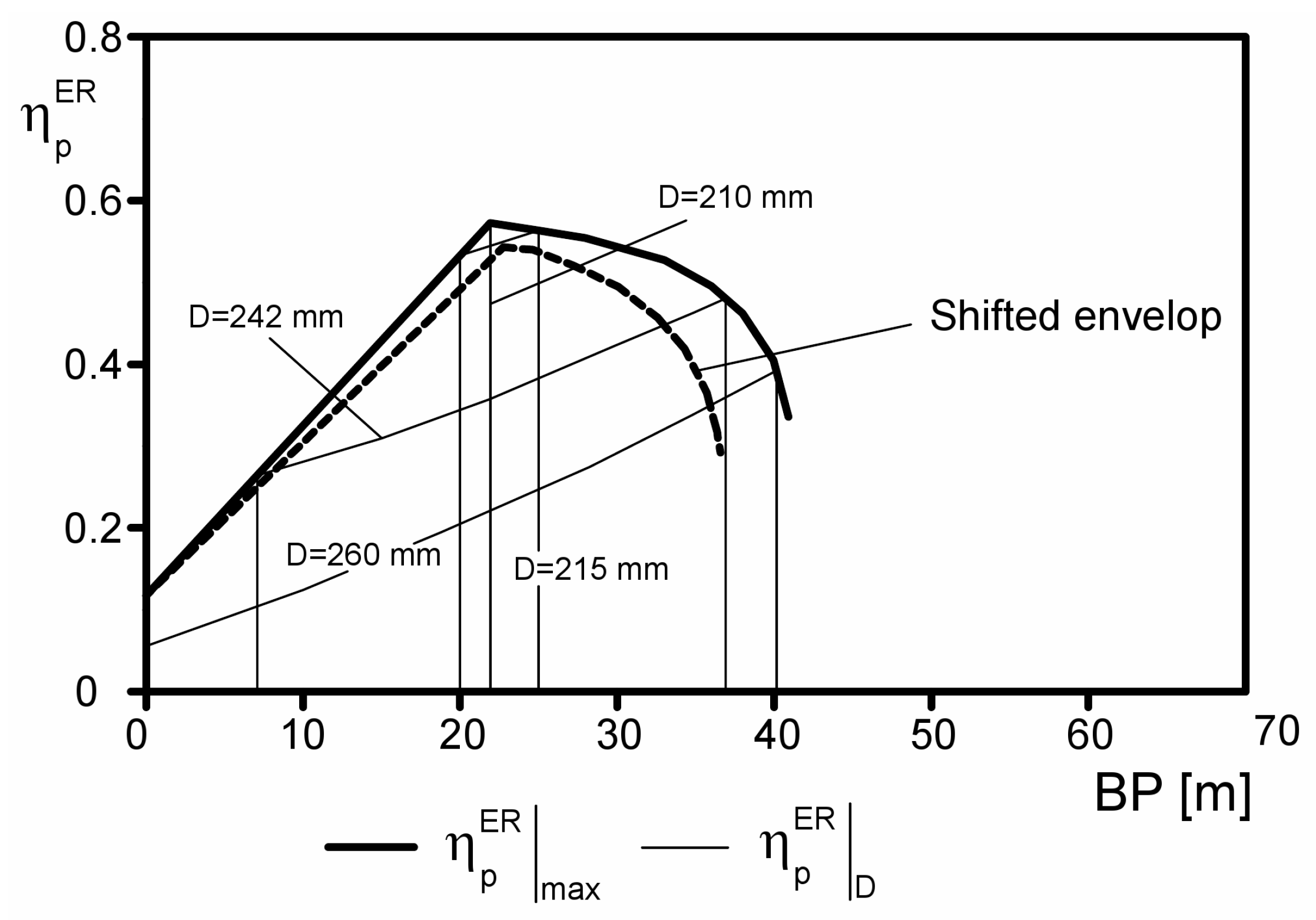
| 10 | 238 | 0.31 |
| 15 | 230 | 0.40 |
| 20 | 220 | 0.50 |
| 23 | 216 | 0.54 |
| 25 | 219 | 0.54 |
| 30 | 232 | 0.49 |
| 35 | 251 | 0.40 |
| 37 | 270 | 0.28 |
| 40 | - | - |
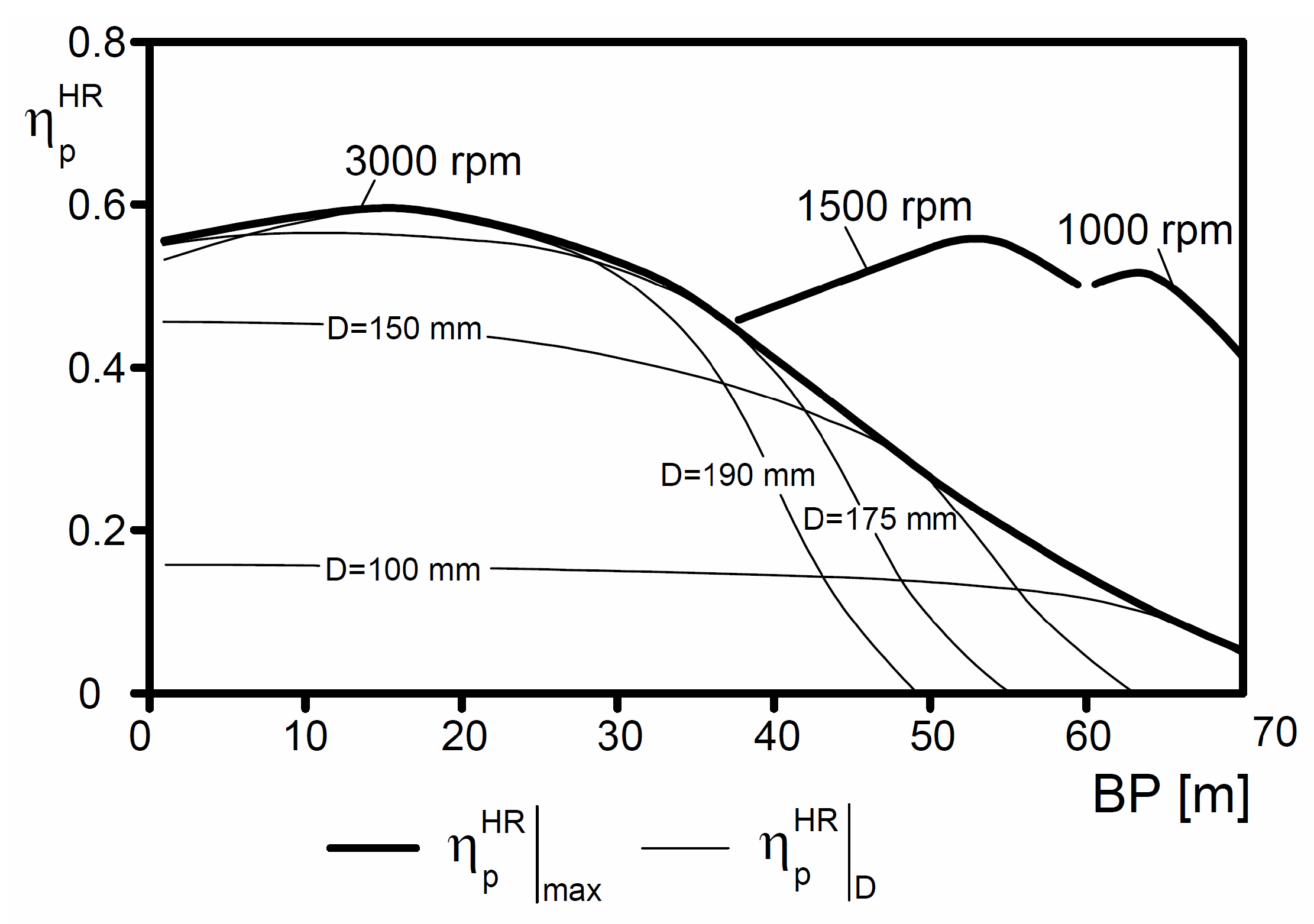
4. Comparison between HR and ER Efficiencies and System Flexibility
| 10 | 186 | 3000 | 0.59 |
| 15 | 190 | 3000 | 0.59 |
| 20 | 191 | 3000 | 0.59 |
| 25 | 187 | 3000 | 0.56 |
| 30 | 181 | 3000 | 0.53 |
| 35 | 176 | 3000 | 0.48 |
| 40 | 208 | 3000 | 0.47 |
| 45 | 219 | 1500 | 0.51 |
| 50 | 232 | 1500 | 0.54 |
| 55 | 237 | 1500 | 0.55 |
| 60 | 221 | 1000 | 0.50 |
| % variation of | % variation of | |||||
|---|---|---|---|---|---|---|
| design | design | |||||
| 10 | 0.586 | −0.485 | 0.387 | 0.305 | −2.349 | 2.244 |
| 20 | 0.585 | 1.045 | −1.492 | 0.502 | −2.418 | 2.246 |
| 30 | 0.531 | 3.356 | −5.285 | 0.488 | −4.497 | 4.126 |
| 35 | 0.484 | 6.405 | −12.791 | 0.403 | −8.473 | 7.450 |
5. Economic Feasibility
| 10 | 20 | 30 | 35 | |||||
|---|---|---|---|---|---|---|---|---|
| Mode | HR | ER | HR | ER | HR | ER | HR | ER |
| D [mm] | 186 | 238 | 191 | 220 | 181 | 232 | 176 | 251 |
| [−] | 0.586 | 0.305 | 0.585 | 0.502 | 0.531 | 0.488 | 0.484 | 0.403 |
| [kW] | 8.49 | 29.12 | 9.69 | 19.65 | 7.41 | 25.63 | 6.44 | 37.99 |
| [kW] | 12.79 | 12.29 | 10.86 | 11.92 | 7.97 | 9.78 | 6.71 | 8.51 |
| [€] | 1953 | 6698 | 2230 | 4520 | 1704 | 5895 | 1481 | 8738 |
| [€] | 1471 | 1414 | 1248 | 1372 | 916 | 1125 | 772 | 978 |
| [€] | - | 2459 | - | 2385 | - | 1957 | - | 1701 |
| [€] | 5000 | - | 5000 | - | 5000 | - | 5000 | - |
| [€] | 8423 | 10570 | 8478 | 8277 | 7620 | 8977 | 7253 | 11418 |
| ADEP [kWh/day] | 266.30 | 139.92 | 146.13 | 123.84 | 159.67 | 147.62 | 84.59 | 70.49 |
| Daily income [€/day] | 53.26 | 27.98 | 29.23 | 24.77 | 31.93 | 29.52 | 16.92 | 14.10 |
| [days] | 158 | 378 | 290 | 334 | 238 | 304 | 428 | 810 |
6. Conclusions
Acknowledgements
References
- Vairavamoorthy, K.; Lumbers, J. Leakage reduction in water distribution systems: Optimal valve control. J. Hydraul. Eng. 1998, 124(11), 1146–1154. [Google Scholar] [CrossRef]
- Tucciarelli, T.; Criminisi, A.; Termini, D. Leak analysis in pipeline systems by means of optimal valve regulation. J. Hydraul. Eng. 1999, 125(3), 277–285. [Google Scholar] [CrossRef]
- Almandoz, J.; Cabrera, E.; Arregui, F.; Cabrera, E.; Cobacho, R. Leakage assessment through water distribution network simulation. J. Water Res. Plan. 2005, 131(6), 458–466. [Google Scholar] [CrossRef]
- Araujo, L.; Ramos, H.; Coelho, S. Pressure control for leakage minimisation in water distribution systems management. Water Res. Manag. 2006, 20(1), 133–149. [Google Scholar] [CrossRef]
- Walsky, T.; Bezts, W.; Posluzny, E.; Weir, M.; Withman, B. Modeling leakage reduction through pressure control. J. Am. Water Work. Assoc. 2006, 98(4), 148–155. [Google Scholar]
- Prescott, S.; Ulanicki, B. Improved control of pressure reducing valves in water distribution networks. J. Hydraul. Eng. 2008, 134(1), 56–65. [Google Scholar] [CrossRef]
- Nazif, S.; Karamouz, M.; Tabesh, M.; Moridi, A. Pressure management model for urban water distribution networks. Water Res. Manag. 2010, 24, 437–458. [Google Scholar] [CrossRef]
- Carravetta, A.; Giugni, M. Functionality factors in the management and rehabilitation of water networks. In Management of Water Networks. Proceedings of the Conference Efficient Management of Water Networks. Design and Rehabilitation Techniques; Franchini, B., Ed.; Franco Angeli: Milano, Italy, 2009. [Google Scholar]
- Gonçalves, F.; Costa, L.; Ramos, H. ANN for hybrid energy system evaluation: Methodology and WSS case study. Water Res. Manag. 2011, 25, 2295–2317. [Google Scholar] [CrossRef]
- Filion, Y.; MacLean, H.; Karney, B. Life cycle energy analysis of a water distribution system. J. Infrastruct. Syst. 2004, 10(3), 120–130. [Google Scholar] [CrossRef]
- Zakkour, P.; M.R., G.; Gochin, R.; Lester, J. Developing a sustainable energy strategy for a water utility. Part II: A review of potential technologies and approaches. J. Environ. Manag. 2002, 66, 115–125. [Google Scholar] [CrossRef]
- Arriaga, M. Pump as turbine—A pico-hydro alternative in Lao People’s Democratic Republic. Renew. Energy 2010, 35, 1109–1115. [Google Scholar] [CrossRef]
- Williams, A.; Smith, P.; Bird, C.; Howard, M. Pumps as turbines and induction motors as generators for energy recovery in water supply systems. Water Environ. J. 1998, 12, 175–178. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Portolano, D. Losses reduction and energy production in water-distribution networks. J. Water Res. Plan. 2012, 138(3), 237–244. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A. The Technical and Economic Feasibility of Energy Recovery in Water Supply Networks. In Proceedings of International Conference on Renewable Energy and Power Quality, Las Palmas de Gran Canaria, Spain, 13–15 April 2011.
- Corcoran, L.; McNabola, A.; Coughlan, P. Energy Recovery Potential of the Dublin Region Water Supply Network. In Proceedings of World Congress on Water, Climate and Energy, Dublin, Ireland, 13–18 May 2012.
- Williams, A. The turbine performance of centrifugal pumps: A comparison of predictione methods. J. Power Energy 1994, 208, 59–66. [Google Scholar] [CrossRef]
- Ramos, H.; Covas, D.; Araujo, L.; Mello, M. Available energy assessment in water supply systems. In Proceedings of XXXI International Association for Hydro-Environment Engineering and Research Congress, Seoul, Korea, 11–16 September 2005.
- Gaius-Obaseki, T. Hydropower opportunities in the water industry. Int. J. Environ. Sci. 2010, 1(3), 392–402. [Google Scholar]
- Khurana, S.; Kumar, A. Small hydro power—A review. Int. J .Therm. Technol. 2011, 1(1), 107–110. [Google Scholar]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6(6), 537–556. [Google Scholar] [CrossRef]
- Sopian, K.; Razak, J. Pico Hydro: Clean Power From Small Streams. In Proceedings of the 3rd World Scientific and Engineering Academy and Society International Conference on Renewable Energy Sources, Tenerife, Spain, 1–3 July 2009.
- Johnston, C.; Pratt, D.; Clarke, J.; Grant, A. A techno-economic analysis of tidal energy technology. Renew. Energy 2012, in press. [Google Scholar] [CrossRef]
- Boccotti, P. On a new wave energy absorber. Ocean. Eng. 2003, 30(9), 1191–1200. [Google Scholar] [CrossRef]
- Buccino, M.; Banfi, D.; Vicinanza, D.; Calabrese, M.; del Giudice, G.; Carravetta, A. Non Breaking wave forces at the front face of seawave slotcone generators. Energies 2012, 5(11), 4779–4803. [Google Scholar] [CrossRef]
- Ramos, H.; Mello, M.; De, P. Clean power in water supply systems as a sustainable solution: From planning to practical implementation. Water Sci. Technol. 2010, 10(1), 39–49. [Google Scholar] [CrossRef]
- Nautiyal, H.; Varun; Kumar, A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Joshi, S.; Holloway, A.; Chang, L.; Kojabadi, H. Development of a Stand Alone Micro-Hydro System using Pump as Turbine Technology for Low Head Sites in Remote Areas. In Proceedings of 20th International Power System Conference, Tehran, Iran, 14–16 November 2005.
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H. Energy production in water distribution networks: A PAT design strategy. Water Res. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Karadirek, I.; Kara, S.; Yilmaz, G.; Muhammetoglu, A.; Muhammetoglu, H. Implementation of hydraulic modelling for water-loss reduction through pressure management. Water Res. Manag. 2012, 26(9), 2555–2568. [Google Scholar] [CrossRef]
- Liberatore, S.; Sechi, G. Location and calibration of valves in water distribution networks using a scatter-search meta-heuristic approach. Water Res. Manag. 2009, 23, 1479–1495. [Google Scholar] [CrossRef]
- Afshar, A.; Jemaa, F.; Marino, M. Optimization of hydropower plant integration in water supply system. J. Water Res. Plan. 1990, 116(5), 665–675. [Google Scholar] [CrossRef]
- Gantar, M. Propeller, Pump running as turbines. In Proceedings of Conference on Hydraulic Machinery, Ljubljana, Yugoslavia, 13–15 September 1988.
- Fernandez, J.; Blanco, E.; Parrondo, J.; Stickland, M.; Scanlon, T. Performance of a centrifugal pump running in inverse mode. J. Power Energy 2004, 218(4), 265–271. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid. Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Rodrigues, A.; Singh, P.; Williams, A.; Nestmann, F.; Lai, E. Hydraulic analysis of a pump as a turbine with CFD and experimental data. In Proceedings of IMechE Seminar, Computational Fluid Dynamics for Fluid Machinery, London, UK, 18 November 2003.
- Natanasabapathi, S.; Kshirsagar, J. Pump as Turbine: An Experience with CFX-5.6. In Proceedings of International ANSYS Conference, Pittsburgh, PA, USA, 24–26 May 2004.
- Carravetta, A.; Fecarotta, O.; Ramos, H. Numerical simulation on Pump As Turbine: Mesh reliability and performance concerns. In Proceedings of International Conference on Clean Electrical Power, Ischia, Italy, 14–16 June 2011.
- Stepanoff, A. Centrifugal and Axial Flow Pumps; John Wiley: New York, NY, USA, 1957. [Google Scholar]
- Childs, S. Convert pumps to turbines and recover HP. Hydrocarb. Process. Pet. Refin. 1962, 41(10), 173–174. [Google Scholar]
- Hanckock, J. Centrifugal Pump or Water Turbine. Pipe Line News 1963, 25–27. [Google Scholar]
- Grover, K. Conversion of Pumps to Turbines; GSA Inter Corp., Katonah: New York, NY, USA, 1980. [Google Scholar]
- Sharma, K. Small Hydroelectric Projects—Use of Centrifugal Pumps as Turbines; Kirloskar Electric Co.: Bangalore, India, 1985. [Google Scholar]
- Schmiedl, E. Serien-Kreiselpumpen im Turbinenbetrieb; Pumpentagung: Karlsruhe, Germany, 1988; Chapter A6. [Google Scholar]
- Alatorre-Frenk, C.; Thomas, T. The pumps as turbines approach to small hydropower. In Proceedings of World Congress on Renewable Energy, Reading, UK, 23–28 September 1990.
- Suter, P. Representation of pump characteristics for calculation of water hammer. Sulzer. Technol. Rev. 1966, 4, 45–48. [Google Scholar]
- Ramos, H.; Almeida, A. Dynamic orifice model on waterhammer analysis of high or medium heads of small hydropower plants. J. Hydraul. Res. 2001, 39(4), 429–436. [Google Scholar] [CrossRef]
- Ramos, H.; Almeida, A. Parametric analysis of water-hammer effects in small hydro schemes. J. Hydraul. Eng. 2002, 128(7), 1–8. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411-424. https://doi.org/10.3390/en6010411
Carravetta A, Del Giudice G, Fecarotta O, Ramos HM. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies. 2013; 6(1):411-424. https://doi.org/10.3390/en6010411
Chicago/Turabian StyleCarravetta, Armando, Giuseppe Del Giudice, Oreste Fecarotta, and Helena M. Ramos. 2013. "PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation" Energies 6, no. 1: 411-424. https://doi.org/10.3390/en6010411
APA StyleCarravetta, A., Del Giudice, G., Fecarotta, O., & Ramos, H. M. (2013). PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies, 6(1), 411-424. https://doi.org/10.3390/en6010411








