DC Flashover Performance of Various Types of Ice-Covered Insulator Strings under Low Air Pressure
Abstract
:1. Introduction
2. Test Facilities and Procedures
2.1. Test Facilities
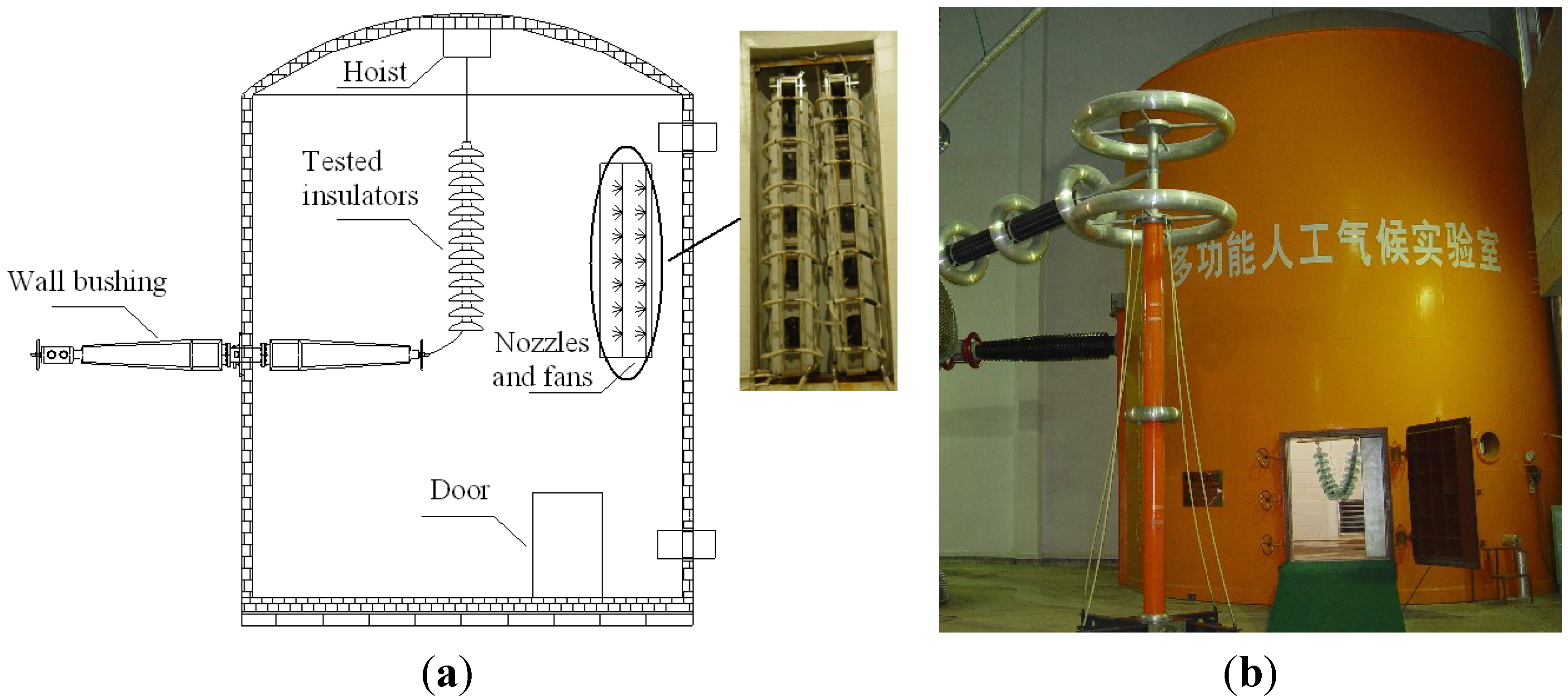
2.2. Specimens
| Type | Profile parameters (mm) | Configuration | ||
|---|---|---|---|---|
| Shed Diameter | Unit Spacing | Leakage Distance | ||
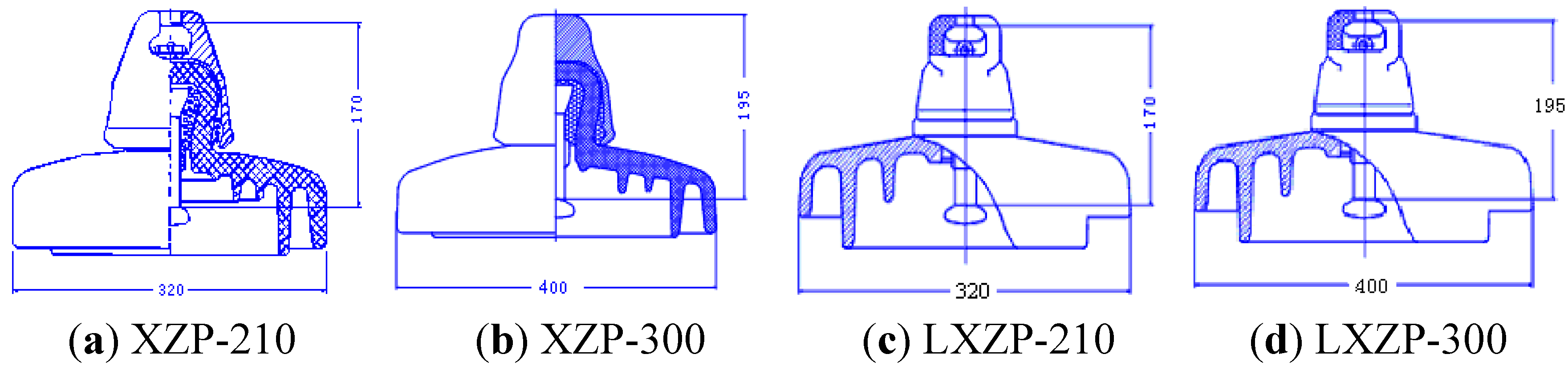
| XZP-210 | 320 | 170 | 545 | Figure 3a |
| XZP-300 | 400 | 195 | 635 | Figure 3b |
| LXZP-210 | 320 | 170 | 545 | Figure 3c |
| LXZP-300 | 400 | 195 | 635 | Figure 3d |
| Type | Profile parameters (mm) | Configuration | |||
|---|---|---|---|---|---|
| Shed Diameter | Dry Arc Distance | Leakage Distance | Housing Diameter | ||
| A | 175(big shed) 87.5(small shed) | 2195 | 7393 | 39 | Figure 4a |
| B | 164(big shed) 125(small shed) | 2290 | 7588 | 32 | Figure 4b |
| C | 190(big shed) 110(small shed) | 3600 | 13100 | 45 | Figure 4c |

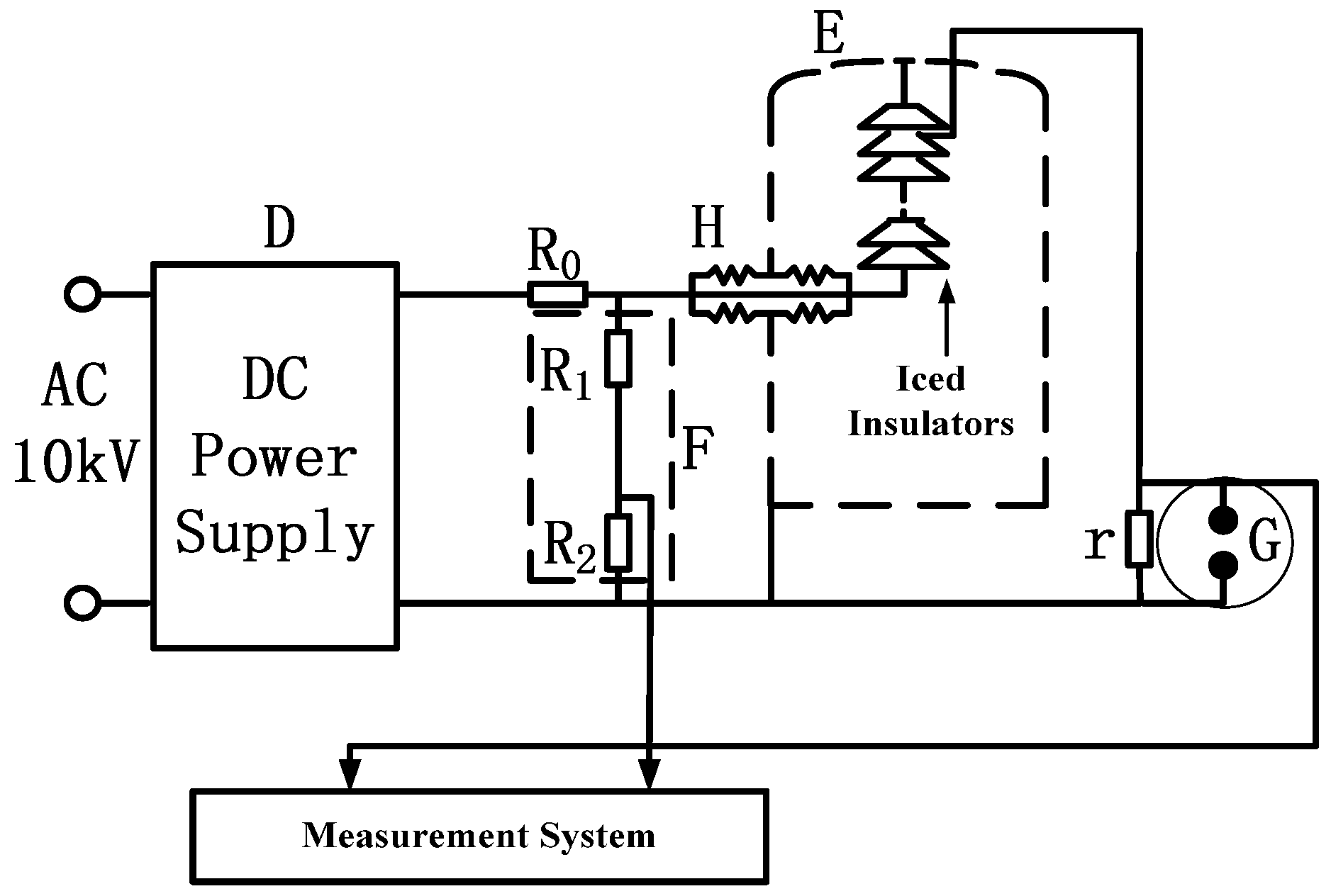
2.3. Test Procedures and Methods
| Droplet (µm) | Freezing water conductivity (µS/cm) | Freezing water flux (L/h·m2) | Air temperature (°C) | Wind velocity (m/s) |
|---|---|---|---|---|
| 80 | 100 | 90 * | −7~−5 | 3.5 * |
- (i)
- Stop spraying steam fog when ice thickness reaches the target value and then remove the monitoring cylinder;
- (ii)
- Lift the iced insulator by the hoist above the wall bushing, and connect the conductor between the wall bushing and the bottom of insulator;
- (iii)
- Maintain the air temperature at −7 °C for 15 min to guarantee complete hardening of the ice and equalization of both insulator and ice temperatures;
- (iv)
- Open the door of the climate chamber to raise the temperature rapidly to −2 °C, and then close the door to recover the temperature to −1.0 °C to 0.5 °C at a speed of 2 °C/h to 3 °C/h;
- (v)
- Apply the flashover voltage to the iced insulator when the ice surface is lucidus and with a layer of water film. First, increase the voltage at a high rate (about 15 kV/s) to the value of about 75% of predicted flashover voltage Up, and then change the rate to the value of 2% × Up/s until the flashover. Finally, record the flashover voltage Uf;
- (vi)
- Repeat the procedure after 2 to 3 min. Stop the flashover test when most of the ice on the insulator is melted. The minimum flashover voltage Ufmin of the test specimen can then be gained;
- (vii)
- Apply the test procedure (i–vi) to another specimen with a similar ice accretion.
2.4. Simulation of High Altitude
3. Results and Analysis
3.1. DC Flashover Characteristics of Iced Insulators under Low Atmospheric Pressure
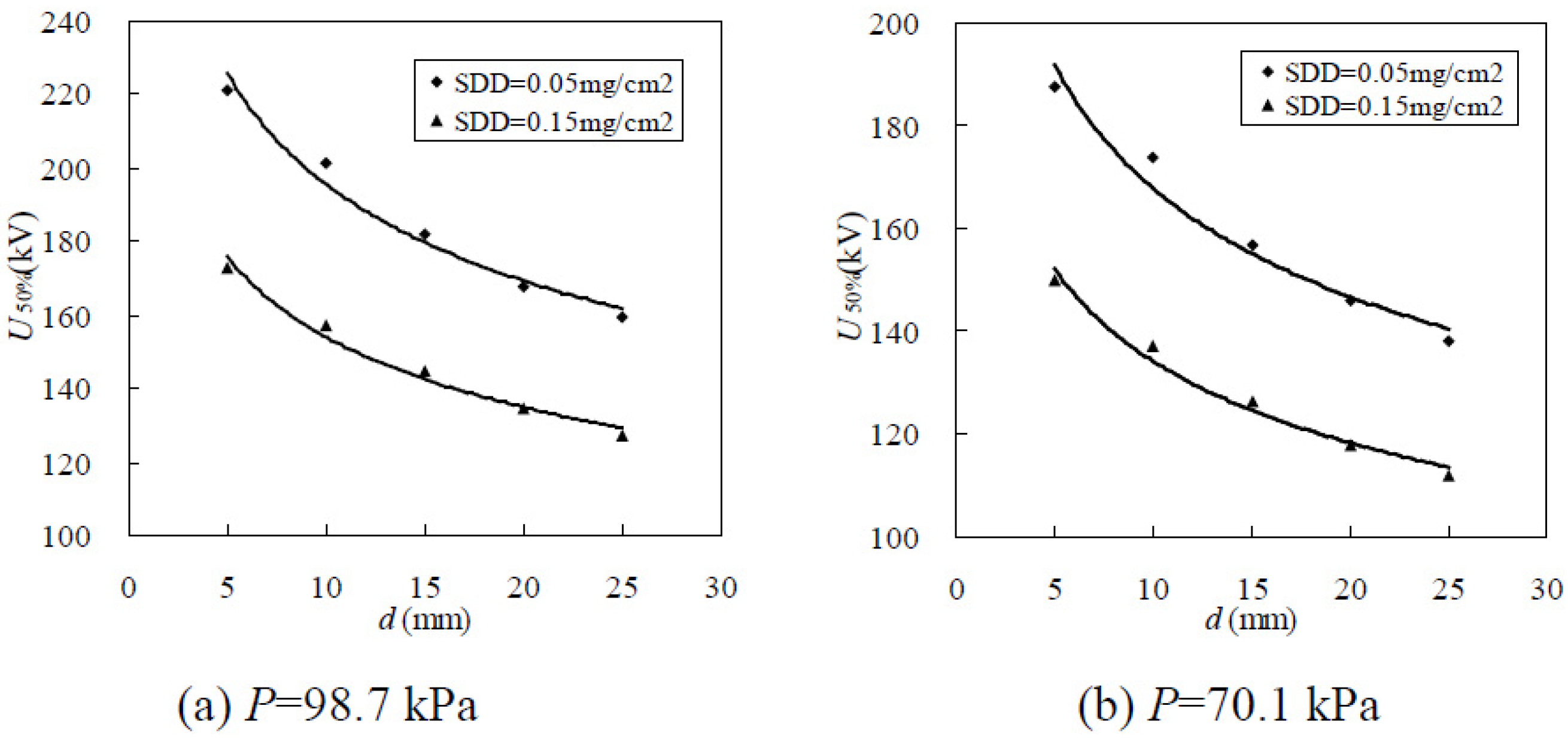
3.1.1. Relationship between U50% and Ice Thickness d
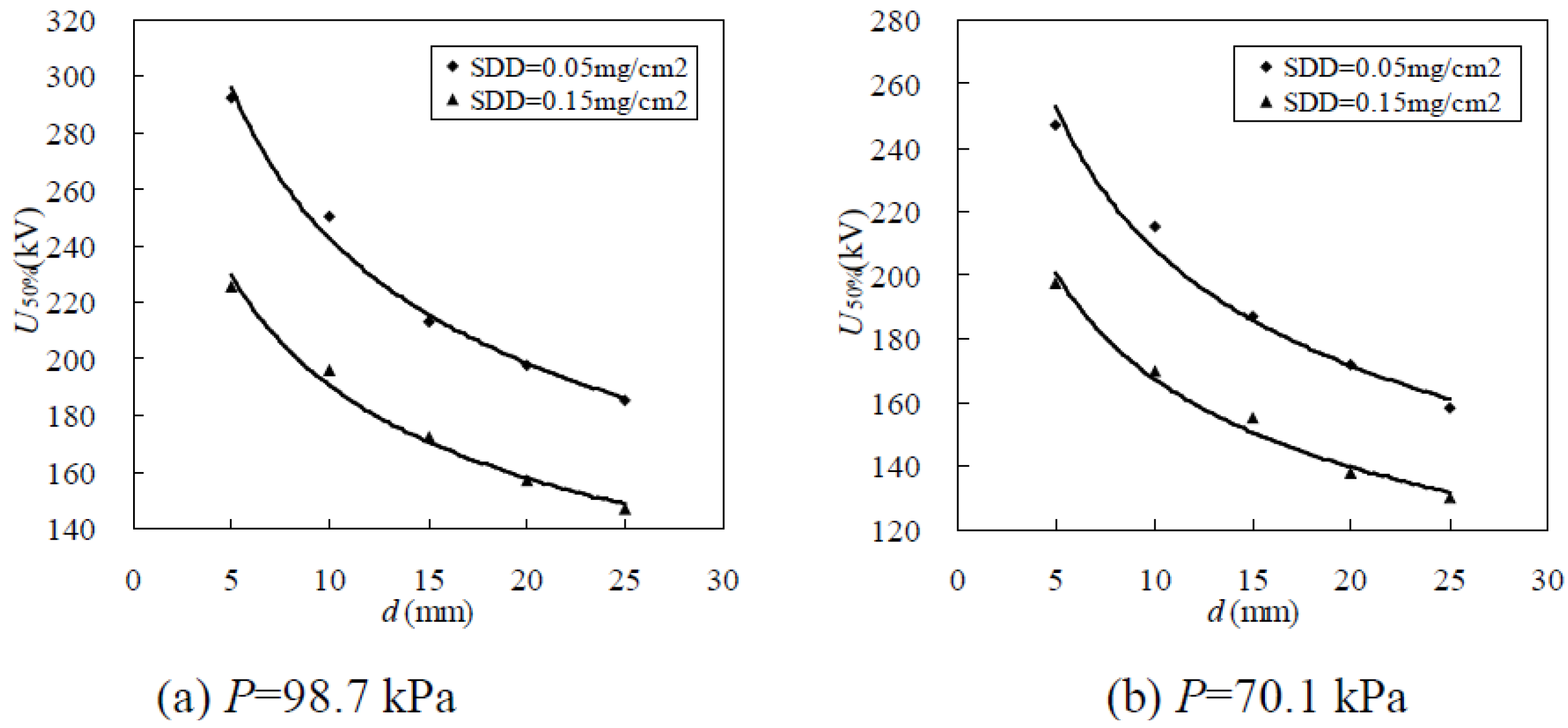
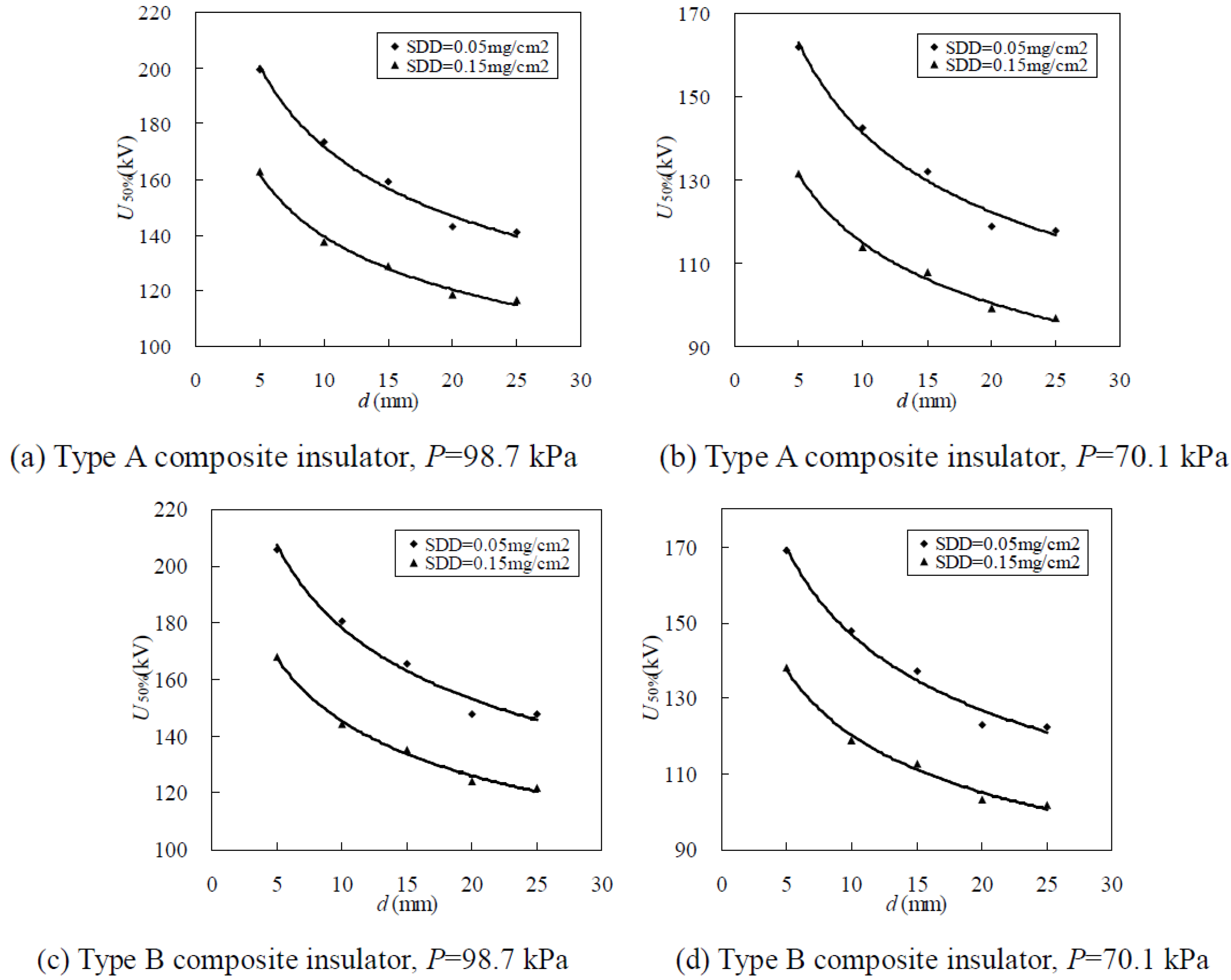
| Type | SDD (mg/cm2) | H = 232 m/P = 98.7 kPa | H = 3000 m/P = 70.1 kPa | ||||
|---|---|---|---|---|---|---|---|
| Ad | c | R2 | Ad | c | R2 | ||
| XZP-210 (15-unit string) | 0.05 | 315.3 | 0.208 | 0.976 | 261.9 | 0.194 | 0.964 |
| 0.15 | 239.2 | 0.191 | 0.978 | 203.6 | 0.182 | 0.979 | |
| XZP-300 (15-unit string) | 0.05 | 470.6 | 0.288 | 0.978 | 428.2 | 0.279 | 0.984 |
| 0.15 | 354.5 | 0.270 | 0.987 | 360.5 | 0.261 | 0.985 | |
| Type A composite insulator | 0.05 | 288.8 | 0.226 | 0.985 | 227.4 | 0.207 | 0.982 |
| 0.15 | 227.6 | 0.213 | 0.990 | 179.1 | 0.193 | 0.991 | |
| Type B composite insulator | 0.05 | 295.2 | 0.217 | 0.978 | 238.0 | 0.210 | 0.980 |
| 0.15 | 232.8 | 0.205 | 0.991 | 187.7 | 0.193 | 0.991 | |
| 0.15 | 238.5 | 0.211 | 0.980 | 186.2 | 0.190 | 0.966 | |
3.1.2. The Effects of SDD on U50%
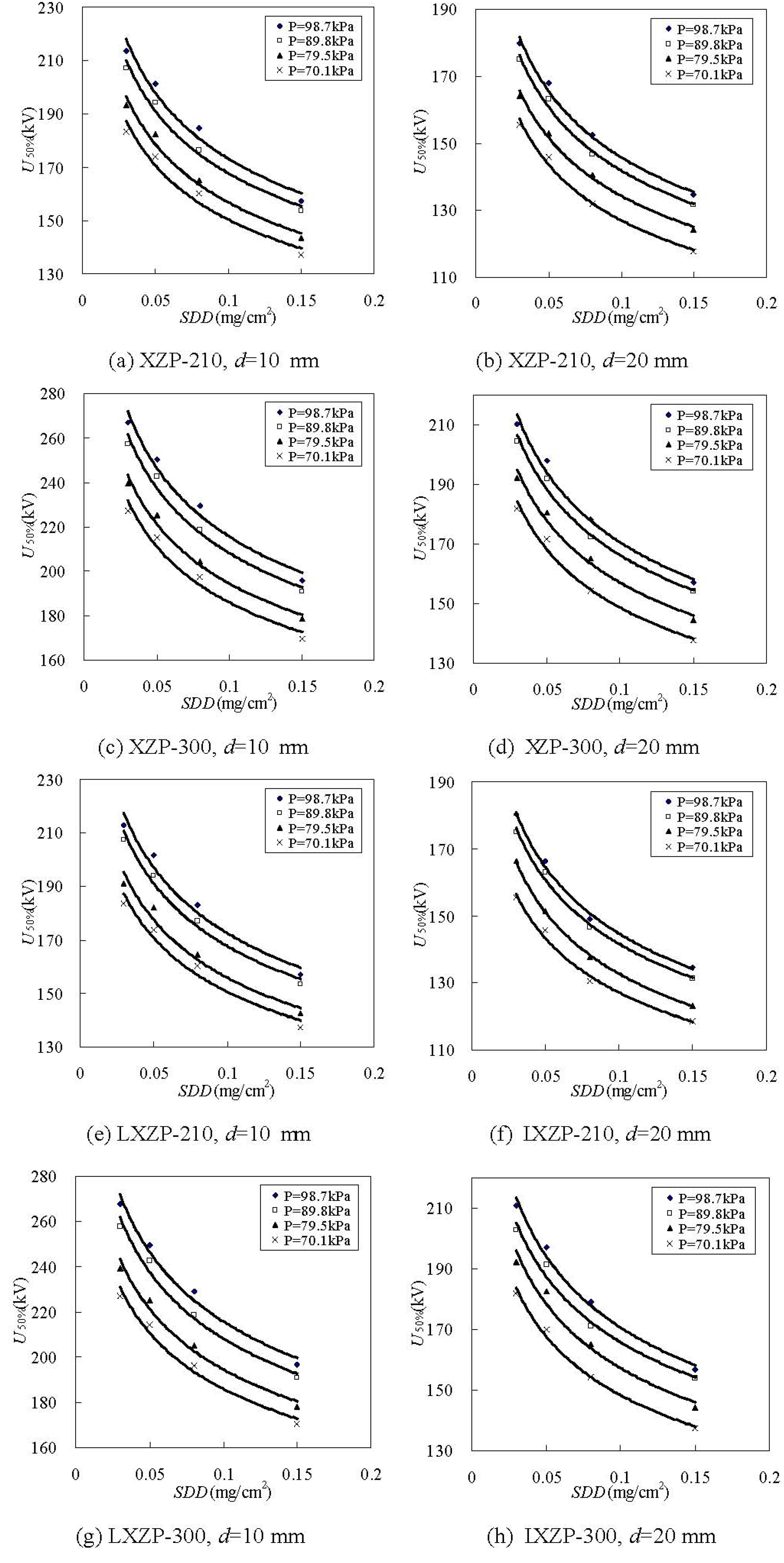
| Type | Ice thickness d (mm) | Fitting values | H (m)/P (kPa) | |||
|---|---|---|---|---|---|---|
| 232/98.6 | 1000/89.8 | 2000/79.5 | 3000/70.1 | |||
| XZP-210 | 10 | AS | 111.5 | 108.9 | 101.7 | 98.8 |
| b | 0.191 | 0.189 | 0.188 | 0.183 | ||
| R2 | 0.971 | 0.985 | 0.981 | 0.965 | ||
| 20 | AS | 95.7 | 93.5 | 89.7 | 84.4 | |
| b | 0.183 | 0.181 | 0.175 | 0.177 | ||
| R2 | 0.992 | 0.992 | 0.993 | 0.991 | ||
| XZP-300 | 10 | AS | 138.2 | 134.5 | 126.8 | 121.9 |
| b | 0.193 | 0.190 | 0.186 | 0.183 | ||
| R2 | 0.976 | 0.982 | 0.984 | 0.970 | ||
| 20 | AS | 111.3 | 109.7 | 104.0 | 98.6 | |
| b | 0.186 | 0.181 | 0.179 | 0.179 | ||
| R2 | 0.986 | 0.988 | 0.985 | 0.986 | ||
| LXZP-210 | 10 | AS | 110.8 | 108.6 | 101.3 | 99.2 |
| b | 0.192 | 0.190 | 0.187 | 0.181 | ||
| R2 | 0.971 | 0.986 | 0.972 | 0.970 | ||
| 20 | AS | 94.4 | 93.1 | 86.3 | 85.3 | |
| b | 0.185 | 0.182 | 0.187 | 0.173 | ||
| R2 | 0.994 | 0.992 | 0.999 | 0.989 | ||
| LXZP-300 | 10 | AS | 138.7 | 134.2 | 126.9 | 122.8 |
| b | 0.192 | 0.191 | 0.186 | 0.180 | ||
| R2 | 0.983 | 0.983 | 0.982 | 0.978 | ||
| 20 | AS | 111.2 | 110.2 | 103.3 | 98.6 | |
| b | 0.186 | 0.177 | 0.182 | 0.177 | ||
| R2 | 0.989 | 0.976 | 0.976 | 0.994 | ||
| Type | Ice thickness d (mm) | Fitting values | H (m)/P (kPa) | |||
|---|---|---|---|---|---|---|
| 232/98.6 | 1000/89.8 | 2000/79.5 | 3000/70.1 | |||
| A | 10 | AS | 93.8 | 89.7 | 85.7 | 79.2 |
| b | 0.201 | 0.192 | 0.191 | 0.191 | ||
| R2 | 0.995 | 0.998 | 0.996 | 0.992 | ||
| 20 | AS | 82.1 | 78.4 | 75.3 | 70.5 | |
| b | 0.188 | 0.186 | 0.180 | 0.177 | ||
| R2 | 0.987 | 0.991 | 0.987 | 0.996 | ||
| B | 10 | AS | 99.8 | 92.6 | 89.5 | 83.8 |
| b | 0.195 | 0.196 | 0.191 | 0.184 | ||
| R2 | 0.997 | 0.996 | 0.996 | 0.993 | ||
| 20 | AS | 86.5 | 82.2 | 78.2 | 73.5 | |
| b | 0.185 | 0.184 | 0.181 | 0.178 | ||
| R2 | 0.994 | 0.997 | 0.993 | 0.992s | ||
| C | 10 | AS | 149.3 | 140.6 | 131.8 | 122.8 |
| b | 0.191 | 0.188 | 0.184 | 0.181 | ||
| R2 | 0.988 | 0.982 | 0.985 | 0.983 | ||
| 20 | AS | 131.1 | 124.6 | 115.8 | 109.4 | |
| b | 0.187 | 0.184 | 0.182 | 0.176 | ||
| R2 | 0.996 | 0.994 | 0.992 | 0.996 | ||
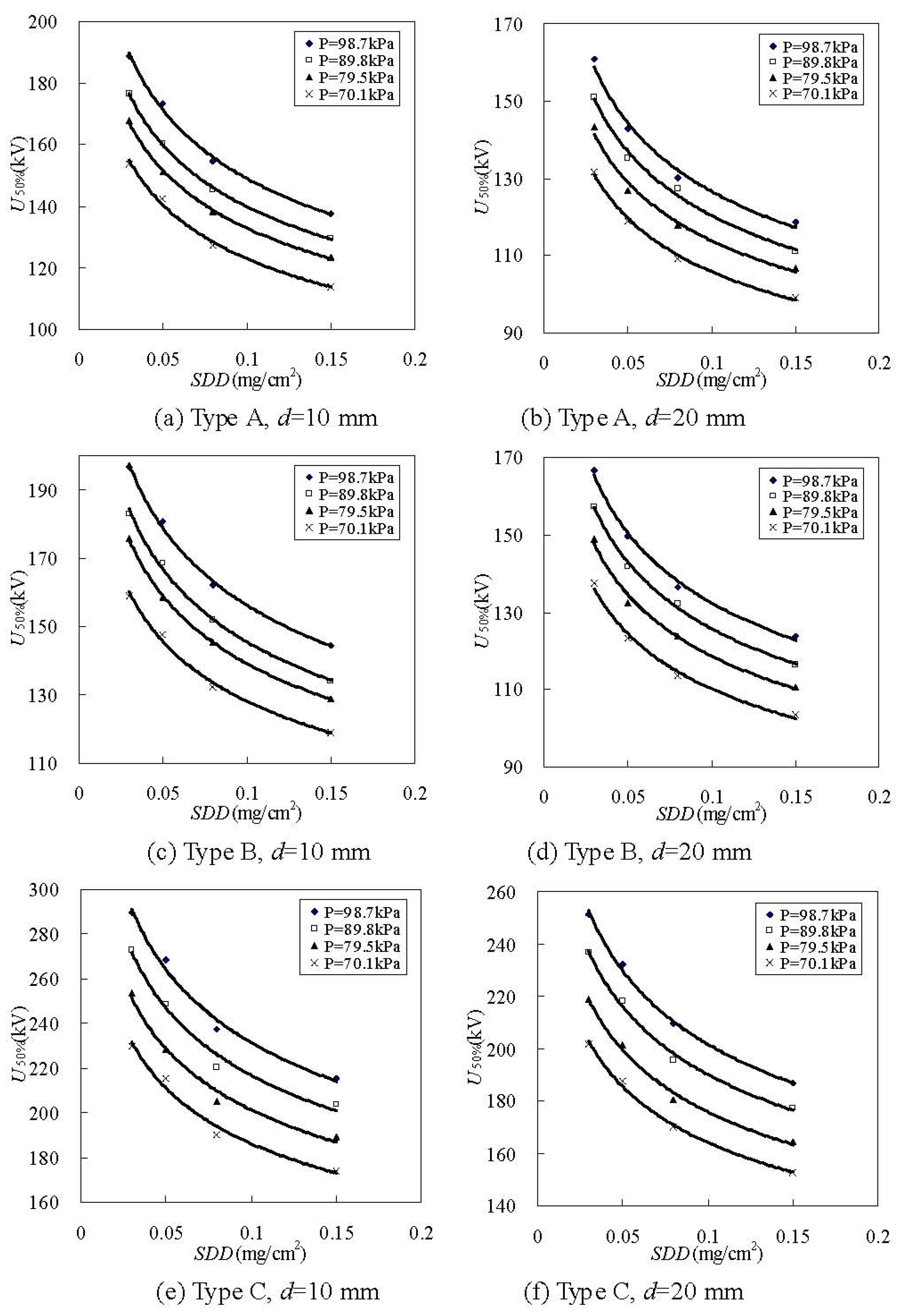
3.1.3. The Effects of Atmospheric Pressure on U50%
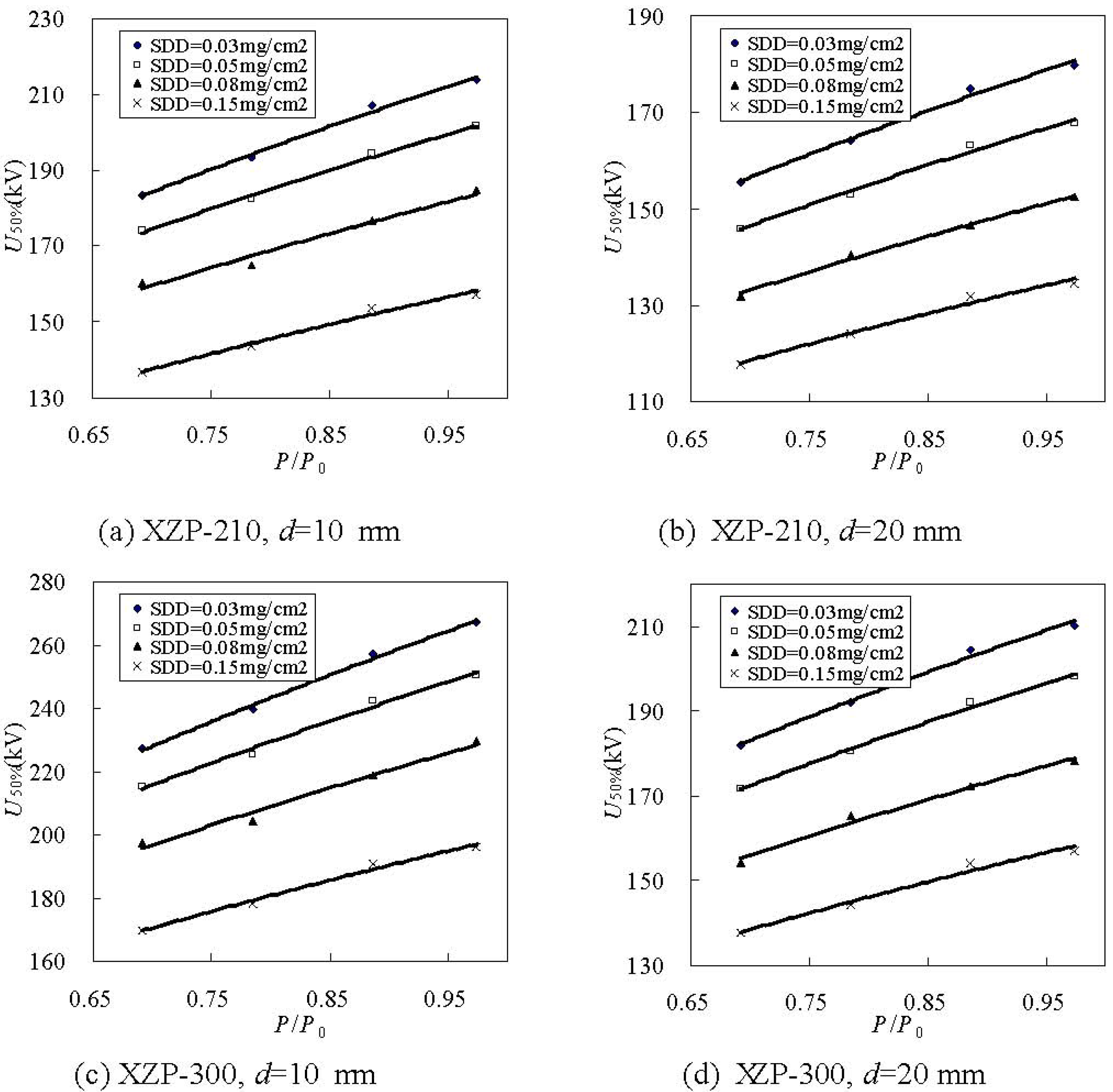
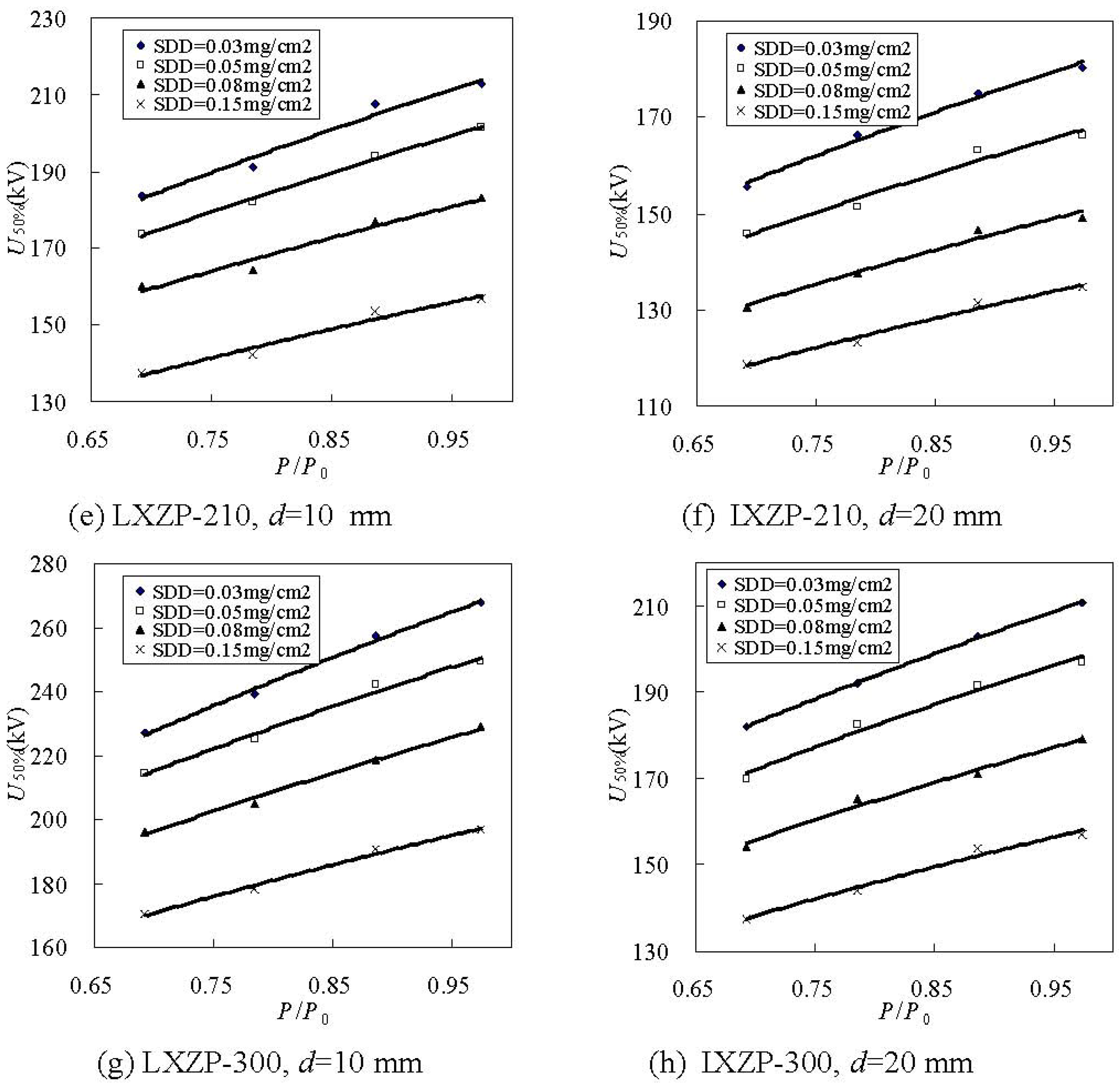
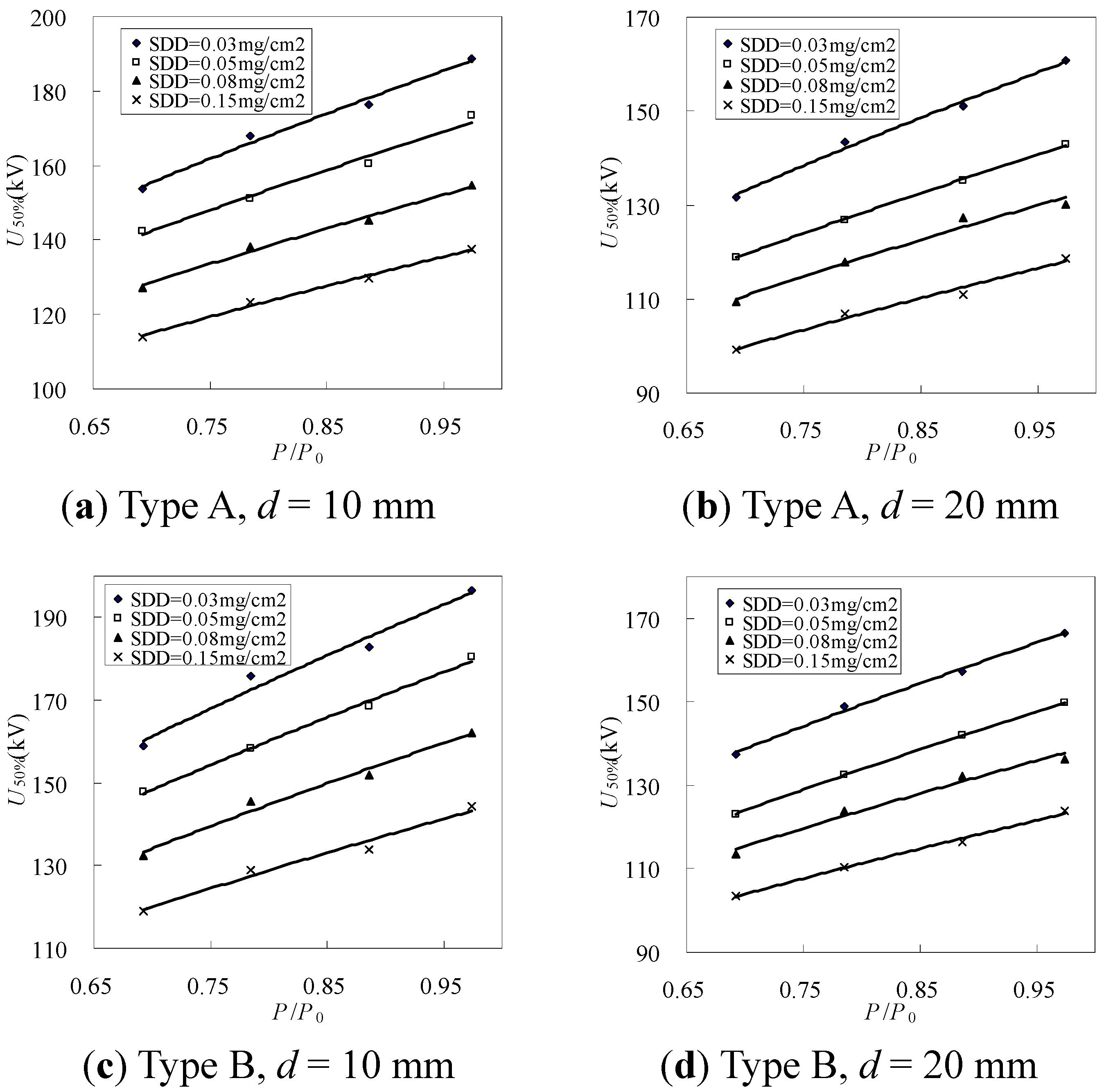
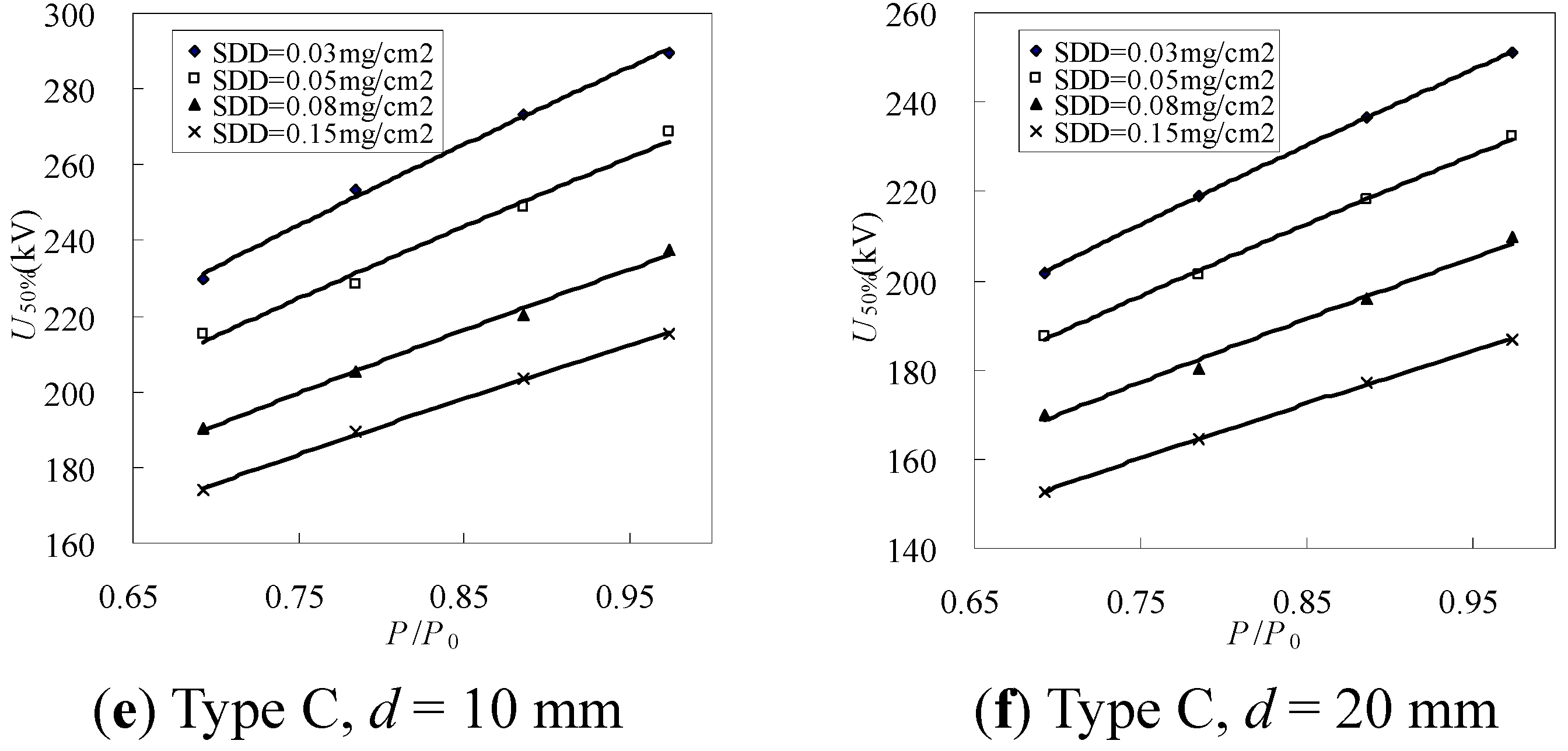
| Type | Ice thickness d (mm) | Fitting values | SDD (mg/cm2) | |||
|---|---|---|---|---|---|---|
| 0.03 | 0.05 | 0.08 | 0.15 | |||
| XZP-210 | 10 | U0 | 217.2 | 203.9 | 185.7 | 160.0 |
| n | 0.462 | 0.440 | 0.427 | 0.425 | ||
| R2 | 0.992 | 0.995 | 0.973 | 0.984 | ||
| 20 | U0 | 182.7 | 170.4 | 154.3 | 136.9 | |
| n | 0.435 | 0.424 | 0.416 | 0.404 | ||
| R2 | 0.991 | 0.991 | 0.993 | 0.986 | ||
| XZP-300 | 10 | U0 | 271.0 | 254.1 | 231.0 | 199.2 |
| n | 0.486 | 0.460 | 0.450 | 0.427 | ||
| R2 | 0.995 | 0.987 | 0.979 | 0.990 | ||
| 20 | U0 | 213.8 | 200.9 | 180.9 | 159.9 | |
| n | 0.434 | 0.429 | 0.416 | 0.403 | ||
| R2 | 0.993 | 0.994 | 0.986 | 0.980 | ||
| LXZP-210 | 10 | U0 | 216.4 | 203.9 | 184.7 | 159.3 |
| n | 0.456 | 0.445 | 0.413 | 0.413 | ||
| R2 | 0.972 | 0.994 | 0.963 | 0.971 | ||
| 20 | U0 | 183.5 | 169.2 | 152.1 | 136.5 | |
| n | 0.435 | 0.413 | 0.407 | 0.387 | ||
| R2 | 0.989 | 0.970 | 0.978 | 0.985 | ||
| LXZP-300 | 10 | U0 | 271.8 | 253.7 | 231.1 | 199.5 |
| n | 0.496 | 0.462 | 0.458 | 0.436 | ||
| R2 | 0.994 | 0.987 | 0.993 | 0.990 | ||
| 20 | U0 | 213.4 | 200.7 | 181.1 | 159.7 | |
| n | 0.432 | 0.431 | 0.421 | 0.405 | ||
| R2 | 0.997 | 0.982 | 0.986 | 0.979 | ||
| Type | Ice thickness d (mm) | Fitting values | SDD (mg/cm2) | |||
|---|---|---|---|---|---|---|
| 0.03 | 0.05 | 0.08 | 0.15 | |||
| Type A | 10 | U0 | 191.0 | 173.9 | 156.5 | 139.3 |
| n | 0.578 | 0.561 | 0.551 | 0.537 | ||
| R2 | 0.989 | 0.981 | 0.992 | 0.992 | ||
| 20 | U0 | 162.9 | 144.5 | 133.4 | 119.6 | |
| n | 0.565 | 0.533 | 0.525 | 0.504 | ||
| R2 | 0.993 | 0.999 | 0.976 | 0.982 | ||
| Type B | 10 | U0 | 199.0 | 182.1 | 164.4 | 145.2 |
| n | 0.590 | 0.575 | 0.569 | 0.536 | ||
| R2 | 0.975 | 0.995 | 0.982 | 0.977 | ||
| 20 | U0 | 168.9 | 152.1 | 139.7 | 124.7 | |
| n | 0.551 | 0.572 | 0.538 | 0.515 | ||
| R2 | 0.995 | 0.997 | 0.981 | 0.993 | ||
| Type C | 10 | U0 | 295.7 | 270.7 | 240.1 | 219.2 |
| n | 0.668 | 0.649 | 0.641 | 0.620 | ||
| R2 | 0.987 | 0.982 | 0.995 | 0.998 | ||
| 20 | U0 | 255.5 | 235.6 | 211.7 | 189.9 | |
| n | 0.638 | 0.629 | 0.617 | 0.590 | ||
| R2 | 0.996 | 0.995 | 0.990 | 0.991 | ||
3.2. Correction of DC Flashover Voltage for Insulators (string) under Combined Conditions of High Altitude, Pollution, and Icing
| Type | Fitting values | Correlation coefficient R2 | |||
|---|---|---|---|---|---|
| q | c | b | n | ||
| XZP-210 | 70.3 | 0.209 | 0.192 | 0.429 | 0.979 |
| XZP-300 | 104.4 | 0.288 | 0.193 | 0.433 | 0.978 |
| LXZP-210 | 70.2 | 0.210 | 0.193 | 0.425 | 0.978 |
| LXZP-300 | 104.9 | 0.289 | 0.192 | 0.435 | 0.983 |
| Type A composite insulator | 74.8 | 0.221 | 0.187 | 0.435 | 0.993 |
| Type B composite insulator | 75.0 | 0.219 | 0.184 | 0.559 | 0.992 |
| Type C composite insulator | 66.7 | 0.195 | 0.186 | 0.638 | 0.994 |
4. Conclusions
Acknowledgments
References
- Meier, A.; Niggli, W.M. The Influence of Snow and Ice Deposits on Supertension Transmission Line Insulator Strings with Special Reference to High Altitude Operations. IEEE Conf. Proc. 1968, 44, 386–395. [Google Scholar]
- Cherney, E.A. Flashover performance of artificially contaminated and iced long-rod transmission line insulators. IEEE Trans. Power App. Syst. 1980, PAS-999, 46–52. [Google Scholar]
- Matsuda, H.; Komuro, H.; Takasu, K. Withstand voltage characteristics of insulator strings covered with snow or ice. IEEE Trans. Power Deliv. 1991, 6, 1243–1250. [Google Scholar]
- Farzaneh, M.; Kiernicki, J. Flashover problems caused by ice build-up on insulators. IEEE Elec. Insul. Mag. 1995, 11, 5–17. [Google Scholar]
- Influence of ice and snow on the flashover performance of outdoor insulators Part I: Effects of ice. CIGRE Task Force 33.04.09 Report. Électra 1999, 187, 90–111, CIGRE Task Force 33.04.09 Report..
- Kannus, K.; Lahti, K. Electrical behaviour of high voltage insulator strings under rime ice. In Proceedings of the 9th International Workshop on Atmospheric Icing of Structures, Chester, UK, 5–8 June 2000; p. 8.
- Jiang, X.L.; Shu, L.C.; Sima, W.X.; Xie, S.J.; Hu, J.L.; Zhang, Z.J. Chinese transmission lines’ icing characteristics and analysis of severe ice accidents. Int. J. Offshore Polar Eng. 2004, 14, 196–201. [Google Scholar]
- Fikke, S.M.; Hanssen, J.E.; Rolfseng, L. Long range transported pollution and conductivity on atmospheric ice on insulators. IEEE Trans. Power Deliv. 1993, 8, 1311–1321. [Google Scholar]
- Farzaneh, M.; Drapeau, J.F. AC flashover performance of insulators covered with artificial ice. IEEE Trans. Power Deliv. 1995, 10, 1038–1051. [Google Scholar]
- Farzaneh, M.; Kiernicki, J. Flashover performance of IEEE standard insulators under ice conditions. IEEE Trans. Power Deliv. 1997, 12, 1602–1613. [Google Scholar]
- Farzaneh, M.; Baker, T.; Bernstorf, A.; Brown, K.; Chisholm, W.A.; de Tourreil, C.; Drapeau, J.F.; Fikke, S.; George, J.M.; Gnandt, E.; et al. Insulator icing test methods and procedures: A position paper prepared by the IEEE task force on insulator icing test methods. IEEE Trans. Power Deliv. 2003, 18, 1503–1515. [Google Scholar]
- Li, Q.F.; Fan, Z.; Wu, Q.; Gao, J.; Su, Z.Y.; Zhou, W.J. Investigation of ice-covered transmission lines and analysis on transmission line failures caused by ice-coating in China. Power Syst. Technol. 2008, 9, 33–36. [Google Scholar]
- Hu, Y. Analysis and countermeasures discussion for large area icing accident on power grid. High Volt. Eng. 2008, 2, 215–219. [Google Scholar]
- Jiang, X.L. Accident analysis of Guizhou power grid ice hazard and its countermeasures. Electr. Power Constr. 2008, 4, 1–4. [Google Scholar]
- Lu, J.Z.; Jiang, Z.L.; Lei, H.C.; Zhang, H.X.; Peng, J.W.; Li, B.; Fang, Z. Analysis of Hunan power grid ice disaster accident in 2008. Autom. Electr. Power Syst. 2008, 11, 16–19. [Google Scholar]
- Fofana, I.; Farzaneh, M. Process of discharge initiation and arc development on an ice-covered insulator. In Proceedings of Transmission and Distribution Conference and Exhibition, 2005/2006 IEEE PES, Dallas, TX, USA, 21–24 May 2006; pp. 115–120.
- Farzaneh, M. Ice accretion on high voltage conductors and insulators and related phenomena. Philos. Trans. R. Soc. Lond. A 2000, 1776, 2971–3005. [Google Scholar]
- Zhang, J.; Farzaneh, M. Propagation of AC and DC arcs on ice surfaces. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 269–276. [Google Scholar]
- Farzaneh, M.; Zhang, J. A multi-arc model for predicting ac critical flashover voltage of ice-covered insulators. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1401–1409. [Google Scholar]
- Farzaneh, M. Atmospheric Icing of Power Networks; Springer: Berlin, Germany, 2008; pp. 269–323. [Google Scholar]
- Jiang, X.L.; Sun, C.X. Study on AC flashover performance and process of ice-covered 10 kV composite insulator. Proc. CSEE 2002, 22, 58–61. [Google Scholar]
- Sun, C.X.; Jiang, X.L.; Shu, L.C.; Sima, W.X.; Gu, L.G. AC/DC flashover performance and its voltage correction of UHV insulators in high altitude and icing and pollution environments. Proc. CSEE 2002, 11, 115–120. [Google Scholar]
- Tian, Y.C.; Jiang, X.L.; Shu, L.C. AC flashover performance and voltage correction of iced 10 kV composite insulator in high altitude area. High Volt. Eng. 2002, 6, 13–15. [Google Scholar]
- Wu, L.H.; Jiang, X.L.; Xiong, Q.X.; Sima, W.X.; Sun, C.X. DC flashover performance and voltage correction of iced XZP-160 insulator at low atmospheric pressure. High Volt. Eng. 2002, 10, 5–7. [Google Scholar]
- Yi, H.; Wang, L.Q. Measures of preventing ice flashover for transmission line insulator string and analysis of mechanism. High Volt. Eng. 2003, 29, 57–58. [Google Scholar]
- Sima, W.X.; Jiang, X.L.; Wu, L.H.; Shu, L.C.; Sun, C.X. DC electrical performance of icing and polluted 10 kV composite insulator at low atmospheric pressures. Proc. CSEE 2004, 7, 122–126. [Google Scholar]
- Jiang, X.L.; Xie, S.J.; Shu, L.C. Ice flashover performance and comparison on three types of DC insulators at low atmosphere pressure. Proc. CSEE 2004, 9, 158–162. [Google Scholar]
- Yuan, J.H.; Jiang, X.L.; Zhang, Z.J.; Hu, J.L.; Sun, C.X. Study on dc flashover performance of three types of iced post insulators at lower atmospheric pressure. Proc. CSEE 2005, 15, 12–15. [Google Scholar]
- Jiang, X.L.; Wu, L.H.; Sima, W.X.; Shu, L.C.; Sun, C.X. Study on flashover mechanism of XZP/XZWP4-160 DC insulator under icing and low atmospheric pressure conditions. Proc. CSEE 2004, 6, 111–115. [Google Scholar]
- Jiang, X.L.; Wang, S.H.; Zhang, Z.J.; Xie, S.J.; Wang, Y. Study on AC flashover performance and discharge process of polluted and iced IEC standard suspension insulator string. IEEE Trans. Power Deliv. 2007, 22, 472–480. [Google Scholar]
- Hu, J.L.; Sun, C.X.; Jiang, X.L.; Shu, L.C. Flashover performance of pre-contaminated and ice-covered composite insulators to be used in 1000 kV UHV AC transmission lines. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1347–1356. [Google Scholar]
- Li, P.; Fan, J.B.; Li, W.F.; Su, Z.Y.; Zhou, J. Flashover performance of hvdc iced insulator strings. IEEE Trans. Dielectr. Electr. Insul. 2007, 6, 1334–1338. [Google Scholar]
- Farzaneh, M.; Baker, A.C.; Allen Bernstorf, R.; Burnhan, J.T.; Cherney, E.A.; Chisholm, W.A.; Gorur, R.S.; Grisham, T.; Gutman, I.; Rolfseng, L.; et al. Selection of line insulators with respect to ice and snow, part i: context and stresses. IEEE Trans. Power Deliv. 2007, 4, 2298–2296. [Google Scholar]
- International Electrotechnical Commission (IEC). Artificial Pollution Tests on High-Voltage Insulators to Be Used on A.C. Systems; Technical Report IEC 60507; IEC: Geneva, Switzerland, 1991. [Google Scholar]
- IEEE Guide for Test Methods and Procedures to Evaluate the Electrical Performance of Insulators in Freezing Conditions; IEEE Standard 1783–2009; The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 2009.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hu, J.; Sun, C.; Jiang, X.; Xiao, D.; Zhang, Z.; Shu, L. DC Flashover Performance of Various Types of Ice-Covered Insulator Strings under Low Air Pressure. Energies 2012, 5, 1554-1576. https://doi.org/10.3390/en5051554
Hu J, Sun C, Jiang X, Xiao D, Zhang Z, Shu L. DC Flashover Performance of Various Types of Ice-Covered Insulator Strings under Low Air Pressure. Energies. 2012; 5(5):1554-1576. https://doi.org/10.3390/en5051554
Chicago/Turabian StyleHu, Jianlin, Caixin Sun, Xingliang Jiang, Daibo Xiao, Zhijin Zhang, and Lichun Shu. 2012. "DC Flashover Performance of Various Types of Ice-Covered Insulator Strings under Low Air Pressure" Energies 5, no. 5: 1554-1576. https://doi.org/10.3390/en5051554




