A Novel Maximum Power Point Tracking Control for Permanent Magnet Direct Drive Wind Energy Conversion Systems
Abstract
:1. Introduction

2. Wind Turbine Model
2.1. Wind Turbine Model

2.2. PMSG Model
3. Proposed MPPT Algorithm
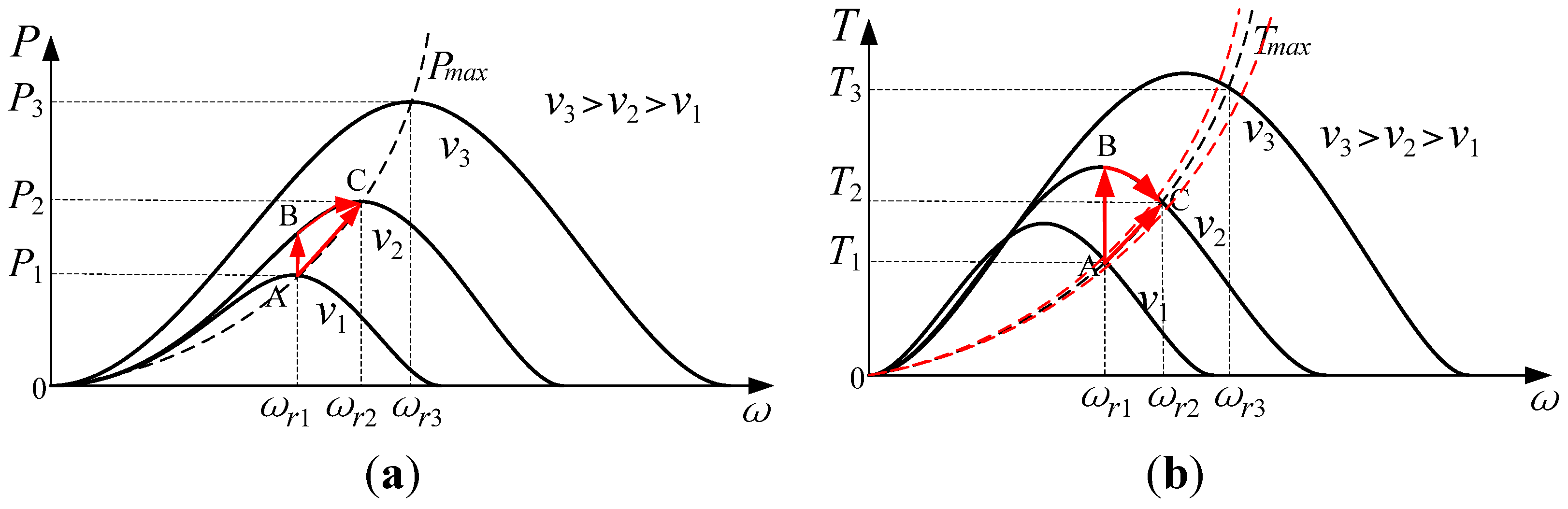
3.1. OCG MPPT Method
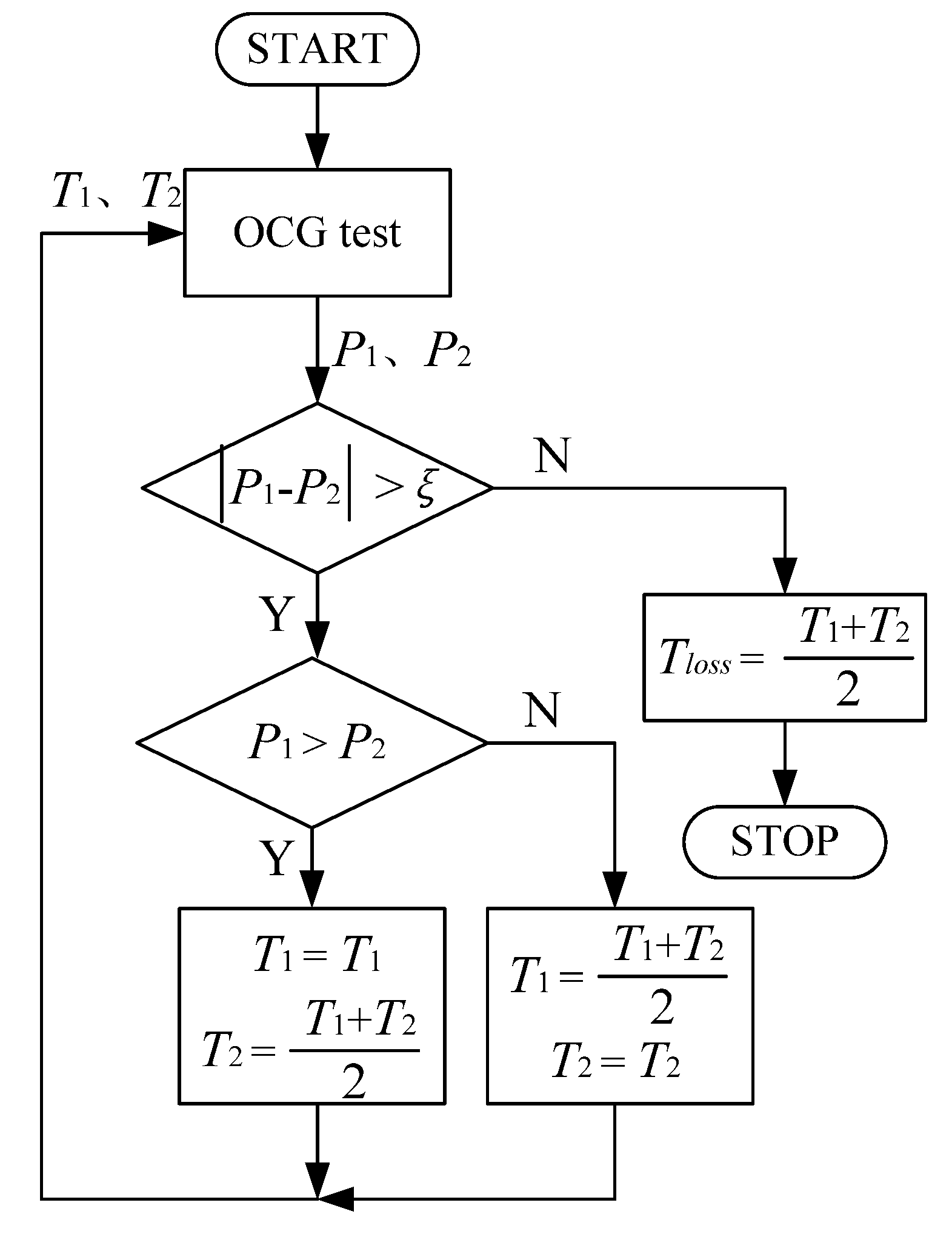
3.2. Estimation of Tloss
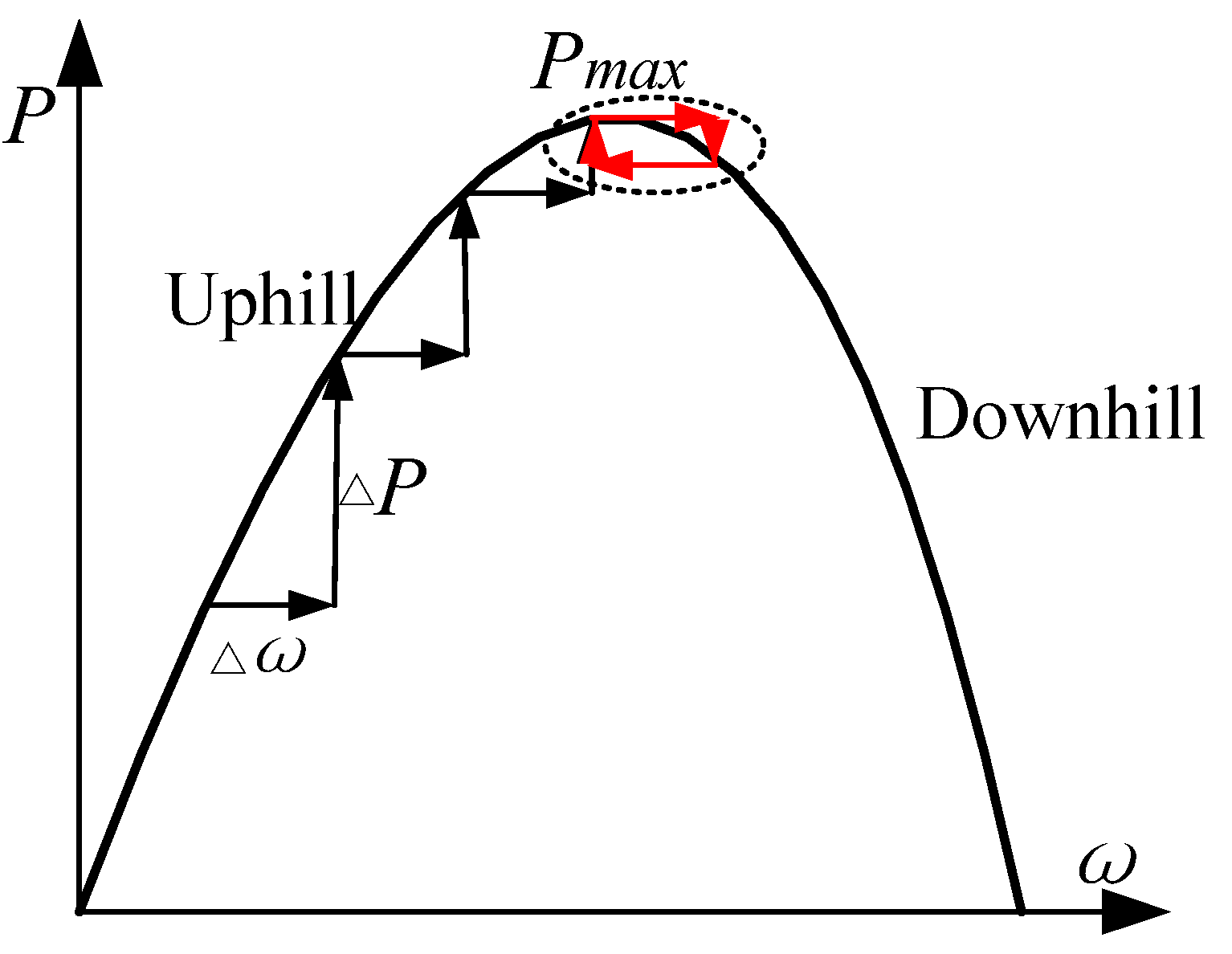
3.3. kopt Obtained by HCS MPPT Method
3.4. Proposed MPPT Method

3.5. Imitation of Wind Turbine

4. Simulation Results
4.1. Simulation Parameters
| PMSG Item | Value | IM Item | Value |
|---|---|---|---|
| Rated power (kW) | 5.5 | Rated power (kW) | 5.5 |
| Resistance (Ω) | 0.665 | Stator resistance (Ω) | 0.628 |
| d-axis inductance (mH) | 7.93 | Rotor resistance (Ω) | 1.192 |
| q-axis inductance (mH) | 7.93 | Stator leakage inductance (mH) | 5.668 |
| Torque coefficient (kg·m2) | 0.04 | Rotor leakage inductance (mH) | 5.668 |
| Permanent Magnet flux-linkage (Wb) | 0.783 | Mutual inductance (H) | 0.1639 |
| Pole pairs | 2 | Pole pairs | 2 |
4.2. Simulation of HCS

4.3. Simulation Results of OCG MPPT
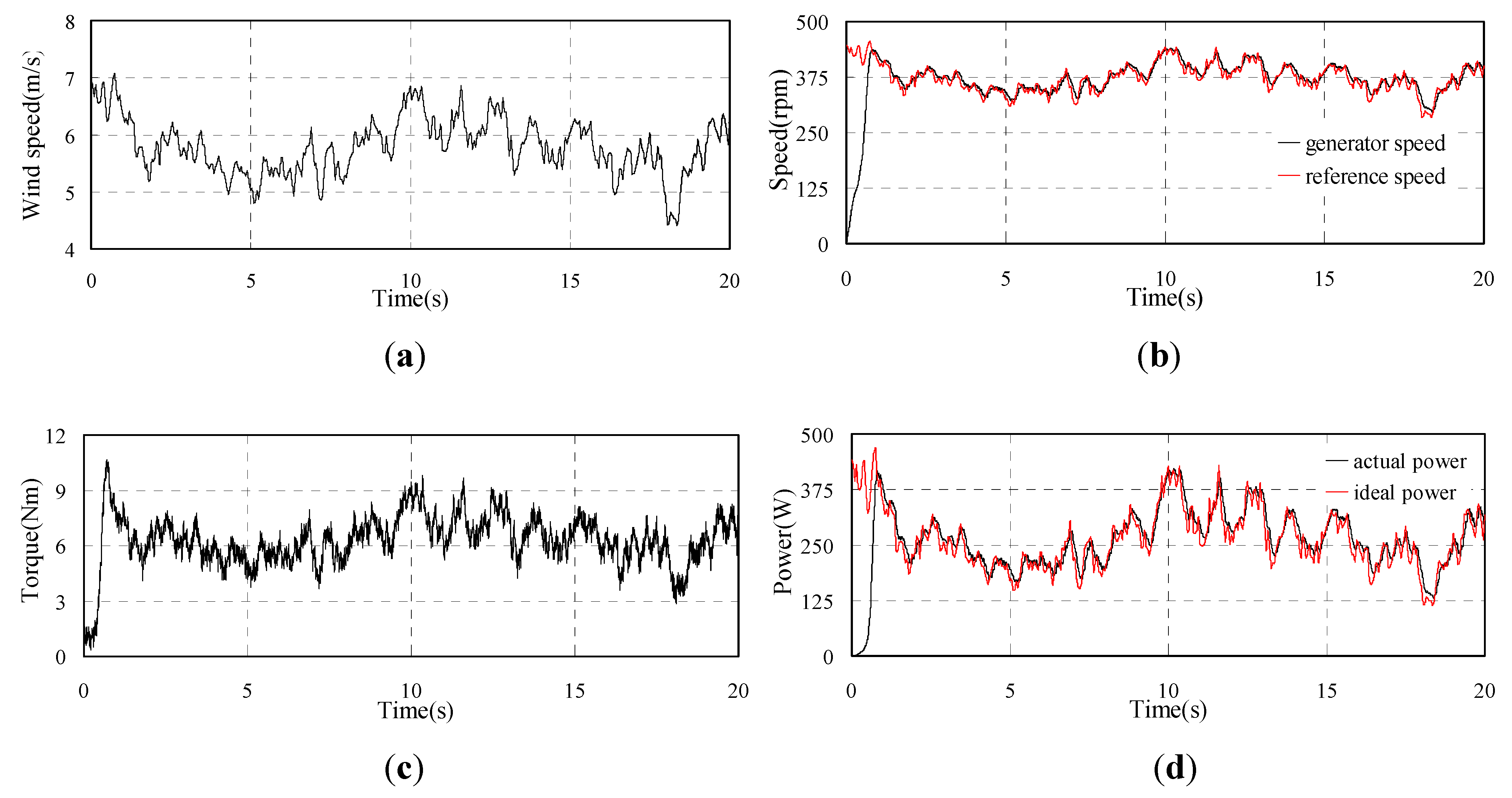
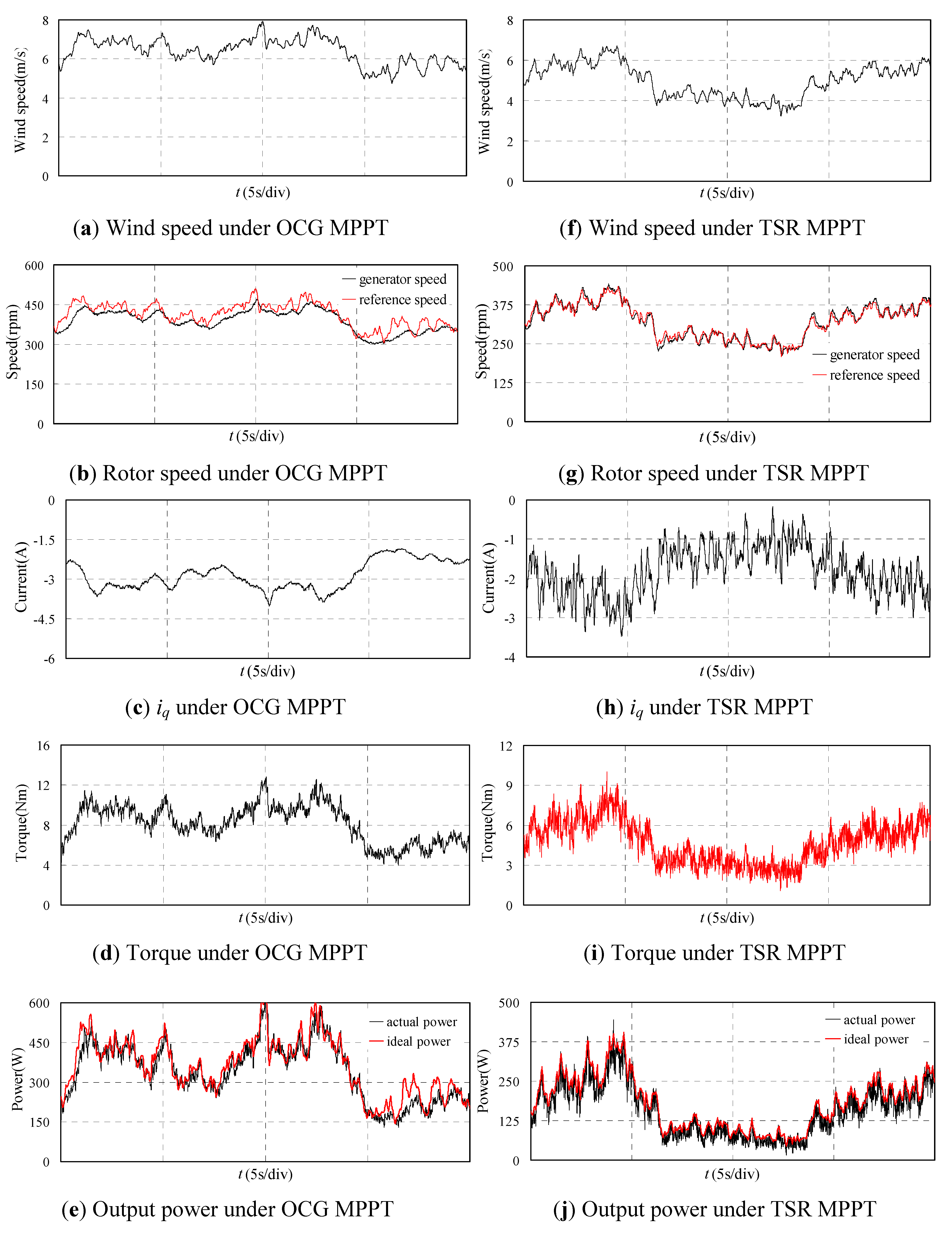
5. Experimental Results
5.1. Experimental Platform

5.2. Experimental Results
6. Conclusions
Acknowledgments
References
- Polinder, H.; Van der Piji, F.F.A.; De Vilder, G.J.; Tavner, P.J. Comparison of direct-drive and geared generator concepts for wind turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Liserre, M.; Cardenas, R.; Molinas, M.; Rodriguez, J. Overview of multi-MW wind turbines and wind parks. IEEE Trans. Ind. Electron. 2011, 58, 1081–1095. [Google Scholar] [CrossRef]
- Haraguchi, H.; Morimoto, S.; Sanada, M. Suitable design of a PMSG for a large-scale wind power generator. In Proceedings of Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 2447–2452.
- Zhang, S.; Tseng, K.; Vilathgamuwa, M.; Nguyen, D. Design of a robust grid interface system for PMSG-based wind turbine generators. IEEE Trans. Ind. Electron. 2010, 58, 316–328. [Google Scholar] [CrossRef]
- Arifujjaman, M.; Lqbal, M.T.; Quaicoe, J.E. A comparative study of the reliability of the power electronics in grid connected small wind turbine systems. In Proceedings of Electrical and Computer Engineering Conference, St. John’s, Canada, 3–6 May 2009; pp. 394–397.
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Agarwal, V.; Aggarwal, R.K.; Patidar, P.; Patki, C. A novel scheme for rapid tracking of maximum power point in wind energy generation systems. IEEE Trans. Energy Convers. 2010, 25, 228–236. [Google Scholar] [CrossRef]
- Tan, K.; Islam, S. Optimal control strategies in energy conversion of PMSG wind turbine system without mechanical sensors. IEEE Trans. Energy Convers. 2004, 19, 392–399. [Google Scholar] [CrossRef]
- Pahlevaninezhad, M.; Eren, S.; Bakhshai, A.; Jain, P. Maximum power point tracking of a Wind Energy Conversion System using adaptive nonlinear approach. In Proceedings of Applied Power Electronics Conference and Exposition, Palm Springs, CA, USA, 21–25 February 2010; pp. 149–154.
- Haque, M.E.; Negnevitsky, M.; Muttaqi, K.M. A novel control strategy for a variable-speed wind turbine with a permanent-magnet synchronous generator. IEEE Trans. Ind. Appl. 2010, 46, 331–339. [Google Scholar] [CrossRef]
- Kun, H.; Guo-Zhu, C. A novel control strategy of wind turbine MPPT implementation for direct-drive PMSG wind generation imitation platform. In Proceedings of Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 2255–2259.
- Kazmi, S.M.R.; Goto, H.; Guo, H.J.; Ichinokura, O. A novel algorithm for fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems. IEEE Trans. Ind. Electron. 2011, 58, 29–36. [Google Scholar] [CrossRef]
- Quincy, W.; Liuchen, C. An intelligent maximum power extraction algorithm for inverter-based variable speed wind turbine systems. IEEE Trans. Power Electron. 2004, 19, 1242–1249. [Google Scholar] [CrossRef]
- Morimoto, S.; Nakayama, H.; Sanada, M.; Takeda, Y. Sensorless output maximization control for variable-speed wind generation system using IPMSG. IEEE Trans. Ind. Appl. 2005, 41, 60–67. [Google Scholar] [CrossRef]
- Galdi, V.; Piccolo, A.; Siano, P. Designing an adaptive fuzzy controller for maximum wind energy extraction. IEEE Trans. Energy Convers. 2008, 23, 559–569. [Google Scholar] [CrossRef]
- Calderaro, V.; Galdi, V.; Piccolo, A.; Siano, P. A fuzzy controller for maximum energy extraction form variable speed wind power generation systems. Electr. Power Syst. Res. 2007, 78, 1109–1118. [Google Scholar] [CrossRef]
- Galdi, V.; Piccolo, A.; Siano, P. Exploiting maximum energy from variable speed wind power generation systems by using an adaptive Takagi-Sugeno-Kang fuzzy model. Energy Convers. Manag. 2009, 50, 413–421. [Google Scholar] [CrossRef]
- Di Tommaso, A.O.; Miceli, R.; Galluzzo, G.R.; Trapanese, M. Optimum performance of permanent magnet synchronous generators coupled to wind turbines. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7.
- Vilathgamuwa, D.M.; Jayasinghe, S.D.G.; Madawala, U.K. Space vector modulated cascade multi-level inverter for PMSG wind generation systems. In Proceedings of IEEE Annual Conference of Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 4600–4605.
- Takahashi, I.; Noguchi, T. A new quick-response and high-efficiency control strategy of an induction motor. IEEE Trans. Ind. Appl. 1986, LA-22, 820–827. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, Y.; Cheng, M.; Hua, W.; Wang, W. A Novel Maximum Power Point Tracking Control for Permanent Magnet Direct Drive Wind Energy Conversion Systems. Energies 2012, 5, 1398-1412. https://doi.org/10.3390/en5051398
Zhu Y, Cheng M, Hua W, Wang W. A Novel Maximum Power Point Tracking Control for Permanent Magnet Direct Drive Wind Energy Conversion Systems. Energies. 2012; 5(5):1398-1412. https://doi.org/10.3390/en5051398
Chicago/Turabian StyleZhu, Ying, Ming Cheng, Wei Hua, and Wei Wang. 2012. "A Novel Maximum Power Point Tracking Control for Permanent Magnet Direct Drive Wind Energy Conversion Systems" Energies 5, no. 5: 1398-1412. https://doi.org/10.3390/en5051398
APA StyleZhu, Y., Cheng, M., Hua, W., & Wang, W. (2012). A Novel Maximum Power Point Tracking Control for Permanent Magnet Direct Drive Wind Energy Conversion Systems. Energies, 5(5), 1398-1412. https://doi.org/10.3390/en5051398








