Numerical Simulation of Methane Production from Hydrates Induced by Different Depressurizing Approaches
Abstract
:1. Introduction
2. Hydrate Depressurization Model
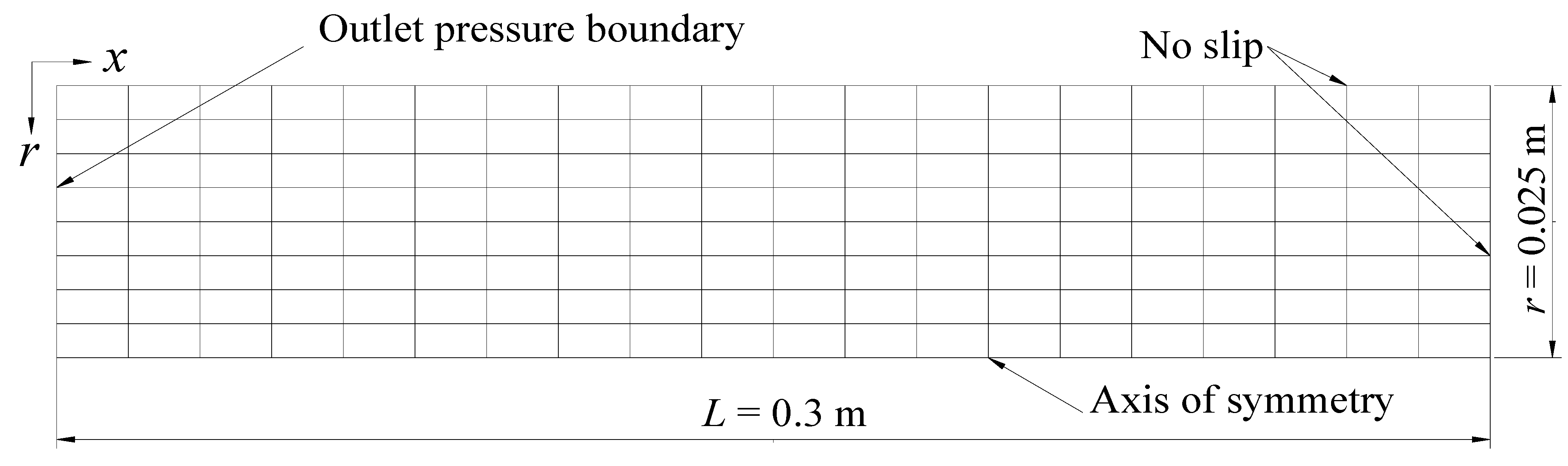
3. Verification of Mathematical Model and Numerical Solution
| Core length, L (m) | 0.3 | Core diameter, D (m) | 0.05 |
| Core pressure, P0 (MPa) | 3.75 | Core temperature, T0 (°C) | 2.3 |
| Intrinsic porosity, Φ0 | 0.182 | Intrinsic permeability, K0 (md) | 97.98 |
| Outlet pressure, Pp0 (MPa) | 2.84 | Bath temperature, Tb (°C) | 2.3 |
| Hydrate saturation, Sh | 0.443 | Water saturation, Sw | 0.206 |
| Gas saturation, Sg | 0.351 | Permeability reduction index, N | 10 |
4. Results and Discussion
4.1. Effect of the Depressurizing Range
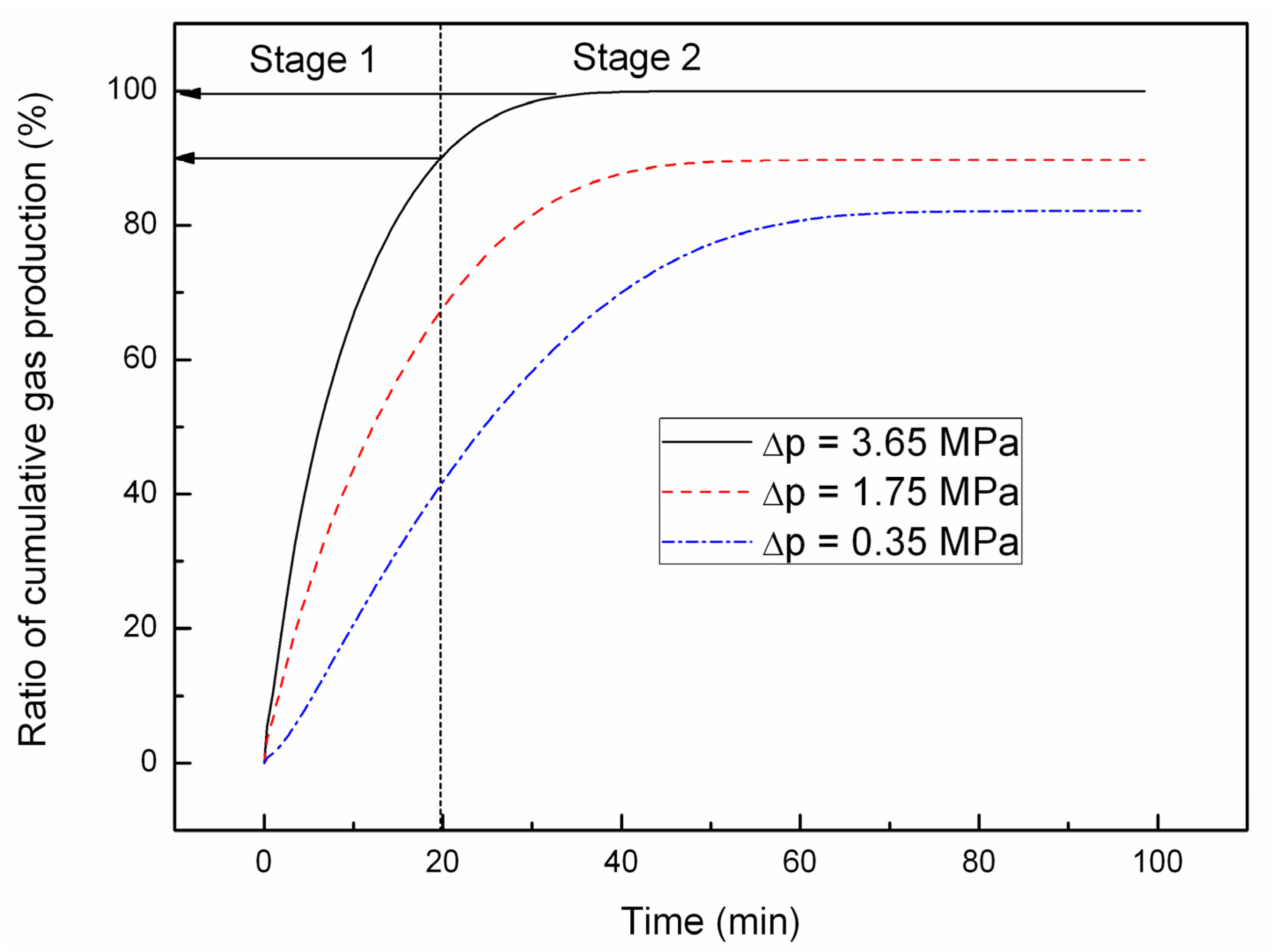
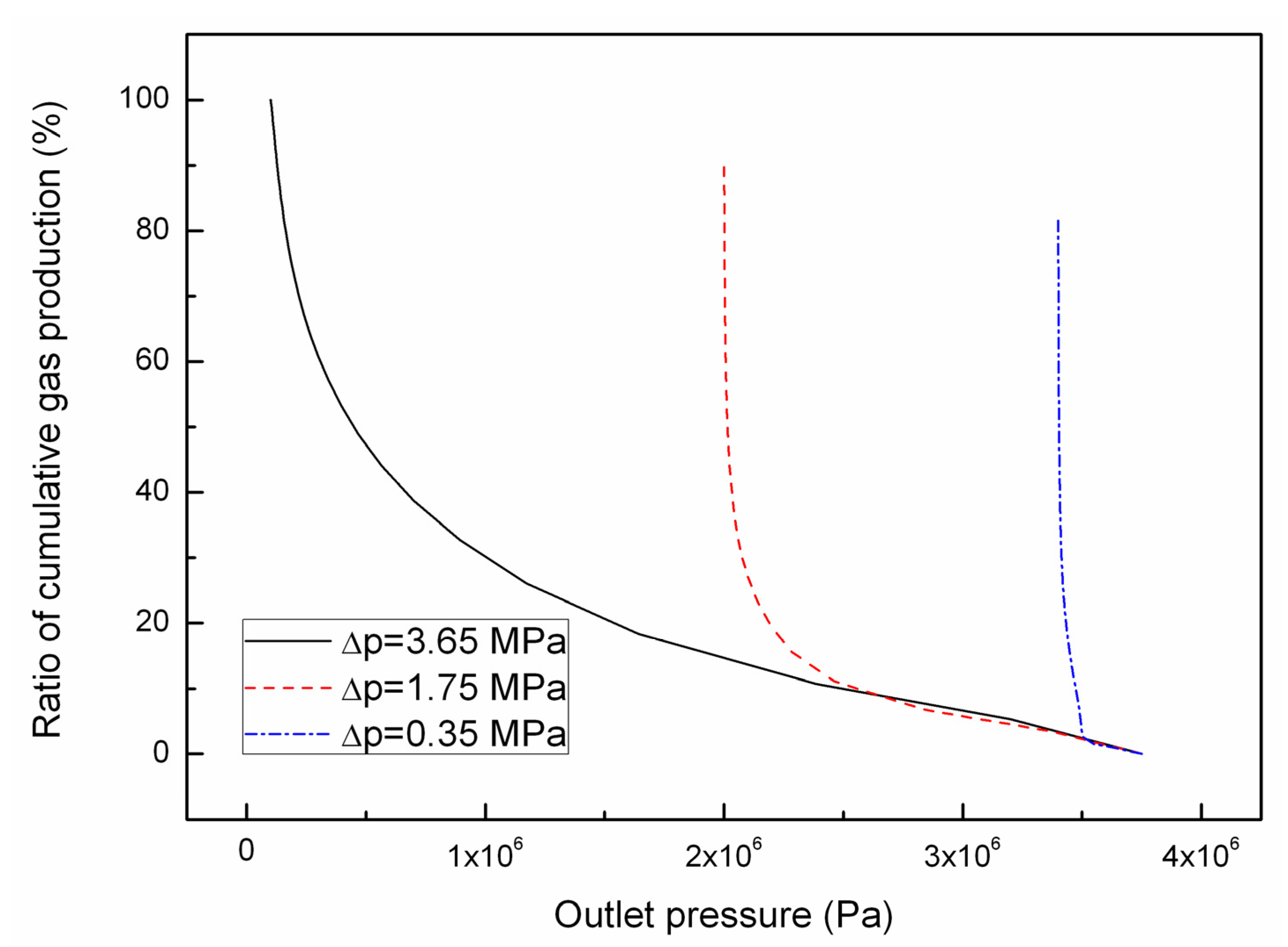
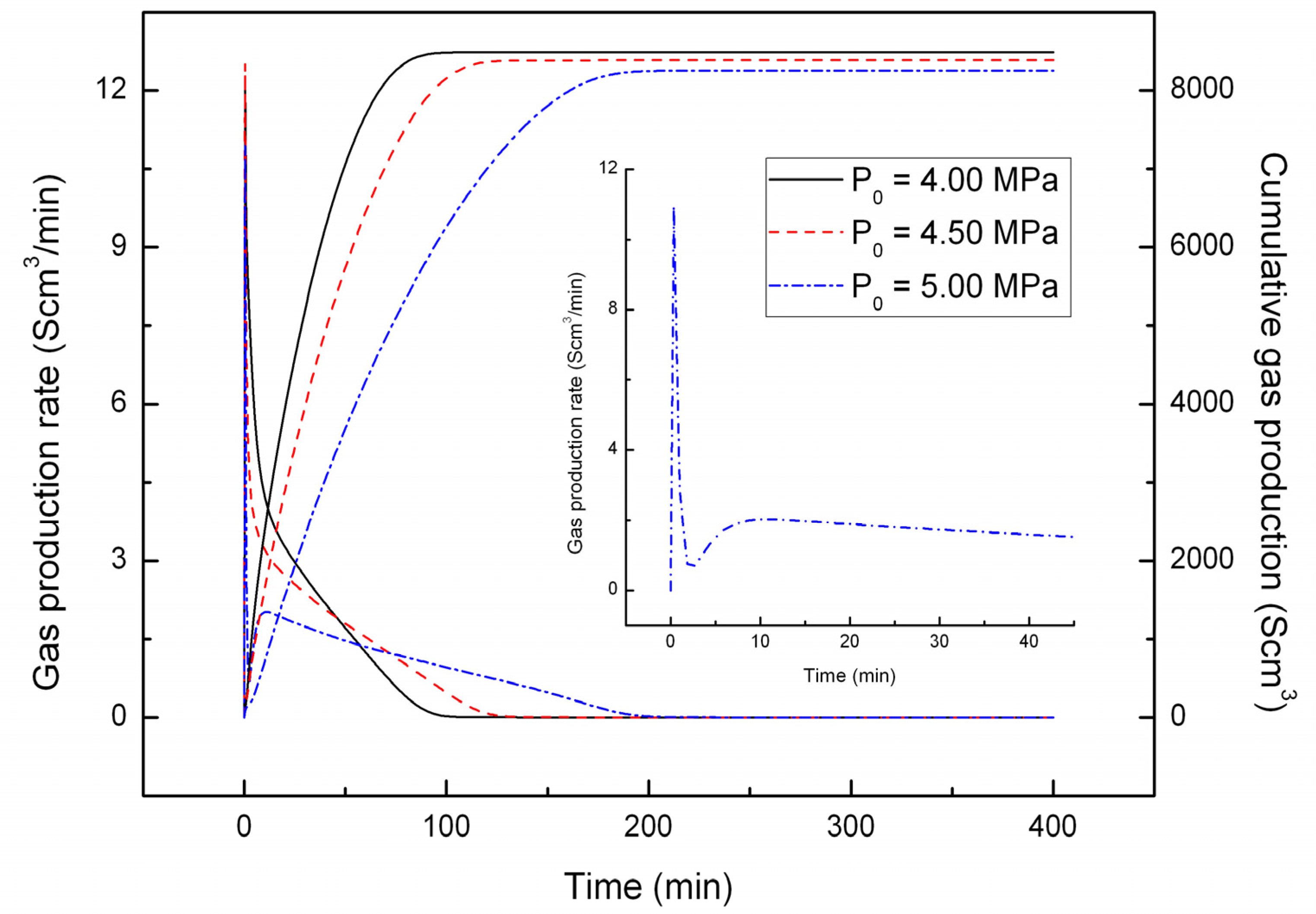
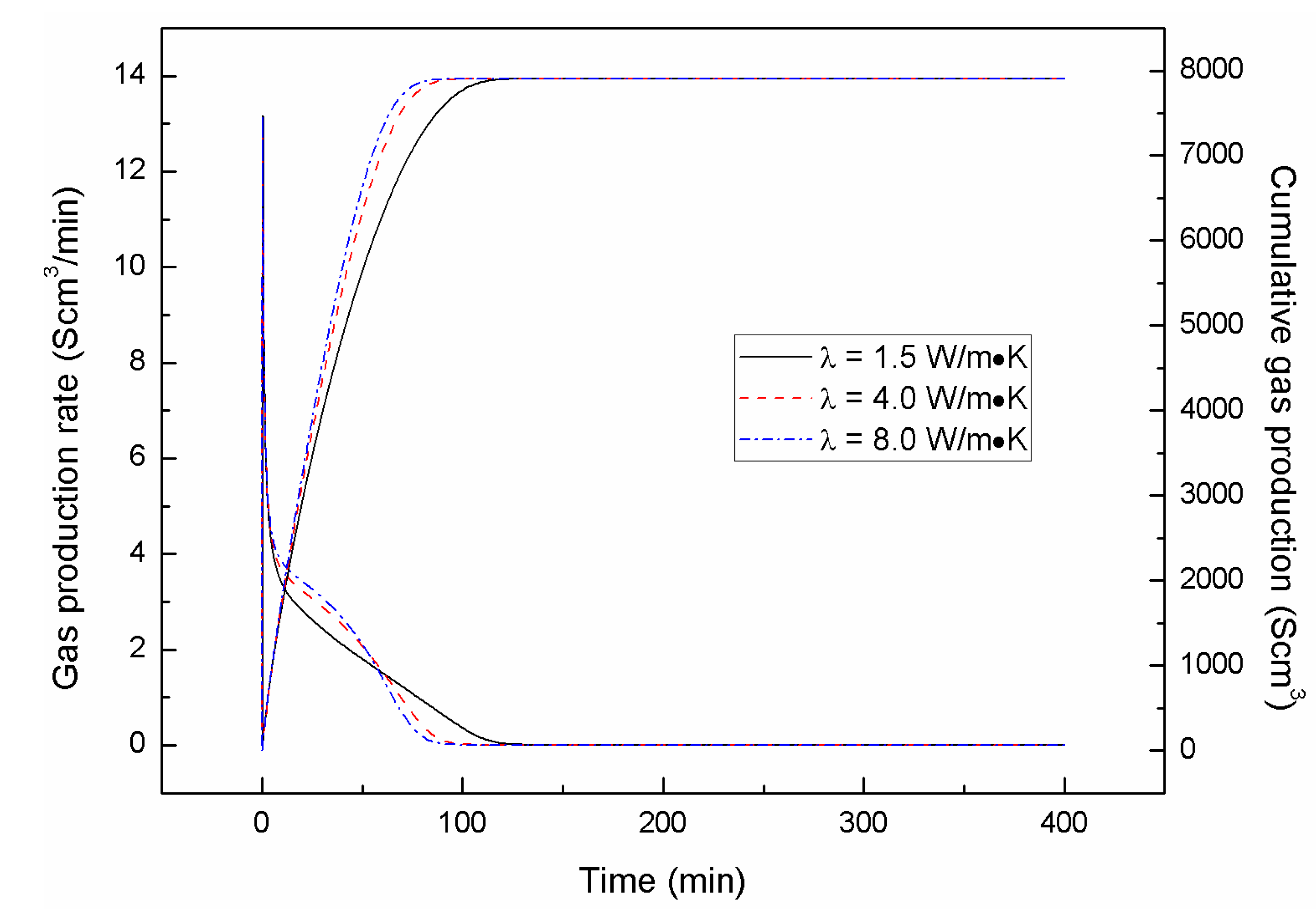
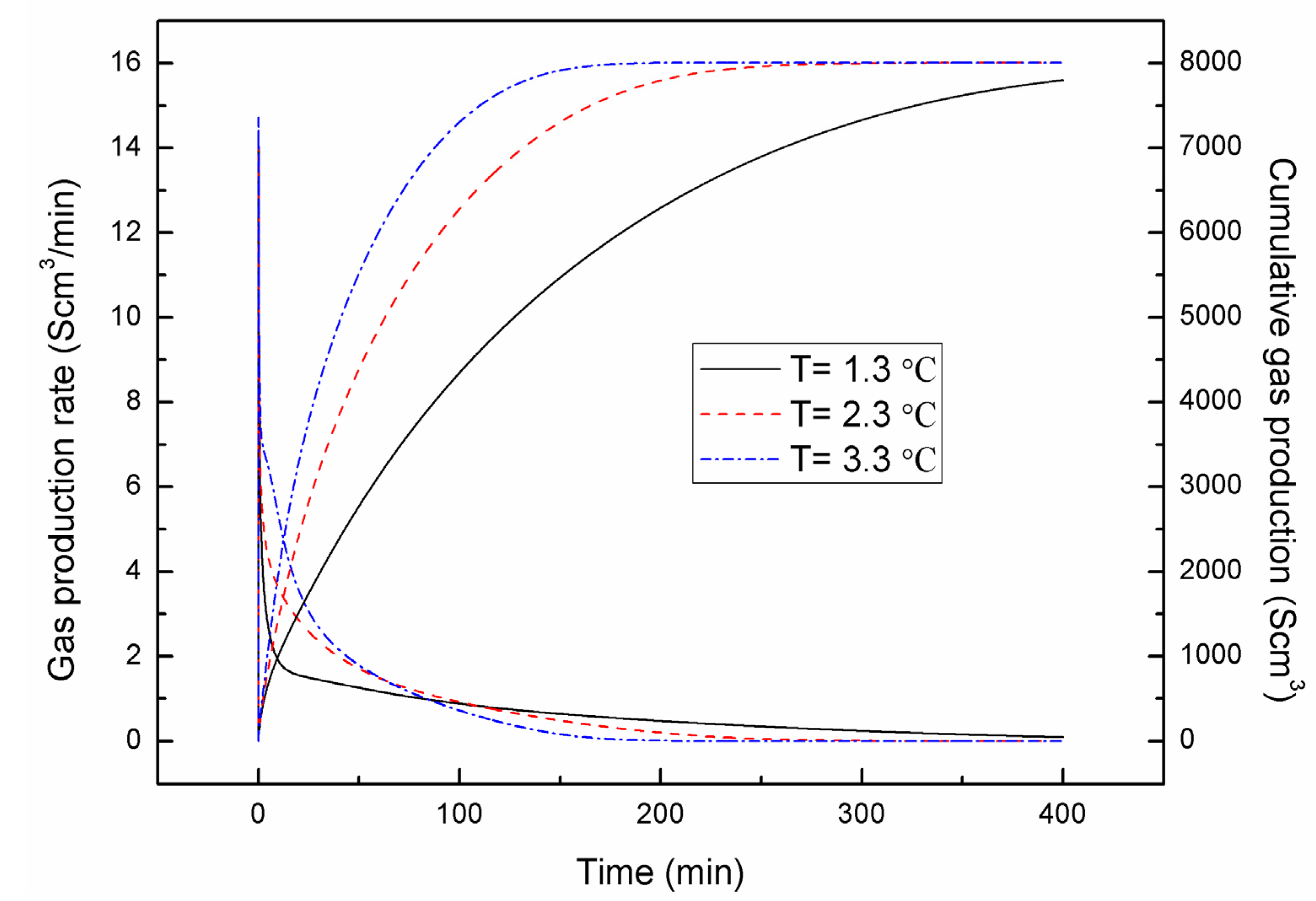
4.2. Effect of the Depressurizing Rate
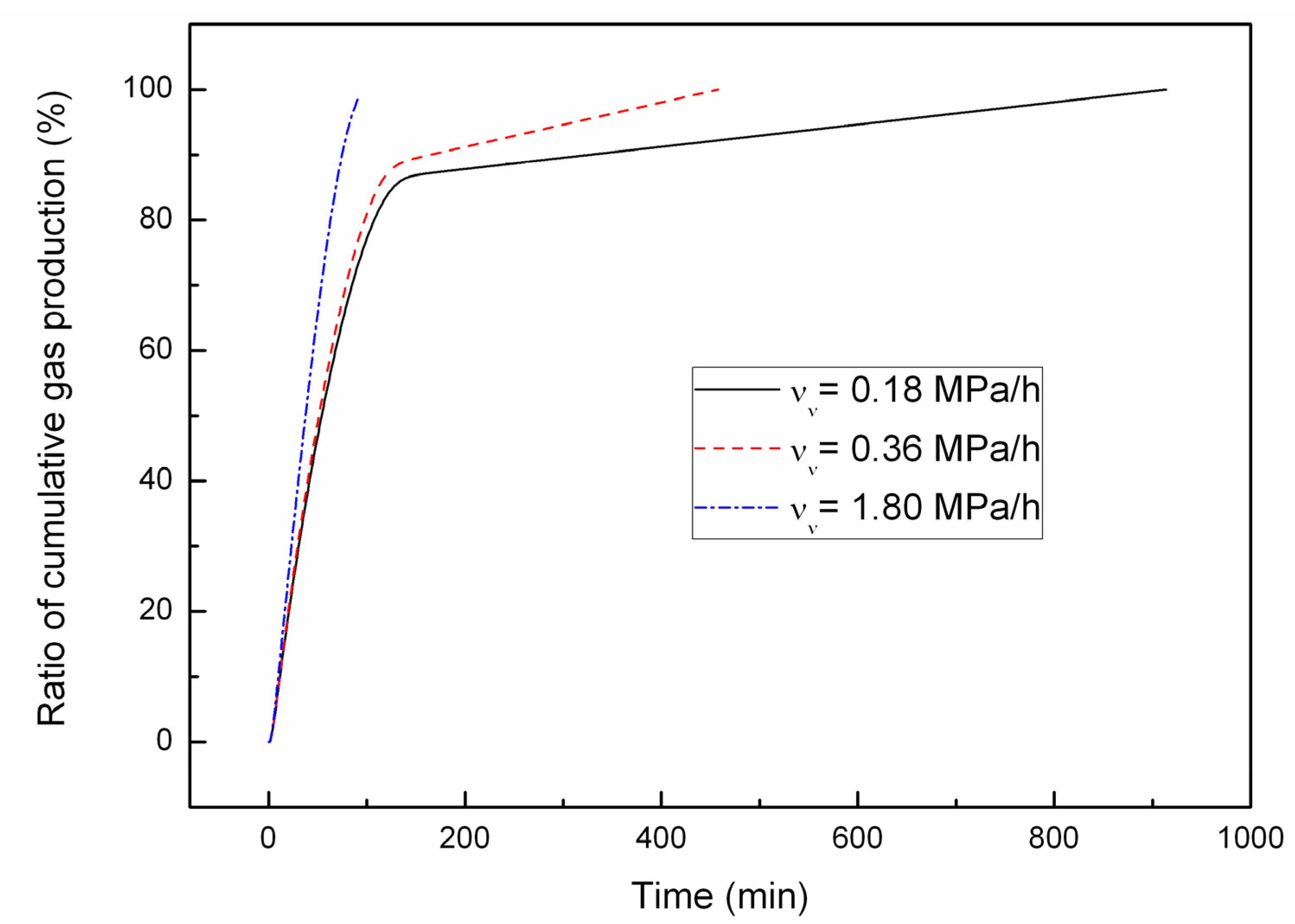
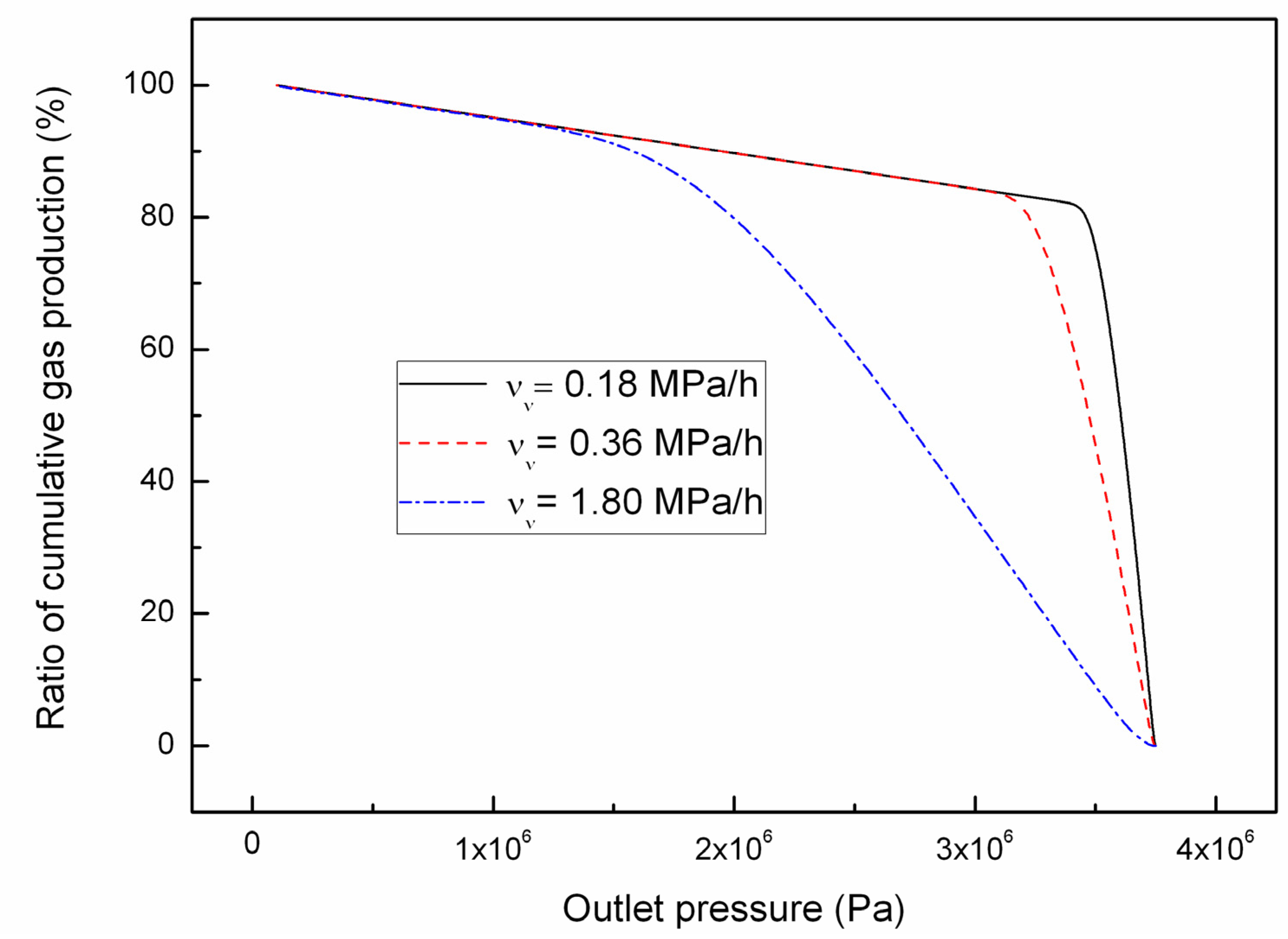
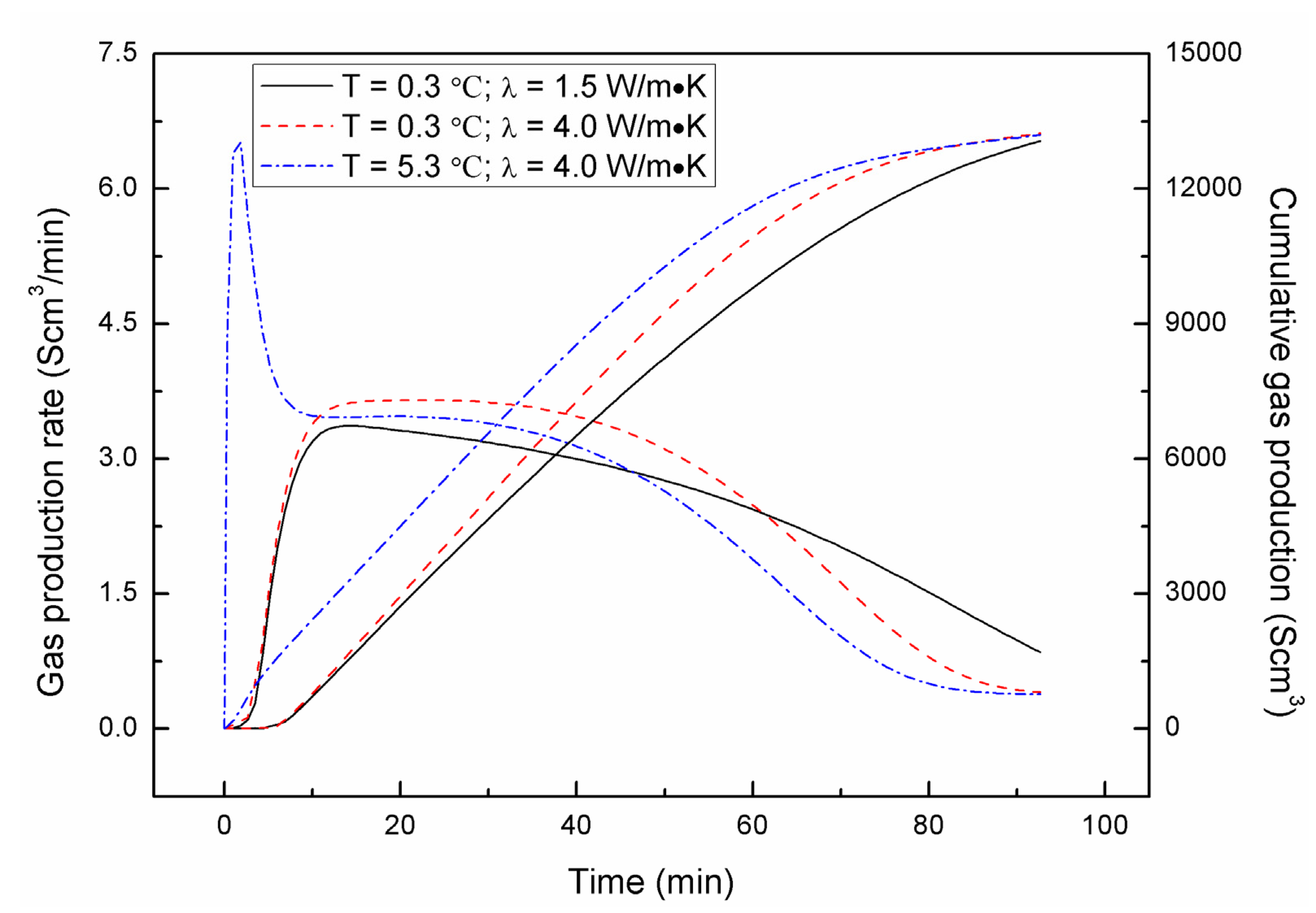
4.3. Effect of Combined Depressurization Approach
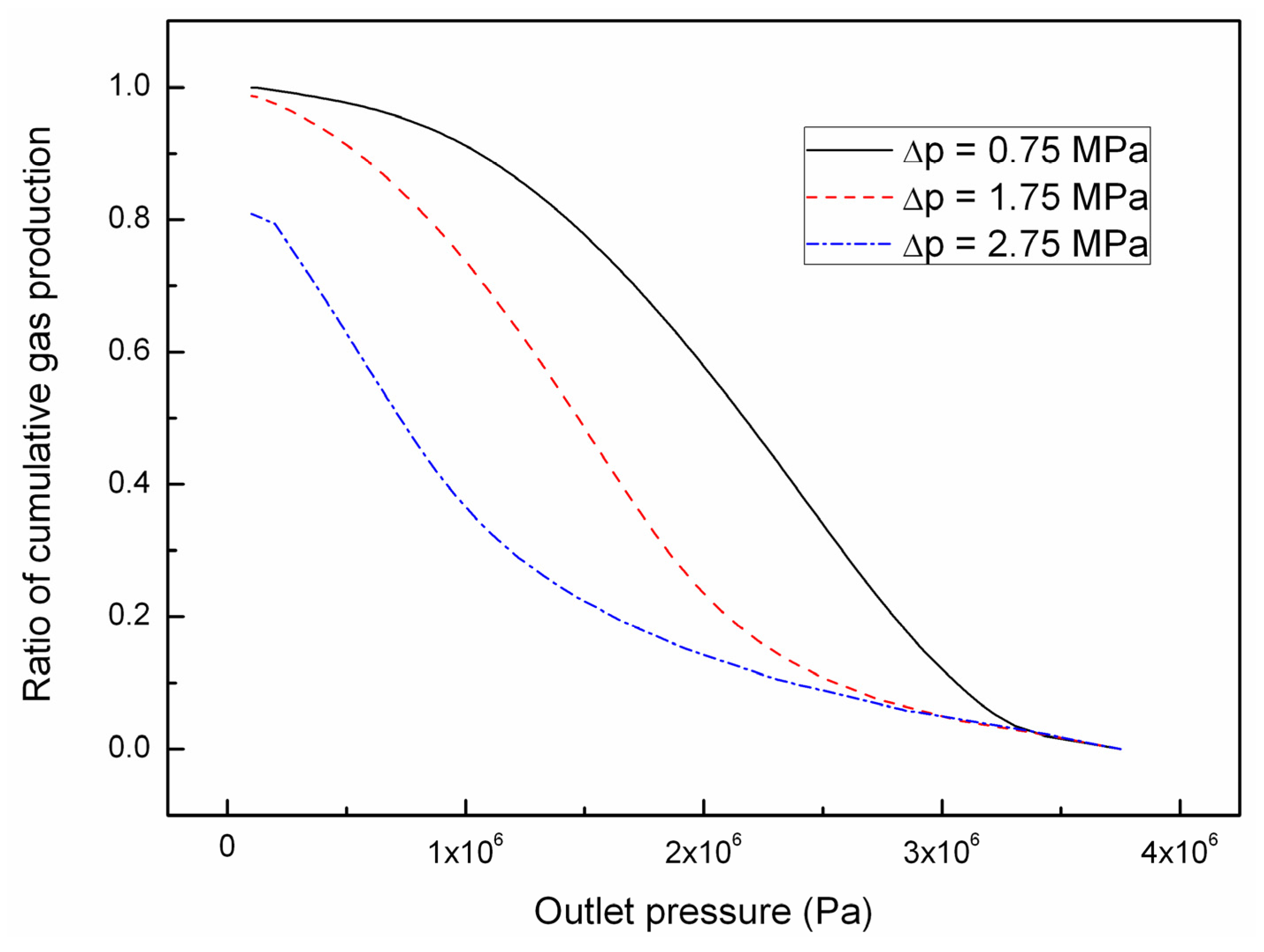

5. Conclusions
Nomenclature:
| As | specific surface area of porous medium bearing gas hydrate |
| Ageo | specific sharp geometry surface area contacting non-hydrate zone |
| Cps | heat capacity of porous media |
| Cpg | heat capacity of gas |
| Cpw | heat capacity of water |
| Cph | heat capacity of hydrate |
| D | core diameter |
| fe | fugacity of gas at the hydrate equilibrium pressure corresponding to the local temperature |
| f | fugacity of gas under the local temperature and pressure |
| hg | enthalpy of gas |
| hw | enthalpy of water |
| hh | enthalpy of hydrate |
| hs | enthalpy of porous media |
the enthalpy change in hydrate dissociation | |
| kc | thermal conductivity coefficient |
| kg | thermal conductivity coefficient of gas |
| kw | thermal conductivity coefficient of water |
| kh | thermal conductivity coefficient of hydrate |
| ks (λ) | thermal conductivity coefficient of porous media |
| kd | dissociation rate constant |
| k0 | intrinsic dissociation rate constant |
| krg | relative permeability of gas phase |
| krw | relative permeability of water phase |
| K | absolute permeability |
| K0 | original permeability without hydrate |
| L | core length |
mass rate of gas generated by hydrate dissociation per unit volume | |
mass rate of water generated by hydrate dissociation per unit volume | |
mass rate by hydrate dissociated per unit volume | |
| Mg | molecular weight of gas |
| Mw | molecular weight of water |
| Nh | hydrate number |
| N | permeability reduction index |
| Pc | capillary pressure between gas and water |
| Pe | equilibrium pressure |
| Pg | gas pressure |
| Pw | water pressure |
| P0 | core initial pressure |
| Pp0 | outlet pressure |
mass rate in terms of injection/production of gas | |
mass rate in terms of injection/production of water | |
heat of hydrate decomposition unit bulk volume | |
heat from the surroundings | |
| r | radial distance |
| R | universal gas constant |
| Sg | hydrate saturation |
| Sw | water saturation |
| Sh | gas saturation |
| Sgr | residual gas saturation |
| Swr | irreducible water saturation |
| t | time |
| T | system temperature |
| Tb | bath temperature |
| T0 | core initial temperature |
| νgr | velocity of gas in r-direction |
| νgx | velocity of gas in x-direction |
| νwr | velocity of water in r-direction |
| vwx | velocity of water in x-direction |
| x | axial distance |
| ρg | density of gas |
| ρw | density of water |
| ρr | density of porous media |
| Φ | porosity |
throttling coefficient for the i phase | |
| μg | viscosity of gas |
| μw | viscosity of water |
Acknowledgments
References
- Sloan, E.D. Clathrate Hydrates of Natural Gas, 2nd ed.; Marcel Dekker Inc: New York, NY, USA, 1998. [Google Scholar]
- Max, M.D.; Dillon, W.P. Oceanic methane hydrate: Character of the Blake Ridge hydrate stability zone and potential for methane extraction. J. Pet. Geol. 1998, 21, 343–358. [Google Scholar] [CrossRef]
- Konno, Y.; Oyama, H.; Nagao, J.; Masuda, Y.; Kurihara, M. Numerical analysis of the dissociation experiment of naturally occurring gas hydrate in sediment cores obtained at the Eastern Nankai Trough, Japan. Energy Fuels 2010, 24, 6353–6358. [Google Scholar] [CrossRef]
- Kumar, A.; Maini, B.; Bishnoi, P.R.; Clarke, M.; Zatsepina, O.; Srinivasan, S. Experimental determination of permeability in the presence of hydrates and its effect on the dissociation characteristics of gas hydrates in porous media. J. Pet. Sci. Eng. 2010, 70, 114–122. [Google Scholar] [CrossRef]
- Khataniar, S.; Kamath, V.A.; Omenihu, S.D.; Patil, S.H.; Dandekar, A.Y. Modelling and economic analysis of gas production from hydrates by depressurization method. Can. J. Chem. Eng. 2002, 80, 135–143. [Google Scholar] [CrossRef]
- Makogon, Y.F. Hydrates of Natural Gas, 1st ed.; Penn Well Publishing Company: Tulsa, OK, USA, 1997. [Google Scholar]
- Pooladi-Darvish, M.; Zatsepina, O.; Hong, H.F. Behaviour of Gas Production from Type III Hydrate Reservoirs. In Proceedings of the 6th International Conference on Gas Hydrates (ICGH 2008), Vancouver, Canada, 6–10 July 2008.
- Yousif, M.H.; Abass, H.H.; Selim, M.S.; Sloan, E.D. Experimental and theoretical investigation of methane-gas-hydrate dissociation in porous media. SPE Reserv. Eng. 1991, 6, 69–76. [Google Scholar] [CrossRef]
- Kim, H.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Masuda, Y.; Fujinaga, Y.; Naganawa, S.; Fujita, K.; Sato, K.; Hayashi, Y. Modeling and Experimental Studies on Dissociation of Methane Gas Hydrates in Bereasandstone Cores. In Proceedings of the 3rd International Conference on Gas Hydrates, Salt Lake City, UT, USA, 8–12 July 1999.
- Ji, C.; Ahmadi, G.; Smith, D.H. Natural gas production from hydrate decomposition by depressurization. Chem. Eng. Sci. 2001, 56, 5801–5814. [Google Scholar] [CrossRef]
- Ji, C.; Ahmadi, G.; Smith, D.H. Constant rate natural gas production from a well in a hydrate reservoir. Energy Convers. Manag. 2003, 44, 2403–2423. [Google Scholar] [CrossRef]
- Sun, X.; Mohanty, K.K. 1-D modeling of hydrate depressurization in porous media. Transp. Porous Media 2005, 58, 315–338. [Google Scholar] [CrossRef]
- Sun, X.; Mohanty, K.K. Kinetic simulation of methane hydrate formation and dissociation in porous media. Chem. Eng. Sci. 2006, 61, 3476–3495. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kowalsky, M.B.; Pruess, K. TOUGH-Fx/HYDRATE V1.0.1 User’s Manual: A Code for the Simulation of System Behavior in Hydrate-Bearing Geological Media; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2005; LBNL/PUB 3185. [Google Scholar]
- Tang, L.G.; Li, X.S.; Feng, Z.P.; Li, G.; Fan, S.S. Control mechanisms for gas hydrate production by depressurization in different scale hydrate reservoirs. Energy Fuels 2007, 21, 227–233. [Google Scholar] [CrossRef]
- Konno, Y.; Masuda, Y.; Hariguchi, Y.; Kurihara, M.; Ouchi, H. Key factors for depressurization-induced gas production from oceanic methane hydrates. Energy Fuels 2010, 24, 1736–1744. [Google Scholar] [CrossRef]
- Liu, Y.; Strumendo, M.; Arastoopour, H. Simulation of methane production from hydrates by depressurization and thermal stimulation. Ind. Eng. Chem. Res. 2009, 48, 2451–2464. [Google Scholar] [CrossRef]
- Gamwo, I.K.; Liu, Y. Mathematical modeling and numerical simulation of methane production in a hydrate reservoir. Ind. Eng. Chem. Res. 2010, 49, 5231–5245. [Google Scholar] [CrossRef]
- Hyodo, M.; Nakata, Y.; Yoshimoto, N.; Ebinuma, T. Basic research on the mechanical behavior of methane hydrate-sediments mixture. Soils Found. 2005, 45, 75–85. [Google Scholar] [CrossRef]
- Winters, W.J.; Waite, W.F.; Mason, D.H.; Gilbert, L.Y.; Pecher, I.A. Methane gas hydrate effect on sediment acoustic and strength properties. J. Pet. Sci. Eng. 2007, 56, 127–135. [Google Scholar] [CrossRef]
- Masui, A.; Miyazaki, K.; Haneda, H.; Ogata, Y.; Aoki, K. Mechanical Characteristics of Natural and Artificial Gas Hydrate Bearing Sediments. In Proceedings of the 6th International Conference on Gas Hydrates (ICGH 2008), Vancouver, Canada, 6–10 July 2008.
- Miyazaki, K.; Masui, A.; Tenma, N.; Ogata, Y.; Aoki, K. Study on mechanical behavior for methane hydrate sediment based on constant strain-rate test and unloading-reloading test under triaxial compression. Int. J. Offshore Polar Eng. 2010, 20, 61–67. [Google Scholar]
- Li, Y.; Song, Y.; Yu, F.; Liu, W.; Zhao, J. Experimental study on mechanical properties of gas hydrate-bearing sediments using kaolin clay. China Ocean Eng. 2011, 25, 113–122. [Google Scholar] [CrossRef]
- Li, Y.; Song, Y.; Liu, W.; Yu, F. Experimental research on the mechanical properties of methane hydrate-ice mixtures. Energies 2012, 5, 181–192. [Google Scholar] [CrossRef]
- Klar, A.; Soga, K. Coupled Deformation-Flow Analysis for Methane Hydrate Production by Depressurized Wells. In Proceedings of the 3rd Biot Conference on Poromechanics, Norman, OK, USA, 24–27 May 2005.
- Rutqvist, J.; Moridis, G. Numerical Studies of Geomechanical Stability of Hydrate-Bearing Sediments. In Proceedings of 2007 Offshore Technology Conference (OTC-18860), Houston, TX, USA, 30 April–3 May 2007.
- Kimoto, S.; Oka, F.; Fushita, T. A chemo-thermo-mechanically coupled analysis of ground deformation induced by gas hydrate dissociation. Int. J. Mech. Sci. 2010, 52, 365–376. [Google Scholar] [CrossRef]
- Selim, M.S.; Sloan, E.D. Heat and mass transfer during the dissociation of hydrate in porous media. AIChE J. 1989, 35, 1049–1052. [Google Scholar] [CrossRef]
- Tester, J.W. Thermodynamics and Its Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Hong, H.; Pooladi-Darvish, M. Simulation of depressurization for gas production from gas hydrate reservoirs. J. Can. Pet. Technol. 2005, 44, 39–46. [Google Scholar] [CrossRef]
- Song, Y.; Liang, H. 2-D Numerical simulation of natural gas hydrate decomposition through depressurization by fully implicit method. China Ocean Eng. 2009, 23, 529–542. [Google Scholar]
- Bai, Y.; Li, Q.; Li, X.; Du, Y. Numerical simulation on gas production from a hydrate reservoir underlain by a free gas zone. Chin. Sci. Bull. 2009, 54, 865–872. [Google Scholar] [CrossRef]
- Liang, H.; Song, Y.; Chen, Y. Numerical simulation for laboratory-scale methane hydrate dissociation by depressurization. Energy Conver. Manag. 2010, 51, 1883–1890. [Google Scholar] [CrossRef]
- Ruan, X.; Song, Y.; Liang, H.; Yang, M.; Dou, B. Numerical simulation of the gas production behavior of hydrate dissociation by depressurization in hydrate-bearing porous medium. Energy Fuels 2012. [Google Scholar] [CrossRef]
- Li, S.; Chen, Y.; Hao, Y.; Du, Q. Experimental research on influence factors of natural gas hydrate production by depressurizing in porous media. J. China Univ. Pet. 2007, 31, 56–59. (in Chinese). [Google Scholar]
- Hong, H.; Pooladi-Darvish, M. A Numerical Study on Gas Production from Formations Containing Gas Hydrates. In Proceedings of Canadian International Petroleum Conference, Calgary, Canada, 12–14 June 2003.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ruan, X.; Song, Y.; Zhao, J.; Liang, H.; Yang, M.; Li, Y. Numerical Simulation of Methane Production from Hydrates Induced by Different Depressurizing Approaches. Energies 2012, 5, 438-458. https://doi.org/10.3390/en5020438
Ruan X, Song Y, Zhao J, Liang H, Yang M, Li Y. Numerical Simulation of Methane Production from Hydrates Induced by Different Depressurizing Approaches. Energies. 2012; 5(2):438-458. https://doi.org/10.3390/en5020438
Chicago/Turabian StyleRuan, Xuke, Yongchen Song, Jiafei Zhao, Haifeng Liang, Mingjun Yang, and Yanghui Li. 2012. "Numerical Simulation of Methane Production from Hydrates Induced by Different Depressurizing Approaches" Energies 5, no. 2: 438-458. https://doi.org/10.3390/en5020438
APA StyleRuan, X., Song, Y., Zhao, J., Liang, H., Yang, M., & Li, Y. (2012). Numerical Simulation of Methane Production from Hydrates Induced by Different Depressurizing Approaches. Energies, 5(2), 438-458. https://doi.org/10.3390/en5020438





