A Novel Multiscale Ensemble Carbon Price Prediction Model Integrating Empirical Mode Decomposition, Genetic Algorithm and Artificial Neural Network
Abstract
:1. Introduction
2. Methodology
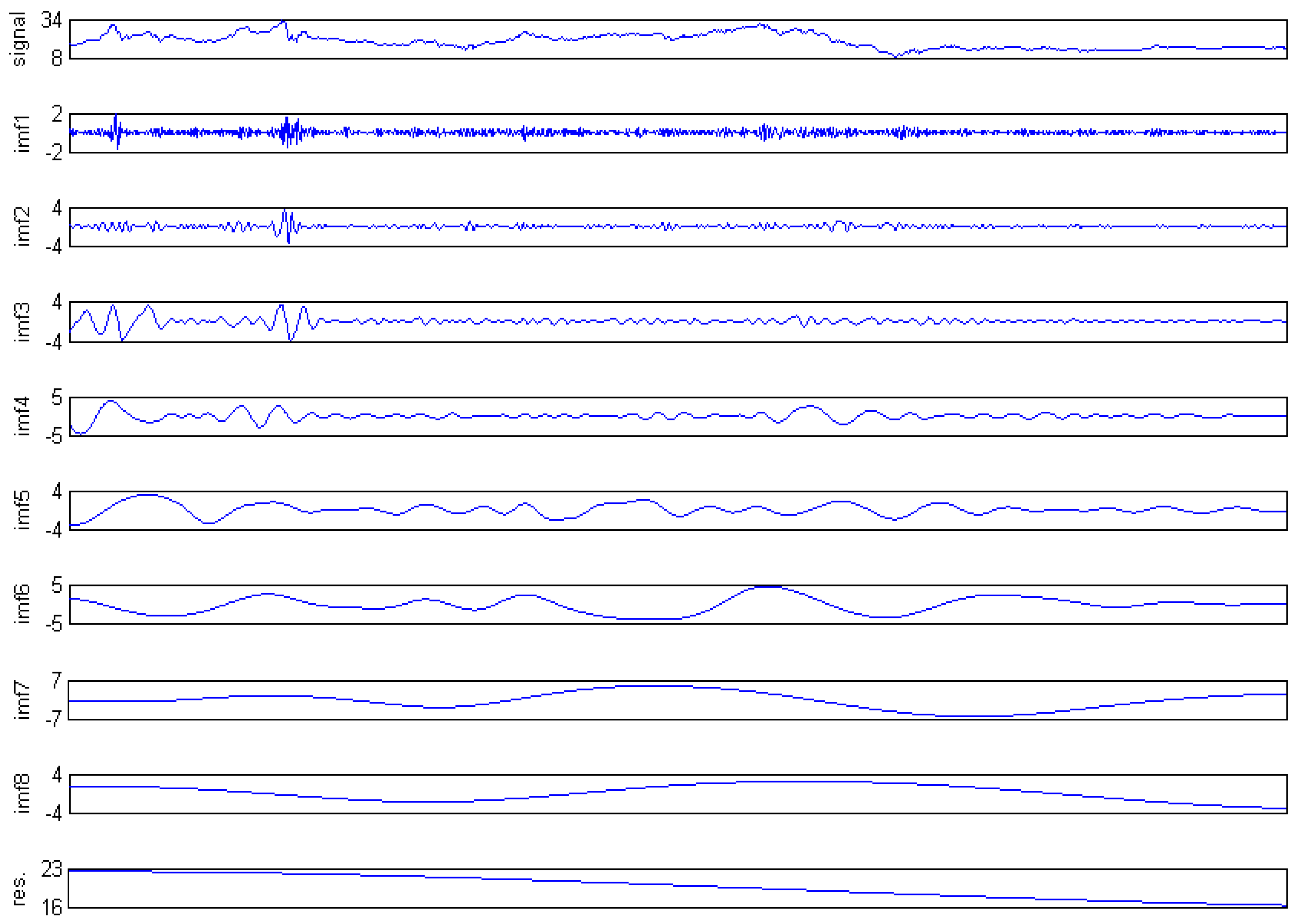
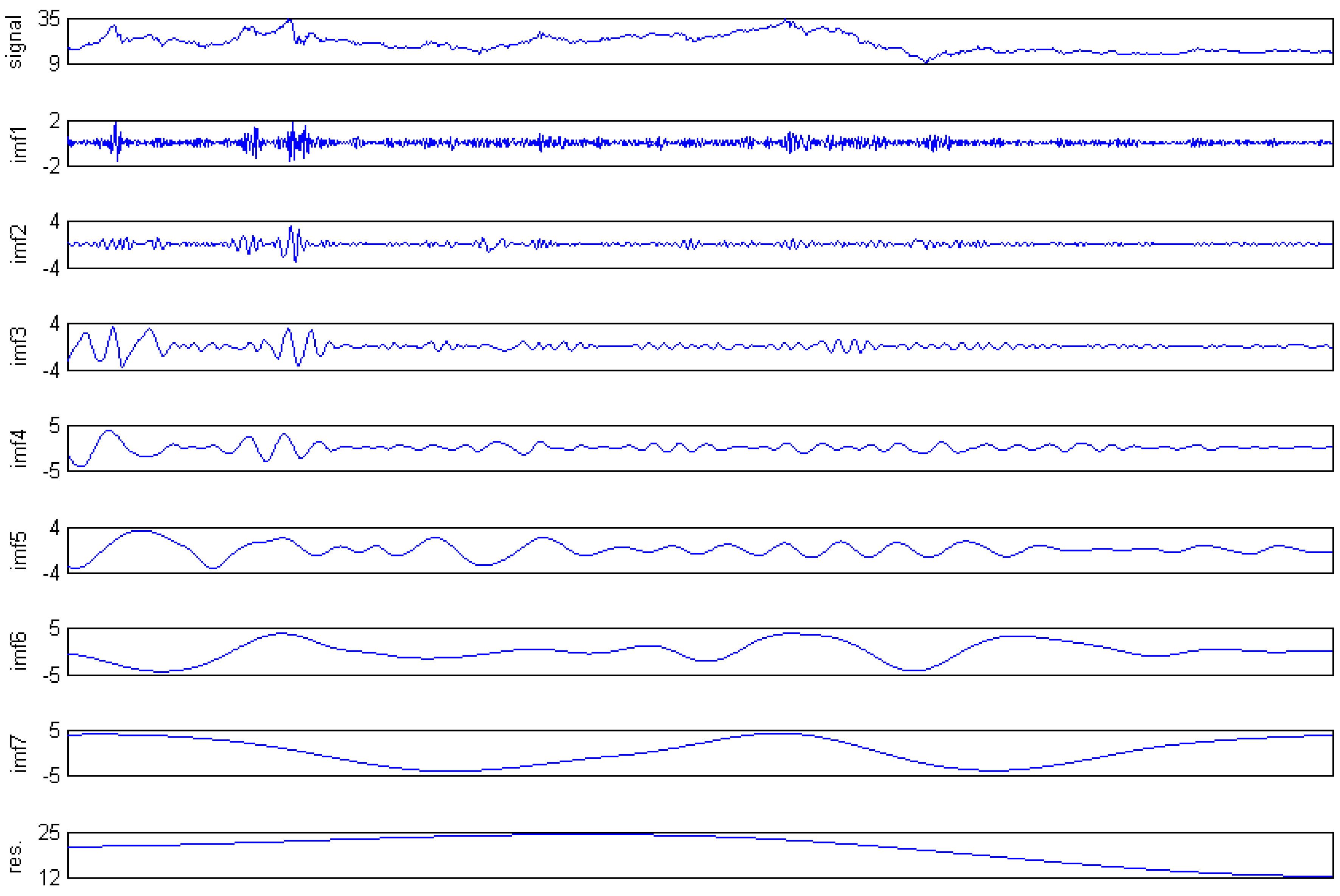
2.1. EMD
- (1)
- Identify all the maxima and minima of carbon price data x(t);
- (2)
- Generate their upper and lower envelopes, emax(t) and emin(t), with cubic spline interpolation;
- (3)
- Calculate the point-by-point mean m(t) from the upper and lower envelopes:m(t) = [emax(t) + emin(t)]/2
- (4)
- Extract the mean from carbon price data and define the difference between x(t) and m(t) as d(t):d(t) = x(t) − m(t)
- (5)
- Check the properties of d(t):
- (a)
- If it is an IMF, denote d(t) as the ith IMF and replace x(t) with the residue r(t) = x(t) − d(t). The ith IMF is often denoted as ci(t) and the i is called its index;
- (b)
- If it is not an IMF, replace x(t) with d(t);
- (6)
- Repeat steps (1)–(5) until the residue satisfies some stopping criteria.
2.2. Fine-to-Coarse Reconstruction
- (1)
- Compute the mean of the sum of c1 to ci(1 ≤ i ≤ m), i.e., for each component (except for the residue);
- (2)
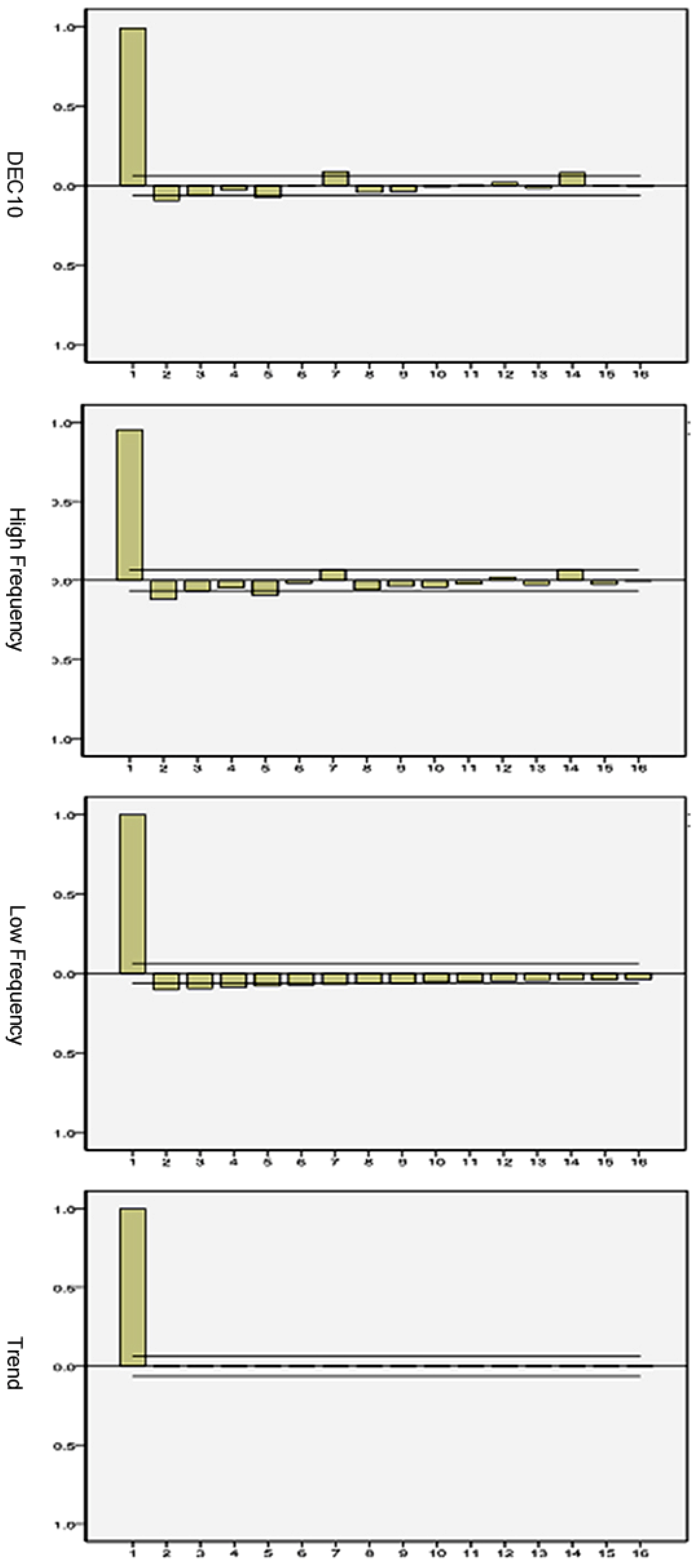
- Select the significance level α and employ t-test to identify for which i the mean significantly departs from zero for the first time;
- (3)
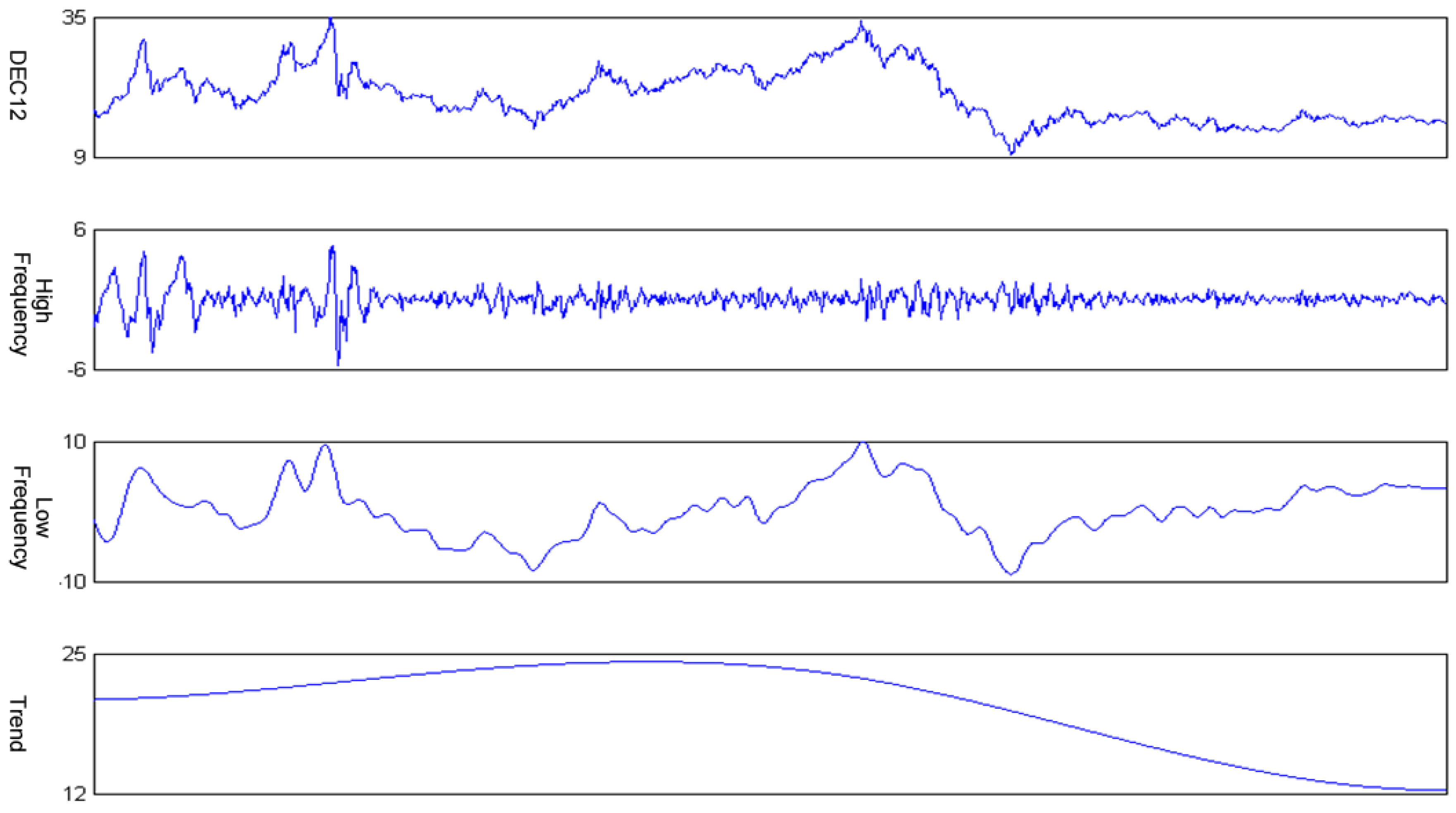
- Once i is identified as a significant change point, partial reconstruction with IMFs from this to the end is identified as a low frequency component, and the partial reconstruction with other IMFs is identified as a high frequency component. The residue is identified as a trend component.
2.3. Combining ANN and GA for Regression
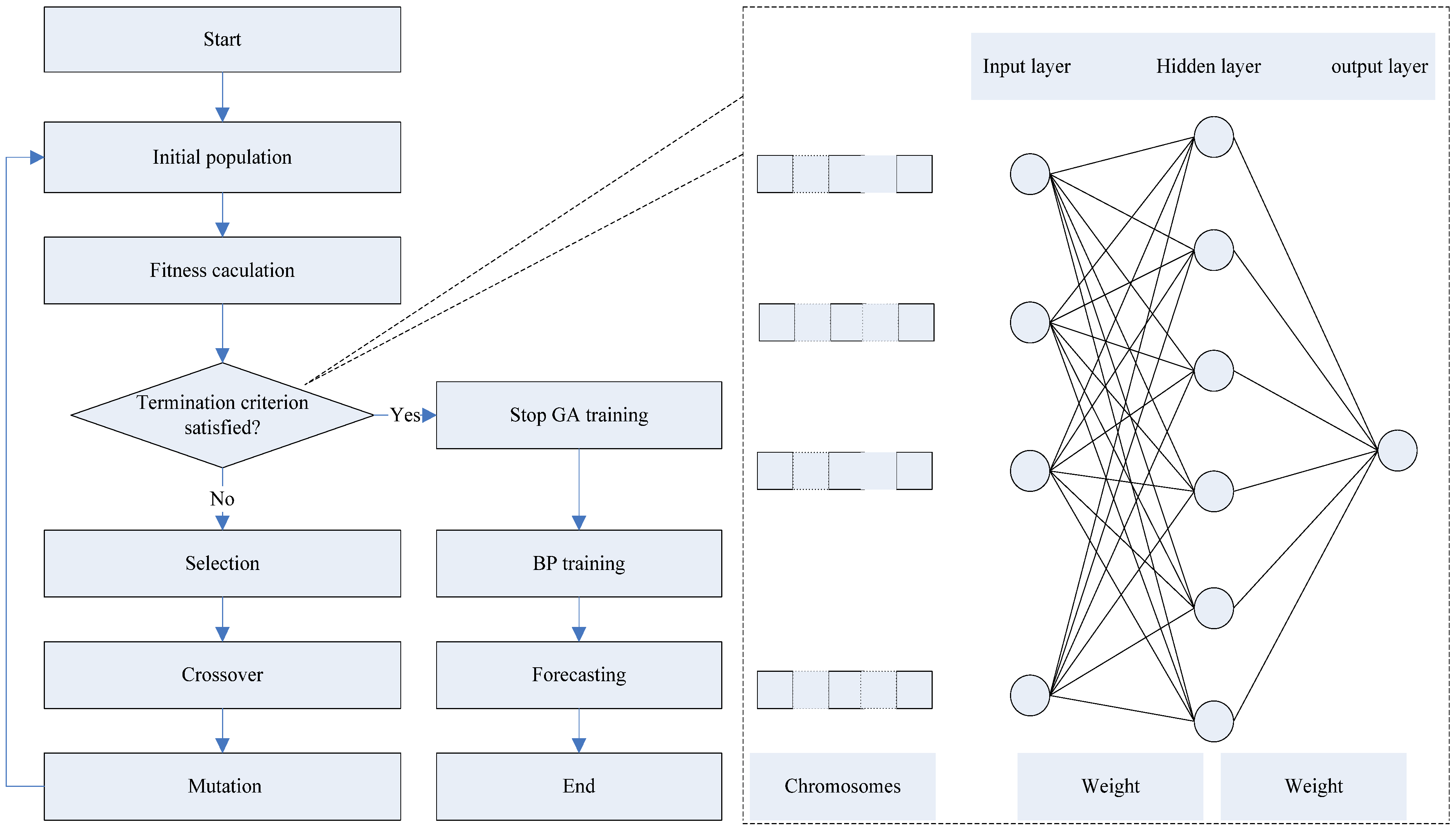
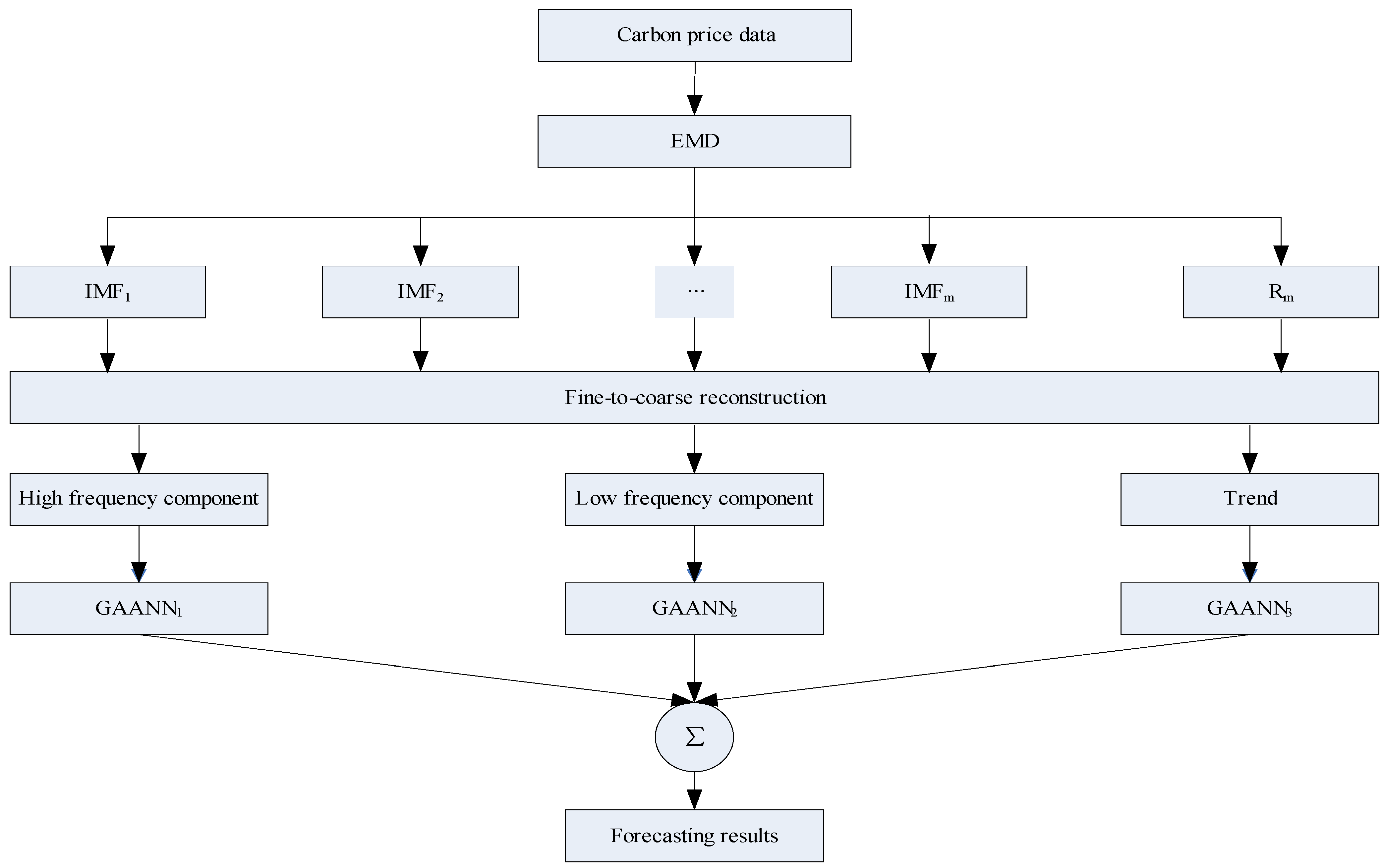
2.4. EMD-Based GAANN Multiscale Ensemble Forecasting Model
- Step 1:
- Use the EMD to decompose the carbon price data into a set of IMFs and one residue.
- Step 2:
- Apply the fine-to-coarse reconstruction algorithm to reconstruct the IMFs and residue obtained from decomposition into a high frequency component, a low frequency component and a trend component.
- Step 3:
- Use the GAANN model to forecast the future one-day values of those three reconstructed components.
- Step 4:
- The forecasting results obtained by the sum of the predicted values in the previous step, can be treated as the final prediction results for the original carbon price.
3. Empirical Analysis
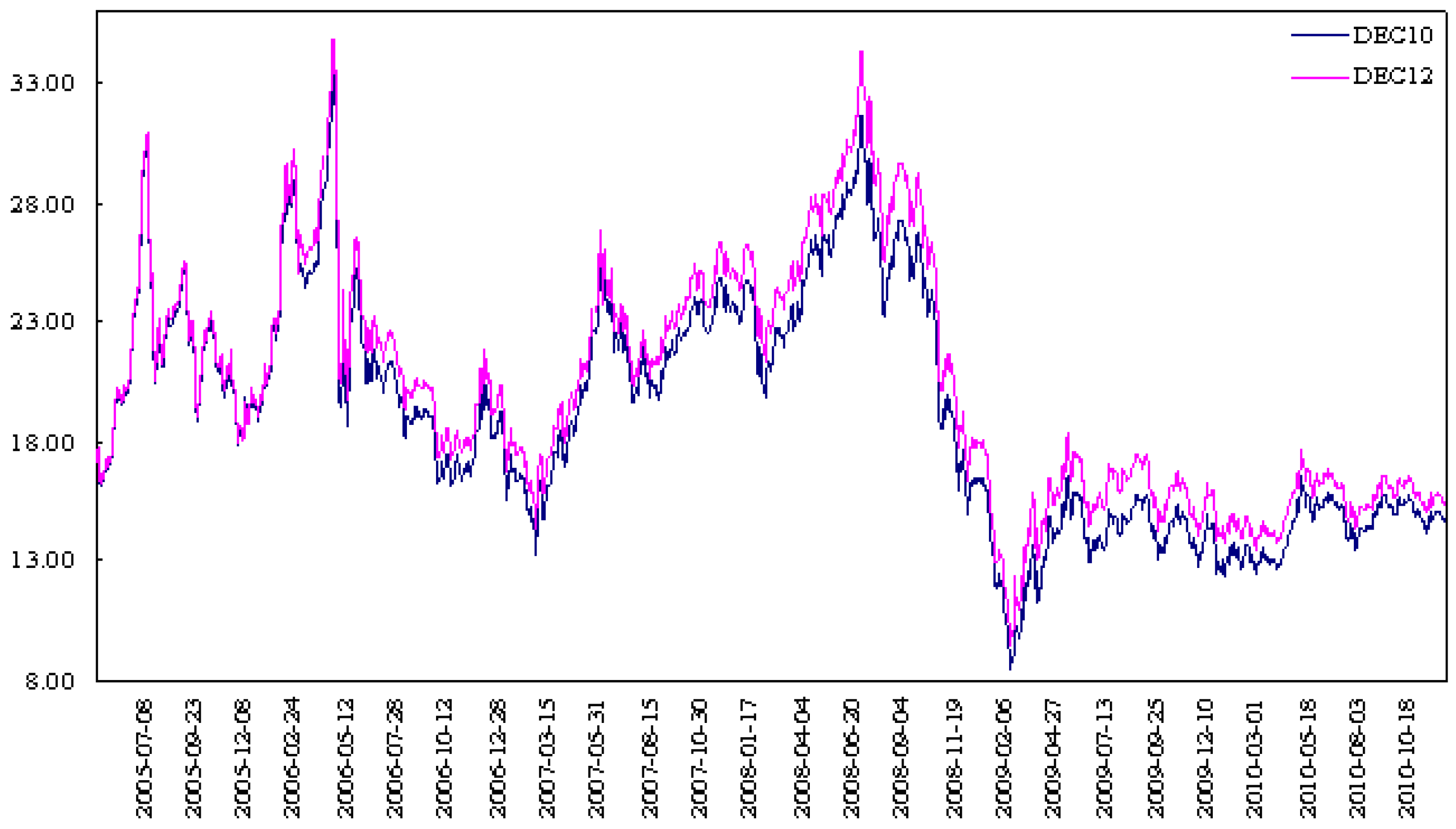
3.1. Data
3.2. Evaluation Criteria
3.3. Forecasting Results
| Item | s1 | s2 | s3 | s4 | s5 | s6 | s7 | s8 |
|---|---|---|---|---|---|---|---|---|
| Mean | −3.23 × 10−4 | 2.54 × 10−3 | −4.52 × 10−4 | −4.90 × 10−3 | 1.20 × 10−2 | −4.13 × 10−2 | −9.71 × 10−2 | −6.55 × 10−2 |
| t value | −0.044 | 0.399 | −0.058 | −0.551 | 1.273 | −3.463 | −6.325 | −4.527 |
| Item | s1 | s2 | s3 | s4 | s5 | s6 | s7 |
|---|---|---|---|---|---|---|---|
| Mean | −1.24 × 10−4 | −1.81 × 10−3 | −5.27 × 10−3 | −1.74 × 10−2 | −6.21 × 10−3 | −1.28 × 10−2 | 2.52 × 10−2 |
| t value | −0.016 | −0.276 | −0.682 | −2.031 | −0.657 | −1.073 | 1.698 |
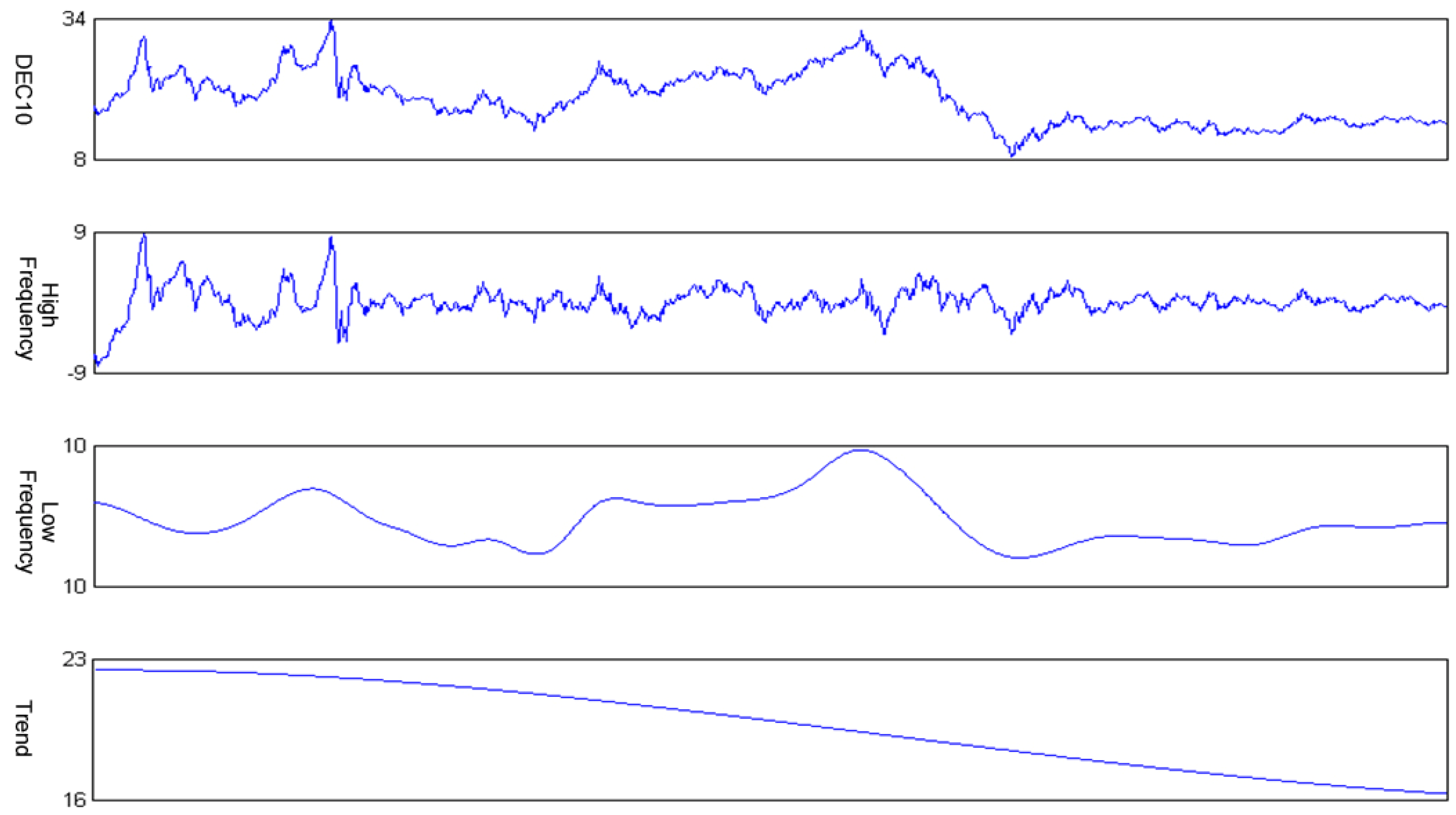
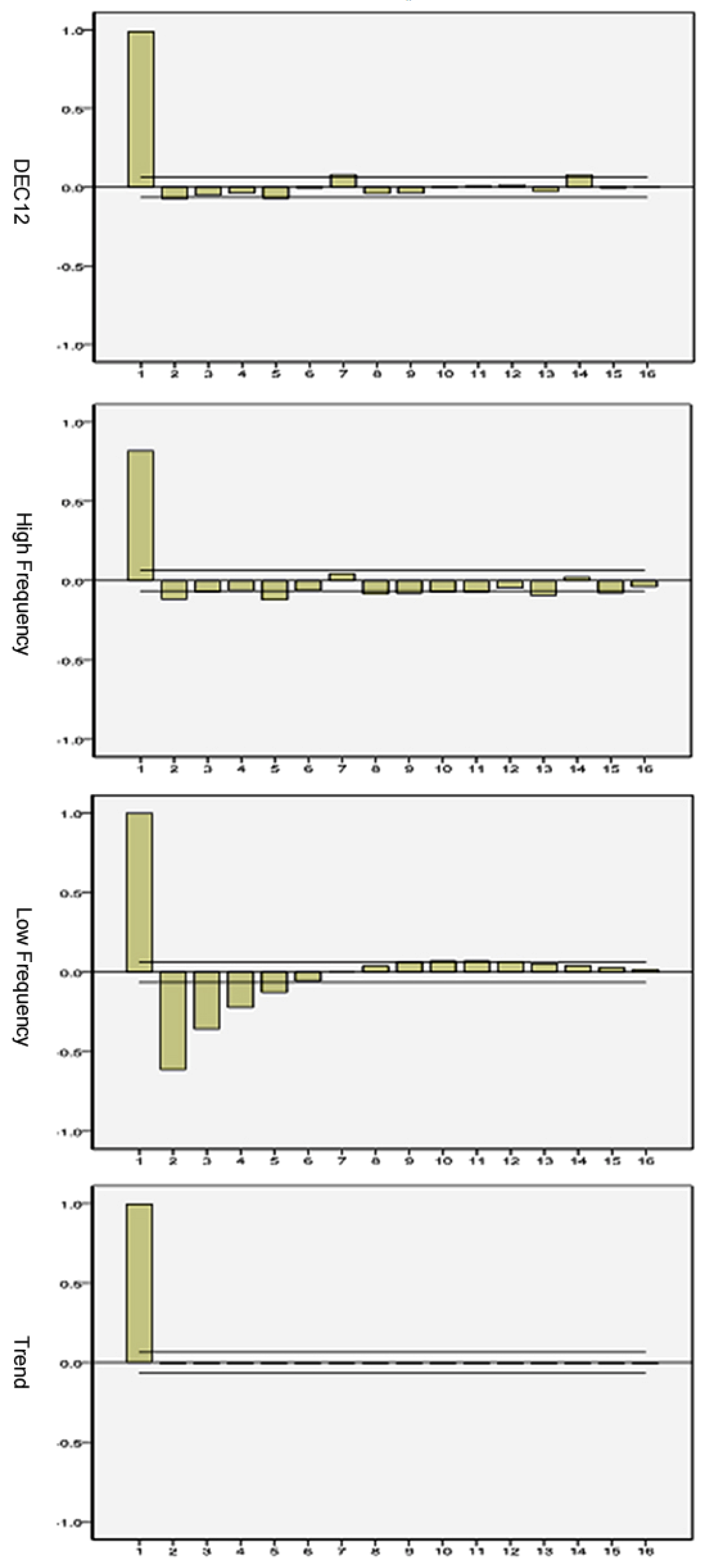
- DEC10: (xt−1, xt−2);
- High frequency component: (xt−1, xt−2);
- Low frequency component: (xt−1, xt−2, xt−3, xt−4);
- Trend component: (xt−1).
| Models | DEC10 | DEC12 | ||
|---|---|---|---|---|
| RMSE | Rank | RMSE | Rank | |
| RW | 0.2962 | 4 | 0.3176 | 5 |
| ARIMA | 0.3002 | 6 | 0.3197 | 6 |
| ANN | 0.2986 | 5 | 0.3078 | 4 |
| GAANN | 0.2952 | 3 | 0.2986 | 3 |
| EMD-ARIMA-∑ | 0.2886 | 2 | 0.2912 | 2 |
| EMD-GAANN-∑ | 0.2817 | 1 | 0.2856 | 1 |
| Models | DEC10 | DEC12 | ||
|---|---|---|---|---|
| Dstat | Rank | Dstat | Rank | |
| RW | 48.40 | 5 | 49.77 | 5 |
| ARIMA | 47.72 | 6 | 48.86 | 6 |
| ANN | 64.38 | 4 | 60.96 | 4 |
| GAANN | 67.58 | 3 | 64.16 | 3 |
| EMD-ARIMA-∑ | 69.18 | 2 | 67.58 | 2 |
| EMD-GAANN-∑ | 70.09 | 1 | 69.63 | 1 |
- DEC12: (xt−1, xt−2);
- High frequency component: (xt−1, xt−2);
- Low frequency component: (xt−1, xt−2, xt−3, xt−4, xt−5);
- Trend component: (xt−1).
4. Conclusions
Acknowledgments
References
- Montagnoli, A.; de Vries, F.P. Carbon trading thickness and market efficiency. Energy Econ. 2010. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wei, Y.M. An Overview of Current Research on EU ETS: Evidence from its Operating Mechanism and Economic Effect. Appl. Energy 2010, 6, 1804–1814. [Google Scholar] [CrossRef]
- Seifert, J.; Marliese, U.H.; Michael, W. Dynamic behavior of CO2 spot prices. J. Environ. Econ. Manag. 2008, 56, 180–194. [Google Scholar] [CrossRef]
- Feng, Z.H.; Zou, L.L.; Wei, Y.M. Carbon price volatility: Evidence from EU ETS. Appl. Energy 2011, 88, 590–598. [Google Scholar] [CrossRef]
- Wang, W.B.; Fei, P.S.; Yi, X.M. Prediction of China stock based on EMD and neural network. Syst. Eng. Theory Pract. 2010, 6, 1027–1033. [Google Scholar]
- Yu, L.; Wang, S.Y.; Lai, K.K. A novel nonlinear ensemble forecasting model incorporating GLAR and ANN for foreign exchange rates. Comput. Oper. Res. 2005, 32, 2523–2541. [Google Scholar] [CrossRef]
- Han, M.; Xi, J.H.; Xu, S.G.; Yin, F.L. Prediction of chaotic time series based on the recurrent network. IEEE Trans. Sign. Proc. 2004, 2, 3409–3416. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Process R. Soc. Lond. 1998, A454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.L.; Qu, W.D.; Long, S.R.; Shen, S.S.P. Applications of Hilbert Huang transform to non-stationary financial time series analysis. Appl. Stoch. Models Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.Y.; Lai, K.K.; Wen, F.H. A multiscale neural network learning paradigm for financial crisis forecasting. Neurocomputing 2010, 73, 716–72. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J.Z. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Riling, G.; Flandrin, P.; Goncalves, P. On Empirical Mode Decomposition and its algorithms. In Proceedings of the IEEE EURASIP Workshop on Nonlinear Signal and Image Processing, Grado, Italy, June 2003.
- Zhang, X.; Lai, K.K.; Wang, S.Y. A new approach for crude oil price analysis based on Empirical Mode Decomposition. Energy Econ. 2008, 30, 905–918. [Google Scholar] [CrossRef]
- Sedki, A.; Ouazar, D.; El Mazoudi, E. Evolving neural network using real coded genetic algorithm for daily rainfall–runoff forecasting. Expert Syst. Appl. 2009, 36, 4523–4527. [Google Scholar] [CrossRef]
- Irani, R.; Nasimi, R. Evolving neural network using real coded genetic algorithm for permeability estimation of the reservoir. Expert Syst. Appl. 2011, 38, 9862–9866. [Google Scholar] [CrossRef]
- ECX EUA Futures Contract: Historic Data 2005-2010. Available online: http://www.ecx.eu (accessed on 5 December 2010).
- Gao, D.Q. On structure of supervised linear basis function feedforward three-layered neural network. Chin. J. Comput. 1998, 1, 81–86. [Google Scholar]
- GAOTV5. Available online: http://www.ise.ncsu.edu/mirage/GAToolBox/gaot/gaotv5.zip (accessed on 16 May 2007).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhu, B. A Novel Multiscale Ensemble Carbon Price Prediction Model Integrating Empirical Mode Decomposition, Genetic Algorithm and Artificial Neural Network. Energies 2012, 5, 355-370. https://doi.org/10.3390/en5020355
Zhu B. A Novel Multiscale Ensemble Carbon Price Prediction Model Integrating Empirical Mode Decomposition, Genetic Algorithm and Artificial Neural Network. Energies. 2012; 5(2):355-370. https://doi.org/10.3390/en5020355
Chicago/Turabian StyleZhu, Bangzhu. 2012. "A Novel Multiscale Ensemble Carbon Price Prediction Model Integrating Empirical Mode Decomposition, Genetic Algorithm and Artificial Neural Network" Energies 5, no. 2: 355-370. https://doi.org/10.3390/en5020355
APA StyleZhu, B. (2012). A Novel Multiscale Ensemble Carbon Price Prediction Model Integrating Empirical Mode Decomposition, Genetic Algorithm and Artificial Neural Network. Energies, 5(2), 355-370. https://doi.org/10.3390/en5020355




