The SSG Wave Energy Converter: Performance, Status and Recent Developments
Abstract
:1. Introduction
- -
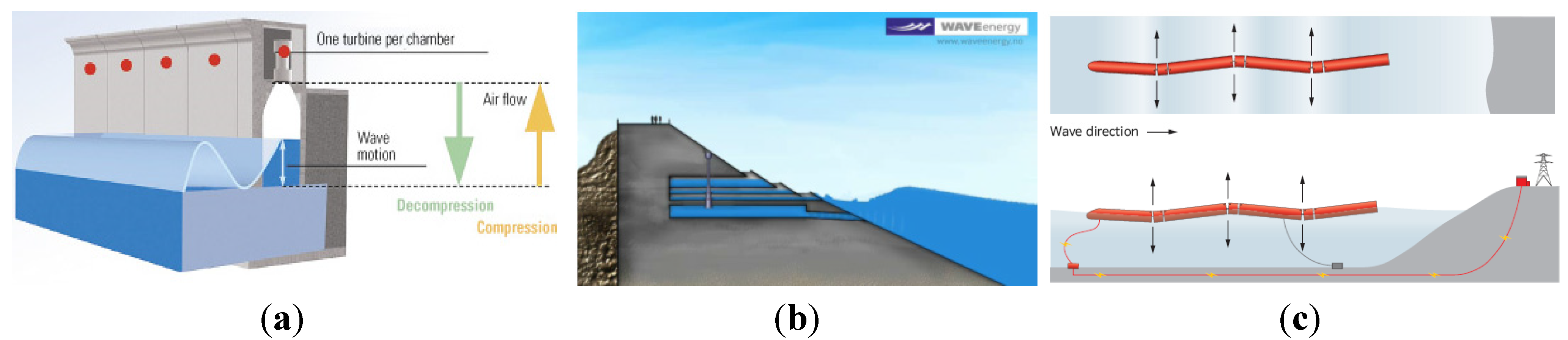
- Oscillating Water Columns (OWC; Figure 1a) can be described as a caisson breakwater with a gap on the seaside face, which encloses a mass of water. Waves cause the water to rise and fall and this alternately compresses and depressurizes an air column. The energy is extracted from the oscillating air flow by using a Wells turbine;
- -
- OverTopping Devices (OTD; Figure 1b) use a sloping plate that leads the waves to overtop into a reservoir located immediately behind it. The energy is extracted via low head turbines, using the difference in water levels between the reservoir and the average sea water level;
- -
- In the Wave Activated Bodies (WAB; Figure 1c), waves cause the body parts of a device to oscillate relative to each other; alternatively, the whole body may oscillate against a fixed reference. The oscillatory motion can be heave, pitch or roll. Hydraulic systems are generally employed to compress oil, air or water, which is then used to drive a generator.
- –
- Sharing structure costs;
- –
- Availability of grid connections and infrastructures;
- –
- Recirculation of water inside the harbors as the outlet of the turbines is on the rear part of the system;
- –
- Easy installation and maintenance;
- –
- No deep-water moorings or long lengths of underwater electrical cable.

2. The Hydraulic Response
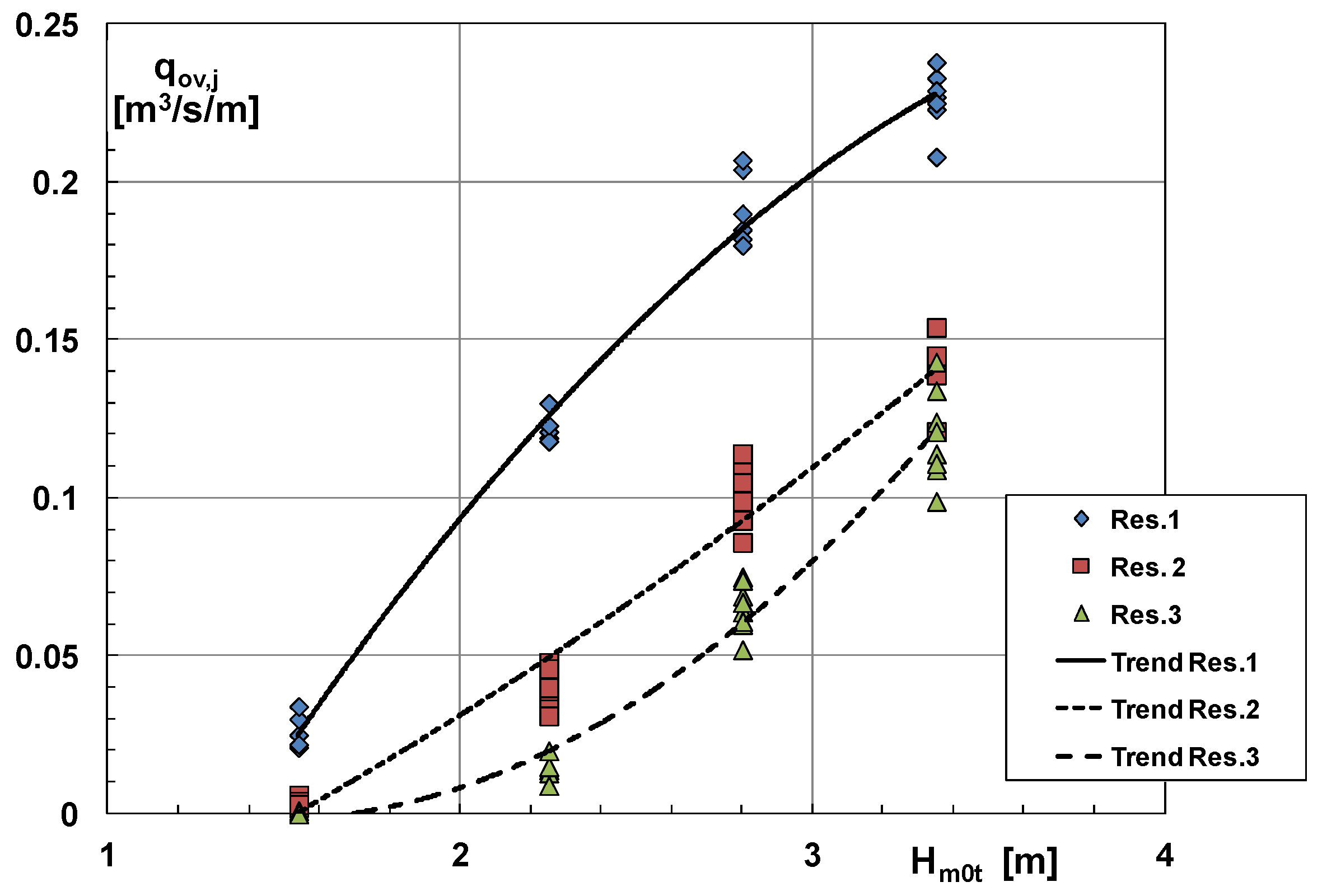
2.1. Overtopping Performance
- √
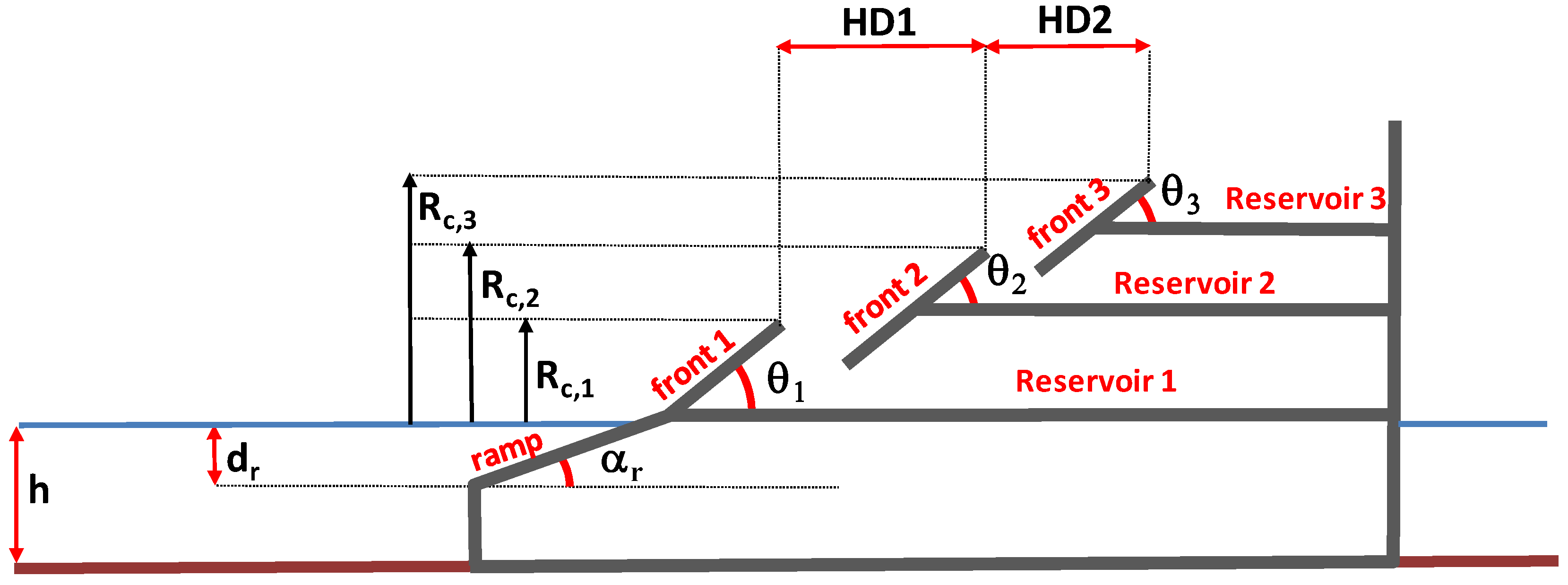
- Reservoir crest levels, Rcj
- √
- Ramp angle, αr;
- √
- Ramp draught, dr;
- √
- Front angles, θj;
- √
- Horizontal distance between the reservoir crests, HDj beside the role of wave height and period.
2.1.1. 2D Waves
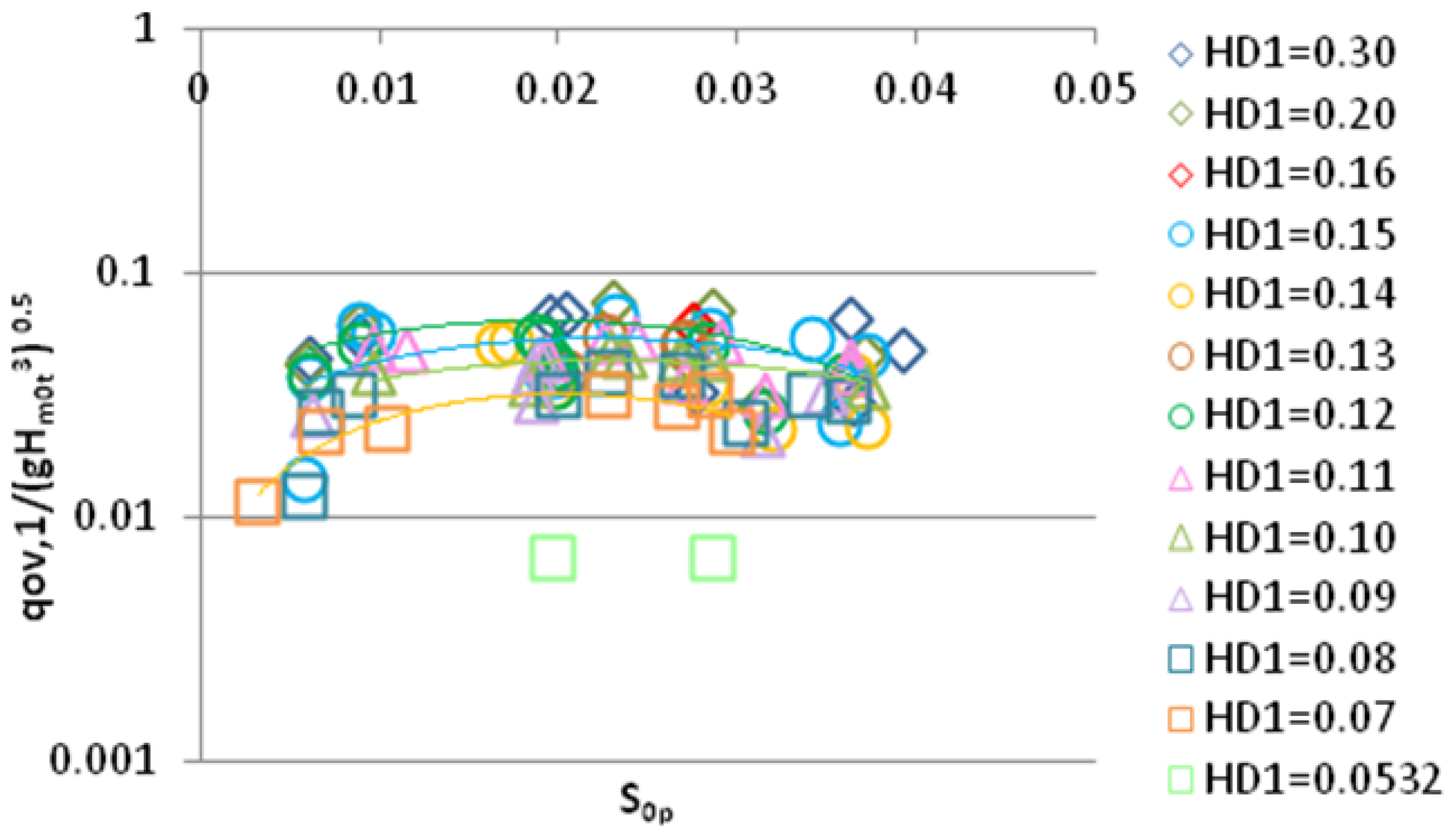

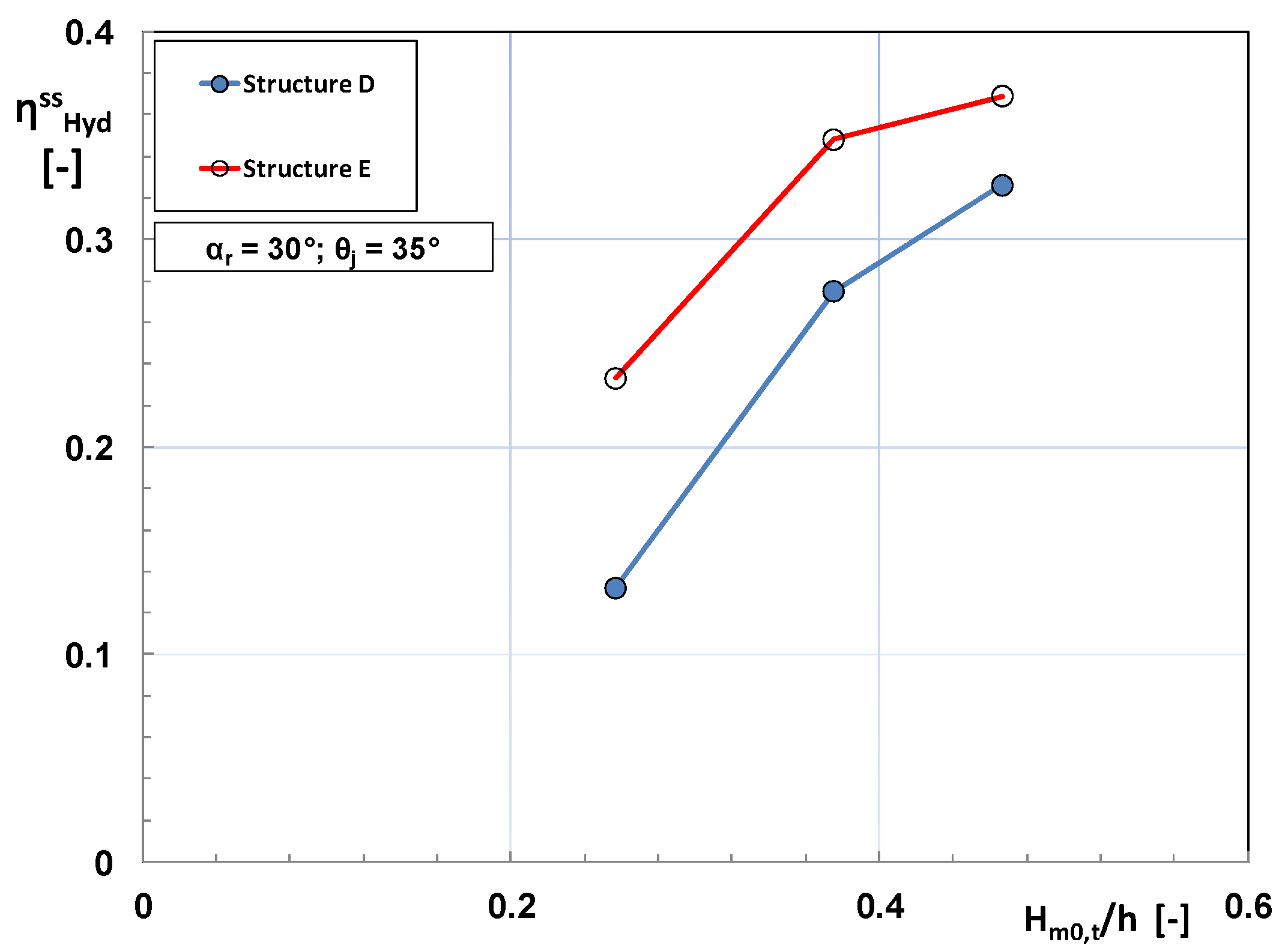
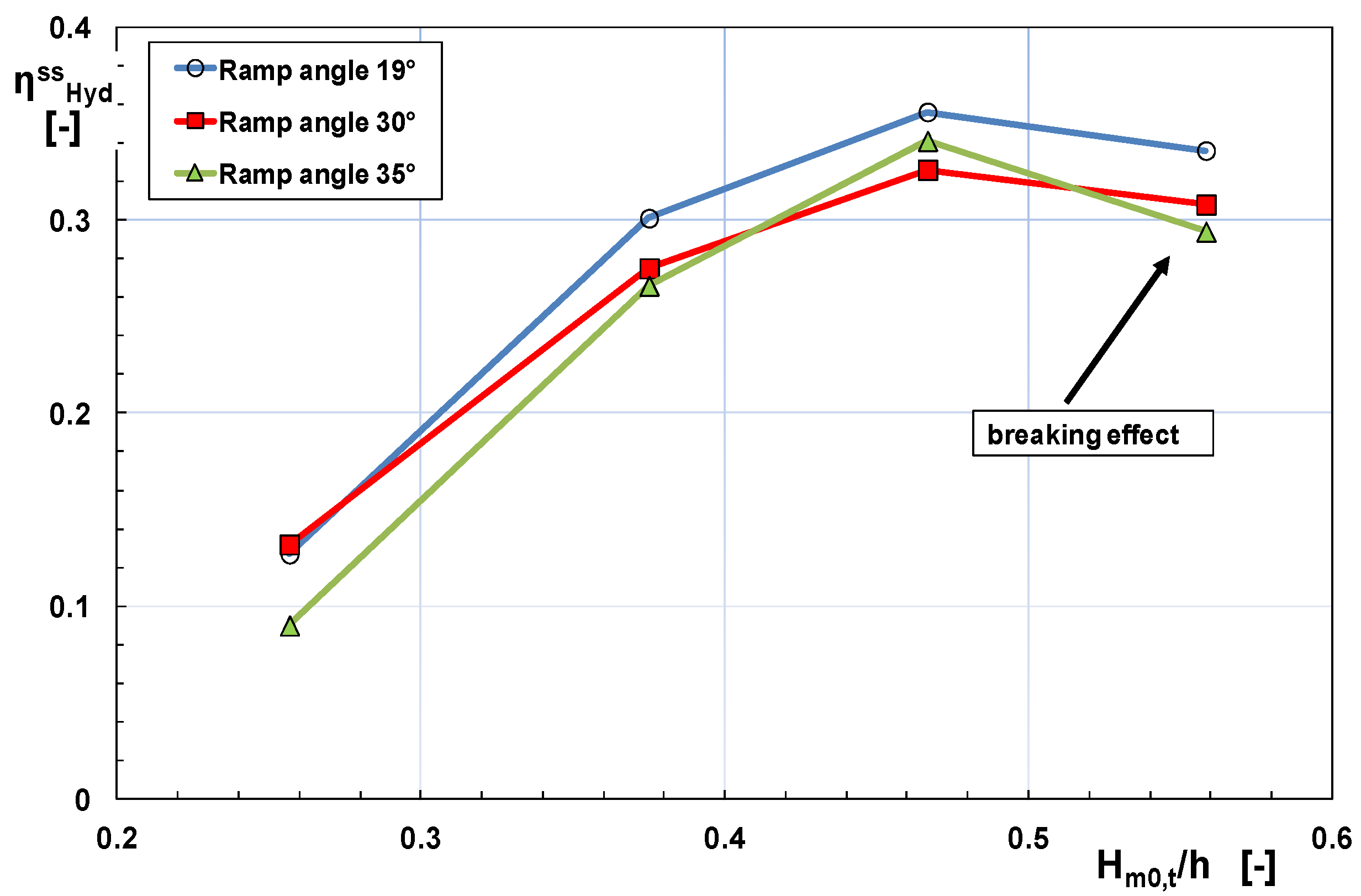

2.1.2. Effect of Wave Directionality
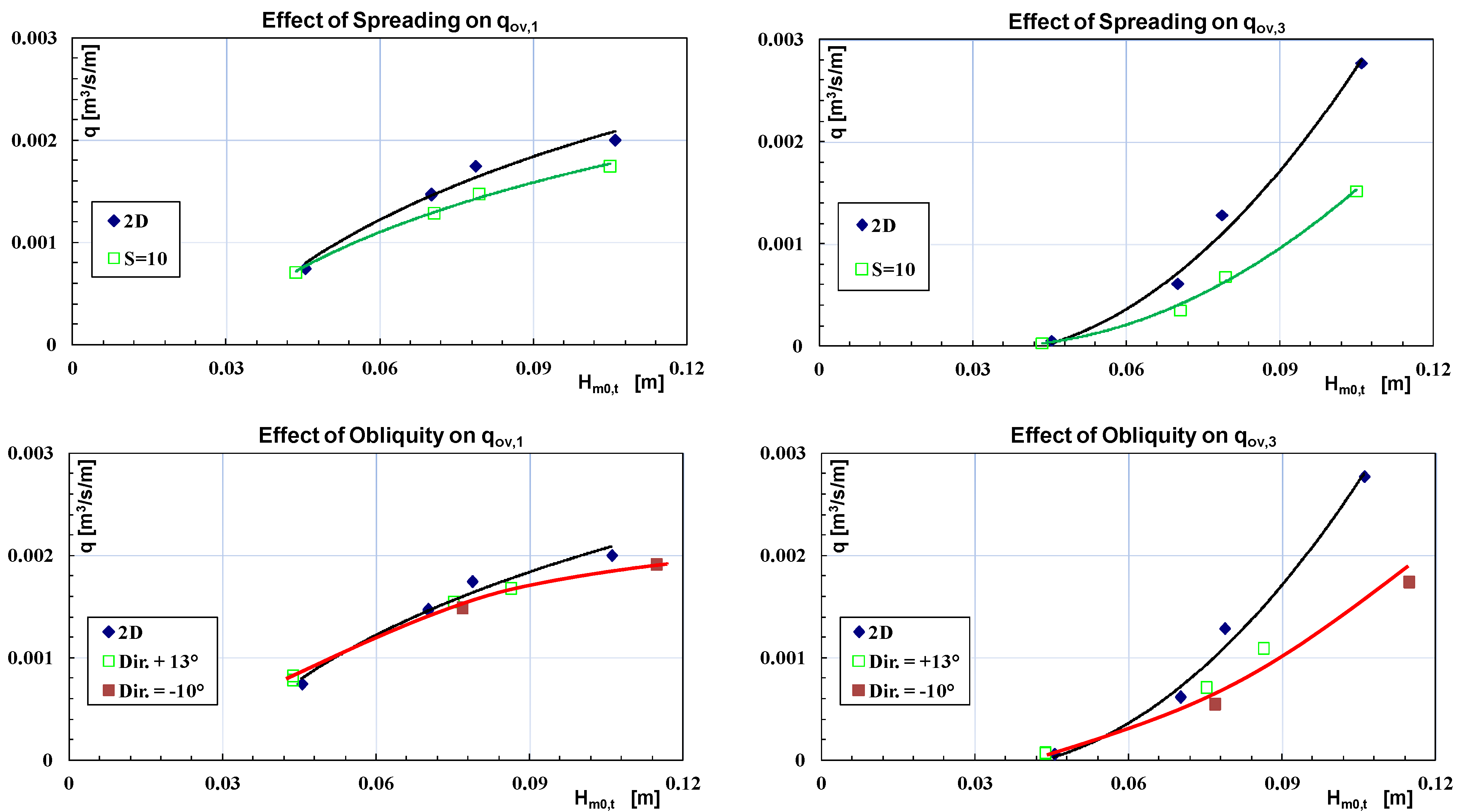
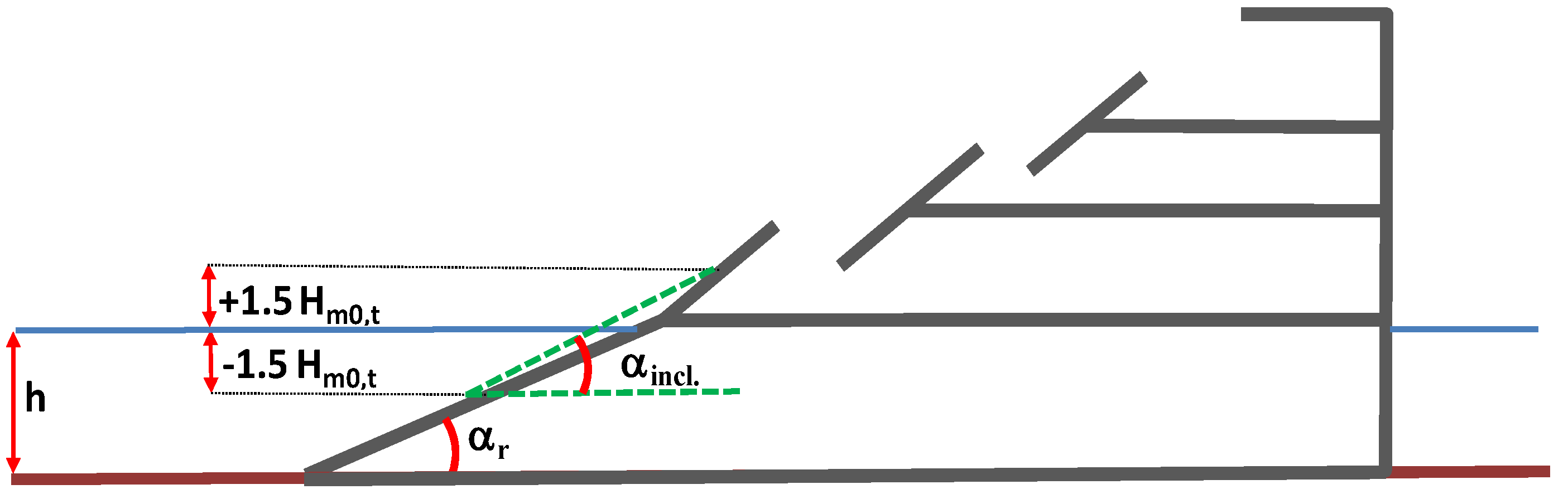
2.1.3. Design Equations

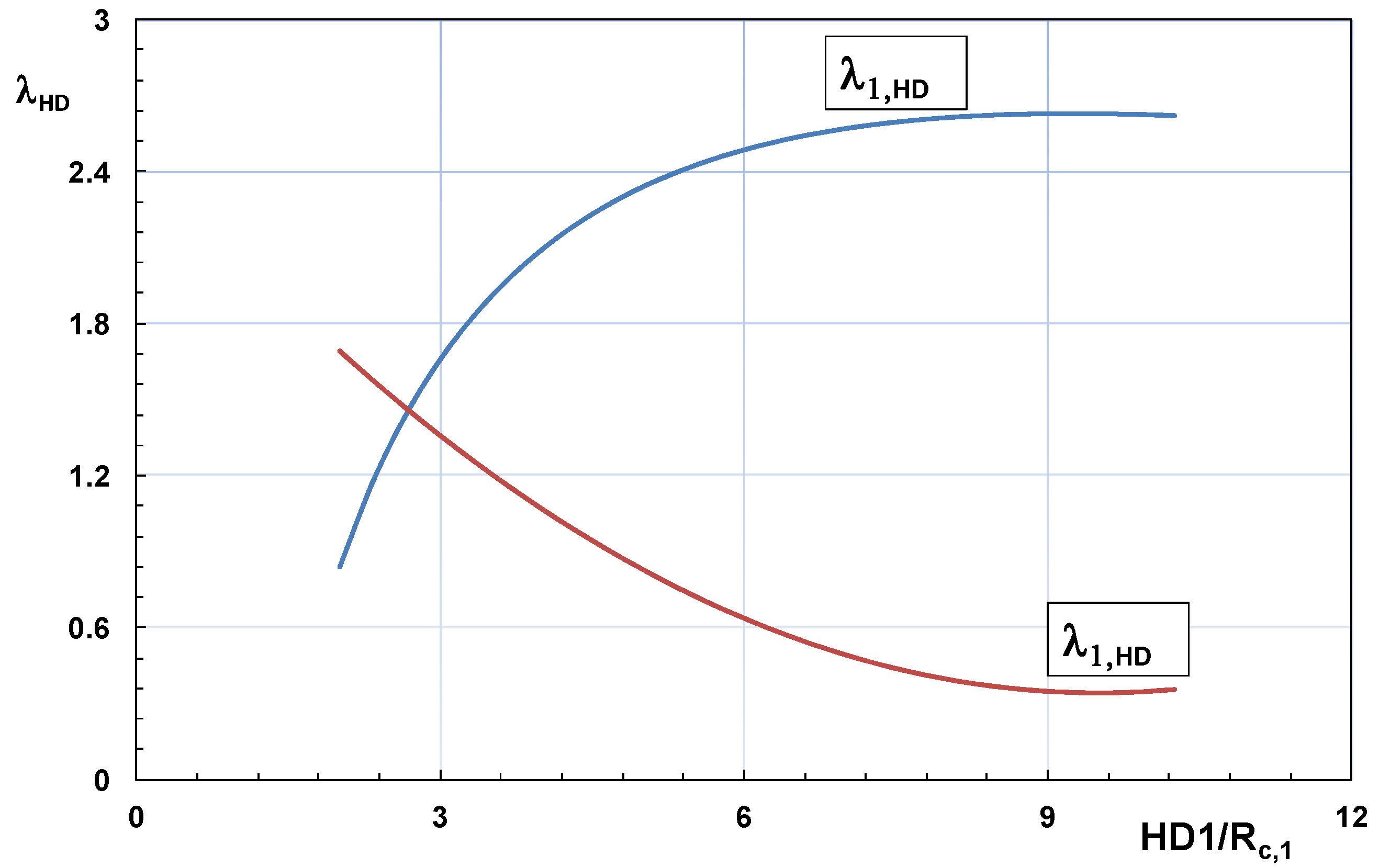
- the draught coefficient λdr given in Equation (11);
- a ramp factor λαr given by:
- a low crest factor:
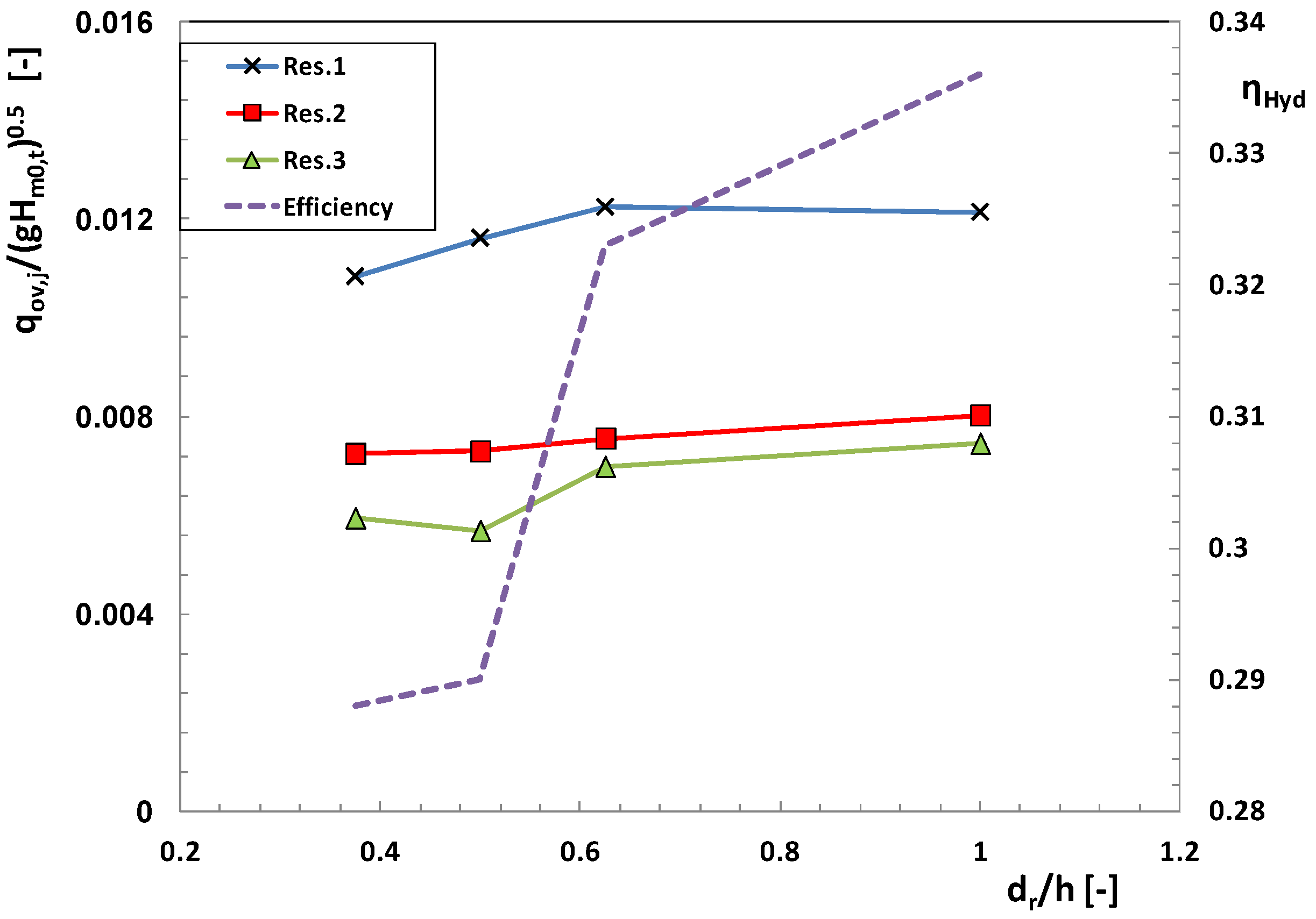
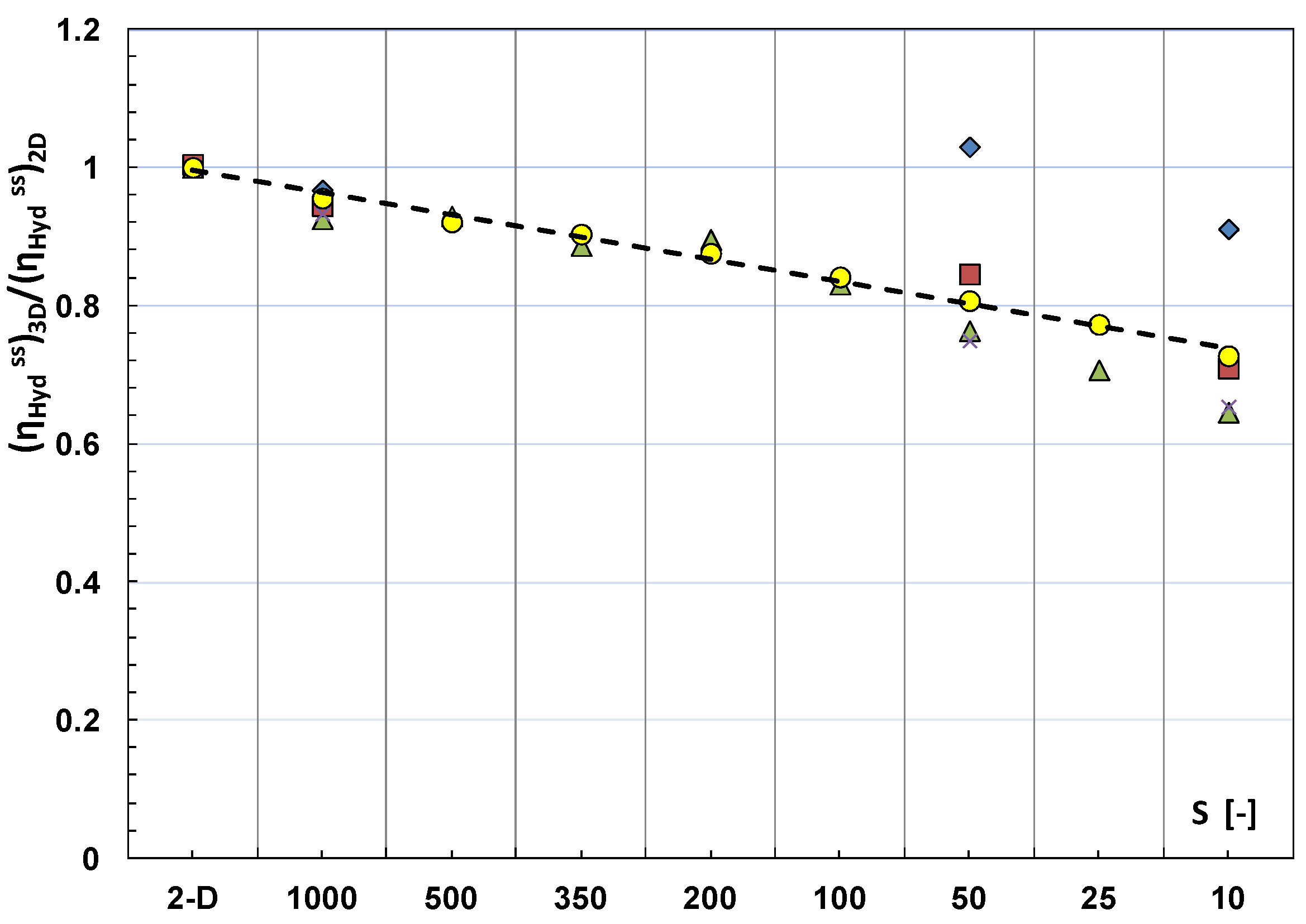
2.2. Two Further Items of the Hydraulic Design: Tide and Number of Reservoirs
2.2.1. The Role of Tide
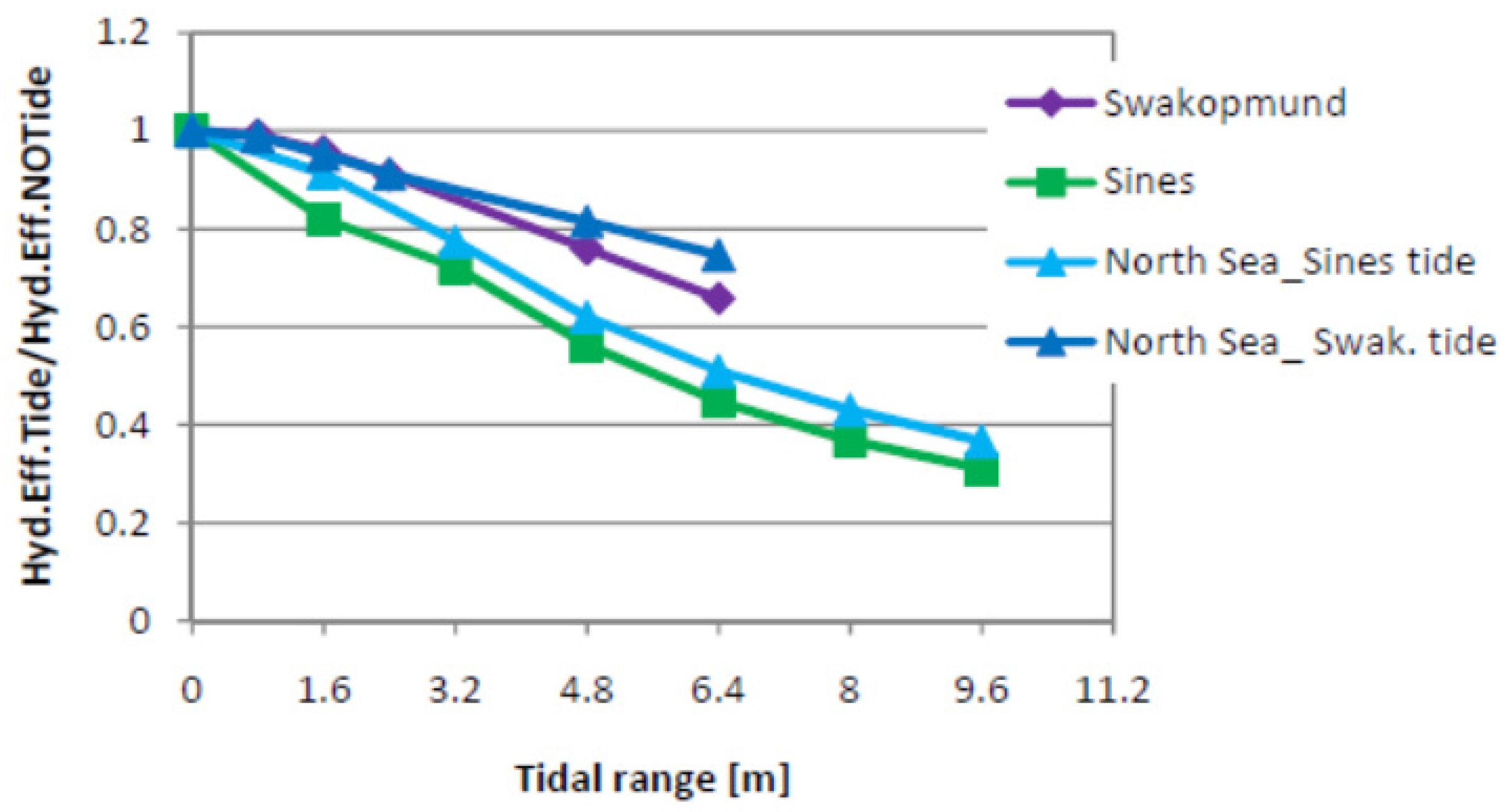
2.2.2. Adding Further Reservoirs
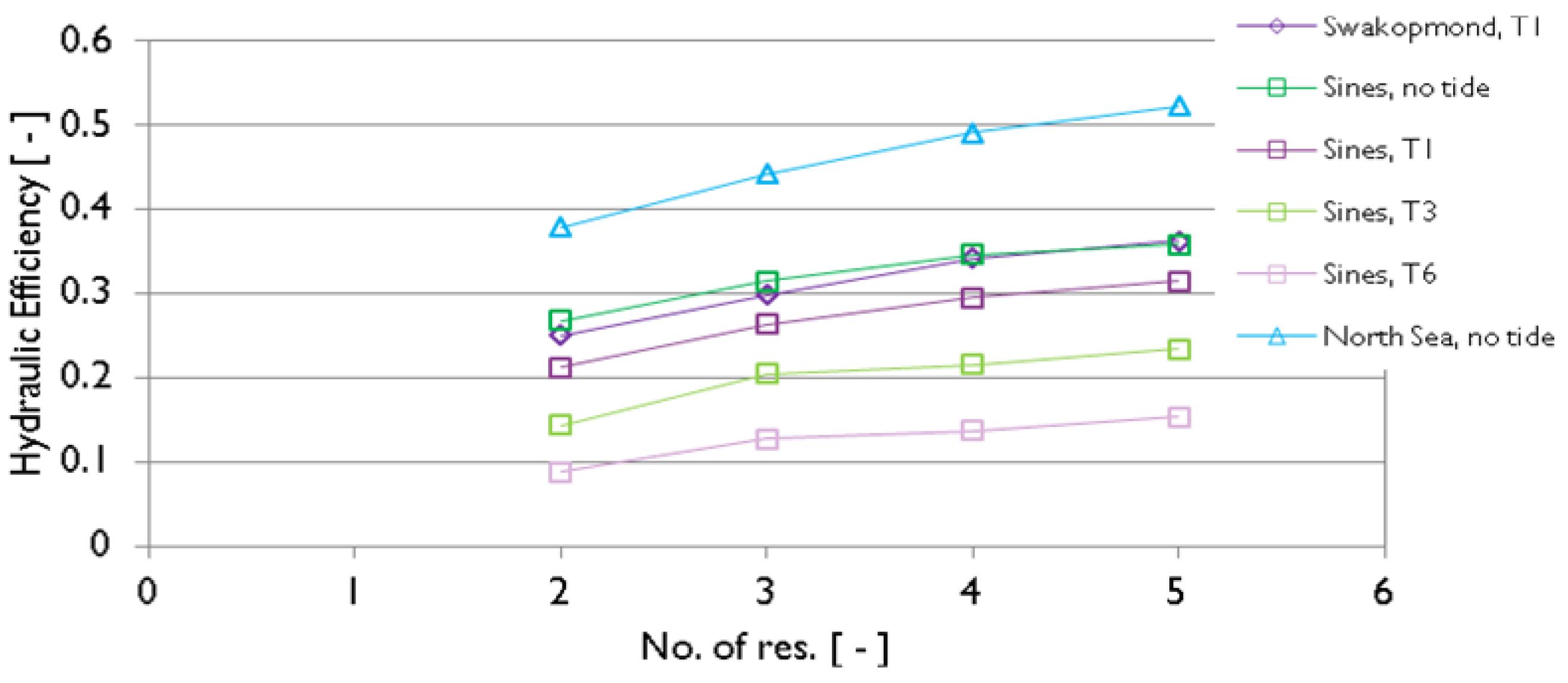
2.3. Reflection Performance
3. Structure Response
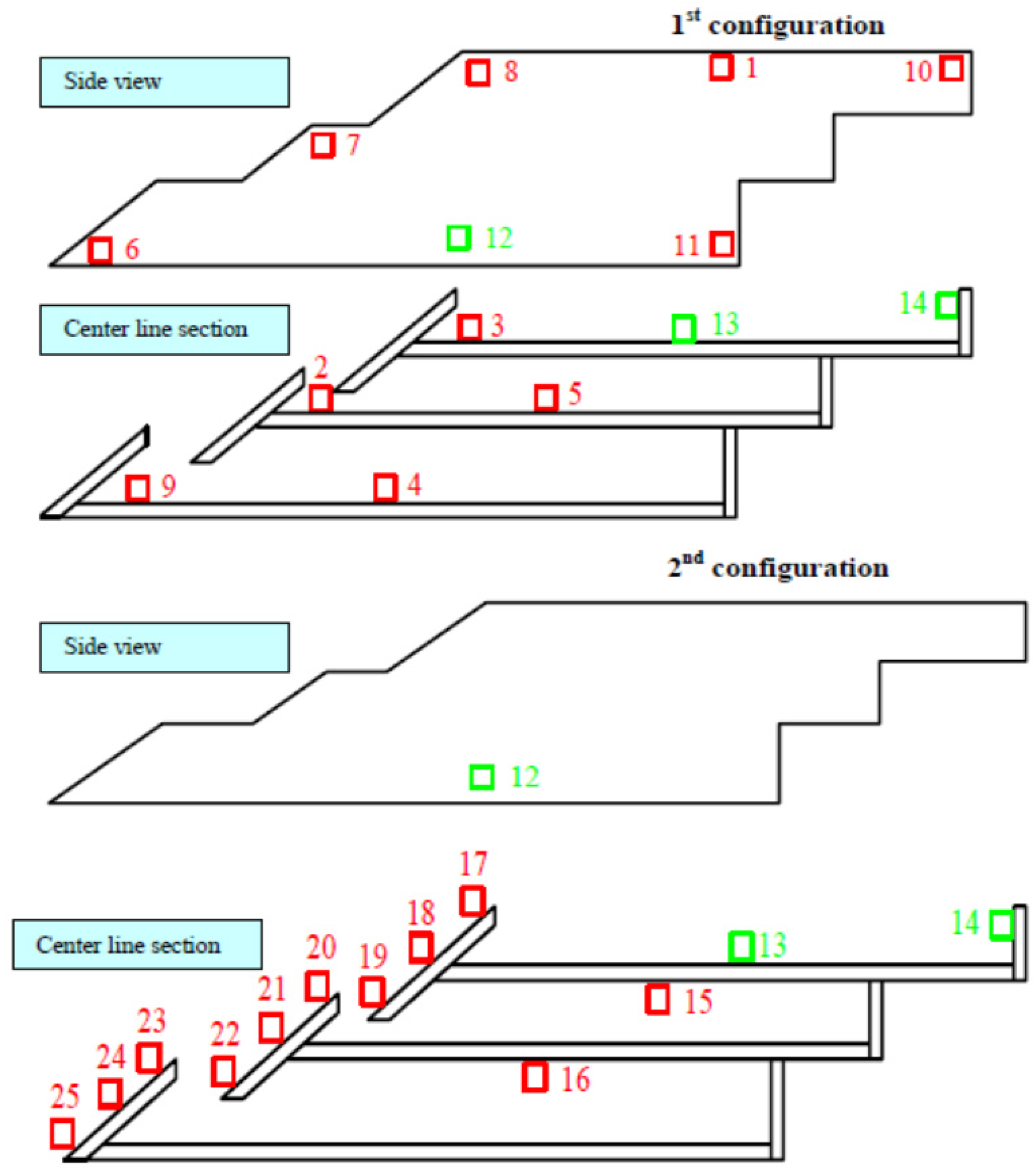
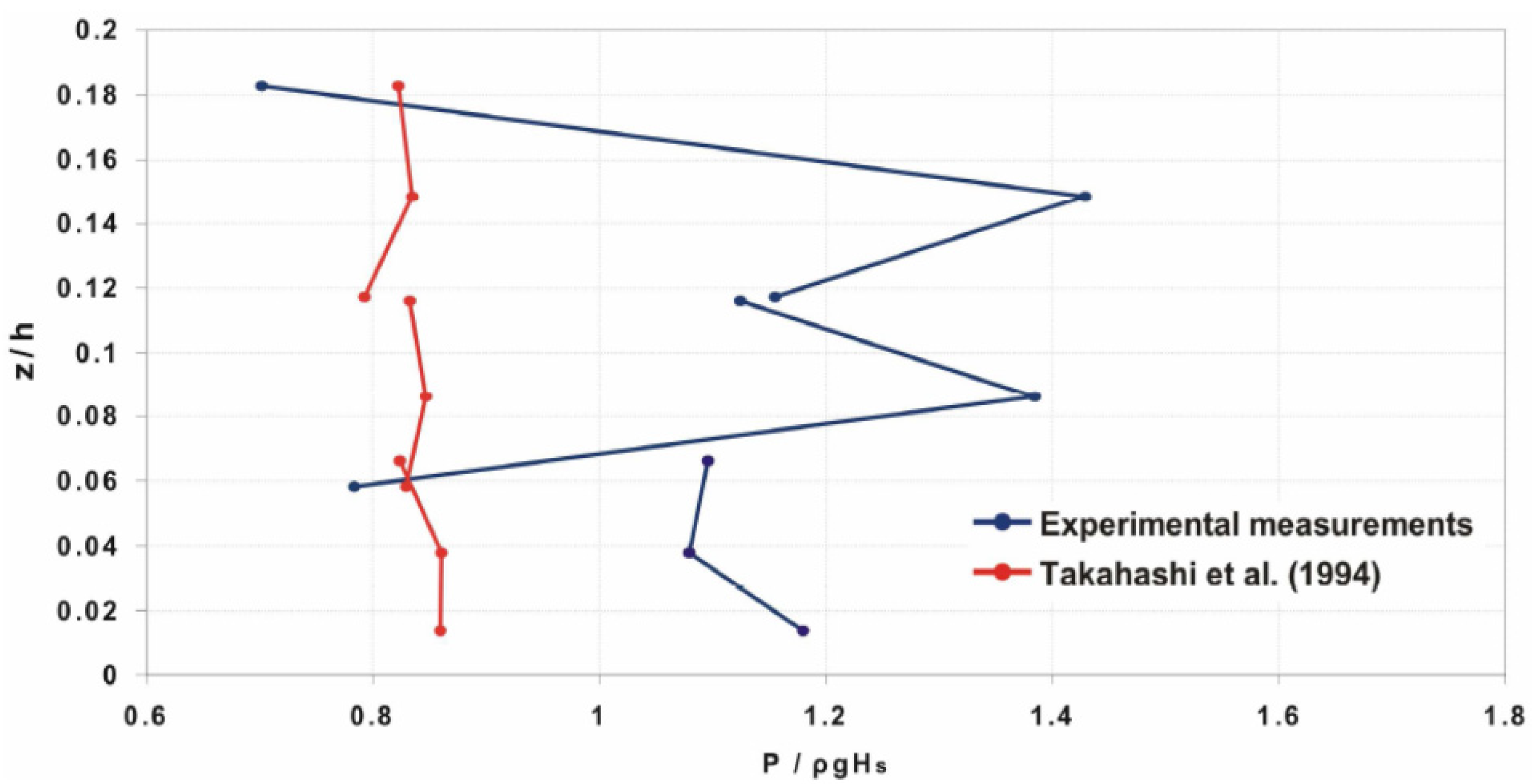
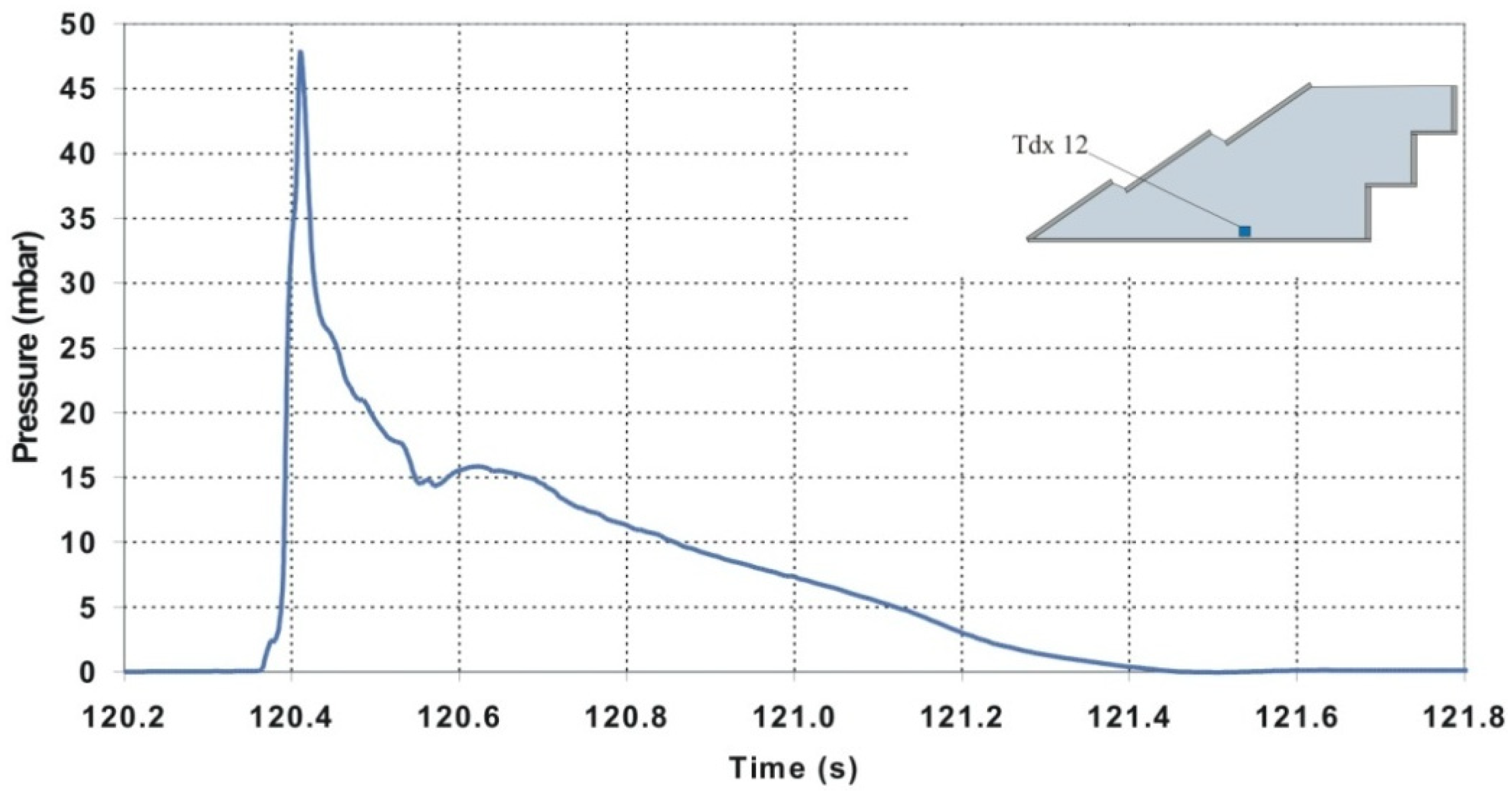
- Under front attacks, surging breakers rapidly rise along the three front plates, originating quasi-static pressure paths. The massive wave overtopping causes a water jet to hit the vertical rear wall in the upper reservoir, which has no roof (position 14 of Figure 17). Figure 18 shows the pressure chronograms at four transducers along the SSG cross section; it is clear that the slamming of the impinging jet at the position 14 induces a quasi-impulsive loading, with a rise time rather short, compared to the other positions, and a magnitude which is about twice the pressure at the front face.
- Under side attacks, the wave experiences a rotation due to refraction. At the structure, only one part of the front climbs the plates with a shape similar to the case 1 (Figure 19a); another part hits the side wall producing a partially damped plunging breaker, which again leads the pressure to get an impulsive or “quasi-impulsive” nature (Figure 20).


4. Efficiency and Energy Production
- Wave to crests, i.e., where the different waves are captured at the crest heights of the reservoirs, Rc,j (j = 1,2…n, n = number of reservoirs). During the of laboratory tests described in the previous sections, it has been measured that around 40% of the available sea state energy (Appendix I) is captured;
- Crests to reservoirs, i.e., where the potential energy relative to the specific crest heights is reduced by falling into the reservoir at a lower height. It is estimated that 75% of the energy from the previous step is maintained;
- Low head water turbines, i.e., where the water in the reservoirs is utilized by the hydraulic turbines with 90% efficiency;
- Electrical generator and electrical equipment, 95% efficiency.
5. Power Take-off

6. Feasibility Studies
- (1)
- sharing of construction costs,
- (2)
- access and therefore operation and maintenance are easier compared to an offshore situation,
- (3)
- sharing of infrastructures.
- (1)
- Recirculation of the water inside the harbor, i.e., improvement of water quality as the outlet of the turbines would be in the rear part of the breakwater,
- (2)
- Potential lower visual impact as a consequence of a lower crest level,
- (3)
- Clean electricity generation.
- (1)
- Local wave and tide climate (determines the number and size of reservoirs, in average passing from three to four reservoirs will see an increase of construction cost of 4%),
- (2)
- Design wave height (determines ballast and size of the structure),
- (3)
- Water depth (determines the construction method and overall size of the caisson).
| Annual wave energy = 15.7 kW/m | |
| Hs = 7.9 m | Hmax = 9.9 m |
| Water depth = 11.3 m | Tidal range = 1.6 (± 0.8) m |
| Capture crest levels: Rc1 = 1 m, Rc2 = 2.5 m, Rc3 = 4 m | |
| Crest level: 8 m | Base width: 28 m |
| Installed capacity: 12.8 kW/m | |
| Expected power production: 18,000 kWh/y/m | |
| Construction costs inclusive of turbines and generators: 150,700 €/m | |
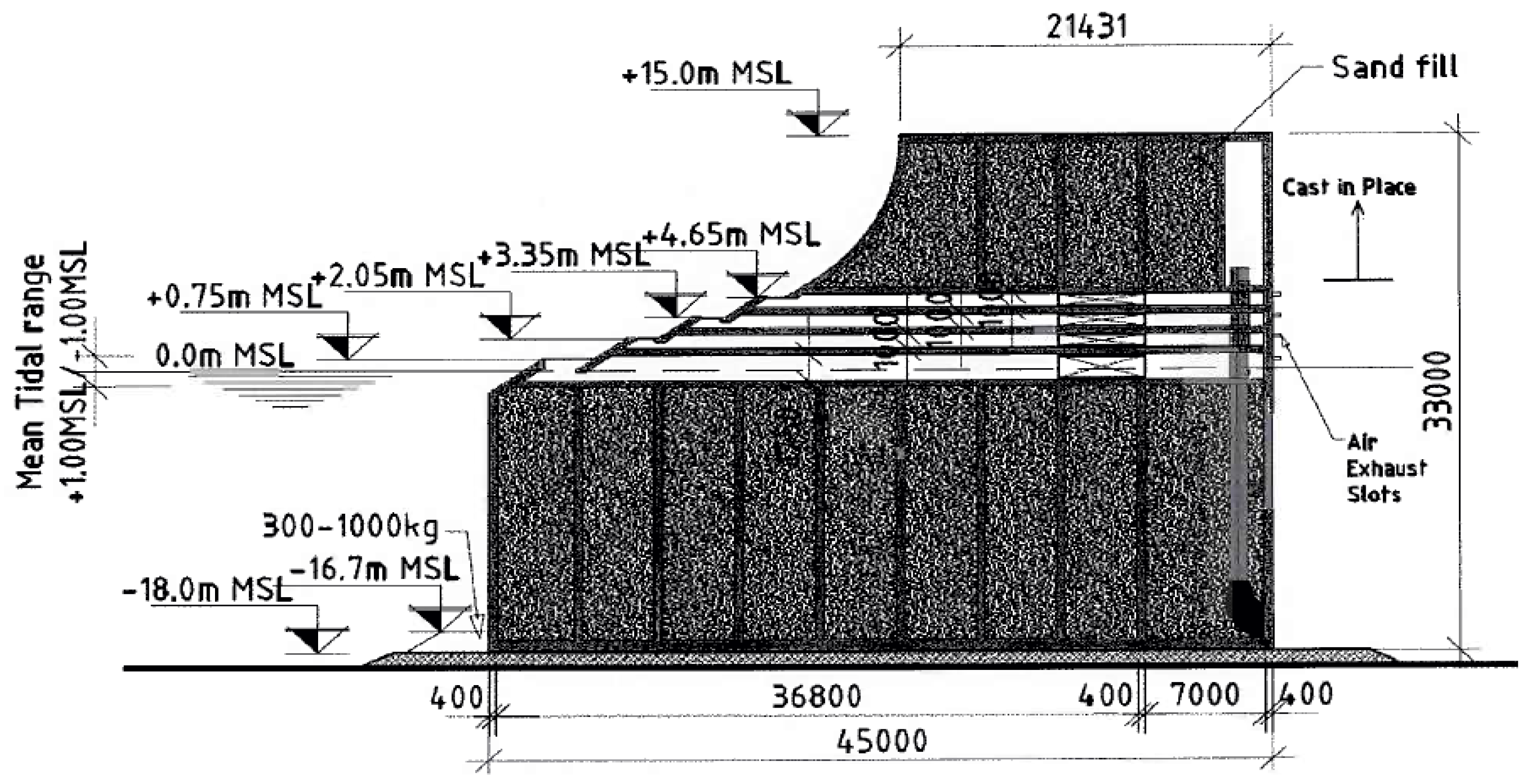
| Annual wave energy = 14.4 kW/m | |
| Hs = 13.9 m | Hmax = 18.1 m |
| Water depth = 18 m | Tidal range = 3.37 (±1.68) m |
| Capture crest levels: Rc1 = 0.75 m, Rc2 =2.05 m, Rc3 =3.35 m, Rc4 = 4.65 m | |
| Crest level: 15 m | Base width: 45 m |
| Installed capacity: 12 kW/m | |
| Expected power production: 12,000 kWh/y/m | |
| Construction costs inclusive of turbines and generators: 285,800 €/m | |

| Location | Rubble mound | Traditional caisson | SSG-breakwater | Additional costs |
|---|---|---|---|---|
| Swakopmund | 67,200 €/m | 124,500 €/m | 150,700 €/m | 83,500 €/m–26,200 €/m |
| Sines | - | 231,000 €/m | 285,800 €/m | 54,800 €/m |
7. Conclusions
Acknowledgements
Nomenclature
| A, B, C | experimental coefficients for overtopping prediction |
| Bu | Hydraulic Head (Bernoulli Trinomial) (m) |
| Cg | group velocity (m/s) |
| D | direction (relative to the orthogonal to the structure) of a single Fourier wave component in the directional power spectrum (deg.) |
| D0 | mean wave direction (deg.) |
| dr | distance between the mean water level and the lower edge of the run-up ramp (draught, (m)) |
| g | gravity acceleration (m/s2) |
| kp |
wave number associated with the peak wavelength Lp (rad/m) |
| Kr | reflection coefficient (-) |
| HD | horizontal distance between the opening of two consecutive reservoir levels |
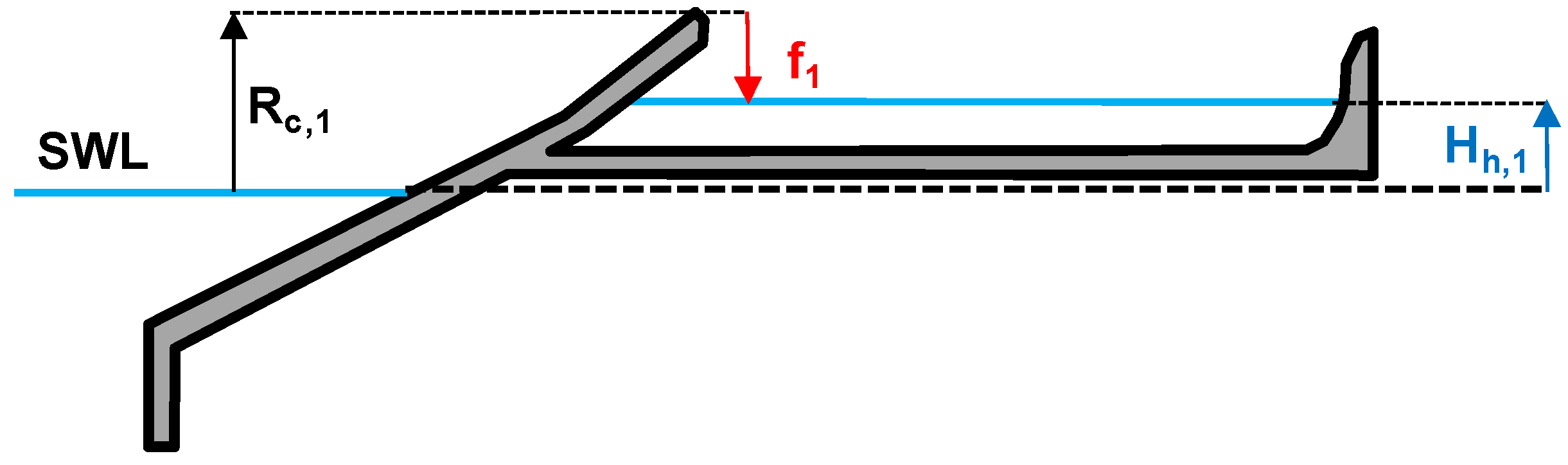
| fj | Rc,j − Hh,j. “freespace” for the j-th reservoir (m) |
| h | water depth at the toe of the structure (m) |
| Hh,j | hydraulic head at the j-th reservoir (m) |
| Hs | significant wave height (m) |
| Hm0,t | spectral estimate of Hs at toe of the structure (m) |
| Hrms | root mean square wave height (m) |
| L0e |
deep water wave length based on the mean period Te (m) |
| L0P |
deep water peak wave length (m) |
| Lp(e) |
= peak (mean) wave length at the depth of placement of the structure (m) |
| mn | nth spectral moment |
| MWL | mean water level (m) |
| Nw | number of waves in a sea state (-) |
| OTD | OverTopping Devices |
| OWC | Oscillating Water Columns |
| PHyd | mean potential power of the overtopping water per unit of width (W/m) |
| PRes | mean power in the reservoirs per unit of width (W/m) |
| PP | mean power production per unit of width (W/m) |
| Pwave | mean power of the waves per unit of width (W/m) |
| Procc. | Probability of occurrence (-) |
| qov,j | sea-state averaged overtopping discharge to the j-th reservoir per unit of width (m3/s/m) |
| Qin,j | individual overtopping discharge to the j-th reservoir per unit of width, averaged over a wave cycle (m3/s/m) |
| Qover,j | rate of overflow at the j-th reservoir (m3/s/m) |
| Qturb,j | flow through the turbine at the j-th reservoir (m3/s/m) |
| QRes,j | volume of water stored in the j-th reservoir during an unitary time-step (m3/s/m) |
| Qover-upper,j | overflow discharge at the (j + 1)-th reservoir, which is re-used at the j-th reservoir (m3/s/m) |
| Rc,j | crest height of the j-th reservoir (m) |
| s0p |
= peak wave steepness (-) |
| s0e |
= mean wave steepness (-) |
| SSG | Seawave Slot-cone Generator |
| Te | energy wave period (in (s)) calculated as
|
| Tm | time domain mean wave period (s) |
| Tp | peak wave period (s) |
| WAB | Wave Activated Bodies |
| WEC | Wave Energy Converter |
Greek Letters:
| αr | front ramp angle on the horizontal (deg.) |
| αeq. | equivalent front angle for reflection analysis |
| αincl | mean front slope in the run-up area |
| Δ | duration of a sea-state (s or hr.) |
SSG efficiency in a sea state (-). ν = (Hyd, Res, P) | |
SSG efficiency for a given wave climate (-). ν = (Hyd, Res, P) | |
turbine efficiency (-) | |
| θj | angle of the front of j-th reservoir (deg.) |
| λj | correction factors (-) |
| ξ0 |
= surf similarity parameter (-) |
| ρ | sea water density (kg/m3) |
Appendix I: Efficiency of SSG
A-I.1. The Wave Power (Mean Sea-State Power)
A-I.2. The Mean Overtopping Power in a Sea-State
A-I.3. The Mean Available Power in a Sea-State
A-I.4. Mean Produced Power
A-I.5. Sea-State and Global Efficiencies
Appendix II: The WOPSim Program
References
- Falcão, A.F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Harris, R.E.; Johanning, L.; Wolfram, J. Mooring Systems for Wave Energy Converters: A Review of Design Issues and Choices. In Proceedings of the World Renewable Energy Congress VII, Denver, CO, USA, 29 August–3 September 2004.
- Tapping the Sun and Moon. Available online: http://www.siemens.com/innovation/pool/en/publikationen/publications_pof/pof_spring_2007/wave_power_plants/pof107art51_pdf_1449430.pdf (accessed on 30 January 2012).
- The Seawave Slot-Cone Generator (SSG) Concept. Available online: http://www.waveenergy.no/WorkingPrinciple.htm (accessed on 30 January 2012).
- Harnessing Energy from Our Oceans; Pelamis Wave Energy Project Information Sheet; E.ON Climate & Renewables UK Ltd.: Coventry, UK; Available online: http://www.eon-uk.com/images/Pelamis_demonstration_project_information_sheet.pdf (accessed on 30 January 2012).
- Kofoed, J.P. Wave Overtopping of Marine Structures—Utilization of Wave Energy. Ph.D. Dissertation, Aalborg University, Aalborg, Denmark, 2002. [Google Scholar]
- Margheritini, L. R&D towards Commercialization of Sea Wave Slot Cone Generator (SSG) Overtopping Wave Energy Converter: Selected Topics in the Field of Wave Energy. Ph.D. Dissertation, Aalborg University, Aalborg, Denmark, 2009. [Google Scholar]
- Kofoed, J.P. Experimental Hydraulic Optimization the Wave Energy Converter Seawave Slot-Cone Generator; Technical Report; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2005; 1603-9874. [Google Scholar]
- Kofoed, J.P. Vertical Distribution of Wave Overtopping for Design of Multi Level Overtopping Based Wave Energy Converters. In Proceedings of the 30th International Conference on Coastal Engineering, San Diego, CA, USA, 3–8 September 2006.
- Margheritini, L.; Vicinanza, D.; Kofoed, J.P. Overtopping performance of Sea wave Slot cone Generator. In Proceedings of the ICE Conference Coasts, Marine Structures and Breakwaters, Edinburgh, UK, 2009.
- Vicinanza, D.; Frigaard, P. Wave pressure acting on a seawave slot-cone generator. Coast. Eng. 2008, 55, 553–568. [Google Scholar] [CrossRef]
- Kofoed, J.P. Model Testing of the Wave Energy Converter Seawave Slot-Cone Generator; Technical Report; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2005; 1603-9874. [Google Scholar]
- Margheritini, L.; Lander, V.; Kofoed, J.P.; Troch, P. Geometrical Optimization for Improved Power Capture of Multi-level Overtopping Based Wave Energy Converters. In Proceedings of the International Society of Offshore and Polar Engineers (ISOPE) Conference, Osaka, Japan, 21–26 June 2009.
- Margheritini, L.; Vicinanza, D.; Frigaard, P. Sea Slot Cone Generator Overtopping Performance in 3D Conditions. In Proceedings of the International Society of Offshore and Polar Engineers (ISOPE) Conference, Vancouver, Canada, 10–12 June 2008.
- De Waal, J.P.; van der Meer, J.W. Wave Runup and Overtopping on Coastal Structures. In Proceedings of 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992.
- Van der Meer, J.W.; Janssen, J.P.F.M. Wave run up and wave overtopping at dikes. In Wave Forces on Inclined and Vertical Wall Structures; Kobayashi, N., Demirbilek, Z., Eds.; American Society of Civil Engineers (ASCE) Publications: Reston, VA, USA, 1995; pp. 1–27. [Google Scholar]
- Le Méhauté, B.; Koh, R.C.Y.; Hwang, L. A systhesis of wave run-up. J. Waterw. Coast. Eng. Div. 1968, 94, 77–92. [Google Scholar]
- Franco, C.; Franco, L. Overtopping formulas for caisson breakwaters with non-breaking 3D waves. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 98–107. [Google Scholar] [CrossRef]
- Margheritini, L.; Kofoed, J.P. Parametrical Numerical Study on Breakwater SSG Application; Contract Reports by Department of Civil Engineering (DCE), Aalborg University: Aalborg, Denmark, 2008. [Google Scholar]
- Meinert, P.; Gilling, L.; Kofoed, J.P. User Manual for SSG Power Simulation 2; Technical Report; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2008; 1603-9874. [Google Scholar]
- Van der Meer, J.W.; d’Agremond, K.; Gerding, E. Toe Structure Stability of Rubble Mound Breakwaters. In Proceedings of the Advances in Coastal Structures and Breakwaters Conference; Institution of Civil Engineers, Thomas Telford Publishing: London, UK, 27–29 April 1995; pp. 308–321. [Google Scholar]
- Tanimoto, K.; Takahashi, S. Design and construction of caisson breakwaters: The Japanese experience. Coast. Eng. 1994, 22, 57–77. [Google Scholar]
- Zanuttigh, B.; Margheritini, L.; Gambles, L.; Martinelli, L. Analysis of Wave Reflection from Wave Energy Converters Installed as Breakwaters in Harbours. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC), Uppsala, Sweden, 7–10 September 2009.
- Zanuttigh, B.; van der Meer, J.W. Wave reflection from coastal structures in design conditions. Coast. Eng. 2008, 55, 771–779. [Google Scholar] [CrossRef]
- Zanuttigh, B.; van der Meer, J.W.; Lykke Andersen, J.W.; Lara, J.L; Losada, I.J. Analysis of wave reflection from structures with berms through an extensive database and 2DV numerical modelling. In Proceedings of 31st International Conference on Coastal Engineering, Hamburg, Germany, 31 August–5 September 2008.
- Salerno, D. Experimental investigation on an overtopping wave energy converter. M.Sc. Thesis, University of Naples “Federico II”, Napoli, Italy, 2011. [Google Scholar]
- Vicinanza, D. Impact pressure/force on vertical and composite breakwaters under breaking waves. Ph.D. Dissertation, University of Naples Federico II, Napoli, Italy, 1997. [Google Scholar]
- Takahashi, S.; Hosoyamada, S.; Yamamoto, S. Hydrodynamic Characteristics of Sloping Top Caissions. In Proceedings of the International Conference on Hydro-Technical Engineering for Port and Harbour Construction; Port and Harbour Research Institute: Yokosuka, Japan, 19–21 October 1994. [Google Scholar]
- Vicinanza, D.; Ciardulli, F.; Buccino, M.; Calabrese, M.; Kofoed, J.P. Wave loadings acting on an innovative breakwaters for energy production. J. Coast. Res. 2011, 64, 608–612. [Google Scholar]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific: Singapore, 1993. [Google Scholar]
- Cuomo, G.; Allsop, N.W.H.; Takahashi, S. Scaling wave impact pressures on vertical walls. Coast. Eng. 2010, 57, 604–609. [Google Scholar] [CrossRef]
- Margheritini, L.; Vicinanza, D.; Frigaard, P. SSG wave energy converter: Design, reliability and hydraulic performance of an innovative overtopping device. J. Renew. Energy 2009, 34, 1371–1380. [Google Scholar] [CrossRef]
- Wave Energy Converters for Electrical Production, Second University of Naples Founded Project PRIST 2007. Available online: http://www.italywavenergy.it (accessed on 30 January 2012).
- Franco, L.; de Gerloni, M.; van der Meer, J.W. Wave Overtopping on Vertical and Composite Breakwaters. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vicinanza, D.; Margheritini, L.; Kofoed, J.P.; Buccino, M. The SSG Wave Energy Converter: Performance, Status and Recent Developments. Energies 2012, 5, 193-226. https://doi.org/10.3390/en5020193
Vicinanza D, Margheritini L, Kofoed JP, Buccino M. The SSG Wave Energy Converter: Performance, Status and Recent Developments. Energies. 2012; 5(2):193-226. https://doi.org/10.3390/en5020193
Chicago/Turabian StyleVicinanza, Diego, Lucia Margheritini, Jens Peter Kofoed, and Mariano Buccino. 2012. "The SSG Wave Energy Converter: Performance, Status and Recent Developments" Energies 5, no. 2: 193-226. https://doi.org/10.3390/en5020193
APA StyleVicinanza, D., Margheritini, L., Kofoed, J. P., & Buccino, M. (2012). The SSG Wave Energy Converter: Performance, Status and Recent Developments. Energies, 5(2), 193-226. https://doi.org/10.3390/en5020193