Abstract
The Sea-wave Slot-cone Generator (SSG) is a Wave Energy Converter based on the wave overtopping principle; it employs several reservoirs placed on top of each other, in which the energy of incoming waves is stored as potential energy. Then, the captured water runs through turbines for electricity production. The system works under a wide spectrum of different wave conditions, giving a high overall efficiency. It can be suitable for shoreline and breakwater applications and presents particular advantages, such as sharing structure costs, availability of grid connection and recirculation of water inside the harbor, as the outlet of the turbines is on the rear part of the system. Recently, plans for the SSG pilot installations are in progress at the Svaaheia site (Norway), the port of Hanstholm (Denmark) and the port of Garibaldi (Oregon, USA). In the last-mentioned two projects, the Sea-wave Slot-cone Generator technology is integrated into the outer harbor breakwater and jetty reconstruction projects. In the last years extensive studies have been performed on the hydraulic and the structural response of this converter, with the aim of optimizing the design process. The investigations have been conducted by physical model tests and numerical simulations and many results have been published on both conference proceedings and journals. The main scope of this paper is reviewing the most significant findings, to provide the reader with an organic overview on the present status of knowledge.
1. Introduction
Ocean energy is a predictable and abundant source of energy with the ability to contribute significantly to the electricity demand of the world. Whether this resource can be exploited economically will depend on the efficiency reached by the wave energy conversion facilities, development of which is still in an immature phase. The number of concepts for Wave Energy Converters (WECs) is very large. Over 1000 WECs are patented worldwide and they can be classified within the following three basic types [1,2]:
- -
- Oscillating Water Columns (OWC; Figure 1a) can be described as a caisson breakwater with a gap on the seaside face, which encloses a mass of water. Waves cause the water to rise and fall and this alternately compresses and depressurizes an air column. The energy is extracted from the oscillating air flow by using a Wells turbine;
- -
- OverTopping Devices (OTD; Figure 1b) use a sloping plate that leads the waves to overtop into a reservoir located immediately behind it. The energy is extracted via low head turbines, using the difference in water levels between the reservoir and the average sea water level;
- -
- In the Wave Activated Bodies (WAB; Figure 1c), waves cause the body parts of a device to oscillate relative to each other; alternatively, the whole body may oscillate against a fixed reference. The oscillatory motion can be heave, pitch or roll. Hydraulic systems are generally employed to compress oil, air or water, which is then used to drive a generator.
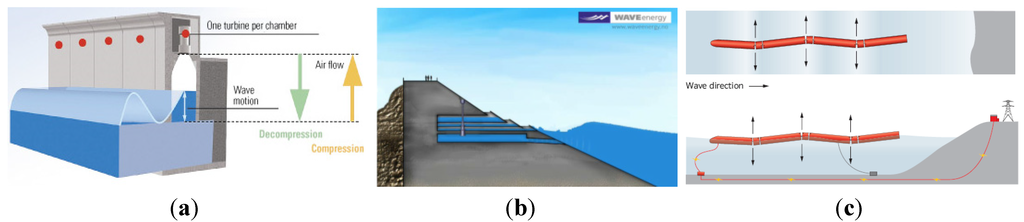
Figure 1.
Examples of WEC types: (a) OWC with courtesy of Voith Siemens Hydro Wavegen [3], (b) OTD with courtesy of WAVEenergy AS [4], (c) WAB with courtesy of Pelamis Wave Power Ltd. [5].
These systems can be installed at the shoreline, nearshore or offshore; both OWCs and OTDs can be designed as caisson breakwaters. Today, the largest problem in harvesting wave energy is ensuring the reliability of the technology and bringing the costs down.
The Seawave Slot-cone Generator (SSG) concept was developed by WAVEenergy (Stavanger, Norway). The SSG is an OTD utilizing a number of reservoirs placed on top of each other, in which the energy of the incoming waves is stored as potential energy (Figure 2).
The water captured in the reservoirs then runs through the multi-stage turbine for electricity production. The use of multiple reservoirs results in a higher overall efficiency compared to a single reservoir structure [6,7,8,9,10]. The SSG technology can be particularly suitable for shoreline and breakwater applications; it presents the following advantages:
- –
- Sharing structure costs;
- –
- Availability of grid connections and infrastructures;
- –
- Recirculation of water inside the harbors as the outlet of the turbines is on the rear part of the system;
- –
- Easy installation and maintenance;
- –
- No deep-water moorings or long lengths of underwater electrical cable.
In practice, an SSG shoreline/nearshore system would experience a slightly less powerful wave regime than offshore systems, but this could be partially compensated by the natural energy concentration due to wave refraction and/or diffraction.

Figure 2.
Artistic representation of a 3-level SSG with multistage turbine.
The system has ondergone six years of R&D, at the Department of Civil Engineering of Aalborg University (Denmark). The research has focused mainly on the maximization of wave power capturing (“hydraulic response” [6,8,9]) and on the nature and magnitude of wave loadings (“structural response”, [11]). However, attention has also been drawn at investigating the technical and economical problems related to the possible integration of SSG in the body of traditional structures for harbor protection.
The main results of the work are reviewed in the following sections, with the aim of providing the reader with an organic overview on the present status of knowledge. The paper is organized as follows: Section 2 deals with the “hydraulic response”; in this field, a good deal of experimental studies have been performed and, accordingly, the status of the research is relatively advanced. Tentative design formulae are given in the subsection 2.1.3 and subsection 2.3 with respect to the mean overtopping discharge and the wave reflection rate.
The results on the “structural response” are still of a qualitative nature; they are described in Section 3. After some discussion on the efficiency of energy production (Section 4) and on the power take off mechanism (Section 5), two previously unpublished feasibility studies are presented in Section 6, where SSG is used as a part of the new structures planned to defend the harbors of Swakopmund (Namibia) and Sines (Portugal).
2. The Hydraulic Response
2.1. Overtopping Performance
The outer geometry of a SSG (Figure 3) should be designed to optimize its hydraulic efficiency,
, i.e., to maximize the captured energy in a given sea environment (wave and tide climates). A detailed discussion on the efficiency of a SSG device is given in the Appendix I at the end of the paper.
However, it is readily understood that the efficiency of this kind of converter (however it may be defined) is primarily ruled by the amount of overtopping water which enters the reservoirs. The ratio between the volume of water captured in a sea state by the j-th reservoir and the duration of the sea state, say Δ, is called “mean overtopping discharge”, qov,j. The latter represents a leading variable in the functional design of SSG as well as of many other maritime structures.
With the purpose of establishing reliable equations to describe how wave tide and structure parameters might affect qov,j, extensive experimental work has been performed between 2004 and 2007, at the Hydraulic and Coastal Engineering Laboratory of the Department of Civil Engineering of Aalborg University.
Physical model tests have been conducted with random waves, both under 2D and 3D conditions. Model length-scale ratios (SR hereafter) have been ranged from 15 to 60. In 2D tests [8,9,12,13], 30 different geometries have been examined; this allowed investigating (referring to Figure 3) the influence of:
- √
- Reservoir crest levels, Rcj
- √
- Ramp angle, αr;
- √
- Ramp draught, dr;
- √
- Front angles, θj;
- √
- Horizontal distance between the reservoir crests, HDj beside the role of wave height and period.
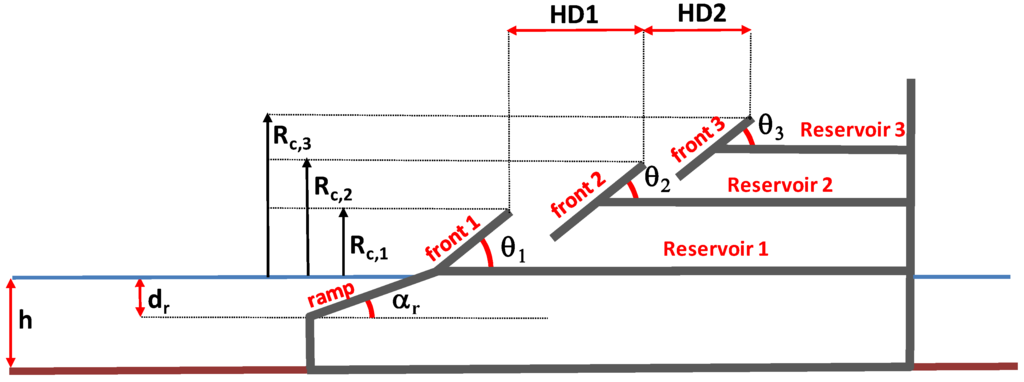
Figure 3.
Definition sketch for a 3-level structure.
The effect of directional seas has subsequently investigated separately in [14]. However, it seems useful to underline that all those tests were performed considering a pilot plant to be deployed in the island of Kvitsøy, Norway; accordingly most of knowledge about the overtopping performance comes from the analysis of a single case study.
2.1.1. 2D Waves
Figure 4 shows how the spectral significant wave height at the toe of the structure, Hm0,t, affects qov,j in a system of three reservoirs [12]. Experimental points refer to different SSG layouts having the same crest levels Rc,j; incident waves have a peak wave steepness, s0p:
nearly constant and close to 0.02.
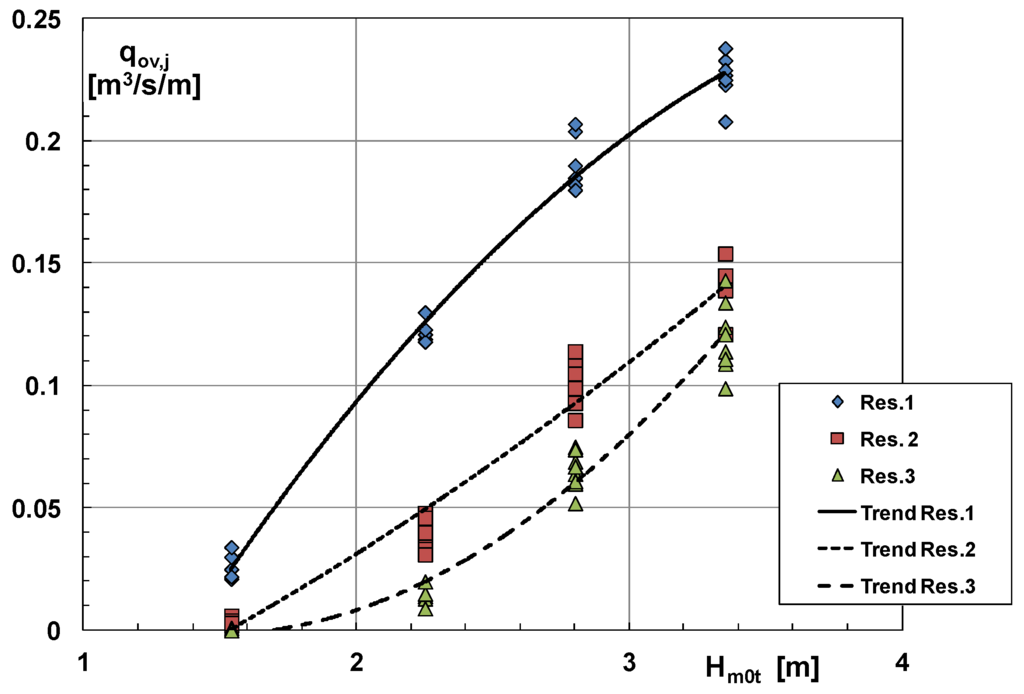
Figure 4.
Overtopping discharge vs. wave height. Redrawn from [12]. Data at prototype scale [SR 1:15].
The graph clearly indicates qov,j to increase with Hm0,t. However, the trend-lines have different shapes: for the lowest reservoir, Res.1, the curve is convex, while for the highest one, Res.3, the flow rate seems to increase, on average, more than linearly. It is of interest that similar trends have also been observed under 3D conditions [14]. The reason of this behavior is rather uncertain: for reservoirs 1 and 2, the distance between the lower and the upper front forms a gap which seems to set an upper limit to the entering volume flux. In other words the presence of the fronts seems to cut the amount of water the lower reservoirs can capture. In the limit, an asymptotic value of qov,1 and qov,2 might be attained when Hm0,t becomes very large. This wouldn’t happen for the highest reservoir, Res.3, as there is no structure above it (Figure 3). More details on this point can be found in [8]. Figure 5 displays the effect of the peak wave steepness.
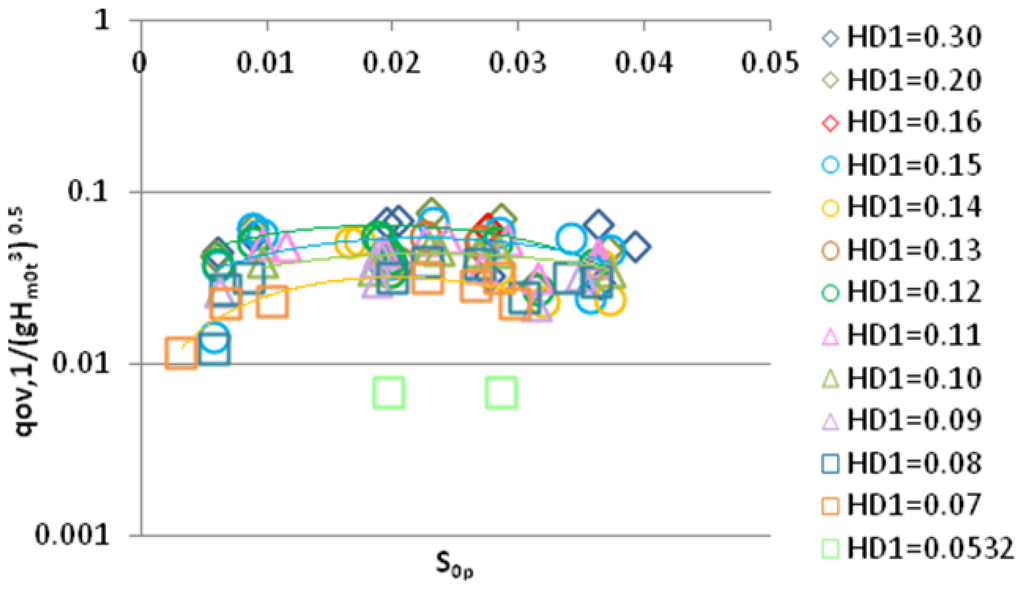
Figure 5.
Effect of peak wave steepness on the overtopping discharge [13]. SR = 1:30.
The graph refers to the lower reservoir in a two element device, with the front plates (ramp and reservoir fronts) inclined by 35° with respect to the horizontal [13]. Experimental points differ by the value of HD1, i.e., the horizontal distance between the first and the second reservoir crest. The mean discharge, qov,1, is made non-dimensional by the significant wave height; all the incident waves were driven by mean JONSWAP spectra.
It seems wave steepness plays a secondary role in the overtopping process, although from the experimental data a slight parabolic trend might be recognizable, with a maximum around 0.022. A similar behavior has been observed for the other reservoir. This result is not surprising given the front face of the structure is generally designed steep enough (35° in this case) to ensure the occurrence of slightly breaking surging waves. Indeed this is among the scopes of the functional design of SSG in order to limit power dissipation by breaking. On the other hand, it has long been known that under surging breakers wave steepness has little influence on in the run-up process [15] and, accordingly, on wave overtopping [16].
As mentioned earlier, 2D model tests used 30 different geometries to investigate the role of many parameters. It is obvious that the primary “geometric” variable for wave overtopping is the front freeboard Rc. A great deal of literature studies (e.g., [15,16]) have revealed that the mean overtopping discharge reduces more than linearly when the height of crest increases; moreover, the rate of reduction increases with increasing wave height. This is partly shown in the top panel of Figure 6; the latter reports the data from two structures where the sole difference is in the height of the lowest reservoir (Rc,1 = 2.25 m in the structure “D” and 1.5 m in the structure “E”). Note that the distance between the curves representing qov,1 increases with wave height. At the same time, the overtopping discharge in the other reservoirs remains basically the same. However it is clear that any reduction of crest freeboard reduces the hydraulic head of the entering flows, besides increasing the discharge. Consequently, its effect in terms of hydraulic efficiency derives from a balance between those two variables (see Appendix I).
This is displayed in the lower panel of Figure 6, where for high waves the efficiency of the two structures seems to tend to the same value, although qov,1 in “E” is nearly twice than in “D” (upper panel). The reason why this would occur is due to the fact that for high Hm0,t the power related to the upper reservoirs should tend to dominate the value of the overall efficiency, because the amount water they capture becomes large and with a high hydraulic head.
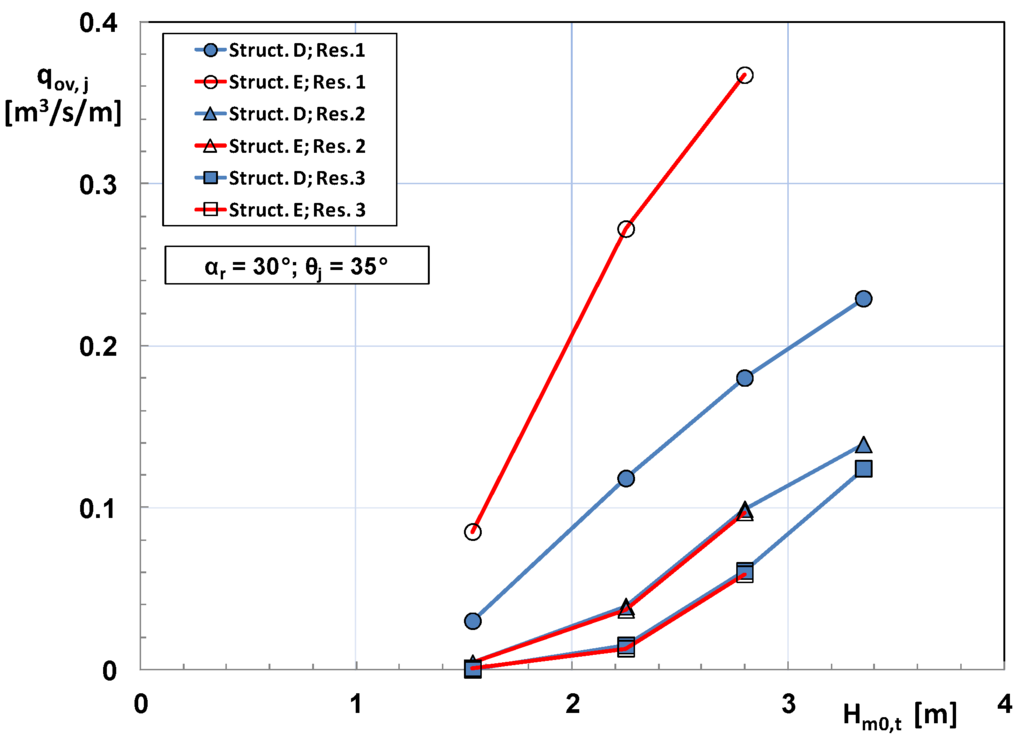
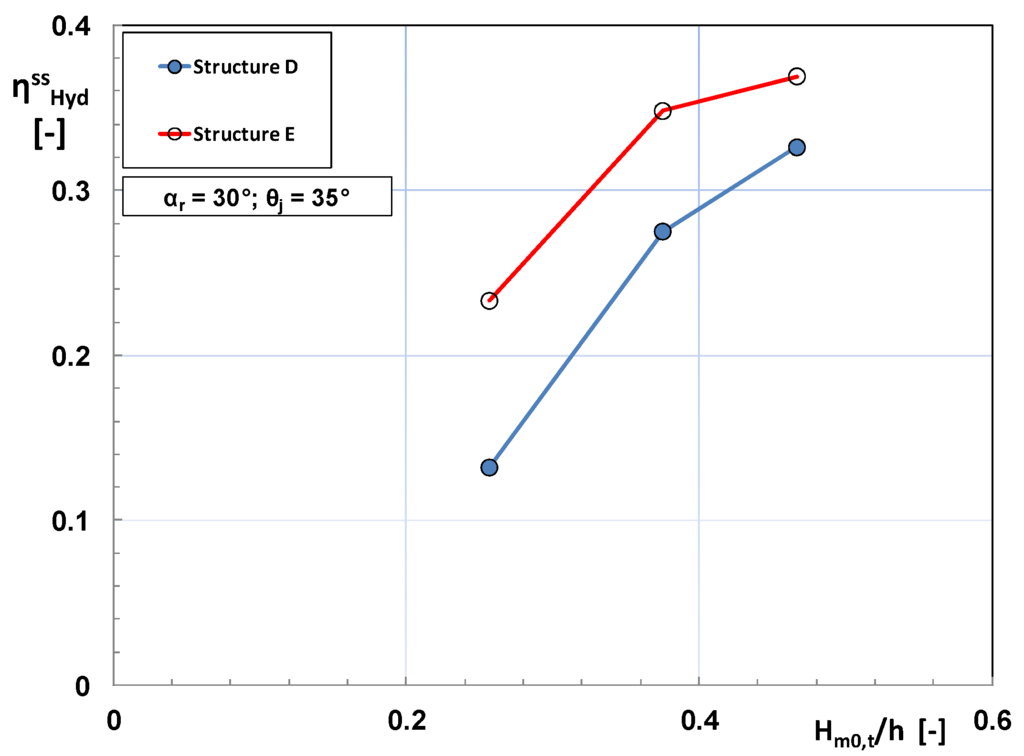
Figure 6.
Top panel: Effect of the reservoir crest on wave overtopping. Lower panel: Effect of the reservoir crest on the sea state hydraulic efficiency. Data in prototype scale [SR = 1:15].
Figure 7 shows the effect of cutting the ramp at a depth dr below the mean water level (see Figure 3 for reference). Data are presented for a single sea state (Hm0,t = 3.5 m, Te = 11.66 s; SR = 1:15) and refer to four structures, which are identical (three reservoirs) but for the value of the draught.
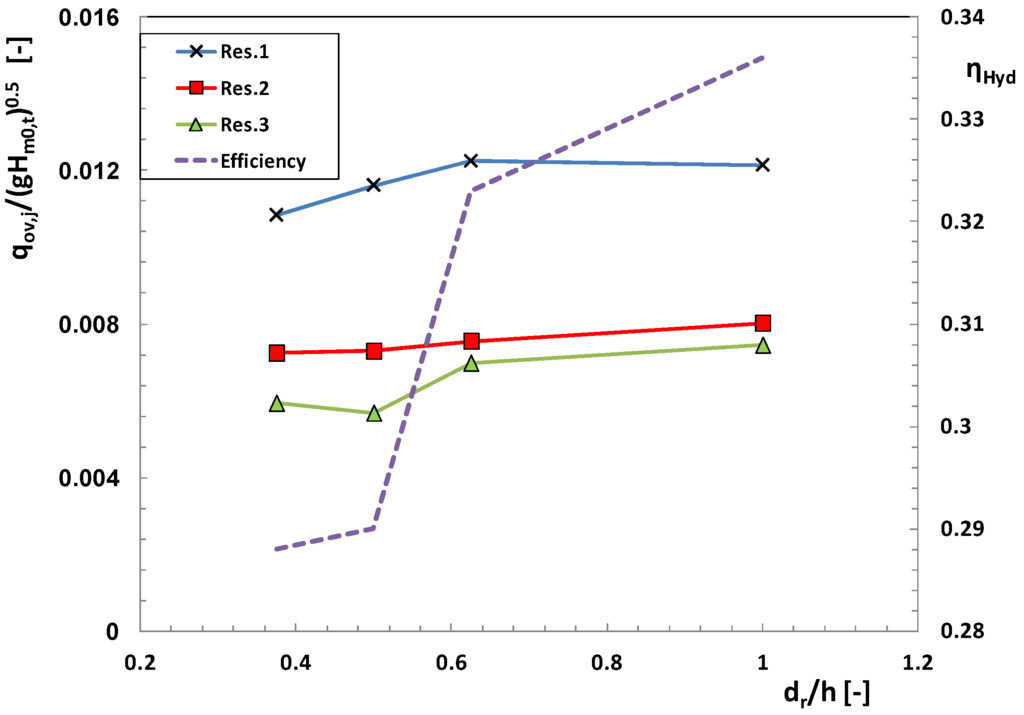
Figure 7.
Effect of the draught on the overtopping rate and on the hydraulic efficiency; [SR = 1:15].
The overtopping rate generally tends to grow with increasing draught. This should be due to the fact that the vertical step reflects back a part of the incoming wave, which will be not involved in the run-up process. The maximum influx is obtained with no vertical front (dr/h = 1), apart from the lowest reservoir, where a constant value seems to be reached between dr/h = 0.625 and dr/h = 1. The dotted line in the graph represents the hydraulic efficiency; a gain of 5% is progressively achieved going from dr/h = 0.375 to dr/h = 1.
The role of the ramp angle, αr, is explained in Figure 8. To facilitate the comprehension, data are presented as (sea state) hydraulic efficiency vs. wave height to depth ratio; in the graph three structure layouts which differ only by αr have been considered, being all the other parameters the same. Accordingly, the results depend uniquely on the overtopping response. Note that all the curves show an efficiency reduction at Hs/h = 0.56, due to some breaking occurrence on the foreshore. The graph suggests 19° is slightly better performing (maximum gain about 4%), while little difference is detected, on average, between 30° and 35°.
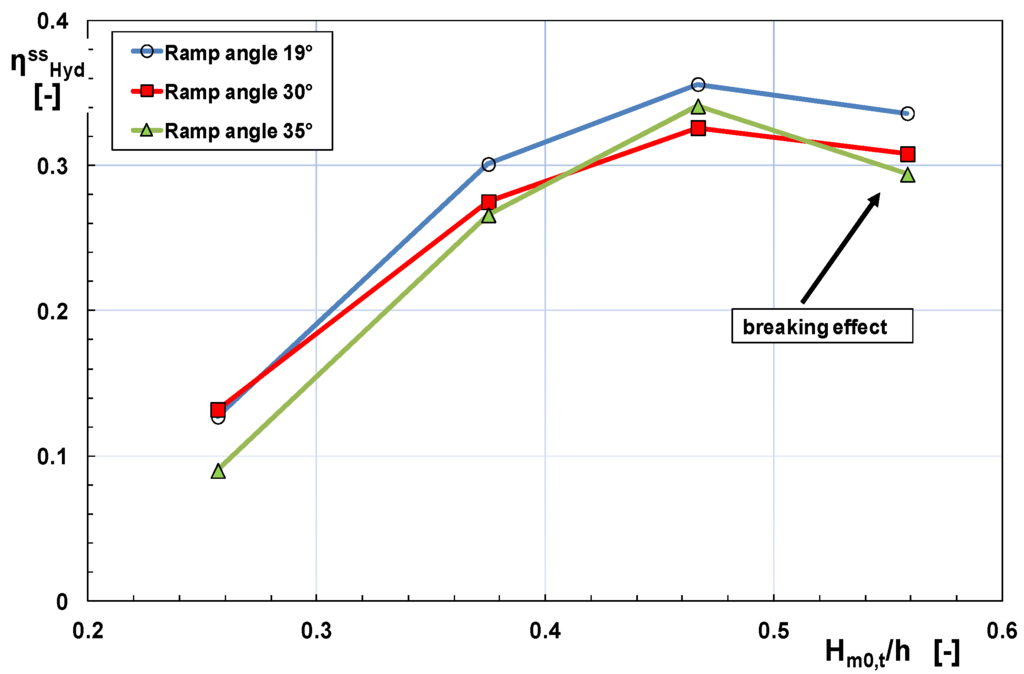
Figure 8.
The effect of the outer ramp angle αr on the hydraulic efficiency [12] (SR = 1:15).
However it has been reasoned that, in general, a ramp angle as slight as 19° could lead the steepest waves to collapse as plunging breakers. This would lead to reduced run-up height and increase the energy losses. Accordingly, an optimal value of the front ramp angle around 35° has been tentatively suggested, in spite of the specific experimental observation, with the aim to render the wave breaking occurrence less probable. This also agrees with the findings in the literature on wave run-up and overtopping (e.g., [6,17]). Following a similar reasoning the use of the same angle for the fronts of the reservoir (θj = 35°; j = 1,…,n) has been proposed.
The effect of the horizontal distance between the crests of the fronts has been studied in [13] for a two reservoirs system. Accordingly, the results shown in the following refer only to HD1 (Figure 3). The tested structures had no vertical front in the ramp (dr/h = 1) and an angle of 35° was used for both αr and θj. As already mentioned, wave attacks were driven by mean JONSWAP spectra; peak wave steepness (Equation (1)) has been varied between 0.005 and 0.05. It has been observed that when HD1 is small compared to the wave height (say, HD1/Hm0,t < 2), the upper level has a significant influence on the water storage in the level below. Figure 9 displays the overtopping discharge in the lower reservoir increases with increasing HD1, whereas the opposite trend is observed for the upper reservoir.
For large values of HD1, the device seems to respond like a structure with a single reservoir at level Rc,1; in this case the value of qov,1 might be calculated by ordinary overtopping formulae for sloping face breakwaters, such as the van der Meer and Janssen equation [16]. The latter is plotted as a solid blue line in the graph. It is also noted that when HD1 becomes small qov,2 appears well predicted by the van der Meer and Janssen formula, although the mean discharge in the lower reservoir does not vanish.
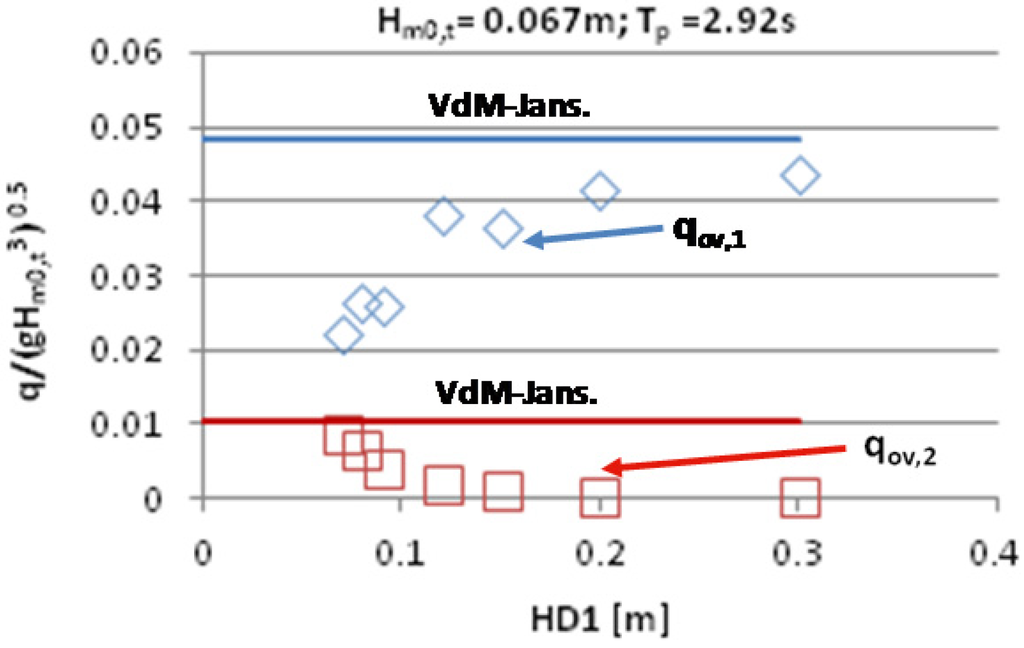
Figure 9.
Non dimensional overtopping rates in the reservoirs as function of HD1 [13]. SR = 1:30.
2.1.2. Effect of Wave Directionality
It is well established that oblique wave attacks can significantly reduce the amount of wave overtopping at coastal structures. On contrary, the role of short-crestedness is never clear; for example van der Meer and Janssen [16] stated that head-on short-crested sea-states produce on sloping structures the same run-up levels (and the same overtopping rates) as the long-crested ones. On the other hand Franco and Franco [18] came to the opposite conclusion for vertical-face breakwaters.
To assess the role of wave directionality, physical model tests have been conducted at the deep wave tank of the Hydraulic and Coastal Laboratory of Aalborg University [14]. A single three-levels device has been employed, which reproduced the pilot plant of Kvitsøy at a 1:60 scale. The model was rigidly fixed to a cliff made of concrete, which simulated the scanned bathymetry of the site. Four irregular sea states have been run as head-on long crested wave attacks (2D, no obliquity, no directional spreading), head-on short-crested storms (no obliquity, nine different spreading levels), and oblique long crested sea-states (seven wave directions between −15° and +15° included, with no directional spreading). In the experiments, a cosine-type angular spreading function has been used, according to the formula:
where D is the direction of the generic Fourier component and D0 is the mean wave direction. D and D0 are taken from the normal to the SSG. n is a spreading index: the larger n, the lower the directional spreading of the waves about D0. The analysis of data revealed that the general effect of both short-crestedness and obliquity is limiting the amount of overtopping discharge (e.g., Figure 10). The reduction is relatively small for the first two levels (qov,1 and qov,2), but is noticeable for the upper one (qov,3), especially under high waves. Altogether, it has been found out that short-crested seas with high spreading (n < 100) decrease the overtopping rate at the lower reservoirs as much as 10%, while a cut by 35% occurs at the top. As far as the role of obliquity is concerned, a similar behavior has been observed.
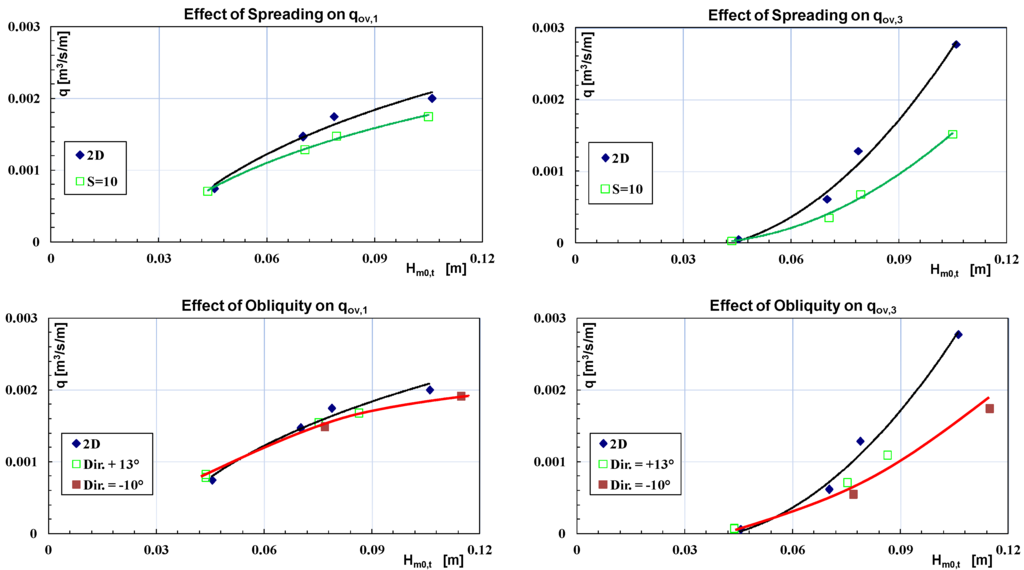
Figure 10.
Effect of directional spreading (up) and obliquity (low) on wave overtopping. Data at model scale. SR = 1:60.
Note Figure 10 indicates that when the incident wave height increases qov,3 becomes larger than qov,1; this should be due to the presence of the fronts that, as commented earlier, “confine” the entering water flow at the lower levels.
The reduction of the mean overtopping discharge reduces the hydraulic efficiency of the device and since the maximum cut occurs at the highest reservoir, which has the maximum hydraulic head, the decreasing rate of
may be higher than that of the overtopping discharge. It was estimated that refraction and short-crestedness may lower the hydraulic efficiency as much as 50%. The effect of the directional spreading is shown in Figure 11. More experiments are needed to support these findings.
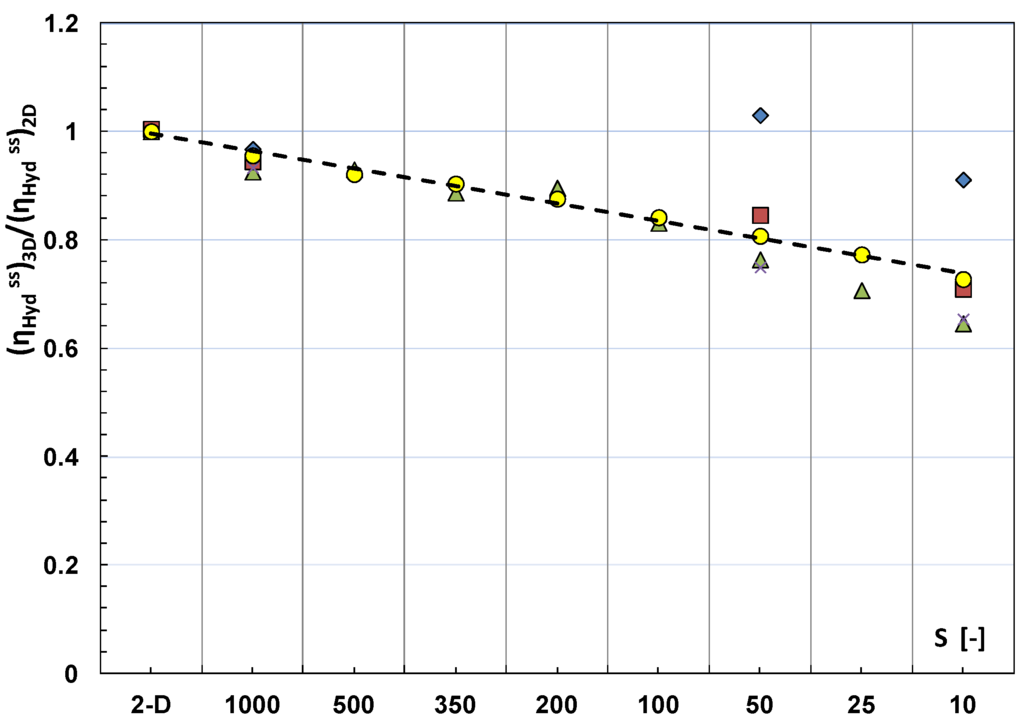
Figure 11.
Effect of short-crestedness on the hydraulic efficiency. Each data series refers to a given sea state. Re-drawn from [14]; SR = 1:60.
2.1.3. Design Equations
In practical applications, the amount of water captured in the reservoirs of a SSG plant can be calculated by integrating the following equation originally proposed by Kofoed [6,9]:
represents the rate of variation of the overtopping discharge, per unit of width, relative to a vertical coordinate, z, measured upward from the still water level. Beyond the incoming wave height, Equation (3) includes three empirical coefficients, A, B and C, which refer to a standard layout; any difference between this reference geometry and that actually designed is taken into account by means of a product of correction factors λj. Note that, according to the previous discussion, neither wave period nor wave steepness are explicitly included in the formula. Finally we can estimate the amount of water entering the j-th reservoir, by integrating between the crest levels Rc,j and Rc,j+1. We get:
For the highest reservoir of a device with no roof (like in Figure 3) Rc,j+1 can be set equal to infinite or to some high value, e.g., 2 times Rc,j.
The experimental work summarized above has suggested that for a standard layout with dr/h =1 and αr = θj = 30°–35°:
As far as the correction factors λj are concerned, it should be emphasized that in most of cases the effects of deviating from the reference configuration have been evaluated “one by one”. That is, in a given test series a single parameter has been varied, whereas the others have been kept constant. Accordingly, there are only few cases where the “cross effect” of two or more λj has been really verified. Then one may conclude that the product at the right hand side of Equations (3) and (4) has been simply “postulated” from the experimental results and that further analyses are needed to investigate the relationships which possibly link the geometric correction indexes. On the other hand, it is also worth noticing that the “one by one” approach described above is a standard in the experimental research on wave run-up and overtopping. In the worldwide known work by van der Meer and Janssen [16], a general run-up formula for sloping structures is established, where a number of correction factors are multiplied by each other to account for the effects of roughness (γf), shallow foreshore (γh), wave obliquity (γβ), presence of berms, etc. In the study, the expressions for calculating those indexes have been derived from different experimental studies with no care about “cross effects”. For example the calibration of γβ comes from 3D tests, whereas the role of roughness and shallow foreshore has been studied through 2D experiments; no results on the “cross effect” of roughness and shallow foreshore in directional seas are presented. Hence one may reason that Equations (3) and (4) are as reliable as most of the practical overtopping formulae of coastal engineering. As a compromise between the two previous views of the problem, it might be suggested that in practical applications the correction coefficients λj are applied within the experimental frame where they have been derived. Some indication is given below.
It has been proved [12] that the presence of a vertical front in the lower ramp of the device may be accounted for by:
where kp is the wave number based on the peak local wavelength Lp. It is of interest that the expression above has been originally formulated for floating devices, when waves were allowed to pass under the structure [6]. This may be not really surprising as in presence of a vertical front in the approaching slope, a portion of the incoming wave energy is however lost, although the loss is caused by reflection instead of under-passing.
Equation (6) has been verified on a SSG model having αr = 19° and θj = 35°; the ratio HD1/Rc,1 (Figure 3) was about 1.25 and dr/d ranged from 0.375 and 1. As shown in Figure 12, λdr increases from 0.6 to 1, when the draught ratio varies from 0 (fully vertical front) to 1 (sloping front).
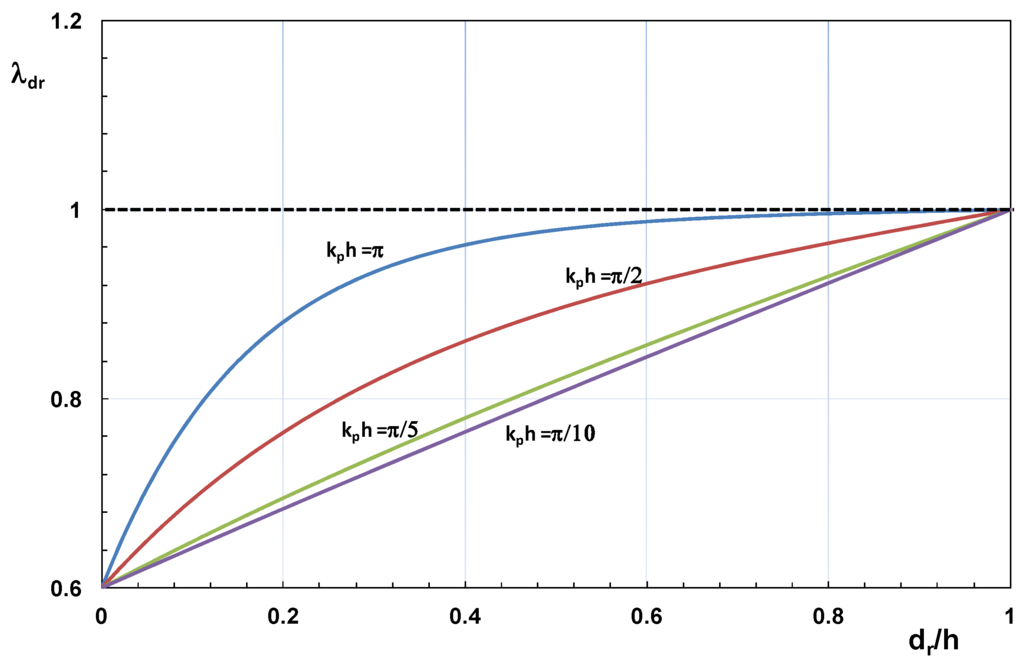
Figure 12.
Values of λdr for varying draught ratio and relative water depth.
As expected, the effect of the draught is lower in deep water (λdr is closer to 1) as the wave energy tends to vanish near the bottom. In [13] the following factors have been introduced to account the effect of HD1 in a two reservoirs system (αr = θj = 35° and dr/d = 1, see above discussion):
where λ1,HD applies to the first reservoir (the lower one) and λ2,HD applies to the second reservoir. The graph of Figure 13 shows that Equation (12) is rather consistent to the experimental findings displayed in Figure 9. No “ad hoc” functional form has been found to account for wave directionality, although it has been suggested [8] that a first estimation of the effect of wave obliquity might come from the van der Meer and Janssen formula [16]:
In Equation (13) D0 is in degree; for an attack of 45° λD0 = 0.85.
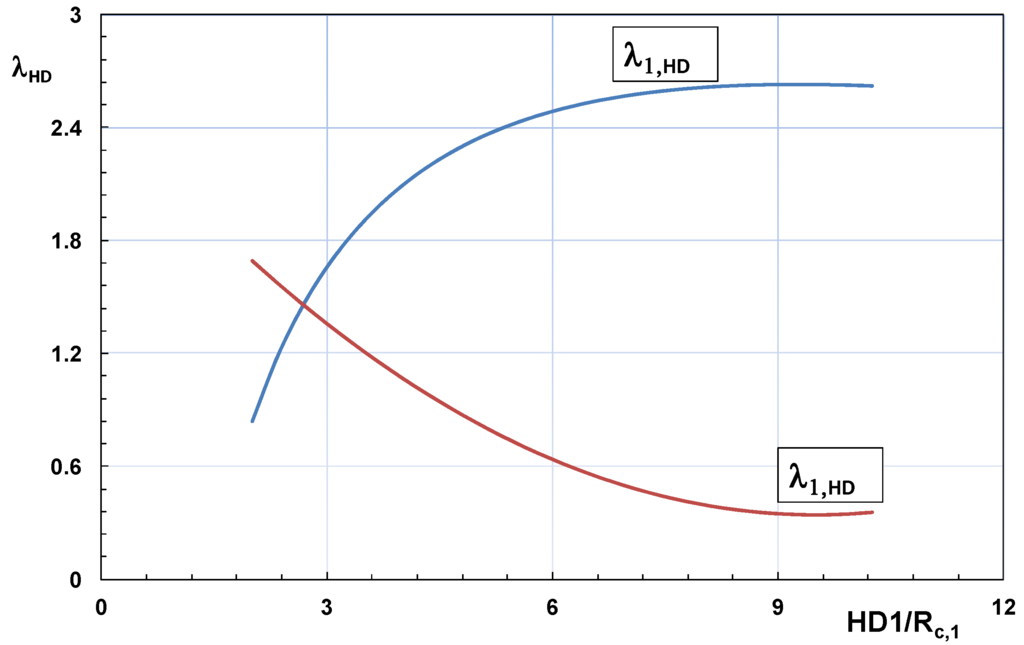
Figure 13.
Correction factors for HD1.
Before concluding this section, it might be useful to remark that experimental data revealed the total discharge which averagely enters the device in a given sea state can be effectively estimated as [12]:
Equation (14) has been introduced by Kofoed [6] for a single level structure; it includes three correction factors and namely:
- the draught coefficient λdr given in Equation (11);
- a ramp factor λαr given by:
- a low crest factor:
Equation (9) proved to be valid for a number of different layouts and consequently the use of the product of the three correction index λj seems plainly justified in this case. It is also noteworthy that λαr is maximum for a ramp angle of 30°, in contrast with the experimental findings discussed above. λs increases from 0.6 to 1, when the relative crest freeboard grows from 0 to 0.75. Equation (9) holds provided that waves do not overpass the device (no overtopping water behind the structure is allowed).
2.2. Two Further Items of the Hydraulic Design: Tide and Number of Reservoirs
2.2.1. The Role of Tide
The studies previously described, focused mainly on the effect of geometry and wave parameters on the sea-state overtopping discharge, qov,j, as well on the sea-state hydraulic efficiency
. In each set of experiments, the water depth has been kept constant and accordingly no information has been obtained about the role of tide. To fill this gap, a number of numerical simulations have been performed by means of the program WOPsim 3.01 [19,20], which is described in detail in Appendix II at the end of the paper. The main inputs to the software are water levels, crest levels, wave conditions and turbine strategy; the output are, among others, power production and overall efficiency (output power to wave power ratio).
Thus, a standard three reservoirs system [Equation (5)] has been supposed to be located at Swakopumd (Namibia), in Sines (Portugal) and in the North Sea (Danish sector). For all these sites the wave climate was known, including wave heights, wave periods and water levels.
Swakopumd and Sines are tidal environments; the tidal range (TR), difference between the mean high level (MHL) and mean low level (MLL) is about 1 m at Swakopumd and 2.0 m at Sines. The North Sea has no relevant tides, so the water level variations of the other two sites have been artificially added to the Danish waves. Furthermore, to simulate different tidal ranges, the actual water levels at Swakopumd and Sines have been multiplied by arbitrary coefficients, so to get a number of fictional tide heights. The analysis procedure is described below.
For each wave climate, the crest freeboards of the reservoirs (Rc,j) have been optimized by maximizing the global hydraulic efficiency,
(see Appendix I), under the assumption of no tide (reference has been made to the chart datum). Once Rc,j have been obtained, the structure has been subjected to the same climates including tides and
has been re-calculated. The ratio between the latter and former value of the efficiency has been considered as an indicator of the influence of tide on the SSG performances.
In Figure 14 this ratio is plotted vs. the tidal range; the graph shows the performance of the device to lower with increasing TR; it can be observed that the response of North Sea_Sines tide (Sines tides virtually superimposed to Danish waves) is similar to the response of Sines (Sines tides + Sines waves). Analogously, the North Sea_Swakopumd tide curve is similar to that of Swakopumd. This indicates the wave climate to be a secondary variable in this process. On average, a loss of order of 10% has been computed for 1.6 m, that is a value halfway between the real TRs of Swakopumd and Sines. However, the rate of reduction seems to depend on the probability density function (pdf ) of tide levels; for Swakopumd the modal value of the pdf is rather close to the Datum (Datum Chart) and this leads to better performances as the probability of no tide is relatively high.
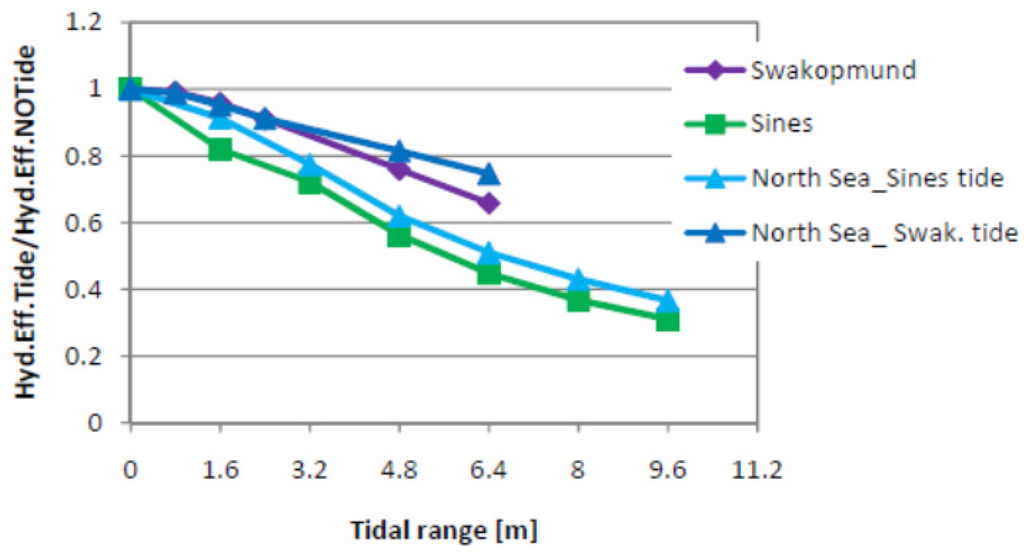
Figure 14.
Decrease of hydraulic efficiency with increasing tidal ranges [19].
Furthermore, it has been found that if Rc,j are optimized taking into account of both wave climate and tidal variations, a larger value of
is obtained (gain up to 3%) compared to the case where the optimization is performed only with respect to the wave climate. In conclusion we may state the time variation of water levels to significantly affect the hydraulic response of SSG.
2.2.2. Adding Further Reservoirs
Besides investigating the tide effect, supplementary simulations have been carried out in [19] to assess how the hydraulic efficiency might grow with growing the number of reservoirs. Accordingly, structures with two, three, four and five reservoirs have been simulated and their Rc,j (j = 1,…,5) have been optimized with respect to
for different values of TR (Figure 15, T1 corresponds to 0.8 m TR, T3 is TR = 4.8 m, T6 is TR = 9.6 m).
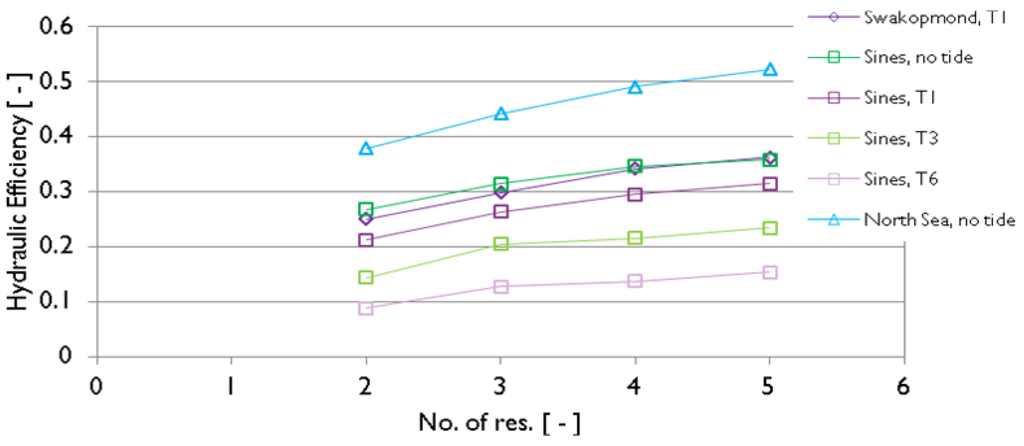
Figure 15.
Effect of number of reservoirs on the hydraulic efficiency [19].
As expected, by increasing the number of mouths the hydraulic efficiency increases as well. On average, the gain is 5% from two to three reservoirs, 3% from three to four, and 2% from four to five. In addition, for a given wave climate, the gain seems to increase with growing TR.
It is important to notice that despite the decision on the number of reservoirs is dependent on economical items also practical aspects deserve to be considered. For example, having four or five reservoirs may mean that the room between the floor of one reservoir and the floor of the above is limited (also considering the thickness of ceiling). A height of less than 1 m makes it impossible to access the reservoirs.
2.3. Reflection Performance
Wave reflection is a leading process for SSGs and one may say it to contribute to the proper working of the device. The need of large run-up heights requires the ramp inclination to be steep (see previous paragraphs) and this leads to large reflection rates. On the other hand, steep slopes are necessary as they favor the occurrence of surging breakers, which dissipate only little energy.
However, high reflection rates could also affect the stability of the structure, in case it is placed on a sandy bottom, due to possible scour events. To prevent this, a proper foot protection must be designed, based on the experience of coastal engineering. Nowadays several design equations are available, but, to select the most suited, a reliable estimate of the reflection coefficient, Kr, is needed. The latter is defined as the reflected to incident significant wave height ratio.
For example if Kr is in the range 30–40%, design formulae for rubble mound breakwaters will be employed [21], whereas, for values in the range 50%–100%, an expression valid for vertical breakwaters will be the most adequate [22].
Thus, with the purpose of quantifying the reflection power of the device, physical model tests have been performed at the Shallow water flume of Aalborg University [23] (SR = 1:30). A three reservoirs system with a 35° ramp has been subjected to random seas driven by mean JONSWAP spectra. Waves had a peak steepness, Equation (6), ranging from 0.009 to 0.063; the same parameter based on the mean wave period Te, referred to as s0e hereafter, ranged between 0.008 and 0.058.
The study has indicated SSG to reflect 45% to 90%, which is similar to vertical face breakwaters on a rubble mound foundation. This result was definitely expected; however, as a supplementary result of the work, a specific predictive equation for Kr was also suggested. The latter reads:
The second term at the right hand side is a well established expression of coastal engineering to predict wave reflection at smooth slopes [24]; here, ξ0 is the surf similarity parameter:
where αfs is the front slope angle.
In case of structures with a segmented front face (like SSGs), an equivalent slope, say αeq, has to be used. In [24] the latter has been calculated as the weighted average of the mean slope in the run-up/run-down area (αincl) and the slope of the approach ramp, αr (Figure 16).
So one gets, according to [25]:
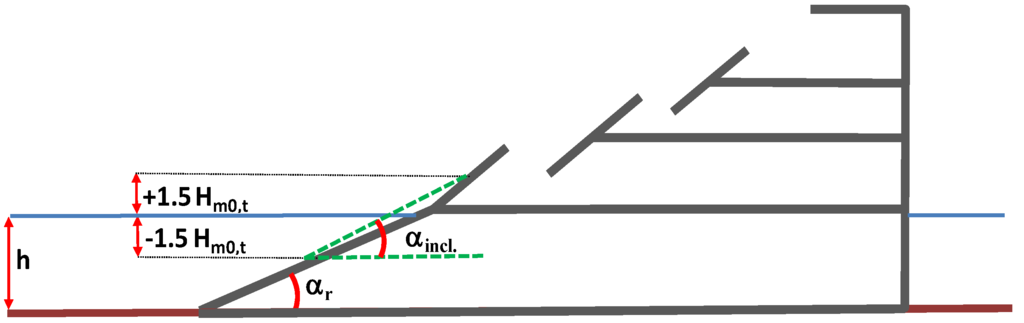
Figure 16.
Definition of equivalent slope angle.
The reduction factor RSSG accounts for the effect of the water volume captured in the lowest reservoir, which is always placed in the run-up/run-down area. It is calculated as:
Equations (12–15) fitted the experimental data reasonably well; the standard error (standard deviation of the difference between the measured value of Kr and that predicted by the formulae) is about 6%. This means the actual (measured) reflection coefficient is in a range of ±0.1 around the predicted one with a 90% probability.
It might be noticed that the formulae given above do not consider the effect of water that overtops the upper reservoir; factually, the latter is subtracted to the down-rush process and this contributes at reducing the reflection rate. The reason why this item has been apparently neglected is that the authors assume reflection is generated mainly below the sea level. For this reason the contribution of overtopping would be a secondary effect. However, recent experiments carried out at the University of Naples Federico II [26] seem to partly contradict this hypothesis. These tests have suggested that a modification might be introduced in the reduction factor (15) in order to improve the reliability of predictions. The latter may be function, for example, of the ratio between the crest freeboard of the highest reservoir and the incoming wave height.
3. Structure Response
Unlike traditional harbor defenses, WECs need to be exposed to large wave forces; they are generally designed to face and challenge the sea as much as possible. Accordingly, design criteria of traditional maritime structures may be not really adequate when designing such innovative structures.
To investigate the nature and the magnitude of wave loadings acting on SSGs, 3D experiments have been conducted at Aalborg University [11], on a 1:60 model of the aforementioned Kvitsøy pilot plant. The latter was conceived as a three reservoirs system with both the ramp and the fronts inclined by 35° to the horizontal. The structure model was located on the top of a concrete cliff and 32 random sea-states were run, including long crested, short crested and oblique (45°) attacks. The storms were representative of the extreme wave climate at the site of Kvitsøy; the peak wave steepness [Equation (1)] was around 0.03 for most of the experiments.
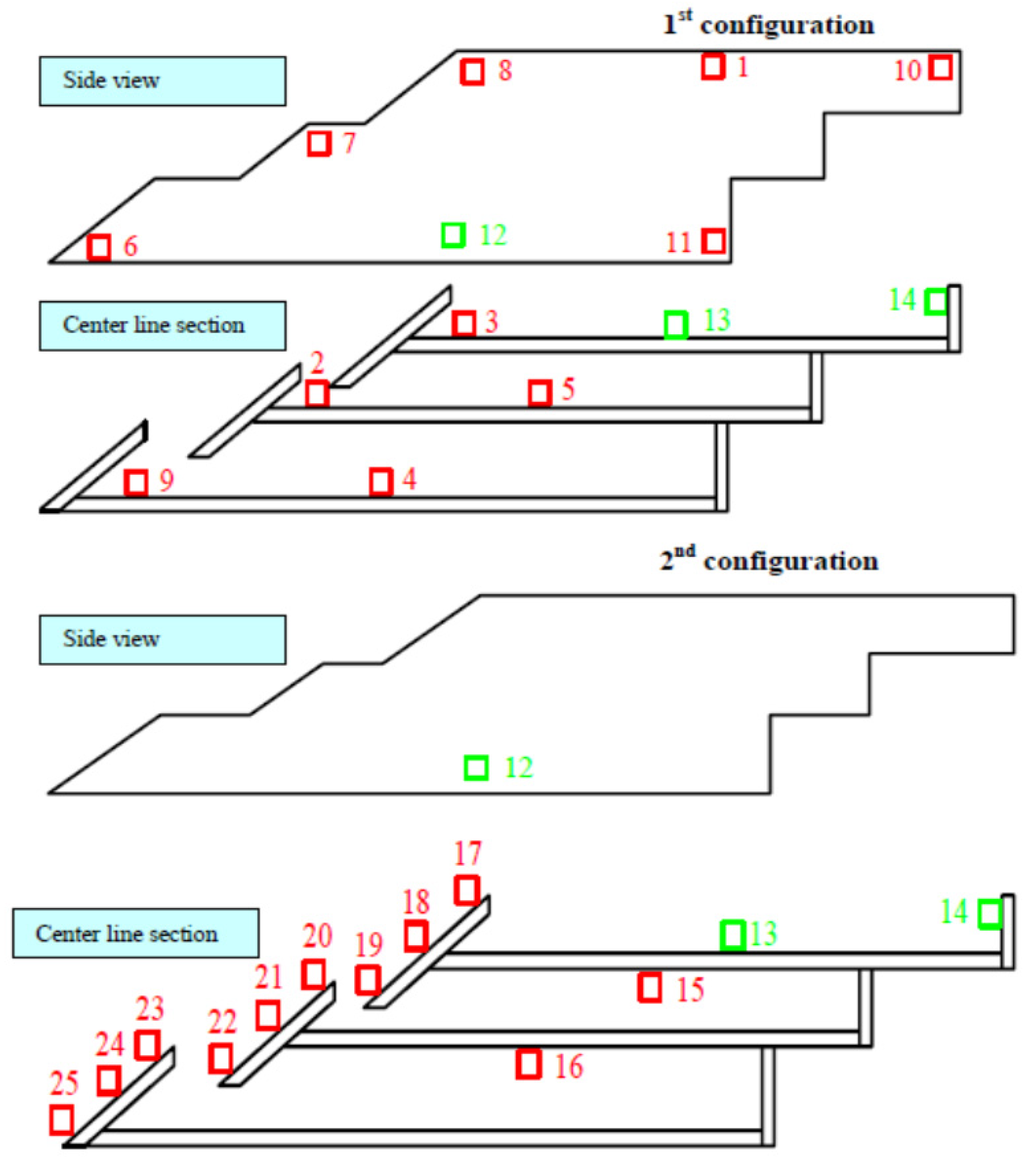
Figure 17.
View of pressure cell positions, after [11].
To measure the pressure at the front face and at the side walls of the device, 14 “Kulite Semiconductor cells”, mainly sampled at 200 Hz, were spread in 25 positions (Figure 17). After combining results of pressure measurements and video camera recordings, two loading cases have been identified:
- Under front attacks, surging breakers rapidly rise along the three front plates, originating quasi-static pressure paths. The massive wave overtopping causes a water jet to hit the vertical rear wall in the upper reservoir, which has no roof (position 14 of Figure 17). Figure 18 shows the pressure chronograms at four transducers along the SSG cross section; it is clear that the slamming of the impinging jet at the position 14 induces a quasi-impulsive loading, with a rise time rather short, compared to the other positions, and a magnitude which is about twice the pressure at the front face.
- Under side attacks, the wave experiences a rotation due to refraction. At the structure, only one part of the front climbs the plates with a shape similar to the case 1 (Figure 19a); another part hits the side wall producing a partially damped plunging breaker, which again leads the pressure to get an impulsive or “quasi-impulsive” nature (Figure 20).
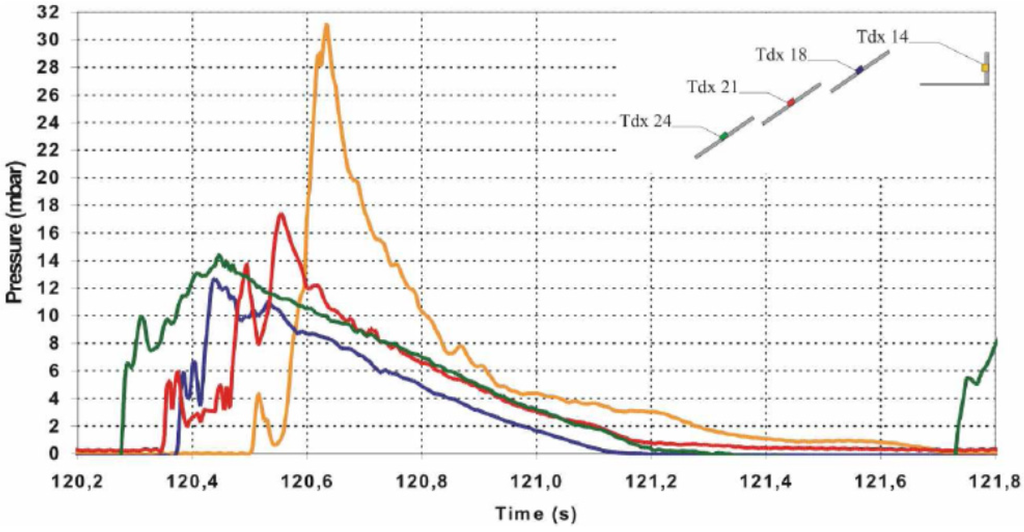
Figure 18.
Pressure signals at the front of SSG [11]. Green curve: transducer # 24; red curve: transducer # 21; blue curve: transducer # 18; yellow curve: transducer # 14.

Figure 19.
Wave shape under side attacks [11].
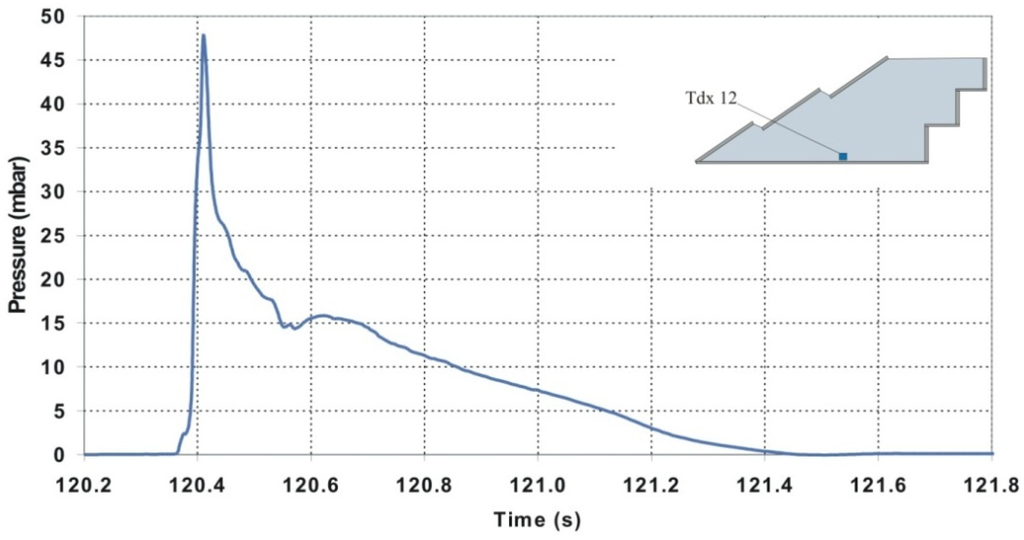
Figure 20.
Quasi impulsive event at position 12 under a side attack [11].
Altogether, the maximum wave pressure at the fronts of the SSG was found to have the same order of magnitude as the incoming significant wave height, whereas in the impulsive events, recorded either at the rear upper wall or laterally, a pressure of about 2–3 Hm0,t was measured. It is worth to notice that plunging breakers impacting vertical-face breakwaters usually produce pressures of order of 10 times the wave height (a factor of 50 times was measured in [27] and this justifies the term “quasi-impulsive” reported above).
Wave directionality seems to have a different effect for each plate. On average, the obliquity loading reduction is around 12%–17%. Spreading loading reduction is about 10% for front attacks and 13% for side attacks.
Finally, to check the reliability of traditional coastal engineering design formulae, measured values of the average 1/250th highest peak pressures were compared to the formula of Takahashi et al. [28]. The authors introduced some corrections to the traditional Goda equation for vertical breakwaters in order to account the presence of a sloping wall at the front face of the structure. As shown by the example reported in Figure 21, measured values may exceed predictions by 20%–50%.
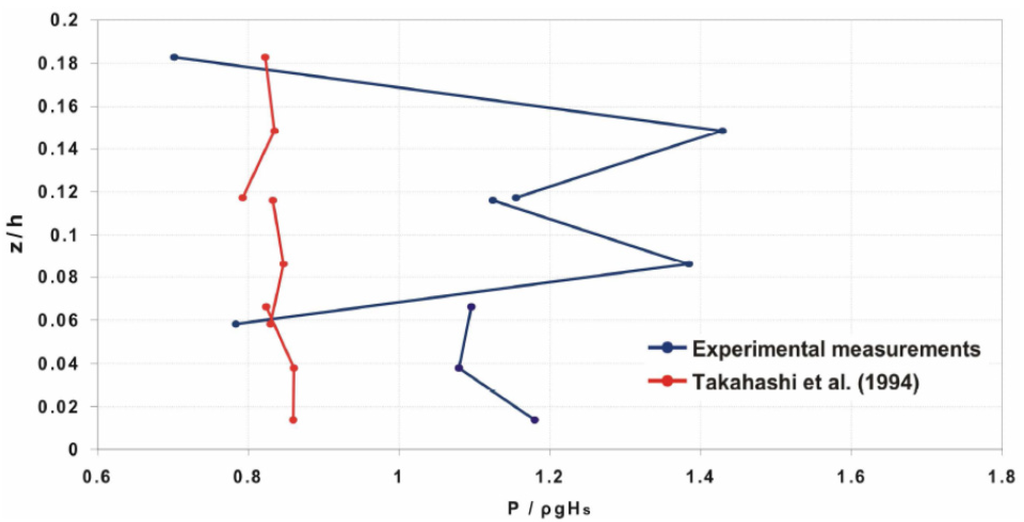
Figure 21.
Takahashi et al. formula [28] compared to measured data [11].
This highlights the need of further investigations, in order to develop a proper and reliable tool for structural design of SSGs. With this purpose, new experiments have been carried out at the University of Naples Federico II ([26] and [29]) using a 1:66 model scale of a new pilot plant to be located at Svåheia, on the NW coast of the Norway. Here, wave height and period have been both widely varied to get all the possible loading cases, including plunging breakers generated by far steep waves. Analysis of those data are now in progress and will be discussed in a subsequent paper.
However, before concluding this section it should be mentioned that a major point, which might limit the validity of the available experimental results, is the small scale at which the tests have been conducted. Indeed when the structure is subjected to surging waves with slight breaking, as in the case of the “Kvitsøy tests” presented above [11], scale effects are not expected to be significant, as there is only a little amount of air involved, which is confined at the tip of the wave that climbs the wall. Moreover, loadings vary quite slowly in the time. On the other hand, under plunging breakers (and possibly under collapsing waves) shock pressures are produced that may have scale effects, which are difficult to define; it is known [30] that the amount of air entrained in laboratory breaking waves is less than in prototype, but the air bubbles are larger because the surface tension is not properly represented.
The problem of scaling impact forces on coastal structures has been recently addressed in [31] with reference to vertical wall.
4. Efficiency and Energy Production
The energy conversion steps in the SSG (and more in general for overtopping devices) are as follows:
- Wave to crests, i.e., where the different waves are captured at the crest heights of the reservoirs, Rc,j (j = 1,2…n, n = number of reservoirs). During the of laboratory tests described in the previous sections, it has been measured that around 40% of the available sea state energy (Appendix I) is captured;
- Crests to reservoirs, i.e., where the potential energy relative to the specific crest heights is reduced by falling into the reservoir at a lower height. It is estimated that 75% of the energy from the previous step is maintained;
- Low head water turbines, i.e., where the water in the reservoirs is utilized by the hydraulic turbines with 90% efficiency;
- Electrical generator and electrical equipment, 95% efficiency.
The overall expected wave-to wire efficiency is 25–35%.
5. Power Take-off
On its way back to the sea, the stored water passes through specially designed low head hydro-turbines generating electricity. The energy extracted from a given volume of water in the reservoir is in direct proportion to its elevation above the mean sea level (turbine head). Different ventilation openings are included in the design of the structure, in order to prevent air pressure to obstruct the water storage.
Part of the concept, which is still under development [32], is the innovative concept of the Multi-Stage Turbine (MST). The design integrated in the structure consists of a number of turbines (depending on the number of reservoirs) staggered concentrically inside each other, which thereby drives a common generator through a common shaft. Each section of the runner is connected to one of the reservoirs by concentric ducts. By taking advantage of different heights of water head, the MST technology is willing to minimize the start/stop sequences and operates, even if only one reservoir is supplying water (Figure 22).
Another option is the use of four Kaplan turbines of identical size i.e., two in the lower reservoir and one in each of the middle and upper reservoirs. The turbines will be manufactured using corrosion resistant steel.
Due to economic considerations, the size of the reservoirs in the SSG will be of the same order of magnitude as the overtopping volume of a single big wave in the design storm. Considering the normal groupiness of ocean waves, this implies that turbines have a high frequency start/stop cycle, approximately every 2 minutes. The cylinder gate has been chosen as the mechanism to regulate the flow to the turbine. It consists of a cylinder directly combined to the turbine that allows the radial water to flow when lifted. The cylinder gate seals by metal-to-metal contact to the outer turbine ring, closing by its own weight and offering a good reliability and transient time. The generators will be allocated at a higher level in order to avoid the risk of floods. They are driven by a tooth belt step-up drive which allows them to be matched with the optimal turbine speed.

Figure 22.
Three-levels Multi-stage Turbine [32].
6. Feasibility Studies
Plans for the construction of SSG wave energy power plants are in progress at the Svaaheia site (Norway), the port of Hanstholm (Denmark) and the port of Garibaldi (Oregon, USA). Preliminary studies have been conducted in other locations too, in order to assess the cost of the structure and compare it to traditional breakwater solutions. The integration of the SSG on breakwater has been taken into account for the renovation of the harbor in Plentzia (Basque Country, Spain), Swakopmund (Namibia) and Sines (Portugal). The presented analysis is based on these two last cases.
In these projects, the SSG technology is integrated into outer harbor breakwaters and jetty reconstruction projects. Additional cost to implement WEC into breakwaters is defined as the cost related to the construction and installation that would not occur in case of a traditional harbor protection. In all the performed studies, the extra cost never exceeded 20% of the cost of a traditional solution.
The application of wave energy converters into breakwaters presents some advantages:
- (1)
- sharing of construction costs,
- (2)
- access and therefore operation and maintenance are easier compared to an offshore situation,
- (3)
- sharing of infrastructures.
Improvements of the SSG-breakwater compared to a traditional solution are:
- (1)
- Recirculation of the water inside the harbor, i.e., improvement of water quality as the outlet of the turbines would be in the rear part of the breakwater,
- (2)
- Potential lower visual impact as a consequence of a lower crest level,
- (3)
- Clean electricity generation.
One issue that has been raided could be the fill in of the reservoirs with sediments especially for installations in water depths less than 15 m. This issue could be solved by sloping floors in the reservoirs or programming adequate maintenance. The most important parameters having an effect on the investment cost of the SSG are:
- (1)
- Local wave and tide climate (determines the number and size of reservoirs, in average passing from three to four reservoirs will see an increase of construction cost of 4%),
- (2)
- Design wave height (determines ballast and size of the structure),
- (3)
- Water depth (determines the construction method and overall size of the caisson).
For Swakopmund, the installation at two different water depths has been proposed using a 3-reservoirs structure. For Sines, the installation of a 4-reservoirs structure is studied. A 4-reservoirs structure has been chosen due to the bigger tidal range at the location. Tidal range is here taken as the difference between the highest high and the lowest low water.
Construction costs have been analyzed including: production of concrete elements, dry dock costs, float and transport elements, immerse and installed elements, gravel bed, sand fill, indirect costs, engineering costs, general costs, profit and risk. The costs of turbines and generators have been added to the total. Following, the main characteristics of the systems are summarized by location in Table 1 and Table 2 (Figure 23 and Figure 24).
The total concrete quantity for a concrete caisson is higher for the SSG-breakwater than for a conventional caisson (because of the floor slabs). Other differences are the higher center of gravity and eccentric location of the center of gravity that have consequences on the draft of the floating caisson into position.

Table 1.
Swakopmund breakwater design parameters, power production and construction costs.
| Annual wave energy = 15.7 kW/m | |
| Hs = 7.9 m | Hmax = 9.9 m |
| Water depth = 11.3 m | Tidal range = 1.6 (± 0.8) m |
| Capture crest levels: Rc1 = 1 m, Rc2 = 2.5 m, Rc3 = 4 m | |
| Crest level: 8 m | Base width: 28 m |
| Installed capacity: 12.8 kW/m | |
| Expected power production: 18,000 kWh/y/m | |
| Construction costs inclusive of turbines and generators: 150,700 €/m | |

Table 2.
Sines breakwater design parameters, power production and construction costs.
| Annual wave energy = 14.4 kW/m | |
| Hs = 13.9 m | Hmax = 18.1 m |
| Water depth = 18 m | Tidal range = 3.37 (±1.68) m |
| Capture crest levels: Rc1 = 0.75 m, Rc2 =2.05 m, Rc3 =3.35 m, Rc4 = 4.65 m | |
| Crest level: 15 m | Base width: 45 m |
| Installed capacity: 12 kW/m | |
| Expected power production: 12,000 kWh/y/m | |
| Construction costs inclusive of turbines and generators: 285,800 €/m | |
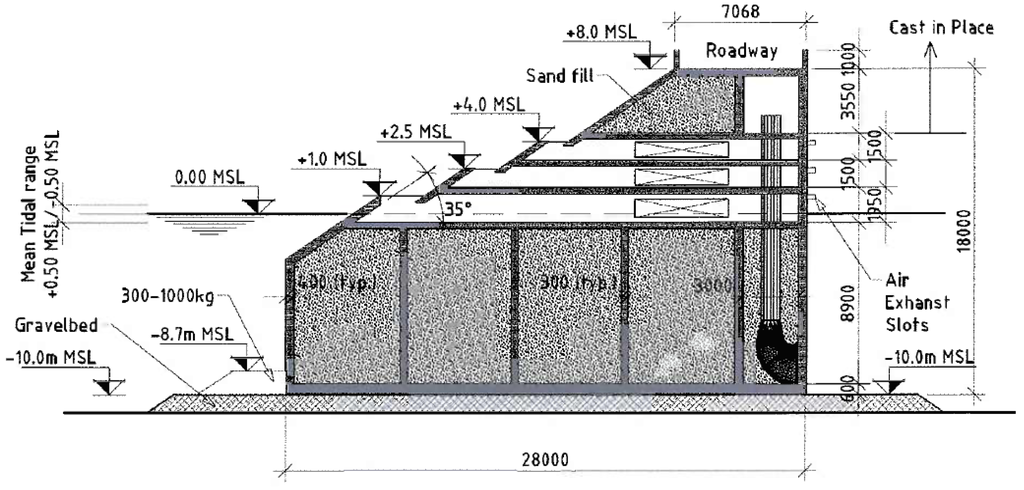
Figure 23.
Section of the SSG-breakwater caisson at Swakopmund.
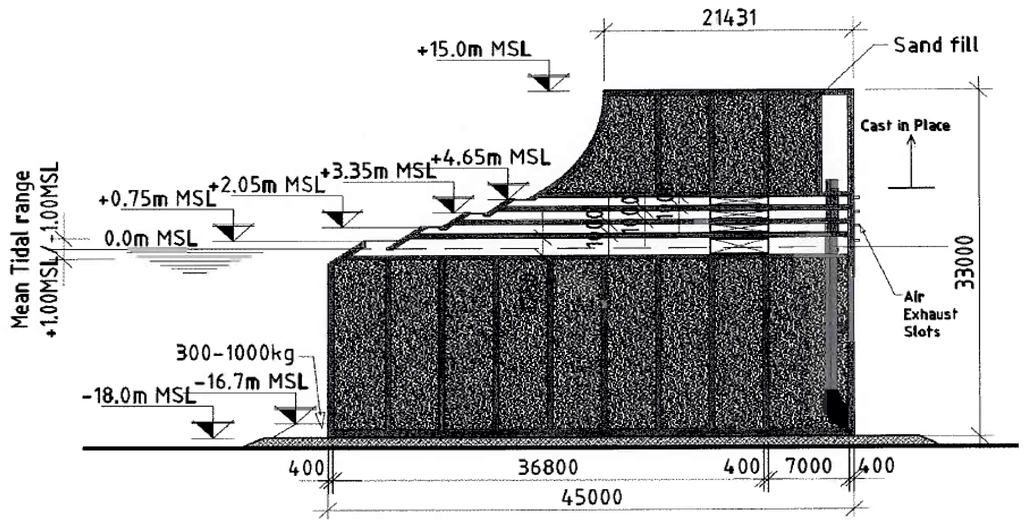
Figure 24.
Section of the SSG-breakwater caisson at Sines.
Indeed for Swakopmund, the draft was revealed to be critical for such shallow water so that the construction will have two separated parts: the lower part reaches to the first slot and consists of elements of 5 m width; the upper part is 10 m wide. The upper part is fixed to the lower by the overhang of the upper part over the lower. To prevent uplift of the upper part, it is secured by tension anchors in the walls. For Sines, the structure is too heavy and cannot be lifted and therefore, they are constructed in a dry dock that will subsequently be flooded and the structure is then towed into position.
Examples of extra costs are: electrical equipment, turbines, etc. By comparison with traditional breakwater solutions, it is possible to reduce the additional costs related to the construction of an SSG-breakwater (Table 3). The additional costs seem to be acceptable; if they are put in a payback scheme of 10 years, the cost of electricity is set around 0.25 €/kWh.

Table 3.
Summary of economics for the SSG-breakwater application.
| Location | Rubble mound | Traditional caisson | SSG-breakwater | Additional costs |
|---|---|---|---|---|
| Swakopmund | 67,200 €/m | 124,500 €/m | 150,700 €/m | 83,500 €/m–26,200 €/m |
| Sines | - | 231,000 €/m | 285,800 €/m | 54,800 €/m |
7. Conclusions
A variety of geometrical factors influence the hydraulic efficiency of the SSG. Due to the possibly high number of combination and interactions of these parameters, laboratory tests for evaluation of hydraulic efficiency of the SSG are fundamental for each application.
The existing overtopping formula used to identify the optimal crest levels related to wave conditions at location has been implemented with a parameter that takes the horizontal distance between the reservoirs into account.
Directional spreading and wave attack angle on the structure are decreasing the overtopping of a single module device, meaning in case of low width to depth ratio, from 40% to 32% and 35% respectively. However, or an array of devices mounted on a breakwater configuration, the reduction on overtopping is not expected to be significant, as side effects will be limited.
The presence of tide also penalizes the efficiency of the system compared to a case with no tide. Nevertheless, it is possible to limit this effect by taking into account tidal variation on the design of the structure and even construct an extra reservoir to obtain a more flexible configuration. However, this last solution should be carefully evaluated both technically and economically for each specific situation.
Preliminary results show that the structure is highly reflective and the reflection coefficient, Kr, which is never lower than 40%, can rise up to 90%. Therefore, it is a design issue to construct a proper toe protection layer to avoid scour holes or a berm to reduce the reflection.
Unlike traditional harbor defenses, WECs need to be exposed to large wave forces and are generally designed to face and challenge the sea as much as possible. The design criteria of traditional maritime structures may not be satisfactory for designing innovative breakwaters such as the SSGs.
Model tests have been carried out measuring pressure and forces on the SSG. Pressure peaks and pressure spatial distribution are sometimes significantly under-predicted by the traditional formulae.
A new design method, to give a more reliable tool for calculating pressure/forces, will be among the scopes of the future research developments.
Part of the SSG concept is the innovative concept of the Multi-Stage Turbine that, using different heights of water head, minimizes the start/stop sequences and operates even if only one reservoir is supplying water. This results in a higher degree of efficiency. The SSG overall expected wave-to wire efficiency is 25%–35%.
Feasibility studies and plans for the construction of the SSG wave energy power plants are in progress in different world sites. The application of the SSG structure as sloping crown wall on a vertical breakwater is suggested in design practices, in this way the placement of the crest of caisson breakwaters will be relatively low, allowing heavy overtopping and reducing wave forces and reflection.
Acknowledgements
The work discussed here is part of the Second University of Naples founded project PRIST 2007 (Progetti di Ricerca di Rilevante Interesse Scientifico e Tecnologico) titled “Convertitori di Energia Ondosa per la produzione di Energia Elettrica” (Wave Energy Converters for Electrical Production, [33]). The Authors gratefully acknowledge Second University of Naples, Department of Civil Engineering of Aalborg University and WaveEnergy A/S for supporting this innovative research and encouraging mobility of researchers. The authors also thank the anonymous reviewers, who contributed at increasing the scientific value of this work.
Nomenclature
| A, B, C | experimental coefficients for overtopping prediction |
| Bu | Hydraulic Head (Bernoulli Trinomial) (m) |
| Cg | group velocity (m/s) |
| D | direction (relative to the orthogonal to the structure) of a single Fourier wave component in the directional power spectrum (deg.) |
| D0 | mean wave direction (deg.) |
| dr | distance between the mean water level and the lower edge of the run-up ramp (draught, (m)) |
| g | gravity acceleration (m/s2) |
| kp |
wave number associated with the peak wavelength Lp (rad/m) |
| Kr | reflection coefficient (-) |
| HD | horizontal distance between the opening of two consecutive reservoir levels |
| fj | Rc,j − Hh,j. “freespace” for the j-th reservoir (m) |
| h | water depth at the toe of the structure (m) |
| Hh,j | hydraulic head at the j-th reservoir (m) |
| Hs | significant wave height (m) |
| Hm0,t | spectral estimate of Hs at toe of the structure (m) |
| Hrms | root mean square wave height (m) |
| L0e |
deep water wave length based on the mean period Te (m) |
| L0P |
deep water peak wave length (m) |
| Lp(e) |
= peak (mean) wave length at the depth of placement of the structure (m) |
| mn | nth spectral moment |
| MWL | mean water level (m) |
| Nw | number of waves in a sea state (-) |
| OTD | OverTopping Devices |
| OWC | Oscillating Water Columns |
| PHyd | mean potential power of the overtopping water per unit of width (W/m) |
| PRes | mean power in the reservoirs per unit of width (W/m) |
| PP | mean power production per unit of width (W/m) |
| Pwave | mean power of the waves per unit of width (W/m) |
| Procc. | Probability of occurrence (-) |
| qov,j | sea-state averaged overtopping discharge to the j-th reservoir per unit of width (m3/s/m) |
| Qin,j | individual overtopping discharge to the j-th reservoir per unit of width, averaged over a wave cycle (m3/s/m) |
| Qover,j | rate of overflow at the j-th reservoir (m3/s/m) |
| Qturb,j | flow through the turbine at the j-th reservoir (m3/s/m) |
| QRes,j | volume of water stored in the j-th reservoir during an unitary time-step (m3/s/m) |
| Qover-upper,j | overflow discharge at the (j + 1)-th reservoir, which is re-used at the j-th reservoir (m3/s/m) |
| Rc,j | crest height of the j-th reservoir (m) |
| s0p |
= peak wave steepness (-) |
| s0e |
= mean wave steepness (-) |
| SSG | Seawave Slot-cone Generator |
| Te | energy wave period (in (s)) calculated as
|
| Tm | time domain mean wave period (s) |
| Tp | peak wave period (s) |
| WAB | Wave Activated Bodies |
| WEC | Wave Energy Converter |
Greek Letters:
| αr | front ramp angle on the horizontal (deg.) |
| αeq. | equivalent front angle for reflection analysis |
| αincl | mean front slope in the run-up area |
| Δ | duration of a sea-state (s or hr.) |
SSG efficiency in a sea state (-). ν = (Hyd, Res, P) | |
SSG efficiency for a given wave climate (-). ν = (Hyd, Res, P) | |
turbine efficiency (-) | |
| θj | angle of the front of j-th reservoir (deg.) |
| λj | correction factors (-) |
| ξ0 |
= surf similarity parameter (-) |
| ρ | sea water density (kg/m3) |
Appendix I: Efficiency of SSG
A-I.1. The Wave Power (Mean Sea-State Power)
For a train of irregular stationary waves in deep water, the mean power per unit of wave front can be calculated as [11]:
where Hrms,0 represents the root mean square wave height and
is the offshore group velocity calculated at the mean period
. The latter equals:
In Equation (A.2), the harmonic average wave period Te is employed for
; the latter is about 1.1 the peak period Tp and is calculated as the ratio between the spectral moment of order −1 and the area of the power spectrum . Now, by noting that the deep water significant wave height Hs,0 , whether spectrally or statistically defined, is approximately √2 Hrms,0, we get:
The power in Equation (A.3) is basically conserved during wave propagation, up to the onset of breaking.
A-I.2. The Mean Overtopping Power in a Sea-State
The wave energy is conveyed to SSG by a number of flows, which originate from wave run-up; obviously, these flows are as many as the number of the reservoirs.
It is known that a stationary current with a volume flux q carries a power:
where ρ is the density of water, g is the gravity acceleration and Bu is the hydraulic head (Bernoulli trinomial).
Similarly, for a SSG of unitary width subjected to a sea state of assigned characteristics, one may set:
In Equation (A.5) qov,j is the mean overtopping discharge, per unit of width, which enters the jth-reservoir; the reservoir has a crest height Rc,j from the mean water level (see Figure 3 and Figure A1). The total number of reservoirs in the device is NRes.
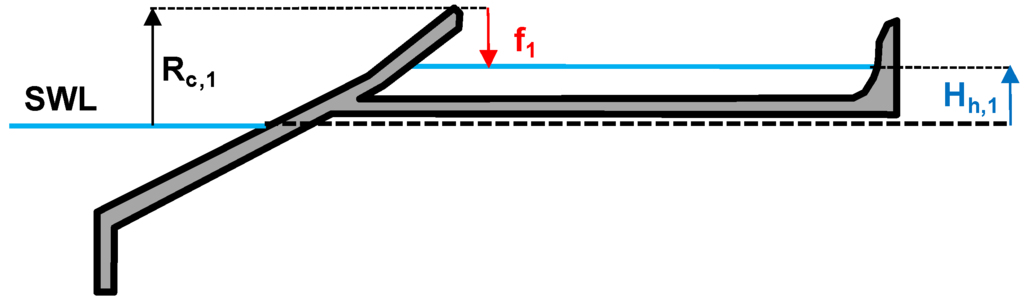
Figure A1.
Definition sketch for the variables used in this appendix (single reservoir structure).
Note the hypothesis
reasonably neglects any pressure contribution to the incoming power, while the kinetic energy of the flows is supposed to be dissipated in the storage process.
A-I.3. The Mean Available Power in a Sea-State
Consider a sea-state of duration Δ, which includes Nw waves. Then a time-domain average wave period, Tm, can be defined as:
Now, it is clear that the amount of potential energy which is actually stored in the j-th reservoir is less than:
This is basically for two reasons. Firstly, the actual hydraulic head available for energy production, Hh,j (Figure A1), is generally less than Rc,j. Secondly, if the water level in the reservoir equals Rc,j, some water will be lost by overflow, because the reservoir is full. Thus, a more realistic estimate of the potential energy theoretically available for electricity production is given by:
in which
is the mean overflow discharge and
is the mean value of the actual water level in the j-th reservoir. Obviously, the quantity included in the square parentheses of Equation (8),
, represents the mean power which might be theoretically converted into electricity by the reservoir j. For the whole SSG one gets:
A-I.4. Mean Produced Power
The sea-state averaged power converted by a turbine of a SSG device is less than (A.9). This is both because the efficiency of the turbines is less than 1 and because there is a time interval in which turbines are turned off. The ensemble of rules that determine when the turbine of a given reservoir starts and stops is termed turbine strategy. In practice when the freespace, fj, between the crest of a reservoir and the water surface (see Figure A1) is less than a threshold value, say Fon, then the turbine starts. Otherwise, when the freespace becomes larger than a second threshold, Foff, then the turbine stops. Both Fon and Foff may be function of the incoming significant wave height.
As far as the turbine is concerned, it should be noted that both the volume flux that passes through it, Qturb,j., and its efficiency, ηturb,j., are function of the hydraulic head, via the so-called turbine characteristics. As Hh,j varies in the time, so do Qturb,j and ηturb,j. Thus, the mean power production related to the j-th reservoir can be calculated as:
and for the entire structure:
Clearly in Equation (A.10) Qturb,j equals 0 when the turbine is turned off.
A-I.5. Sea-State and Global Efficiencies
According to previous definitions, for a given sea-state the efficiency of a SSG device can calculated by the following indexes:
The superscript “ss” has been introduced to remark that they refer to a single sea state. The first of the above efficiencies is termed sea-state hydraulic efficiency and describes the capability of the device of capturing the water coming from the overtopping waves. The second one represents a (sea-state) storage efficiency and gives the percentage of wave power, which is actually available for electricity production. The third one is a power production efficiency (in the sea state) and accounts of both the turbine strategy and the turbine efficiency.
When the entire climate at a given location is considered, rather than a single sea-state, then significant wave heights, wave periods and water levels are clustered in bins of assigned probability of occurrence, say
. Hence, for a given structure, the global efficiency indexes can be introduced as follows:
In Equation (A.13), the superscript “k” refers to the k-th combination of wave height, wave period and water level, to which corresponds the probability
Appendix II: The WOPSim Program
The acronym WOPSim stands for Wave Overtopping Power Simulation [20]. The program is capable of simulating a Sea Slot-cone structure with NRes reservoirs, each reservoir with an independent turbine set-up. It produces a time series of overtopping discharges and calculates the power produced by the turbines. The intention of WOPSim is to allow the user to optimize both the structure layout and the turbine strategy. Once the SSG geometry and the sea-state duration have been inputted, the software works on the mass balance, which must be satisfied at each time-step, Δt, and for each separate reservoir, j:
In Equation (A.14) Qin,j is the volume of overtopping water during the time Δt, Qturb, j is the flow through the turbine for the same time interval, Qres,j is the amount of water stored in the reservoir and Qover,j is the water overflow if the reservoir will be full. Furthermore, an option called “overflow to next reservoir” can be enabled, where the overflow at the j-th reservoir can be re-used (spillage) by the lower reservoirs (1 to j − 1). In that case Equation (A.14) is re-formulated as:
The time step Δt is assumed to be a fraction of the time domain wave period Tm. As far as the volume influx Qin,j is concerned, it is supposed to be constant over a “wave cycle” of duration Tm and to vary wave by wave. Thus, a random series of overtopping discharges is simulated, using the approach described in [34], which is based on a three parameters Weibull distribution. One of these parameters is the mean overtopping discharge, qov,j, whose estimation is discussed in Section 2.
Qturb, j is computed at each time step based on both the turbine strategy and the turbine characteristics:
where the hydraulic head Hh and the freespace fj (which rules the ON/OFF periods) come from the preceding calculation step. Analogously, the power production during Δt can be evaluated as [Equation (A.10)]:
The knowledge of Qin,j and Qturb, j allows calculating, by difference, the amount of water stored in the reservoir and, accordingly, the new values of the hydraulic head Hh and of the freespace fj. If the water level in the reservoir overcomes the crest level Rc,j, then overflow takes place. Once the simulation has been completed, the program computes all the efficiency indexes defined in Appendix I.
References
- Falcão, A.F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Harris, R.E.; Johanning, L.; Wolfram, J. Mooring Systems for Wave Energy Converters: A Review of Design Issues and Choices. In Proceedings of the World Renewable Energy Congress VII, Denver, CO, USA, 29 August–3 September 2004.
- Tapping the Sun and Moon. Available online: http://www.siemens.com/innovation/pool/en/publikationen/publications_pof/pof_spring_2007/wave_power_plants/pof107art51_pdf_1449430.pdf (accessed on 30 January 2012).
- The Seawave Slot-Cone Generator (SSG) Concept. Available online: http://www.waveenergy.no/WorkingPrinciple.htm (accessed on 30 January 2012).
- Harnessing Energy from Our Oceans; Pelamis Wave Energy Project Information Sheet; E.ON Climate & Renewables UK Ltd.: Coventry, UK; Available online: http://www.eon-uk.com/images/Pelamis_demonstration_project_information_sheet.pdf (accessed on 30 January 2012).
- Kofoed, J.P. Wave Overtopping of Marine Structures—Utilization of Wave Energy. Ph.D. Dissertation, Aalborg University, Aalborg, Denmark, 2002. [Google Scholar]
- Margheritini, L. R&D towards Commercialization of Sea Wave Slot Cone Generator (SSG) Overtopping Wave Energy Converter: Selected Topics in the Field of Wave Energy. Ph.D. Dissertation, Aalborg University, Aalborg, Denmark, 2009. [Google Scholar]
- Kofoed, J.P. Experimental Hydraulic Optimization the Wave Energy Converter Seawave Slot-Cone Generator; Technical Report; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2005; 1603-9874. [Google Scholar]
- Kofoed, J.P. Vertical Distribution of Wave Overtopping for Design of Multi Level Overtopping Based Wave Energy Converters. In Proceedings of the 30th International Conference on Coastal Engineering, San Diego, CA, USA, 3–8 September 2006.
- Margheritini, L.; Vicinanza, D.; Kofoed, J.P. Overtopping performance of Sea wave Slot cone Generator. In Proceedings of the ICE Conference Coasts, Marine Structures and Breakwaters, Edinburgh, UK, 2009.
- Vicinanza, D.; Frigaard, P. Wave pressure acting on a seawave slot-cone generator. Coast. Eng. 2008, 55, 553–568. [Google Scholar] [CrossRef]
- Kofoed, J.P. Model Testing of the Wave Energy Converter Seawave Slot-Cone Generator; Technical Report; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2005; 1603-9874. [Google Scholar]
- Margheritini, L.; Lander, V.; Kofoed, J.P.; Troch, P. Geometrical Optimization for Improved Power Capture of Multi-level Overtopping Based Wave Energy Converters. In Proceedings of the International Society of Offshore and Polar Engineers (ISOPE) Conference, Osaka, Japan, 21–26 June 2009.
- Margheritini, L.; Vicinanza, D.; Frigaard, P. Sea Slot Cone Generator Overtopping Performance in 3D Conditions. In Proceedings of the International Society of Offshore and Polar Engineers (ISOPE) Conference, Vancouver, Canada, 10–12 June 2008.
- De Waal, J.P.; van der Meer, J.W. Wave Runup and Overtopping on Coastal Structures. In Proceedings of 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992.
- Van der Meer, J.W.; Janssen, J.P.F.M. Wave run up and wave overtopping at dikes. In Wave Forces on Inclined and Vertical Wall Structures; Kobayashi, N., Demirbilek, Z., Eds.; American Society of Civil Engineers (ASCE) Publications: Reston, VA, USA, 1995; pp. 1–27. [Google Scholar]
- Le Méhauté, B.; Koh, R.C.Y.; Hwang, L. A systhesis of wave run-up. J. Waterw. Coast. Eng. Div. 1968, 94, 77–92. [Google Scholar]
- Franco, C.; Franco, L. Overtopping formulas for caisson breakwaters with non-breaking 3D waves. J. Waterw. Port Coast. Ocean Eng. 1999, 125, 98–107. [Google Scholar] [CrossRef]
- Margheritini, L.; Kofoed, J.P. Parametrical Numerical Study on Breakwater SSG Application; Contract Reports by Department of Civil Engineering (DCE), Aalborg University: Aalborg, Denmark, 2008. [Google Scholar]
- Meinert, P.; Gilling, L.; Kofoed, J.P. User Manual for SSG Power Simulation 2; Technical Report; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2008; 1603-9874. [Google Scholar]
- Van der Meer, J.W.; d’Agremond, K.; Gerding, E. Toe Structure Stability of Rubble Mound Breakwaters. In Proceedings of the Advances in Coastal Structures and Breakwaters Conference; Institution of Civil Engineers, Thomas Telford Publishing: London, UK, 27–29 April 1995; pp. 308–321. [Google Scholar]
- Tanimoto, K.; Takahashi, S. Design and construction of caisson breakwaters: The Japanese experience. Coast. Eng. 1994, 22, 57–77. [Google Scholar]
- Zanuttigh, B.; Margheritini, L.; Gambles, L.; Martinelli, L. Analysis of Wave Reflection from Wave Energy Converters Installed as Breakwaters in Harbours. In Proceedings of the European Wave and Tidal Energy Conference (EWTEC), Uppsala, Sweden, 7–10 September 2009.
- Zanuttigh, B.; van der Meer, J.W. Wave reflection from coastal structures in design conditions. Coast. Eng. 2008, 55, 771–779. [Google Scholar] [CrossRef]
- Zanuttigh, B.; van der Meer, J.W.; Lykke Andersen, J.W.; Lara, J.L; Losada, I.J. Analysis of wave reflection from structures with berms through an extensive database and 2DV numerical modelling. In Proceedings of 31st International Conference on Coastal Engineering, Hamburg, Germany, 31 August–5 September 2008.
- Salerno, D. Experimental investigation on an overtopping wave energy converter. M.Sc. Thesis, University of Naples “Federico II”, Napoli, Italy, 2011. [Google Scholar]
- Vicinanza, D. Impact pressure/force on vertical and composite breakwaters under breaking waves. Ph.D. Dissertation, University of Naples Federico II, Napoli, Italy, 1997. [Google Scholar]
- Takahashi, S.; Hosoyamada, S.; Yamamoto, S. Hydrodynamic Characteristics of Sloping Top Caissions. In Proceedings of the International Conference on Hydro-Technical Engineering for Port and Harbour Construction; Port and Harbour Research Institute: Yokosuka, Japan, 19–21 October 1994. [Google Scholar]
- Vicinanza, D.; Ciardulli, F.; Buccino, M.; Calabrese, M.; Kofoed, J.P. Wave loadings acting on an innovative breakwaters for energy production. J. Coast. Res. 2011, 64, 608–612. [Google Scholar]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific: Singapore, 1993. [Google Scholar]
- Cuomo, G.; Allsop, N.W.H.; Takahashi, S. Scaling wave impact pressures on vertical walls. Coast. Eng. 2010, 57, 604–609. [Google Scholar] [CrossRef]
- Margheritini, L.; Vicinanza, D.; Frigaard, P. SSG wave energy converter: Design, reliability and hydraulic performance of an innovative overtopping device. J. Renew. Energy 2009, 34, 1371–1380. [Google Scholar] [CrossRef]
- Wave Energy Converters for Electrical Production, Second University of Naples Founded Project PRIST 2007. Available online: http://www.italywavenergy.it (accessed on 30 January 2012).
- Franco, L.; de Gerloni, M.; van der Meer, J.W. Wave Overtopping on Vertical and Composite Breakwaters. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).