1. Introduction
Developing some renewable alternative energy in remote areas where the fuel delivery and the grid extension are both costly is an imminent requirement [
1]. Wind power systems are becoming increasingly cost competitive as compared with conventional power systems and are gradually accepted as the cheapest renewable energy source in many countries all over the world [
2]. Solar energy has expressed its unique advantage in the remote area where the cost of the power transmission is very high or even has no power supplies, although solar power is too costly to be economic. Integrating wind and solar resources in a proper combination can overcome the drawback of their unpredictable nature and dependence on weather and climatic changes. Therefore, it is convenient to develop a microgrid that consists of wind-turbine generator (WT), photovoltaic array (PV) and battery backups to satisfy power demands in remote areas.
In order to utilize the renewable energy cost effectively, many researchers have studied the algorithm to calculate the capacity of applicable generator units that can constitute a reliable power system with low cost. Many different sizing methods [
3,
4], such as iterative method and artificial intelligence method, have been reported to design a techno-economically optimum hybrid renewable energy system.
The iterative method traverses almost all the possible combinations of generator units by linearly changing the values of the corresponding decision variables, and the optimum configuration can be identified finally by calculating the reliability and system cost for each combination. Borowy and Salameh [
5] presented a methodology to calculate the optimum combinations of the number of batteries and PV arrays for a stand-alone hybrid PV/wind system. In the design process, for each wind turbine of different type and capacity, all combinations of the number of batteries and the number of PV arrays were compared by judging whether the system cost was the lowest and whether the system reliability was satisfied. Habib [
6] calculated the optimal percentage of power produced by PV and WT based on analyzing different solar/wind ratio to satisfy a constant power demand and achieve the minimal capital cost. The Hybrid Solar-Wind System Optimization Sizing (HSWSO) model was presented in [
7] to select the configuration of the hybrid solar-wind systems employing a battery bank by seeking the optimal economic index of Loss of Power Supply Probability (LPSP) through changing number of PV arrays, the orientations of PV arrays, the capacity of wind turbine, the tower height of wind turbine, and the battery capacity. Diaf
et al. [
8] presented a sizing model to estimate the appropriate dimensions of a stand-alone hybrid PV/wind system on the basis of LCE (Levelised Cost of Energy). The curves of PV power capacity versus the wind power capacity are summarized for five different storage capacity in that study. While the wind/total energy production ratio is varying from 0 to 1, the optimum ratio will be found to guarantee a zero LPSP with minimum LCE. Prasad [
9] also developed a new method in which the computational procedure involves sequential processing of three loops, namely outer, middle and inner loops, for calculating the required size of wind turbines, solar arrays and batteries.
The use of heuristic techniques, such as evolutionary algorithms, has been proposed in order to obtain solutions in a reasonable time. Due to their ability of handling complex nonlinear problem, more decision variables can be involved without extending computing time. Using genetic algorithms, Koutroulis
et al., [
10] calculated the optimal number and type of each component of the stand-alone PV/wind system to minimize the 20-year round total system cost. The load power requirement was considered as constraint condition of the optimization problem and must be completely met. The same method has been applied to analyze a hybrid power system that supplies power for a telecommunication relay station on a remote island [
11]. Two new decision variables (PV array slope angle and turbine installation height) were involved in the calculation. Besides, the LPSP and annualized cost of system (ACS) were both considered as optimization objectives. To avoid being trapped in local minima, other different evolutionary algorithm like simulated annealing was performed to obtain optimum size of a PV/wind integrated hybrid energy system with battery storage [
12] .
As the number of optimization variables rises, the computation time increases exponentially when using the classic iterative method but is unaffected when the evolutionary algorithm is used. However, evolutionary algorithm has its shortcomings in that it may fall into local optimum.
In this paper, a simple optimization algorithm to determine the optimum component size for a stand-alone microgrid power system employing an iterative scheme is introduced. Taking into account the relationship of decision variables, the number of iterations will be reduced effectively. As the assistant device, the batteries must have sufficient capacity to store excess energy and supply power when there is a shortage of the renewable energy. Strictly speaking, the battery cannot be seen as a power generation unit, because its supply of electricity comes from the storage of previously generated excess electricity. Firstly, based on the observation that the state of charge (SOC) of battery should be periodically invariant, the needed number of generator units in the microgrid power system can be calculated directly. Then, to satisfy load power requirement entirely, the appropriate capacity of battery can be easily decided. Finally, the optimal sizing of hybrid microgrid is given in the sense that the life cycle cost of system is minimized.
2. Stand-Alone Microgrid Power System
The power system considered here is composed of three parts: WT, PV and battery bank. The two former units generate electricity, in accordance with the local wind and solar energy resources, to supply load; the battery bank forms the energy storage system that can supply the load when there is lack of electricity, and store the surplus power when the power generated exceeds the load. Energy storage system is essential to cover the shortage of the renewable energy’s unpredictable and fluctuant nature, but its existence brings difficulties to the sizing problem.
2.1. Estimating the Output Power of Wind Turbine
The speed of wind is often represented by a random variable. The Weibull distribution function with two parameters is commonly used to describe wind speed data [
13,
14]. It provides a convenient representation of the wind speed data for wind energy calculation purposes. The general representation of the Weibull distribution is given by:
where
is the wind speed (m/s),
c is the scale factor of Weibull distribution with unit of speed, and
k is the shape factor of Weibull distribution, which is dimensionless. There are several methods for calculating the parameters of the Weibull wind speed distribution for wind energy analysis [
15]. In this paper we calculate the two parameters using:
where the Γ( ) is the gamma function,
is the average value of wind speed data, and
is the standard deviation of wind speed data.
The available wind generator power
can be expressed by a function of
:
where
is the rated power of the turbine,
is the cut-in wind speed,
is the rated wind speed,
is the cut-out wind speed,
k is the Weibull shape parameter.
The distribution functions of the wind speed were calculated for every hour in a day. Then, the average output power of the wind turbine, whose specifications are provided by the manufacturer, can be calculated using the following equation:
where
, and
.
2.2. Estimating the Output Power of PV Array
When there are different level of temperatures and irradiation effects on the PV module, the I-V characteristic of PV module could be different. The power generated by the PV array is not only dependent on the solar irradiation but also dependent on the ambient temperature of the site. A maximum power point tracker (MPPT) is often used in the PV array to reach the maximum output power at any radiation level [
16,
17]. The maximum output power at different radiation and temperature is calculated by the following equation:
where
is the total area of the PV module (
),
is the temperature error of the PV module between the cell temperature
and the reference cell temperature
(
),
is the temperature coefficient, and
is the PV module generation efficiency.
Because of cloud cover and other insolation reducing phenomena, the solar irradiance
G can also be represented by a random variable [
18]. It has been shown that the beta distribution with parameters
α and
β can describe the solar irradiance
G:
where the
is the maximum solar irradiance during a certain interval. The two parameters can be evaluated by the mean value
and the variance
as shown below:
Once the solar irradiance and temperature were given for every hour of a day, the average output power of a PV array whose specifications are provided by the manufacturer can be calculated using Equation (
8):
2.3. Performance of Battery
Energy storage is necessary because the generation of renewable energy is inherently intermittent. The stored energy can supply the load when there is a lack of electricity, and store surplus power when the generated power exceeds the load. The battery behavior is mainly characterized by the SOC [
19]. The charging/discharging and self-discharge efficiency are both ignored in the model formula of battery. The simplification is carried to this point where the model is still amenable to mathematical treatment. Alternatively, the charging/discharging efficiency can be approximated by multiplying an empirical coefficient (larger than 1) of the
. The state of charge at the moment
t can be obtained using the following equation:
where
is the electric power demand at moment
t,
is the battery voltage,
is the capacity of battery bank,
denote the number of WT, and
is the number of PV.
If , the power generated by both the PV arrays and the wind turbines exceeds the load, hence the battery will be charging.
If , the power generated by both the PV arrays and the wind turbines is insufficient to supply the load, hence the battery will be discharging.
3. Simple Sizing Algorithm
Before starting the algorithm, the sizing problem to determine the number of WT (), the number of PV and the required battery capacity is formulated as follows.
Sizing problem for , and
Given:
- (1)
A time horizon ;
- (2)
Average powers and respectively generated by WT and PV, and average power demanded by the load , at every moment t in the time horizon .
- (3)
A cost index
Find: The optimal solution,
(WT) and
(PV) and the required battery capacity
such that
3.1. Analysis of the System Cost
It is crucial that the stand-alone microgrid power system can be built under the optimum configuration considering both investment and system power reliability. The analysis of cost is necessary to utilize the renewable energy resources efficiently and economically. There are many ways to calculate the system cost [
20,
21]. Here the concept of life cycle cost of system, consisting of the initial capital cost, the operation and maintenance cost and the components replacement cost, is adopted in this paper, which is expressed by the following equations [
9]:
where
,
and
are the number of wind turbines, PV arrays and batteries combined in the hybrid system respectively,
,
and
are the initial capital cost of wind turbines, PV arrays and batteries respectively,
,
is specified percentage of the initial capital,
is the life time of the system and often equals to the life time of the PV array as it has longer service life than the other two components,
and
are the service time of the battery and wind turbine respectively,
is the actual interest rate,
e is the nominal rate and
d is the escalation rate.
If the specifications of wind turbine, PV array and battery are given, the cost can be calculated by the unit sizing in terms of the function .
3.2. SOC Cycle Invariance
It is the existence of the battery banks that make the sizing problem very difficult. As shown in (
9), SOC depends on the history data and the difference between the generated power and the demanded power. When the power generated by the wind turbines and the PV arrays is larger than the load demands, the battery bank serves as the energy storage to save the redundant power; when the generated power is less than the load demands, the battery bank works as the generator to provide the lacked power.
In fact, the power generated by the battery bank is the power that the battery bank stored in the past. The battery bank is not an energy source but an assistant device. To ensure good performance of the battery bank, SOC should be returned to the initial state each period of time; otherwise, SOC will be gradually decreasing over time. This leads to the following SOC cycle invariance criterion.
SOC cycle invariance criterion: The SOC of battery bank should be invariant at the end of time horizon.
With this criterion, our sizing algorithm no longer considers the SOC value of each time instant, but directly determines the numbers of WT and PV according to the load demand. The SOC cycle invariance criterion implies that:
From Equation (
9), it follows that:
Combination of (
14) and (
15) yields,
Once the number of WT is determined, the number of PV arrays can be directly calculated by
After
and
are obtained, the remainder is to determine the capacity of battery. According to the power generated by
wind turbines and
PV arrays (
) and the load demand (
) at every instant
t, we can calculate the power flowing into or out of the battery
by:
At present, the capacity of battery
is undetermined, then we let
denote the available energy capacity in battery bank at the moment
t:
here the initial condition
is set to be zero in the calculation, which means the battery is empty at the beginning.
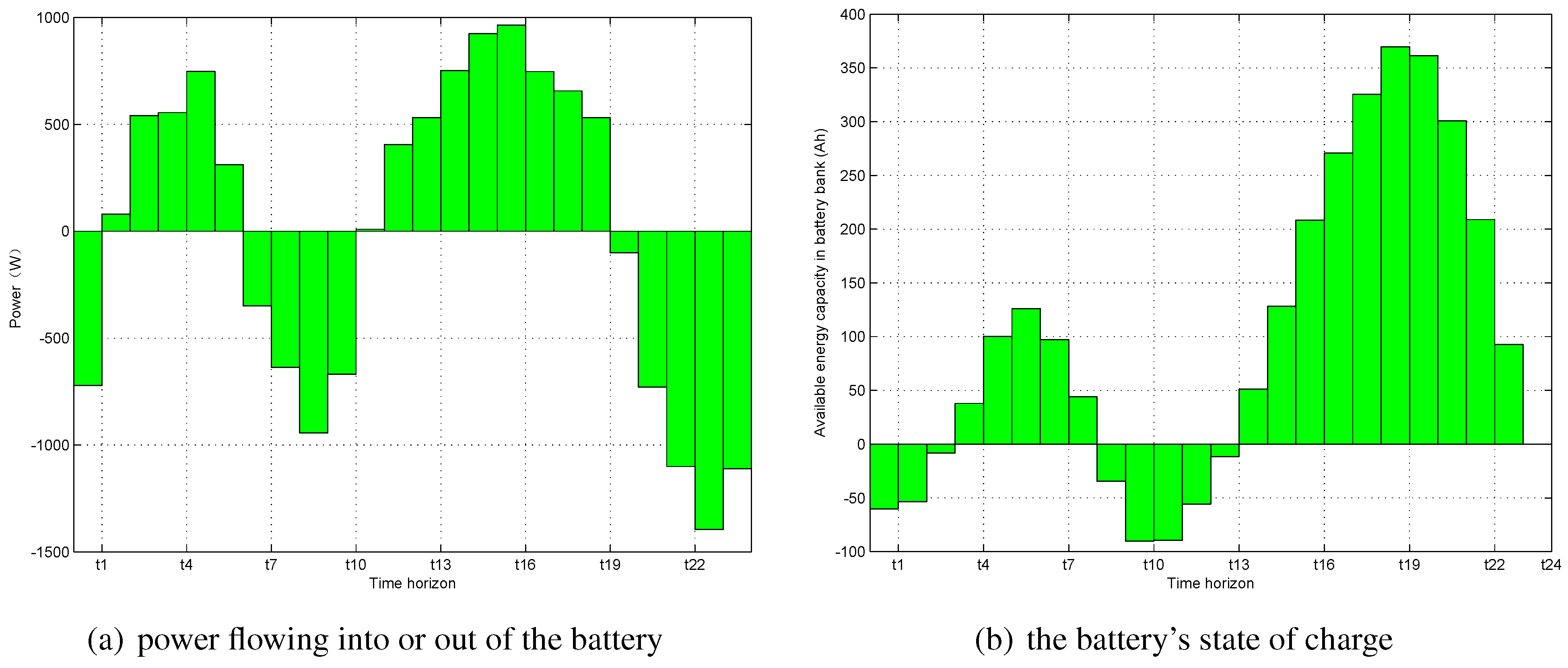
Figure 1 illustrates an example of the calculated
and
of every hour in the time horizon
. As shown in the right subfigure, there are moments when the available energy capacity in battery bank is less than zero. This is because of the zero value initial condition and can be overcome by a suitable initial value.
In fact, what we focus on is the variation of
in the specified time horizon, rather than the absolute value of
at each time instant.
. Let the
and
represent the maximum and minimum available energy capacity in battery bank over the time horizon
:
Since
should be no less than zero, the capacity of battery
should satisfy
Figure 1.
The battery SOC and power flowing every hour of a typical day.
Figure 1.
The battery SOC and power flowing every hour of a typical day.
On the other hand, in order to improve the battery life and efficiency, the current flowing through the battery must be limited within a certain range, and then the maximum absorbable power [
22] must be considered in the calculation. The suggested limit is 1 C in the charging phase, that is,
Battery has a limited range of depth of discharge (DOD) [
23,
24], which means the amount of capacity withdrawn from a battery expressed as a percentage of its maximum capacity. Therefore, the allowable DOD must be taken into account so as to extend the working life of the battery. Combination of the above two inequalities yields
As addressed above, for a given , and can be directly calculated such that the power system composed of WT, PV and battery banks can satisfy the varying electricity demand of load.
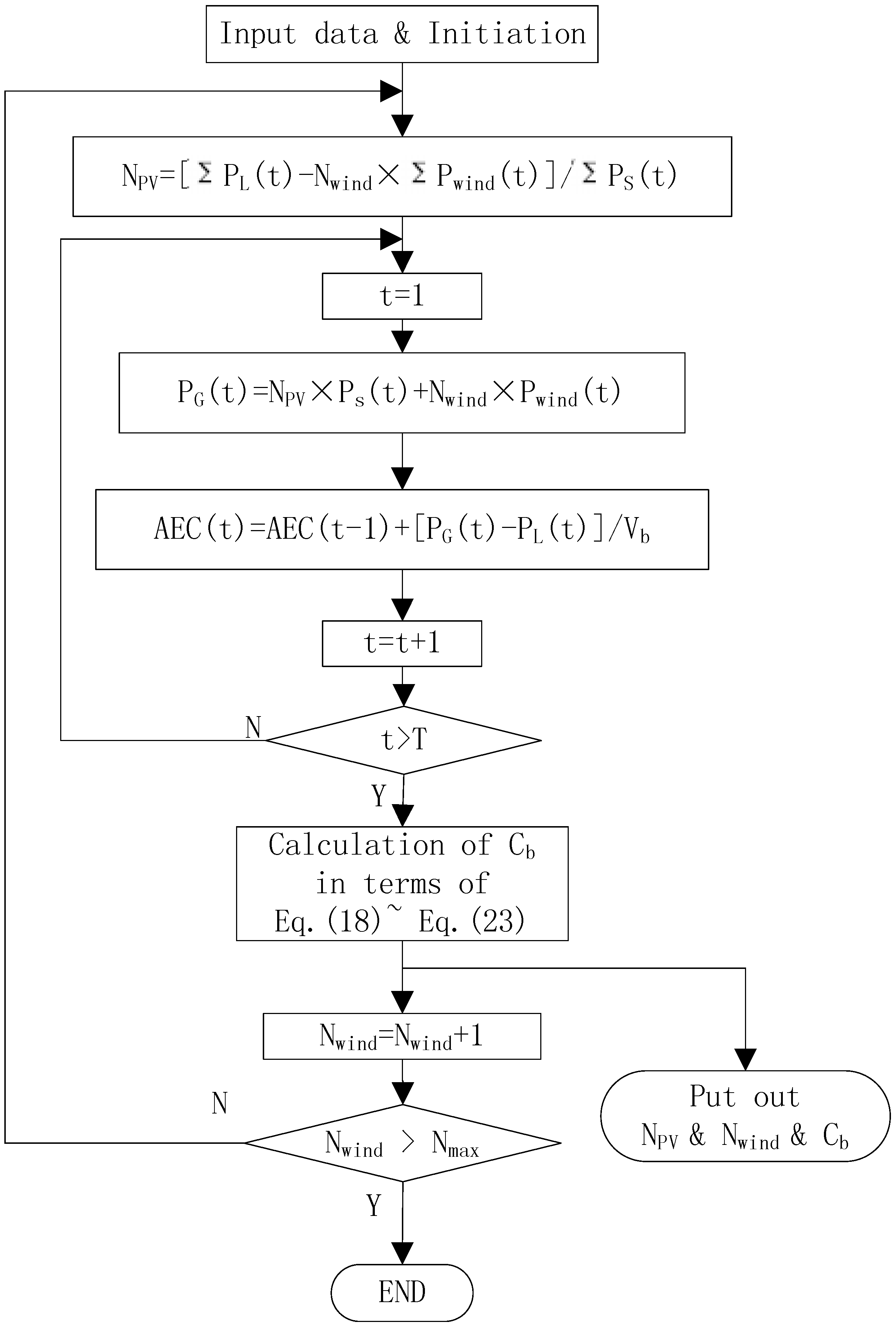
3.3. The Flowchart of Algorithm
The flowchart diagram of the proposed algorithm for getting feasible configurations is shown in
Figure 2. The input data for this program consists of: the hourly wind speed and solar radiation data; the daily load profiles [
]; the specifications of wind turbine, PV array and battery. The initialization includes the calculation of power generated by both the given wind turbine and the PV array, which is based on the collection of the wind speed and solar radiation data at the same hour every day to get the average daily curves.
is the maximum number of wind turbines allowed in the wind turbine alone system to meet load demand. Firstly, all the configurations of the system (
,
and
) satisfying the demand can be calculated by the algorithm as shown in
Figure 2. Then these solutions were applied to Equations (
10–
13) to obtain the corresponding
. Finally, the optimal solution that has the smallest
can be easily obtained.
Figure 2.
Flowchart of the algorithm for getting feasible configurations.
Figure 2.
Flowchart of the algorithm for getting feasible configurations.
4. A Case Study
In this section, we take the Zhoushan islands of China as an example to illustrate the efficacy of the proposed algorithm.
The Zhoushan islands have abundant light irradiation and are under the influence of subtropical oceanic monsoons. The whole archipelago is cool in summer and warm in winter, where August is the hottest and January is the coldest. The geographical coordinates of the region are N, E, 206 m above sea level. The average temperature of the whole year is about , the annual mean sunlight duration is about 2257 hours, and the total solar radiation is 4126∼4598 J/m. Due to the effect of the unstable season wind, this area has always been attacked by tropical storm in the early autumn and strong wind in the winter. The periodic and seasonal variation in wind and solar energy will be analyzed in the following section.
The chronological weather data of the Zhoushan islands over about the last four years period is chosen during the power potential analysis. These data were recorded by a cup generator anemometer, radiation sensor and thermometer at a height of 70 m. Weather data in time series was processed in advance. March, April and May have been considered as spring; June, July and August have been considered as summer; September, October and November have been considered as autumn; December, January and February have been considered as winter. In this paper, these irradiance level and wind speed data are calculated for every hour of a typical day in each season. The time horizon is 24 hours a day beginning at 8:00 am until 8:00 am of the next day.
4.1. Wind and Solar Power Potential
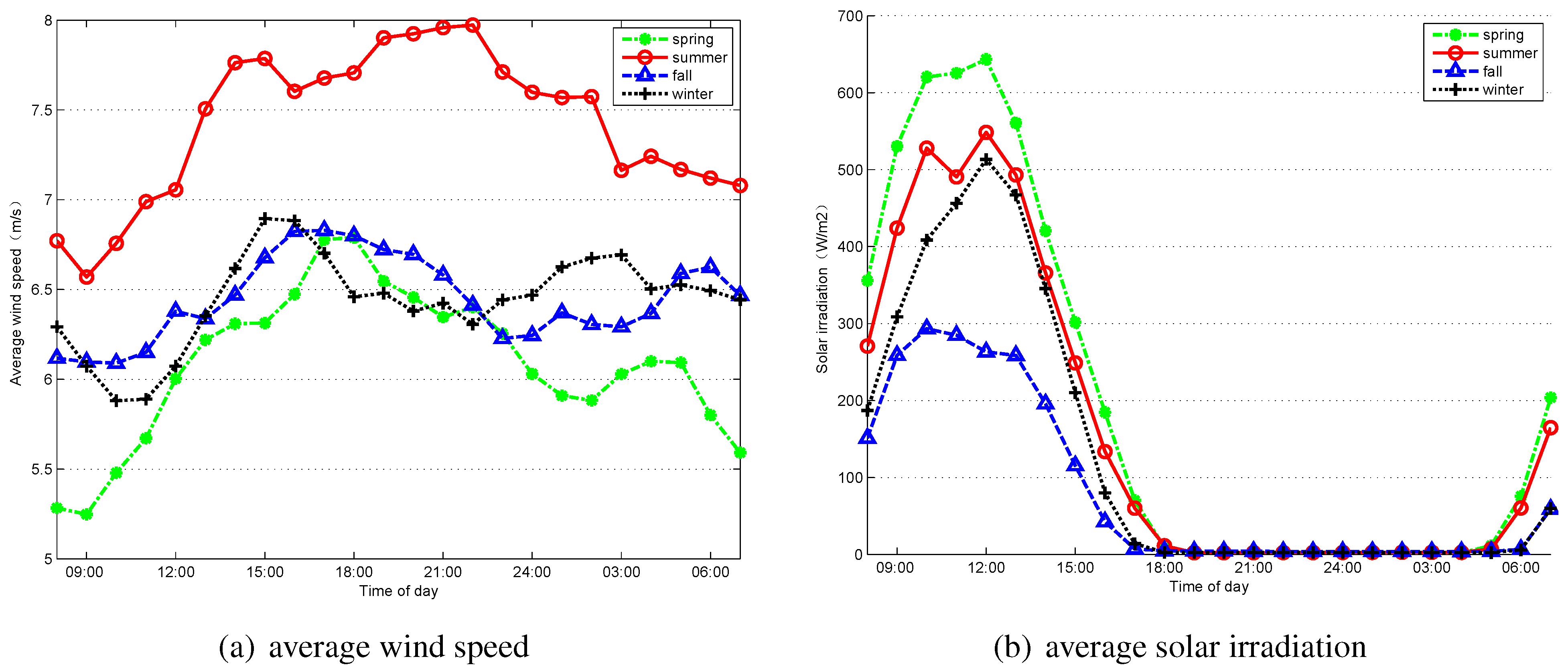
The Weibull distribution is the most commonly used function to describe the wind speed data. The mean speed of wind, shown in the left figure of
Figure 3, is respectively calculated at the same hour for each day in every season. Likewise, the right of
Figure 3 shows the hourly mean solar radiation of a day in every season (
am ,
am,
am,
hour ). A maximum power point tracker (MPPT) is often used in the PV array to calculate the maximum output power at any radiation level.
Figure 3.
Hourly seasonal mean solar irradiation and wind speed distribution in island.
Figure 3.
Hourly seasonal mean solar irradiation and wind speed distribution in island.
By comparing the left and right plots in
Figure 3, we can easily see that wind energy and solar energy resources could compensate each other well. In spring, the wind speed is relatively lower, but the solar radiation is the highest. Due to the influence of the plum rain season in early summer and the tropical storm in late summer, the average solar radiation in summer is poor, but the high wind speed can compensate for this. The solar radiation reaches a high level at about 10:00 am and drops until 1:00 pm. The energy generated by wind turbine becomes the main generator within the system at night.
4.2. Load Characteristic
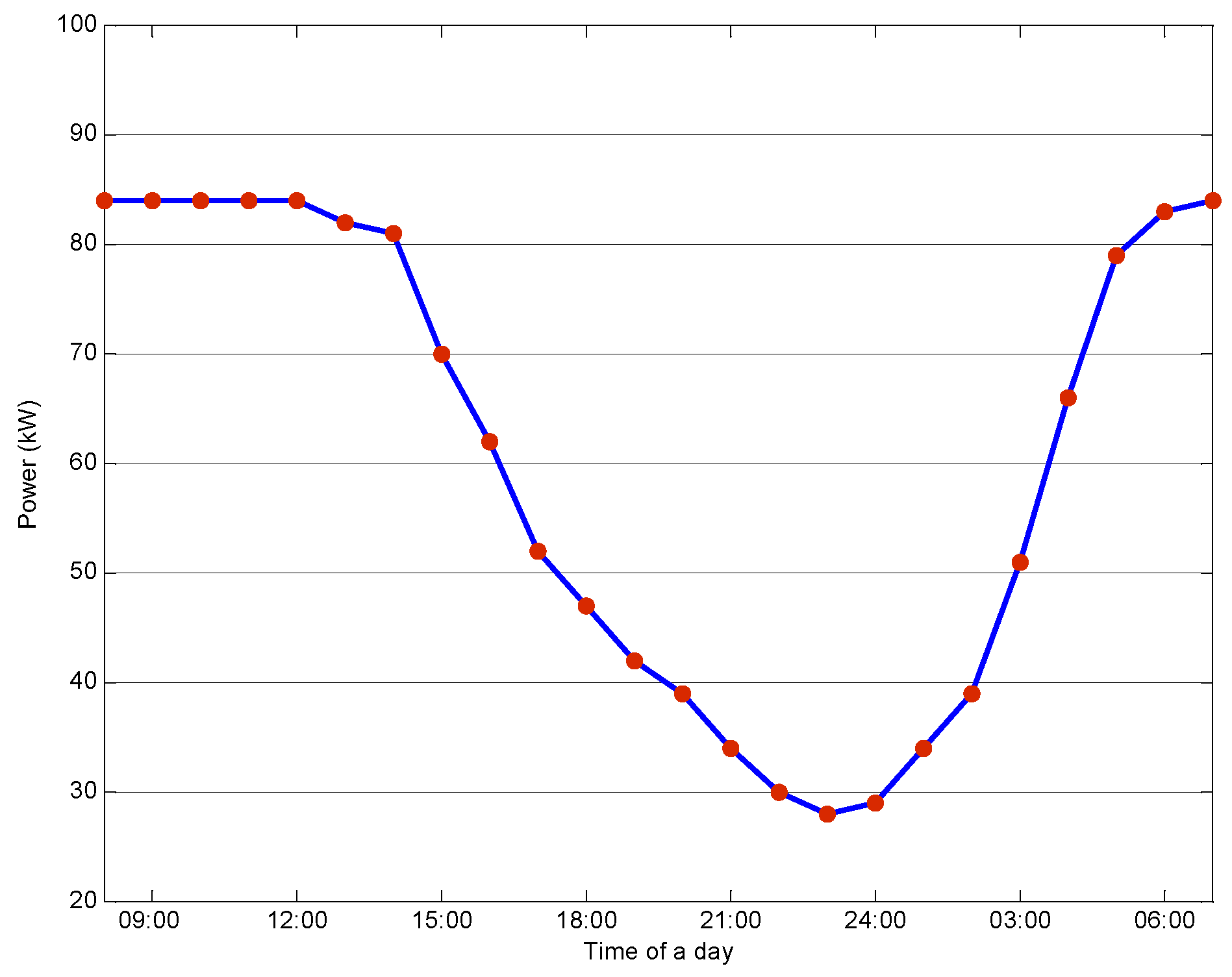
The daily load profiles in four different seasons have been considered.
Figure 4 shows the average office power demand of a day. Furthermore, depending on the season there are another two kinds of load,
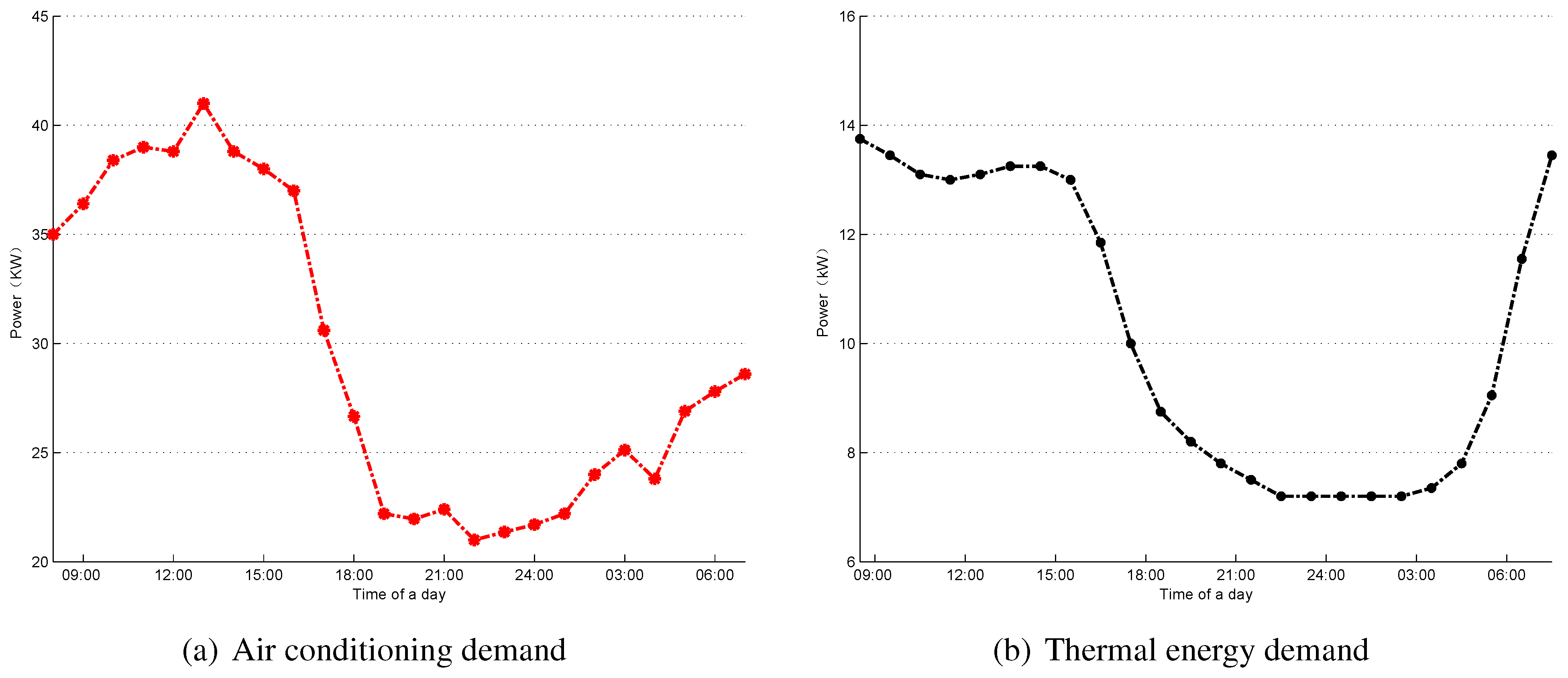
i.e., air condition and heat supply (
Figure 5). It has been assumed that the daily load does not change throughout all seasons, and the additional load will be considered when either air conditioning is needed in the hot summer or heat supply is needed in the cold winter.
Figure 4.
Hourly average office power demand of a day in the island.
Figure 4.
Hourly average office power demand of a day in the island.
Figure 5.
Load characteristic of air condition in summer and heat supply demand in winter.
Figure 5.
Load characteristic of air condition in summer and heat supply demand in winter.
According to the analysis of weather data above, a hybrid PV/wind power system is the most suitable solution. The installation of the energy storing system is essential to cover the shortage of the renewable energy’s unpredictable and fluctuant nature [
25].
5. Results and Discussion
The presented algorithm has been used to get the sizing of one microgrid project, which is designed to supply power for an office station (
Figure 4,
5) on a remote island in Zhoushan. Solar radiation and wind speed data in hourly time series for this region were applied to calculate the power generated by the generator unit of the system. As the previous treatment of weather data, the distribution functions for wind speed and the average solar radiation were calculated for every hour of a typical day, e.g., there are 1460 wind speed and solar radiation data collected for an hour considering a 365-day-long year.
Because the wind speed changes with height, the power output of a wind turbine must be calculated with consideration of the installation height and the hub height in addition to the specifications listed in
Table 1. Using the specifications of the PV arrays listed in
Table 2, the available energy generated from a PV array can be calculated according to the PV system model discussed above as well as the local solar radiation and temperature data. The capacity of a single employed colloidal battery is 100 Ah (12V), which has a round-trip efficiency of 0.85 and a depth of discharge (DOD) of 80%. The colloidal battery’s lifetime is 12 years, and the cost of one battery is 2700 RMB with a replacement cost of 1890 RMB. The cost of one turbine is considered to be 70737 RMB with a replacement cost of 41550 RMB, and the lifetime of a turbine is considered to be 20 years. The lifetime of the PV array is 25 years, which is the lifetime of this project, and its cost is considered to be 900 RMB. Considering the project lifetime to be 25 years, the annual real interest rate is taken as 8%.
Table 1.
Specifications of wind turbine used in the system.
Table 1.
Specifications of wind turbine used in the system.
Rated
Power (kW) | Hub
Height (m) | Rotor
Diameter (m) | Cut in
Speed (m/s) | Cut off
Speed (m/s) | Rated
Speed (m/s) |
|---|
| 10 | 15 | 8 | 3 | 40 | 10 |
Table 2.
Specifications of PV arrays used in the system.
Table 2.
Specifications of PV arrays used in the system.
Maximum
Power(W) | Temperature
Range () | Temperature
Coefficients | Module
Efficiency | Size of
module (mm) |
|---|
| 180 | | 0.5% | 15.8% | 1580 × 808 |
With the utilization of the program presented in the former section, a series of possible sizing results can be calculated for the office station load case. By Equation (
17), every needed number of PV arrays can be directly calculated as the chosen number of wind turbines increases from 1 to
. The results are tabulated in
Table 3. It can be seen that the number of PV arrays is decreased as the number of wind turbines in the project increases. According to these different combinations of wind turbines and PV arrays, the corresponding capacity of battery can be selected according to the method described by Equation (
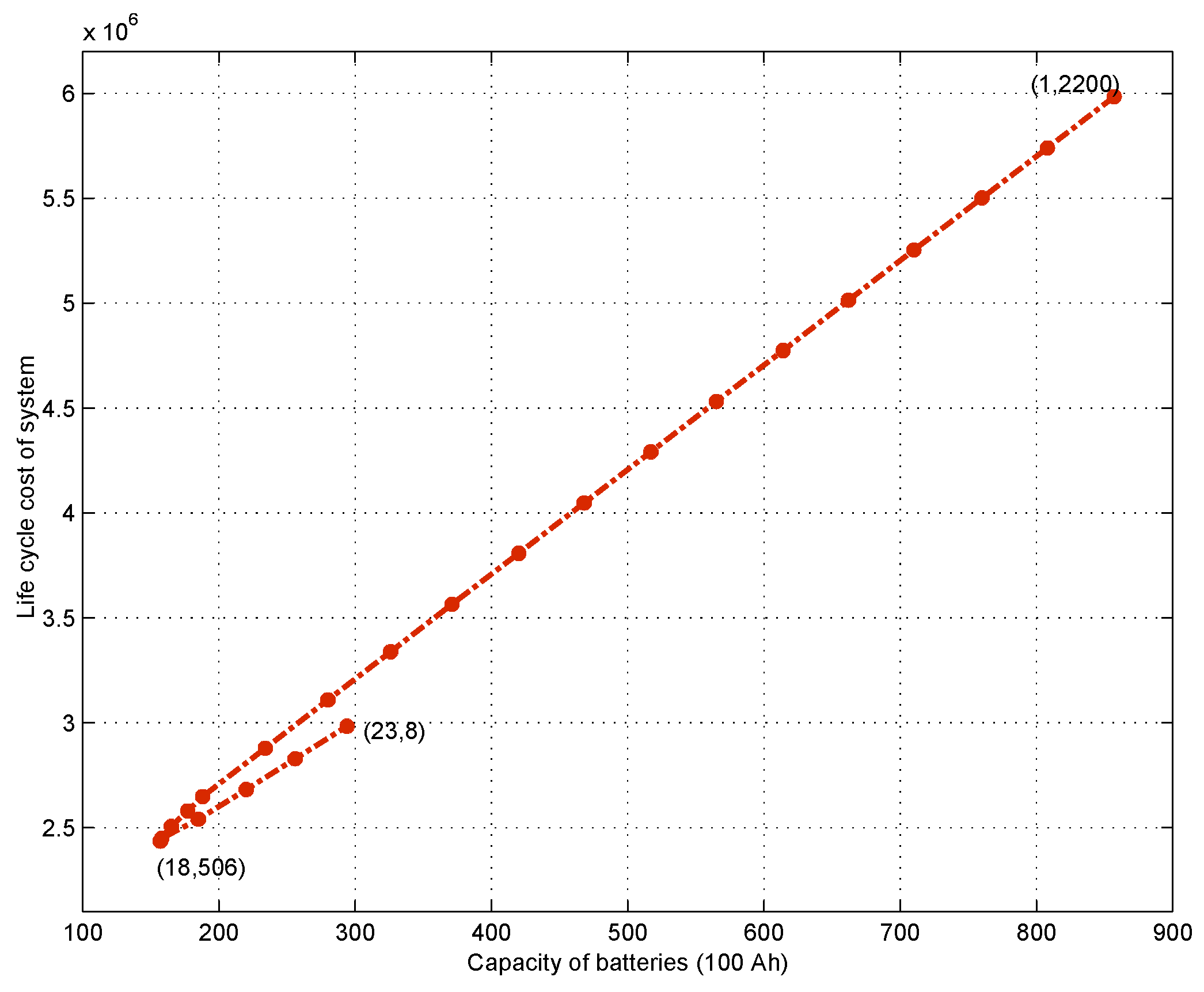
23). Here we assume that the DOD is approximately 65% such that the microgrid system can supply power to reliably meet the load demand. Then the curves of the life cycle cost of the system for different numbers of employed batteries are plotted in
Figure 6. An optimal solution is derived when the system consists of 180 kW wind turbine, 506 m
PV arrays and 160 battery banks with a life cycle cost of 2,435,523 RMB.
Table 3.
Numbers of wind turbines and PV arrays.
Table 3.
Numbers of wind turbines and PV arrays.
| | | | | |
|---|
| 1 | 2200 | 9 | 1403 | 17 | 606 |
| 2 | 2100 | 10 | 1303 | 18 | 506 |
| 3 | 2001 | 11 | 1204 | 19 | 407 |
| 4 | 1902 | 12 | 1104 | 20 | 307 |
| 5 | 1802 | 13 | 1005 | 21 | 207 |
| 6 | 1702 | 14 | 905 | 22 | 108 |
| 7 | 1603 | 15 | 805 | 23 | 8 |
| 8 | 1503 | 16 | 706 | | |
Figure 6.
Sizing results of the hybrid system in each season.
Figure 6.
Sizing results of the hybrid system in each season.
It can be seen that the optimal configuration of system with lower life cycle cost can be found after
iterations. Like in [
5], the needed iteration number is equal to the product of the maximum number of batteries
and the maximum number of PV arrays
when the capacity of wind turbine is given. Also in [
9], the computational procedure involves sequential processing of the three loops, namely the outer, middle and inner loops, for calculating the required size of wind turbines, solar arrays and batteries. The optimal configuration will be obtained after
iterations, which is the product of these three values.
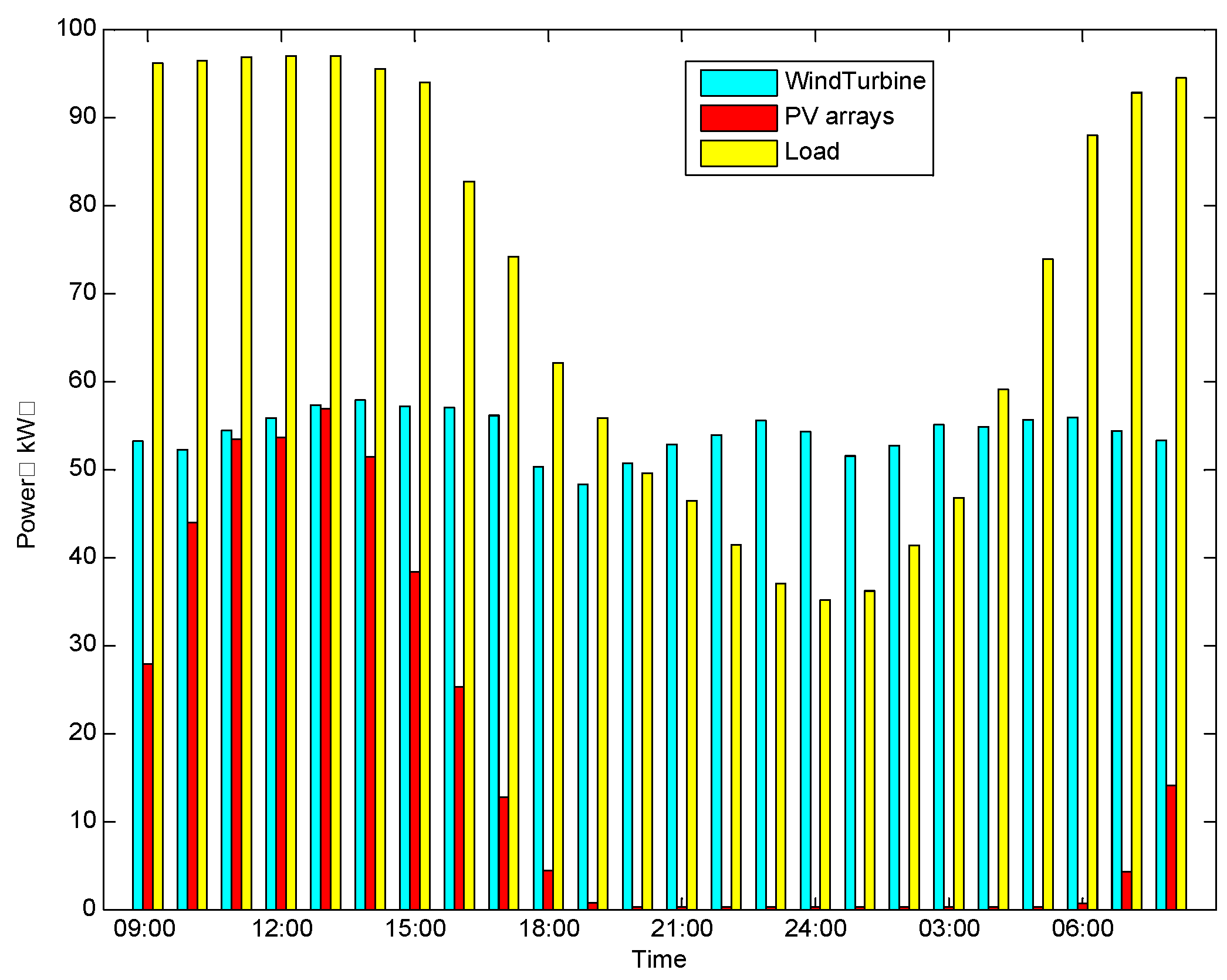
For the optimal system configuration studied, the hourly power generated by these wind turbines and PV arrays that constitute the microgrid system and the hourly average load are shown in
Figure 7. Before this microgrid with battery banks is put into operation, the initial battery SOC is assumed to be about 60% to better show its charging/discharging pattern.
Figure 8 shows the trajectory of SOC of the battery without considering seasonal effects. The results clearly reveal that the SOC at the start of every day is invariant, except for the first day when the initial battery SOC is larger than the invariant point.
Figure 7.
Hourly average output power of wind turbines and PV arrays and the hourly average demand of load.
Figure 7.
Hourly average output power of wind turbines and PV arrays and the hourly average demand of load.
Figure 8.
Battery SOC fluctuation without considering seasonal effects.
Figure 8.
Battery SOC fluctuation without considering seasonal effects.
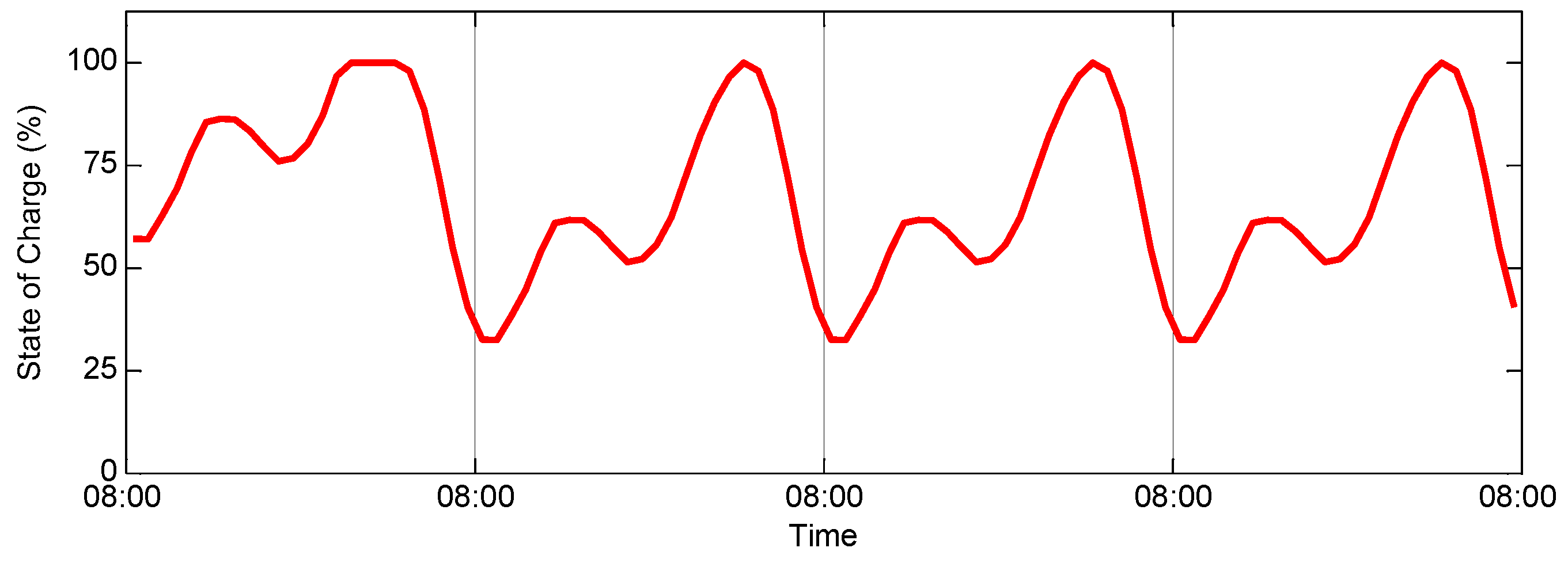
The wind energy and solar energy vary with the season and the load varies due to the application of air conditioning and heat supply in summer and in winter. The average seasonal daily curves of wind speed and solar radiation are shown in
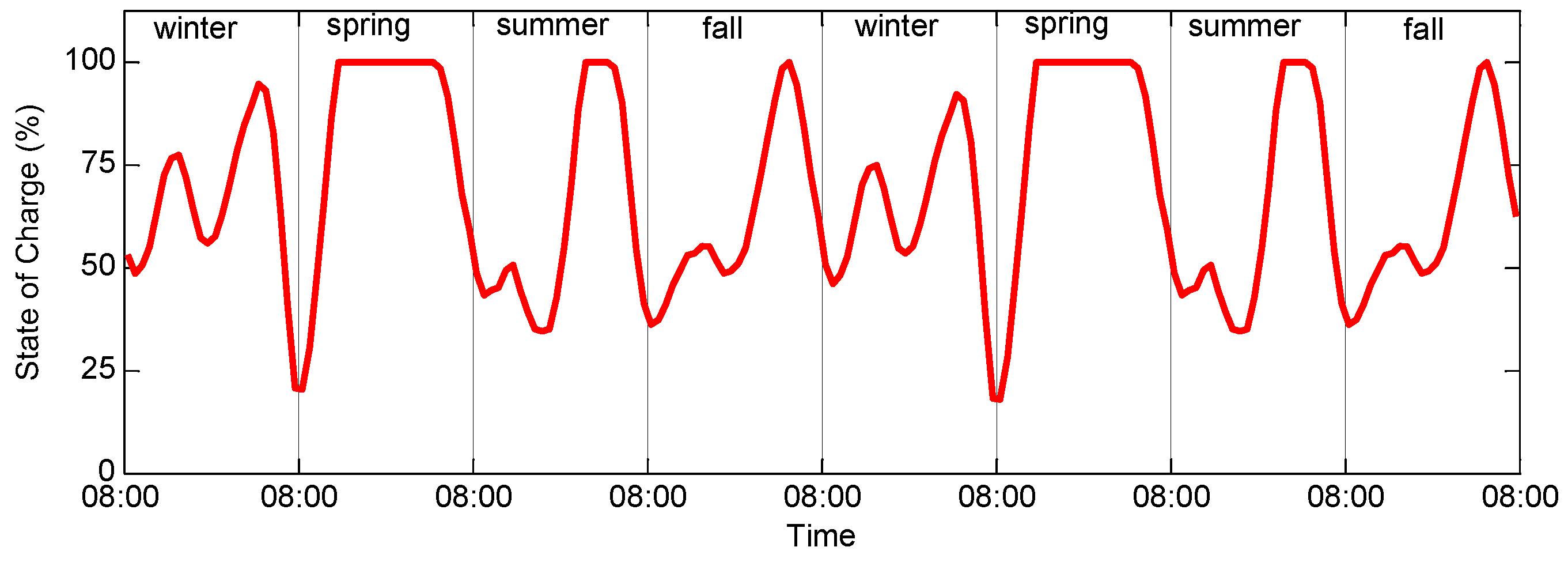
Figure 3. The robustness of this algorithm is verified in
Figure 9, where the average spring day, the average summer day, the average autumn day and the average winter day happens successively in a periodic order. The obtained optimal system configuration can still work well for different average seasonal days and therefore is robust against the changes of the environment. The smaller battery SOC occurs in the end of the average winter day because the total energy generation of microgrid system is relatively low. This deficiency is compensated by the following spring day, where much more power is supplied so that the battery SOC reaches the maximum point. Our method is based on the average data during the time interval and therefore is robust against a certain degree of data fluctuation around the average level. In engineering practice, there exist some rare worst-case situations such as persistent low-wind and low solar radiation weather. None of the sizing methods that use historical weather data can be completely immune to such situations. The stochastic sizing optimization is probably a good solution and is one focus of our further research.
Figure 9.
Battery SOC fluctuation considering seasonal effects.
Figure 9.
Battery SOC fluctuation considering seasonal effects.