Degradation Characteristics of Wood Using Supercritical Alcohols

Jeeban Poudel; Sea Cheon Oh

doi:10.3390/en5125038

and

Department of Environmental Engineering, Kongju National University, 275 Budae-dong, Cheonan, Chungnam 330-717, South Korea

^*

Author to whom correspondence should be addressed.

Energies2012, 5(12), 5038-5052;https://doi.org/10.3390/en5125038

This article belongs to the Special Issue Wood to Energy

Version Notes

Order Reprints

Abstract

In this work, the characteristics of wood degradation using supercritical alcohols have been studied. Supercritical ethanol and supercritical methanol were used as solvents. The kinetics of wood degradation were analyzed using the nonisothermal weight loss technique with heating rates of 3.1, 9.8, and 14.5 °C/min for ethanol and 5.2, 11.3, and 16.3 °C/min for methanol. Three different kinetic analysis methods were implemented to obtain the apparent activation energy and the overall reaction order for wood degradation using supercritical alcohols. These were used to compare with previous data for supercritical methanol. From this work, the activation energies of wood degradation in supercritical ethanol were obtained as 78.0–86.0, 40.1–48.1, and 114 kJ/mol for the different kinetic analysis methods used in this work. The activation energies of wood degradation in supercritical ethanol were obtained as 78.0–86.0, 40.1–48.1, and 114 kJ/mol. This paper also includes the analysis of the liquid products obtained from this work. The characteristic analysis of liquid products on increasing reaction temperature and time has been performed by GC-MS. The liquid products were categorized according to carbon numbers and aromatic/aliphatic components. It was found that higher conversion in supercritical ethanol occurs at a lower temperature than that of supercritical methanol. The product analysis shows that the majority of products fall in the 2 to 15 carbon number range.

Keywords:

wood degradation; supercritical ethanol; supercritical methanol; kinetic analysis; liquid product analysis

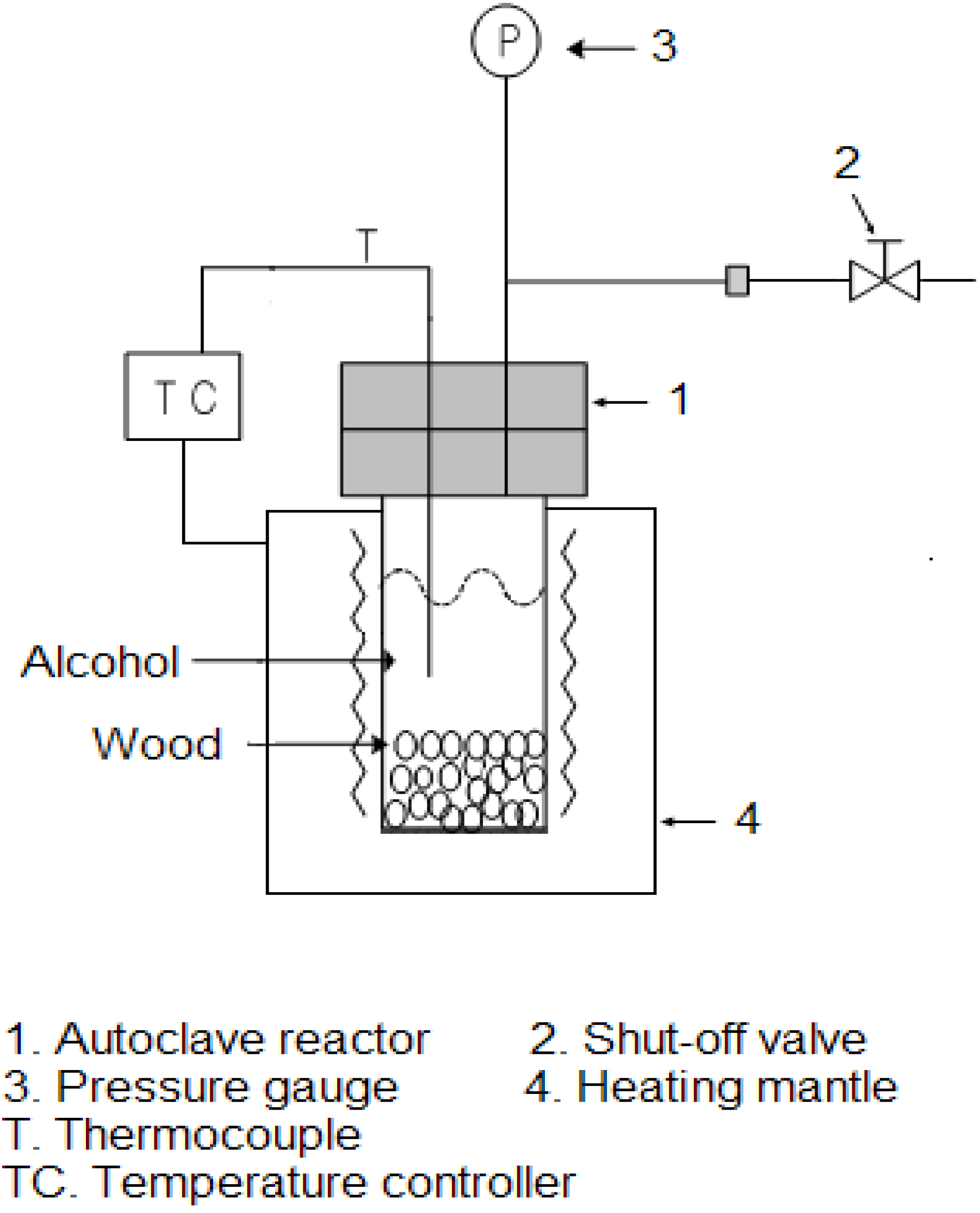
1. Introduction

When the World is seeking an environmentally benign fuel source, supercritical techniques can be a good support for other available technologies. Due to human activities of mass production, mass consumption, and mass waste since the early twentieth century, environmental issues such as global warming and acid rain have become increasingly serious problems in the World. Environmentally friendly biomass resources such as lignocelluloses could be utilized effectively as an alternative to fossil resources []. Biomass, as an energy source, has two striking characteristics. Firstly, biomass is the only renewable organic resource and is also one of the most abundant resources. Secondly, biomass fixes carbon dioxide in the atmosphere by photosynthesis []. Due to the limitations of homogeneous and heterogeneous catalytic reactions for biodiesel production from biomass, a sustainable and environmentally friendly technology using supercritical alcohol (SCA) has been receiving considerable attention. The liquid products in alcohol can be used directly as liquid fuel because alcohol itself is a good fuel []. Supercritical fluids are regarded as promising solvents for industrial use in the coming decades and their special physical properties have caught worldwide attention for a long period of time [,]. Several reviews have highlighted developments in theory, application, and instrumentation [,]. Supercritical fluids are also extremely compressible media, being both dense and compressible at the same time; their heat diffusion coefficient is generally very small compared to standard gases, while their mass diffusion coefficients are generally much larger than those of most liquids []. The advantages of supercritical fluid (SCF) technology in biodiesel production compared to conventional catalytic reactions are enormous and vital in solving issues involving energy security in the future. The use of supercritical fluid technology as a sustainable route for biodiesel production has vast potential compared to the catalytic processes [].

SCA technology is a noncatalytic process which makes separation and purification of biodiesel relatively easy and simple. Supercritical fluids (SCF) have the properties of both liquid and gaseous elements. Having a density close to liquids, the supercritical fluid has the ability to dissolve many components, whereas the high diffusivity and low viscosity of the supercritical fluid also enable it to behave like a gas. Such mobility properties of the supercritical fluid tend to maximize the yields of the products. Along with this major advantage of SCF, others have been mentioned in the referred papers [,]. Supercritical ethanol (SCE, T_c = 513.9 K, P_c = 61.4 bars) and supercritical methanol (SCM, T_c = 512.6 K, P_c = 80.9 bars) have lower critical temperatures and pressures than water (T_c = 647.1 K, P_c = 220.6 bars), which shows that SCA can offer milder conditions for the reactions [,,]. In addition, alcohols are expected to readily dissolve relatively high molecular weight products from cellulose, hemicelluloses, and lignin due to their high dielectric constants when compared with those of water. Further, methanol and ethanol are ubiquitous solvents. The alcohols may be alternatives to water as supercritical solvents considering their less corrosive and aggressive chemical nature, lower critical temperatures and pressures, and reasonably high dielectric constants [,,].

Wood and other forms of biomass can be used in various ways to provide energy through combustion, gasification, pyrolysis, etc. []. SCA have not been studied extensively so far; however, SCA, like SCE and SCM, shows some promising results for better conditions. High conversions (80%–100%) were obtained when the reaction was conducted in SCA []. The kinetics of wood degradation using SCA were studied in this work, but factors including hard reaction conditions, complicated compositions of degradation products, and difficulty of continuous operation tend to limit the kinetic study on the wood degradation in SCF. For SCA, although they are important cosolvents and excellent substitutes for supercritical water [], questions regarding their intermolecular forces, microscopic structure, dynamic property, and hydrogen bonding still remain unanswered. In this work, the kinetics of wood decomposition has been analyzed to make a comparative study of the activation energy using various kinetic analysis methods. This paper also includes the analysis of the liquid products obtained from this work. The analysis of the characteristics of the liquid products on increasing reaction temperature and time has been performed through Gas Chromatography Mass Spectrometry (GC-MS).

2. Experimental Details

2.1. Materials and Apparatus

Crushed chopsticks were used as wood samples which were subjected to supercritical treatment. Proximate and elemental analysis of the wood samples is shown in Table 1. As shown in Table 1, the volatile material is a major component of wood samples used in this work while the initial moisture and fixed carbon are 7.78% and 13.25%, respectively. From the elemental analysis, it was seen that carbon and oxygen were major components, with weight percentages 52.35% and 39.75%, respectively. As solvent, ethanol (99.9% purity) and methanol (99.5% purity) produced by OCI Company Ltd. (Seoul, Korea) was purchased and used.

Table 1. Proximate and elemental analyses of wood sample used in this work.

**Table 1.** Proximate and elemental analyses of wood sample used in this work.
Proximate analysis		Elemental analysis
Items	Weight fraction (%)	Elements	Weight fraction (%)
Initial moisture	7.78	Carbon	52.35
Volatile matter	78.52	Hydrogen	6.63
Fixed carbon	13.25	Nitrogen	0.16
Ash	0.45	Oxygen	39.75
		Sulfur	0.01

2.2. Apparatus and Procedure

Figure 1 shows the schematic diagram of 25 mL, batch-type reactor manufactured by Parr Instrument Co. (Moline, IL, USA). The permissible reactor conditions are 500 °C and 55 MPa. The experiments were conducted under unstirred conditions. Initially, the wood sample was put in a 105 °C oven for at least 24 h to dry. At room temperature, a total of 1 g of wood sample was charged the stainless steel autoclave with 16 g of ethanol. The reaction was started by heating the vessel in an electric furnace, and the reaction temperature was controlled by a PID controller in order to raise the temperature to a set value. The pressure inside the vessel was monitored by a pressure gauge. When the reaction temperature got to the preset condition, the heating of the vessel was interrupted and the vessel was moved into a water bath. After the vessel was cooled to room temperature, the product was taken out of the vessel. In the kinetic analysis experiments, the solid residue was rinsed with alcohol to remove the absorbed liquid organic fraction and weighed after the removal of the solvent in the oven for 24 h. The heating rate was 3.1, 9.8, and 14.5 °C/min for SCE. The conversion α of wood was calculated as follows:

α = \frac{W_{o} - W}{W_{0}}

(1)

where W_o and W are the initial and final masses of the sample, respectively.

In the experiments for product analysis, the reaction temperature was 300, 315, and 330 °C while the reaction holding time was taken as 0, 30, 60, 120, and 180 min. The reaction temperature was defined according to the experiment for kinetic analysis in which maximum conversion was obtained at this range.

Figure 1. Schematic diagram of the experimental apparatus.

2.3. Analysis

The moisture content, volatile material, and fixed carbon were obtained using the ASTM D3173, ASTM D3175, and ASTM D5142 tests, respectively. The ash content was obtained using a Shimadzu TG model TGA-50 (Shimadzu, Tokyo, Japan). In Table 1, C, H, N, and S values were obtained using a Thermo Scientific FLASH EA-2000 Elemental Analyzer (Thermo Scientific, Pittsburgh, PA, USA) and the oxygen was obtained using a Thermo Finnigan FLASH EA-1112 Elemental Analyzer (Conquer Scientific, San Diego, CA, USA). The liquid products obtained from this work were analyzed by GC-MS (Agilent GC-6890 with MSD detector, Agilent Technologies, California, CA, USA) as shown in Table 2.

Table 2. Operation conditions of GC-MS analysis used in this work.

**Table 2.** Operation conditions of GC-MS analysis used in this work.
Instrument	Condition
GC	6890GC, Agilent
MSD	5975, Agilent
Methods
Detector	DB-WAX (30 m × 250 µm, 0.25 µm thickness)
Column	From 70 °C (4 min) to 150 °C (5 min) at 5 °C/min
Over Temp	From 150 °C (5 min) to 230 °C (5 min) at 5 °C/min
	From 230 °C (5 min) to 250 °C (10 min) at 5 °C/min
He gas flow (mL/min)	1
Injection Vol. (µL)	1
Inlet Temp. (°C)	250
Detector temperature (°C)	250

3. Kinetic Models

Based on the basic Arrhenius equation, the overall rate equation of conversion, α for thermal degradation is expressed as:

\frac{d α}{d t} = Aexp (- \frac{E}{R T}) {(1 - α)}^{n}

(2)

where A, E, T, and R are the pre-exponential factor (1/min), the apparent activation energy (J/mol), the temperature of reaction (K), and the gas constant (8.314 J/mol K), respectively, and n denotes the overall reaction order. If the basic Equation (2) is used and a heating rate of

β = \frac{d T}{d t}

is employed, it can be shown that:

\frac{d α}{d T} = (\frac{A}{β}) \exp (- \frac{E}{R T}) {(1 - α)}^{n}

(3)

3.1. Method 1

In an integration using a series of approximations and simplifications [], Equation (3) becomes:

\frac{{(1 - α)}^{1 - n} - 1}{1 - n} = \frac{A}{β} \frac{R {T_{s}}^{2}}{E} exp [- \frac{E}{R T_{s}} (1 - \frac{θ}{T_{s}})]

(4)

where

θ = T - T_{s}

and

T_{s}

is defined as the temperature at which

\frac{1}{1 - α} = \frac{1}{exp} = 0.368

. With an unknown reaction order n and a generally applicable method to choose

T_{s}

where

d (1 - α) / d T

is maximum or

\frac{d^{2} (1 - α)}{d T^{2}} = 0

. At

\frac{d^{2} (1 - α)}{d T^{2}} = 0

, Equation (4) becomes:

\frac{{(1 - α)}^{1 - n} - 1}{1 - n} = - \frac{1}{n} {(1 - α_{s})}^{1 - n} exp (\frac{E θ}{R T_{s}^{2}})

(5)

when

θ = 0, (1 - α) = (1 - α_{s})

, Equation (5) yields:

(1 - α_{s}) = n^{\frac{1}{1 - n}}

(6)

In Equation (6), when we know α_s, we can obtain the corresponding n. Considering integral approximation and logarithm on Equations (3) and (5) yields:

ln [\frac{1 - {(1 - α)}^{1 - n}}{1 - n}] = \frac{E}{R T_{s}^{2}} θ for n \neq 1

(7)

ln [- ln (1 - α)] = \frac{E}{R T_{s}^{2}} θ for n = 1

(8)

Plotting

Y = ln [\frac{1 - {(1 - α)}^{1 - n}}{1 - n}]

versus

θ

in Equation (7) and

Y = ln [- ln (1 - α)]

versus

θ

in Equation (8), we can obtain the activation energy, E, from the slope of the line.

3.2. Method 2

Integrating Equation (3) yields:

F (α) = \int_{0}^{α} \frac{d α}{{(1 - α)}^{n}} = - \frac{A}{β} \int_{T_{o}}^{T} \exp (- \frac{E}{R T}) d T

(9)

Applying integral approximation and integration to Equation (9) yields []:

ln {\frac{1 - {(1 - α)}^{1 - n}}{T^{2} (1 - n)}} = \frac{ln A R}{β E} (1 - \frac{2 R T}{E}) + \frac{- E}{R T} for n \neq 1

(10)

ln {\frac{- ln (1 - α)}{T^{2}}} = ln \frac{A R}{β E} (1 - \frac{2 R T}{E}) + \frac{- E}{R T} for n = 1

(11)

Plotting

ln {\frac{1 - {(1 - α)}^{1 - n}}{T^{2} (1 - n)}}

versus 1/T in Equation (10) and

ln {\frac{- ln (1 - α)}{T^{2}}}

versus 1/T in Equation (11), we can obtain the value of activation energy, E, from the slopes.

3.3. Method 3

The variables given in Equation (9) may be separated and integrated to give in a logarithmic form []:

log F (α) = log (\frac{A E}{R}) - log β - 2.315 - \frac{0.4567 E}{R T}

(12)

The apparent activation energy (E) can therefore be obtained from a plot of logβ against 1/T for a fixed degree of conversion since the slope of such a line is given by 0.4567E/R. In conventional nonisothermal thermogravimetric techniques, this technique is also known as the Ozawa method [].

4. Results and Discussion

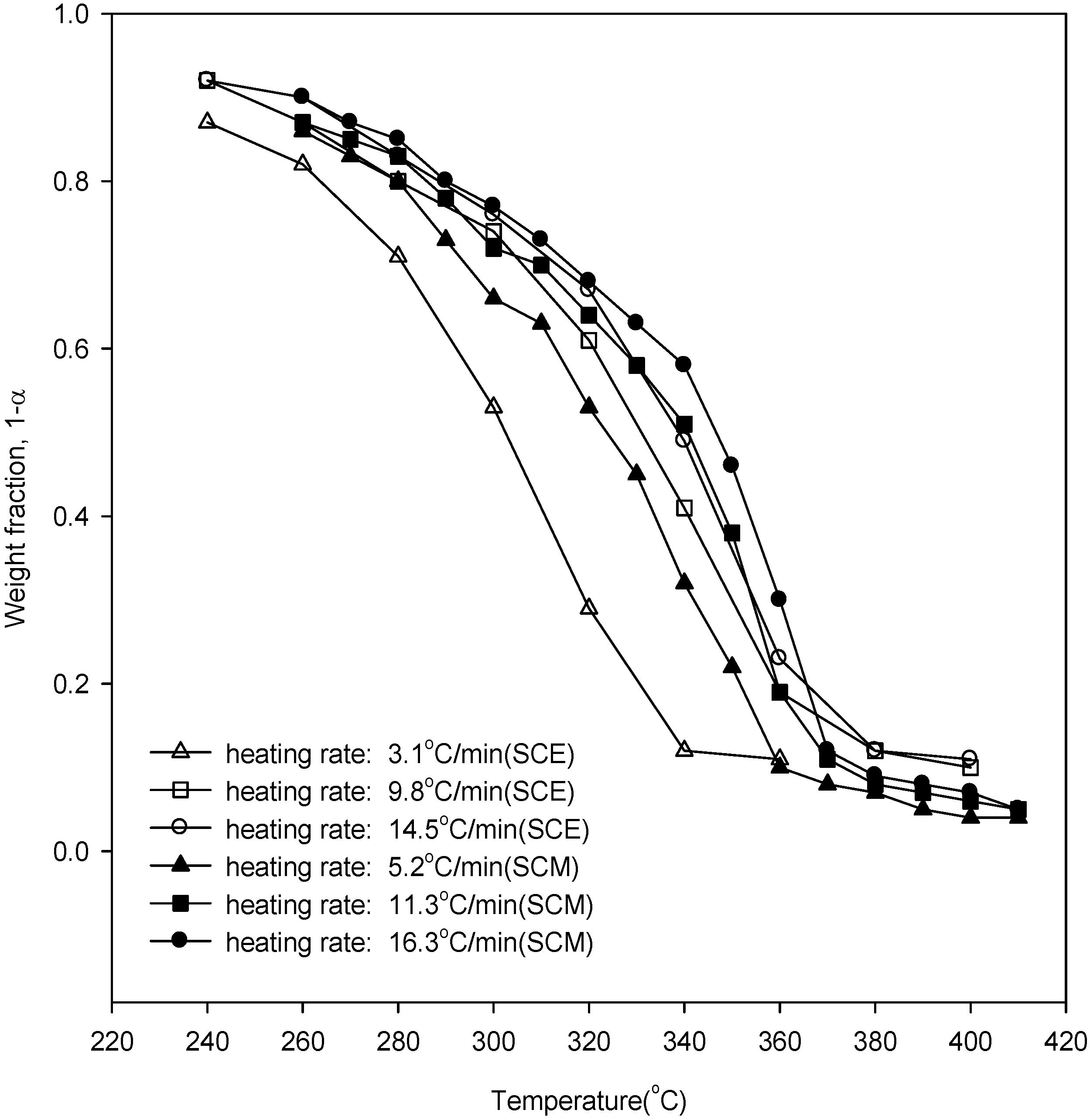
Figure 2 shows the weight loss curves of wood in SCE and SCM. It can be seen that with increased heating rate the weight loss curves of wood degradation were displaced to higher temperatures due to the heat transfer lag. Further, there is a higher conversion in SCE yields at a lower temperature than in SCM yields. In our previous work [], it was shown that the degree of hydrogen bonding of ethanol was slightly weaker in comparison to that in methanol in the supercritical region [].

Figure 2. Weight loss data of wood degradation in SCE and SCM.

Using Figure 2, the points of inflection, along with their respective weight fractions, were obtained and are listed in Table 3. From Table 3 and Equation (6), the overall reaction orders for SCE were obtained as 1.26, 1.26, and 0.96 for heating rates of 3.1, 9.8, and 14.5 °C/min, while from our previous work [], the overall reaction orders for SCM were 0.59, 0.62, and 0.64 for heating rates of 5.2, 11.3, and 16.3 °C/min, respectively. 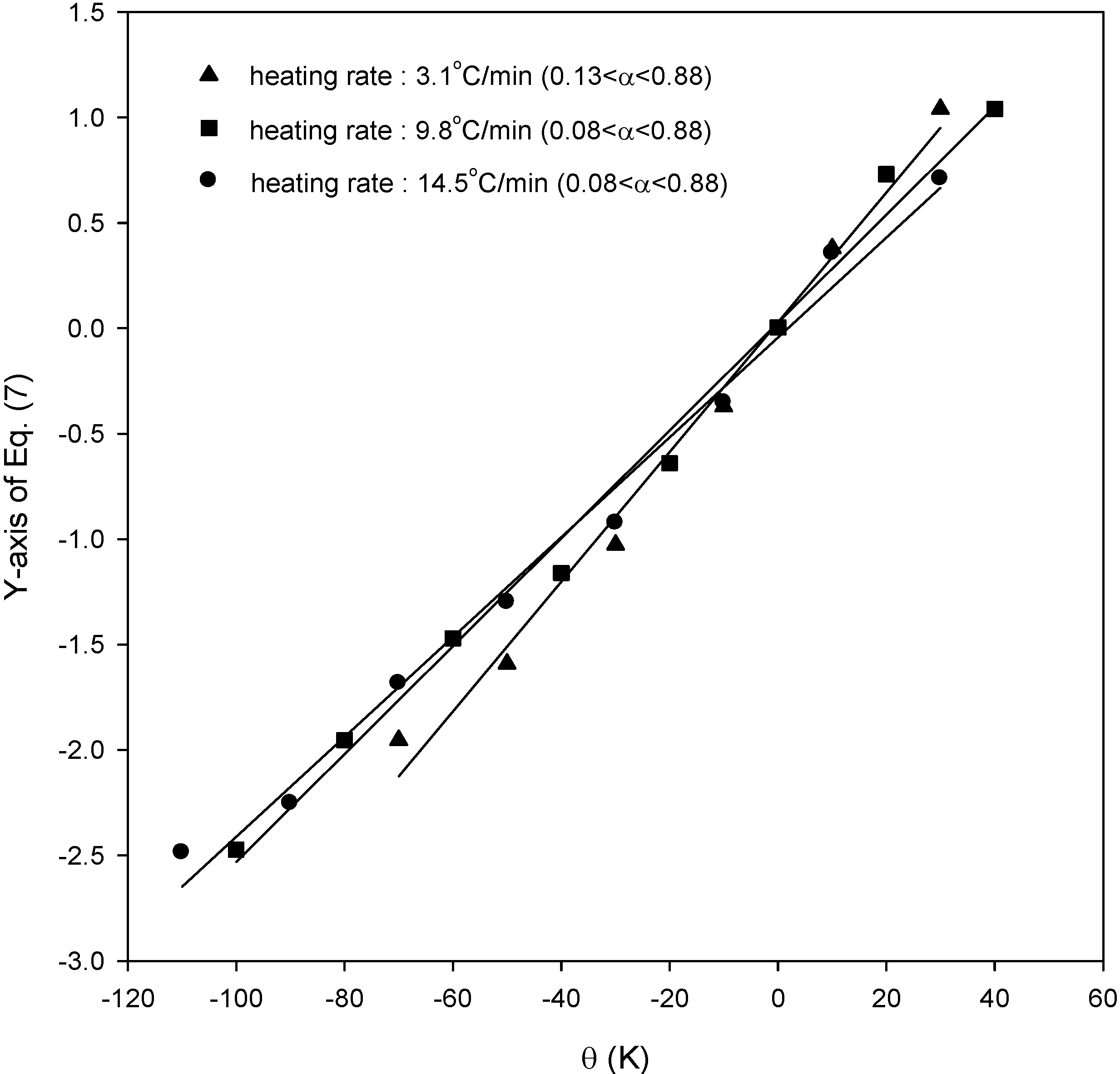Figure 3 shows the results for SCE from Equation (7). From the slope in this figure, the activation energies for SCE were obtained as 86.0, 79.1, and 78.0 kJ/mol for heating rates of 3.1, 9.8, and 14.5 °C/min, respectively, while the activation energies for SCM were 73.7, 73.5, and 74.5 kJ/mol for heating rates of 5.2, 11.3, and 16.3 °C/min from our previous work [].

Table 3. Weight fraction and temperature at which the inflection occurs in weight loss curve.

**Table 3.** Weight fraction and temperature at which the inflection occurs in weight loss curve.
	Heating rates, β (°C/min)	Temperature, T_s (°C)	Weight fraction, (1 − α_s)
SCE	3.1	310	0.41
	9.8	340	0.41
	14.5	350	0.36
SCM	5.2	345	0.26
	11.3	355	0.28
	16.3	360	0.20

Figure 3. Plots of Equation (7) for the application of kinetic analysis for SCE.

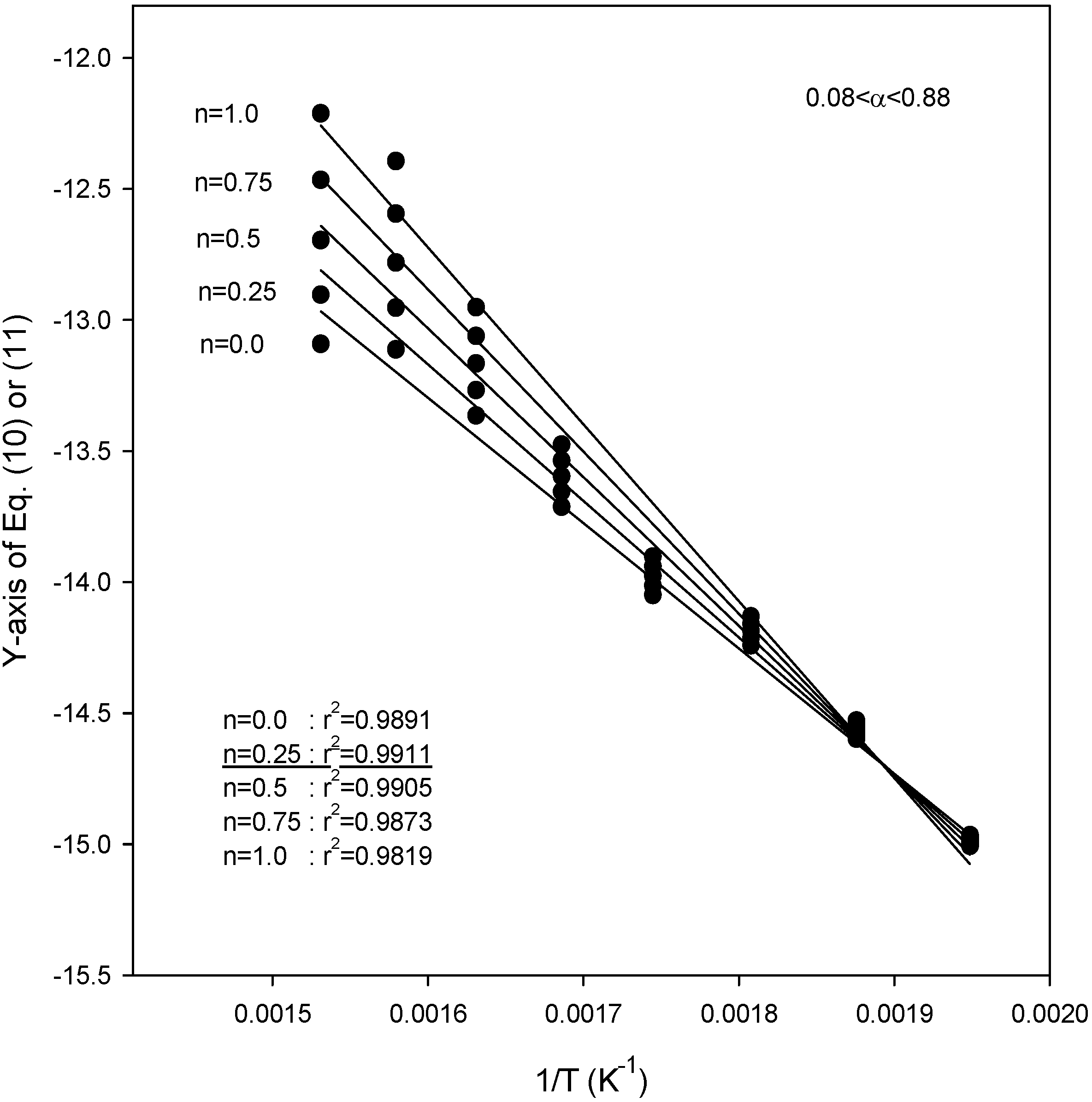
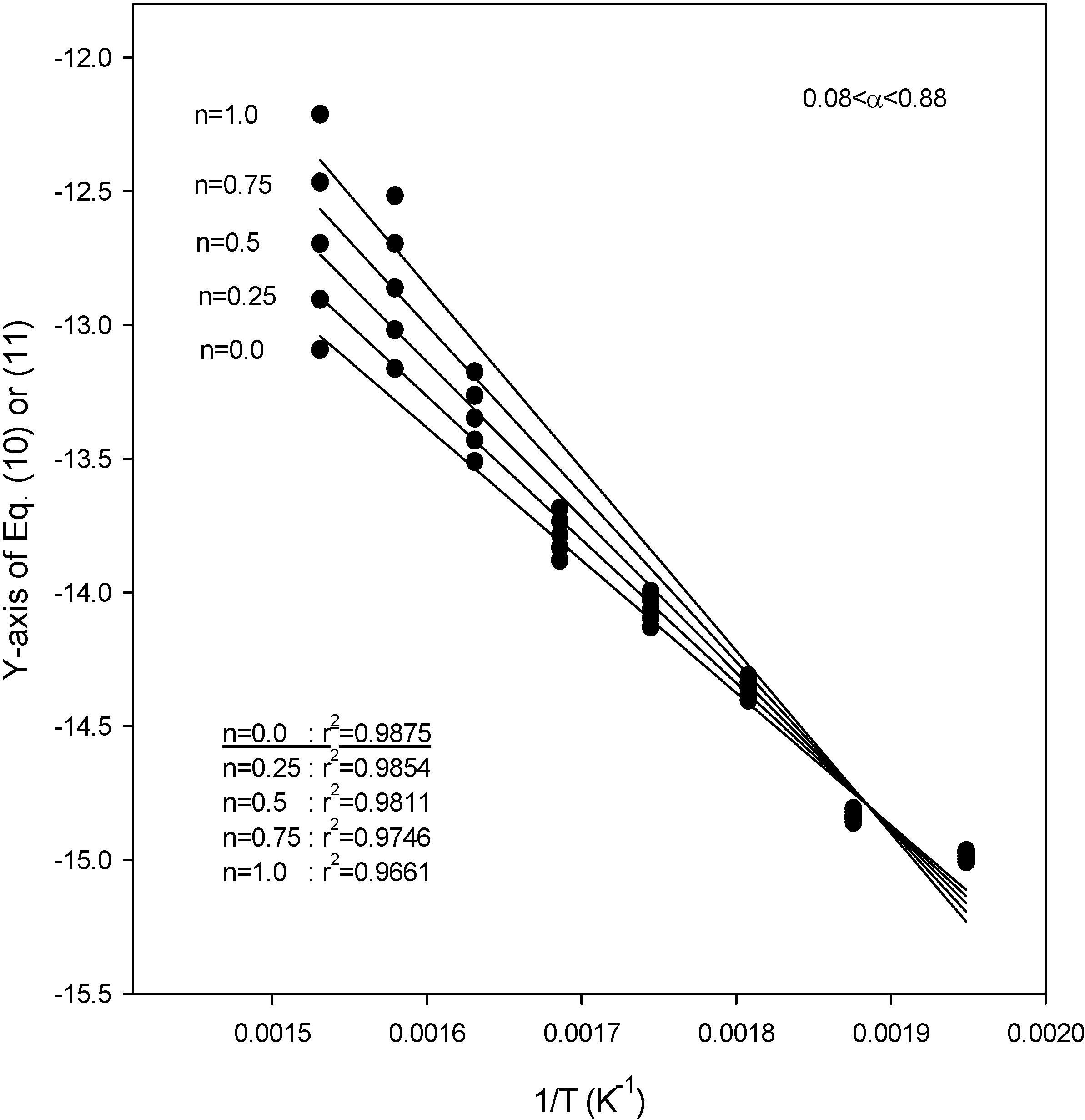
Figure 4, Figure 5 and Figure 6 also show the plot of Equations (10) and (11) for the application of the second kinetic analysis method used in this work at heating rates of 3.1, 9.8, and 14.5 °C/min for SCE, respectively. This method has been applied to our data and the best fit values for each heating rate were determined by employing reaction order values (n) of 0, 0.25, 0.5, 0.75, and 1.0. The best overall fit values were obtained using a value of n = 0.25, with the exception of a heating rate of 14.5 °C/min, for which the best fit of the data was obtained using a value of n = 0.0. From the slope of the lines in Figure 4, Figure 5 and Figure 6, the activation energies were obtained as 48.1, 43.3 and 40.1 kJ/mol for heating rates of 3.1, 9.8, and 14.5 °C/min, respectively. The best overall fit values in SCM were n = 0.25 for all heating rates, while the activation energies were 48.8, 45.2, and 47.6 kJ/mol for heating rates of 5.2, 11.3, and 16.3 °C/min, respectively []. All the parameters were obtained under unstirred condition. Although stirring was not implemented in this study because of experimental setup limitations, we considered the significance of stirring in this study. The rate of thermal reaction would surely be affected by any stirring. Since the stirring keeps the biomass particles mixed with the SCA, thus increasing the weight loss and then increasing the rate of reaction, considering it in supercritical reactions will increase the conversion.

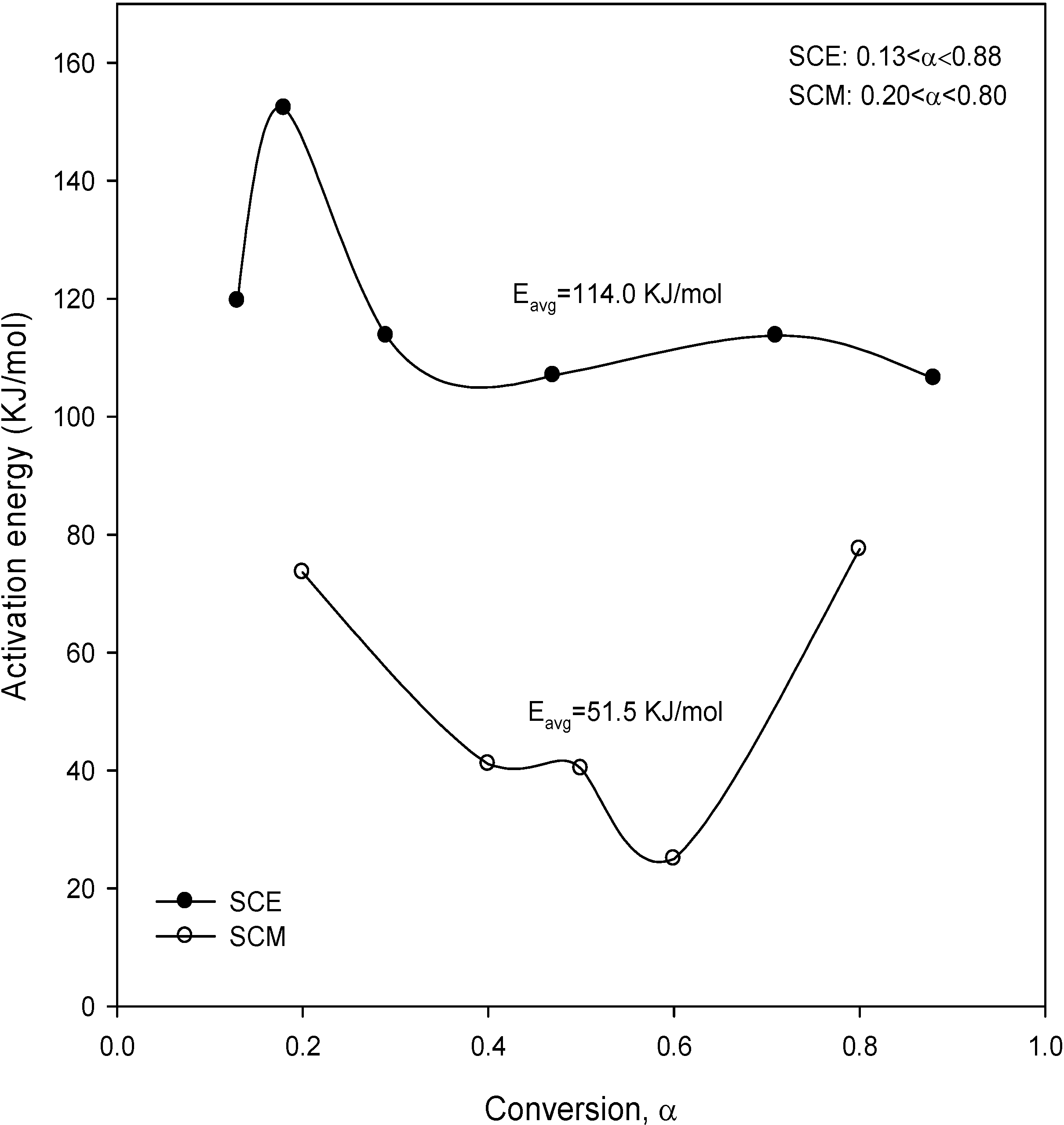
Figure 7 shows the result obtained for the activation energies from Equation (12). The average activation energies by this method were 114 kJ/mol and 51.5 kJ/mol for SCE and SCM, respectively, and this method yielded the highest activation energy for SCE. For comparative purposes, the results from the analytical methods used in this work are summarized in Table 4. In Methods 1 and 2, it was seen that the activation energies of SCE were similar to those of SCM, while it was obtained from Method 3 that the activation energy of SCM was lower than that of SCE.

Figure 4. Plots of Equations (10) or (11) for the application of the kinetic analysis method at a heating rate of 3.1 °C/min for SCE.

Figure 5. Plots of Equations (10) or (11) for the application of the kinetic analysis method at a heating rate of 9.8 °C/min for SCE.

Figure 6. Plots of Equations (10) or (11) for the application of the kinetic analysis method at a heating rate of 14.5 °C/min for SCE.

Figure 7. Activation energy upon conversion obtained from Equation (12) for SCE and SCM.

It was also found from Table 4 that there were tremendous variations in the calculated kinetic parameters, depending on the mathematical approach. This observation clearly indicated the problems in the selection and utilization of the different analytical methods to describe the wood degradation under supercritical conditions.

Table 4. Summary of the kinetic parameters obtained from this work.

**Table 4.** Summary of the kinetic parameters obtained from this work.
		Heating rates, β (°C/min)	Activation energy, E (kJ/mol)	Reaction order, n
Method 1	SCE	3.1	86.0	1.26
		9.8	79.1	1.26
		14.5	78.0	0.96
	SCM []	5.2	73.7	0.59
		11.3	73.5	0.62
		16.3	74.5	0.64
Method 2	SCE	3.1	48.1	0.25
		9.8	43.3	0.25
		14.5	40.1	0.0
	SCM []	5.2	48.8	0.25
		11.3	45.2	0.25
		16.3	47.6	0.25
Method 3	SCE	-	114.0 ^a	-
Method 3	SCM	-	51.5 ^a	-

^a average value.

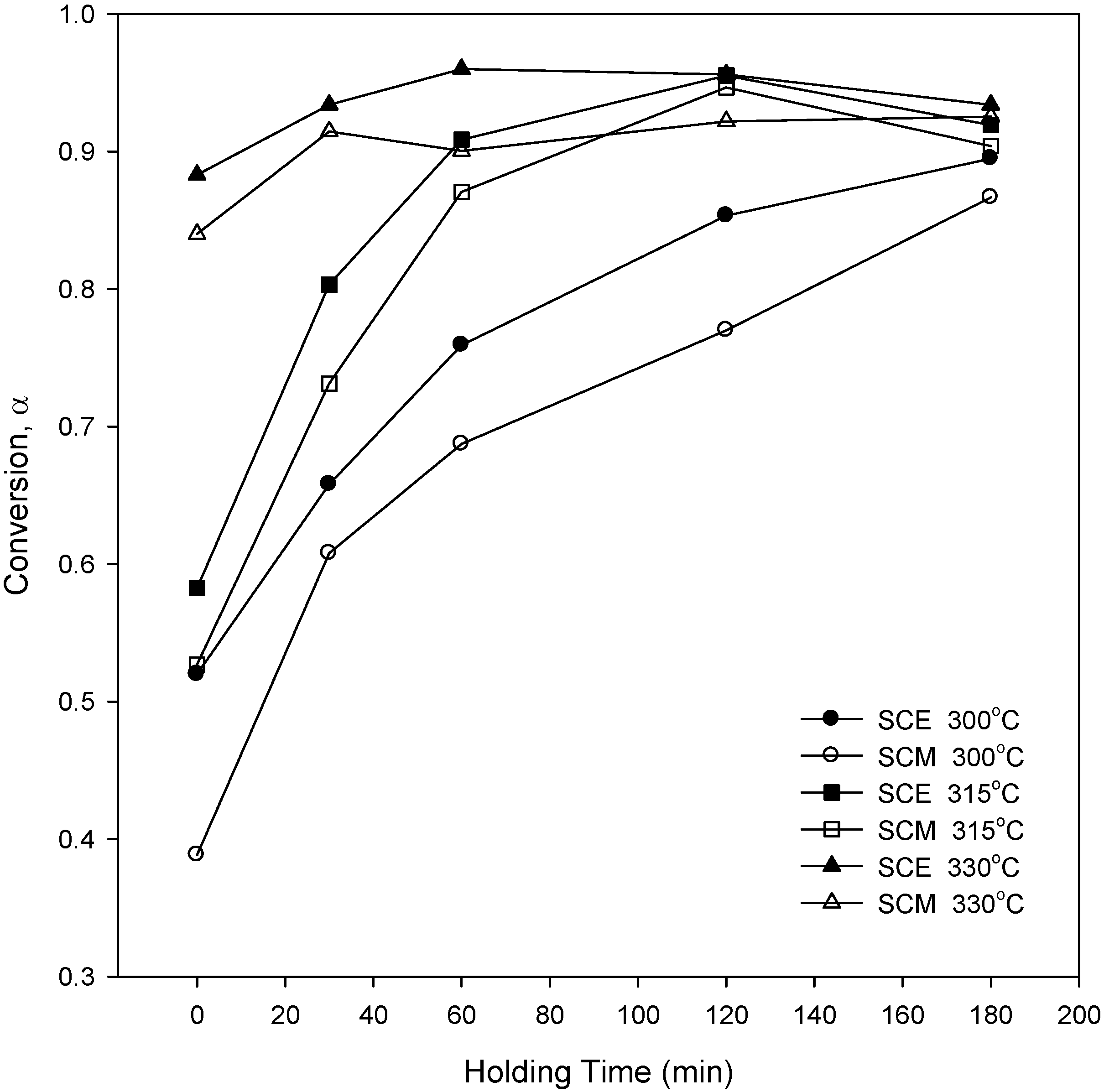
The qualitative analysis of wood degradation in SCA is absolutely necessary to study its effects. The liquid products were obtained from the experiments conducted at 300, 315, and 330 °C. Figure 8 shows the conversion to liquid products of wood at various reaction temperatures for SCA. The conversion increased with the increase of reaction temperature and holding time, and the conversions in SCE were higher than those of SCM. This result is similar to the experimental results of weight loss for the kinetic analysis of Figure 2, which shows the possibility that ethanol can act as a better solvent under supercritical conditions. It was also found that the conversion increased with the increase of reaction holding time for reaction temperatures of 315 and 330 °C, and then decreased again. At the initial stage, biomass was decomposed and depolymerized into small compounds, and these compounds may then rearrange through condensation, cyclization, and polymerization reactions to form new compounds. Thus, the conversion is less for longer holding times [].

Table 5 shows the grouping of the compounds obtained from the product analysis for SCE and SCM. This table shows the compounds, in terms of carbon number, for a reaction holding time of 0, 30, 60, 120, and 180 min and for reaction temperatures of 300, 315, and 330 °C. This data shows that the compounds with carbon numbers ranging from 2 to 15 are the major products. The products do not show much difference in terms of holding time and reaction temperature.

Figure 8. Percentage conversion at various reaction temperatures using SCM and SCE.

Table 5. The weight percentage of compounds according to the carbon number of liquid products obtained at different holding times.

**Table 5.** The weight percentage of compounds according to the carbon number of liquid products obtained at different holding times.
	Temperature (°C)	Carbon number	Holding time (min)
	Temperature (°C)	Carbon number	0	30	60	120	180
SCE	315	–C₅	60.5735	55.1467	48.8496	40.2349	42.3631
		C₆–C₁₀	21.3746	30.6275	42.3841	43.2205	38.7331
		C₁₁–C₁₅	8.9993	9.7628	6.4340	16.5445	18.9037
		C₁₅+	9.0523	4.4629	2.3321	0	0
	315	–C₅	49.8866	48.9922	49.7882	53.3591	52.1675
		C₆–C₁₀	22.6942	38.9051	38.1877	36.9808	40.2991
		C₁₁–C₁₅	22.5731	12.1026	7.9642	9.6600	3.1626
		C₁₅+	4.8460	0	4.0597	0	5.6382
	330	–C₅	62.308	45.1746	47.3825	56.9097	53.5084
		C₆–C₁₀	26.395	42.3808	35.3924	27.54808	35.2916
		C₁₁–C₁₅	11.297	12.4444	10.4425	11.1417	10.1567
		C₁₅+	0	0	6.78253	4.4003	1.0432
SCM	300	–C₅	59.3559	35.7655	29.4561	44.4425	45.7245
		C₆–C₁₀	24.2777	41.4319	54.2352	41.2186	41.8139
		C₁₁–C₁₅	16.3662	22.8025	16.3086	12.6105	9.2282
		C₁₅+	0	0	0	1.72831	3.2331
	315	–C₅	41.6373	57.4272	58.3233	40.0128	32.9110
		C₆–C₁₀	38.8932	28.4824	36.3414	50.7345	38.8445
		C₁₁–C₁₅	17.7693	10.3694	4.5028	4.5284	28.2444
		C₁₅+	1.70001	3.7207	0.8322	4.7240	0
	330	–C₅	54.0369	41.5547	31.5717	40.8246	30.9853
		C₆–C₁₀	32.1226	41.5144	55.8919	46.6675	59.9668
		C₁₁–C₁₅	5.0866	16.9307	10.8452	4.7987	3.3761
		C₁₅+	8.7538	0	1.6910	7.70905	5.6716

Table 6 shows the product in terms of their aliphatic and aromatic composition for SCE and SCM at 300, 315, and 330 °C. From Table 6 it can be seen that the aliphatic component increases with an increase in reaction temperature and holding time, while the aromatic component decreases with an increase in temperature and holding time for SCE. This clearly shows the conversion of aromatic components to aliphatic components with an increase of temperature and holding time. Similar results concerning a decrease in the aromatic components are shown in other works []. However, the change in reaction temperature and holding time for SCM doesn’t show significant changes. From this, it can be seen that the degradation of wood in SCM occurs very randomly, while it is not very random for SCE. From our previous work [] and as this result, SCE shows significant possibilities as a solvent for supercritical reactions, although further exploration is indispensable.

Table 6. The weight percentages of aromatic and aliphatic components in the liquid products obtained from this work.

**Table 6.** The weight percentages of aromatic and aliphatic components in the liquid products obtained from this work.
Temperature (°C)	Holding time (min)	SCE		SCM
Temperature (°C)	Holding time (min)	Aliphatic	Aromatic	Aliphatic	Aromatic
300	0	37.21739	62.78261	50.19121	49.80879
	30	58.82611	41.17389	54.17968	45.82032
	60	39.52417	60.47583	62.57999	37.42001
	120	52.41277	47.58723	40.96126	59.03874
	180	63.28477	36.71523	61.40423	38.59577
315	0	44.53008	55.46992	45.87700	54.12300
	30	57.82844	42.17156	45.99045	54.00955
	60	58.09071	41.90929	45.58905	54.41095
	120	61.00901	38.99099	60.89976	39.10024
	180	71.61326	28.38674	50.72985	49.27015
330	0	67.01420	32.98580	70.58513	29.41487
	30	58.57076	41.42924	62.86133	37.13867
	60	68.27741	31.72259	48.98633	51.01367
	120	58.71955	41.28045	61.42090	38.57910
	180	77.04858	22.95142	77.27807	22.72193

5. Conclusions

In this work, the kinetics of wood degradation have been analyzed using a nonisothermal weight loss technique with heating rates of 3.1, 9.8, and 14.5 °C/min for SCE and 5.2, 11.3, and 16.3 °C/min for SCM. Three different kinetic analysis methods were implemented to obtain the kinetic parameters such as apparent activation energy and overall reaction order for wood degradation in supercritical alcohols. From this work, the activation energies of wood degradation in SCE were obtained as 78.0–86.0, 40.1–48.1, and 114 kJ/mol according to the kinetic analysis method used in this work. In addition, the activation energies for SCM were obtained as 73.5–77.8, 45.2–48.8, and 52 kJ/mol, according to the same kinetic analysis methods followed previously. It was also found that there were variations in the calculated kinetic parameters, depending on the mathematical approach.

At the supercritical region, it was found that conversion is higher in SCE at lower temperatures than in SCM. The product analysis shows that the majority of products fall in the carbon number range of 2 to 15. The products do not show many differences in terms of reaction temperature and holding time. SCE shows a specific pattern with change of reaction temperature and holding time, while SCE doesn’t show any specific pattern with these changes. Overall, SCE shows significant potential as a solvent for supercritical reactions, although further exploration is necessary.

Acknowledgements

This work was supported with a Technology Development Program of the Korea Evaluation Institute of Industrial Technology (KEIT) grant funded by the Korean government’s Ministry of Knowledge Economy.

References

Demirbaş, A. Supercritical fluid extraction and chemicals from biomass with supercritical fluids. Energy Convers. Manag. 2001, 42, 279–294. [Google Scholar] [CrossRef]
Qian, Y.; Zuo, C.; Tan, J.; He, J. Structural analysis of bio-oils from sub-and supercritical water liquefaction of woody biomass. Energy 2007, 32, 196–202. [Google Scholar] [CrossRef]
Saka, S. Recent progress in supercritical fluid science for biofuel production from woody biomass. For. Stud. China 2006, 8, 9–15. [Google Scholar] [CrossRef]
Chester, T.; Pinkston, J.; Raynie, D. Supercritical fluid chromatography and extraction. Anal. Chem. (USA) 1998, 70, 301–319. [Google Scholar] [CrossRef]
Yamazaki, J.; Minami, E.; Saka, S. Liquefaction of beech wood in various supercritical alcohols. J. Wood Sci. 2006, 52, 527–532. [Google Scholar] [CrossRef]
Yamaguchi, T.; Matubayasi, N.; Nakahara, M. NMR study on the reorientational relaxation in supercritical alcohols. J. Phys. Chem. A 2004, 108, 1319–1324. [Google Scholar] [CrossRef]
Carlès, P. A brief review of the thermophysical properties of supercritical fluids. J. Supercrit. Fluids 2010, 53, 2–11. [Google Scholar] [CrossRef]
Deshpande, P.; Kulkarni, K.; Kulkarni, A. Supercritical fluid technology in biodiesel production: A review. Chem. Mater. Res. 2011, 1, 27–32. [Google Scholar]
Oh, S.C.; Kwak, H.; Bae, S.Y. A kinetic analysis of polymer degradation in supercritical fluid. J. Chem. Eng. Jpn. 2006, 39, 1004–1009. [Google Scholar] [CrossRef]
Hwang, G.C.; Kim, B.K.; Bae, S.Y.; Yi, S.C.; Kumazawa, H. Degradation of polystyrene in supercritical acetone. J. Ind. Eng. Chem. 1999, 5, 150–154. [Google Scholar]
Minami, E.; Saka, S. Comparison of the decomposition behaviors of hardwood and softwood in supercritical methanol. J. Wood Sci. 2003, 49, 73–78. [Google Scholar] [CrossRef]
Hoffmann, M.M.; Conradi, M.S. Are there hydrogen bonds in supercritical methanol and ethanol? J. Phys. Chem. B 1998, 102, 263–271. [Google Scholar] [CrossRef]
Poudel, J.; Oh, S.C. A kinetic analysis of wood degradation in supercritical alcohols. Ind. Eng. Chem. Res. 2012, 51, 4509–4514. [Google Scholar] [CrossRef]
Liu, Q.; Wang, S.; Wang, K.; Luo, Z.; Cen, K. Pyrolysis of wood species based on the compositional analysis. Korean J. Chem. Eng. 2009, 26, 548–553. [Google Scholar] [CrossRef]
Madras, G.; Kolluru, C.; Kumar, R. Synthesis of biodiesel in supercritical fluids. Fuel 2004, 83, 2029–2033. [Google Scholar] [CrossRef]
Lalanne, P.; Andanson, J.; Soetens, J.C.; Tassaing, T.; Danten, Y.; Besnard, M. Hydrogen bonding in supercritical ethanol assessed by infrared and Raman spectroscopies. J. Phys. Chem. A 2004, 108, 3902–3909. [Google Scholar] [CrossRef]
Horowitz, H.H.; Metzger, G. A new analysis of thermogravimetric traces. Anal. Chem. 1996, 35, 1464–1468. [Google Scholar] [CrossRef]
Cooney, J.D.; Wilis, D.M. Thermal degradation of poly(ethylene tetrephthalate): A kinetic analysis of thermogravimetric data. J. Appl. Polym. Sci. 1983, 28, 2887–2902. [Google Scholar] [CrossRef]
Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
You, B.R.; Oh, S.C. Nonisothermal kinetics of wood degradation in supercritical methanol. Korean J. Chem. Eng. 2010, 27, 1159–1163. [Google Scholar] [CrossRef]
Carrier, M.; Loppinet-Serani, A.; Absalon, C.; Marias, F.; Aymonier, C.; Mench, M. Conversion of fern (Pteris vittata L.) biomass from a phytoremediation trial in sub-and supercritical water conditions. Biomass Bioenergy 2011, 35, 872–883. [Google Scholar] [CrossRef]

© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).