Modeling and Control of a Flux-Modulated Compound-Structure Permanent-Magnet Synchronous Machine for Hybrid Electric Vehicles

Abstract

The compound-structure permanent-magnet synchronous machine (CS-PMSM), comprising a double rotor machine (DRM) and a permanent-magnet (PM) motor, is a promising electronic-continuously variable transmission (e-CVT) concept for hybrid electric vehicles (HEVs). By CS-PMSM, independent speed and torque control of the vehicle engine is realized without a planetary gear unit. However, the slip rings and brushes of the conventional CS-PMSM are considered a major drawback for vehicle application. In this paper, a brushless flux-modulated CS-PMSM is investigated. The operating principle and basic working modes of the CS-PMSM are discussed. Mathematical models of the CS-PMSM system are given, and joint control of the two integrated machines is proposed. As one rotor of the DRM is mechanically connected with the rotor of the PM motor, special rotor position detection and torque allocation methods are required. Simulation is carried out by Matlab/Simulink, and the feasibility of the control system is proven. Considering the complexity of the controller, a single digital signal processor (DSP) is used to perform the interconnected control of dual machines instead of two separate ones, and a typical hardware implementation is proposed.

1. Introduction

The increasing energy crisis and environmental concerns have helped revive interest in electric vehicles [1]. As a trade-off between driving performance and emissions, hybrid propulsion architectures have been proven successful during the last two decades. Hybrid electric vehicles (HEVs) like the Toyota Prius utilize a planetary gear unit for power splitting. The planetary gear unit enables independent output speed and torque control of the internal combustion engine (ICE) to maximize system efficiency, yet adds additional mechanical complexity and maintenance [2]. To get rid of the planetary gear unit, a compound-structure permanent-magnet synchronous machine (CS-PMSM), as shown in Figure 1, is proposed [3].

Figure 1. Schematic diagram of a hybrid electric drive system based on CS-PMSM.

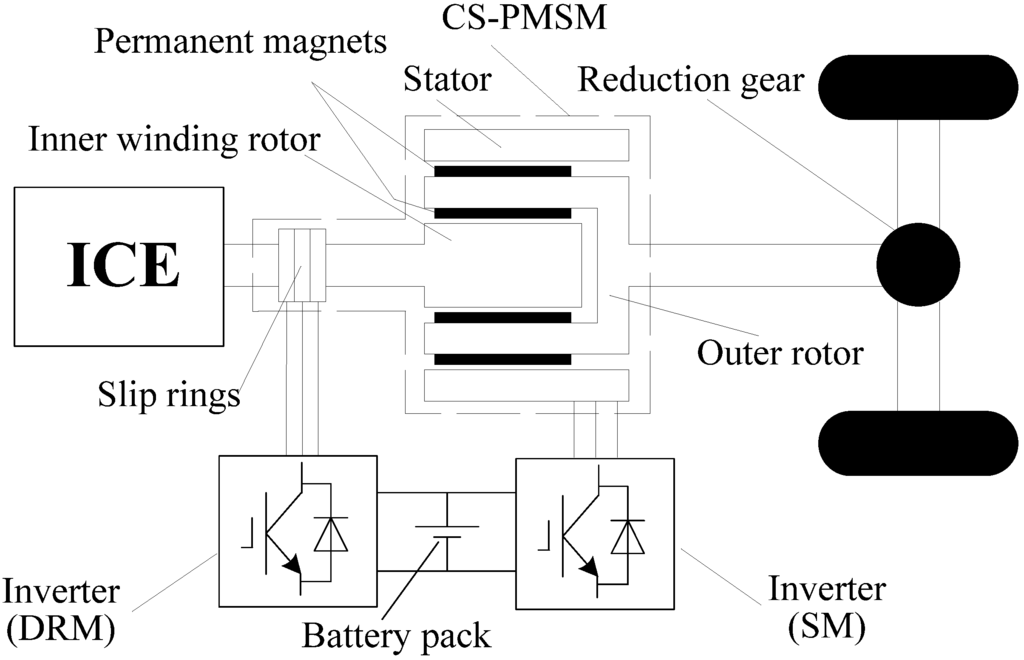
Figure 1. Schematic diagram of a hybrid electric drive system based on CS-PMSM.

The CS-PMSM, also known as four-quadrant transducer (4QT), or dual mechanical port (DMP) machine, comprises a stator machine (SM) and a double-rotor machine (DRM) [4,5,6,7]. The inner rotor is mechanically connected with the ICE and the outer rotor is coupled to the final gear. The DRM decouples speed between the ICE and final drive, and the SM provides supplementary torque. Hence, the CS-PMSM represents the functional integration of the planetary gear unit, generator and motor in the Toyota Hybrid System (THS). Without the use of gearbox or clutch, the CS-PMSM enables a simple HEV drive train configuration. Nevertheless, brushes and slip rings are required to feed the inner winding rotor, which increases friction losses and maintenance costs. Besides, the cooling of the inner rotating winding rotor needs special design to prevent overheating.

The magnetic-geared motor has drawn wide interests since Howe proposed the flux-modulated magnetic gear [8]. By modulating the magnetic field between the stator and a permanent-magnet (PM) rotor, “pseudo” direct drive is achieved for low-speed applications such as wind power and electric vehicles [9,10,11,12,13]. When both the PM rotor and modulating ring are designed to be rotary, the magnetic-geared motor becomes a brushless DRM. By coupling the DRM with a conventional motor, a brushless flux-modulated CS-PMSM can be realized.

In this paper, the operating principle of the flux-modulated CS-PMSM as an energy transducer is discussed. Then the mathematical model is built up and further joint control for the two machines of the CS-PMSM is investigated for HEVs. Consequently, one realization of the controller is recommended.

2. The Hybrid Electric Drive System Based on Flux-Modulated CS-PMSM

2.1. The Operating Principle of Flux-Modulated CS-PMSM

Like the conventional CS-PMSM, the flux-modulated CS-PMSM has dual mechanical and dual electrical ports, as shown in Figure 2. The PM rotor-1, modulating ring rotor and stator-1 comprise the DRM. Stator-2 and PM rotor-2 form motor-2. The modulating ring rotor is mechanically coupled with PM rotor-2 that is connected to the final gear, while PM rotor-1 is connected with the ICE. Compared with conventional radial-radial flux CS-PMSM, no slip rings and brushes are required, and the outer stator of DRM enables more flexible cooling designs.

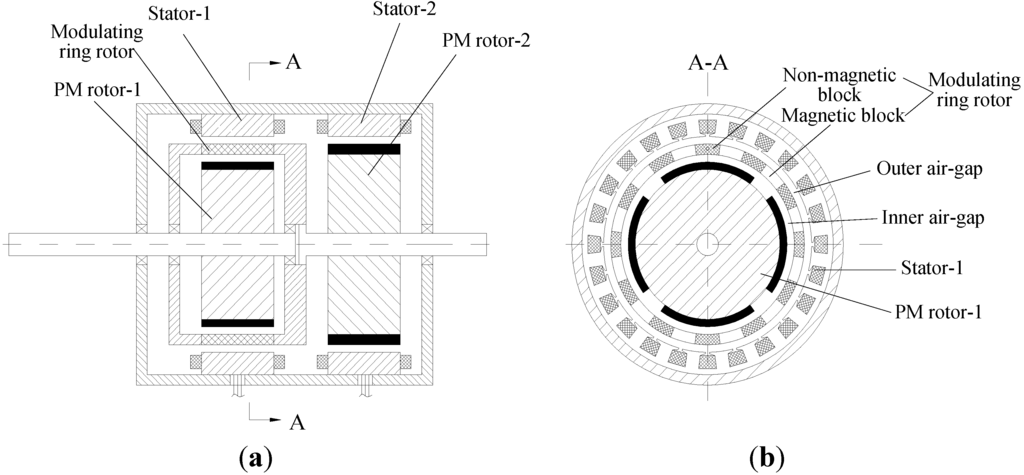
Figure 2. (a) The flux-modulated CS-PMSM; (b) The cross section of the brushless DRM.

Figure 2. (a) The flux-modulated CS-PMSM; (b) The cross section of the brushless DRM.

According to the operating principle of flux-modulated magnetic gear [14,15], the pole pair numbers of the PM rotor-1, the stator and magnetic blocks satisfies:

$$p_1+p_{S1}=N_R$$

(1)

where p₁ and p_S1 are the pole pair numbers of the PM rotor-1 and stator-1, respectively, N_R is number of magnetic blocks of the modulating ring rotor.

To generate steady torque, the rotating magnetic field speed of stator-1 can be expressed by:

$${\mathrm{\Omega }}_{S1}=\frac{1}{p_{S1}}\left({\mathrm{\Omega }}_R{N}_R-p_1{\mathrm{\Omega }}_1\right)$$

(2)

where Ω₁, Ω_R, Ω_S1 are the rotating speeds of PM rotor-1, the modulating ring and magnetic field generated by stator-1, respectively.

When all losses are not considered, the power balance equation of DRM can be written as follows:

$$\begin{array}{l}{T}_R{\mathrm{\Omega }}_R=\left(T_1+T_{S1}\right){\mathrm{\Omega }}_R\\ =T_1{\mathrm{\Omega }}_1+T_{S1}{\mathrm{\Omega }}_{S1}\end{array}$$

(3)

where T_R, T₁ and T_S1 are the output torque delivered to modulating ring rotor, the input torque of PM rotor-1, and the electromagnetic torque of stator-1.

The torque equation of DRM can be further described according to Equations (2) and (3):

$$\frac{T_1}{T_{S1}}=-\frac{{\mathrm{\Omega }}_{S1}-{\mathrm{\Omega }}_R}{{\mathrm{\Omega }}_1-{\mathrm{\Omega }}_R}=\frac{p_1}{p_{S1}}$$

(4)

Under steady operation, the output speed and torque of the CS-PMSM can be written as:

$${\mathrm{\Omega }}_O=\frac{p_1}{N_R}{\mathrm{\Omega }}_{ICE}+\frac{p_{S1}}{N_R}{\mathrm{\Omega }}_{S1}$$

(5)

$$\begin{array}{l}{T}_O=T_{ICE}+T_{S1}+T_{M2}\\ =\frac{N_R}{p_{S1}}{T}_{S1}+T_{M2}\\ =\frac{N_R}{p_1}{T}_{ICE}+T_{M2}\end{array}$$

(6)

where Ω_O and Ω_ICE are the mechanical speeds of output and input shafts connected with final gear and ICE, respectively; T_O, T_ICE and T_M2 are the output torque, input torque of ICE and torque of motor-2.

By changing the electromagnetic torque of stator-1, the speed of ICE is adjustable for a given throttle opening. The rotating speed of magnetic field generated by stator-1 changes in response to speed variations of ICE and output shaft according to Equation (5) while motor-2 makes torque compensation according to Equation (6), so that driving demands are satisfied. Hence, both the operating speed and torque between ICE and output are decoupled, which means the ICE can work within an efficient speed-torque domain, independent of driving demand.

2.2. Basic Operating Modes of Flux-Modulated CS-PMSM

By defining ${\mathrm{\Omega }}_{ICE}^{\prime }=\frac{p_1}{N_R}{\mathrm{\Omega }}_{ICE}$ and $T_{ICE}^{\prime }=\frac{N_R}{p_1}{T}_{ICE}$, Equations (5) and (6) can be transformed as:

$${\mathrm{\Omega }}_O={\mathrm{\Omega }}_{ICE}^{\prime }+\frac{p_{S1}}{N_R}{\mathrm{\Omega }}_{S1}$$

(7)

$$T_O=T_{ICE}^{\prime }+T_{M2}$$

(8)

where ${\mathrm{\Omega }}_{ICE}^{\prime }$ and $T_{ICE}^{\prime }$ can be regarded as the transferred speed and torque by magnetic gearing. Numerically, ${\mathrm{\Omega }}_{ICE}^{\prime }$ is the output speed of modulating ring when ${\mathrm{\Omega }}_{S1}$ is zero, while $T_{ICE}^{\prime }$ is the output torque when $T_{M2}$ equals zero.

Unlike the conventional CS-PMSM, the origin of speed and torque coordinate that divides the plane into four quadrants is not the actual operating point of ICE [16], as shown in Figure 3. When all losses are not considered, for an optimal ICE working point A$\left({\mathrm{\Omega }}_{ICE},T_{ICE}\right)$, the transferred point B$\left({\mathrm{\Omega }}_{ICE}^{\prime },T_{ICE}^{\prime }\right)$ lies on the same constant-power line. $\Delta \mathrm{\Omega }$ and $\Delta T$ are the speed and torque difference between point B and required output point C$\left({\mathrm{\Omega }}_O,T_O\right)$. The basic operating modes of flux-modulated CS-PMSM can be described as follows:

(1)

When $\Delta \mathrm{\Omega }$ > 0 and $\Delta T$ > 0, point C lies in quadrant I and both DRM and motor-2 work as motors. The CS-PMSM draws energy from battery packs to increase the output speed and torque. In this case, the vehicle runs under high speed and heavy load with added battery power. So the maximum lasting time of this mode depends on the state of charge (SOC). Generally, this mode is used for shot-time high-speed acceleration, e.g., overtaking.

(2)

When $\Delta \mathrm{\Omega }$ < 0 and $\Delta T$ > 0, point C lies in quadrant II. DRM works with negative speed and generates power for motor-2 or charging the battery. Motor-2 draws power from DC bus to increase output torque. This mode is used for low speed and high torque propulsion.

(3)

When $\Delta \mathrm{\Omega }$ < 0 and $\Delta T$ < 0, point C lies in quadrant III. Both DRM and motor-2 operate in generating mode charging the battery. In this case, the ICE delivers additional power as well as power required by driving demand.

(4)

When $\Delta \mathrm{\Omega }$ > 0 and $\Delta T$ < 0, point C lies in quadrant IV. DRM works as a motor to increase output speed while motor-2 as a generator to reduce output torque. This mode can be used for high-speed light-load cruising.

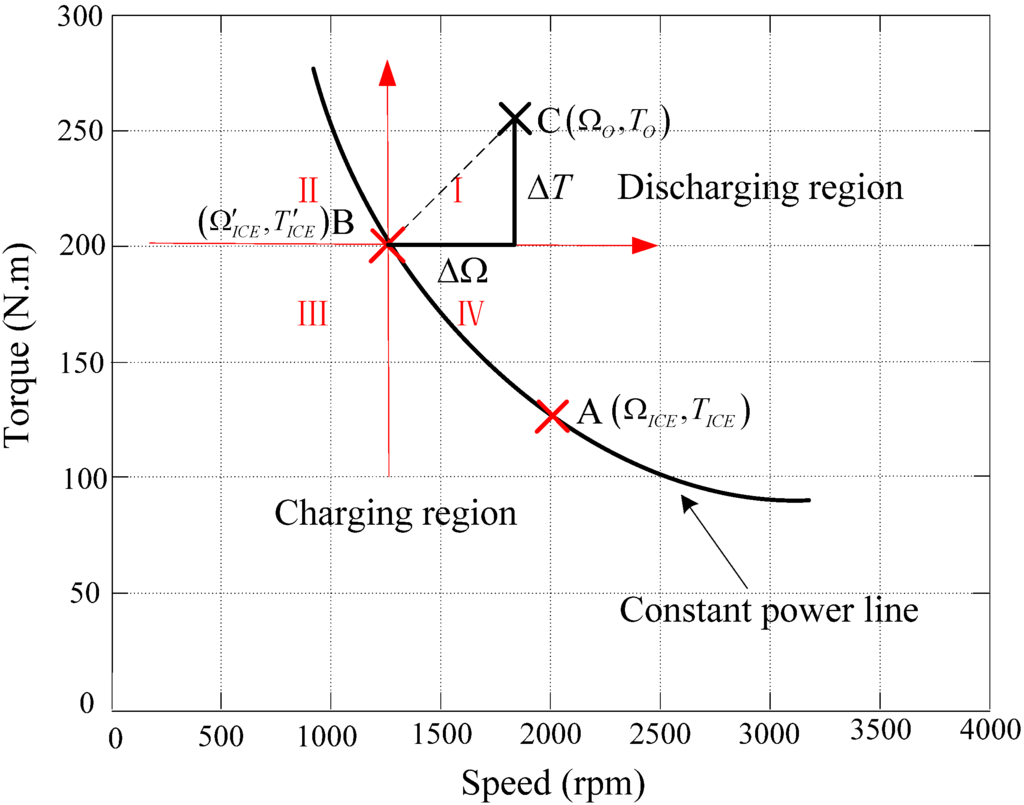
Figure 3. Energy transducing diagram of the flux-modulated CS-PMSM.

Figure 3. Energy transducing diagram of the flux-modulated CS-PMSM.

When ICE is shut down and PM rotor-1 is locked, the system works in pure electric mode, and both DRM and motor-2 can be used to propel the vehicle. When the two rotors are locked together, the ICE is directly connected with final gear, and the system works in pure ICE mode. For these cases, clutches and mechanical locks are required. For simplicity, only motor-2 is used in pure electric mode so no clutch and lock are needed. To realize pure ICE mode without locking the two rotors, the generated power of DRM is solely used to feed motor-2, hence no power is drawn from or injected to the battery. The simplicity, however, is achieved in sacrifice of lower driving performance and efficiency.

For all possible driving output, the battery is discharged when the point C is above the constant power line and charged when it is under the line. By dynamic controlling the operating point of ICE, the battery SOC can be maintained for sustainable running.

Compared with power-split HEVs based on planetary gear units, e.g., the Toyota Prius, the flux-modulated CS-PMSM removes complex mechanical transmission, and dramatically simplifies the drive train, so simpler vehicle system control is possible. Gear cogging noise is diminished and less lubrication is required. Disadvantages may be the complex control of CS-PMSM. In the Prius, both the generator and motor can be controlled as conventional machines, while the control of CS-PMSM has to be specially treated, which will be discussed in the following section. Besides, the electromagnetic and mechanical design of CS-PMSM is much different from conventional PM machines. Non-conductive material with low permeability and high strength is required to support the magnetic blocks. Overall, though, the flux-modulated CS-PMSM is a promising concept for HEVs.

3. Modeling and Control of Flux-Modulated CS-PMSM System

3.1. Mathematical Models of Flux-Modulated CS-PMSM

For simplicity, saturation, eddy currents and hysteresis losses are neglected for the following analysis [17].

Flux linkage equation can be written as follows:

$$\left[\begin{array}{c}{\psi }_{d1}\\ {\psi }_{q1}\\ {\psi }_{d2}\\ {\psi }_{q2}\end{array}\right]=\left[\begin{array}{cccc}{L}_{d1}& 0& 0& 0\\ 0& L_{q1}& 0& 0\\ 0& 0& L_{d2}& 0\\ 0& 0& 0& L_{q2}\end{array}\right]\left[\begin{array}{c}{i}_{d1}\\ i_{q1}\\ i_{d2}\\ i_{q2}\end{array}\right]+\left[\begin{array}{c}{\psi }_{f1}\\ 0\\ {\psi }_{f2}\\ 0\end{array}\right]$$

(9)

where Ψ_d1, Ψ_q1, Ψ_d2, Ψ_q2 are d- and q- axis flux linkages of stator-1 and stator-2; Ψ_f1 is the flux linkage in the DRM outer air gap generated by PM rotor-1 and modulating ring; Ψ_f2 is the flux linkage generated by PM rotor-2; L_d1, L_q1, L_d2, L_q2 are the d- and q- axis inductances of stator-1 and stator-2; i_d1, i_q1, i_d2, i_q2 are d- and q- axis currents of stator-1 and stator-2, respectively.

The electrical angular position of motor-2 is simply determined by the position of PM rotor-2, while for DRM both rotors are involved. As the magnetic field in the outer air gap of DRM relies on the position of rotary parts, the synchronization of electrical angle needs position acquisition of two rotors. As a result, the voltage equations of the CS-PMSM are given by:

$$\left[\begin{array}{c}{u}_{d1}\\ u_{q1}\\ u_{d2}\\ u_{q2}\end{array}\right]=\left[\begin{array}{c}{R}_1{i}_{d1}\\ R_1{i}_{q1}\\ R_2{i}_{d2}\\ R_2{i}_{q2}\end{array}\right]+p\left[\begin{array}{c}{\psi }_{d1}\\ {\psi }_{q1}\\ {\psi }_{d2}\\ {\psi }_{q2}\end{array}\right]+\left[\begin{array}{l}(p_1{\Omega }_1-N_R{\Omega }_2){\psi }_{q1}\\ (N_R{\Omega }_2-p_1{\Omega }_1){\psi }_{d1}\\ -p_2{\Omega }_2{\psi }_{q2}\\ p_2{\Omega }_2{\psi }_{d2}\end{array}\right]$$

(10)

where u_d1, u_q1, u_d2, u_q2 are d- and q- axis voltages of stator-1 and stator-2; R₁, R₂ are winding resistances of stator-1 and stator-2; p is differential operator; p₂ are pole pair number of PM rotor-2; Ω₂ is the mechanical speed of PM rotor-2 that equals that of modulating ring rotor.

The electromagnetic torque generated by stator-1 and motor-2 can be calculated independently:

$$\left[\begin{array}{c}{T}_{S1}\\ T_{M2}\end{array}\right]=\frac{3}{2}\left[\begin{array}{cccc}-p_{S1}{\psi }_{q1}& p_{S1}{\psi }_{d1}& 0& 0\\ 0& 0& -p_2{\psi }_{q2}& p_2{\psi }_{d2}\end{array}\right]\left[\begin{array}{c}{i}_{d1}\\ i_{q1}\\ i_{d2}\\ i_{q2}\end{array}\right]$$

(11)

Hence, the motion equations are written as:

$$\left[\begin{array}{c}{T}_{ICE}\\ T_o\\ {\Omega }_{ICE}\\ {\Omega }_o\end{array}\right]=\left[\begin{array}{cccc}\frac{p_1}{p_{S1}}& 0& 0& 0\\ \frac{N_R}{p_{S1}}& 1& 0& 0\\ 0& 0& -\frac{p_{S1}}{p_1}& \frac{N_R}{p_1}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{T}_{S1}\\ T_{M2}\\ {\Omega }_{S1}\\ {\Omega }_{M2}\end{array}\right]-\left[\begin{array}{c}{J}_{1}p{\Omega }_1\\ J_{2}p{\Omega }_2\\ 0\\ 0\end{array}\right]-\left[\begin{array}{c}{D}_1{\Omega }_1\\ D_2{\Omega }_2\\ 0\\ 0\end{array}\right]$$

(12)

where J₁, J₂ are the rotary inertias of input rotor (i.e., PM rotor-1) and output rotor (i.e., PM rotor-2 connected with modulating ring rotor); D₁, D₂ are the drag coefficients of input and output rotors, respectively.

3.2. Control Strategy of Flux-Modulated CS-PMSM System

The CS-PMSM has proposed two challenges for conventional controllers. Firstly, the mechanical speed coupling between the DRM and motor-2 requires dual position feedback of the input and output rotors for the DRM controller. Secondly, the overall output torque comprises the contributions of both machines, although they are electrically independent, and coordinated system control is required for joint operation. Considering the compound structure and HEV application, the use of two individual conventional controllers is not justified. Since conventional controllers only accept absolute position or speed feedback and are simply applied to control one machine, a special controller is proposed in this paper, as shown in Figure 4. Control algorithm is implemented by one digital signal processor (DSP; e.g., TMS320F2812) instead of two separate ones, which is preferred for both functional and cost concerns.

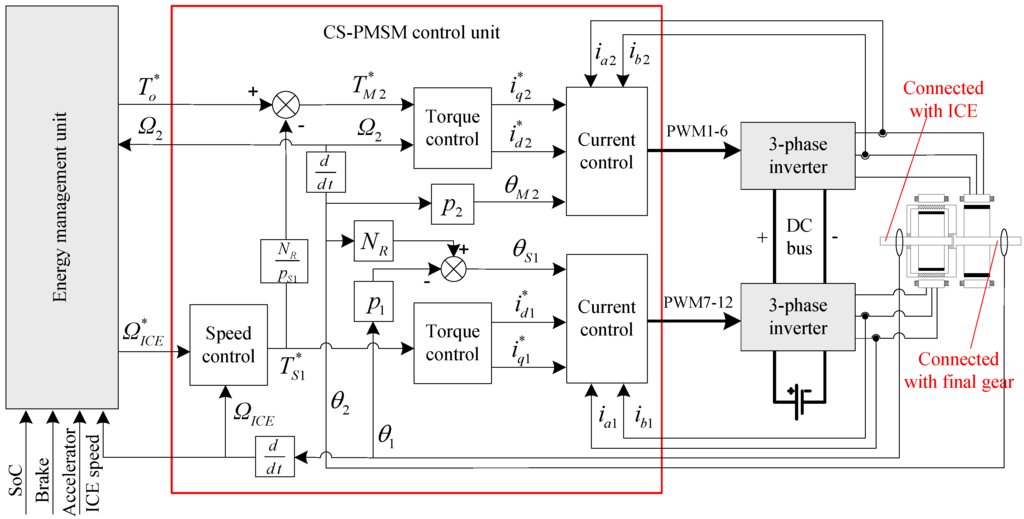
Figure 4. Control diagram of the flux-modulated CS-PMSM system.

Figure 4. Control diagram of the flux-modulated CS-PMSM system.

Two resolvers are installed for position feedback of the dual rotors, so the instantaneous electrical angular of the DRM can be calculated according to its operating principle. The two 6-switch inverters share the same DC bus. A DC-DC converter may be used to boost the low battery voltage for the inverters or buck the high DC link voltage for battery charge. This is useful for reducing the size of machine without increasing the number of battery packs needed. In that case, voltage control of DC bus is required like in the THS II [18,19].

Field oriented control (FOC) is applicable to both DRM and motor-2. The DRM shown in Figure 2(b) exhibits little reluctance torque in tentative simulations. The winding inductions of d- and q-axis of stator-1 are quite close. Thus the DRM can be treated as a surface-mounted PM machine and i_d = 0 method is adequate for the torque control. The reference value for the torque control loop of DRM is given by speed control loop of ICE. Torque reference for motor-2 is then calculated according to the transferred torque input (i.e., ICE torque delivered via PM rotor-1 to modulating ring rotor) and required overall torque output. Rotary inertia and resistance drag are neglected, as $T_o^{*}$ is adjusted according to driver demand. The magnets of motor-2 are inset on the outer rotor with salient-pole structure, so field weakening methods can be used to extend its operating domain.

The controller together with CS-PMSM serves as a continuous variable transmission between the ICE and final gear with three energy ports, i.e., the DC bus, engine input shaft and output shaft. Power flow of the three ports is controlled by vehicle controller according to components efficiency, SOC, vehicle speed, brake and accelerator signal. In fact, the CS-PMSM system has much in common with the THS. The DRM and motor-2 of CS-PMSM are actually the counterparts of the generator and motor in the THS. The vehicle energy management strategies of THS are still viable for the CS-PMSM system only after slight modification.

3.3. System Simulation

The system model is built in Matlab/Simulink, as shown in Figure 5, and a designed drive cycle is simulated.

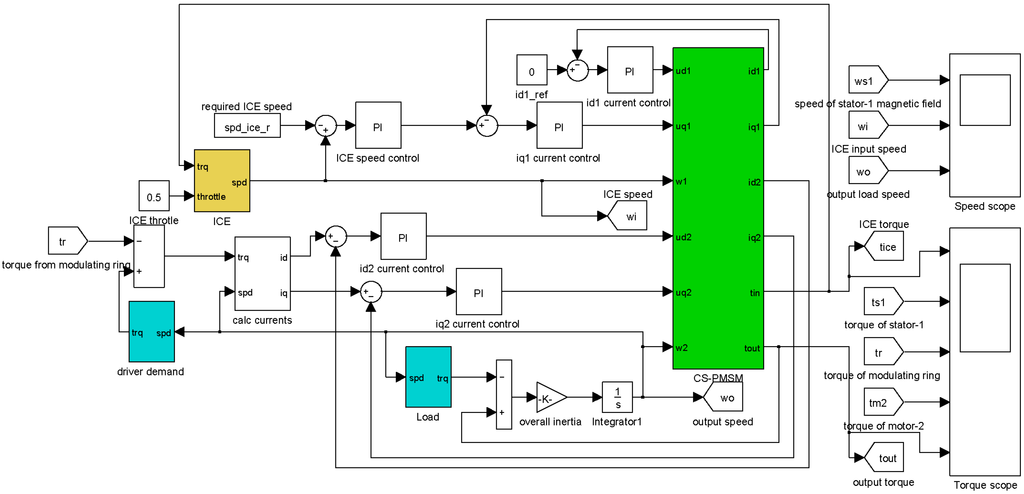
Figure 5. System model of the flux-modulated CS-PMSM system in Matlab/Simulink.

Figure 5. System model of the flux-modulated CS-PMSM system in Matlab/Simulink.

The pole pair numbers of PM rotor-1 and PM rotor-2 are 19 and 4, respectively, and the magnetic block number of modulating ring is 23. The output moment of inertia is considered, so the transient process of speed change can be observed. Vehicle air drag, rolling resistance and road grade are employed in the load submodule. The ICE is controlled to an optimal operating speed at a fixed throttle. Simulation results are shown in Figure 6, Figure 7 and Figure 8.

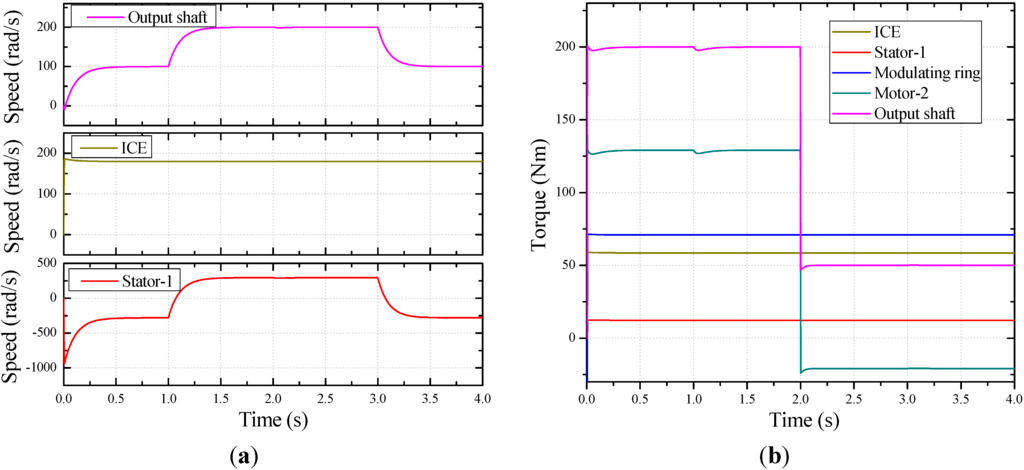
Figure 6. Simulated speed and torque waveforms: (a) Speeds of output shaft, ICE and rotating magnetic field generated by stator-1; (b) Torque delivered from ICE, electromagnetic torque of stator-1, torque delivered to modulating ring, electromagnetic torque of motor-2 and torque of output shaft.

Figure 6. Simulated speed and torque waveforms: (a) Speeds of output shaft, ICE and rotating magnetic field generated by stator-1; (b) Torque delivered from ICE, electromagnetic torque of stator-1, torque delivered to modulating ring, electromagnetic torque of motor-2 and torque of output shaft.

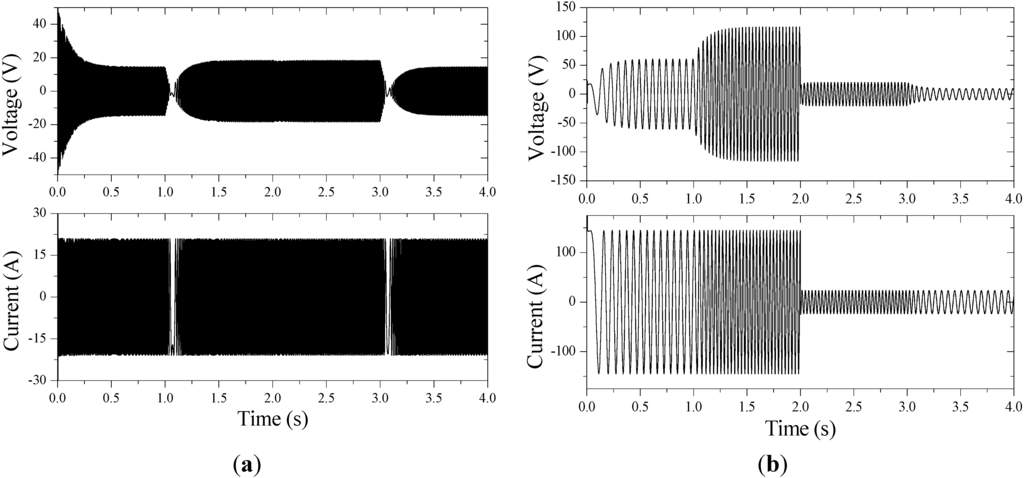
Figure 7. Phase voltage and current waveforms of DRM and motor-2: (a) DRM; (b) Motor-2.

Figure 7. Phase voltage and current waveforms of DRM and motor-2: (a) DRM; (b) Motor-2.

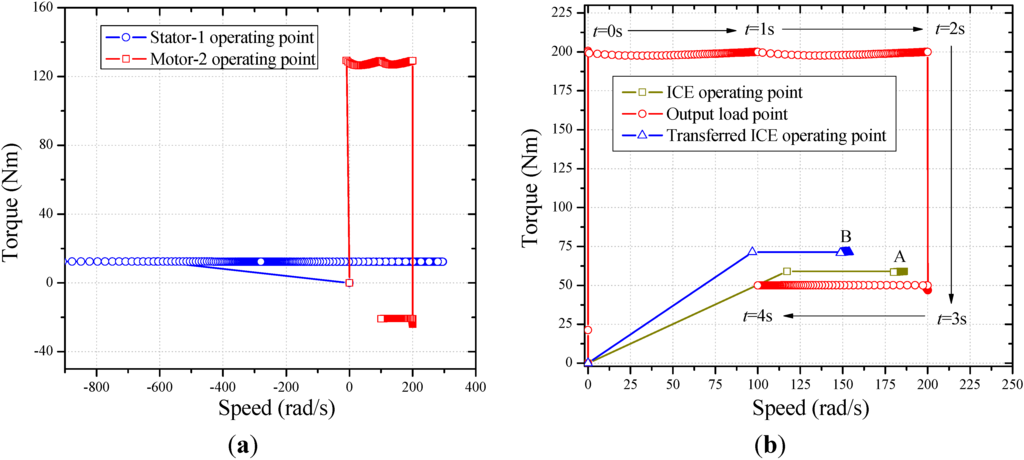
Figure 8. Historical speed-torque points: (a) Stator-1 and motor-2 operating points; (b) ICE, output load and transferred ICE operating points.

Figure 8. Historical speed-torque points: (a) Stator-1 and motor-2 operating points; (b) ICE, output load and transferred ICE operating points.

The speed-torque correlation of the ICE, stator-1 and modulating ring shown in Figure 6 satisfied Equations (5) and (6) derived in Section 2. Due to the speed-torque transfer characteristic of the DRM, the rotating speed of magnetic field generated by stator-1 may be much higher than that of ICE and output shaft. At a given throttle, the current of stator-1 was controlled to adjust the ICE torque, so it could run at the optimal speed, as shown in Figure 6 and Figure 7. Likewise, the current of motor-2 was controlled to deliver the torque difference between output shaft and modulating ring.

As shown in Figure 8, both DRM and motor-2 could operate as a generator or motor. Points A and B denote the actual and transferred operating speed-torque points of ICE, respectively. During the whole driving cycle the CS-PMSM system successively experienced all the four modes discussed in Section 2.2, i.e., decreased speed and increased torque, increased speed and torque, increased speed and decreased torque, and decreased speed and torque. Hence, the control strategy and the energy transducing function of CS-PMSM system are proved.

4. Implementation of the CS-PMSM Controller

The controller is designed with two cores: one DSP and one ARM microcontroller, as shown in Figure 9. The DSP implements the CS-PMSM control algorithms. The inverter and resolver interface enables control of two inverters and position acquisition of two resolvers. The ARM microcontroller is used for human-machine interface and communication, so the DSP can handle the control algorithms in time. A dual-port static RAM is employed as the data buffer between the DSP and the ARM microcontroller. The DSP messages the ARM microcontroller status data such as current, speed and torque values, via the dual-ports RAM. Likewise, ARM microcontroller notifies the DSP the values of control parameters, such as reference values of ICE speed, output torque, and brake or accelerator position. Figure 10 shows the designed controller and two inverters for a 20 kW CS-PMSM.

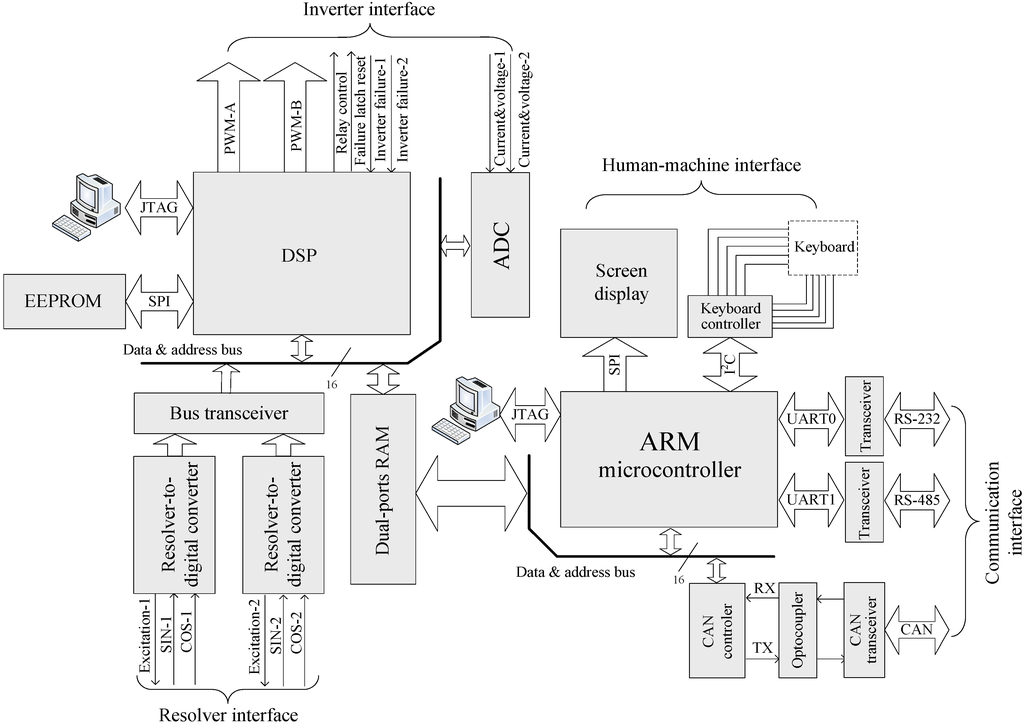
Figure 9. Hardware implementation of the flux-modulated CS-PMSM controller.

Figure 9. Hardware implementation of the flux-modulated CS-PMSM controller.

Figure 10. Photograph of the CS-PMSM controller.

Figure 10. Photograph of the CS-PMSM controller.

5. Conclusions and Future Work

The operating principle and basic working modes of the flux-modulated CS-PMSM are discussed. Joint control of the two integrated machines is proposed based on the mathematical models of the CS-PMSM system. The control of DRM requires position acquisition of dual rotors to synchronize the magnetic field generated by stator with the modulated harmonic component. The i_d = 0 torque control is applicable for DRM as little reluctance torque is observed. It is recommended to run the control algorithm by single DSP instead of two in order to implement the interconnected control of dual electrical and dual mechanical ports of CS-PMSM. Feasibility of the control system is further validated by Matlab/Simulink and a typical hardware design of the controller is given.

Experiments with the controller will be carried out in the future work and various standard driving cycles will be employed to test the flux-modulated CS-PMSM system. In a HEV system, the CS-PMSM and its controller constitute the power-split subsystem controlled by the vehicle energy management unit. The vehicle driving performance and fuel efficiency rest with the power-split ratio between engine and battery. Hence, the vehicle energy management strategy in particular will be investigated in the future.