Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer
Abstract
:1. Introduction
2. Modeling of Lithium-Ion Battery Pack
2.1. Battery Model
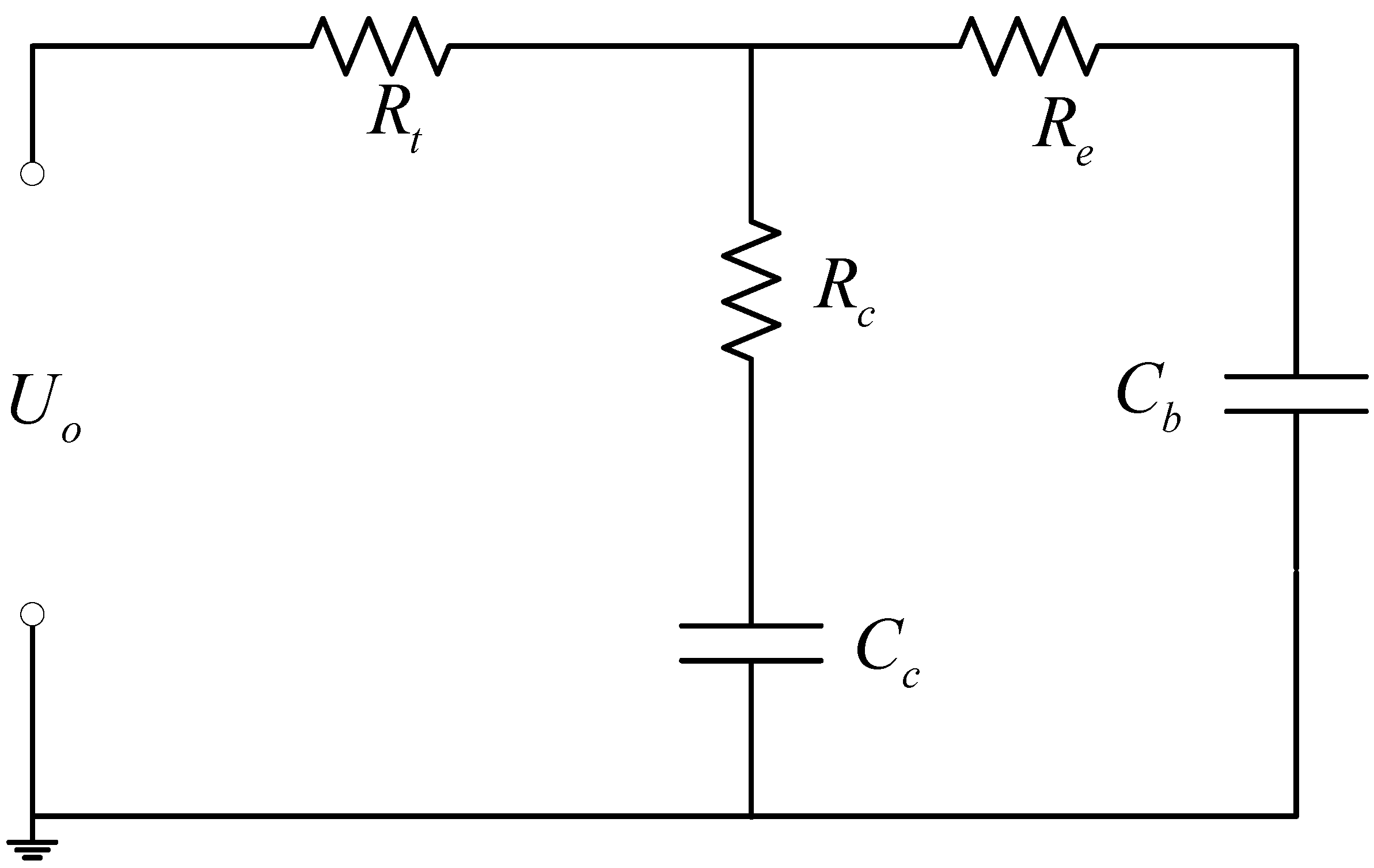
2.2. Parameter Estimation
2.2.1. Battery Test Bench
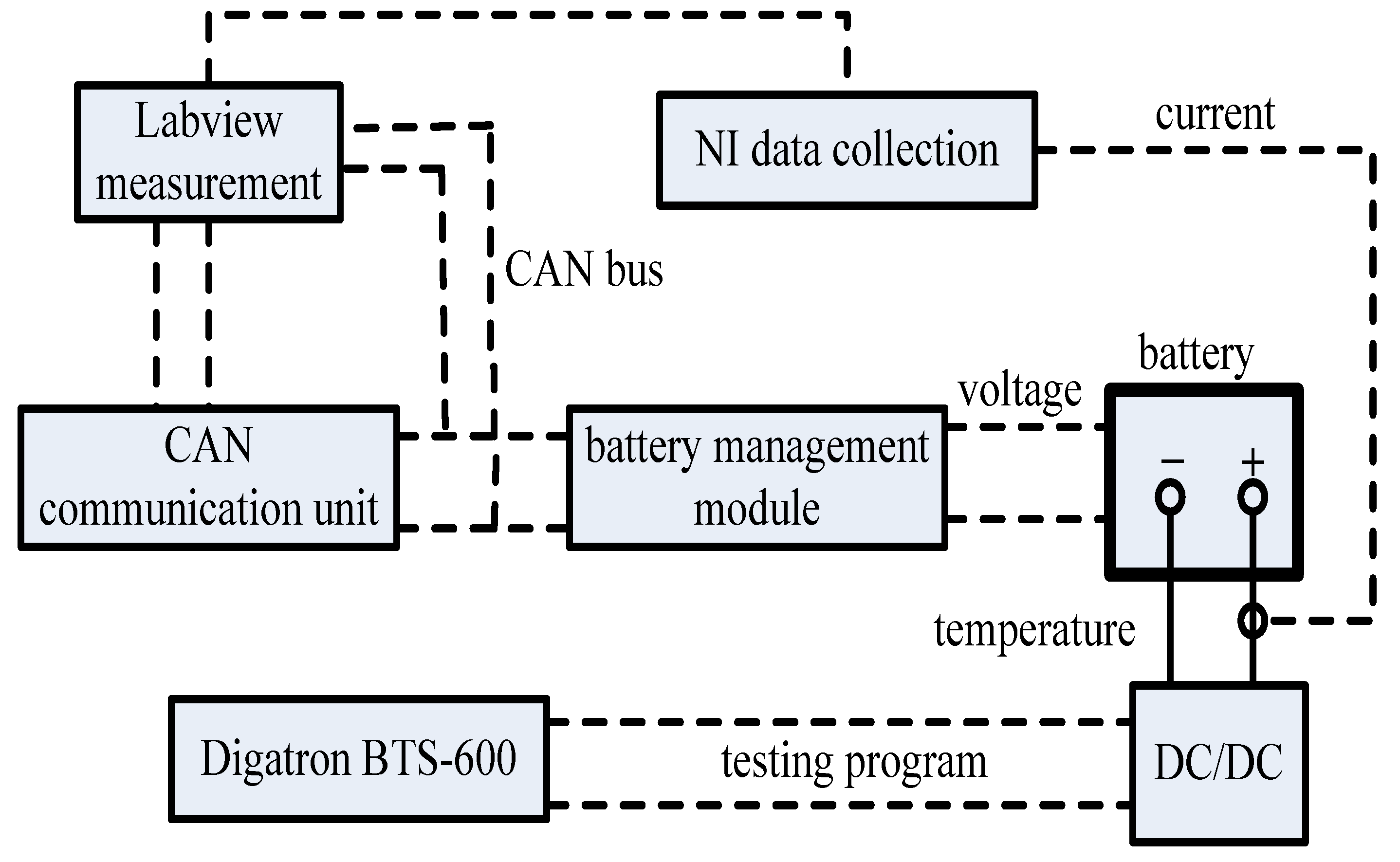
2.2.2. Acquisition of Estimation Data
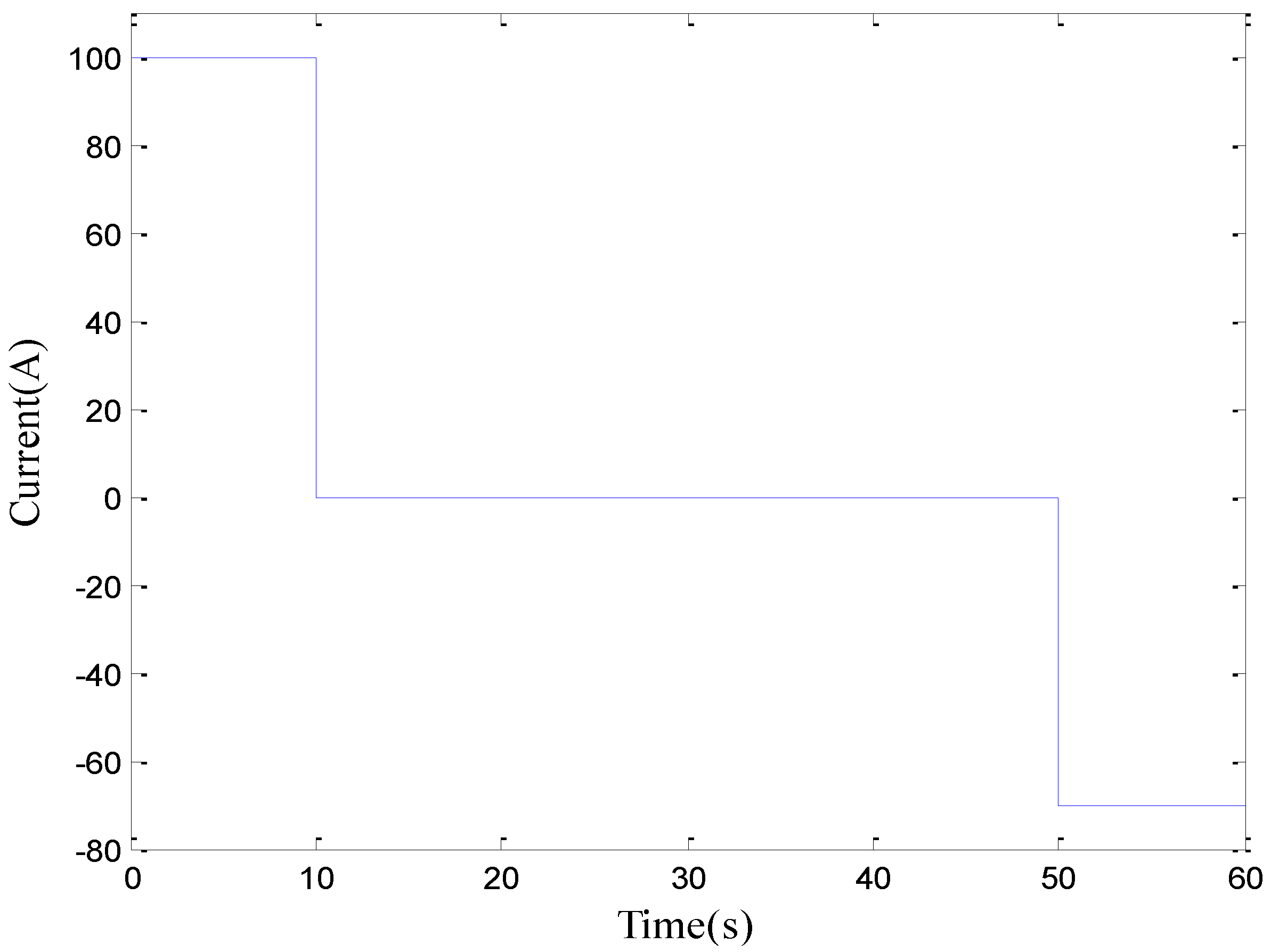
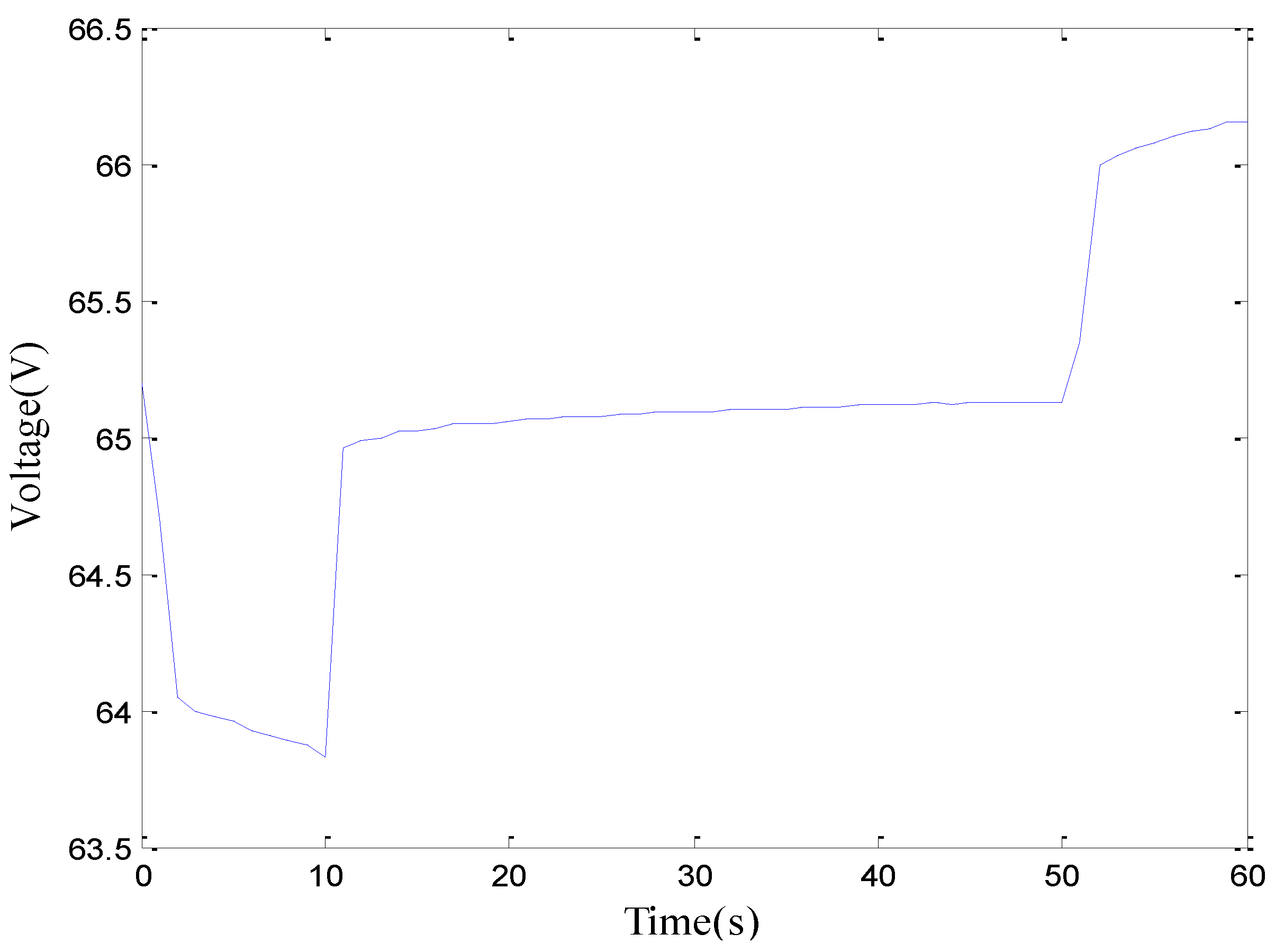
2.2.3. Determination of Initial Model Parameters
| SoC | Cb (F) | Cc (F) | Re (Ω) | Rc (Ω) | Rt (Ω) |
|---|---|---|---|---|---|
| 0.9 | 52360 | 65.04 | 0.0091 | 0.0091 | 0.00445 |
| 0.8 | 52360 | 74.56 | 0.0088 | 0.0088 | 0.00440 |
| 0.7 | 52360 | 74.51 | 0.0086 | 0.0086 | 0.00432 |
| 0.6 | 52360 | 68.37 | 0.0087 | 0.0087 | 0.00425 |
| 0.5 | 52360 | 63.14 | 0.0087 | 0.0087 | 0.00425 |
| 0.4 | 52360 | 50.90 | 0.0090 | 0.0090 | 0.00434 |
| 0.3 | 52360 | 47.93 | 0.0091 | 0.0091 | 0.00445 |
| 0.2 | 52360 | 46.44 | 0.0092 | 0.0092 | 0.00448 |
| 0.1 | 52360 | 45.32 | 0.0095 | 0.0095 | 0.00453 |
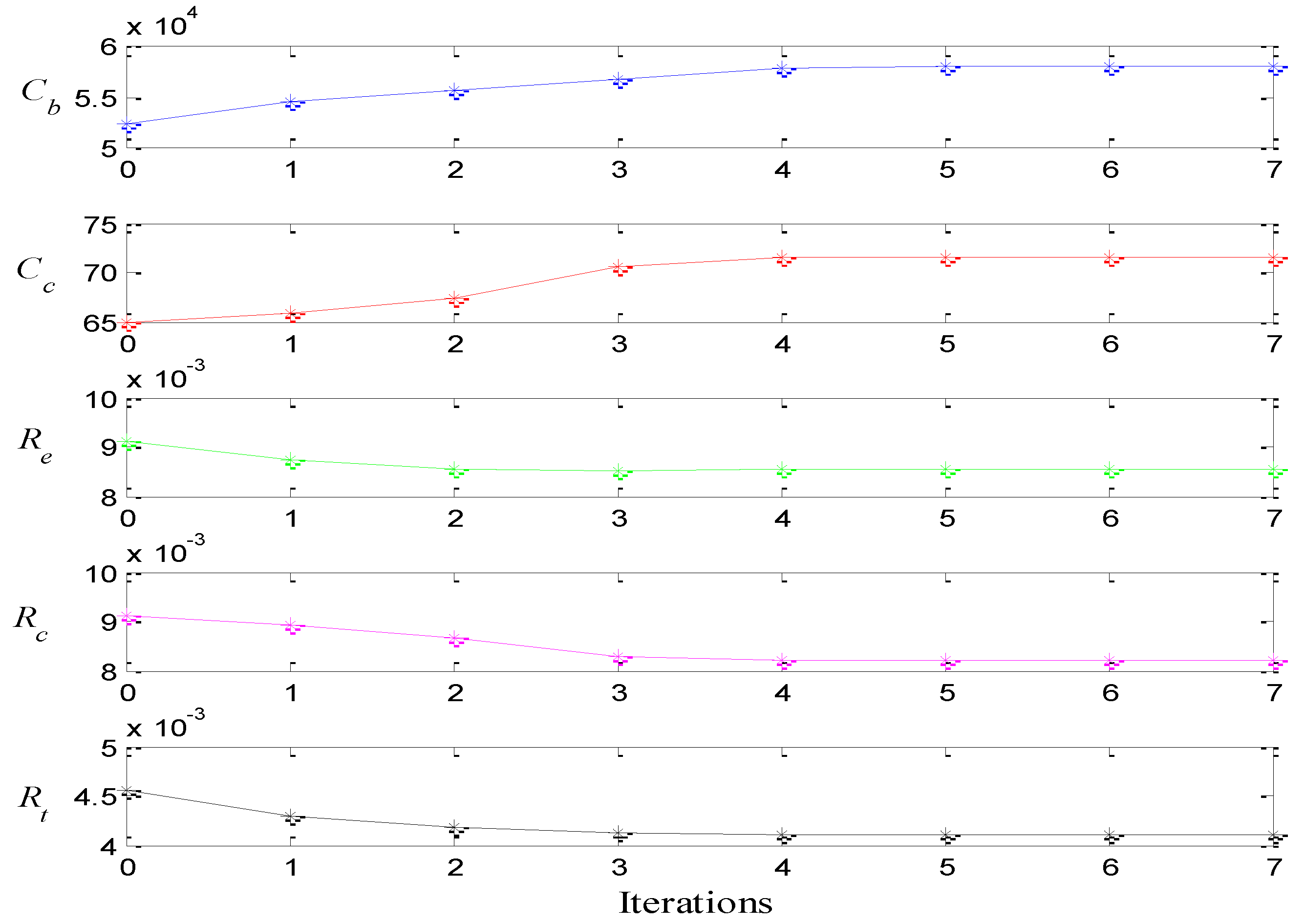
2.2.4. Optimization of Model Parameters
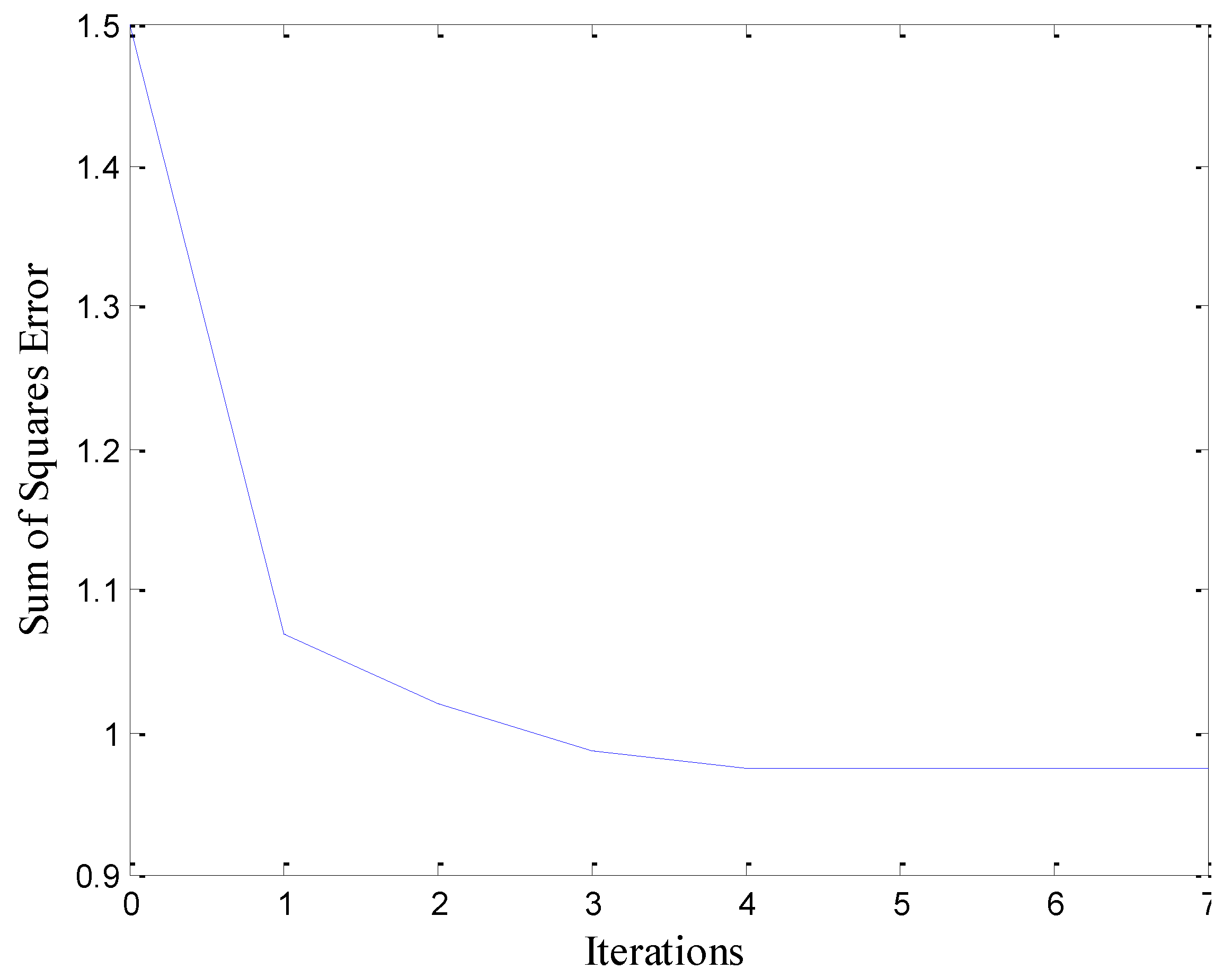
2.2.5. Model Evaluation
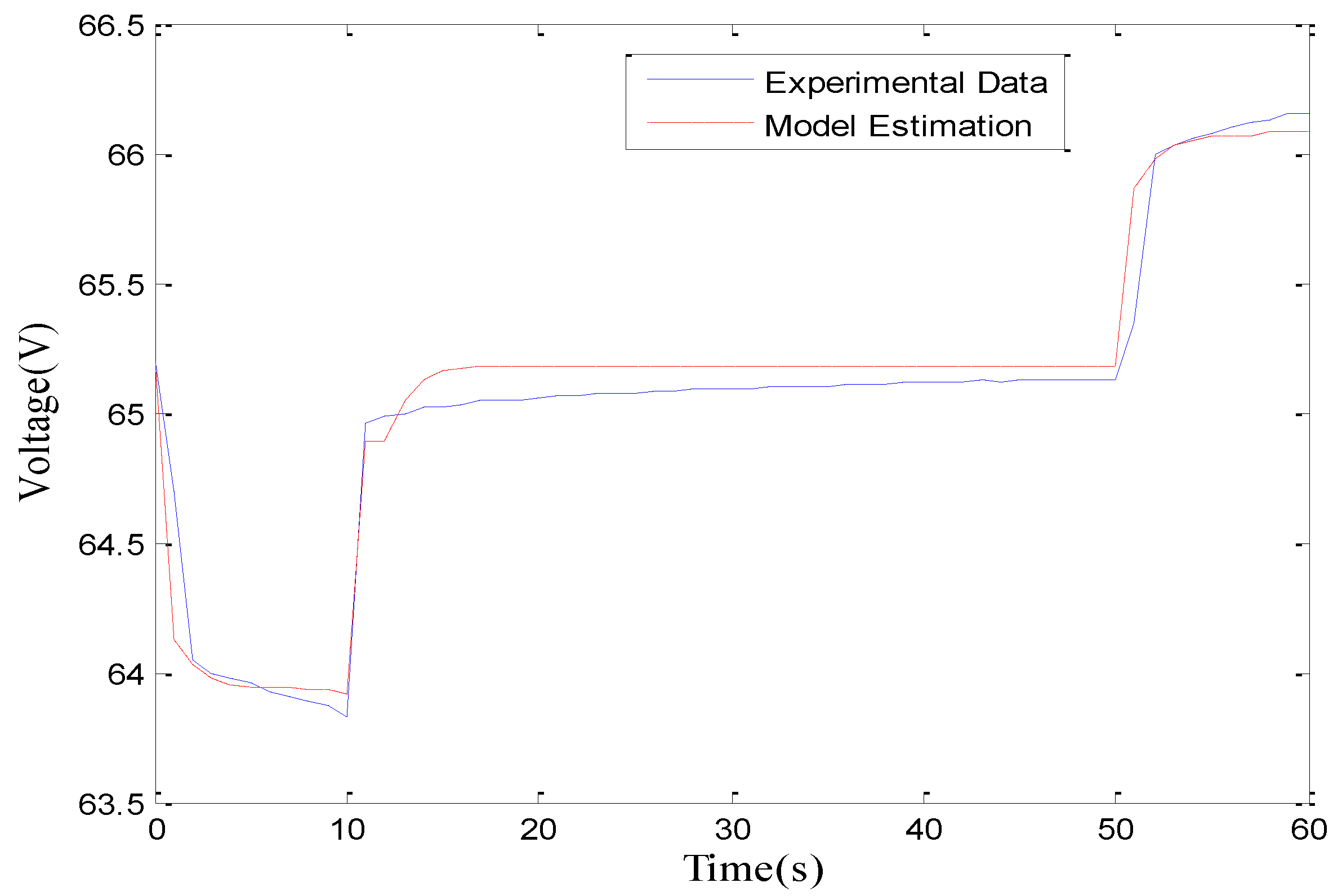
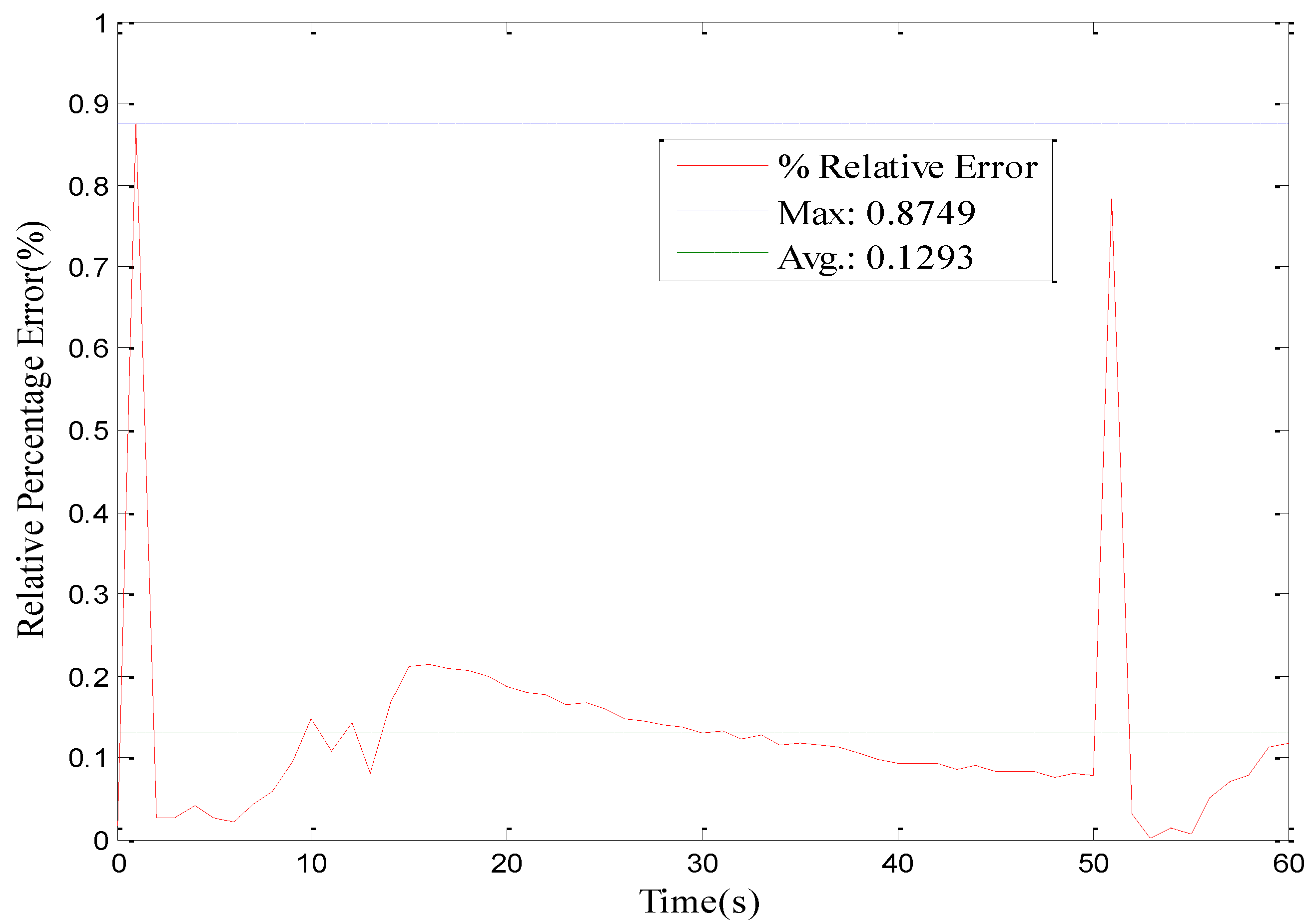
| SoC | Cb (F) | Cc (F) | Re (Ω) | Rc (Ω) | Rt (Ω) |
|---|---|---|---|---|---|
| 0.9 | 58002 | 71.55 | 0.00854 | 0.00819 | 0.00409 |
| 0.8 | 58002 | 82.01 | 0.00848 | 0.00812 | 0.00396 |
| 0.7 | 58002 | 81.97 | 0.00840 | 0.00803 | 0.00394 |
| 0.6 | 58002 | 75.20 | 0.00832 | 0.00795 | 0.00392 |
| 0.5 | 58002 | 69.45 | 0.00783 | 0.00783 | 0.00391 |
| 0.4 | 58002 | 55.99 | 0.00841 | 0.00810 | 0.00405 |
| 0.3 | 58002 | 52.73 | 0.00851 | 0.00819 | 0.00410 |
| 0.2 | 58002 | 51.09 | 0.00862 | 0.00822 | 0.00416 |
| 0.1 | 58002 | 50.12 | 0.00868 | 0.00825 | 0.00416 |
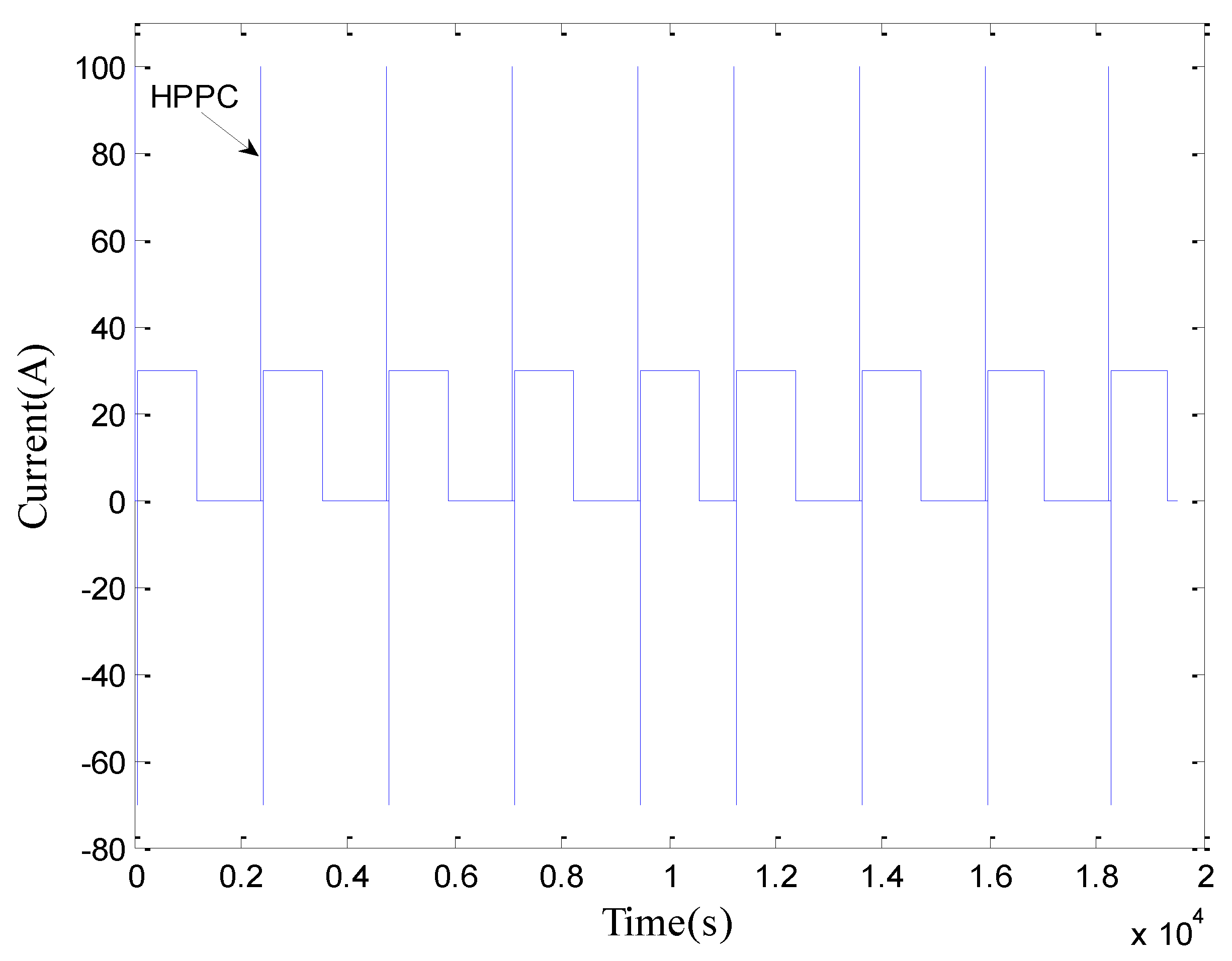
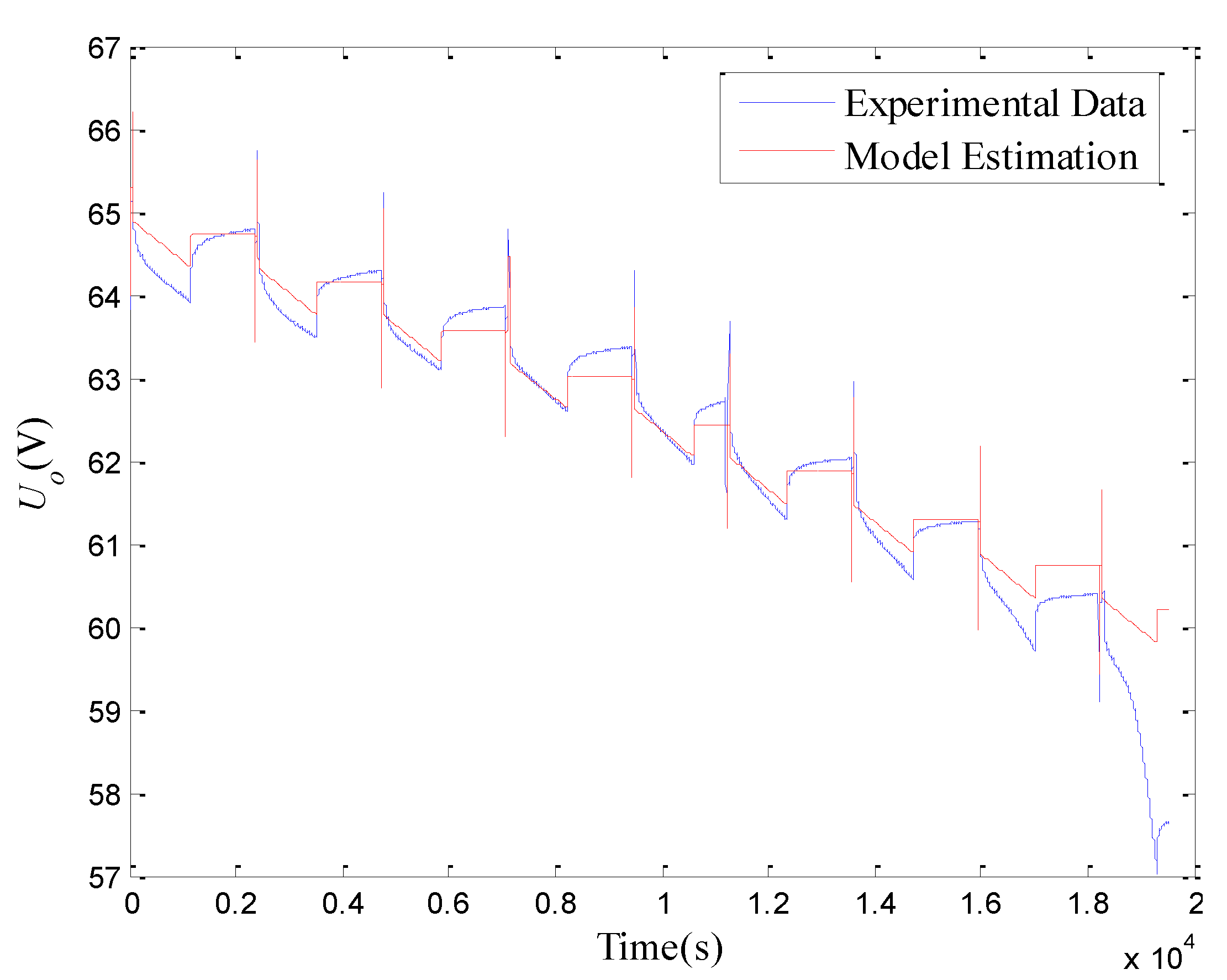
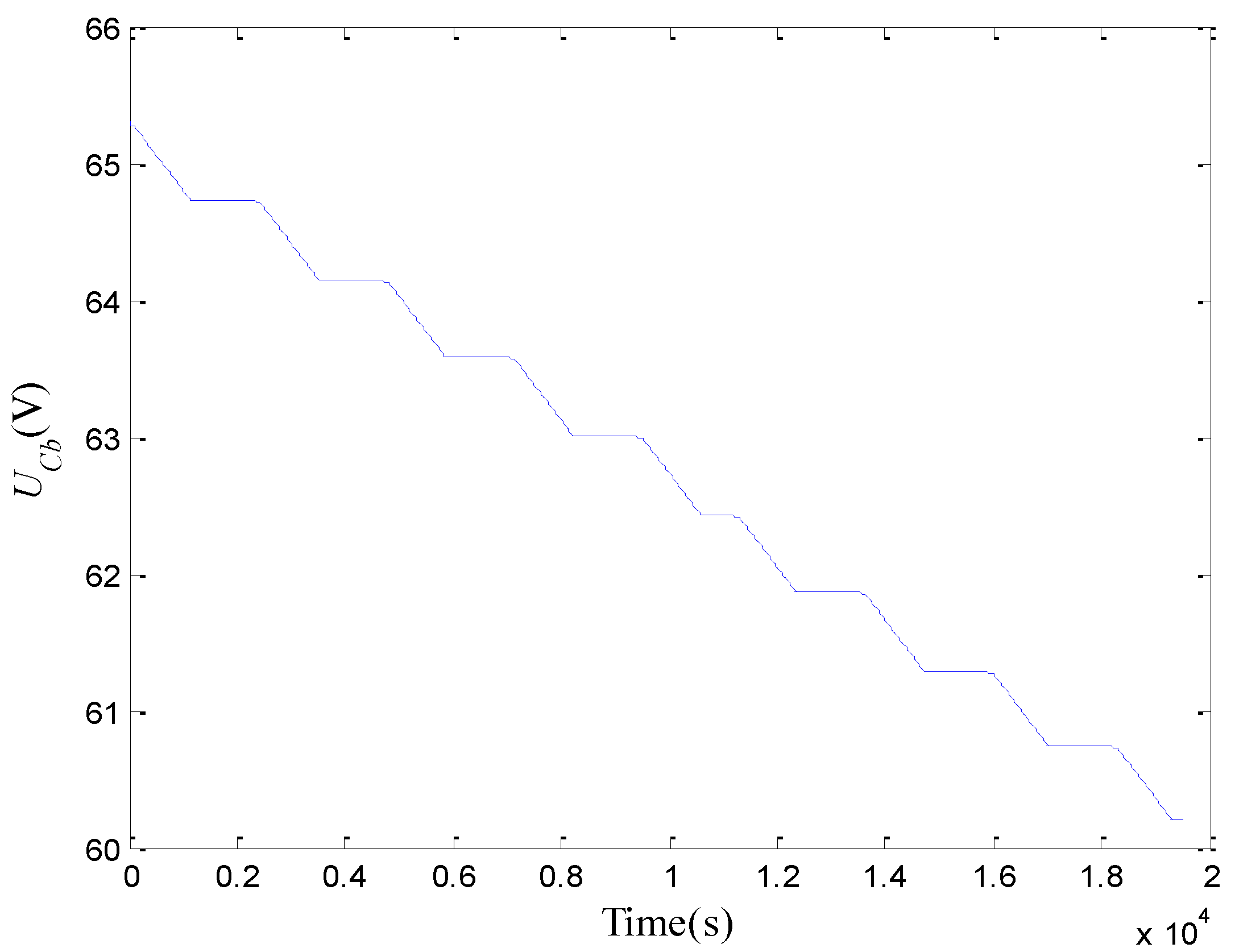
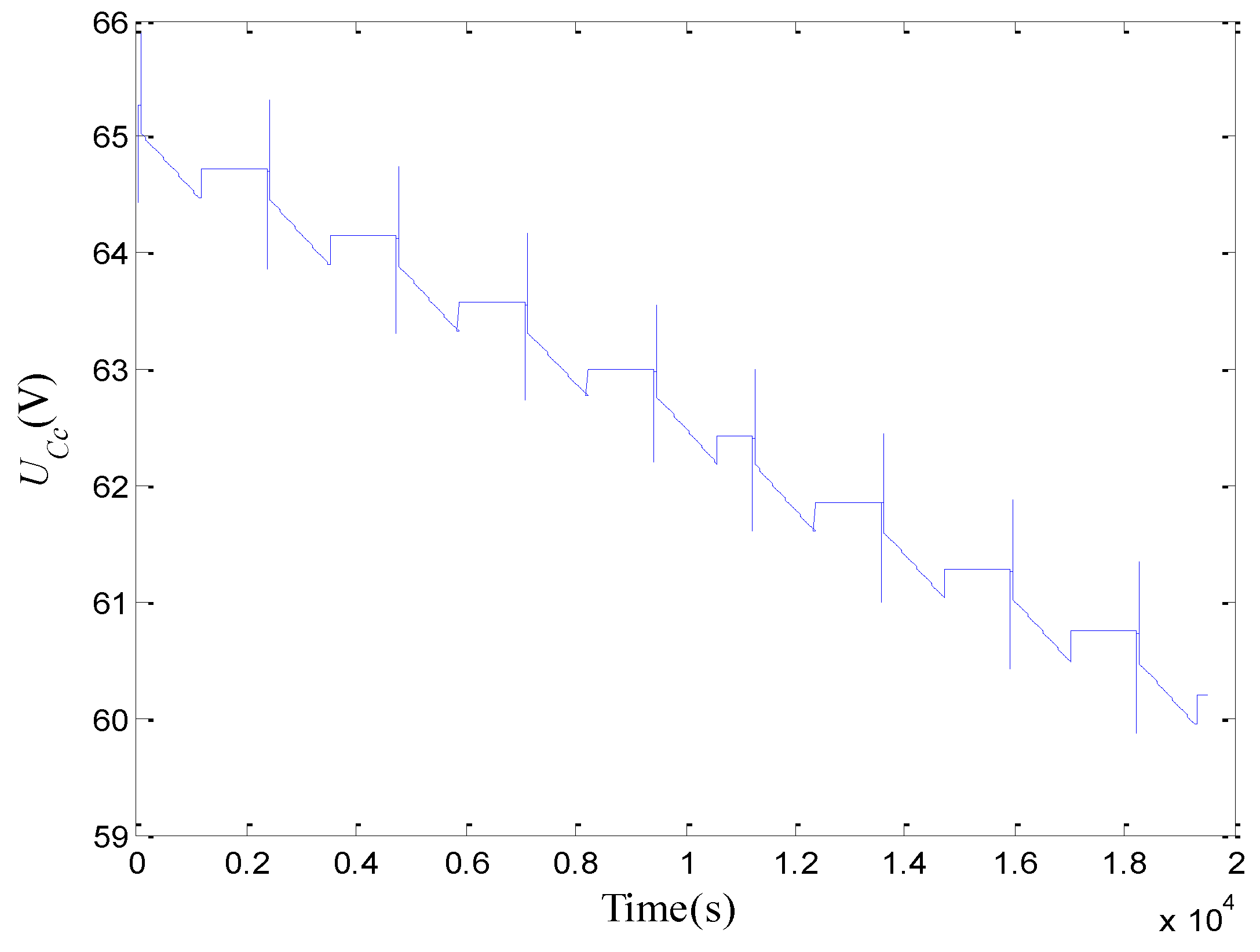
3. SoC Estimation Using Adaptive Luenberger Observer
3.1. The Adaptive Luenberger Observer
3.2. SoC Estimation Algorithm Based on the Optimized Battery Model
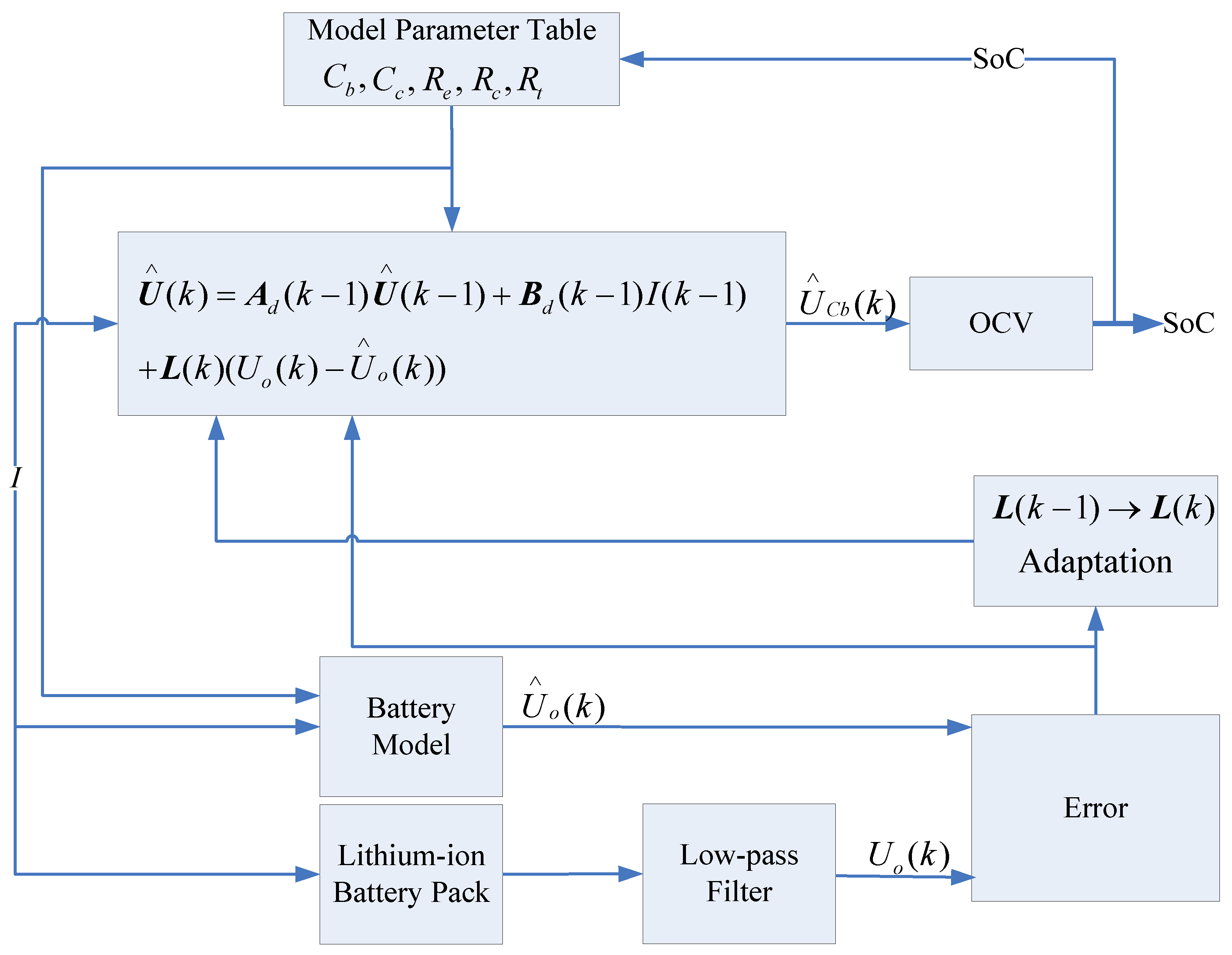
3.3. SoC Estimation Result
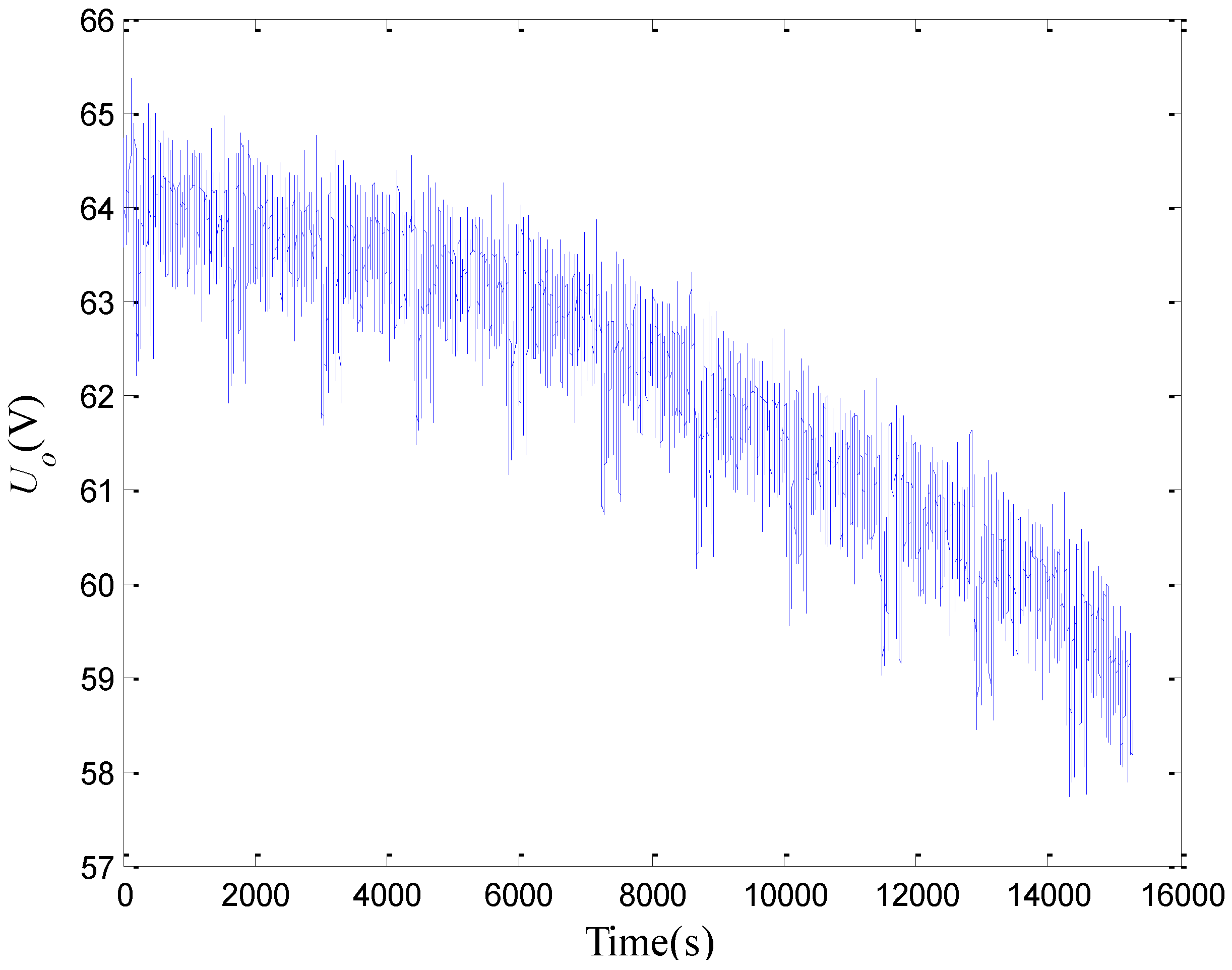
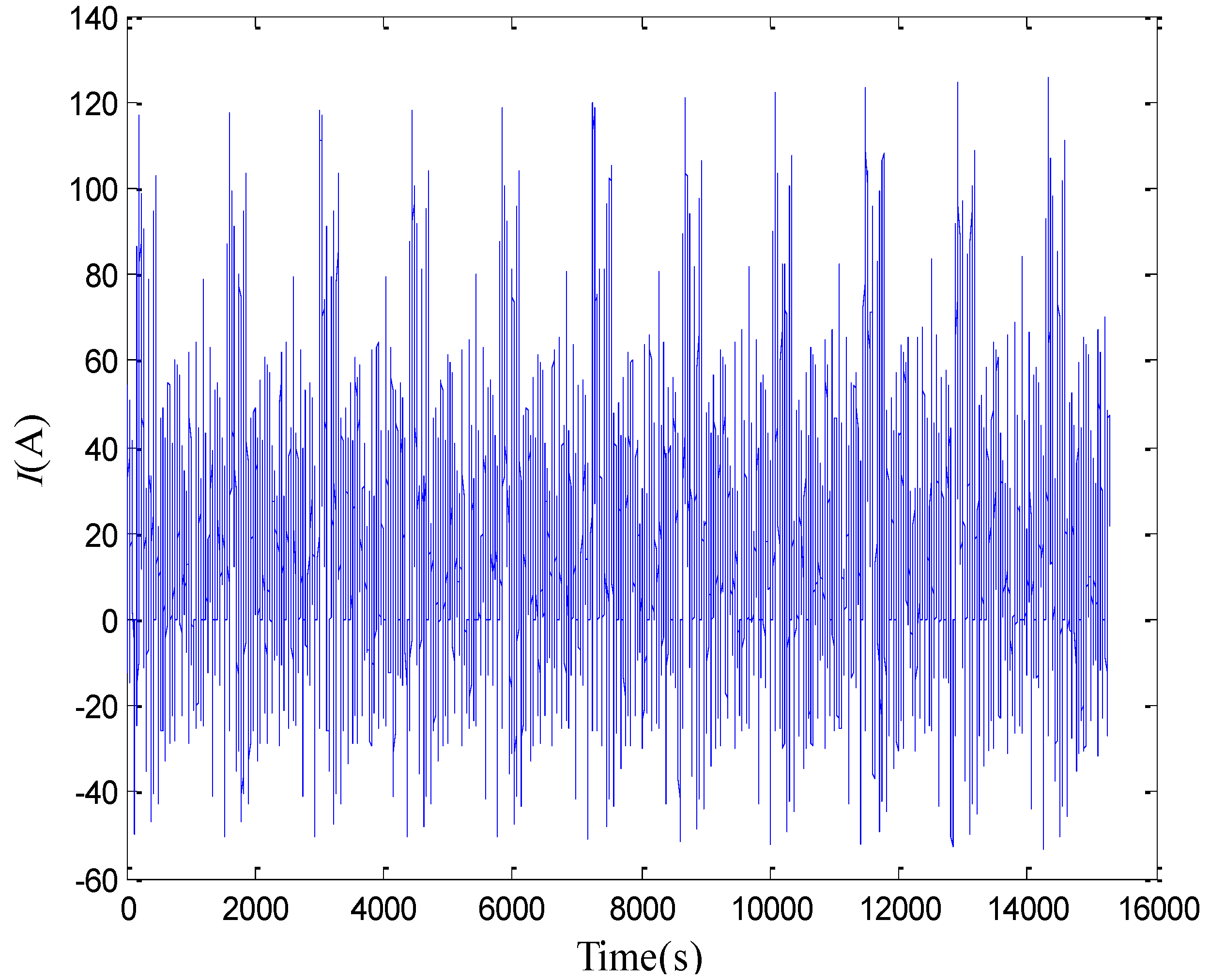
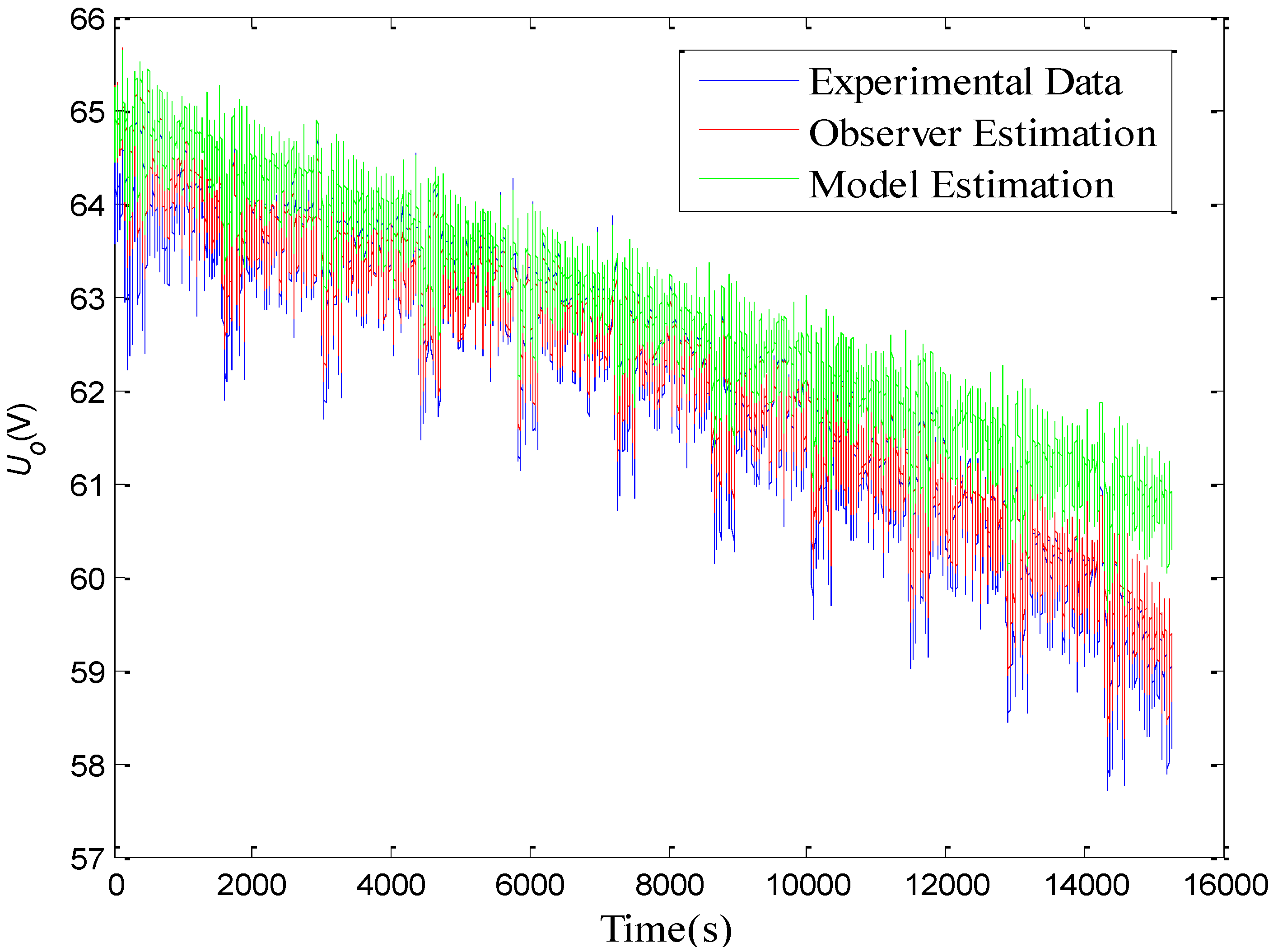
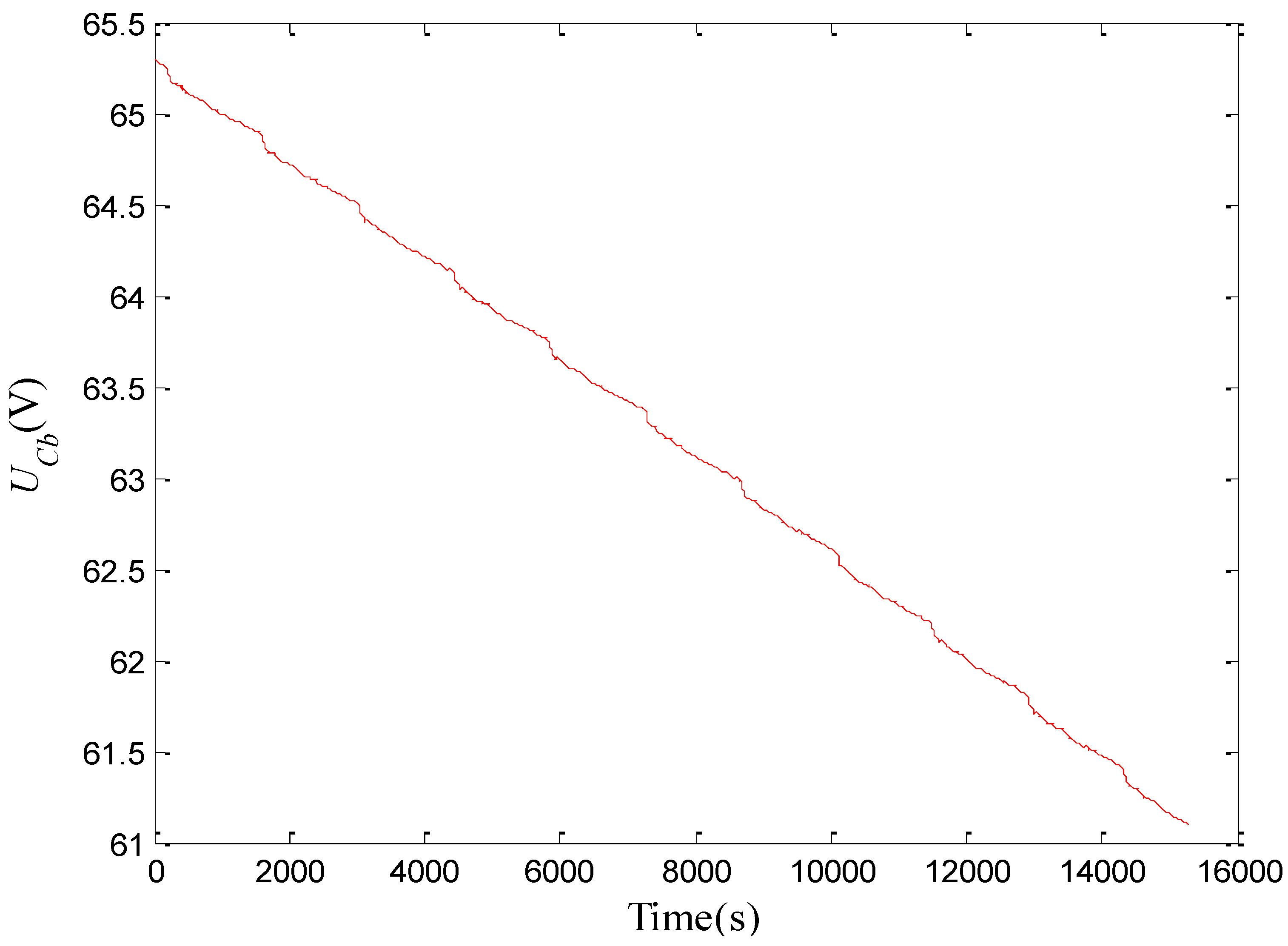

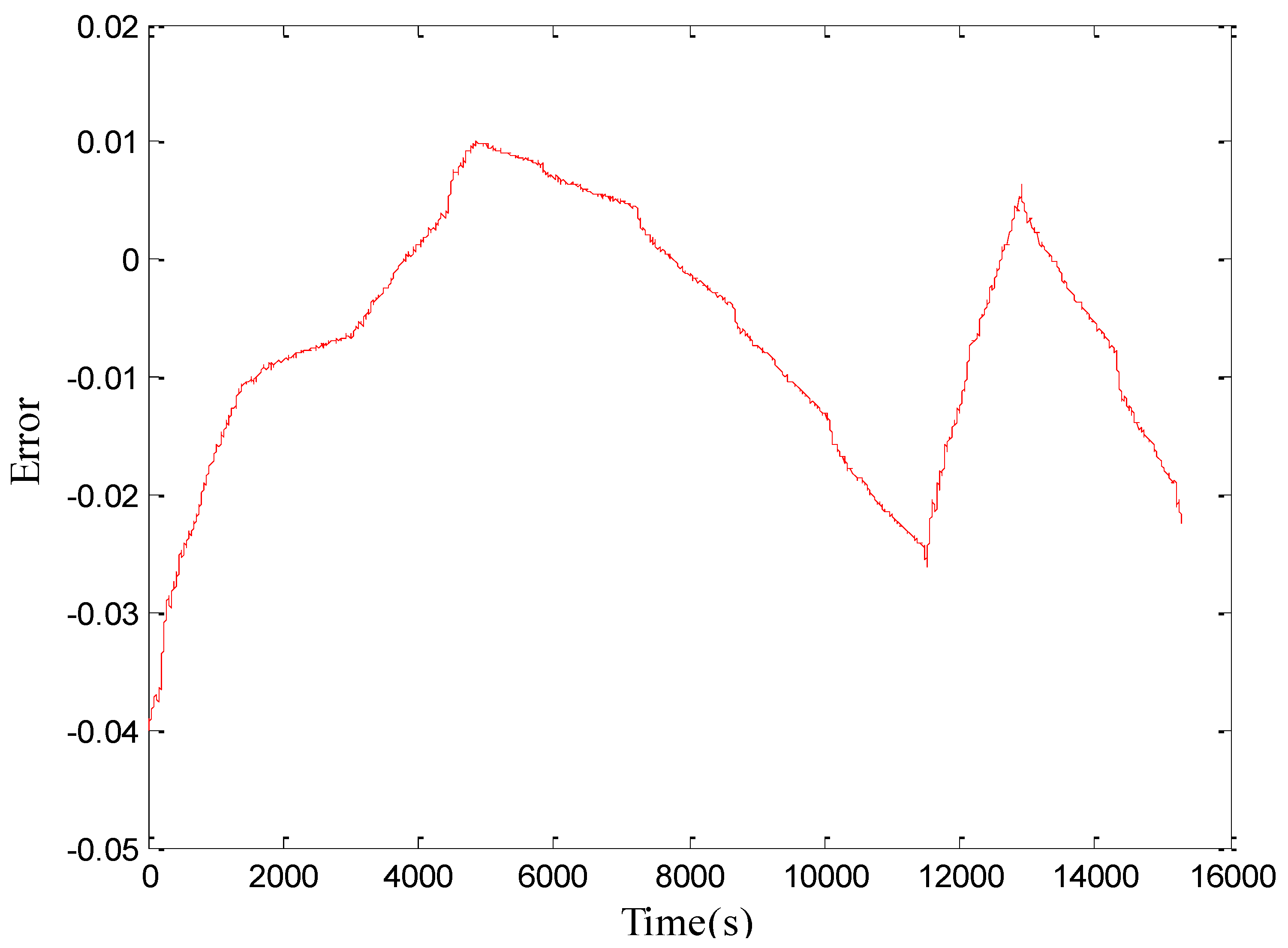
4. Conclusions
Acknowledgements
References
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Aylor, J.H.; Johnson, B.W. A battery state-of-charge indicator for electric wheelchairs. IEEE Trans. Ind. Electron. 1992, 39, 398–409. [Google Scholar] [CrossRef]
- Liu, T.H.; Chen, D.F.; Fang, C.C. Design and implementation of a battery charger with a state-of-charge estimator. Int. J. Electron. 2000, 87, 211–226. [Google Scholar] [CrossRef]
- Çadırcı, Y.; Özkazanç, Y. Microcontroller-based on-line state-of-charge estimator for sealed lead-acid batteries. J. Power Sources 2004, 129, 330–342. [Google Scholar] [CrossRef]
- Bhangu, B.S.; Bentley, P.; Stone, D.A.; Bingham, C.M. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. IEEE Trans. Veh. Tech. 2005, 54, 783–794. [Google Scholar] [CrossRef]
- Chan, C.C.; Lo, E.W.C.; Shen, W. The available capacity computation model based on artificial neural network for lead-acid batteries in electrical vehicles. J. Power Sources 2000, 87, 201–204. [Google Scholar] [CrossRef]
- Shen, W.X.; Chan, C.C.; Lo, E.W.C.; Chau, K.T. A new battery available capacity indicator for electric vehicles using neural network. Energy Convers. Manage. 2002, 43, 817–826. [Google Scholar] [CrossRef]
- Shen, W.X.; Chau, K.T.; Chan, C.C. Neural network-based residual capacity indicator for nickel-metal hydride batteries in electric vehicles. IEEE Trans. Veh. Tech. 2005, 54, 1705–1712. [Google Scholar] [CrossRef]
- Morita, Y.; Yamamoto, S.; Lee, S. H.; Mizuno, N. On-line detection of state-of-charge in lead acid battery using radial basis function neural network. Asian J. Control 2006, 8, 268–273. [Google Scholar] [CrossRef]
- Shen, W.X. State of available capacity estimation for lead-acid batteries in electric vehicles using neural network. Energy Convers. Manage. 2007, 48, 433–442. [Google Scholar] [CrossRef]
- Cheng, B.; Bai, Z.F.; Cao, B.G. State of charge estimation based on evolutionary neural network. Energy Convers. Manage. 2008, 49, 2788–2794. [Google Scholar] [CrossRef]
- Wang, J.P.; Xu, L.; Guo, J.G.; Ding, L. Modelling of a battery pack for electric vehicles using a stochastic fuzzy neural network. Proc. IMechE. Part D: J. Automobile Eng. 2009, 223, 27–35. [Google Scholar] [CrossRef]
- Cheng, B.; Zhou, Y.L.; Zhang, J.X.; Wang, J.P.; Cao, B.G. Ni–MH batteries state-of-charge prediction based on immune evolutionary network. Energy Convers. Manage. 2009, 50, 3078–3086. [Google Scholar] [CrossRef]
- Salkind, A.J.; Fennie, C.; Singh, P.; Atwater, T.; Reisne, D.E. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology. J. Power Sources 1999, 80, 293–300. [Google Scholar] [CrossRef]
- Chau, K.T.; Wu, K.C.; Chan, C.C.; Shen, W.X. A new battery capacity indicator for nickel-metal hydride battery powered electric vehicles using adaptive neuro-fuzzy inference system. Energy Convers. Manage. 2003, 44, 2059–2071. [Google Scholar] [CrossRef]
- Chau, K.T.; Wu, K.C.; Chan, C.C. A new battery capacity indicator for lithium-ion battery powered electric vehicles using adaptive neuro-fuzzy inference system. Energy Convers. Manage. 2004, 45, 1681–1692. [Google Scholar] [CrossRef]
- Singh, P.; Vinjamu, R.; Wang, X.P.; Reisne, D. Design and implementation of a fuzzy logic-based state-of-charge meter for Li-ion batteries used in portable defibrillators. J. Power Sources 2006, 162, 829–836. [Google Scholar] [CrossRef]
- Malkhandi, S. Fuzzy logic-based learning system and estimation of state of charge of lead-acid battery. Eng. Appl. Artif. Intel. 2006, 19, 479–485. [Google Scholar] [CrossRef]
- Hansen, T.; Wang, C.J. Support vector based battery state of charge estimator. J. Power Sources 2005, 141, 351–358. [Google Scholar] [CrossRef]
- Wang, J.P.; Chen, Q.S.; Cao, B.G. Support vector machine based battery model for electric vehicles. Energy Convers. Manage. 2006, 47, 858–864. [Google Scholar] [CrossRef]
- Shi, Q.S.; Zhang, C.H.; Cui, N.X. Estimation of battery state-of-charge using ν -support vector regression algorithm. Int. J. Auto. Tech. 2008, 9, 759–764. [Google Scholar] [CrossRef]
- Hu, X.S.; Sun, F.C. Fuzzy clustering based multi-model support vector regression state of charge estimator for lithium-ion battery of electric vehicle. In Proceedings of International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, Zhejiang, China, 26–27 August 2009; pp. 392–396.
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs-Part1: Background, Part2: Modeling and identification, Part3: State and parameter estimation. J. Power Sources 2004, 134, 252–292. [Google Scholar] [CrossRef]
- Vasebi, A.; Bathaee, S.M.T.; Partovibakhsh, M. Predicting state of charge of lead-acid batteries for hybrid electric vehicles by extended Kalman filter. Energy Convers. Manage. 2008, 49, 75–82. [Google Scholar] [CrossRef]
- Plett, G.L. Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs-Part 1: Introduction and state estimation, Part 2: Simultaneous state and parameter estimation. J. Power Sources 2006, 161, 1356–1384. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. State of charge estimation using an unscented filter for high power lithium ion cells. Int. J. Energy Res. 2010, 34, 152–163. [Google Scholar] [CrossRef]
- Wipke, K. ADVISOR 3.2 Documentation; NREL: Golden, CO, USA, 2001. [Google Scholar]
- Luenberger, D.G. Observers for multivariable systems. IEEE Trans. Automat. Contr. 1966, 11, 190–197. [Google Scholar] [CrossRef]
- Zeitz, M. The extended Luenberger observer for nonlinear systems. Sys. Control Lett. 1987, 9, 149–156. [Google Scholar] [CrossRef]
- Elmas, C. Zelaya de la Parra H. Application of a full-order Luenberger observer for a position sensorless operation of a switched reluctance motor drive. IEE Proc. Contr. Theor. Appl. 1996, 143, 401–408. [Google Scholar]
- Du, T.; Stronach, P.F. Design and application of extended observers for joint state and parameter estimation in high-performance AC drives. IEE Proc. Elec. Power Appl. 1995, 142, 71–78. [Google Scholar] [CrossRef]
- Erdogmus, D.; Genc, A.U.; Principe, J.C. A neural network perspective to extended Luenberger observers. Inst. Meas. Control 2002, 35, 10–16. [Google Scholar] [CrossRef]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Widrow, B.; Kamenetsky, M. On the Efficiency of Adaptive Algorithms. In Least-Mean-Square Adaptive Filters; Haykin, S., Widrow, B., Eds.; Wiley-Interscience: Hoboken, NJ, USA, 2003; pp. 1–34. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hu, X.; Sun, F.; Zou, Y. Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies 2010, 3, 1586-1603. https://doi.org/10.3390/en3091586
Hu X, Sun F, Zou Y. Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies. 2010; 3(9):1586-1603. https://doi.org/10.3390/en3091586
Chicago/Turabian StyleHu, Xiaosong, Fengchun Sun, and Yuan Zou. 2010. "Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer" Energies 3, no. 9: 1586-1603. https://doi.org/10.3390/en3091586
APA StyleHu, X., Sun, F., & Zou, Y. (2010). Estimation of State of Charge of a Lithium-Ion Battery Pack for Electric Vehicles Using an Adaptive Luenberger Observer. Energies, 3(9), 1586-1603. https://doi.org/10.3390/en3091586





