New Approaches for Very Short-term Steady-State Analysis of An Electrical Distribution System with Wind Farms
Abstract
:1. Introduction
- frequency regulation (a few seconds to about a minute);
- load following (a few minutes to a couple of hours);
- unit commitment (from several hours to one or more days into the future).
- Physical methods – methods that use physical information about the site (e.g., wind conditions at the height of turbine hubs and weather conditions). These methods are typically characterized by significant computational complexity and are mainly used for long-term forecasting.
- Statistical methods—methods that can forecast either a wind-speed/power value (“point-forecast” methods) or a wind-speed/power probability density function (“pdf-forecast” methods). Both are obtained from statistical analyses of time series from past data, and they usually employ recursive techniques. They can furnish useful information with reduced computational efforts for short-term forecasting (a few hours ahead).
- Artificial neural network methods—methods that are designed to determine the relationship between wind power and the time series from past data.
- Hybrid methods – methods that are combinations of the previous methods.
2. Very Short-Term, Steady-State Analysis of a Distribution System with Wind Farms
- (i)
- Step 1: forecast “at hour t” the wind power “at hour t + k” at the sites where the wind farms are installed; and
- (ii)
- Step 2: perform the very-short-term (VST), steady-state analysis of the electrical distribution system.
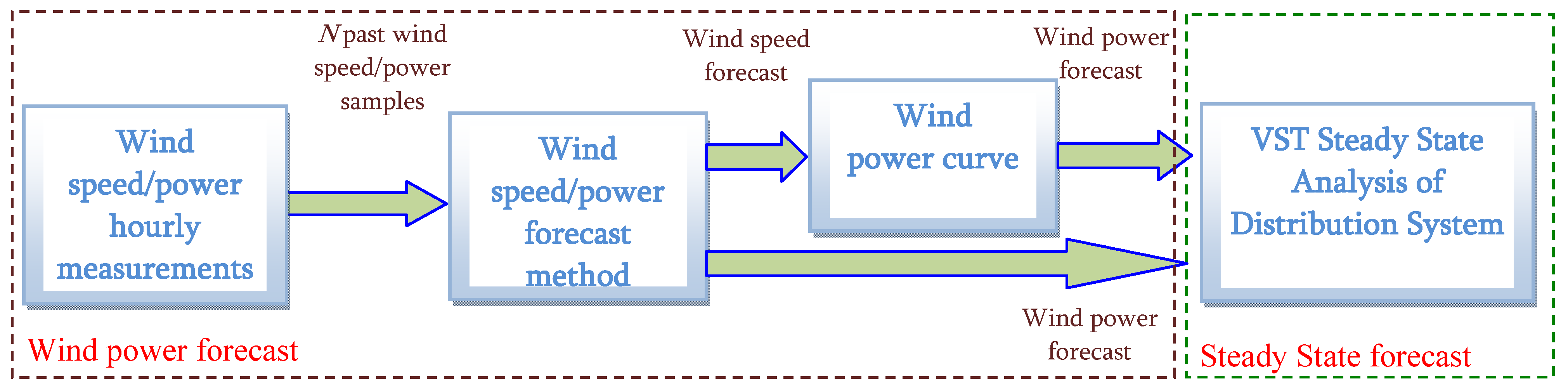
3. Wind Power Forecast Methods
3.1. “Point-forecast” Methods [5]
3.2. “Pdf-forecast” Methods
- a.
- Bayesian Method
- b.
- Markov Method
- weight the generic element of the wind power time series with the coefficient (1-), where is the correlation coefficient defined in Equation 4; and
- add the results obtained in 1. to the last observed power Pt weighted with the correlation coefficient .
4. Load flow equations for distribution systems with wind farms
4.1. Deterministic Load Flow
- fixed speed WTGUs (induction generators directly connected to the distribution system that are driven by wind turbines with either a fixed turbine blade angle or a pitch controller to regulate the blade angle);
- semi-variable-speed WTGUs (induction generators with a rotor-resistance converter); and
- variable-speed WTGUs (doubly-fed induction generators or synchronous/induction generators with full-scale static converters).
- a.
- Fixed-speed WTGUs
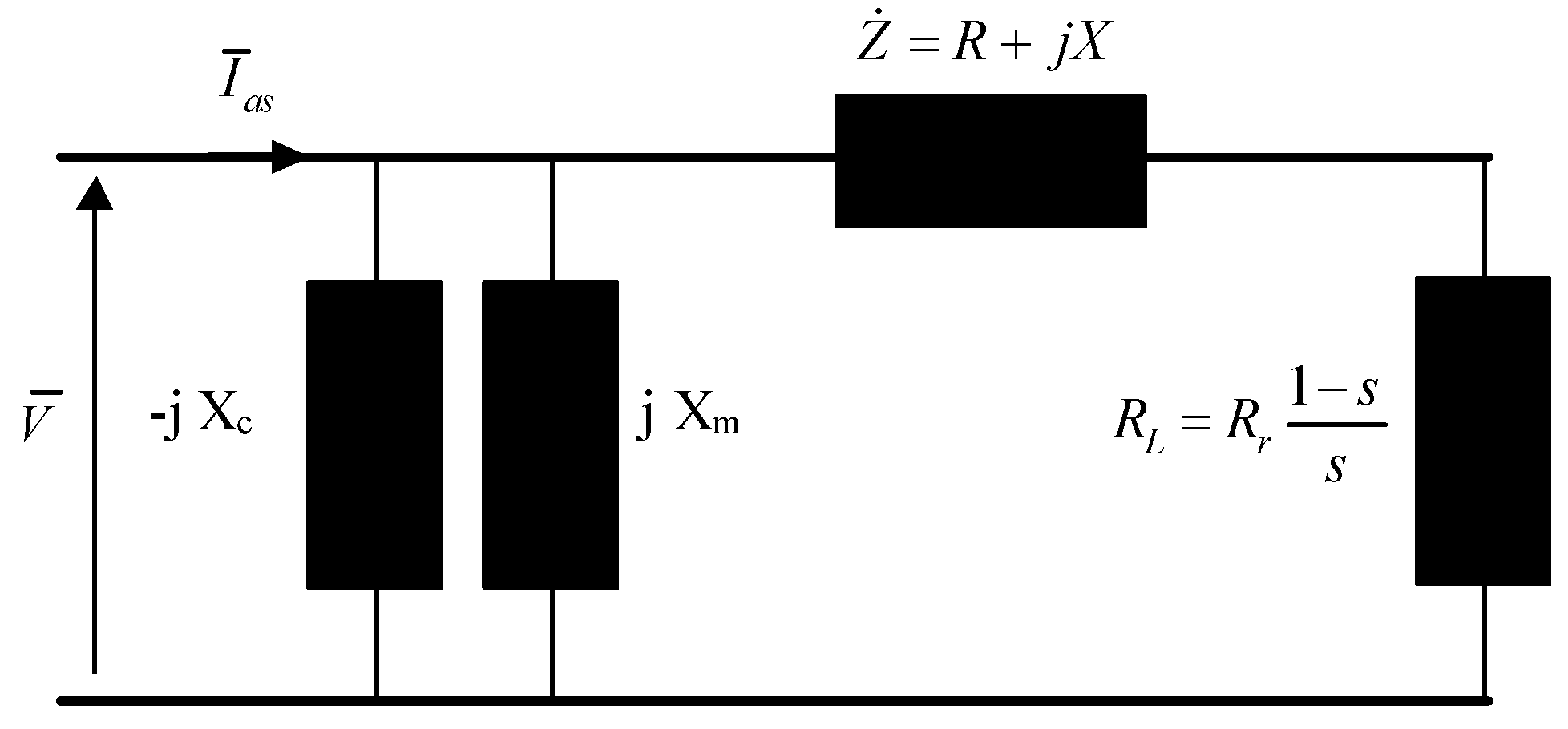
- b.
- Semi-variable speed WTGUs
- c.
- Variable-speed WTGUs
4.2. Probabilistic Load Flow
5. Experimental Section
- -
- 1.0 MW, semi-variable-speed WTGU at bus #9;
- -
- 1.0 MW GBBC, variable-speed WTGU at bus #13;
- -
- 1.0 MW DFIG, variable-speed WTGU at bus #15;
- -
- 1.0 MW stall-regulated, fixed-speed WTGU at bus #17.
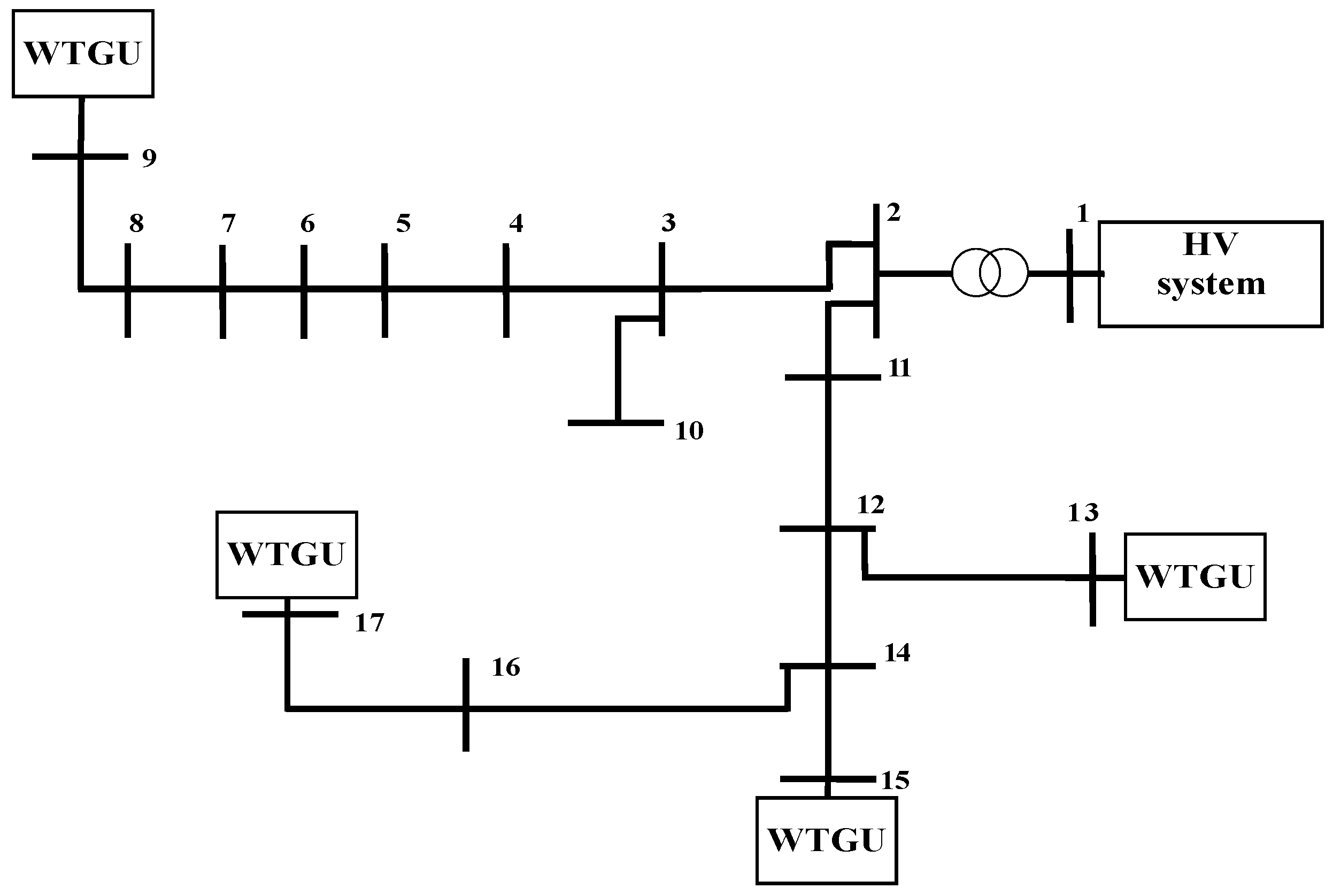
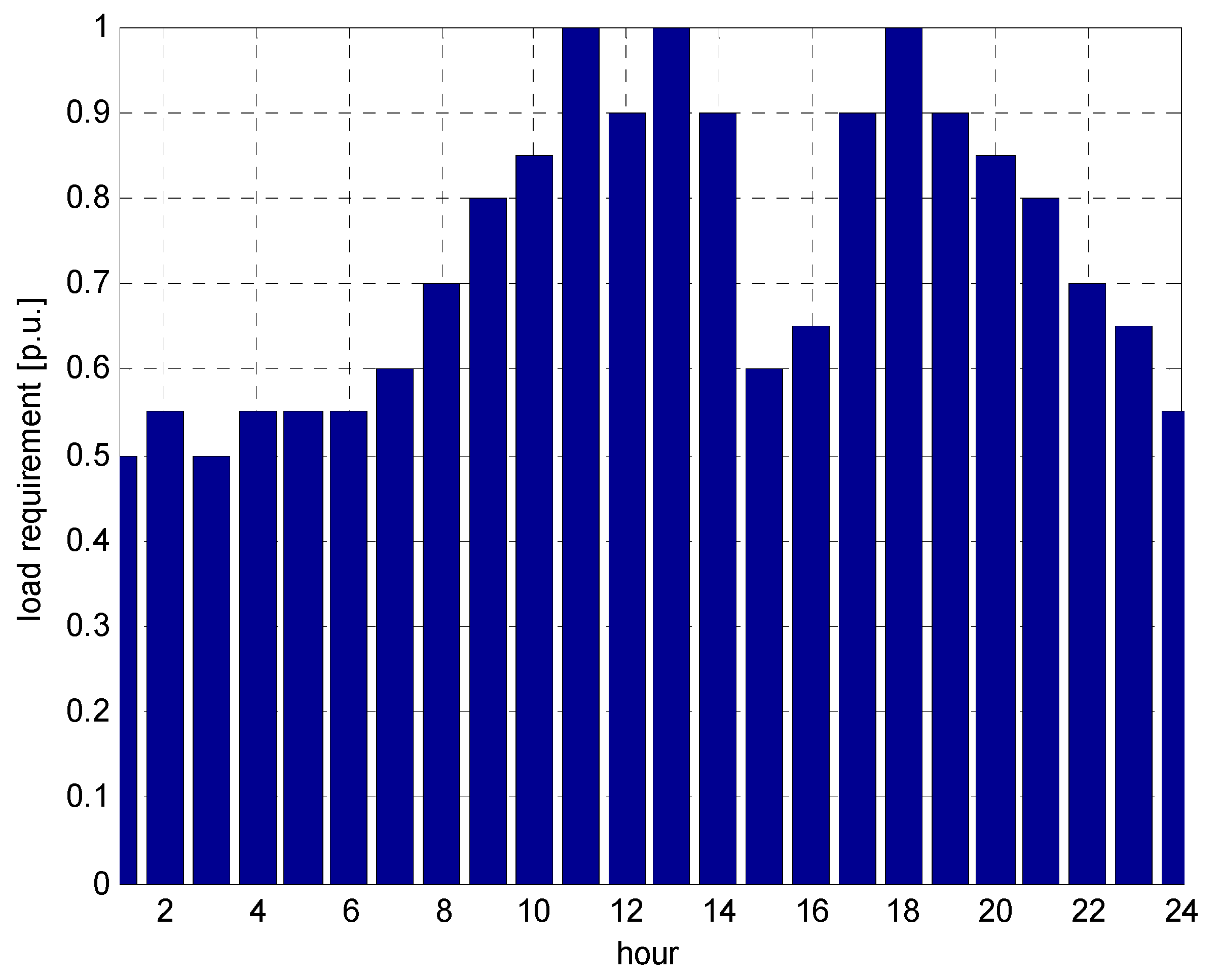
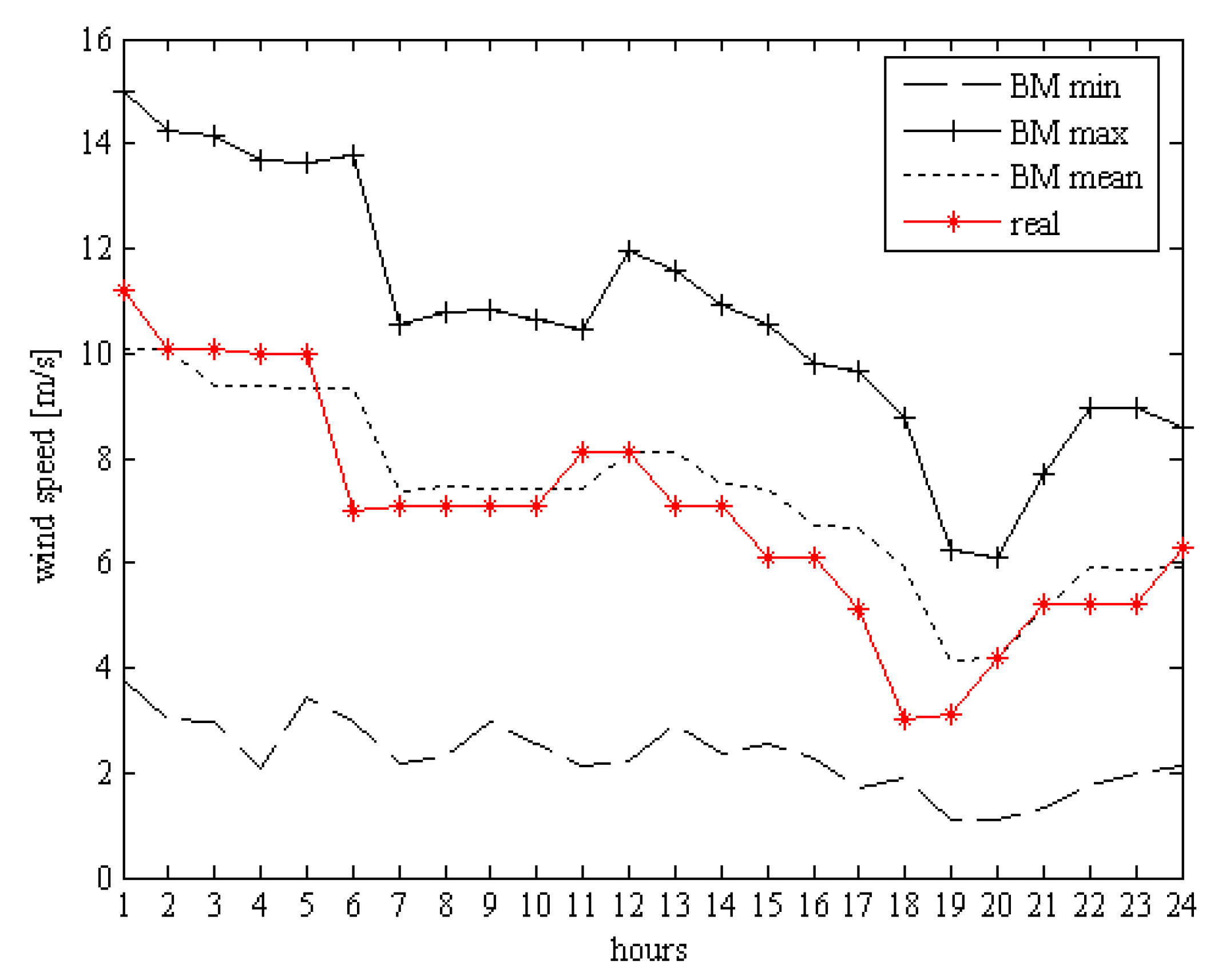
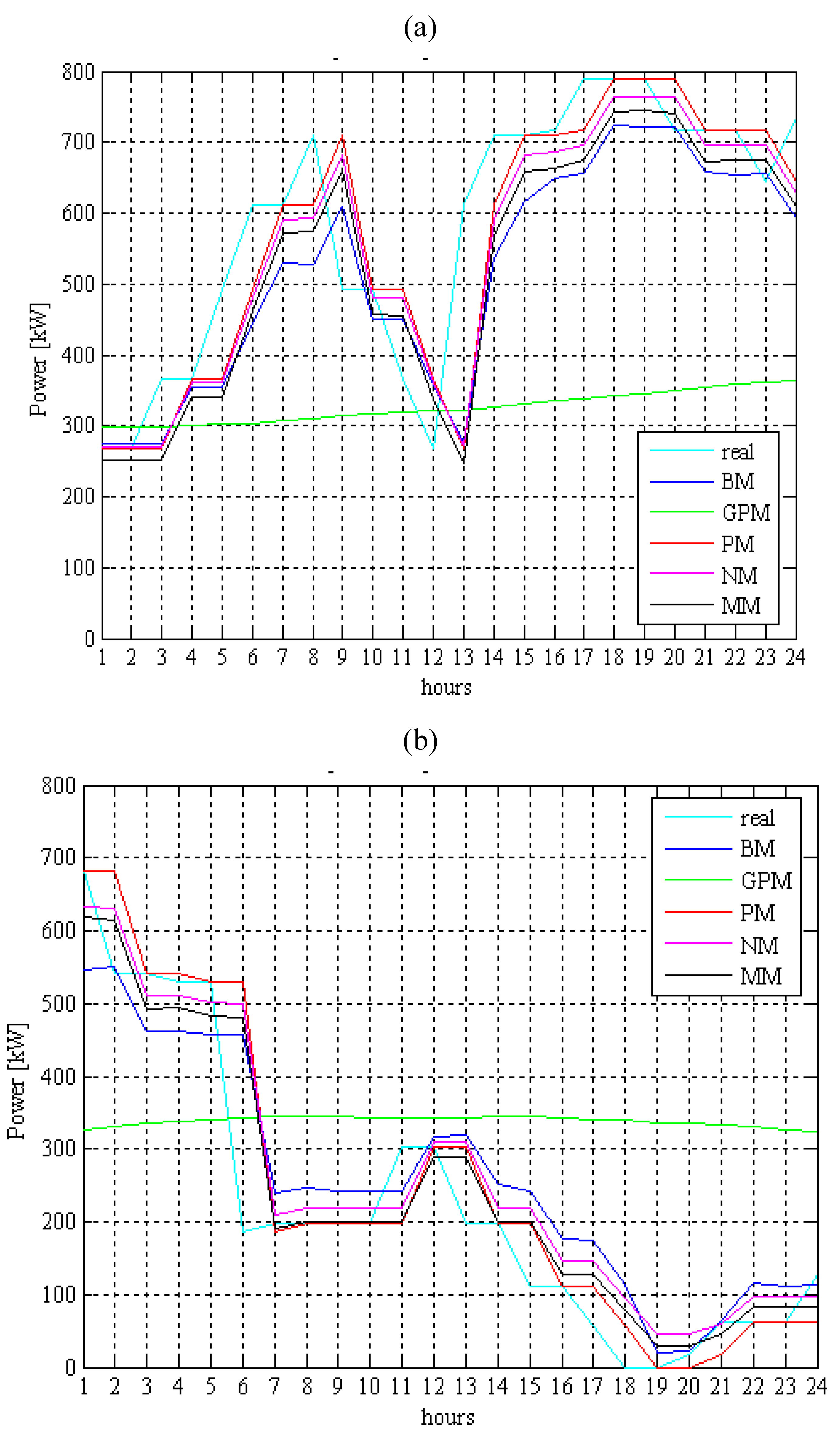
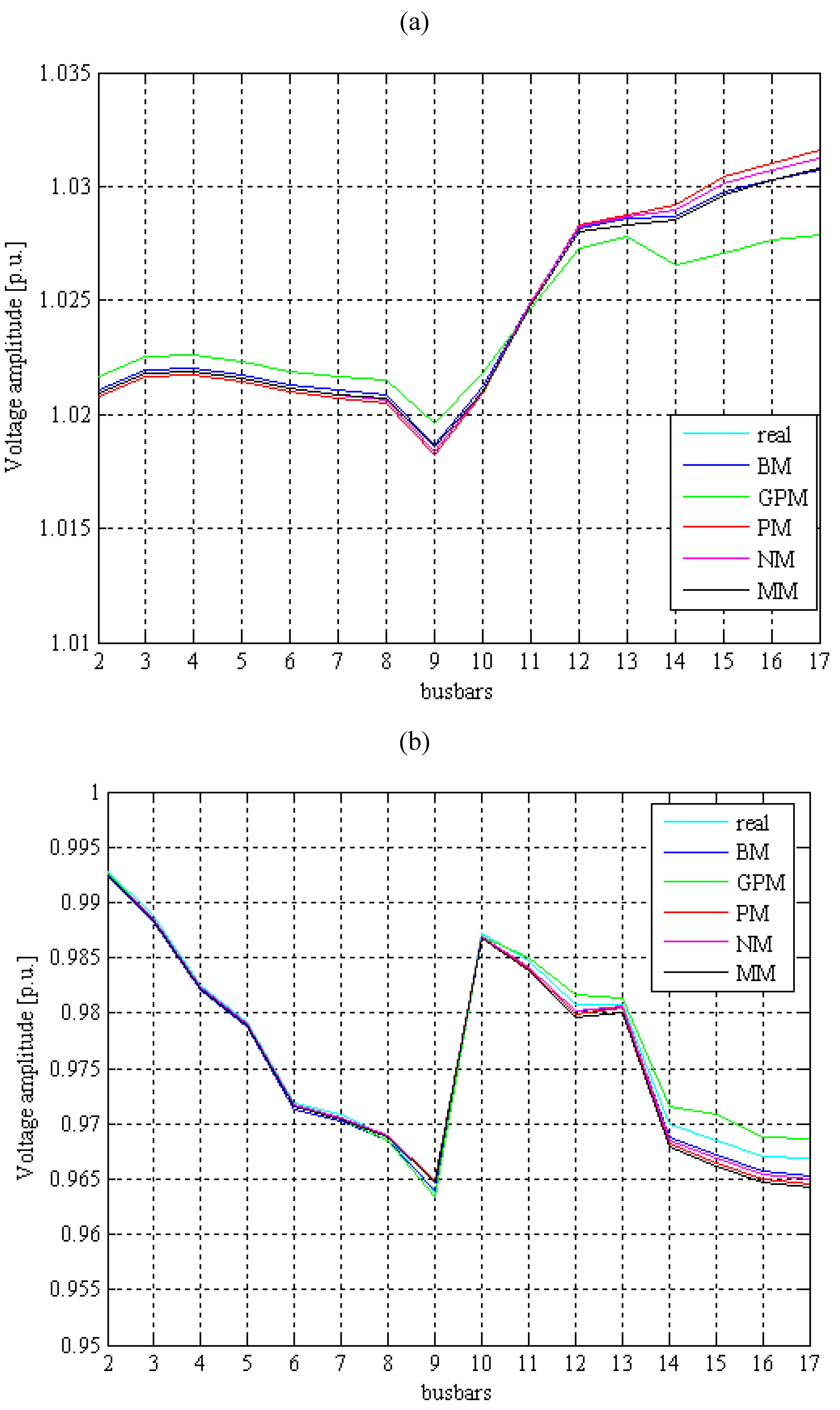
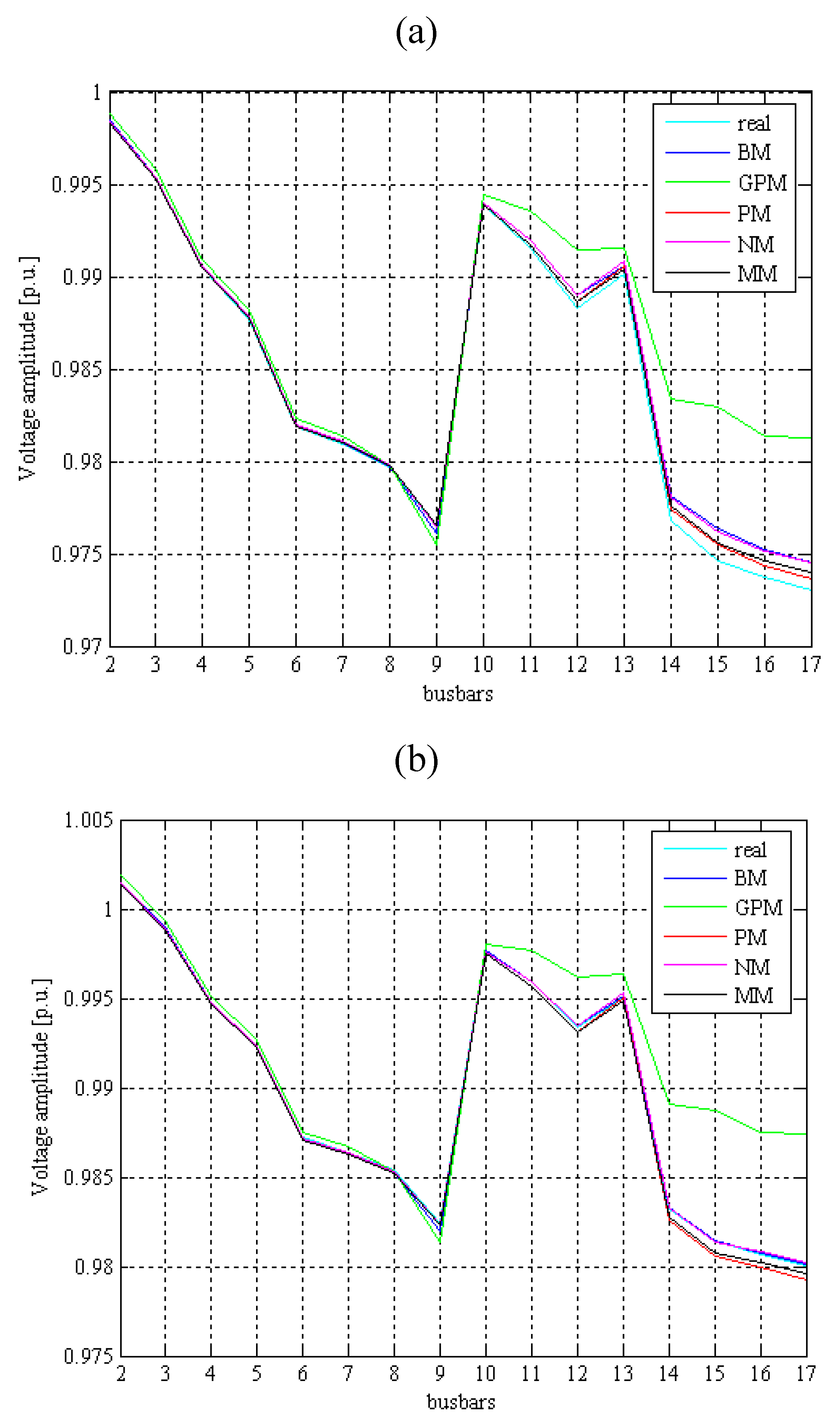
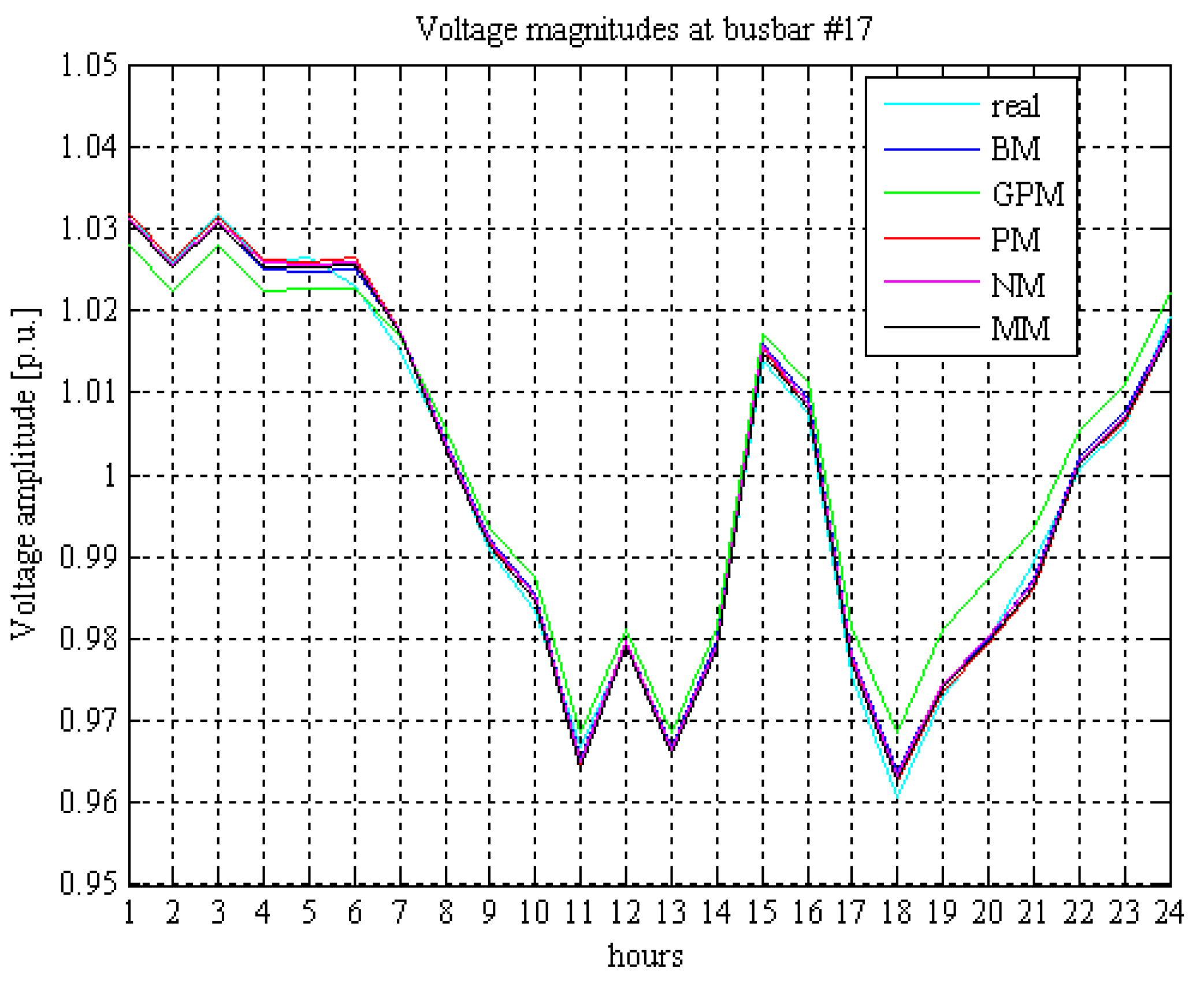
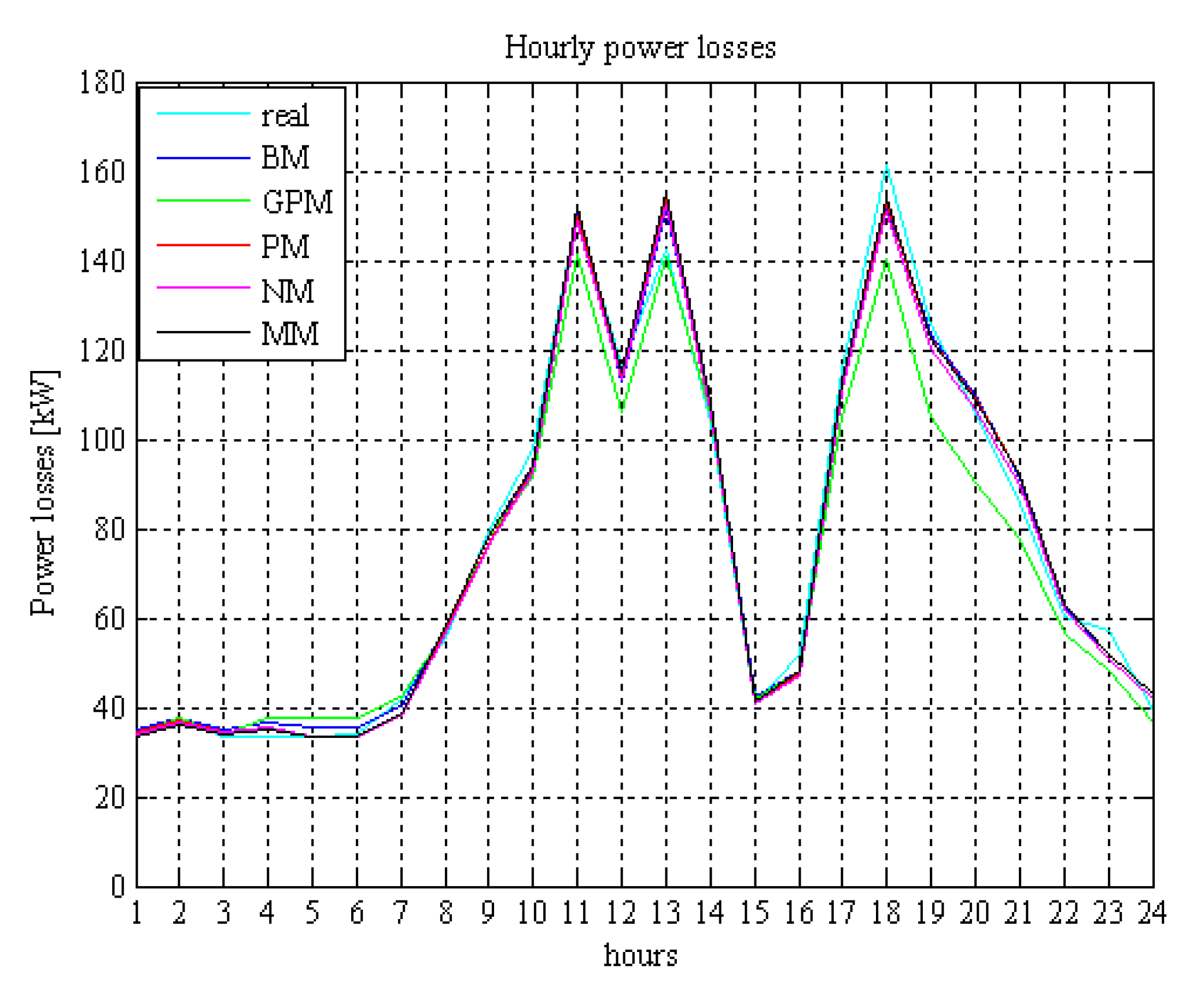
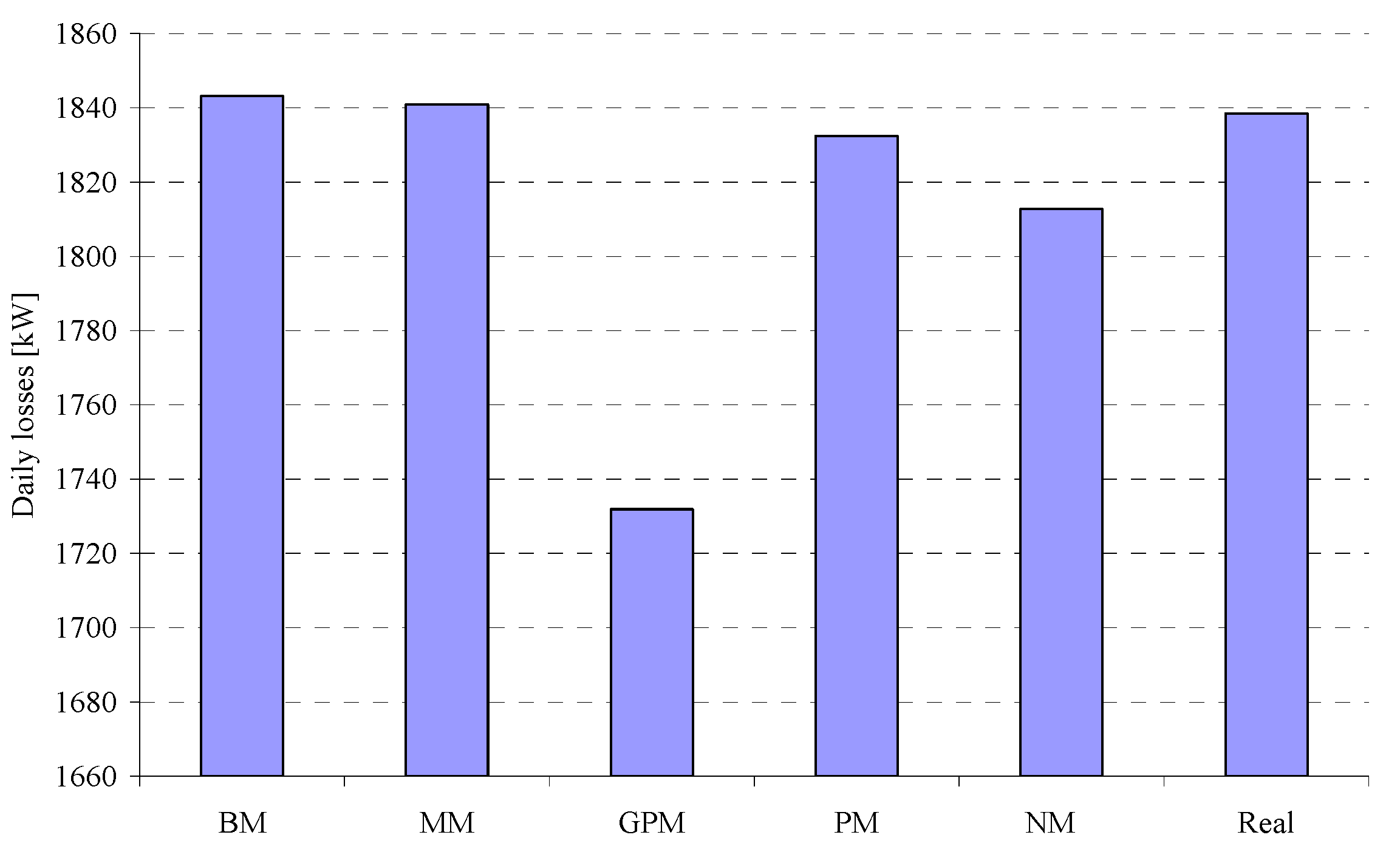
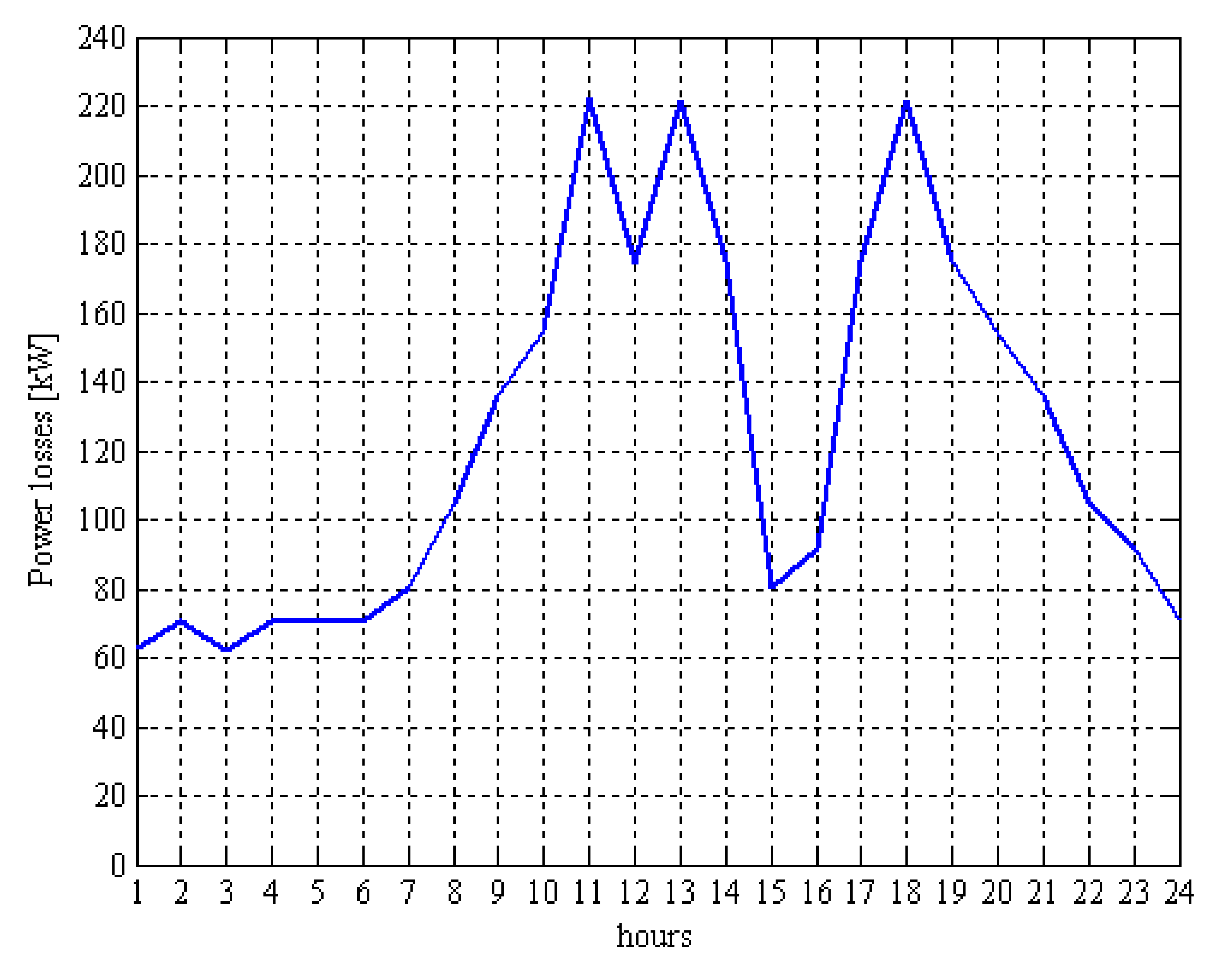
4. Conclusions
- The steady-state analysis of a distribution system is mandatory in order to determine the voltage profile and the losses, which are strongly influenced by the presence of the wind farm.
- All wind-forecasting methods, with the exception of the Generalized Persistence Method, furnished similar acceptable results in terms of both voltage profile and losses.
- In the case of the probabilistic approaches, the mean value seems to be the most reliable statistical figure to take into account.
- Probabilistic approaches seems to be the most useful, since they are capable of taking into account the unavoidable time-varying nature of wind speed and of the loads on the steady-state behavior of the distribution system.
Acknowledgments
References and Notes
- Smith, J.C. Winds of change. IEEE Power Energy 2005, 3, 20–24. [Google Scholar] [CrossRef]
- Ahlstrom, M.L.; Zavadil, R.M. The role of wind forecasting in grid operations and reliability. In Proceedings of IEEE/PES Transmission and Distribution Conference and Exhibition, Asia and Pacific, Dalian, Liaoning, China, 23–25 August 2005.
- De Meo, E.A.; Grant, W.; Milligan, M.R.; Schuerger, M.J. Wind plant integration. IEEE Power Energy 2005, 3, 38–46. [Google Scholar] [CrossRef]
- Costaa, A.; Crespob, A.; Navarroa, J.; Lizcanoc, G.; Madsend, H.; Feitosa, E. A review on the young history of the wind power short-term prediction. Renew. Sustain. Energy Rev. 2008, 12, 1725–1744. [Google Scholar] [CrossRef] [Green Version]
- Bracale, A.; Carpinelli, G.; Mangoni, M.; Proto, D. Wind power forecast methods and very short-term steady-state analysis of an electrical distribution system. Elec. Eng. Res. Rep. 2009, 1, 1–8. [Google Scholar]
- Feijòo, A.E.; Cidràs, J. Modeling of wind farms in the load flow analysis. IEEE Trans. Power Deliv. 2000, 15, 110–115. [Google Scholar] [CrossRef]
- Giebel, G.; Brownsword, R.; Kariniotakis, G. The state-of-the-art in short-term prediction of wind power. A Literature Overview, 2003. Riso National Laboratory Publication: Denmark. Available online: http://anemos.cma.fr (Accessed on 23 March 2010).
- Nielsen, T.S.; Joensen, A.; Madsen, H. A new reference for wind power forecasting. Wind Energy 1998, 1, 29–34. [Google Scholar] [CrossRef]
- Mc Calley, J.; Zhang, J.; Pu, J.; Stern, H.; Gallus, W. A Bayesian approach to short term transmission line thermal overload risk assessment. IEEE Trans. Power Deliv. 2002, 17, 770–778. [Google Scholar] [CrossRef]
- Bracale, A.; Caramia, P.; Carpinelli, G.; Varilone, P. A probability method for very short-term steady state analysis of a distribution system with wind farms. Int. J. Emerg. Elec. Pow. Syst. 2008, 9, 5. [Google Scholar]
- Masters, C.L.; Mutale, J.; Strbac, G.; Curcic, S.; Jenkins, N. Statistical evaluation of voltages in distribution systems with embedded wind generation. IEE Proc. Generat. Transm. Distrib. 2000, 147, 207–212. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Klockl, B. MCMC for wind power simulation. IEEE Trans. Energ. Convers. 2008, 23, 234–240. [Google Scholar] [CrossRef]
- Amada, J.M.; Bayod-Rújula, Á.A. Wind Power Variability Model: Part I-Foundations. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilization, Barcelona, Spain, October 2007.
- Conlon, M.F.; Mumtaz, A.; Farrell, M.; Spooner, E. Probabilistic Techniques for Network Assessment with Significant Wind Generation. In Proceedings of the 11th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, May 2008; pp. 351–356.
- Divya, K.C.; Nagendra, R.P.S. Models for Wind Turbine Generating Systems and Their Application in Load Flow Studies. Elec. Power Syst. Res. 2006, 76, 9–10, 844–856. [Google Scholar]
- Bracale, A.; Carpinelli, G.; Di Fazio, A.; Russo, A. Probabilistic Approaches for Steady State Analysis in Distribution Systems with Wind Farms. In Handbook of Wind Power Systems: Operation, Modeling, Simulation and Economic Aspects; Pardalos, P.M., Pereira, M.V.F., Rebennack, S., Boyko, N., Eds.; Springer; in press.
- Chang, W.K.; Grady, W.M.; Samotji, M.J. Meeting IEEE-519 harmonic voltage and voltage distortion constraints with an active power line conditioner. IEEE Trans. Power Deliv. 1994, 9, 1531–1537. [Google Scholar]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bracale, A.; Carpinelli, G.; Proto, D.; Russo, A.; Varilone, P. New Approaches for Very Short-term Steady-State Analysis of An Electrical Distribution System with Wind Farms. Energies 2010, 3, 650-670. https://doi.org/10.3390/en3040650
Bracale A, Carpinelli G, Proto D, Russo A, Varilone P. New Approaches for Very Short-term Steady-State Analysis of An Electrical Distribution System with Wind Farms. Energies. 2010; 3(4):650-670. https://doi.org/10.3390/en3040650
Chicago/Turabian StyleBracale, Antonio, Guido Carpinelli, Daniela Proto, Angela Russo, and Pietro Varilone. 2010. "New Approaches for Very Short-term Steady-State Analysis of An Electrical Distribution System with Wind Farms" Energies 3, no. 4: 650-670. https://doi.org/10.3390/en3040650
APA StyleBracale, A., Carpinelli, G., Proto, D., Russo, A., & Varilone, P. (2010). New Approaches for Very Short-term Steady-State Analysis of An Electrical Distribution System with Wind Farms. Energies, 3(4), 650-670. https://doi.org/10.3390/en3040650








