Abstract
This paper describes an analytical approach to investigate the nature of short overbalanced conditions and time effects during underbalanced drilling (UBD) in a naturally fractured reservoir. This study uses an analytical model which is developed for kinetic invasion of mud into the fractures. The model is based on fluid flow between two parallel plates, which is further extended to model the fluid flow in a fractured formation. The effect of short overbalanced pressure and the time effect during UBD as well as the aspects of well productivity and flow efficiency are explained. This model is an Excel-based program and provides a fast and convenient tool for analysis and evaluation of drilling conditions (mud properties, time, and pressure of drilling) in a fractured formation. The model can also predict the impact of the fracture and mud properties on the depth of invasion in the fractured formations.
1. Introduction
Minimizing formation damage that occurs during conventional drilling is a critical point for optimizing an oil field development, especially in fractured carbonate reservoirs that often exhibit low matrix permeability. Drilling fluid invasion into fractured formations can create severe formation damage around the wellbore and reduce the productivity of the well and ultimately the recovery factor for the field. Therefore, minimizing fluid invasion in this type of reservoir is very important. The drilling operation in which the drilling fluid pressure in the borehole is maintained below the pressure in the formation pressure is called underbalanced drilling (UBD). The productivity benefits of underbalanced drilling are well known in the industry. When UBD is implemented correctly, it may considerably reduce or eliminate mud invasion into the fracture systems. Even though UBD has many advantages over overbalanced drilling (OBD), quantification of possible formation damage effects by comprehensive reservoir characterization and feasibility studies is central to judge the feasibility of UBD [1].
Different approaches to analyze the feasibility of UBD are reported in the literature. Ding et al. [2] presented a model for evaluation of well performance by taking into account the near-wellbore formation damage. This model applies laboratory data related to filter cake properties in analyzing formation damage for horizontal wells, using relative permeabilities to represent effects of formation damage due to polymer adsorption/retention, water blocking, etc. The model can be used to evaluate formation damage in heterogeneous media. In their next work, Ding et al. [3] presented a model of near wellbore formation damage in anisotropic media, which is particularly important for horizontal wells.
Leising and Rike [4] used an analytical model to estimate the productivity index (PI) for UBD and OBD cases, respectively. Different skin factors were applied; however, no feature was included in the model to represent the dynamic filtration process. Lietard and Unwin [5] presented an analytical equation to predict the invasion radius in fractured reservoirs as function of drilling parameters and fracture aperture. This equation is limited to infinite fracture conductivity and the basic model reflects the fluid flow between two parallel plates with constant width. They used numerical methods to solve the equation and concluded that an analytical solution was not possible for mud with positive yield values.
Suryanarayana et al. [6] introduced an approach for a formation damage study by incorporating a model calibrated on dynamic core flood test results into a dynamic reservoir simulator. The simulator is based on an ultra-fine grid, and it applies an effective permeability distribution within the invaded zone based on the return permeability data from the laboratory study. This study did not include the fractured reservoir case and used only a single porosity model.
Salimi and Andersen [7] have studied formation damage in fractured reservoir formations. They considered a dual porosity model including a Warren-Root configuration to simulate the mechanism of productivity improvement by an UBD operation. Xiong and Shan [8] have studied reservoir criteria for selecting underbalanced drilling candidates. They used an incremental net present value (NPV) model to analyze economic benefits of UBD operations. In their work, they employed a numerical simulation method that considers formation damage mechanisms to investigate productivity improvement mechanisms by UBD.
Ding et al. [3] presented a numerical approach to modelling possible formation damage during UBD in a homogenous reservoir. In their work, they used a two-phase flow model to describe invasive formation damage during UBD. To simulate temporary overbalanced time periods, the model developed for OBD in their previous work was used. However, in their paper they did not discuss the aspects of fractures or heterogeneous reservoirs.
This paper focuses on the analytical approach to simulate the effect of short overbalanced conditions, time effect during UBD and evaluating well performance in a naturally fractured reservoir. In this paper, an analytical model is developed for kinetic invasion of mud into the fractures. The model is extended to describe the effect of short pulse overbalanced pressure during UBD and aspects of well productivity and flow efficiency. This model is an Excel-based program and provides a fast and convenient tool for analysis and evaluation of drilling conditions (mud properties, time, and pressure of drilling) in a fractured formation. The model can also predict the impact of the fracture and mud properties on the depth of invasion in fractured formations.
2. Description of the Problem
The high productivity of wells in naturally fractured formations is due to the presence of large and continuous fracture networks that have a dramatic impact on reservoir performance. Most of the drilling mud invasion in naturally fractured reservoirs occurs in the fractures, and the invasion radius is large (rd>>rw) because the fracture porosity is a small component of total rock porosity. Thus, filling the natural fractures with mud solids can impair the productivity. Therefore, minimizing fluid invasion is very important in this type of reservoir. The productivity benefits of underbalanced drilling are well known in the industry. When UBD is implemented correctly, it may considerably reduce or eliminate mud invasion into the fracture systems[9]. Even though UBD has many advantages over OBD, possible formation damage effects during UBD is crucial to judge the proper application of UBD.
Two main problems during UBD may cause severe damage around the well [10]:
- 1-Temporary overbalanced condition.
- 2-Capillary imbibition.
In the first damage category, an overbalanced pressure can be applied to the formation during short periods of time for various reasons like tripping operations or pipe connection. Due to the lack of external protection filter-cake, high filtration and mud invasion into the fracture system and formation may occur, decreasing the fracture conductivity. Mud invasion may change the relative permeability and wettability in the near wellbore region by phase trapping in the rock matrix and solid retention in the fracture.
When capillary force is important, counter–current imbibition occurs with flow of reservoir fluid toward the well while the mud filtrate invades the formation. Imbibition effect is a less important issue when the well is drilled in a naturally fractured formation, due to large fracture width in this type of reservoir. This study focuses on the short overbalance conditions and time effects during UBD, causing deep invasion into the fracture system, with corresponding reduced well productivity and reservoir recovery.
3. Modeling of Invasion in a Fractured Reservoir
Lietard et al. [5] assumed the rheological behavior of the non-Newtonian drilling fluid mud as a Bringham fluid, represented by Bird et al.:
in which y is the distance from the fracture wall (Figure 1), v is velocity, μp denotes the plastic viscosity and τy is the drilling fluid yield value. Hence, they expressed the pressure loss dp/dr occurring during laminar flow of drilling fluid through a fracture width wf by:
where νm denotes the local velocity of the mud in the fracture under radial flow conditions around the well, given by:
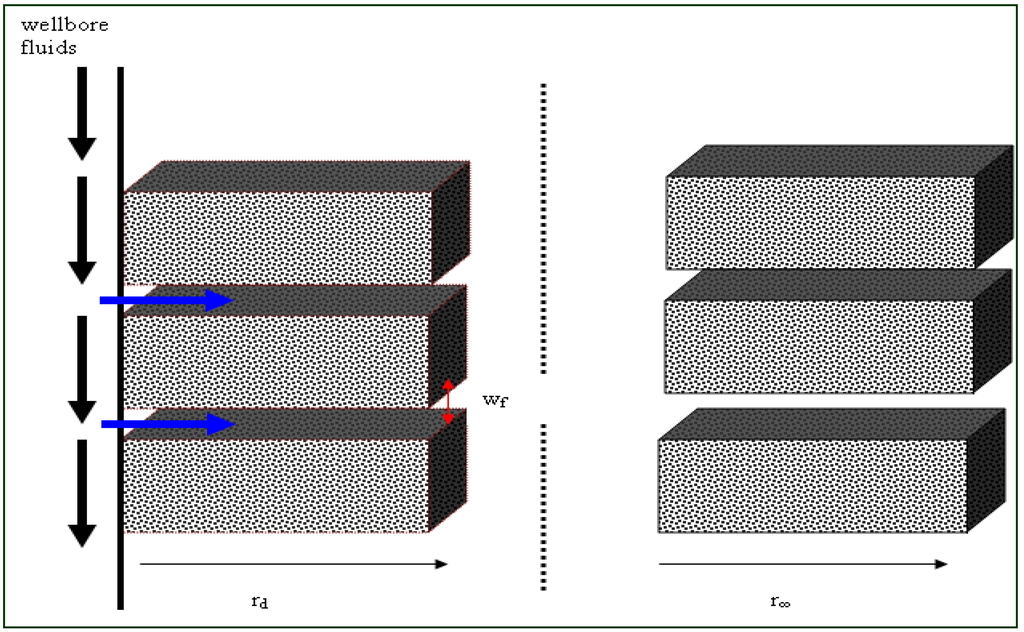
Figure 1.
One-half of wellbore area in a fractured reservoir during drilling operation (modified after Civan[11])
If qm isthe volumetric rate of mud invasion, then Vm represents the cumulative volume of mud loss at a given time, and is given by:
where wf = fracture width, in m; rd(t) = invasion radius, in m; nf = number of fractures intersecting the well and Vm = total mud loss, in cubic m.
Thus, substituting equations 3 and 4 into equation 2 results in:
By use of dimensionless analysis the ordinary differential equation is simplified as follows (Lietard et al., [12]) , expressing the dimensionless mud-invasion radius rD with respect to the dimensionless time tD:
In addition, tC and a new parameter αD, referred to as the dimensionless mud invasion factor, are defined as:
Appendix A1 illustrates in detail the dimensionless analysis for equation 5.
Civan and Rasmussen [13] applied an analytical solution for the above equation under initial conditions of rD = 1 ,tD = 0 presented as :
The partial differential equation was solved by using mathematic software and yields a solution as follows:
The function of Polylog(x) was tested for different values of x. Since x values are smaller than other parameters in this equation it can be simplified to:
Figure 2 shows the comparison of two solutions which are presented by Civan and mathematical program. To validate the analytical model, some references have made studies based on real field data. A summary of these results is attached in Appendix A2.
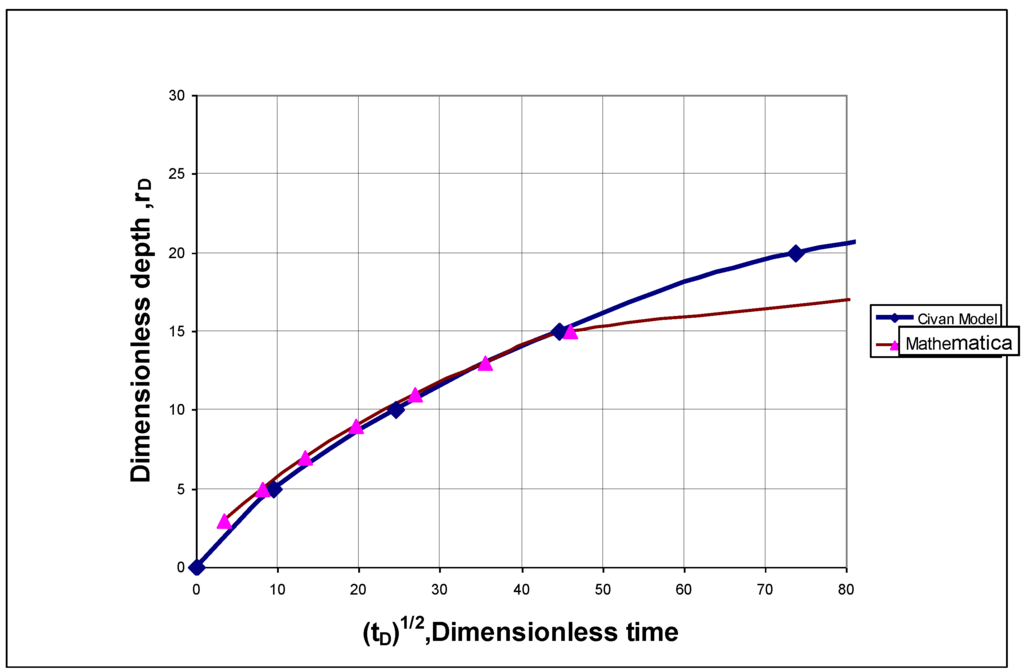
Figure 2.
Comparisons between two analytical solutions by Civan and Mathematica.
4. Application of the Approach for UBD; the Impact of Short Overbalanced Conditions
Muskat and Jones [14] have shown that the permeability kf and the porosity φf of a system of parallel fractures spread all over a reservoir are given by:
where (wf) is the average width and (xf) the average spacing, (i.e., the average distance between two fractures) and h is pay zone height.
When a well fully intercepts the fracture network, it has also been shown that a negative skin exists. This pseudo skin (sf) stems from a larger apparent permeability in the vicinity of the wellbore, where full connectivity to the fracture(s) is present:
where (rw) is the wellbore radius.
Giger [15] gives the productivity index (Q/ΔP) of a horizontal well in an oil reservoir (no permeability anisotropy):
where:
- k = reservoir matrix permeability, mD
- h = payzone height, m
- µ = oil viscosity, cp
- B = formation volume factor, rb/stb
- re = drainage radius, m
- rw = wellbore radius, m
- L = well length, m (L < re)
- q = production rate, stb/day
- ∆p = production drawdown pressure, pa
Horizontal wells are of particular interest in naturally fractured reservoirs since the fracture planes typically are vertical (drilling horizontally maximizes the chances of intercepting the fractures) and the in-plane fracture conductivity is isotropic. Lietard [12] has verified the definition of the skin (s) and found it to be quite similar to the expression given by Renard and Dupuy [16]:
Here (kd) is the permeability of the damaged zone containing fractures with radius (rd) around the wellbore. Most of the mud invasion damage in naturally fractured reservoirs is in the fractures, and the invasion radius is very large (rd>>rw) due to the very small value for fracture porosity.
Considering that the damage permeability (kd) is about equal to the matrix permeability (km) around the wellbore, and by replacing (k) by kf in equation (14) since km<<kf (usual case), it comes:
Golan and Whitson [17] expressed the effect of damage in terms of flow efficiency EF , defined as the ratio of actual rate (with skin) to ideal rate (no skin) for given pressure drawdown:
EF = Flow rate with skin / Flow rate with no skin
Another expression used to quantify flow conditions is damage ratio (DR) which is the reciprocal of flow efficiency (DR = 1/EF). Replacing the skin in the flow equation gives:
Then substituting, in the DR equation, the damage ratio is proportional to fracture and damage radius:
The following flow chart (Figure 3) will be used to study the effect of short overbalanced conditions and time effects during UBD. For ease in using this method, it has been abbreviated as FEUBD. This toolbox is simple and it can be calculated with an Excel-based program.
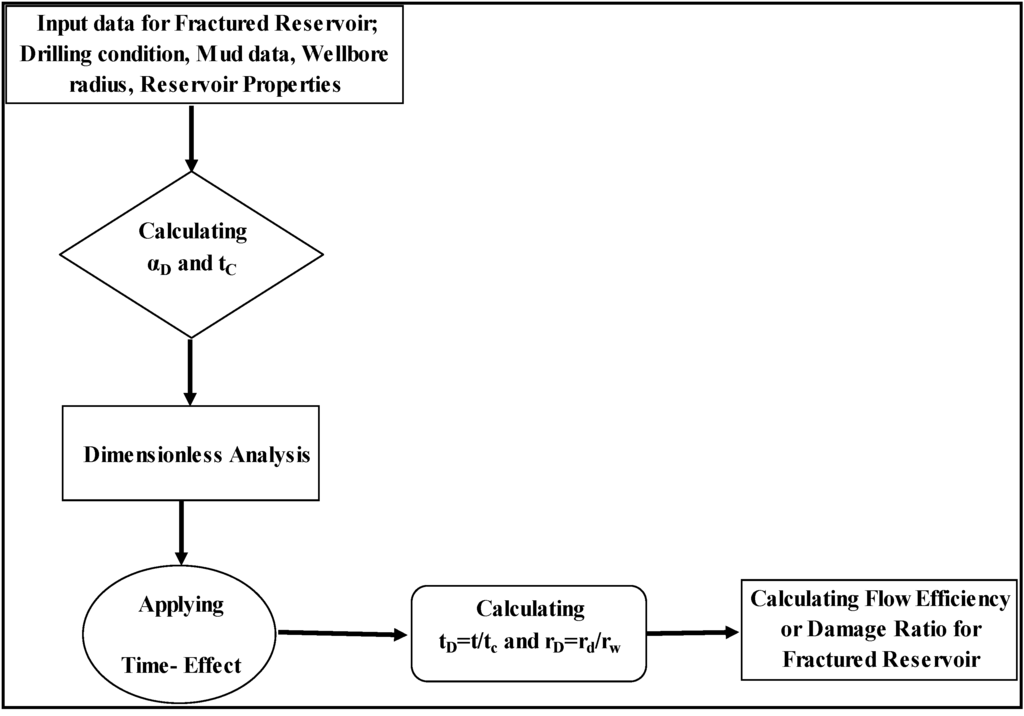
Figure 3.
Flow diagram for FEUBD, the effect of time and short overbalanced pressure during UBD.
5. Model Assumptions
This paper and its included equations are used for both vertical and horizontal wells and are not specific to horizontal wells only. What is important is the well direction relative to the fractures. The model assumes the well being non-parallel to the fractures, and thus anisotropy of fracture conductivity may not play an important role to the model results.
Lietard et al. (1999) [5] considered a reservoir formation separated into matrix blocks and a combined system of parallel fractures. According to Civan [11],” a vertical or horizontal well drilled in an isotropic reservoir and running orthogonal to the fracture plane with full fracture connectivity was considered “(Figure 1). Lietard et al. (1999) [19] considered that mud invasion in naturally fractured formations primarily occurs in the fractured systems, because the fracture permeability is much greater than the matrix permeability and thus the reservoir permeability k = kf+ km≈ kf. It is assumed also, that damage radius (rd) is much larger than the wellbore radius (rw), because the fracture porosity is sufficiently small. Therefore, when fractures are plugged by the invading mud, the damaged permeability kd of the formation becomes approximately equal to the matrix permeability km and thus kd = km. [11].
6. Results and Discussions
The FEUBD toolbox as an analytical model will enable evaluation of drilling conditions using a quick and simple function. Input factors like Fracture dimensions, rock properties and drilling conditions such as underbalanced or overbalanced pressure can be evaluated by FEUBD.
Numerical simulation for the near wellbore region in a fractured formation requires full and extensive information from reservoir and well bore region such as geometry, fluid and rock properties. The analytical model provides a fast tool to analyze drilling conditions (mud properties, time, and pressure of drilling) in a fracture formation. For this study, two separate mud systems have been considered. Their properties are given in Table 1 below.

Table 1.
Drilling and reservoir input data for model sensitivity evaluation.
In the mud I and II the ratio of yield point to plastic viscosity, τy/μp (Ibf/100 sq.ft/ cp) are 21/35 and 42/30, respectively. Fracture aperture is 500 micron and pressure of overbalanced drilling is 100 psia. The results for the two muds are given in Figure 4. It can be seen that flow efficiency is reduced very fast for both muds. In less than 5 minutes, severe formation damage occurs in near wellbore region and then productivity and flow efficiency decreases dramatically. It also clearly demonstrates the role of the fracture dimension around wellbore and resulting impact on production rate. Decreasing both the plastic viscosity and the yield value, under similar conditions of overpressure, may lead to larger losses and low flow efficiency.
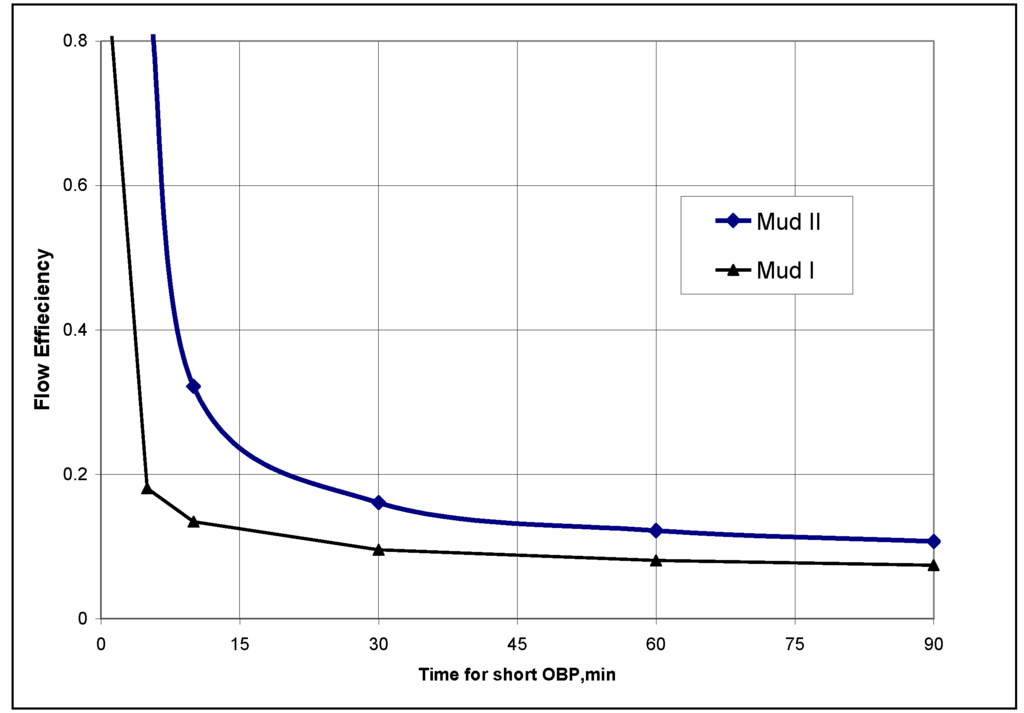
Figure 4.
The Analytical model results-The flow efficiency vs. time of OBP, for two mud systems.
The results clearly illustrate that even time duration lasting between 5 to 20 minutes overbalanced pressure during UBD, the flow efficiency will be significantly decreased comparing with 100% UBD.
Figure 5 shows the flow efficiency over time of short overbalance pressure for Mud 1 when two different rock—fracture systems have been considered. The narrower fracture shows higher value of flow efficiency, while for wider fracture severe formation damage occurs, and flow efficiency is decreased significantly.
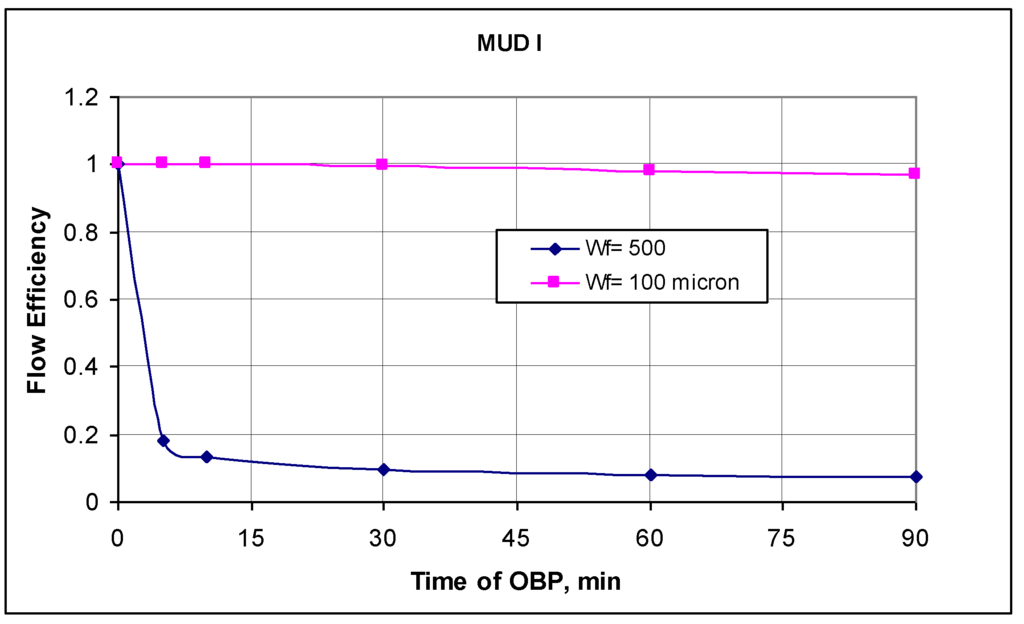
Figure 5.
Analytical model results-the flow efficiency vs. time of OBP, for two rock systems.
7. Sensitivity of the Model to Fracture Parameters
In naturally fractured reservoir, the following idealized models (Figure 6) are used in the literature for fracture and matrix system and presented by Van-Golf Racht [20]:
- Kazemi model - formed by alternate horizontal layers of matrix and fractures.
- Warren-Root model—formed by a number of matrix blocks (cubes) intersected by an orthogonal network of fractures.
Infinite and continuous fractures are considered for both models. A schematic of the fracture and matrix system for our model is shown in Figure 1. The idea of a fractured reservoir model is that the fracture network covers the entire reservoir to its boundary. Thus, for such a network fracture length may be regarded “infinite”. In the naturally fractured reservoir the length of the fracture is not playing an important role contrary toa hydraulic fracture in a well in a continuous reservoir, where the fracture and its length has significant impact on the well productivity. However, the results of this model are not affected by length of the fracture and only aperture of the fracture is important parameter in order to calculate the flow efficiency and productivity index.
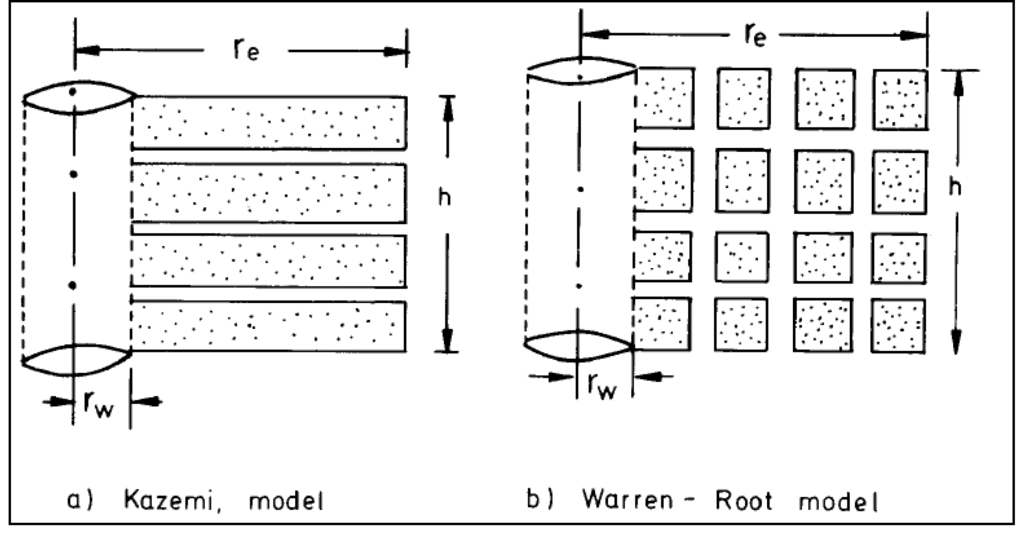
Figure 6.
The idealized models for naturally fractured reservoirs[20].
8. Conclusions
- The simple analytical approach presented provides a fast tool to analyze and evaluate drilling conditions (mud properties, time, and pressure of drilling) in a fractured formation.
- The results clearly illustrate that for even short time duration of overbalanced pressure condition during UBD, the flow efficiency is significantly decreased comparing with 100% UBD.
- The narrower fracture shows higher retained flow efficiency, while in wider fractures severe formation damage and invasion occurs, reducing flow efficiency significantly.
- Decreasing both the plastic viscosity and the yield value, under similar conditions of overpressure, may lead to larger losses and therefore low calculated values for flow efficiency.
Appendixes
A1-Dimensionless Analysis
An integration of Equation 5 over the mud invasion region extending from the wellbore at rw to the depth of mud invasion rd = rd(t) yields:
where:
- ∆P = overbalance pressure drilling, Pa
- pd(t) = formation pressure , pa
- pw = wellbore pressure, Pa
- μp = plastic viscosity of fluid, Pa.sec
- wf = fracture width, m
Substituting equation 1 for a single fracture (nf = 1) into Equation 2 yields an expression for constant the overbalanced pressure drilling (OBD) as:
The dimensionless mud-invasion radius and time are defined as:
In which the characteristic time scale is taken as:
A2-Fluid Loss Parameters
The fluid loss parameter is very important with respect to the risk of formation damage. The study was aimed at calculating the flow efficiency and damage ratio for a given naturally fractured formation. In the Excel tool box “FEUBD” the fluid loss for each time step is calculated by equation (4).
The fluid loss value is very important for the drilling discipline. Production and reservoir engineers would like to estimate the formation damage induced by the drilling operation in different terms such as skin or Productivity Index. Thus, results of output are defined for by the term damage ratio (DR) which incorporates mud loss into the fractured formations.
In order to calculate fluid loss, first αD and tc are calculated by equation (A.4). Most of these parameters (overbalanced pressure, wellbore radius, and fluid properties) are assumed to be known. The relation between rD and tD is defined by equation (10). Then, for each time step (t), rd is calculated and the fluid loss volume (Vm) is determined by equation (4).
A3–Model Validation by Case Study
The Machar field was discovered in 1976 and is located in UKCS block 23/26a in 95 m water depth, approximately 240 km east of Aberdeen. The field is a normally pressured oil reservoir with approximately 410 mmstb oil in place, (expected reserves 135 mmstb oil) contained in steeply dipping, fractured Cretaceous chalk and Palaeocene sandstone in a high relief structure over a salt diapir. Production flow rates from recent development wells have increased dramatically compared with earlier appraisal wells. The methods used to deliver highly productive wells from tight, fractured chalk reservoirs are described.
SPE 36832 reported the well data of 18Z and 20Z. These wells have been completed and stimulated the same way, however right at the top of the diapir in a zone of intense fissuration. Pre- and post-stimulation productivity indices are even more impressive, beating Machar 18Z and its productivity soared from 1.02 to 470 stb/day/psi after a mud and silt remover acid treatment performed in August 1995 by the same stimulation vessel, which had pumped Machar 182 job in December 1993. The comparison with well 18Z productivity evolution - 2.9 to 147 stb/day/psi – already signals the larger reservoir permeability at the top of the dome: indeed, a larger number of wider natural fractures over a shorter payzone length (1,270 feet) means increased damage build-up and removal potentials at the same time.
Table A.2 is a summary of loss events after the 9 5/8 casing was set too deep - past the Paleocene sandstone - and whilst drilling the final 8 ½ inch (0.36 ft) hole section. Because losses at the very top of the payzone (2, 189 bbl) occurred during long, unexpected trips into the 12 M hole, the following circulations do not take them into account and only consider 2,844 barrels of losses and 8 events over 1,130 ft.

Table A.1.
Reservoir data for Machar Field (SPE 36832, 56974).

Table A.2.
Mud loss data for Machar Field (SPE 36832, 56974).
 |
Creating data as was done for Machar 1flz leads to the following estimates: spacing i5 = 141.5 ft. sf = -3.62 and the dimensionless factor of productivity = 2.04 (with re = 20,000 ft - about 6 kilometers), Reservoir (or fissure) permeability (kf) is 231 mD, therefore the average width (wf) is 620 microns and ∆P/τy = 828,320 . To estimate the average mud loss rate for our example well, we use an average τy/μp = 0.64 in field units, corresponding to 306 reciprocal seconds. This leads to tC = 2346 (1/sec) Hence for t = 1 hour, tD, = 8,448,438 . For αD = 0.0006, then rD = 133 ft from equation 16, the mud loss for given one hour will be given by Eq.(7-6) as :
The calculated mud loss rate is quite similar to reported value in the given Table A.2, which is 12 bbl/hr.
A4- Invasion Behavior and Effect of Yield Point
Lietard [19] studied some sensitivity analysis on the equation 6. The following figure shows that rheological properties of the mud (yield point) can control the invasion of mud into fracture system. This result illustrates that for a Newtonian mud (yield point is zero) would not stop invading natural fracture since (rD) in this case doesn’t tend to any limit when tD goes to infinity. On other hand, when yield point becomes higher (we assume that others drilling parameters such as pressure are constant) the invasion would be stopped in the small time.
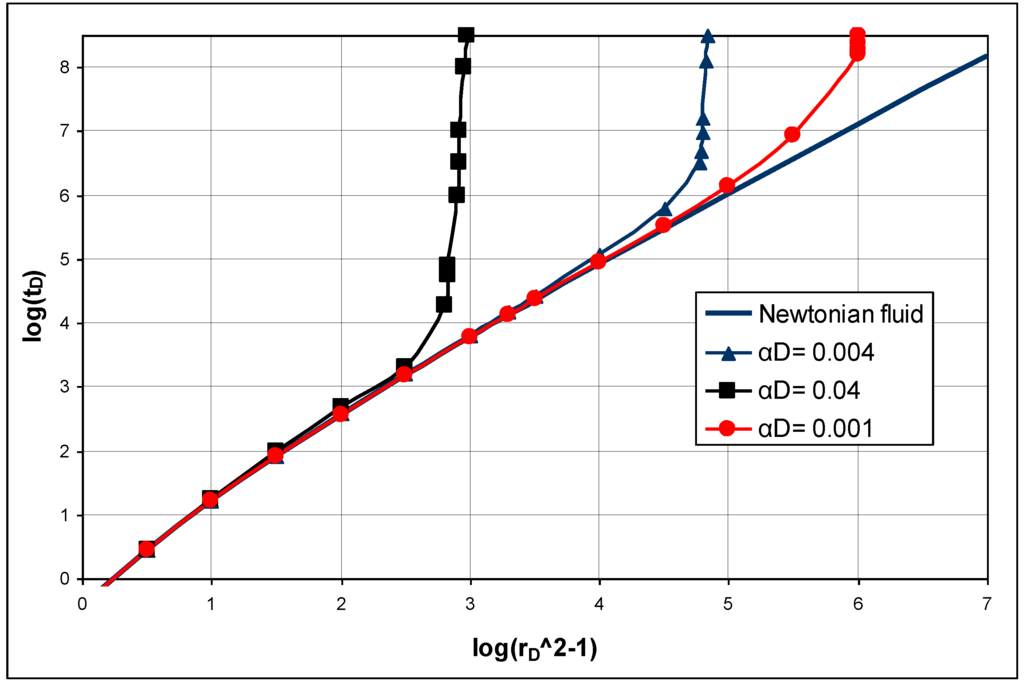
Figure A.1.
The effect of yield point of the mud system on the invasion model [19].
Acknowledgements
Department of Petroleum Engineering and Applied Geophysics. of Norwegian University of Science and Technology (NTNU) and specially Jon Kleppe are highly acknowledged for their assistance in publishing this work.
References
- Bennion, D.B. Underbalanced Drilling of Horizontal Wells—Does it Really Eliminate Formation Damage. In Proceedings of Formation Damage Symposium, Lafayette, LA, USA, 7–10 February 1994.
- Ding, Y.; Longeron, D.; Renard, G.; Audibert, A. Modeling of Both Near-Wellbore Damage and Natural Cleanup of Horizontal Wells Drilled With a Water-Based Mud. In Proceedings of SPE Int.Symp.& Exhibition on Formation Damage Control, Lafayette, LA, USA, 20–21 February 2002.
- Ding, Y.; Herzhaft, B.; Renard, G. Near-wellbore Damage Effects on Well Performance-A Comparison Between Underbalanced and Overbalanced Drilling. In Proceedings of The SPE Symp. & Exhibition on Formation Damage Control, Lafayette, LA, USA, 18–20 February 2004.
- Leising, L.J.; Rike, E.A. Underbalanced Drilling With Coiled Tubing and Well Productivity. In Proceedings of The SPE European Petroleum Conference, London, UK, 25–27 October 1994.
- Lietard, O.; Unwin, T.; Guillot, D.; Hodder, M. Fracture Width LWD and Drilling Mud/LCM Selection Guidelines in Naturally Fractured Reservoirs. In Proceedings of European Petroleum Conference, Milan, Italy, 22–24 October 1996.
- Suryanarayan, S.V.; Wu, Zh.; Ramalho, J.; Himes, R. Dynamic modeling of invasion damage and impact on production in horizontal wells. SPE Reservoir Eval. Eng. 2007, 10, 348–358. [Google Scholar] [CrossRef]
- Salimi, S.; Andersen, K.I. Enhancement Well Productivity-Investigating the Feasibility of UBD for Minimizing Formation Damage in Naturally Fractured Carbonate Reservoirs. In Proceedings of SPE/IADC Underbalanced Technology Conference and Exhibition, Houston, TX, USA, 11–12 October 2004.
- Xiong, H.; Shan, D. Reservoir Criteria for selecting Underbalanced Drilling Candidates. In Proceedings of Underbalanced Technology Conference, Houston, TX, USA, 25–26 March 2003.
- Bennion, D.B.; Thomas, F.B. Underbalanced Drilling a Reservoir Design Prespective. In Proceedings of Horizontal Well Technology, Calgary, Canada, 3 November 1999.
- Bennion, D.B.; Thomas, F.B.; Bietz, R.F.; Bennion, D.W. Underbalanced Drilling, Praises and Perils: Lab and Field Experience. In Proceedings of Horizontal Well Technology, Calgary, Canada, 21 November 1995.
- Civan, F. Reservoir Formation Damage,Fundamentals,Modeling,Assessment,and Mitigation, 2nd ed.; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Lietard, O. Permeabilities and Skins in Naturally Fractured Reservoirs: An Overview and an Update for Wells at Any Deviation. In Proceedings of SPE European Formation Damage Conference, The Hague, The Netherlands, 31 May–1 June 1999.
- Civan, F.; Rasmussen, M.L. Discussion of fracture width logging while drilling and drilling mud/loss-circulation-materials selection guidelines in naturally fractured reservoirs. SPE Drill. Completion J. 2002, 14, 249–250. [Google Scholar]
- Muskat, M. Physical Principles of Oil Production; McGraw-Hill Book Co. Inc.: New York, NY, USA, 1949. [Google Scholar]
- Giger, F.; Reiss, L.H.; Jourdan, A. The Reservoir Engineering Aspects of Horizontal Drilling. In Proceedings of Anual Technical Conference and Exhibition, Houston, TX, USA, 16–19 September 1984.
- Renard, G.; Dupuy, J.G. Influence of Formation Damage oil the Flow Efficiency of Horizontal Wells. In Proceedings of Formation Damage Control Symposium,SPE 19414, Lafayette, LA, USA, 22–23 Februray 1990.
- Golan, M.; Whitson, C.H. Well Performance; Tapir: Trondheim, Norway, 1996. [Google Scholar]
- Lietard, O.; Bellarby, J.; Holcoinb, D. Design, Execution and Evaluation of Acid Treatments of Naturally Fractured Carbonate. Oil Reservoirs of the North Sea. SPE Prod. Facil. J. 1998, 13, 133–140. [Google Scholar] [CrossRef]
- Lietard, O.; Unwin, T.; Guillot, D.; Hodder, M. Fracture Width LWD and Drilling Mud/LCM Selection Guidelines in Naturally Fractured Reservoirs. SPE Drill. Completion J. 1999. [Google Scholar] [CrossRef]
- Van Golf-Racht, T.D. Fundamentals of Fractured Reservoirs Engineering; Elsevier/North- Holland Inc.: New York, NY, USA, 1982. [Google Scholar]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).