1. Introduction
Few issues, maybe none, are as important to industrial societies and their economies as the future of oil and gas supplies. Oil and gas provide nearly 60% of the world’s energy [
1]. Global food production and most economies rely heavily on oil and gas, and historical restrictions in the availability of oil have had large economic impacts [
2,
3]. There are those who claim that unexploited supplies are limited and that world oil production will soon peak if it has not already [
4]. Others maintain that remaining reserves are large and that, as in the past, technological advances will help stave off a peak in production for at least another thirty or so years [
5]. What is increasingly apparent to all is that we no longer find large, cheap and easy to exploit reserves, and that oil and gas production is moving to more remote and challenging areas [
6,
7]. A critical issue missing from this debate is not how much oil is in the ground, or not even how much we might be able to extract, but rather how much we can extract with a significant energy surplus. In other words what we need to know is the net, not gross, energy available. A second, related, issue is the role of technology, which some argue can offset the depletion of easily accessible oil and gas reserves by advances that allow the exploitation of more technically challenging resources.
These issues can be addressed, perhaps even resolved, through the use of what is called EROI analysis. EROI is the ratio of energy that is produced by a process (in this case oil and gas extraction) to the energy that is consumed in carrying out that process. In other words, it is the proportion of the energy produced that is required to run the production process. If the EROI of a fuel is high, then only a small fraction of the energy produced is required to maintain production, and the majority of that energy produced can be used to run the general economy. On the other hand, if the EROI is very low, the majority of the energy produced must be used to ensure continued energy production and very little net energy is available to do useful economic work. High EROI fuels are vital to economic growth and productivity [
8].
One would think that there should be a good data base on the energy cost of all of the energy we exploit, since it seems very important to examine this process over time. One might even imagine that such data might be amongst the most important information our entire civilization needs to know. Unfortunately this is not the general case, as there are only a few countries that maintain and make public such information, let alone insure quality control. An even larger problem is that a large proportion (roughly half) of oil is produced by national oil companies (NOCs), which show little interest in making any of their information public, let alone having it audited. What we do have is: 1) reasonably good analyses for the United States, which has maintained for many years statistics on the energy use by all major industries, including oil and gas; 2) similar data for the United Kingdom for a less extended period of time and 3) a quite good data base on dollar costs on a large majority of publicly traded oil and gas companies maintained by John S. Herold Incorporated. This data base accounted for about 40% of the oil produced in the world in 2006. Thus we consider this a reasonably large but probably biased sample of the total “population” of oil and gas production. The data is normally aggregated as both oil and gas because they are frequently found together as a result of the same drilling effort.
What is clear in the Herold data base is that the amount of oil and gas produced per dollar spent between 1999 and 2006 shows a decline. In 1999 the industry produced about one tenth of a barrel of oil equivalent (boe) per 2005 dollar spent globally in exploration, development and production. By 2006 that number had declined to approximately 50% of that (these numbers reflect data for publicly traded oil companies only) [
9]. What we do here is convert these dollar cost numbers to energy costs and then calculate a time series for the EROI for oil and gas production globally. We then compare the results to time trends for the United States where we have explicit data on energy gains and costs over a more extended period of time to see if our new results make sense. Our simplistic hypothesis is that global EROI values over time should have a similar pattern to, but higher than, the EROI for the United States.
We can also use this data to examine the impact of technology vs. that of depletion. While we do not know how either effect can be derived independently, their combined effect can be estimated by the time trend in EROI. There is a sort of “race” in which technological advancement is in constant contention with depletion [
10]. The question of which is “winning” cannot be answered theoretically, but must be addressed empirically. We do this by assessing the time trends in the efficiency (i.e., EROI) with which we produce oil and gas. We need to know how much energy is returned to society in the form of oil and gas compared to that which is invested by the industry in getting it, and how that ratio is changing over time. If the energy return on that invested by the industry is increasing over time, then we would have evidence that new technologies are currently outpacing depletion, and the converse. The rate of change of EROI may also give us some indication of how close we are to the point at which it takes as much energy to extract the resource as we gain through its production.
2. Results and Discussion
The quality-corrected EROI for global oil and gas production, as measured by megajoules (MJ) of oil and gas produced divided by the MJ equivalent of the dollars spent on exploration, development, and production was approximately 26:1 in 1992, increased to about 35:1 in 1999, and has since declined steadily to 18:1 in 2006. The non-quality-corrected EROI was roughly 26:1 in 1992, rose to about 33:1 in 1999, and declined to 18:1 in 2006 (
Figure 1).
Figure 1.
Energy return on investment for oil and gas production worldwide.Quality-corrected (solid line) and heat equivalent (dashed line) estimates are shown.
Figure 1.
Energy return on investment for oil and gas production worldwide.Quality-corrected (solid line) and heat equivalent (dashed line) estimates are shown.
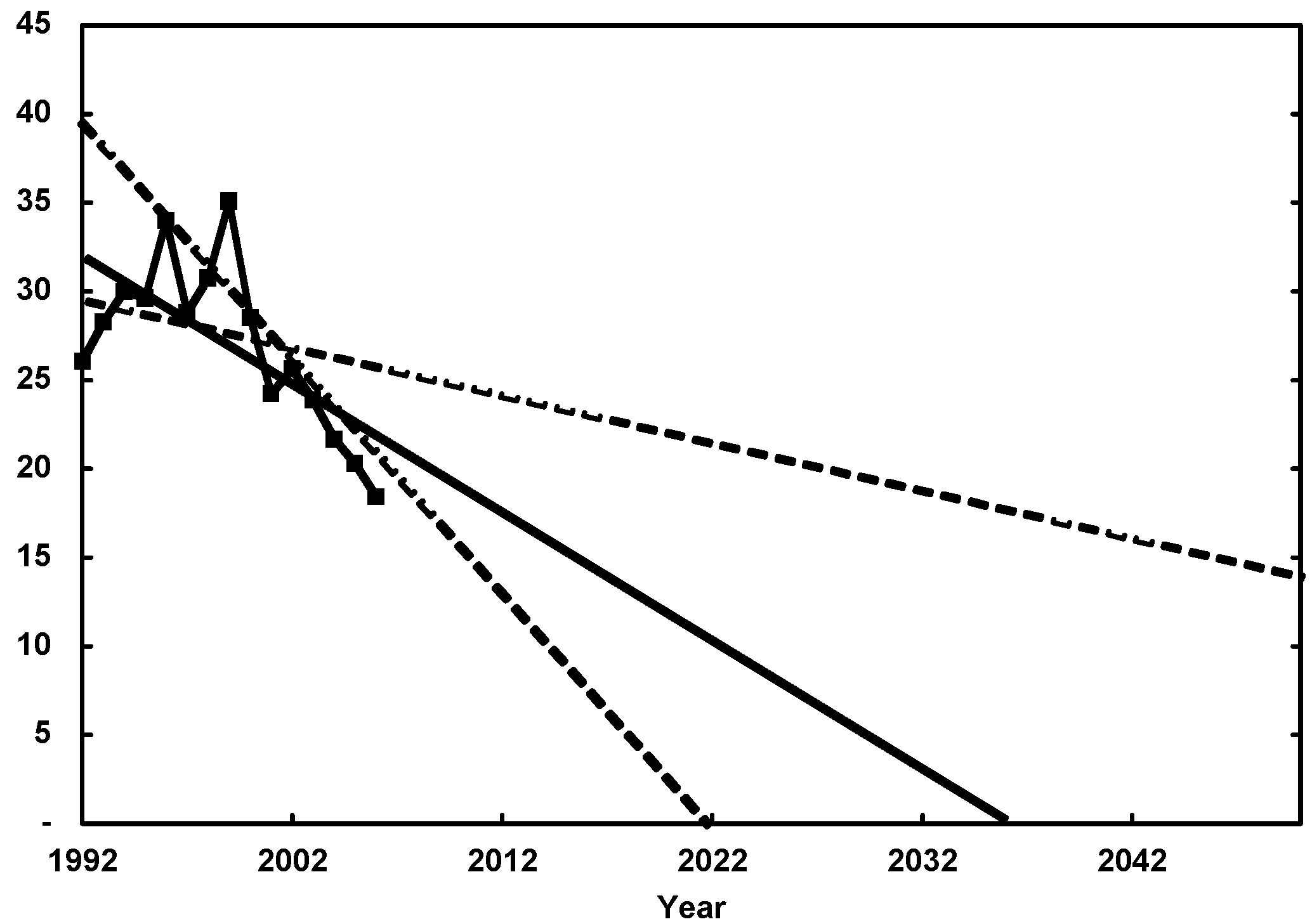
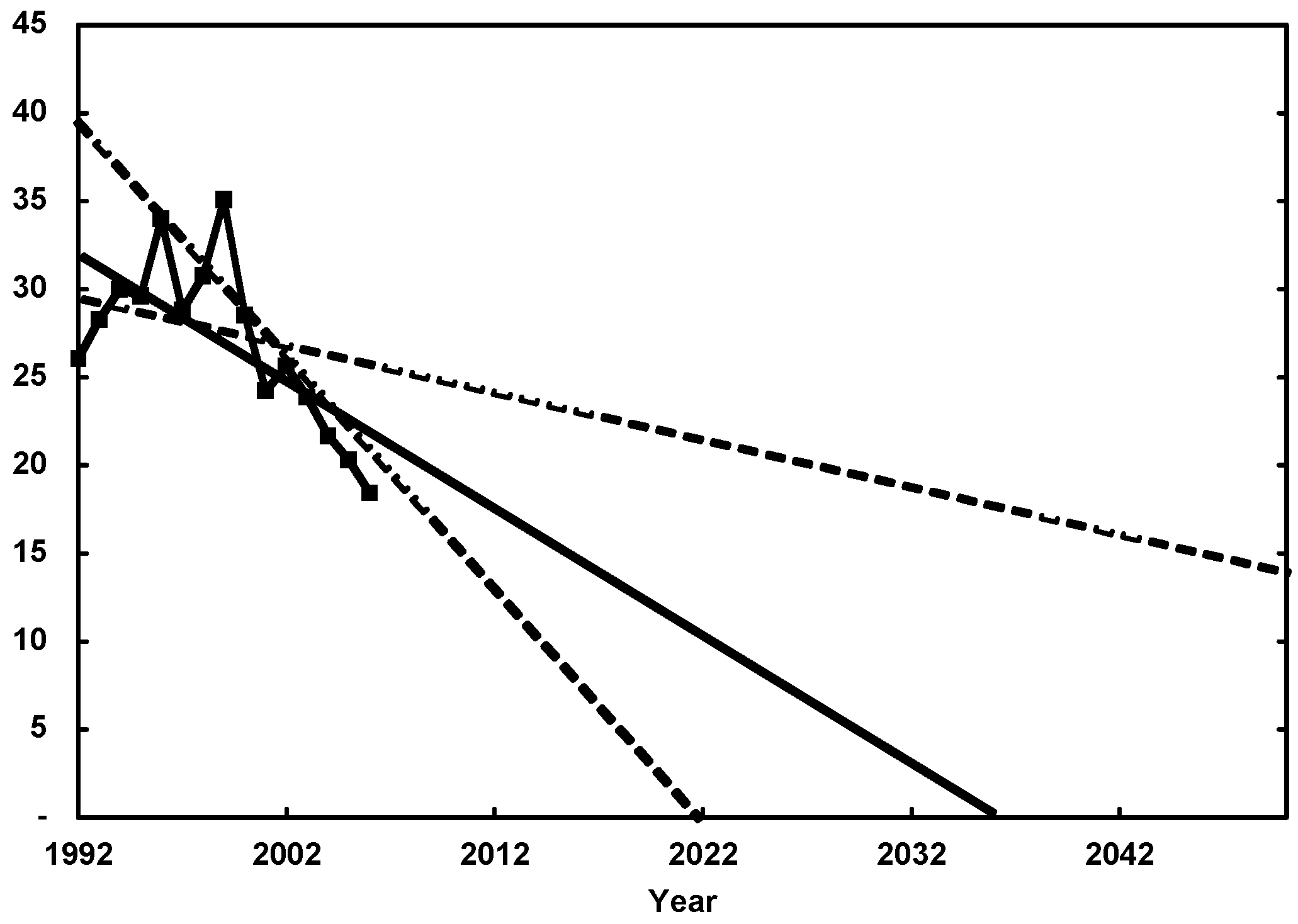
Figure 2.
Linear extrapolation of the trend in our best estimate of EROI for oil and gas extraction globally (solid line, R2 of 0.46). Also shown are linear extrapolations of the steepest and most gradual trends in EROI resulting from different methods of calculating energy input (dashed lines). These were obtained by calculating energy input using energy intensity defined as energy use per real (2005) dollar of gross product of the oil and gas extraction sector with a unique energy intensity for each year (steep slope), and using the average energy intensity over all years (gradual slope).
Figure 2.
Linear extrapolation of the trend in our best estimate of EROI for oil and gas extraction globally (solid line, R2 of 0.46). Also shown are linear extrapolations of the steepest and most gradual trends in EROI resulting from different methods of calculating energy input (dashed lines). These were obtained by calculating energy input using energy intensity defined as energy use per real (2005) dollar of gross product of the oil and gas extraction sector with a unique energy intensity for each year (steep slope), and using the average energy intensity over all years (gradual slope).
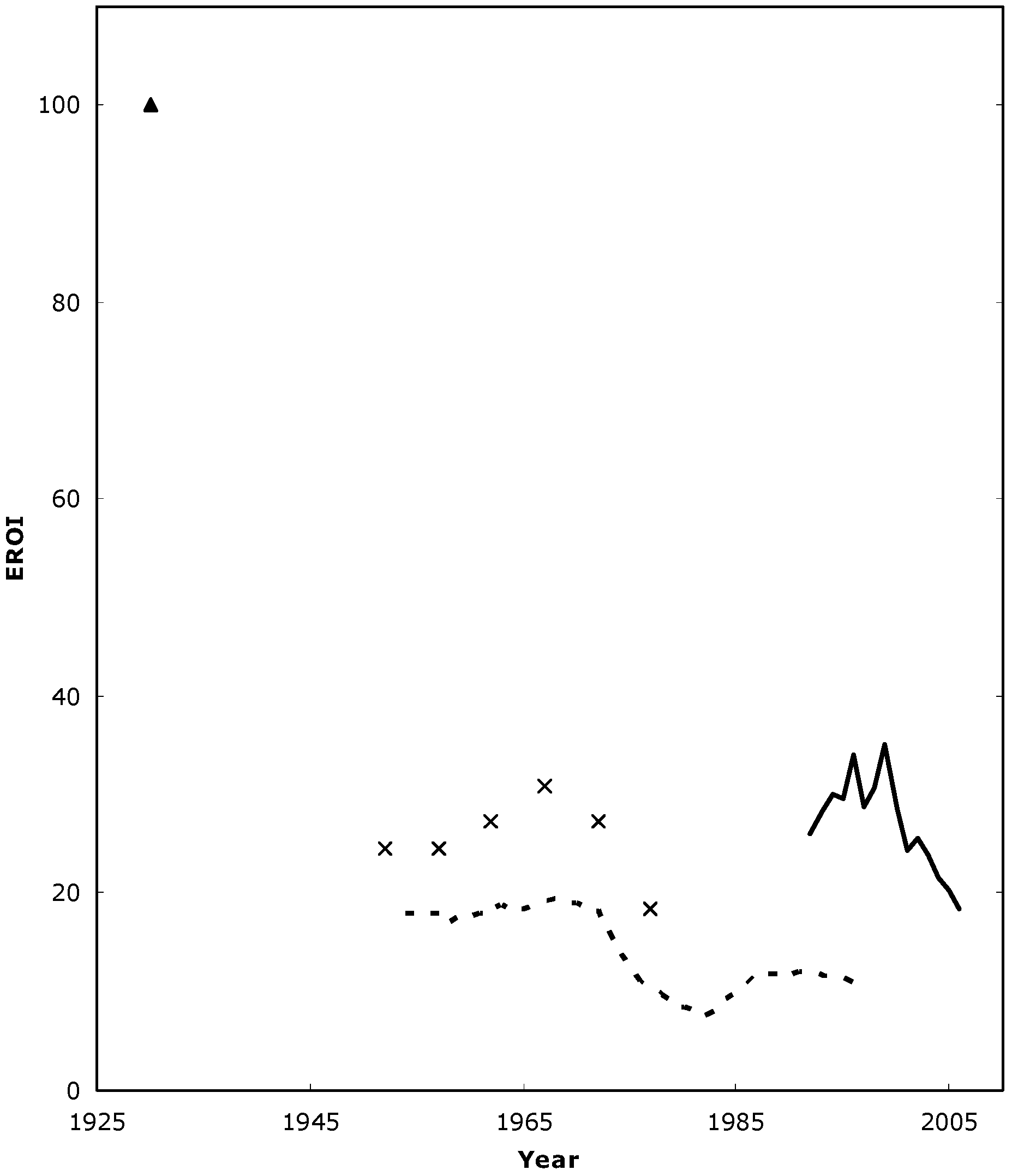
Figure 3.
All estimates of EROI for oil and gas known to us. The triangle is a crude estimate for the EROI of U.S. oil and gas discoveries (not production which could not be derived) in 1930 [
8]. Crosses are Cleveland
et al.’s estimates for production in the U.S. [
8], which also gives values for discoveries that are mostly about half those of production. The dashed line is Cleveland’s assessment of US EROI [
11] that includes a “divisia” (see below) correction for quality. Model-derived estimates for the US Gulf of Mexico are broadly similar [
10]. The solid line represents values derived for the world in this study.
Figure 3.
All estimates of EROI for oil and gas known to us. The triangle is a crude estimate for the EROI of U.S. oil and gas discoveries (not production which could not be derived) in 1930 [
8]. Crosses are Cleveland
et al.’s estimates for production in the U.S. [
8], which also gives values for discoveries that are mostly about half those of production. The dashed line is Cleveland’s assessment of US EROI [
11] that includes a “divisia” (see below) correction for quality. Model-derived estimates for the US Gulf of Mexico are broadly similar [
10]. The solid line represents values derived for the world in this study.
Our results indicate that indirect energy use (the energy cost of materials and supplies) represents 11% of total energy input in 1992 and 9% in 2006, with an average of approximately 11% over the entire study period. If the EROI for global oil and gas extraction continues to follow the trend that it has over the period of this analysis, and if a linear extrapolation of that trend is appropriate, then the EROI would drop to 1:1 in about three decades (
Figure 2).
This declining trend in EROI for the world has a pattern similar to, although is higher than, data from the United States that is based on direct estimates of energy costs and energy gains (
Figure 3). This pattern is consistent with our hypothesis that the global pattern is similar to that of the United States, i.e., that depletion is a serious problem in all or most oil producing areas and that the world is, so far, less depleted than the United States.
2.1. Uncertainty Analysis
The energy output values are almost certainly about right, as they are examined fairly carefully by many people and there is a broad general agreement among various sources (i.e., EIA, IEA, BP). Our input data sources are another matter. For starters they publish no estimates of uncertainty. However any error in the data itself is likely to be qualitative in nature, i.e., stemming from inaccurate reporting by the oil and gas industry, clerical errors, and so on, and cannot be quantified. The overall trend in our results is unlikely to be affected significantly by this uncertainty as we see no reason it would change much over time. We are able to examine the uncertainty that is introduced to this analysis by the necessity of estimating energy inputs for regions and years in which we have no energy input data. The total energy used was derived by multiplying the total money spent “upstream” by an energy intensity appropriate for that year, which could be derived only from data from the US and Great Britain. Since usually this ratio decreases over time due to inflation (or may change for technical reasons) it was necessary to correct for those factors. We used three approaches to do that. For our base case (where there was no need to correct for inflation) we multiplied the nominal dollars of all expenditures for our “total” sample (i.e., Herold data not corrected for inflation) times the ratio of energy used per nominal dollar spent, derived for the mean of the energy intensity for the US and Great Britain for that year, interpolating or extrapolating for years with no energy use data. For our second approach we corrected the total expenditures for inflation to 2005 dollars and then multiplied that by year-by-year inflation-corrected intensity ratios derived by fitting a line to the mean of US and Great Britain (energy use) / money spent ratios. Our third method was to multiply inflation-corrected expenditures by an energy intensity ratio derived as the mean of all the energy intensities derived for all years and both countries.
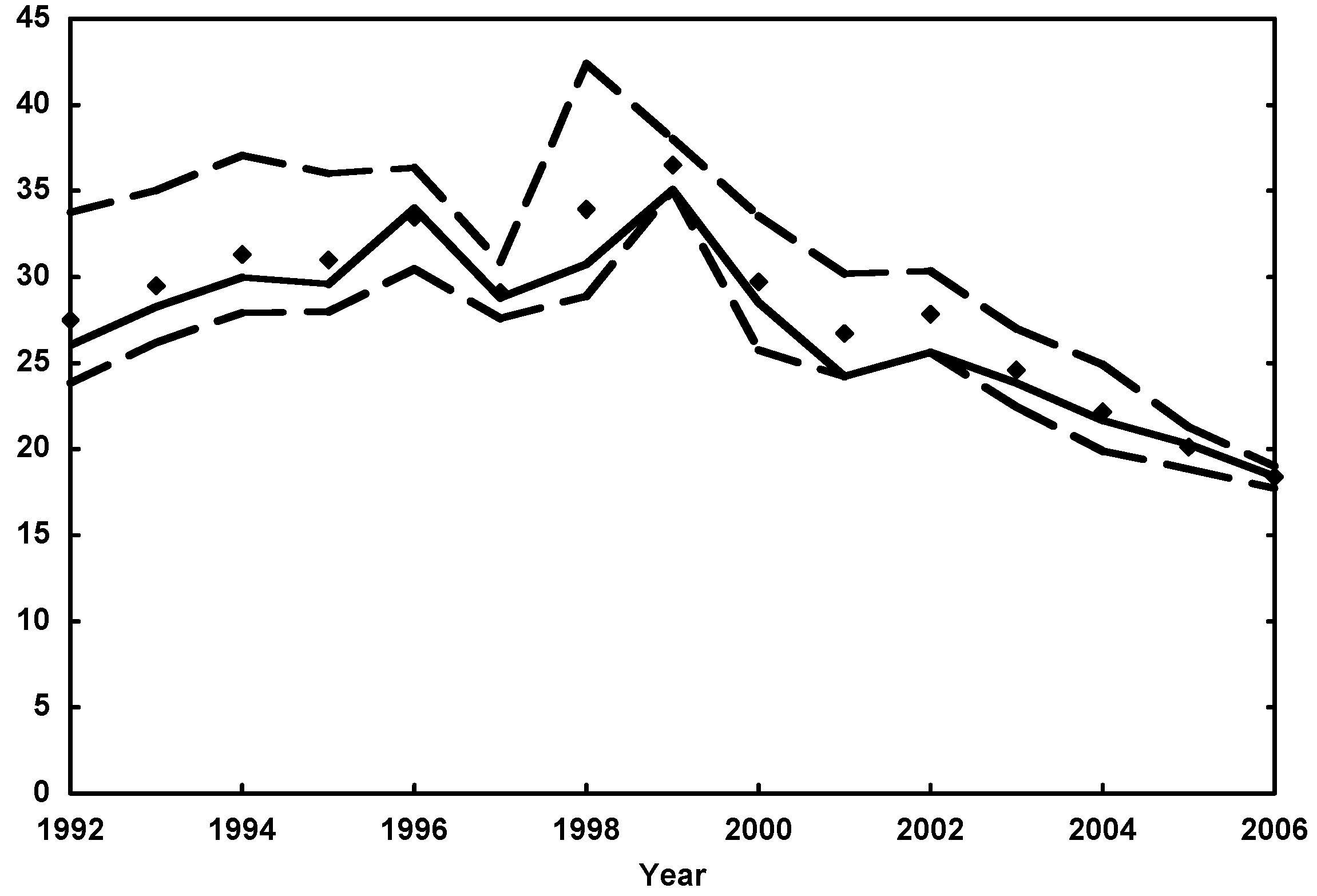
The mean EROI for each year produced by the various methods of estimating energy inputs differ from the values obtained from our base case by an average of 4% (
Figure 4). The greatest difference between our base case and an alternative occurs in 1998. In this case the high EROI estimate generated by calculating energy intensity as energy use per dollar of gross product in real (2005) dollars is greater than our base case by 35%. None of this uncertainty changes the basic slopes of our extrapolations.
Figure 4.
Range of EROI estimates derived from different methods of estimating energy inputs (area between dashed lines), the mean of those estimates (diamonds), and our base case EROI estimate (solid line).
Figure 4.
Range of EROI estimates derived from different methods of estimating energy inputs (area between dashed lines), the mean of those estimates (diamonds), and our base case EROI estimate (solid line).
3. Methods
In general EROI is calculated at the wellhead or equivalent as simply energy output (in this case the energy content of oil and gas produced) divided by energy input (in this case the estimated energy cost of exploration, development, and production). This ratio is often calculated over the lifetime of an individual project or facility. For example, the EROI of a nuclear plant can be calculated as the ratio of all of the electricity produced over the life of the plant to the sum total of the on and off site costs of construction, operation, maintenance, and cleanup costs over the same period.
There are two major drawbacks to applying this approach to oil and gas extraction. The first is a paucity of data. In order to carry out this type of analysis it would be necessary to have data on total energy inputs and outputs on a well-by-well or field-by-field basis. This would not be practical because such information is proprietary and because of the enormous number of individual wells. Second, the sum total of energy inputs and outputs over the life of most oil and gas fields is unknown simply because most oil and gas fields are still in production. For this reason we use a “rolling average” calculation of EROI. That is, we compare energy input to the oil and gas extraction industry in a given year to the energy output of the industry in that same year. We compare inputs and outputs in the same year (rather than comparing input this year to output in some future year) because our data suggest that 86% of the input is used for development and production, which affect oil yield essentially immediately, rather than exploration, the activity that would affect future production [
9]. This method also would seem to be of greatest interest to society more generally. We do not include the energy cost of maintaining e.g. executive salaries or national governments although for some purposes these might be considered some of the cost to the rest of society. Below we estimate the EROI for global oil and gas extraction in each year over the period 1992–2006. Both global and regional production data (output) for the entire period are available in terms of volume of fuel (barrels of oil or cubic feet of natural gas) produced per unit time, and these are converted readily to energy units using their heat equivalents (approximately 6,100 megajoules per barrel of oil and 1.1 MJ per cubic foot of natural gas, with some unknown regional variation that would not affect our global results). Quality (as defined by the ease of locating, extracting, storing, and transporting a fuel, as well as the ability of that fuel to do work of various types) varies across fuel types; therefore we have done our calculations both with and without corrections for the relative quality of each fuel, which varies over time. Our sources of production data are John S. Herold, Inc. (JSH) [
9], and the U.S. Energy Information Administration (EIA) (
Table 1) [
12,
13].
Table 1.
The total amount of crude oil/liquids and natural gas produced worldwide (millions of MJ), in the United States, and from the North Sea/Northern Europe as reported by John S. Herold, Inc. (JSH) and the United States Energy Information Administration (EIA). The Herold data pertain to a more limited universe, which includes only publicly traded companies.
Table 1.
The total amount of crude oil/liquids and natural gas produced worldwide (millions of MJ), in the United States, and from the North Sea/Northern Europe as reported by John S. Herold, Inc. (JSH) and the United States Energy Information Administration (EIA). The Herold data pertain to a more limited universe, which includes only publicly traded companies.
| | Worldwide | USA | North Sea/Northern Europe |
|---|
| Year | JSH | JSH | EIA | JSH | EIA |
| 1992 | 55,146 | 22,099 | 36,574 | 10,194 | 17,151 |
| 1993 | 56,736 | 21,767 | 36,094 | 10,659 | 18,066 |
| 1994 | 60,120 | 22,495 | 36,470 | 12,066 | 19,946 |
| 1995 | 62,094 | 22,630 | 36,020 | 11,779 | 20,971 |
| 1996 | 80,041 | 23,317 | 36,179 | 12,736 | 23,434 |
| 1997 | 85,955 | 23,481 | 36,169 | 11,726 | 23,077 |
| 1998 | 96,792 | 23,842 | 35,823 | 14,946 | 22,946 |
| 1999 | 97,286 | 22,965 | 34,819 | 15,620 | 23,558 |
| 2000 | 99,923 | 22,296 | 35,149 | 16,042 | 23,632 |
| 2001 | 103,685 | 23,049 | 35,474 | 16,073 | 23,723 |
| 2002 | 107,729 | 22,706 | 34,601 | 16,090 | 24,040 |
| 2003 | 108,467 | 22,519 | 34,552 | 16,463 | 23,565 |
| 2004 | 111,573 | 21,554 | 33,499 | 15,933 | 23,360 |
| 2005 | 118,866 | 20,270 | 32,281 | 14,495 | 21,613 |
| 2006 | 121,710 | 20,196 | 32,605 | 13,787 | 20,492 |
3.1. Energy Input
Ideally one would derive the energy costs (input) of oil and gas production from explicit data kept for that purpose, but such data do not exist on a global scale. Therefore this first estimate of the global energy cost of oil and gas extraction is based on the “upstream” financial data obtained and maintained by JSH (the only comprehensive data source available to us) (
Table 2). In this context “upstream” refers to the exploration for, and development and production of, oil and gas resources.
Table 2.
Money spent by the oil and gas industry (billions of nominal USD) on exploration, development and production worldwide, in the United States, and in the North Sea/Northern Europe.
Table 2.
Money spent by the oil and gas industry (billions of nominal USD) on exploration, development and production worldwide, in the United States, and in the North Sea/Northern Europe.
| | Worldwide | USA | North Sea/Northern Europe |
|---|
| Year | Exp | Dev | Prod | Exp | Dev | Prod | Exp | Dev | Prod |
| 1992 | 12.63 | 34.48 | 37.43 | 2.84 | 8.43 | 14.30 | 3.37 | 12.99 | 6.78 |
| 1993 | 11.52 | 33.73 | 36.07 | 3.26 | 9.66 | 13.99 | 2.45 | 9.97 | 6.08 |
| 1994 | 12.39 | 33.61 | 36.59 | 3.82 | 10.29 | 13.77 | 2.05 | 8.66 | 8.42 |
| 1995 | 13.57 | 36.90 | 37.43 | 3.98 | 11.04 | 13.30 | 2.26 | 9.85 | 8.89 |
| 1996 | 17.23 | 43.24 | 41.73 | 5.65 | 12.93 | 13.40 | 2.31 | 9.98 | 8.55 |
| 1997 | 21.65 | 58.64 | 52.21 | 6.93 | 17.18 | 13.04 | 2.20 | 9.97 | 7.49 |
| 1998 | 24.53 | 67.09 | 53.89 | 7.63 | 17.13 | 13.24 | 2.41 | 13.73 | 9.07 |
| 1999 | 16.93 | 53.82 | 50.72 | 4.91 | 12.04 | 11.99 | 1.45 | 10.18 | 8.38 |
| 2000 | 19.79 | 63.50 | 59.22 | 6.50 | 17.28 | 13.62 | 1.23 | 8.33 | 8.37 |
| 2001 | 23.73 | 82.27 | 62.57 | 8.40 | 25.20 | 15.11 | 1.55 | 9.44 | 8.44 |
| 2002 | 22.39 | 88.16 | 65.35 | 6.87 | 22.11 | 15.01 | 1.28 | 10.08 | 9.08 |
| 2003 | 25.66 | 103.40 | 75.17 | 7.15 | 23.81 | 16.37 | 1.40 | 12.51 | 10.03 |
| 2004 | 28.00 | 120.65 | 85.91 | 7.48 | 26.88 | 17.42 | 1.45 | 13.70 | 10.93 |
| 2005 | 36.16 | 160.86 | 104.49 | 10.18 | 35.94 | 20.77 | 2.11 | 16.55 | 12.47 |
| 2006 | 49.05 | 208.10 | 123.95 | 14.86 | 51.35 | 24.51 | 3.18 | 20.81 | 14.26 |
We were able to obtain specific data on energy costs only for the U.S. and the U.K. In order to estimate global energy costs of oil and gas extraction we first calculated the ratio of energy (E) consumption, in MJ, to monetary expenditures ($), in nominal dollars, in these countries to derive energy intensities:
We did not need to correct the dollar values we use in this analysis for inflation because we derived independent energy intensity (EI) ratios for each year. In this way we avoided uncertainty about which method of inflation correction to use.
Next we took the average of the energy intensities for the U.S. and the U.K. (EI
avg which was about 20 MJ per dollar for both countries in 2005) and multiplied this number by the total worldwide dollar expenditures (by public companies) reported by JSH ($) to generate an estimate of global energy cost in MJ (E
i). We assume that changes in monetary expenditures indicate commensurate changes in energy use:
We calculated global EROI for oil and gas by dividing global oil and gas production in MJ (E
o) for each year by the estimated global energy investment in that same year (E
i):
The “universe” of the JSH data is comprised of the vast majority of publicly traded oil and gas companies, the proportion of which has increased over time. This database does not include fully state-owned national oil companies (NOCs) such as Saudi Aramco. We do not know whether NOCs are more or less efficient than the publicly traded companies in the JSH database, but we have made the assumption that they are similar across the world. The JSH data represent about one quarter of the global oil industry (based on production) in 1992 and approximately 41% by 2006. The data are given by region and by company, include explicit dollar values, and span the time period from 1992 to 2006. Thus we were careful to insure that the energy costs and energy gains were derived using the same boundaries (i.e., that the energy costs used were used to recover the energy output used in the calculation).
In the U.S., the Census Bureau publishes a Census of Mineral Industries every five years. Three of these publications (1992, 1997 and 2002) fall within our study period (1992–2006). In these reports are data on the fuels and materials used by the major U.S. industries, including oil and gas extraction [
11,
14,
15]. Similarly, the U.K. Department for Business Enterprise and Regulatory Reform (BERR) publishes data annually on the energy used directly by the oil and gas extraction industry in the U.K. going back to 1998 [
16,
17]. Since these reports (both Census and BERR) specify how much of each fuel type is used we were able to correct for the quality of the different fuel inputs using a modified Divisia index [
18], a method to adjust for relative qualities of fuels that is based essentially on relative price. In other words the Divisia index assumes that the market is willing to pay for fuels of higher quality and that price reflects that quality.
It was also necessary for us to insure that both input and output data were applicable to the same boundaries. For example, one cannot compare input data for the entire North Sea to output from only the UK. While simple in principle, the boundaries of the JSH data do not always match those of our other data sources, making this sometimes difficult in practice. The following sections detail our methods for adjusting the datasets so that the input and output boundaries match.
3.2. Calibration Using USA Data
We obtained data on the fuel (direct energy) and the materials and supplies (indirect energy) used in the U.S. oil and gas industry from the Census of Mineral Industries. The fuel, or direct energy, costs are given in terms of routine units (e.g., gallons of gasoline, kilowatt-hours of electricity, and so on). We converted each to MJ using their heat equivalents (
Table 3). The material and supply costs are given in terms of dollar amounts spent for each category (cement, valves and pipe fittings,
etc.). Since the actual energy costs of these materials and supplies are not available from any source, these indirect energy costs needed to be derived from the dollar expenditures. For this we used the Economic Input-Output Life Cycle Assessment Model constructed by the Green Design Institute at Carnegie-Mellon University (
Table 4) [
19], which generates estimates of the energy use throughout the economy that is associated with the production of each dollar’s worth of goods and services in various sectors of the US economy. The model is based on energy use in 1997.
We prorated the JSH data to the entire US industry using the annual relation between US production reported by the EIA and the JSH production values, a factor of 1.7. When we had made this correction, the new JSH dollar cost data represented, presumably, the same boundaries as the Census energy cost data.
Table 3.
Selected fuels and their heat equivalents.
Table 3.
Selected fuels and their heat equivalents.
| Fuel | Heat Equivalent (MJ) |
|---|
| Residual oil (1 barrel) | 6,626.5 |
| Crude oil (1 barrel) | 6,163.8 |
| Distillate oil (1 barrel) | 6,139.6 |
| Gasoline (1 gallon) | 131.8 |
| Electricity (1 kilowatt-hour) | 3.6 |
| Natural gas (1 cubic foot) | 1.1 |
Table 4.
MJ used per dollar spent in select sectors of the economy. Source: Economic Input-Output Life Cycle Assessment Model developed by the Green Design Institute at Carnegie-Mellon University. (We suspect that the nominal precision given does not reflect reality).
Table 4.
MJ used per dollar spent in select sectors of the economy. Source: Economic Input-Output Life Cycle Assessment Model developed by the Green Design Institute at Carnegie-Mellon University. (We suspect that the nominal precision given does not reflect reality).
| Sector | MJ |
|---|
| Oil and gas field machinery and equipment | 7.36 |
| Petroleum lubricating oil and grease manufacturing | 61.30 |
| Cement manufacturing | 68.4 |
| Rolled steel shape manufacturing | 15.60 |
| Fabricated pipe and pipe fitting manufacturing | 9.84 |
| Water transportation | 48.80 |
| Other miscellaneous chemical product manufacturing | 16.30 |
| Other basic organic chemical manufacturing | 21.70 |
| Explosives manufacturing | 22.70 |
| Watch, clock, and other measuring device manufacturing | 5.65 |
| Oil and gas extraction | 9.26 |
| Drilling oil and gas wells | 9.87 |
| Support activities for oil and gas operations | 6.98 |
Our study period includes data points from three Census years (1992, 1997 and 2002). To estimate the annual energy cost values in non-Census years we interpolated between Census years the ratios of fuel use by type to the JSH-reported US dollar costs (in constant dollars). We then multiplied these estimated values by the dollar cost in each non-census year (Equation 2). For the three fuel categories for which no 2002 data are available (residual oil and heavy diesel, gasoline, and crude petroleum produced and used at the same plant) we assumed a constant ratio from 1997. Similarly, for the years after 2002 we assumed a constant ratio from 2002 for each fuel type.
We calculated total direct energy expenditure for the U.S. oil and gas industry for each year by adding up fuel consumption across fuel types using the modified Divisia index to account for differences in fuel quality. We derived the energy intensity of each dollar spent (MJ/$) in the U.S. in each year by dividing the total energy used by the U.S. oil and gas industry by the prorated dollar cost values from JSH (Equation 1). In years after 2002, the last Census year, we assume a constant energy intensity ratio in the U.S. at the 2002 level.
3.3. Calibration Using UK Data
We obtained data on the direct energy consumption, by fuel type, of the oil and gas extraction industry in the UK from the Digest of UK Energy Statistics, published by the BERR. No data on indirect energy costs were available so we multiplied the direct energy value for each year by the ratio of total energy cost to direct energy cost for the US for each year. These corrections were fairly small (+11% on average).
The JSH dollar cost data for the North Sea/Northern Europe aggregates data principally for the UK, Norway, Denmark, The Netherlands, Germany, and Ireland. We prorated the JSH data for the North Sea to represent only the UK using the annual relation between U.K. production reported by the EIA and the JSH North Sea production values for each year (61% in 1992 to 46% in 2006) so that our estimates of energy costs and gains shared the same boundaries.
We calculated the total upstream energy costs for the UK by aggregating across fuel types, with and without using the Divisia index to correct for differences in relative fuel quality. Finally we derived the energy intensity of each dollar spent in the UK in each year (MJ/$) by dividing the total energy cost by the dollar cost (Equation 1). For years prior to 1998, the first year for which BERR data are available, we assume constant energy intensity in the U.K. at the 1998 level.
The energy intensities per dollar spent ranged from 30 MJ/$ to 18 MJ/$ for the US and from 31 MJ/$ to 18 MJ/$ for the UK, the differences are due principally to inflation and are similar for both countries for each year. We do not know why they are about twice those derived by Carnegie-Mellon (
Table 4) but have greater faith in our values because we think our process is very srtaightforwartd and because we got similar results for both the US and UK.
4. Conclusions
While we are well aware of the limitations of having to depend upon financial data for our energy cost estimates we consider this work a best available estimate of the trend over the last fifteen years in EROI for global oil and gas extraction. We think this is a very important step in evaluating the planet’s remaining usable oil and gas resources and planning how to most wisely invest human, technological, and capital resources in future energy supplies. The fact that the EROI for global oil and gas extraction declined by nearly half from 1999 to 2006 is cause for concern. We rely on surplus energy, that is, a quantity of energy above that required to maintain energy production, to drive our economy. Surplus energy from petroleum production supplies the majority of the energy used to develop and maintain our vast infrastructure, produce food, and make possible the functioning of government and financial systems. If the decline in EROI continues, then the amount of energy that will be available to sustain and grow the economy, both nationally and worldwide, will decline as well. The recent paper by Hall
et al. [
20] on the minimum EROI for society indicates that society, even at its most basic level, cannot function on an EROI at the wellhead of less than about 3:1, and that considerably more than that would be required for the full suite of goods and services (such as medical care and education) that we have come to expect. At this time oil and gas still represent a favorable EROI compared to most alternatives (except coal) [
21].
We hope that this first estimate will spark debate and ultimately yield better reporting, especially of energy costs, so that more refined and accurate estimates can be generated. Quite curiously we as a society do not maintain explicitly the data to definitively assess either the status of our current energy resources or that of potential replacements, nor do we have government programs in place to provide support for objective analyses of this very critical issue.
It is important to note that the data we used in this analysis group oil and natural gas production together, since they are commonly produced from the same reservoirs. However, the effort required to pump oil out of the ground is generally much greater than that required to bring natural gas to the surface. We therefore expect that the true EROI of oil is somewhat lower than our results suggest, while that of conventional natural gas is higher.
What are the reasons for the decline in the EROI estimates, especially since 1999? Probably the most important thing is that it appears that depletion is a somewhat more powerful force than technological improvement. A second, possibly equally important effect is that of drilling intensity. Previous studies have shown that exploitation efficiency in the petroleum industry declines when exploitation intensity increases [
22,
23]. Exploitation intensity increased substantially from 1999 to 2008 in response to price increases. This increased drilling intensity may be the cause of both the inflection and some or much of the decline in EROI, and may not result in as much additional net energy delivered to society as would seem to be the case at first thought. The integrated effects of depletion and variable drilling effort may also explain much of the variability in both the US and the global data, all of which shows both a general secular decline over the entire period but also a flattening or even increase in EROI during periods of reduced drilling effort (i.e., the 1960s and early-mid 1990s) and a sharp decline when oil prices and drilling intensity increase as in the 1970s and also the late 1990s through 2006. The complexities of oil price and drilling intensity changes in the past several years may make any simple assessment of recent years difficult! Finally the steep initial decline 1930–1960 may imply that an exponential decline would be a better predictor than the linear extrapolations we use.
To generate this first assessment of the EROI of global oil and gas extraction we were forced to make many assumptions that introduced varying degrees of error to our analysis. The first of these is the assumption that changes in monetary expenditures indicate changes in energy expenditures. There are other factors, such as scarcity of drilling rigs, which can change the dollar cost of exploration, development, and production without affecting the energy cost. We believe we address this issue by calculating discreet energy intensity ratios for each year of our analysis in our base case. In this way our estimated energy costs in a given year will be related to the monetary expenditures in that same year only. Then sensitivity analysis of inflation-corrected estimates gave similar values.
Similarly, we have applied the energy intensity ratios calculated from US and UK data to the entire world. We realize that this requires the possibly unrealistic assumption that energy intensities are the same the world over. However, the data necessary for calculating energy intensities on a regional basis are not publicly available.
Our final assumptions concern our methods for estimating energy intensities in years for which no energy input data were available. We assume a constant energy intensity in the US after 2002, and constant energy intensity in the UK prior to 1998 because there are no data available for those time periods. These intensities could of course change, but in the absence of any data we do not assume a trend one way or the other. In addition, we assume that a linear interpolation between our three energy intensity values for the U.S. is appropriate. In the absence of any energy input data between Census years we have chosen the simplest estimation — a straight line. Additionally, straight lines represent the average of all of the possible ways of connecting the existing data points. As of press times there were no new assessments of energy costs (e.g., for 2007) available, and additionally we have some concerns about the apparent increase in the variability of fuel type from one past census to the next.
Finally, our analysis suggests that the critical issue facing humanity is not just “peak oil” or “how much oil is left?”, about which there is considerable debate. Rather the most important issue facing the global economy is likely to be “how much oil is left that can be extracted with a significant energy profit?” and “what are the EROIs of possible substitutes?” In 1984 Cleveland
et al. concluded that, “If we are to sustain…economic growth and productivity as minimum long run goals, alternative fuel technologies with EROI ratios comparable to that of petroleum today must be developed” [
8]. This need has become only more pressing with time. It is important to get more comprehensive and more reliable data on energy costs in order to truly understand this issue. On the other hand our analysis here and elsewhere showing declining EROI of main fuels and low EROI of most alternatives, as well as the many economic difficulties of the past year suggest that we are indeed reaching the “limits to growth” and must adjust our perspectives and economic goals accordingly [
21].