Lead-acid batteries are widely utilized in diverse applications, including automotive, railway, marine, and telecommunications industries, and backup power systems, due to their low cost and superior high-rate discharge performance. For systems that use lead-acid batteries, the State of Health (SOH) of these batteries critically influences overall system stability. Therefore, accurate SOH assessment is essential. Currently, research on the health status of lead-acid batteries remains significantly less extensive compared to that on lithium-ion batteries; hence, methodologies developed for lithium batteries will be referenced in this study. Methods for predicting battery health status primarily fall into two categories: model-driven and data-driven approaches [
1,
2,
3,
4,
5]. Model-driven methods mainly rely on battery physical mechanism models or empirical degradation models. Physical mechanism models usually require an in-depth understanding of the battery’s internal electrochemical mechanisms to establish the relationship between model parameters and SOH from the physical mechanism of batteries [
6]. Empirical degradation models, such as those utilizing the ampere-hour integral method or internal resistance measurements, analyze historical capacity fade trends or quantitatively estimate remaining capacity to assess battery health [
7,
8,
9]. Data-driven methods, by contrast, bypass the explicit modeling of internal degradation mechanisms. Instead, these approaches extract features indicative of capacity fade (e.g., voltage/current profiles during charge–discharge cycles) from operational data and construct predictive mappings between these features and SOH through machine learning. Based on the multi-phase Weiner process degradation model, Yang et al. [
10] proposed a prediction method for lead-acid battery health state estimation and Remaining Useful Life (RUL). However, the Weiner process assumes that the degradation noise is a Gaussian distribution, but in fact the battery degradation may have non-Gaussian noise or mutation phenomenon, which may affect the prediction accuracy. Sun et al. [
11] utilized Convolutional Neural Networks (CNNs) to extract local spatial features such as voltage from battery charge and discharge data. By employing Bidirectional Long Short-Term Memory (BiLSTM) networks to capture temporal dependencies, they introduced attention mechanisms to dynamically weight the importance of features at different time steps, thereby enhancing the model’s sensitivity to degradation features. Yu et al. [
12] proposed a Time-series Convolutional Network (TCN) model based on multi-health feature extraction and Particle Swarm Optimization (PSO). The high accuracy and robustness of this method in different training datasets and lithium battery systems were verified by experiments. Fu et al. [
13] proposed a VMD-PE-IDBO-TCN prediction model, which used the method of VMD combined with Permutation Entropy (PE) to reconstruct the original lithium battery SOH data and used the Improved Dung Beetle Optimization (IDBO) algorithm to optimize the hyperparameters of the TCN model, so as to achieve high precision SOH prediction. Xu et al. [
14] proposed a hybrid method combining the Transformer model with the Unscented Particle Filter (UPF) to predict the health status of lithium-ion batteries. By leveraging the global prediction capability of Transformer and the online correction capability of the UPF-based local correction model, high-precision battery health predictions can be achieved under different aging conditions. Guijun Ma et al. [
15] employed convolutional neural networks to automatically extract features from raw charging voltage curves and implemented transfer learning for the personalized SOH estimation of new batteries. Winata et al. [
16] used three machine-learning algorithms—Gaussian Process Regression, Support Vector Machine, and Random Forest—to predict the degradation of lead-acid batteries based on real-time monitored voltage and temperature as features and proved that Random Forest had the best prediction performance. Zhang et al. [
17] used a Long Short-Term Memory (LSTM) recurrent neural network to capture long-term dependencies in lithium-ion battery capacity fade, optimizing their model with resilient mean square back-propagation and dropout techniques. Overall, data-driven methods have gained prominence due to their ability to circumvent complex battery modeling. These techniques typically exploit machine learning to uncover latent relationships between measurable battery parameters (e.g., voltage, current) and internal health states, thereby enabling robust SOH prediction.
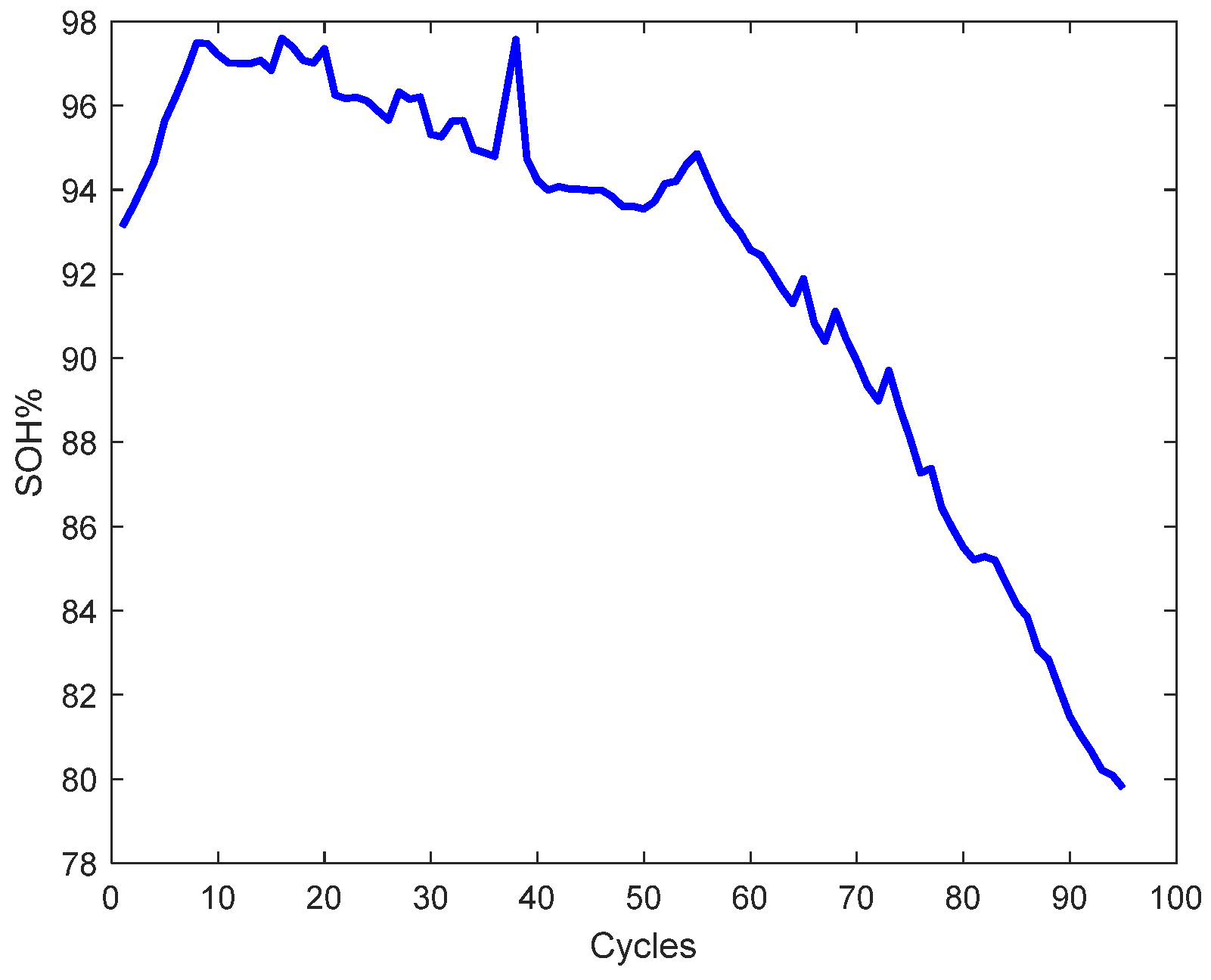
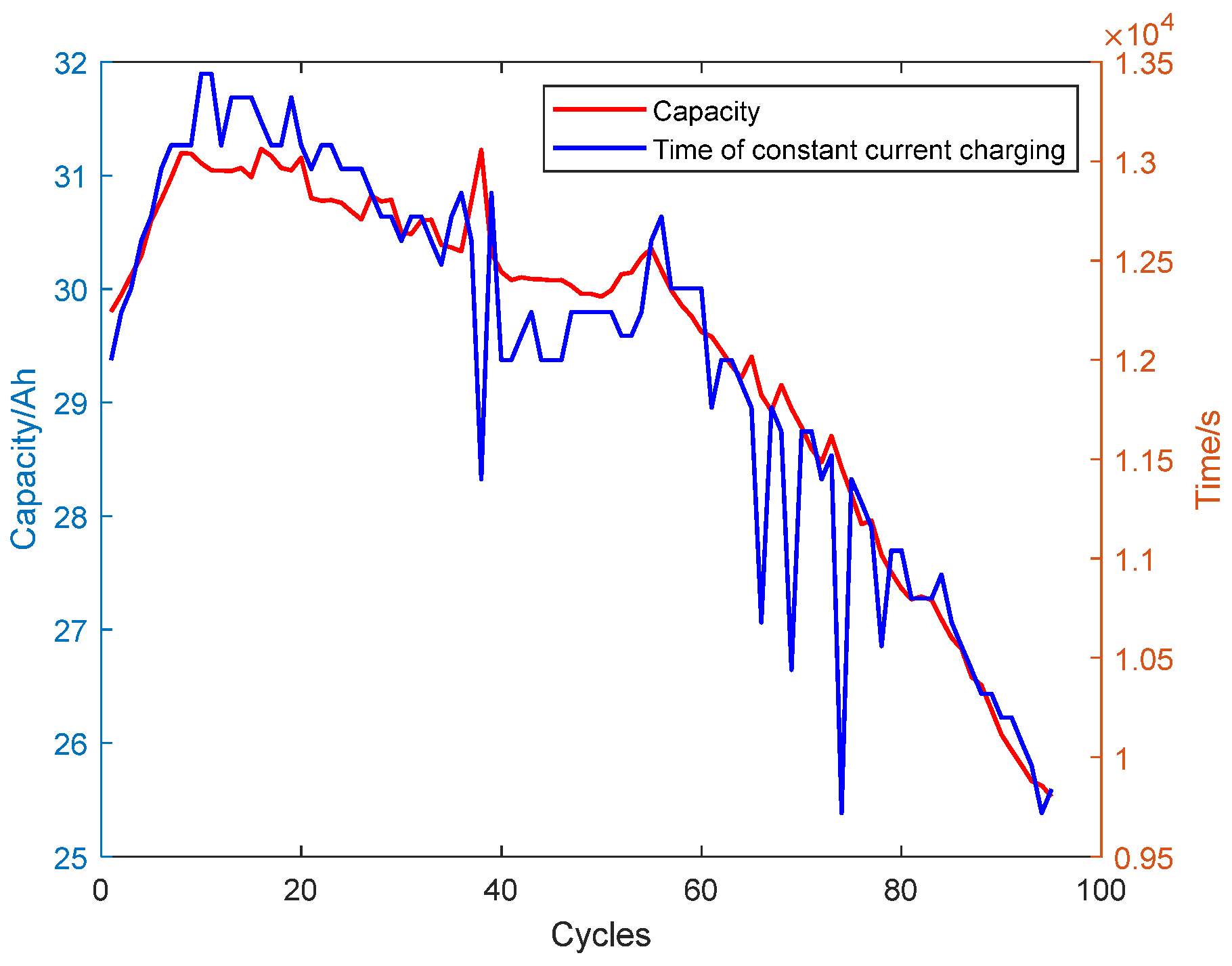
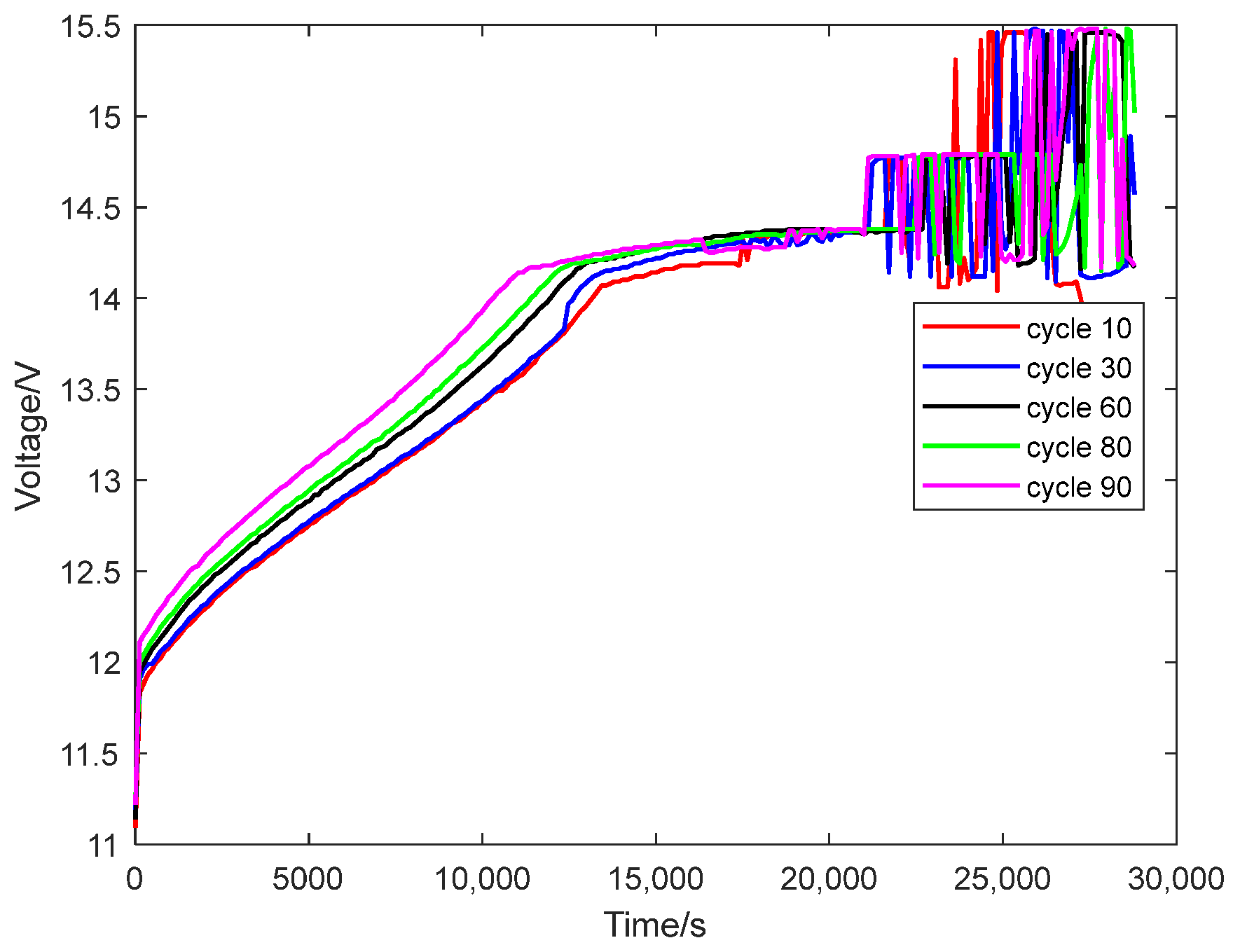
The capacity degradation of lead-acid batteries stems from their internal electrochemical mechanisms, resulting in nonlinear and non-stationary degradation data. This inherent complexity poses significant challenges for accurate battery health status prediction. The operational data collected during battery cycling can be characterized as nonlinear and non-stationary time series. To maximize information extraction while mitigating noise interference, researchers often decompose such time series into multiple components with distinct temporal scales. Subsequent analysis and recombination of these individual components enable effective noise separation [
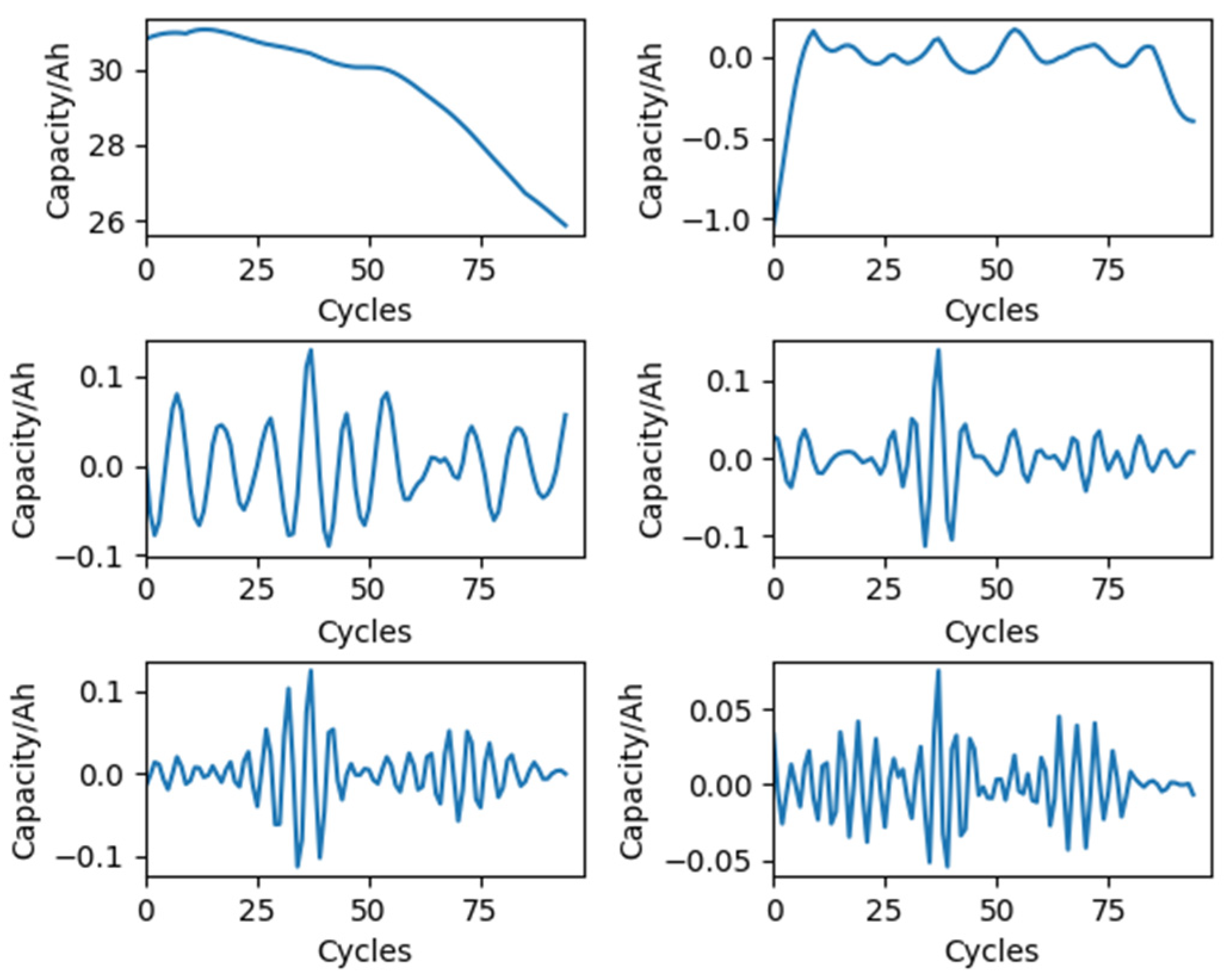
18]. Singular Spectrum Analysis (SSA) is an efficient method for processing non-stationary time-series data [
19]. The ability of SSA to separate noise, trend, and harmonic is consistent with the physical degradation of lead-acid batteries and can perform interpretable feature extraction. Requiring no prior assumptions, SSA preserves critical data features while demonstrating superior noise suppression capabilities compared to Empirical Mode Decomposition (EMD) and wavelet decomposition, as evidenced in [
20,
21].
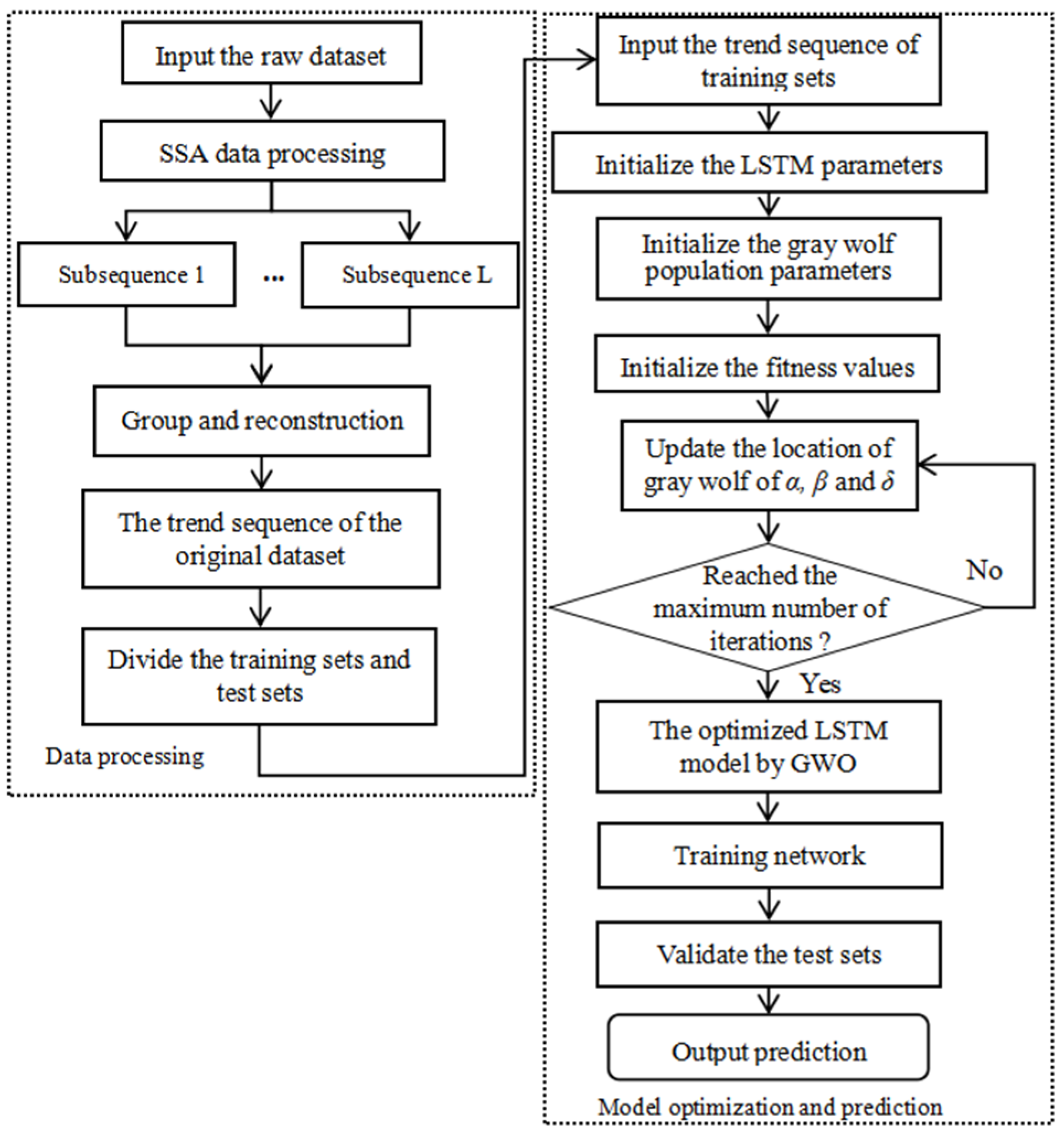
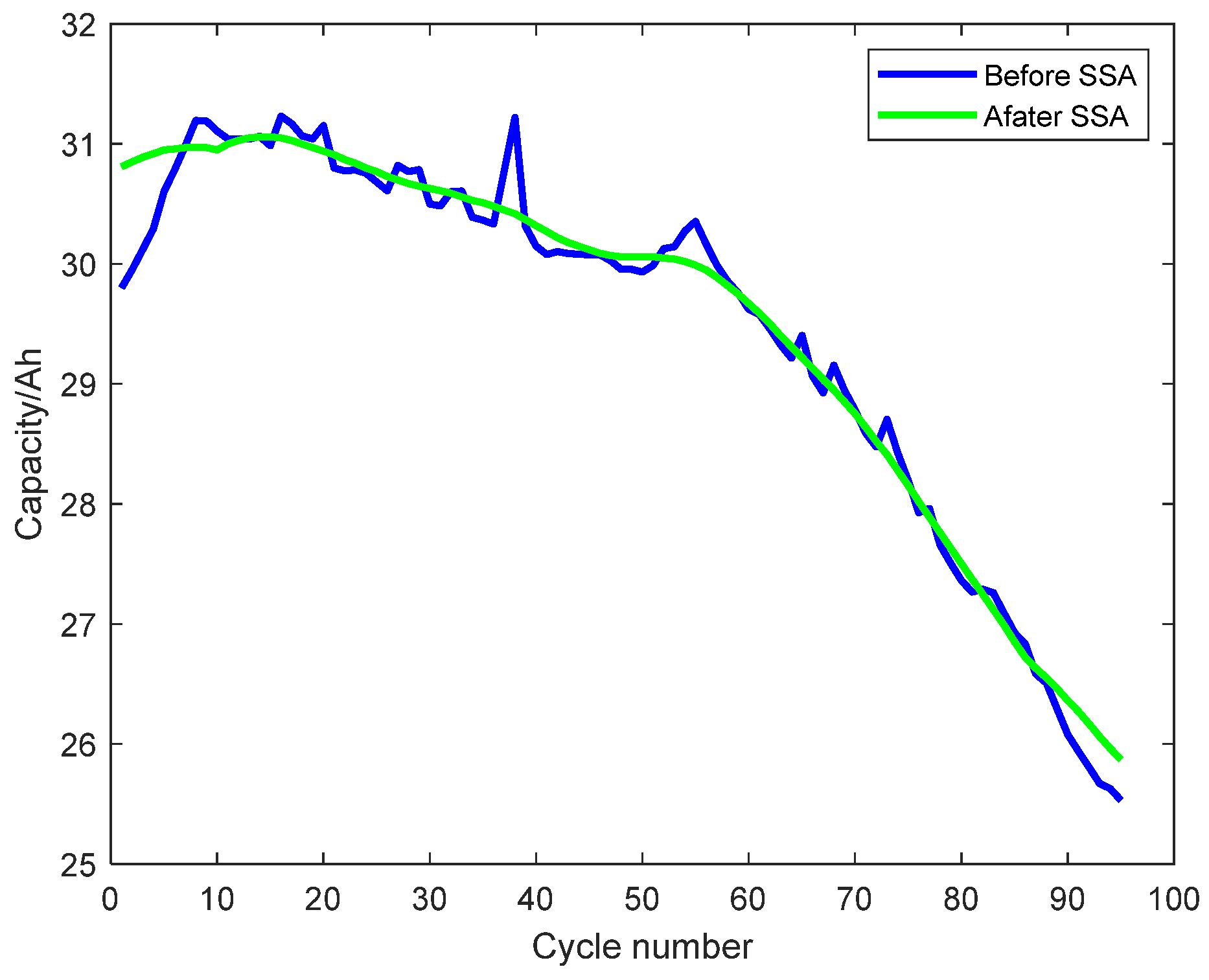
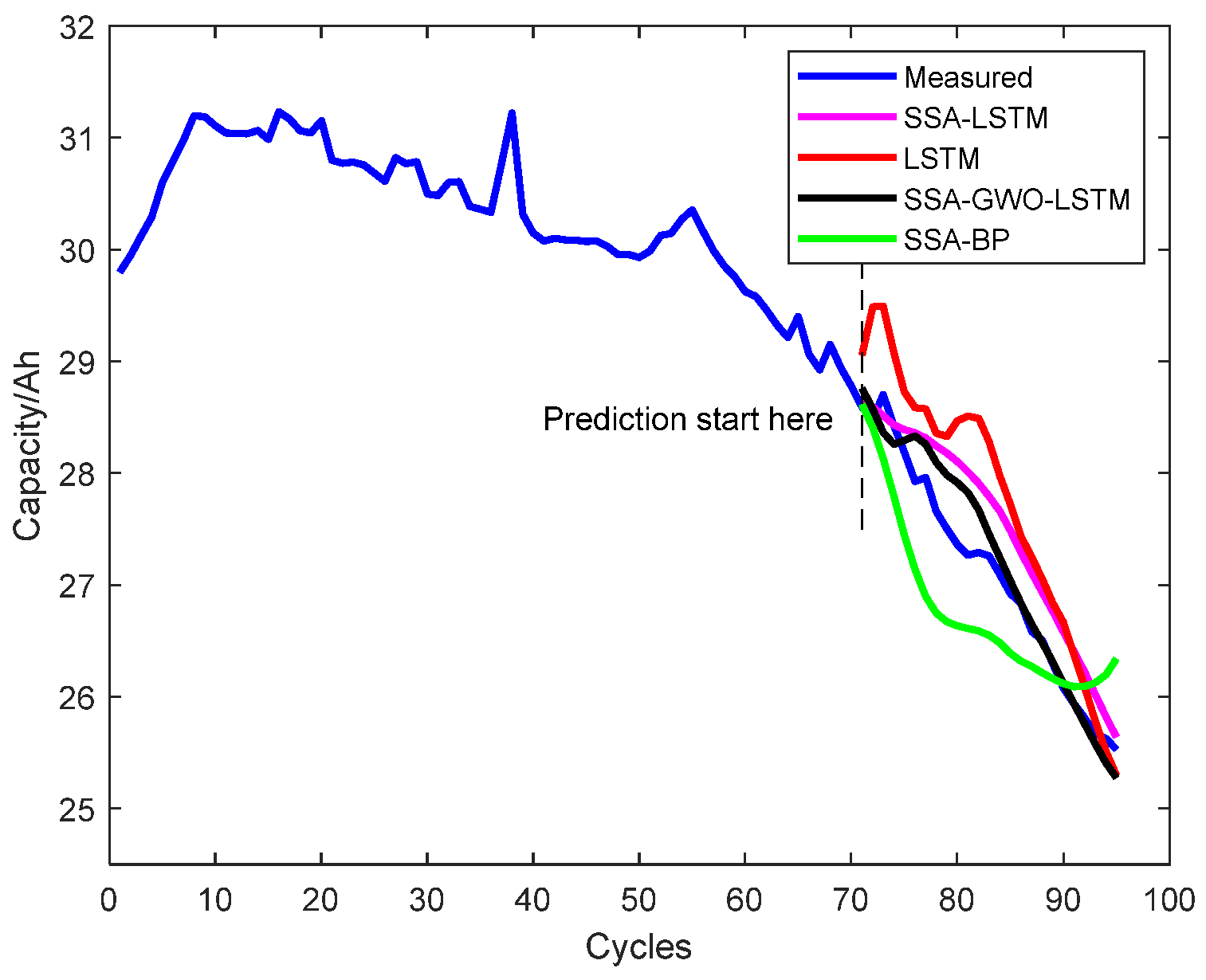
Based on the preceding analysis, this study employs a data-driven approach to evaluate the SOH of lead-acid batteries. To enhance prediction accuracy, the singular spectral analysis is integrated to preprocess the sequence of degradation features. Subsequently, the processed data are fed into an LSTM network for model training and prediction.
Our main contributions are as follows: (i) Combining the SSA method with the LSTM network algorithm to form an efficient SOH prediction model; (ii) Using the SSA method to preprocess battery capacity degradation data and extract the trend sequence of the data, which makes the characteristics of the data more significant; (iii) Optimizing the parameters of the LSTM network by using the Grey Wolf Optimization (GWO) algorithm, improving the robustness and accuracy of the model.