Research on Resource Utilization of Bi-Level Non-Cooperative Game Systems Based on Unit Resource Return
Abstract
:1. Introduction
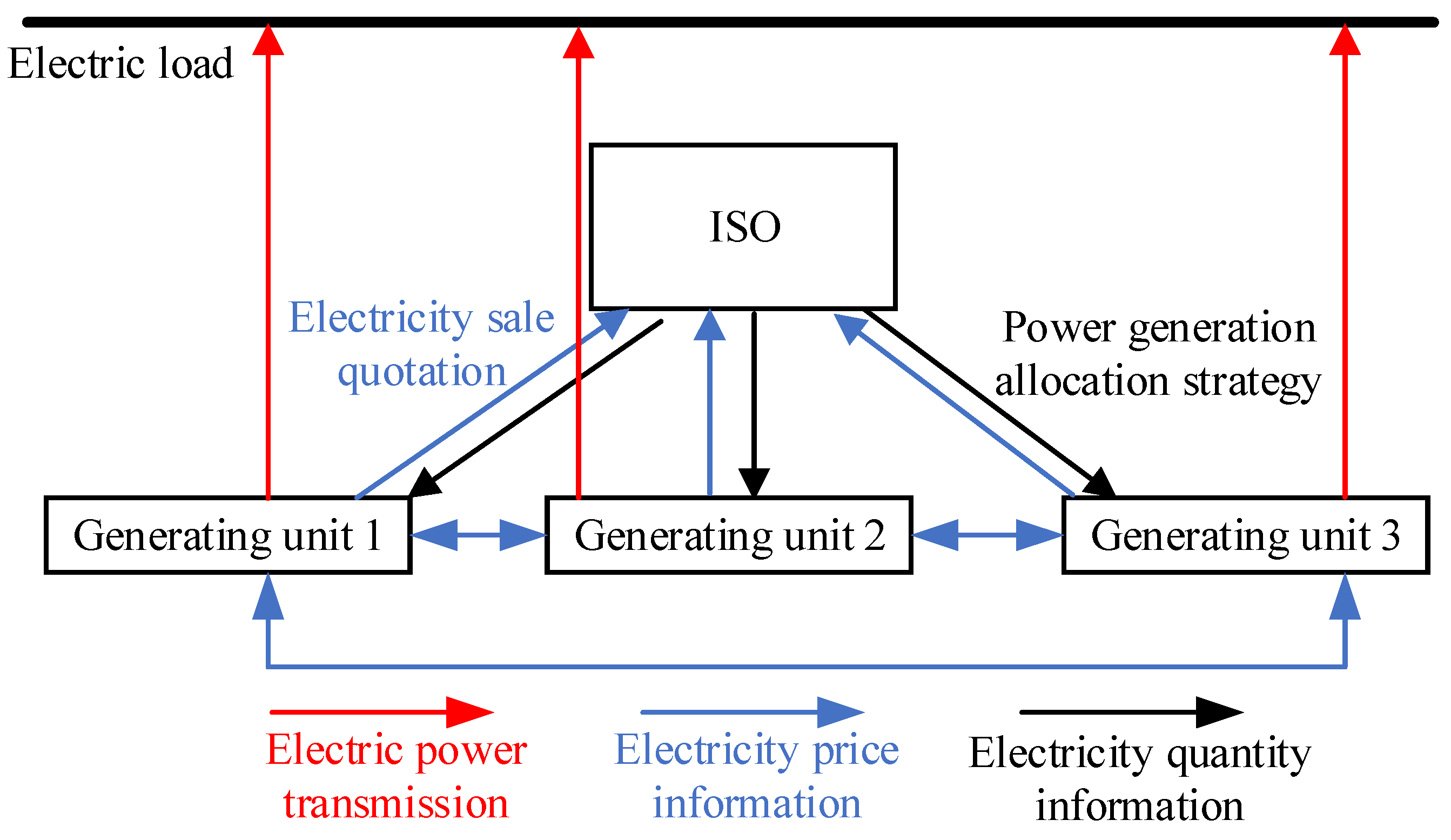
2. System Energy-Trading Framework
3. Analysis of System Resource Utilization Rate
3.1. Unit Resource Return
- URR of Wind and Photovoltaic Generation Units
- 2.
- URR of Thermal Power Generation Units
3.2. System Resource Utilization Function
4. Bi-Level Non-Cooperative Game Model
4.1. Bi-Level Non-Cooperative Game Optimization Framework
4.2. Modeling of Lower-Level Generating Units
4.2.1. Objective Function
- Wind and Photovoltaic Generation Units
- 2.
- Thermal Power Generation Unit
4.2.2. Constraints
- Electricity Selling Price Constraints
- 2.
- Overall System Electricity Selling Revenue Constraints
4.3. ISO Objective Modeling
4.3.1. Objective Function
4.3.2. Constraints
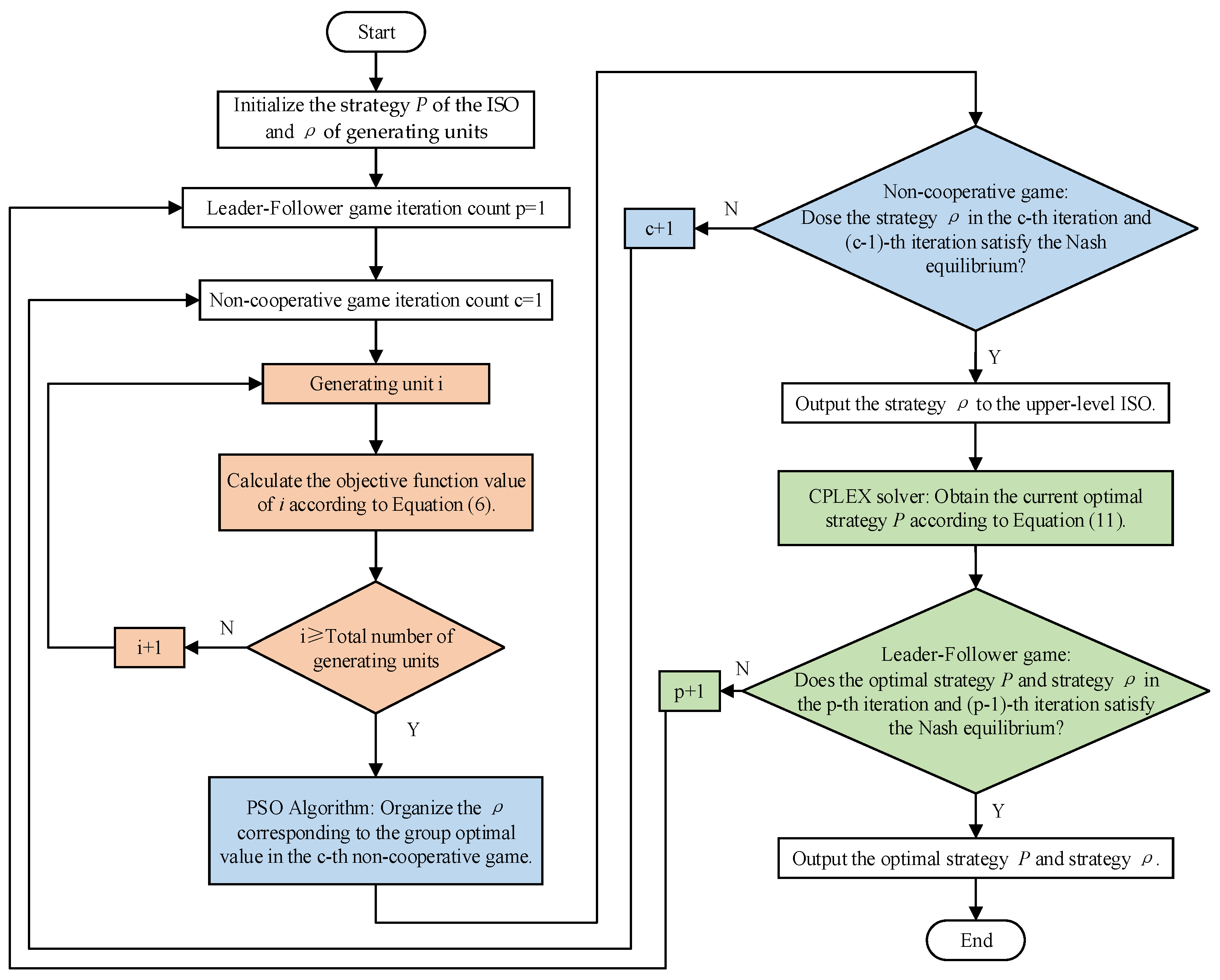
5. Algorithm Solution Analysis
5.1. Upper-Level Leader–Follower Game in the Bi-Level Non-Cooperative Game Model
- Participants: ISO, and n generating units
- Strategy: The strategy of the ISO is N-dimensional and represents the generation allocation for each generating unit adjusted based on their bidding prices. It is expressed in vector form as .
- Objective: The ISO, as the upper-level guiding module, does not consider its interests. However, as the overall system coordinator, it must ensure that the contributions of power generation units receive reasonable returns and improve the system’s resource utilization efficiency. Its objective function is calculated by Formula (11).
5.2. Lower-Level Non-Cooperative Game in the Bi-Level Non-Cooperative Game Model
- Participants: n different types of generating units
- Strategy: The strategy of each generating unit is an N-dimensional bidding strategy, which can be represented in vector form as .
- Profit: The objective function of each generating unit can be calculated using Formula (6).
5.3. Algorithm Flowchart
6. Case Analysis
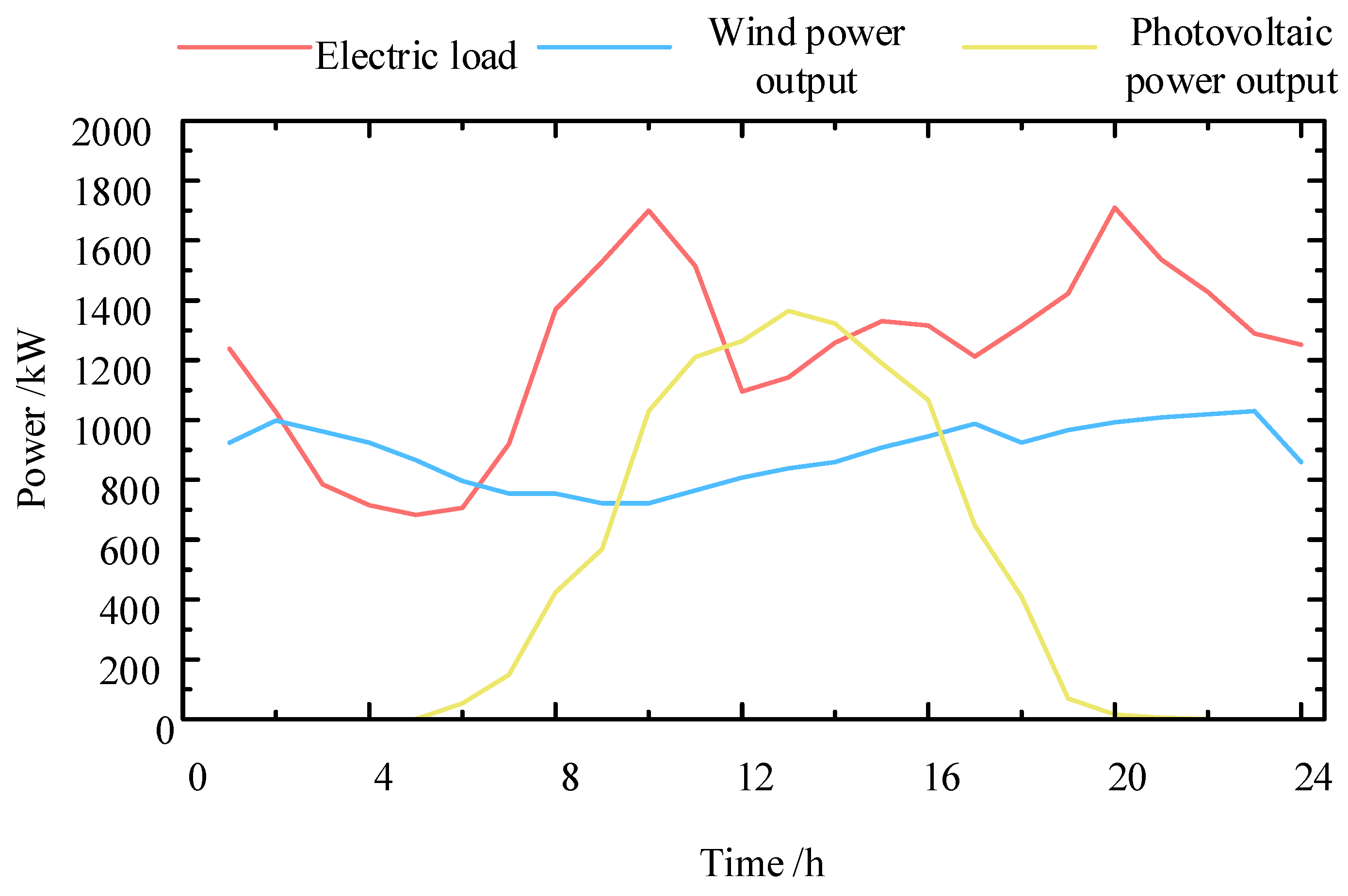
6.1. Basic Case Data
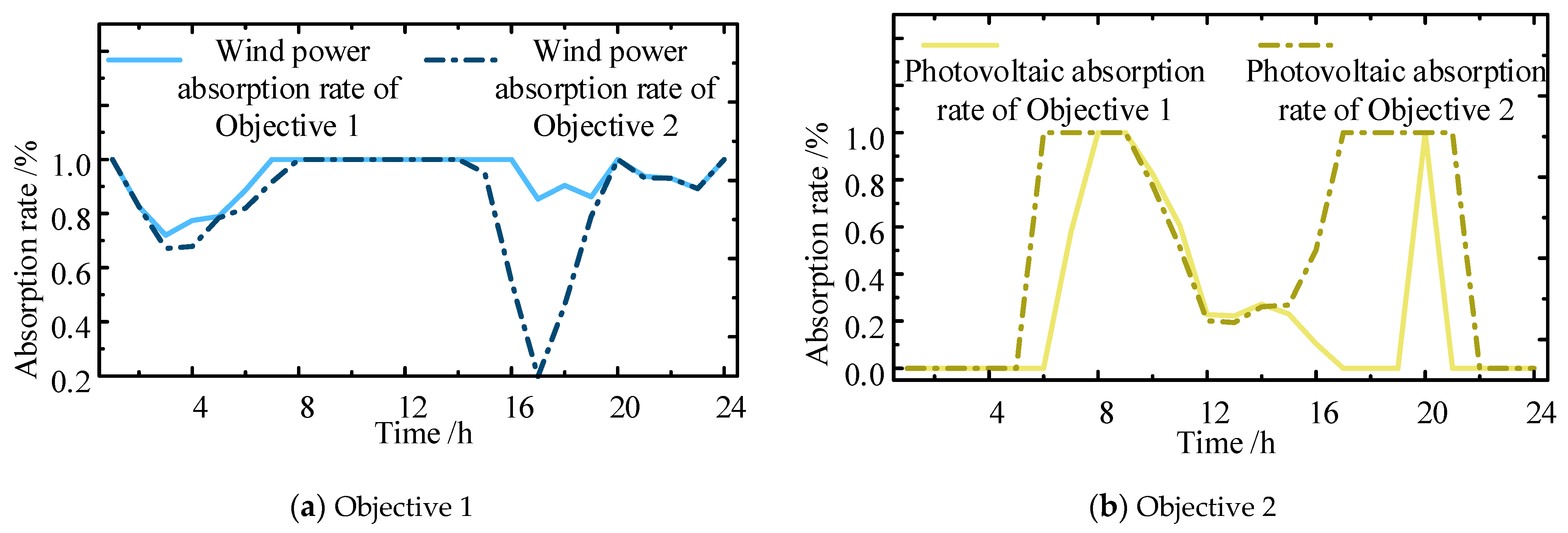
6.2. Analysis of the Impact of Different Objectives on the System
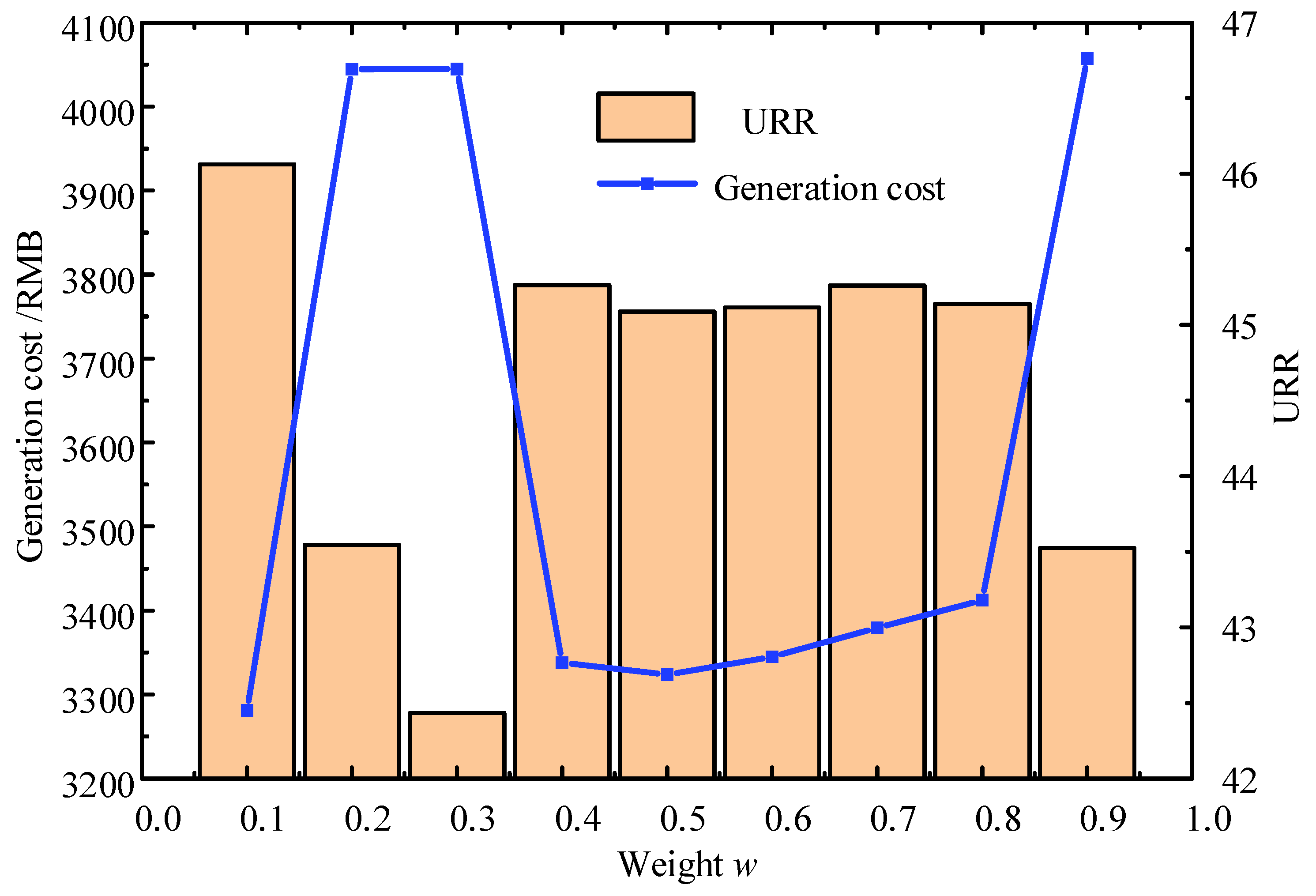
6.3. The Impact of Weight Proportions on Scheduling Results
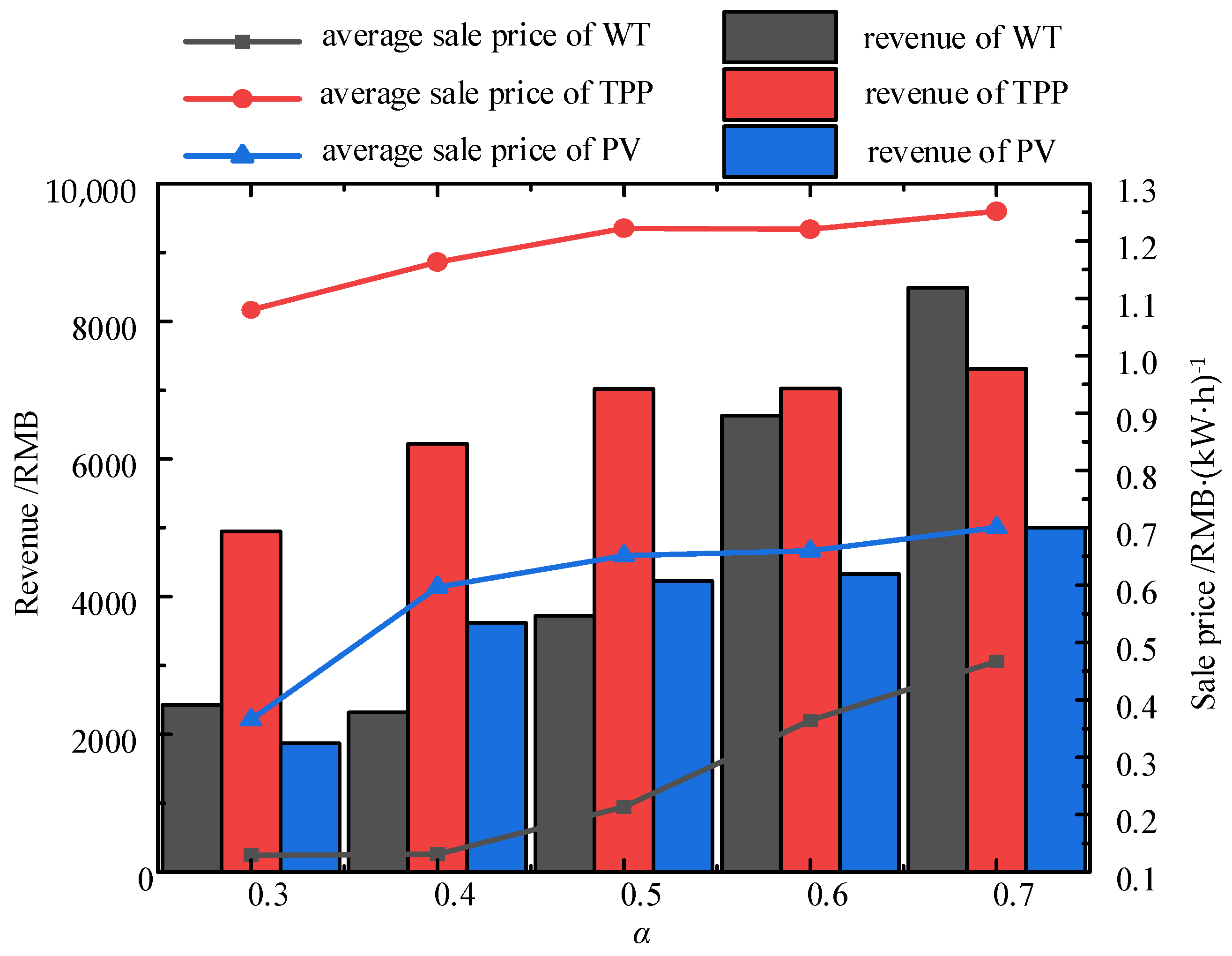
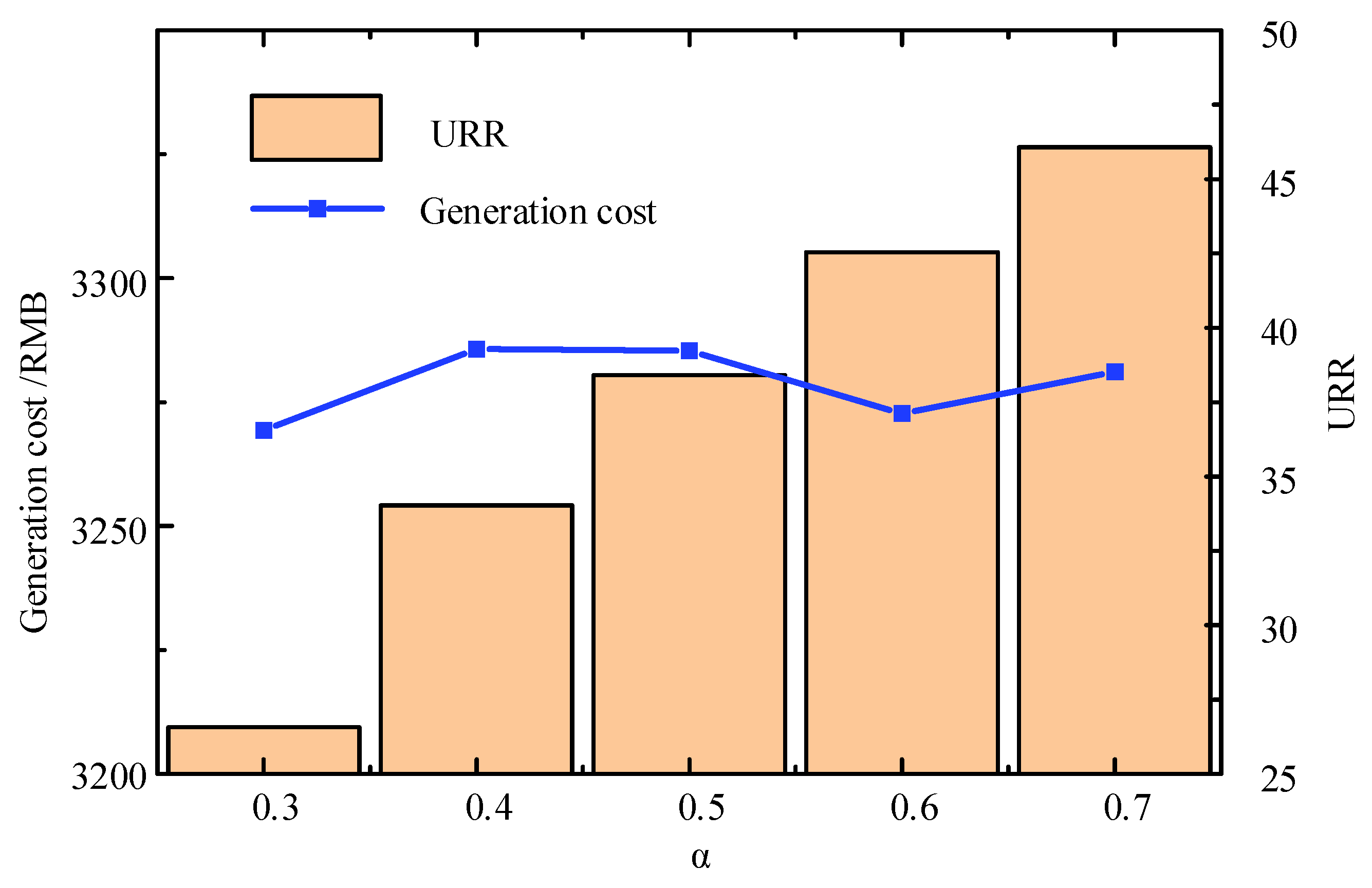
6.4. The Impact of the Total Revenue Constraint for Power Generation Units Issued by ISO on the Results
7. Conclusions
- The establishment of the bi-level non-cooperative game model enables a balance between the autonomy of individual generation units and the overall efficiency of the power system. In this framework, different generation units adopt distinct bidding strategies, fostering fairer competition among them. This ensures that each unit of output receives a reasonable return, encouraging the system to dispatch various types of generation units more equitably and avoiding situations where certain units are either excessively utilized or left idle.
- Incorporating URR into the ISO’s dispatch objective can effectively guide system-level scheduling while ensuring a fair return on the contributions of generation units. The model simultaneously considers both generation cost and resource utilization efficiency. URR encourages all units to improve their operational efficiency, achieving a significant increase in unit resource returns at a relatively low cost. This approach maintains a competitive balance among different types of generation units, enhances the equity of profit distribution, and promotes sustained participation and operational enthusiasm across the system.
- In the current model, generation units do not submit bids based on their true production costs. Instead, they optimize their bidding strategies by anticipating competitor behavior and system conditions in order to maximize their own profit—reflecting strategic bidding behavior. Future research may incorporate constraints on truthful bidding, regulatory mechanisms, or multi-agent evolutionary game approaches to enhance the model’s applicability in real-world electricity markets.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Zhang, K.; Zhang, S.; Wang, F. Game Analysis of Multi-Energy Markets Considering Wind Power Bidding. Acta Energ. Solaris Sin. 2021, 42, 279–285. [Google Scholar]
- Mei, S.; Wang, Y.; Liu, F. A Game Theory Based Planning Model and Analysis for Hybrid Power System with Wind Generators-Photovoltaic Panels-Storage Batteries. Autom. Electr. Power Syst. 2011, 35, 13–19. [Google Scholar]
- Dong, L.; Tu, S.Q.; Li, Y.; Pu, T. A Stackelberg Game Model for Dynamic Pricing and Energy Management of Multiple Virtual Power Plants Using Metamodel-Based Optimization Method. Power Syst. Technol. 2020, 44, 973–981. [Google Scholar]
- Li, F.; Yu, K.; Chen, X.; Hua, H.C. Price Decision Optimization for Electricity Retailers Based on Dual Game under Carbon Constraints. Electr. Power 2024, 57, 126–136. [Google Scholar]
- Chen, L.; Zhu, Z.; Wang, K.; Guo, B.; Shuai, W.L. Optimal Operation of Distribution Networks and Multiple Integrated Energy Microgrids Based on Mixed Game Theory. Power Syst. Technol. 2023, 47, 2229–2243. [Google Scholar]
- Mi, Y.; Zhao, H.; Fu, Q.; Ma, S.Y.; Cai, P.C.; Yuan, M.H. Two-level Game Optimal Operation of Regional Integrated Energy System Considering Wind and Solar Uncertainty and Carbon Trading. Power Syst. Technol. 2023, 47, 2174–2188. [Google Scholar]
- Yang, D.; Wang, Y.; Yang, S.; Jiang, C.; Liu, X. Multi-microgrid and Shared Energy Storage Two-layer Energy Trading Strategy Based on Hybrid Game. High Volt. Eng. 2024, 50, 1392–1402. [Google Scholar]
- Feng, C.; Wang, X. Review of Unit Maintenance Scheduling in Market Environment. Power Syst. Prot. Control. 2011, 39, 138–147. [Google Scholar]
- Haghighat, H.; Karimianfard, H.; Zeng, B. Integrating Energy Management of Autonomous Smart Grids in Electricity Market Operation. IEEE Trans. Smart Grid 2020, 11, 4044–4055. [Google Scholar] [CrossRef]
- Yang, N.; Ding, L.; Liu, Z.; Yan, J.; Xing, C.; Zhu, B.X.; Huang, Y.H.; Zhang, X.T.; Ren, Y.L. Power System Planning Method Considering Uncertainty Value and Entire Market Element Game under Market Background. Power Syst. Prot. Control 2022, 50, 11–23. [Google Scholar]
- Chen, Z.; Lin, K.; Wang, B. Design of Demand Response Incentive Mechanism Considering Lowest Efficiency Loss Based on Stackelberg Equilibrium Analysis in Unilateral Liberalization Market. Power Syst. Technol. 2022, 46, 1790–1800. [Google Scholar]
- Hong, Q.; Meng, F.; Liu, J.; Bo, R. A Bilevel Game-Theoretic Decision-Making Framework for Strategic Retailers in Both Local and Wholesale Electricity Markets. Appl. Energy 2023, 330, 120311. [Google Scholar] [CrossRef]
- Luan, T.; Yang, Z.; Li, J.; Deng, Y.X.; Feng, S.H. Design of Electricity Market Mechanism Adapting to Cost Characteristics of Electrochemical Energy Storage. Autom. Electr. Power Syst. 2024, 48, 101–110. [Google Scholar]
- Zhong, H.; Wu, F.; Zhang, L.; Dong, X.W.; Xia, X.; Shu, D. Optimal Capacity Allocation of Pumping and Storage Power Station Based on Multi-time Scale Decision-making in Power Market. High Volt. Eng. 2023, 49, 4109–4119. [Google Scholar]
- Zhang, L.; Shi, Z.; Zhou, W.; Ma, J.; Chen, K.; Yang, D.W.; Wan, J. Capacity Optimization Configuration of Battery, Thermal and Hydrogen Hybrid Energy Storage System Considering Battery Life. Power Syst. Technol. 2025, 49, 998–1006. [Google Scholar]
- Yu, Y.; Yan, W.; Zhong, Y.; Ge, X.H. Joint Optimization of Return on Investment and Carbon Efficiency for Green Cellular Networks with Hybrid Energy Supply. J. Chongqing Univ. Posts Telecommun. Nat. Sci. Ed. 2024, 36, 106–117. [Google Scholar]
- Sadat, S.A.; Mittal, K.; Pearce, J.M. Using Investments in Solar Photovoltaics as Inflation Hedges. Energies 2025, 18, 890. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, H. An Agent-Based Hierarchical Bargaining Framework for Power Management of Multiple Cooperative Microgrids. IEEE Trans. Smart Grid 2019, 10, 514–522. [Google Scholar] [CrossRef]
- Zhu, R.; Ren, Y.; Meng, Q.; He, J.W.; Pan, Y.; He, B. Electricity-Heat-Gas Cooperative Optimal Operation Strategy of Integrated Energy System Based on Cooperative Game. Acta Energ. Solaris Sin. 2022, 43, 20. [Google Scholar]
- Chen, J.; Hu, Z.; Chen, Y.; Chen, J.B.; Chen, W.N.; Gao, M.X.; Lin, M.R.; Du, Y.X. Thermoelectric Optimization of Integrated Energy System Considering Ladder-Type Carbon Trading Mechanism and Electric Hydrogen Production. Electr. Power Autom. Equip. 2021, 41, 48–55. [Google Scholar]
- Mao, K. Non Cooperative Games of Three Oligarch Firms on Output. J. Sci. Teach. Coll. Univ. 2024, 44, 16–20. [Google Scholar]
- Wu, L.; Jing, Z.; Wu, Q.; Deng, S. Equilibrium Strategies for Integrated Energy Systems Based on Stackelberg Game Model. Autom. Electr. Power Syst. 2018, 42, 142–150, 207. [Google Scholar]
- Li, P.; Wu, D.; Li, Y.; Liu, H.T.; Wang, N.; Zhou, X.C. Optimal Dispatch of Multimicrogrids Integrated Energy System Based on Integrated Demand Response and Stackelberg Game. Proc. CSEE 2021, 41, 1307–1321. [Google Scholar]
- Shuai, Z.; Wei, P.; Tengfei, M. Noncooperative Game Model of Prosumer P2P Electricity Trading Considering Markov Decision. Autom. Electr. Power Syst. 2023, 47, 18–27. [Google Scholar]
- Wang, X.; Yan, L.; Liu, B.; Zhao, F.J.; Gao, B.F. Cooperative Operational Strategies of Photovoltaic, Energy Storage, Load and Power Grid Based on Cooperative and Non-Cooperative Game. Acta Energ. Solaris Sin. 2023, 44, 128–138. [Google Scholar]
- Cao, P.; Deng, C.; Zhang, X.; Zhang, Y.; Dong, Y. Real-Time Coordinated Optimal Scheduling Strategy for Thermal Power Units with Adaptive Time Division and Variable Objective. Power Syst. Technol. 2024, 1–12. [Google Scholar]
- Li, G.; Li, Q.; Liu, Y.; Liu, H.; Song, W.; Ding, R. A Cooperative Stackelberg Game Based Energy Management Considering Price Discrimination and Risk Assessment. Int. J. Electr. Power Energy Syst. 2022, 135, 107461. [Google Scholar] [CrossRef]




| Objective | 1 | 2 |
|---|---|---|
| Profit of WT | 11,388.67976 | 8710.521313 |
| Profit of TPP | 2749.394016 | 5188.411317 |
| Profit of PV | 3697.211194 | 3627.456385 |
| Total profit | 17,835.28497 | 17,526.38901 |
| Total electricity sale revenue | 21,094.87503 | 21,003.7032 |
| Total generation cost | 3259.590059 | 3477.314186 |
| Profit standard deviation | 3868.595844 | 2126.013175 |
| Wind power absorption rate | 0.927866965 | 0.840815262 |
| Photovoltaic absorption rate | 0.372000025 | 0.507971136 |
| Total renewable energy absorption rate | 0.741169176 | 0.729023648 |
| URR of WT | 12.6083658 | 10.61315561 |
| URR of TPP | 7.569878432 | 20.19290866 |
| URR of PV | 4.262690436 | 14.4884504 |
| Total URR | 24.44093467 | 45.29451467 |
| URR standard deviation | 3.431458139 | 3.934610277 |
| Standardized URR standard deviation | 0.140397992 | 0.086867258 |
| Price Corresponding to the Objective | 1 | 2 |
|---|---|---|
| Average sale price of WT | 0.581621283 | 0.501662503 |
| Average sale price of TPP | 0.616589138 | 1.221805977 |
| Average sale price of PV | 0.459579423 | 0.652547483 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, B.; Li, P.; Quan, Y. Research on Resource Utilization of Bi-Level Non-Cooperative Game Systems Based on Unit Resource Return. Energies 2025, 18, 2396. https://doi.org/10.3390/en18092396
Fu B, Li P, Quan Y. Research on Resource Utilization of Bi-Level Non-Cooperative Game Systems Based on Unit Resource Return. Energies. 2025; 18(9):2396. https://doi.org/10.3390/en18092396
Chicago/Turabian StyleFu, Bo, Peiwen Li, and Yi Quan. 2025. "Research on Resource Utilization of Bi-Level Non-Cooperative Game Systems Based on Unit Resource Return" Energies 18, no. 9: 2396. https://doi.org/10.3390/en18092396
APA StyleFu, B., Li, P., & Quan, Y. (2025). Research on Resource Utilization of Bi-Level Non-Cooperative Game Systems Based on Unit Resource Return. Energies, 18(9), 2396. https://doi.org/10.3390/en18092396






