A Computationally Efficient Learning-Based Control of a Three-Phase AC/DC Converter for DC Microgrids
Abstract
1. Introduction
- Superior control performance: Compared with some popular AC/DC converter control methods, such as PI control and MPC, the proposed algorithm provides superior dynamic and steady-state responses;
- Low computational burden: In comparison with the existing AI-based AC/DC converter controllers, the proposed method significantly reduces the computational burden in both offline neural network training and online implementation;
- Verifiable closed-loop control stability: Unlike nearly all of the other AI-based converter control algorithms that solely or mainly rely on the offline-trained neural network, the proposed algorithm offers closed-loop control stability that can be explicitly verified.
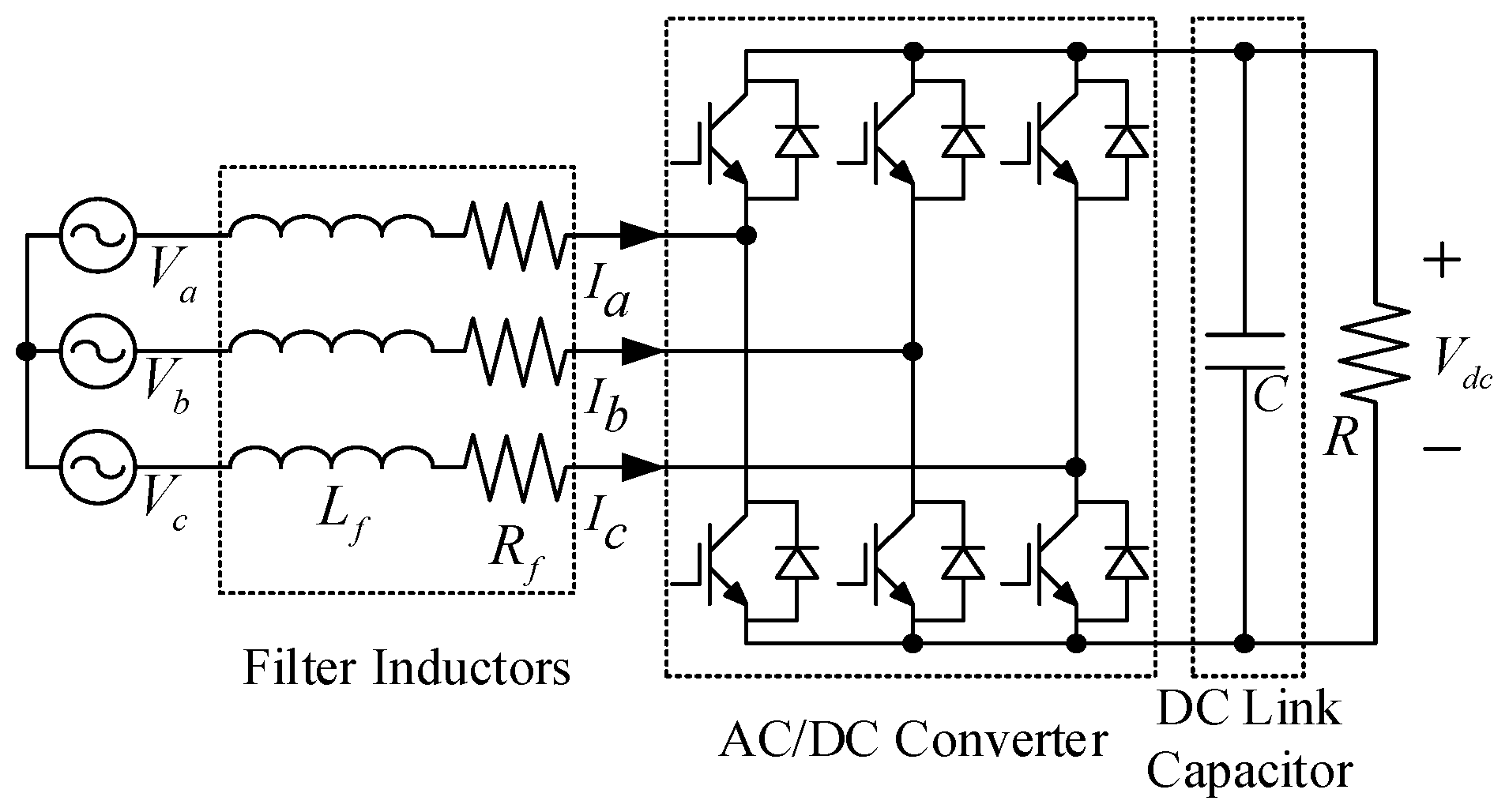
2. Mathematical Model
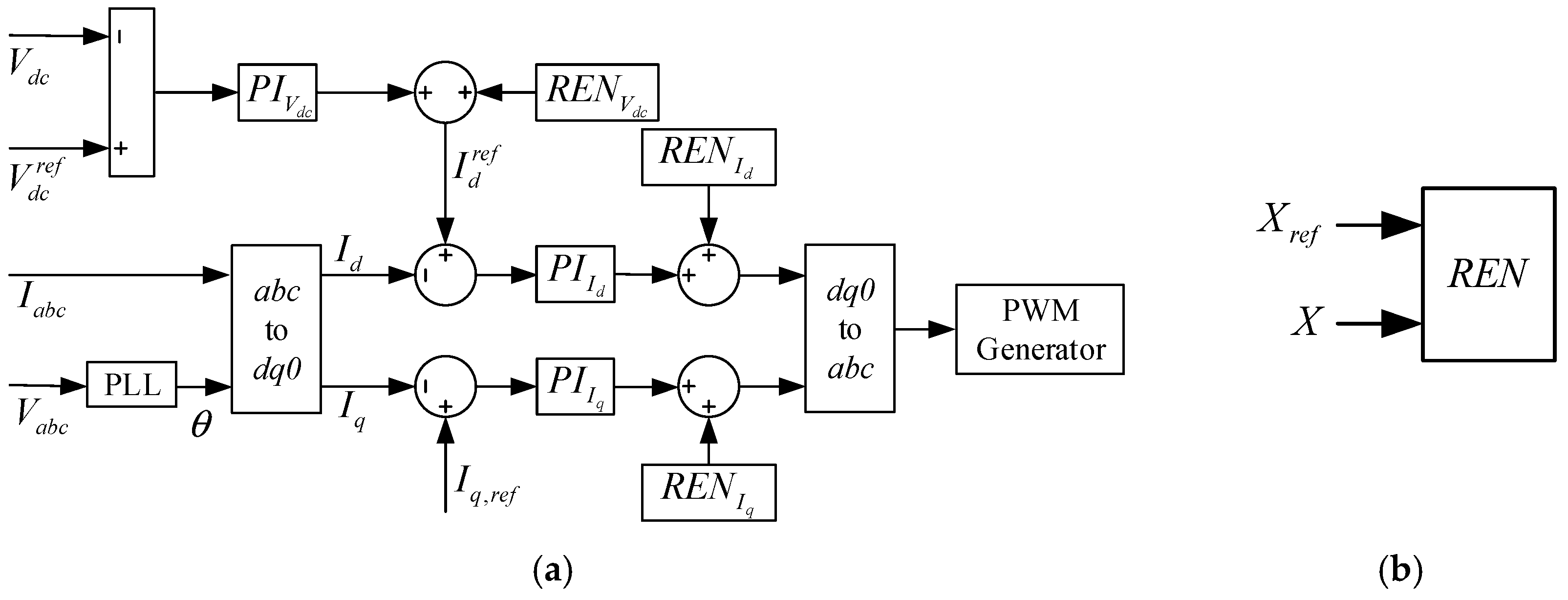
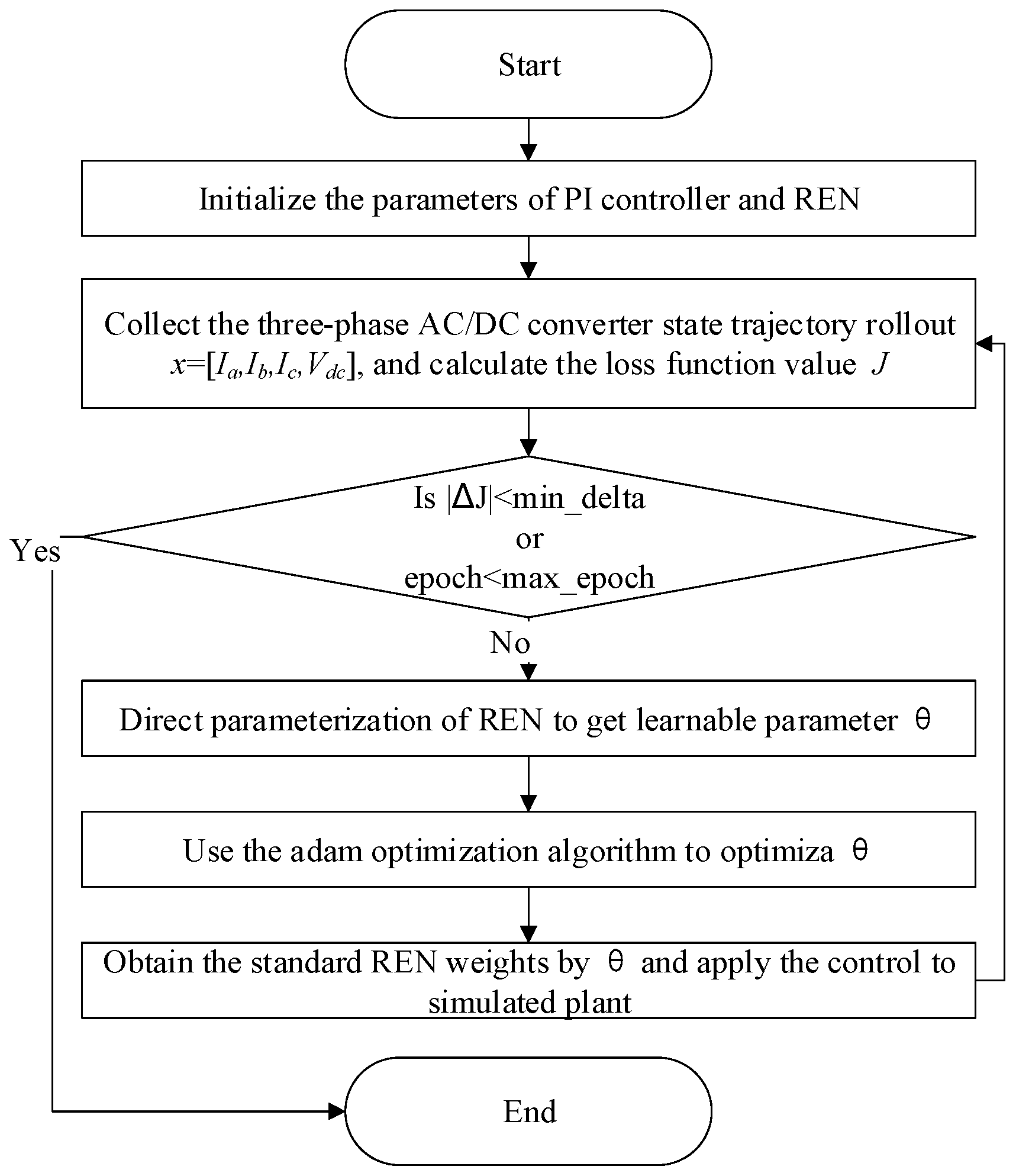
3. The Proposed REN Control Algorithm
3.1. Base Controller
3.2. Configuration of REN
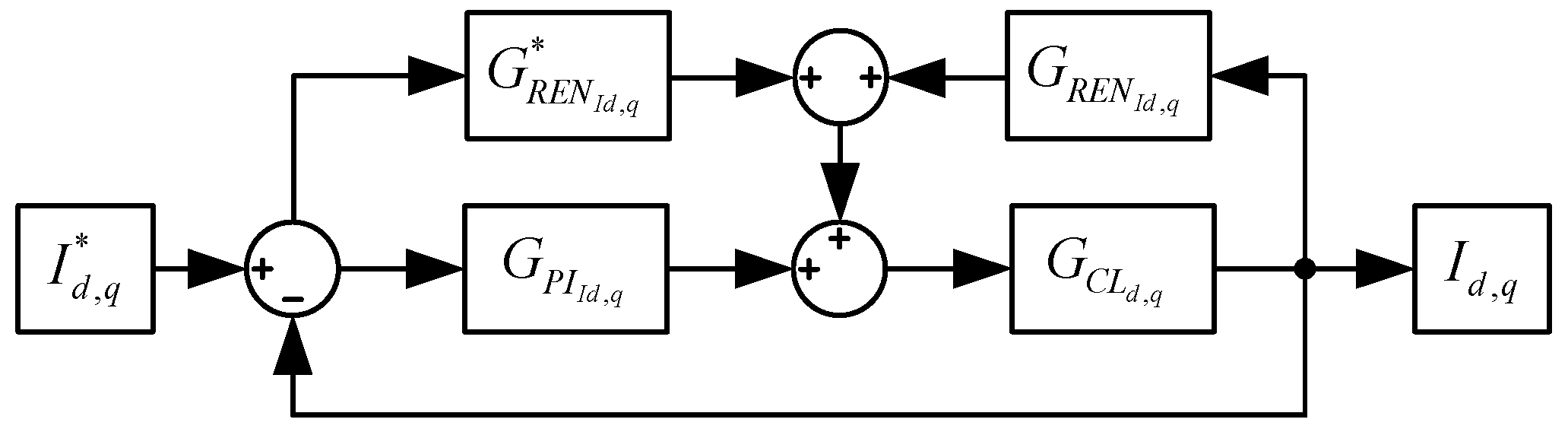
3.3. Stability Analysis of Current Loop
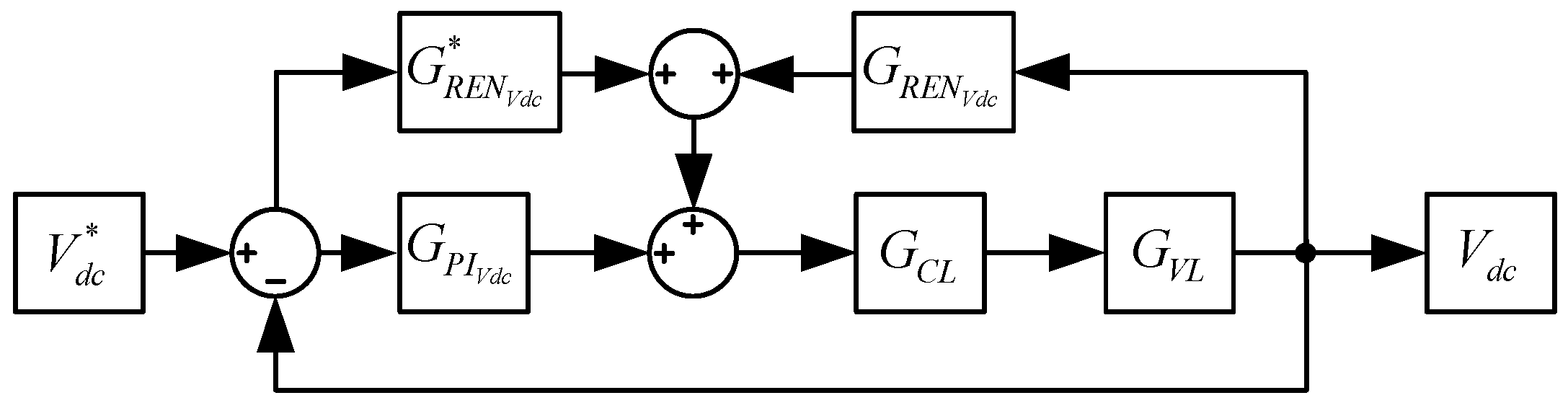
3.4. Stability Analysis of Voltage Loop
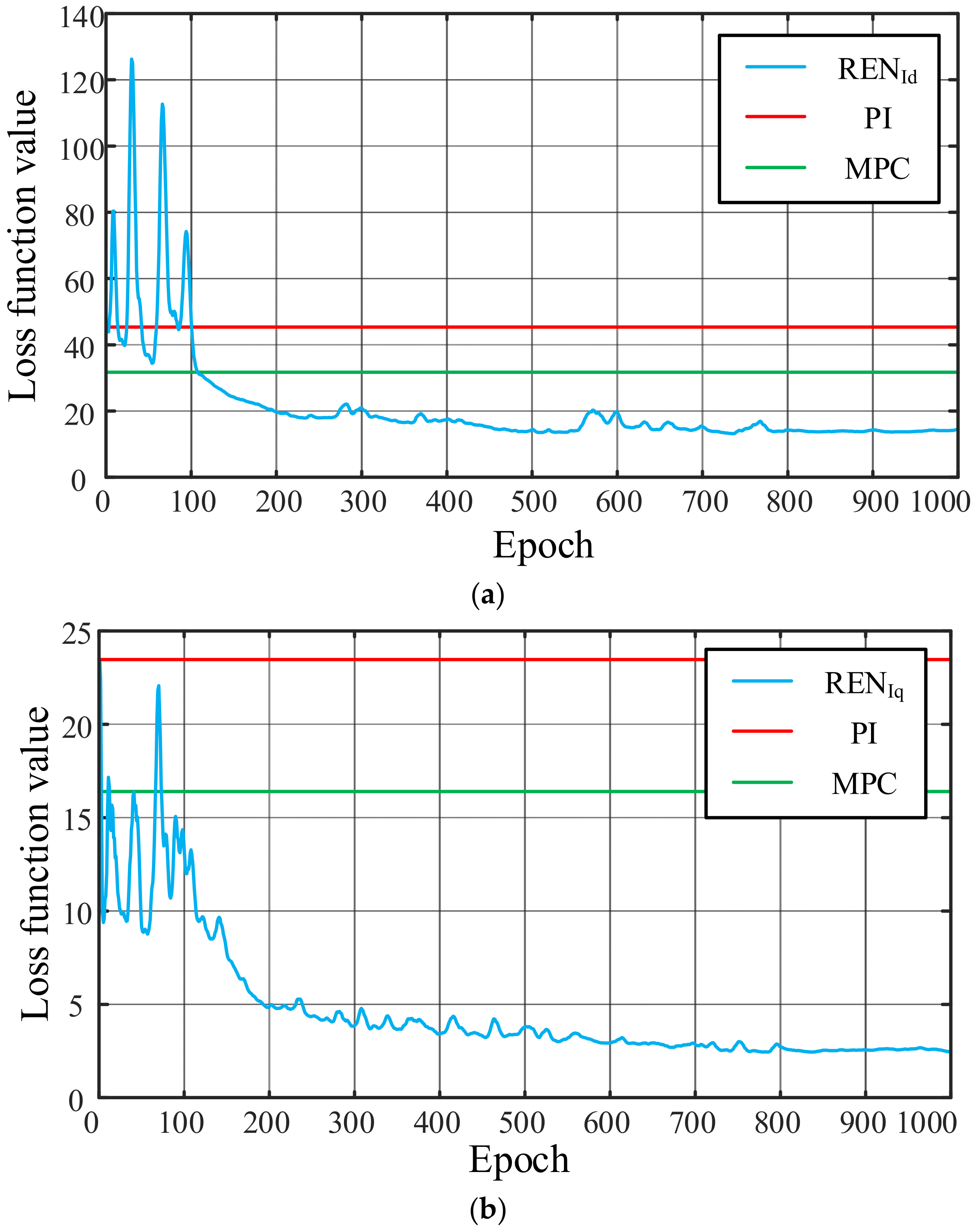
3.5. Policy Training Details
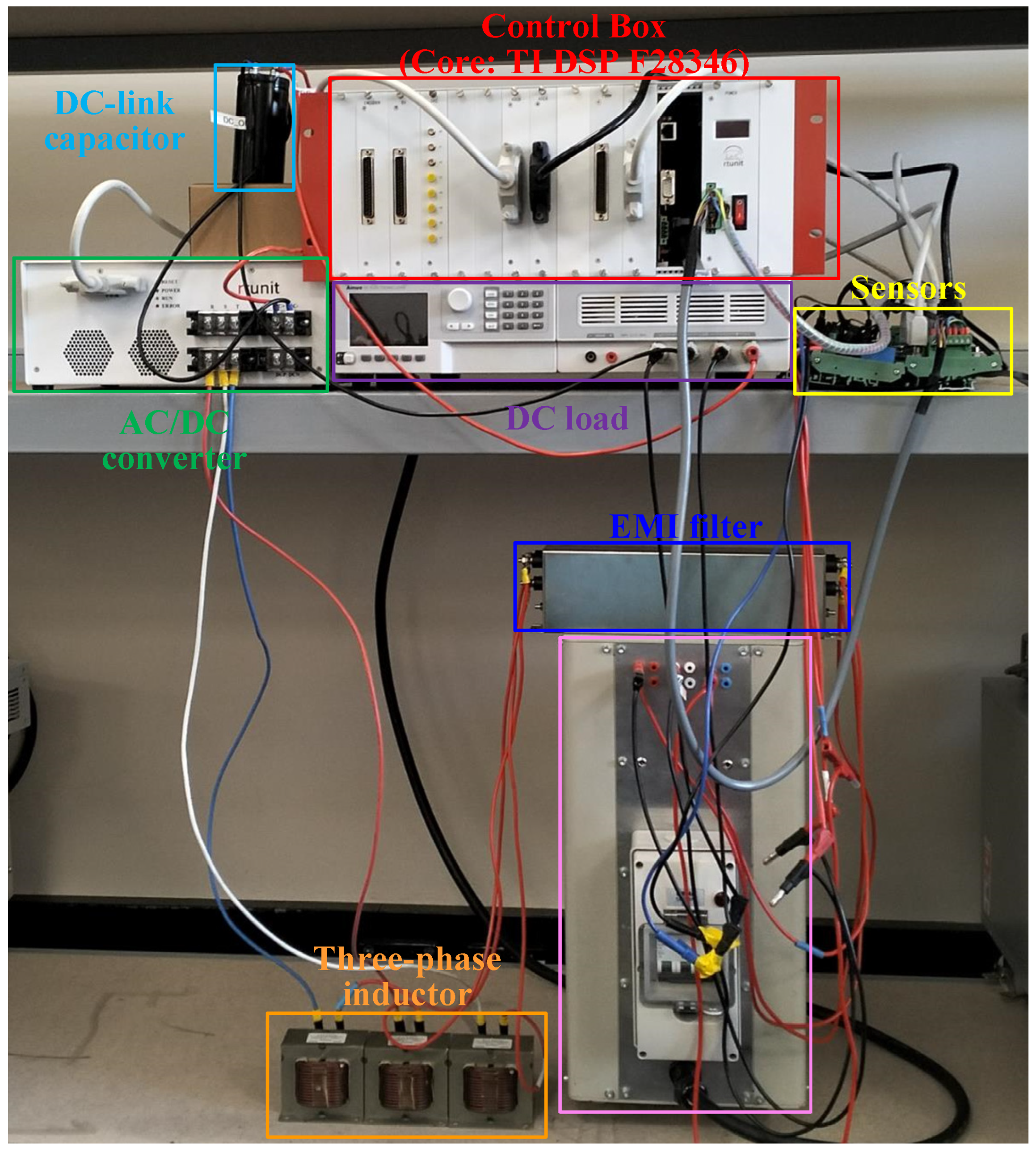
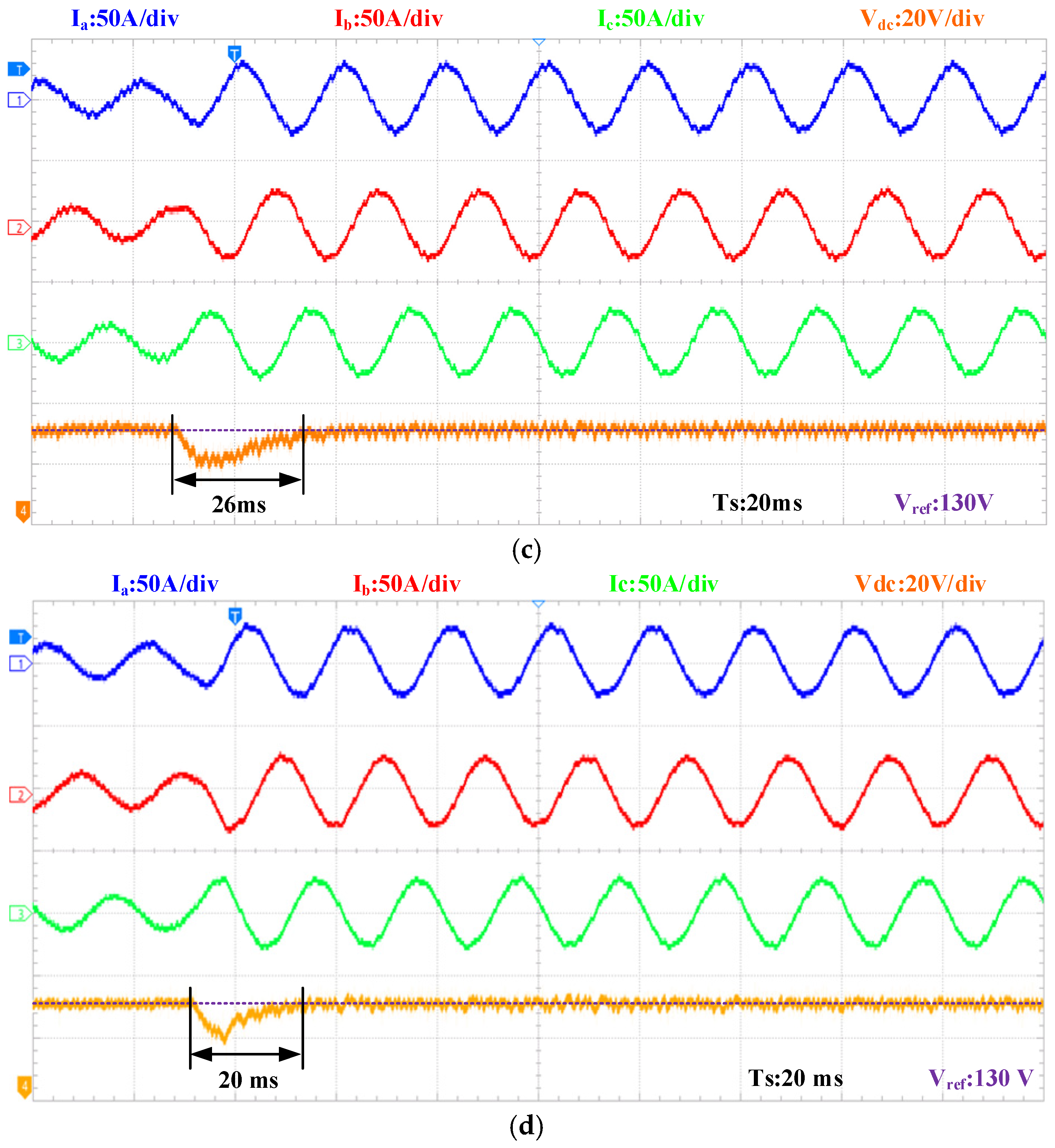
4. Experiment Results
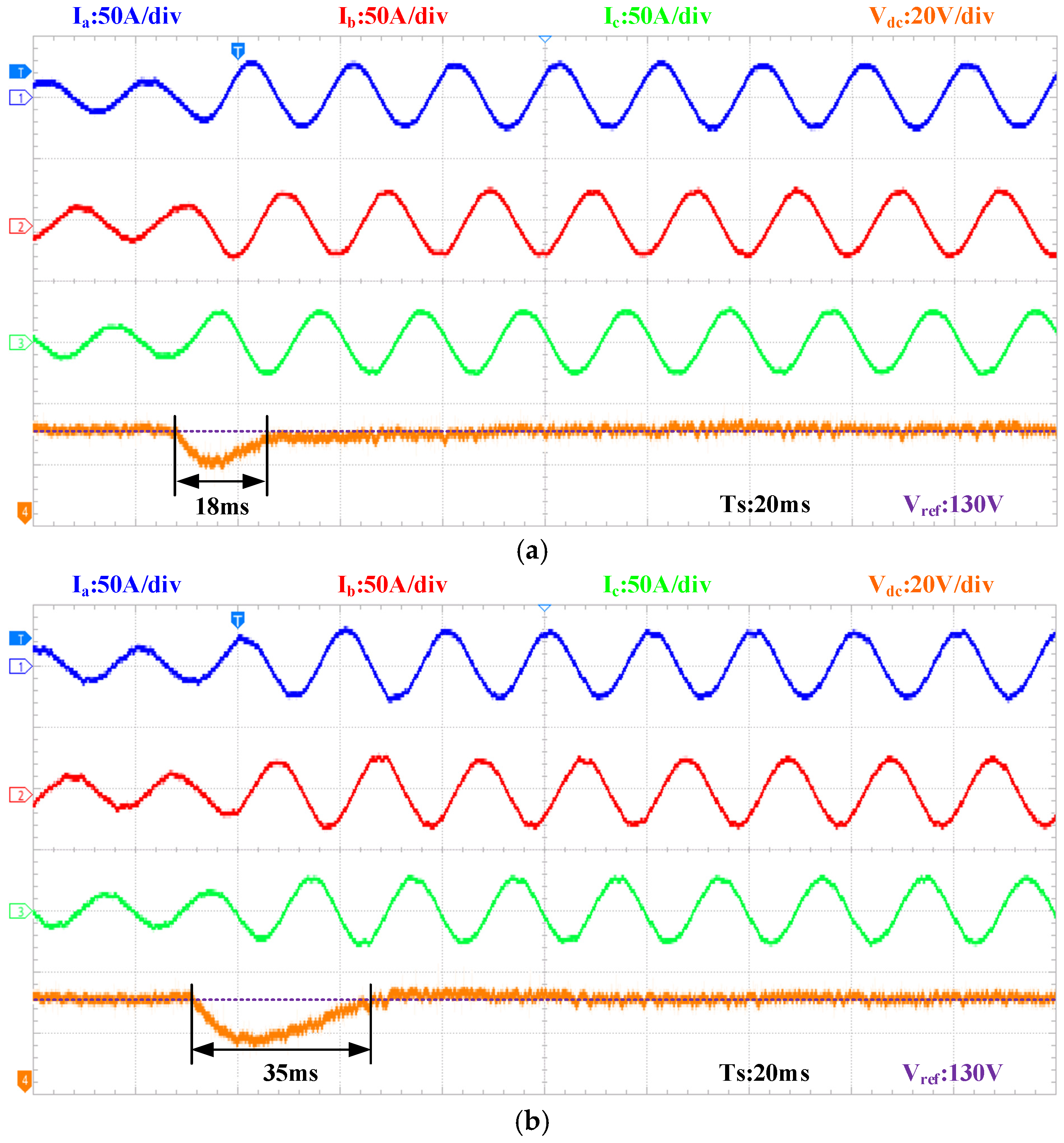
4.1. Transient Performance Under Step Load Charge
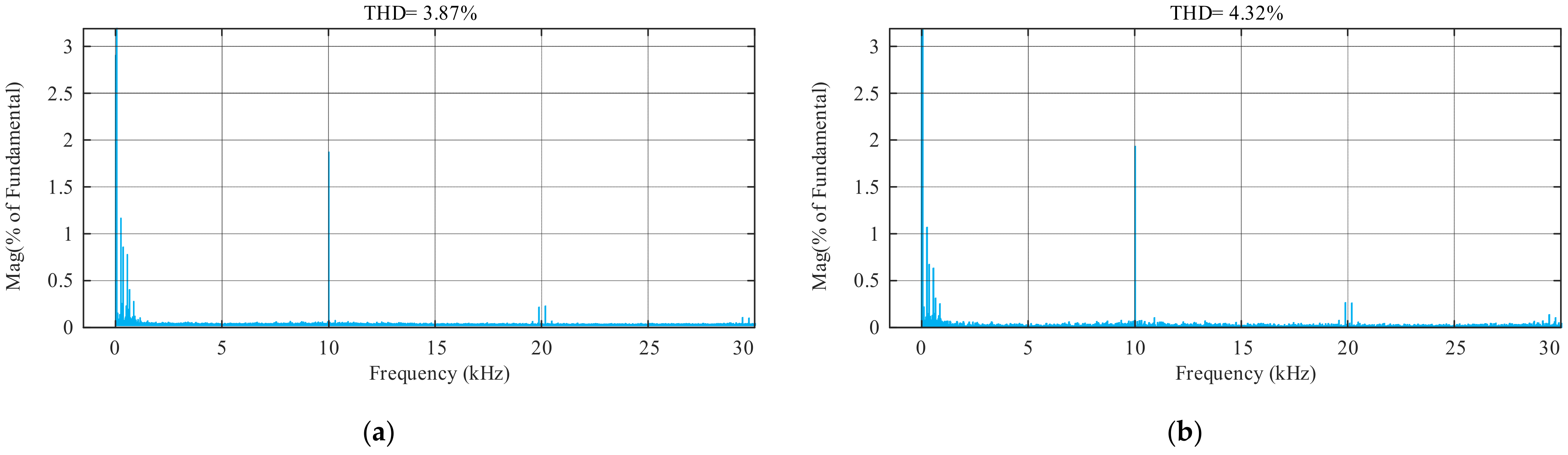
4.2. Steady-State Performance with Nominal System Parameters
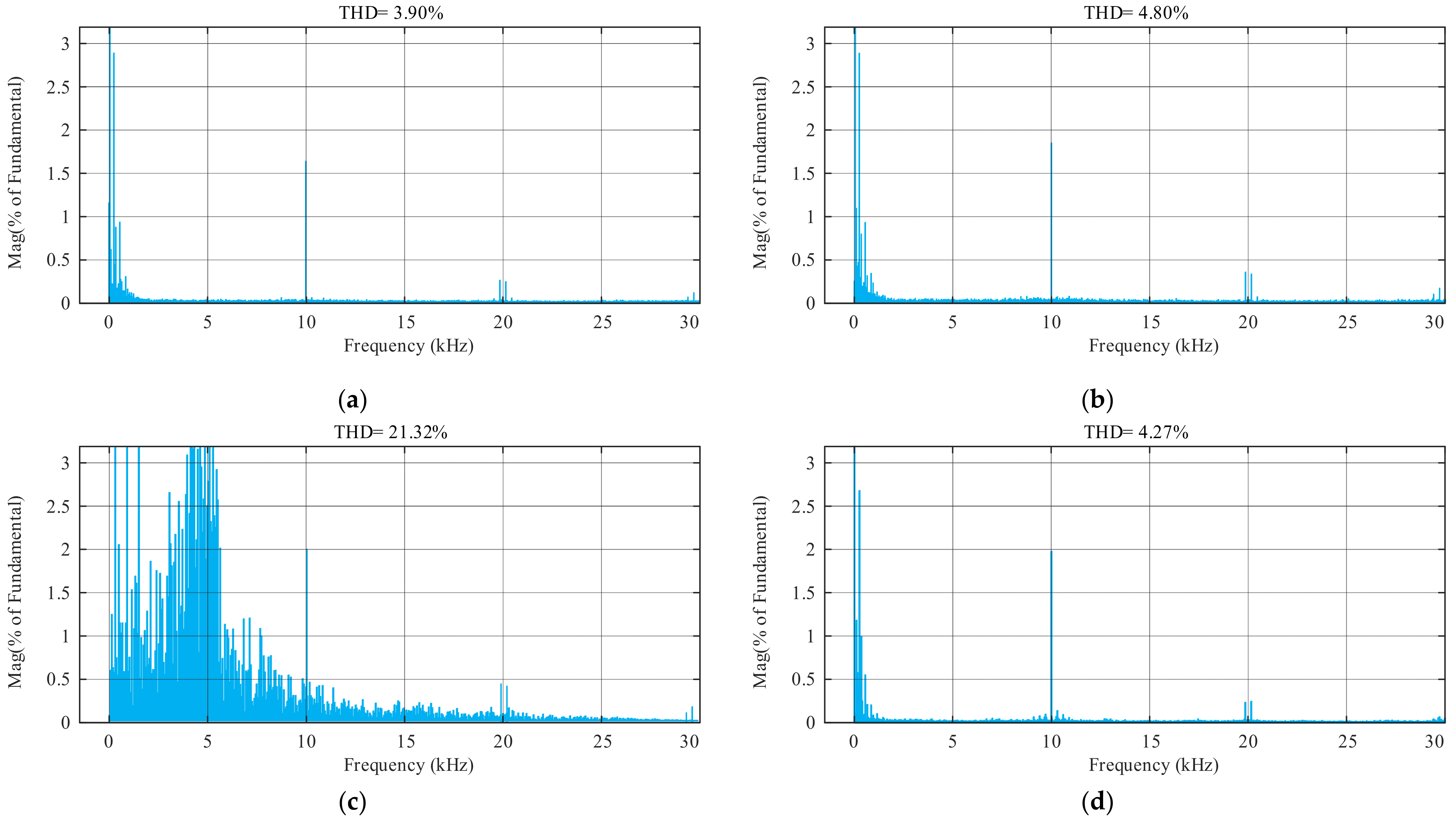
4.3. Control Performance Under Detuned Model Parameter
4.4. Computational Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Wang, J.; Liu, T.; Yang, T.; Xing, Y. Modified SVPWM-Controlled Three-Port Three-Phase AC–DC Converters with Reduced Power Conversion Stages for Wide Voltage Range Applications. IEEE Trans. Power Electron. 2018, 33, 6672–6686. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, C.; Zhang, G.; Song, J.; Zhang, C.; Duan, B. Disturbance Observer-Based Finite-Time Control for Three-Phase AC–DC Converter. IEEE Trans. Ind. Electron. 2022, 69, 5637–5647. [Google Scholar] [CrossRef]
- Tomida, K.; Natori, K.; Xu, J.; Shimosato, N.; Sato, Y. A New Control Method to Realize Wide Output Voltage Range for Three Phase AC/DC Converter Based on Matrix Converter. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022-ECCE Asia), Himeji, Japan, 15–19 May 2022. [Google Scholar]
- Ran, X.; Xu, B.; Liu, K.; Liu, Y. A Three-Vector Finite Control Set Model Predictive Control Variant with Low Power Fluctuations of AC/DC Converters. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 1338–1343. [Google Scholar] [CrossRef]
- Zargari, N.R.; Joos, G. Performance investigation of a current-controlled voltage-regulated PWM rectifier in rotating and stationary frames. IEEE Trans. Ind. Electron. 1995, 42, 396–401. [Google Scholar] [CrossRef]
- Blasko, V.; Kaura, V. A new mathematical model and control of a three-phase AC-DC voltage source converter. IEEE Trans. Power Electron. 1997, 12, 116–123. [Google Scholar] [CrossRef]
- Verdelho, P.; Marques, G.D. DC voltage control and stability analysis of PWM-voltage-type reversible rectifiers. IEEE Trans. Ind. Electron. 1998, 45, 263–273. [Google Scholar] [CrossRef]
- Shtessel, Y.; Baev, S.; Biglari, H. Unity Power Factor Control in Three-Phase AC/DC Boost Converter Using Sliding Modes. IEEE Trans. Ind. Electron. 2008, 55, 3874–3882. [Google Scholar] [CrossRef]
- Zhang, X.N.; Vilathgamuwa, D.M.; Foo, G.; Tseng, K.J.; Kandasamy, K.; Gupta, A.K.; Chandana, G. Cascaded sliding mode control for global stability of three phase AC/DC PWM rectifier with rapidly varying power electronic loads. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar]
- He, T.; Lu, D.D.-C.; Li, L.; Zhang, J.; Zheng, L.; Zhu, J. Model-Predictive Sliding-Mode Control for Three-Phase AC/DC Converters. IEEE Trans. Power Electron. 2018, 33, 8982–8993. [Google Scholar] [CrossRef]
- Jeeranantasin, N.; Nungam, S. Sliding Mode Control of Three-Phase AC/DC Converters using Exponential Rate Reaching Law. J. Syst. Eng. Electron. 2022, 33, 210–221. [Google Scholar] [CrossRef]
- Lu, J.; Savaghebi, M.; Ghias, A.M.Y.M.; Hou, X.; Guerrero, J.M. A Reduced-Order Generalized Proportional Integral Observer-Based Resonant Super-Twisting Sliding Mode Control for Grid-Connected Power Converters. IEEE Trans. Ind. Electron. 2021, 68, 5897–5908. [Google Scholar] [CrossRef]
- Kim, S.-K.; Choi, D.-K.; Lee, K.-B.; Lee, Y.I. Offset-Free Model Predictive Control for the Power Control of Three-Phase AC/DC Converters. IEEE Trans. Ind. Electron. 2015, 62, 7114–7126. [Google Scholar] [CrossRef]
- Falkowski, P.; Sikorski, A. Finite Control Set Model Predictive Control for Grid-Connected AC–DC Converters with LCL Filter. IEEE Trans. Ind. Electron. 2018, 65, 2844–2852. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q. Relationship between finite control set model predictive control and direct current control for three-phase voltage source converters. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014. [Google Scholar]
- Zerouali, S.; Allag, A.; Mimoune, S.M.; Ayad, M.Y.; Becherif, M.; Miraoui, A.; Khanniche, S. An Adaptive Optimal Linear Quadratic Regulator Applied to Three Phases PWM AC-DC Converter. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006. [Google Scholar]
- Kedjar, B.; Al-Haddad, K. DSP-Based Implementation of an LQR With Integral Action for a Three-Phase Three-Wire Shunt Active Power Filter. IEEE Trans. Ind. Electron. 2009, 56, 2821–2828. [Google Scholar] [CrossRef]
- Patarroyo-Montenegro, J.F.; Andrade, F.; Guerrero, J.M.; Vasquez, J.C. A Linear Quadratic Regulator with Optimal Reference Tracking for Three-Phase Inverter-Based Islanded Microgrids. IEEE Trans. Power Electron. 2021, 36, 7112–7122. [Google Scholar] [CrossRef]
- Rakhshani, E.; Cantarellas, A.M.; Remon, D.; Rodriguez, P.; Candela, I. Modeling and control of multi modular converters using optimal LQR controller with integral action. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013. [Google Scholar]
- Kanieski, J.M.; Cardoso, R.; Pinheiro, H.; Gründling, H.A. Kalman Filter-Based Control System for Power Quality Conditioning Devices. IEEE Trans. Ind. Electron. 2013, 60, 5214–5227. [Google Scholar] [CrossRef]
- Soliman, S.; Rafin, S.M.S.H.; Mohammad, O.A. Enhanced DC Voltage and Power Regulation Using Intelligent Data-Driven Control for AC/DC Converters in DC Microgrid Applications. IEEE Trans. Ind. Appl. 2024, 60, 8383–8392. [Google Scholar] [CrossRef]
- Davari, M.; Zhao, J.; Yang, C.; Gao, W.; Chai, T. Reinforcement Learning to Stabilize Singularly Perturbed DC-Side Dynamics of Grid-Connected Voltage-Source Converters in Modern AC–DC Grids Using Singular Perturbation Theory and Adaptive Dynamic Programming. IEEE Trans. Ind. Electron. 2025, 72, 2914–2926. [Google Scholar] [CrossRef]
- El Ghaoui, L.; Gu, F.; Travacca, B.; Askari, A.; Tsai, A. Implicit deep learning. SIAM J. Math. Data Sci. 2021, 3, 930–958. [Google Scholar] [CrossRef]
- Lohmiller, W.; Slotine, J.-J.E. On contraction analysis for non-linear systems. Automatica 1998, 34, 683–696. [Google Scholar] [CrossRef]


| Quantity | KP | KI |
|---|---|---|
| DC voltage controller | 0.0018 | 0.00005 |
| d-axis current controller | 6 | 60 |
| q-axis current controller | 10 | 4.2 |
| Quantity | Values |
|---|---|
| Input AC voltage | 30 V |
| Nominal DC-link voltage | 130 V |
| Grid frequency | 50 Hz |
| DC-link capacitance | 2.7 mF |
| Filter inductance | 5.2 mH |
| Load resistance | 20 Ω |
| Switching frequency | 10 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Feng, W.; Qie, T.; Liu, Y.; Fernando, T.; Iu, H.H.; Zhang, X. A Computationally Efficient Learning-Based Control of a Three-Phase AC/DC Converter for DC Microgrids. Energies 2025, 18, 2383. https://doi.org/10.3390/en18092383
Li R, Feng W, Qie T, Liu Y, Fernando T, Iu HH, Zhang X. A Computationally Efficient Learning-Based Control of a Three-Phase AC/DC Converter for DC Microgrids. Energies. 2025; 18(9):2383. https://doi.org/10.3390/en18092383
Chicago/Turabian StyleLi, Ran, Wendong Feng, Tianhao Qie, Yulin Liu, Tyrone Fernando, Herbert HoChing Iu, and Xinan Zhang. 2025. "A Computationally Efficient Learning-Based Control of a Three-Phase AC/DC Converter for DC Microgrids" Energies 18, no. 9: 2383. https://doi.org/10.3390/en18092383
APA StyleLi, R., Feng, W., Qie, T., Liu, Y., Fernando, T., Iu, H. H., & Zhang, X. (2025). A Computationally Efficient Learning-Based Control of a Three-Phase AC/DC Converter for DC Microgrids. Energies, 18(9), 2383. https://doi.org/10.3390/en18092383









