Comparing Fast Fourier Transform and Prony Method for Analysing Frequency Oscillation in Real Power System Interconnection
Abstract
:1. Introduction
2. Materials and Method
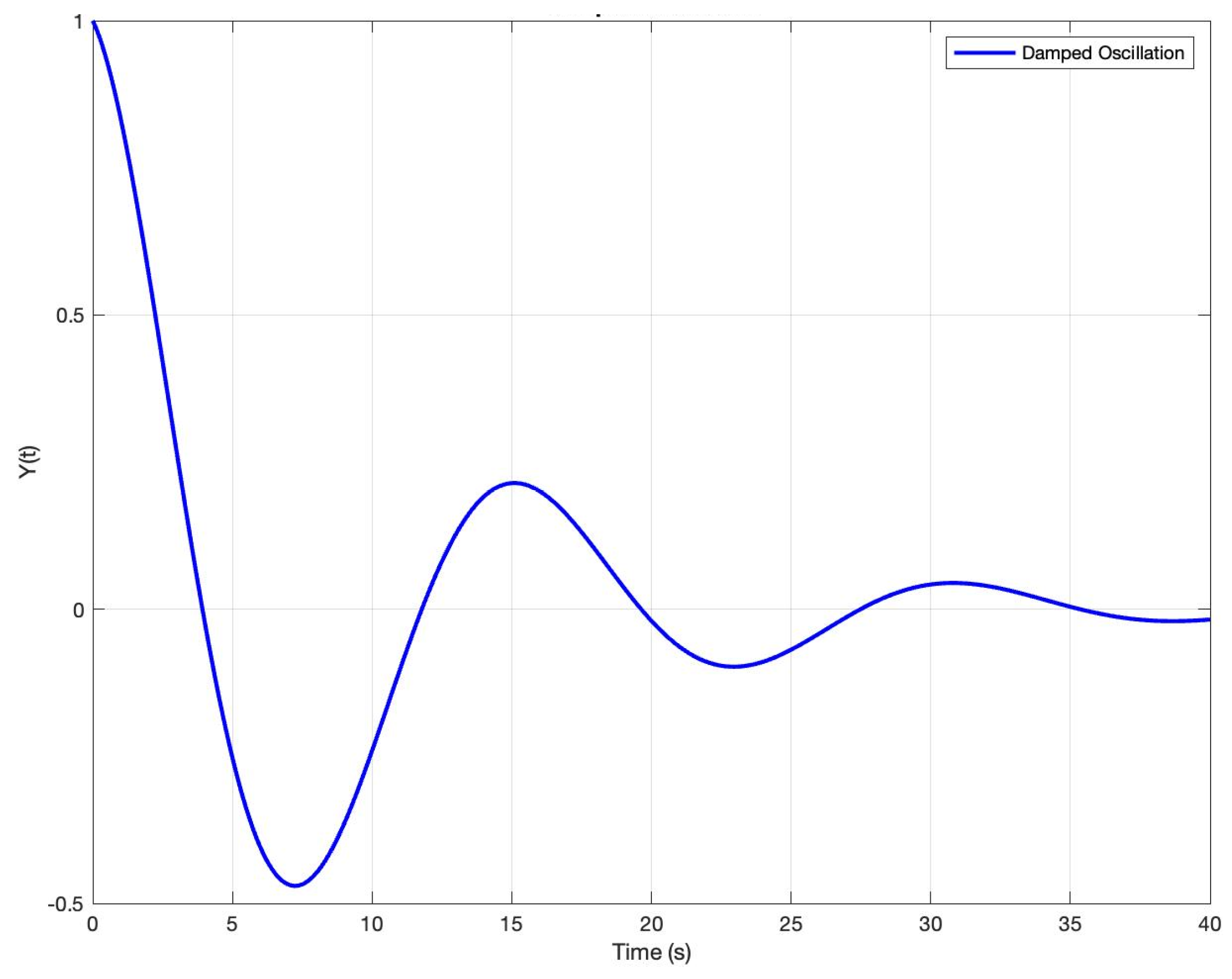
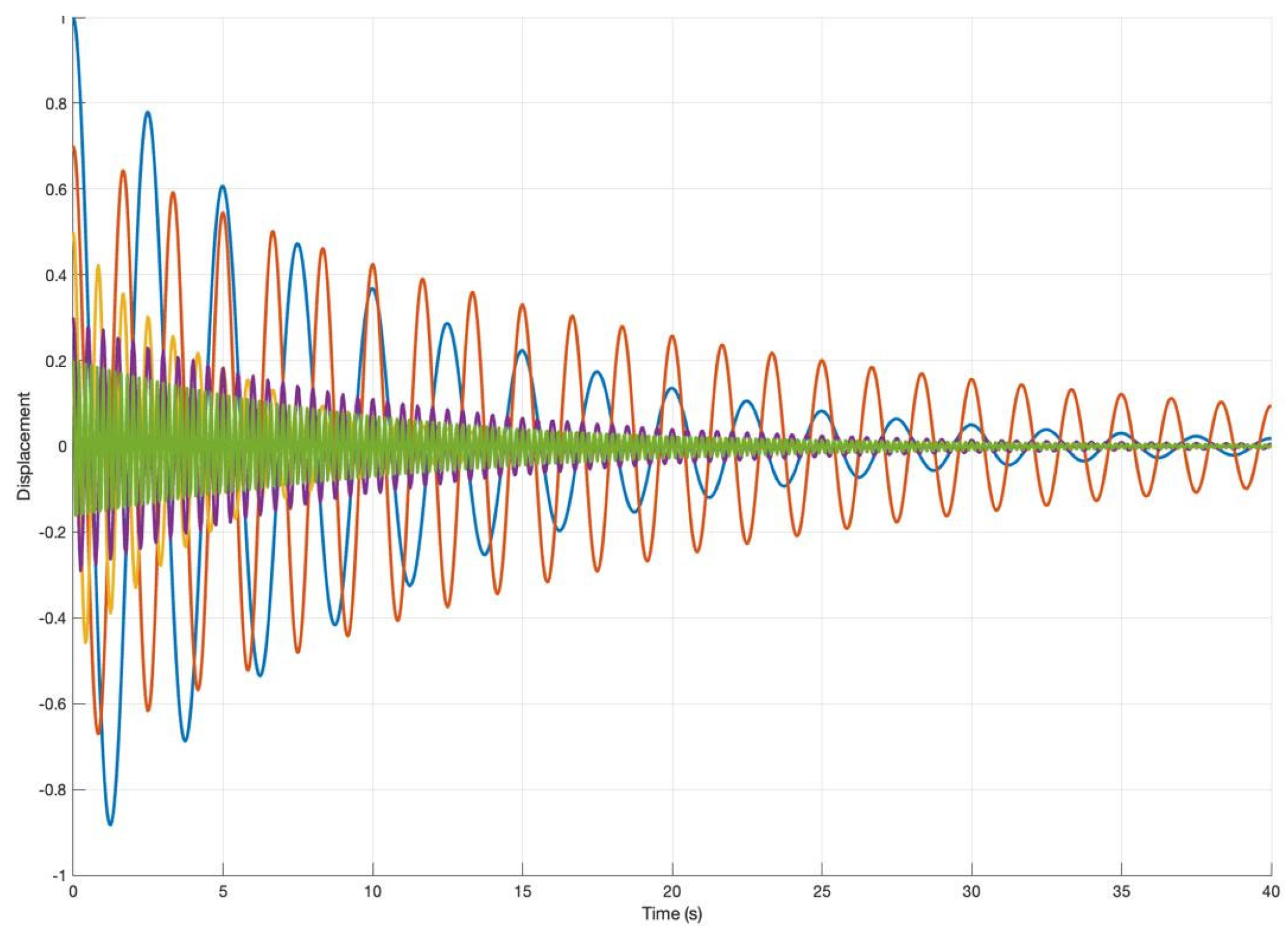
2.1. Small-Signal Stability
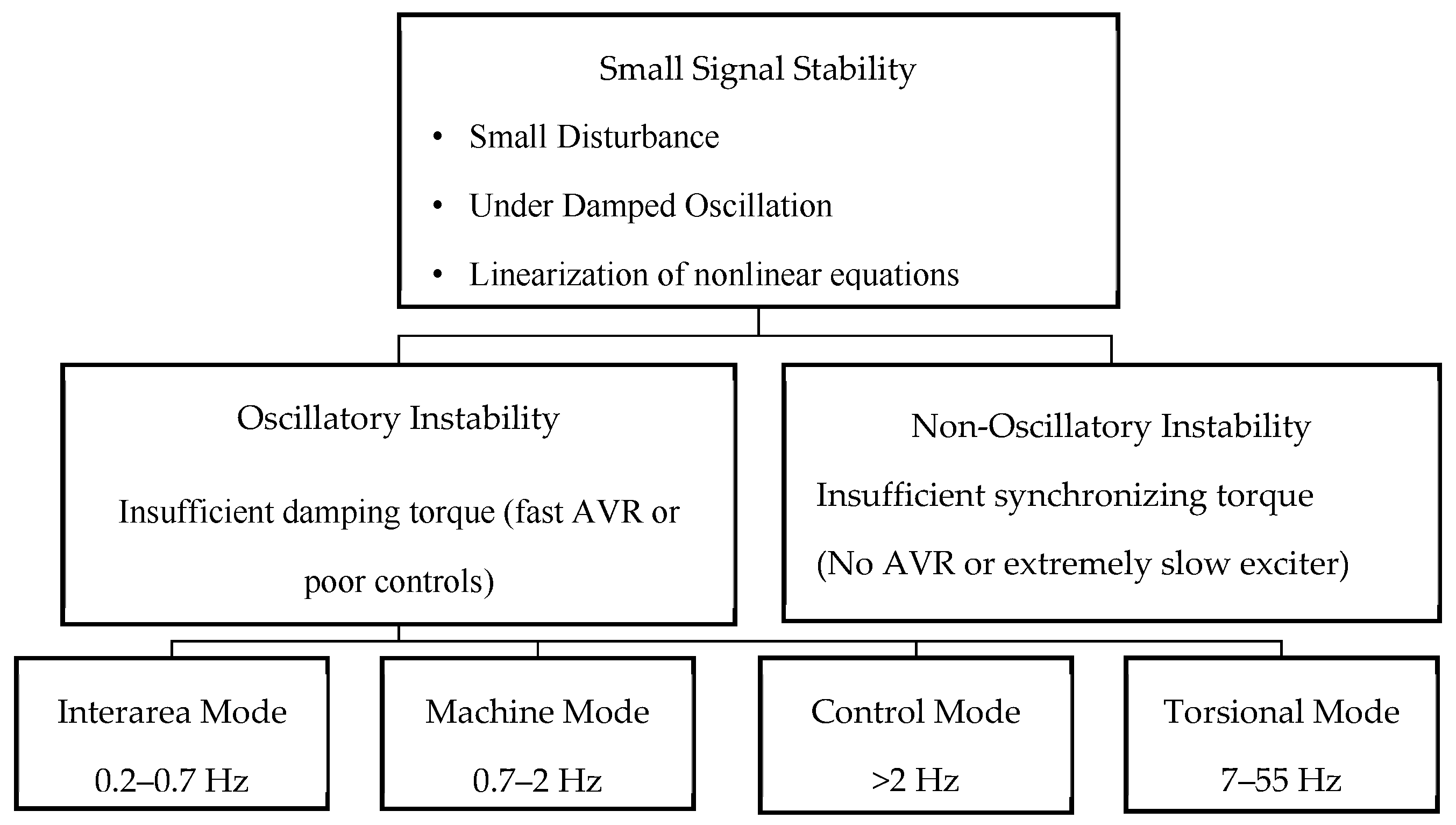
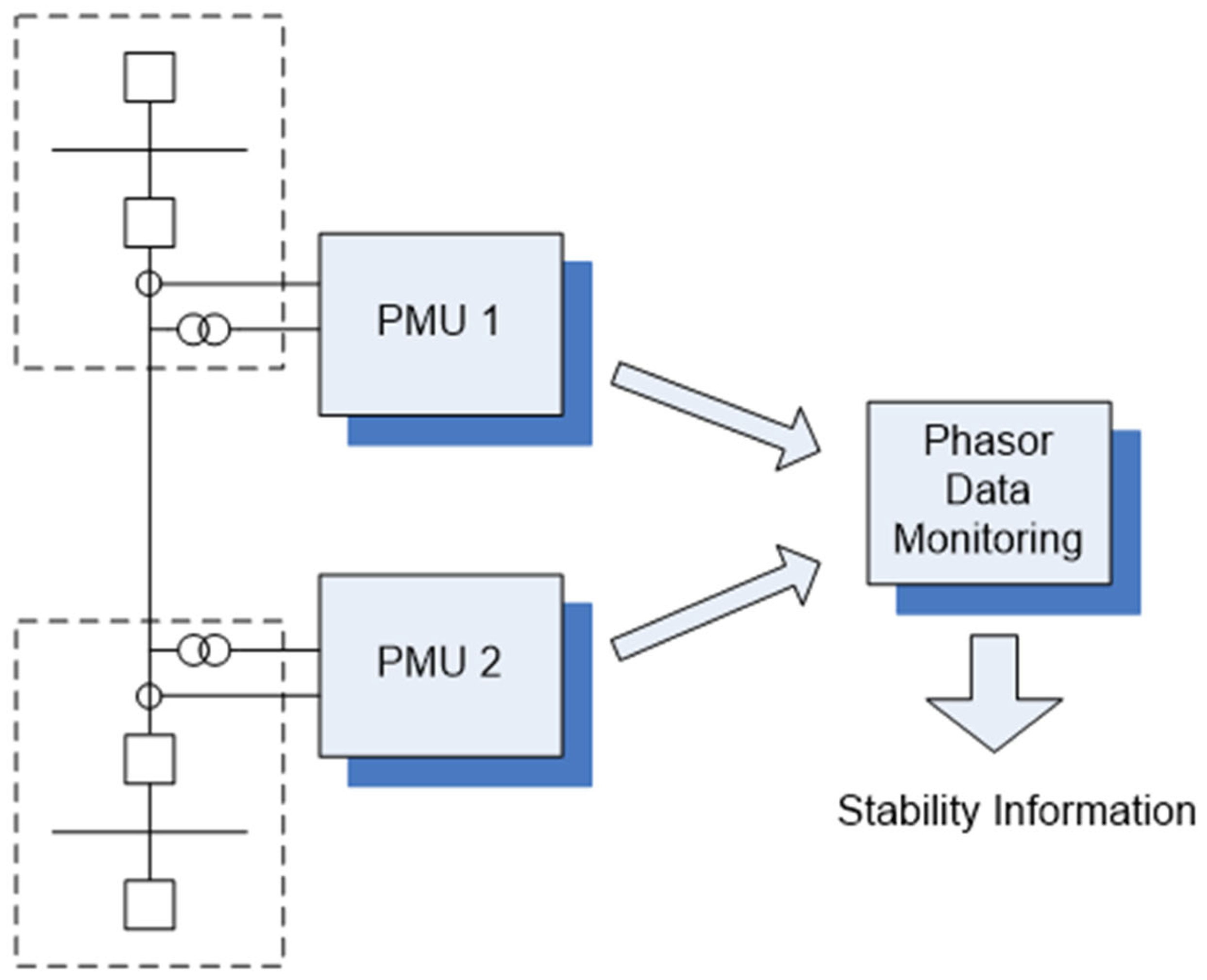
2.2. Phasor Measurement Unit
2.3. Fast Fourier Transform
- X(k) represents the frequency-domain components;
- x(n) is the time-domain signal;
- N is the total number of samples;
- k denotes the frequency index;
- represents the complex exponential basis function.
2.4. Prony Method
- represents the eigenvalues of the system;
- represents the damping components;
3. Result and Discussion
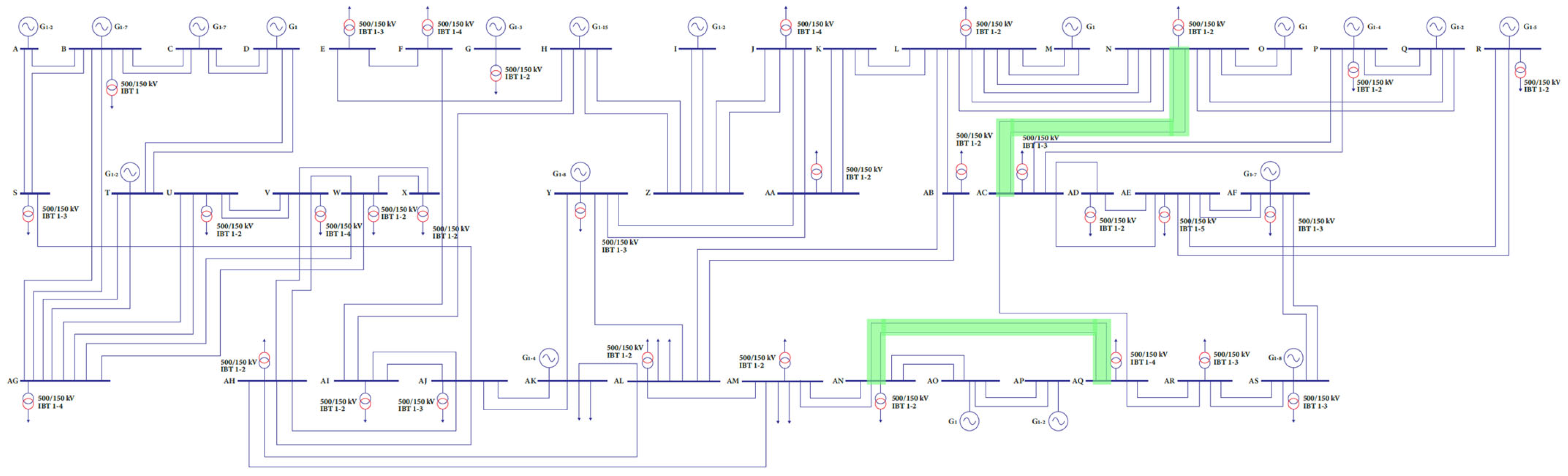
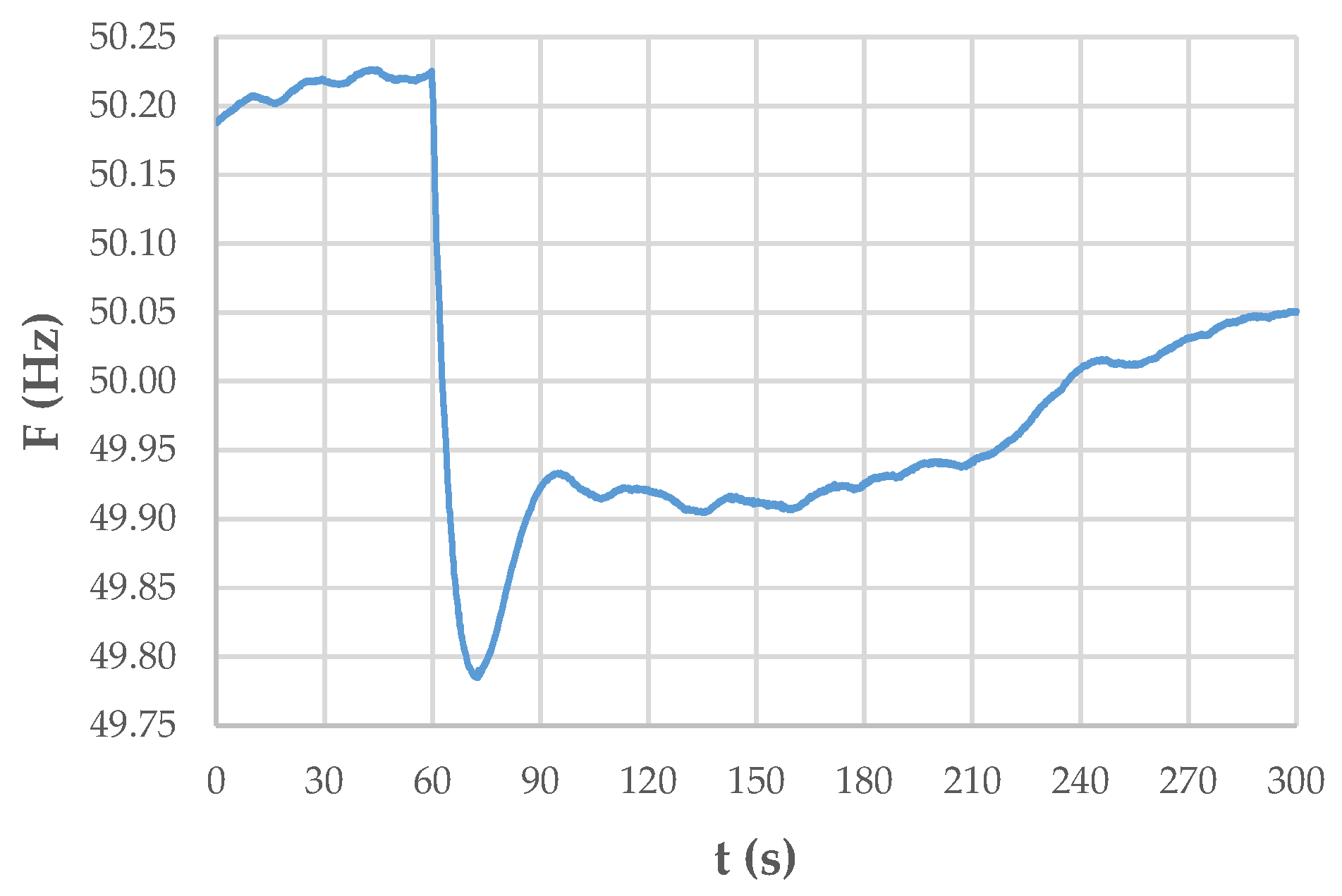
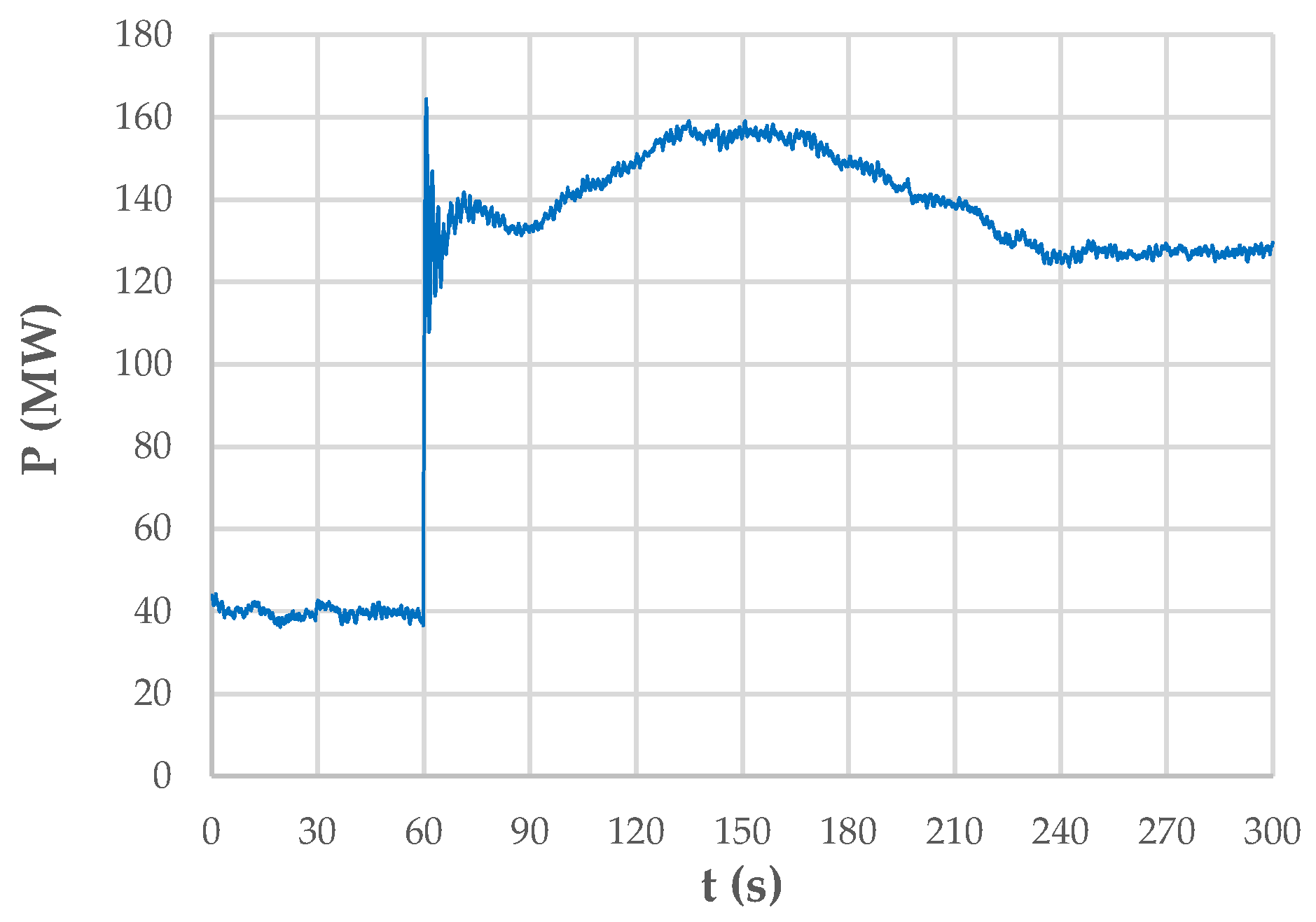
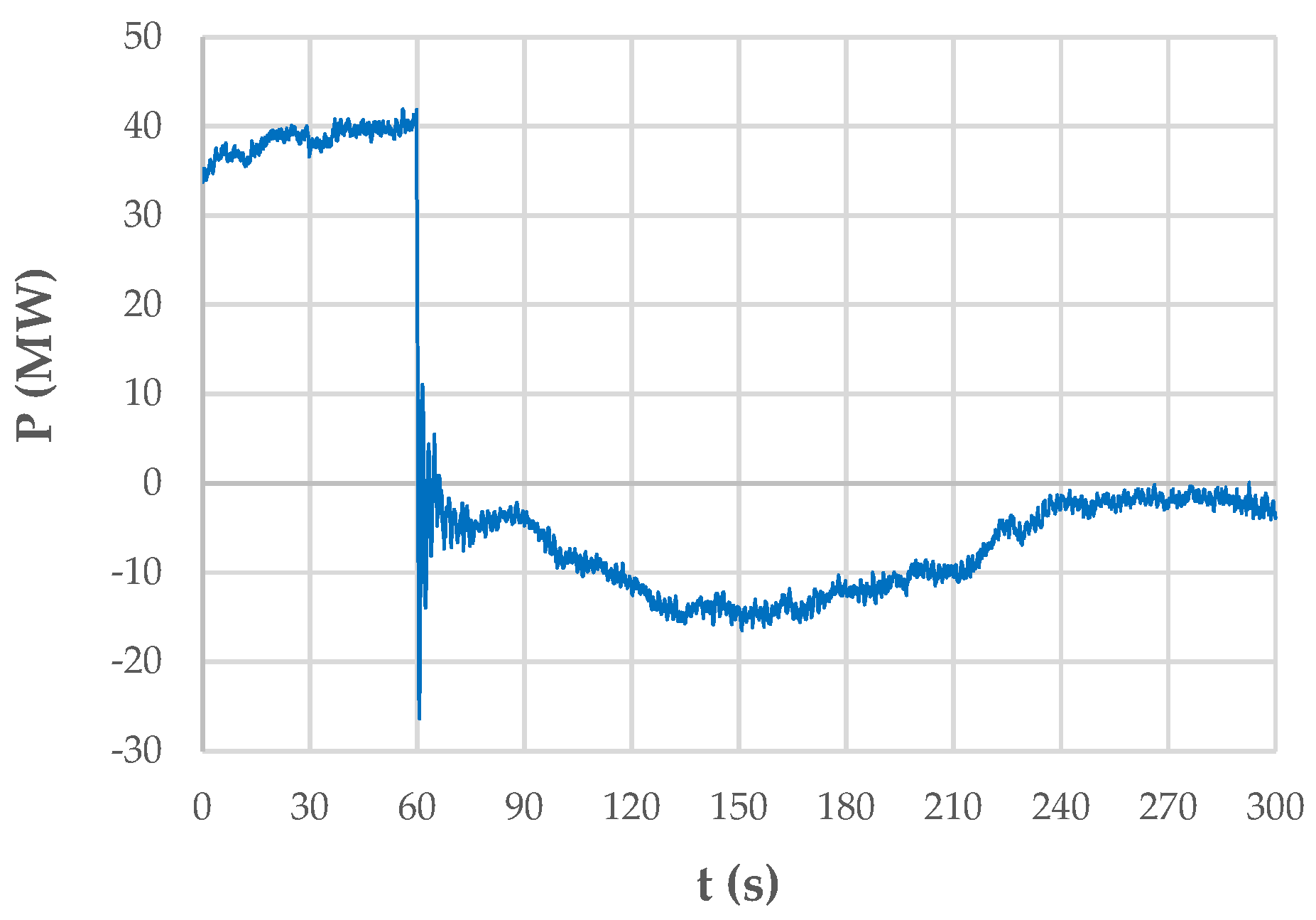
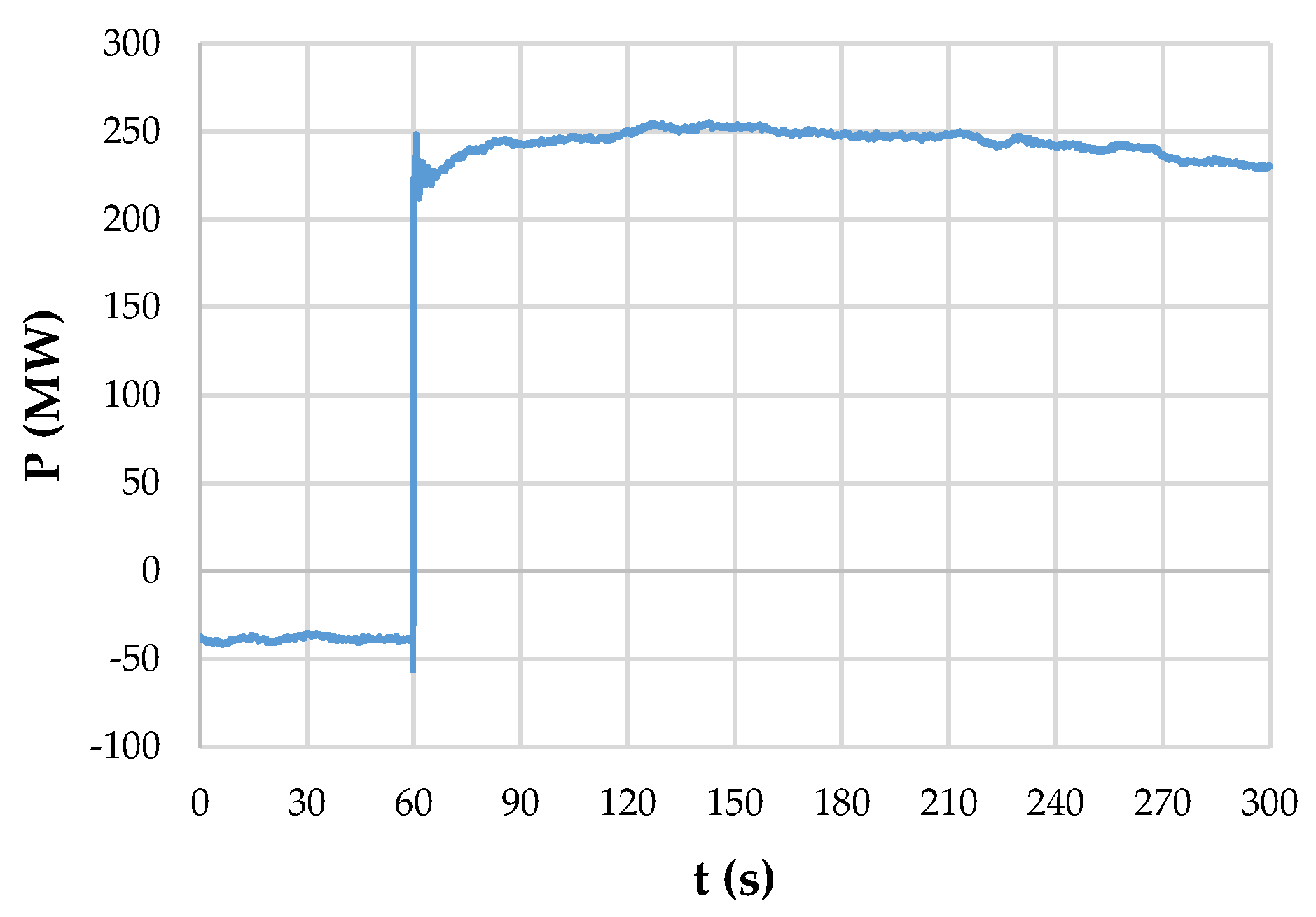
3.1. Case Study
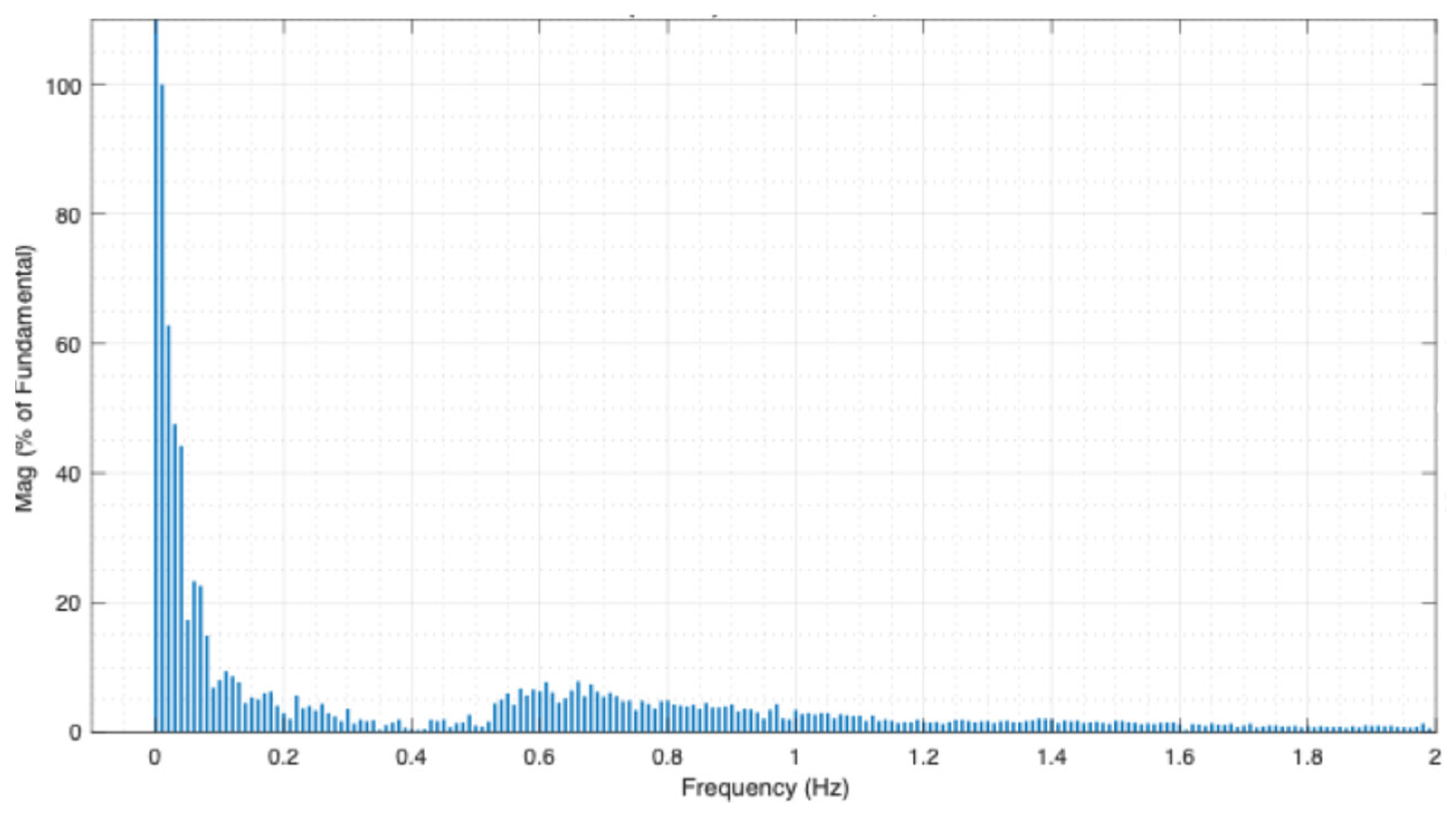
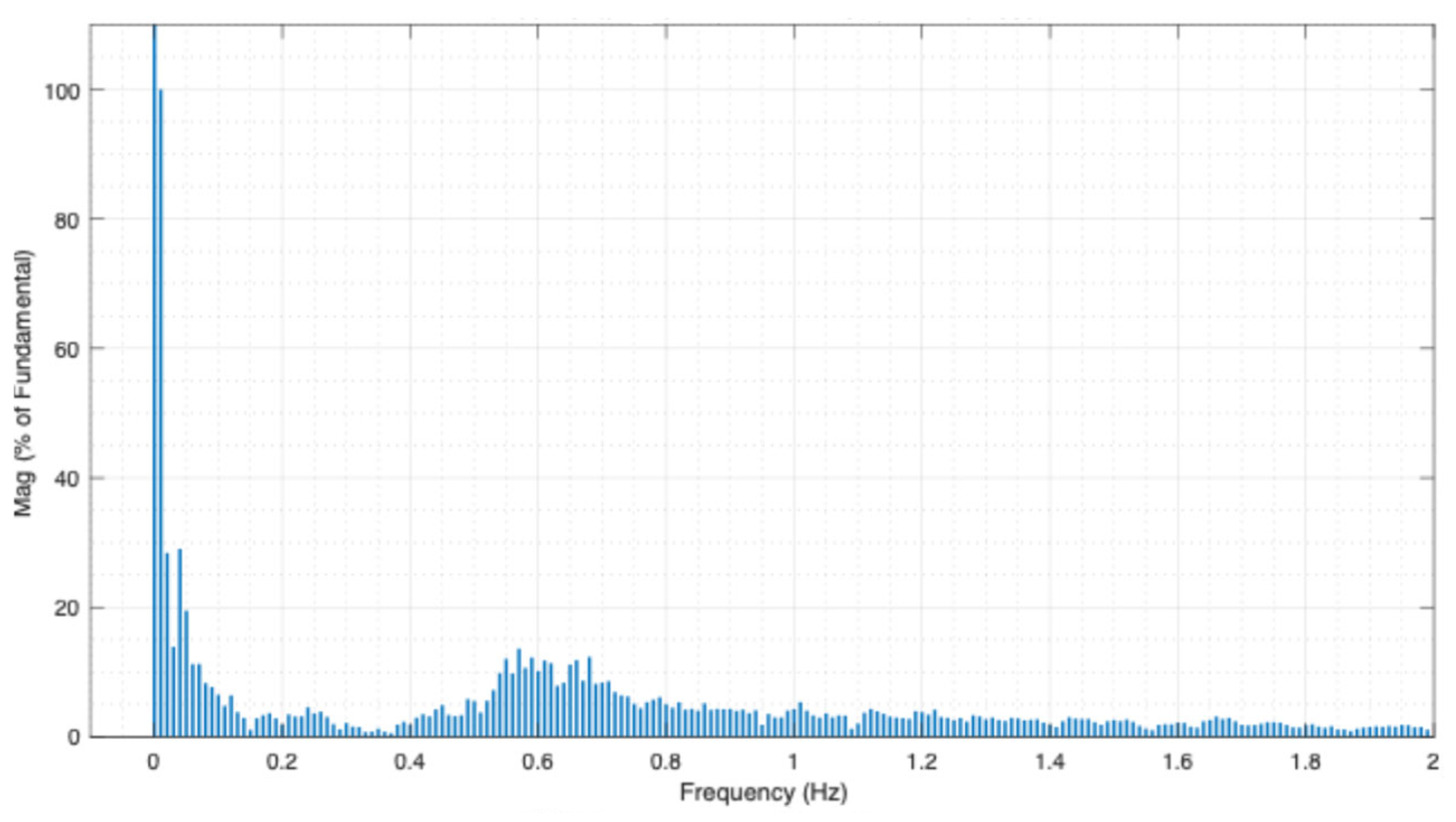
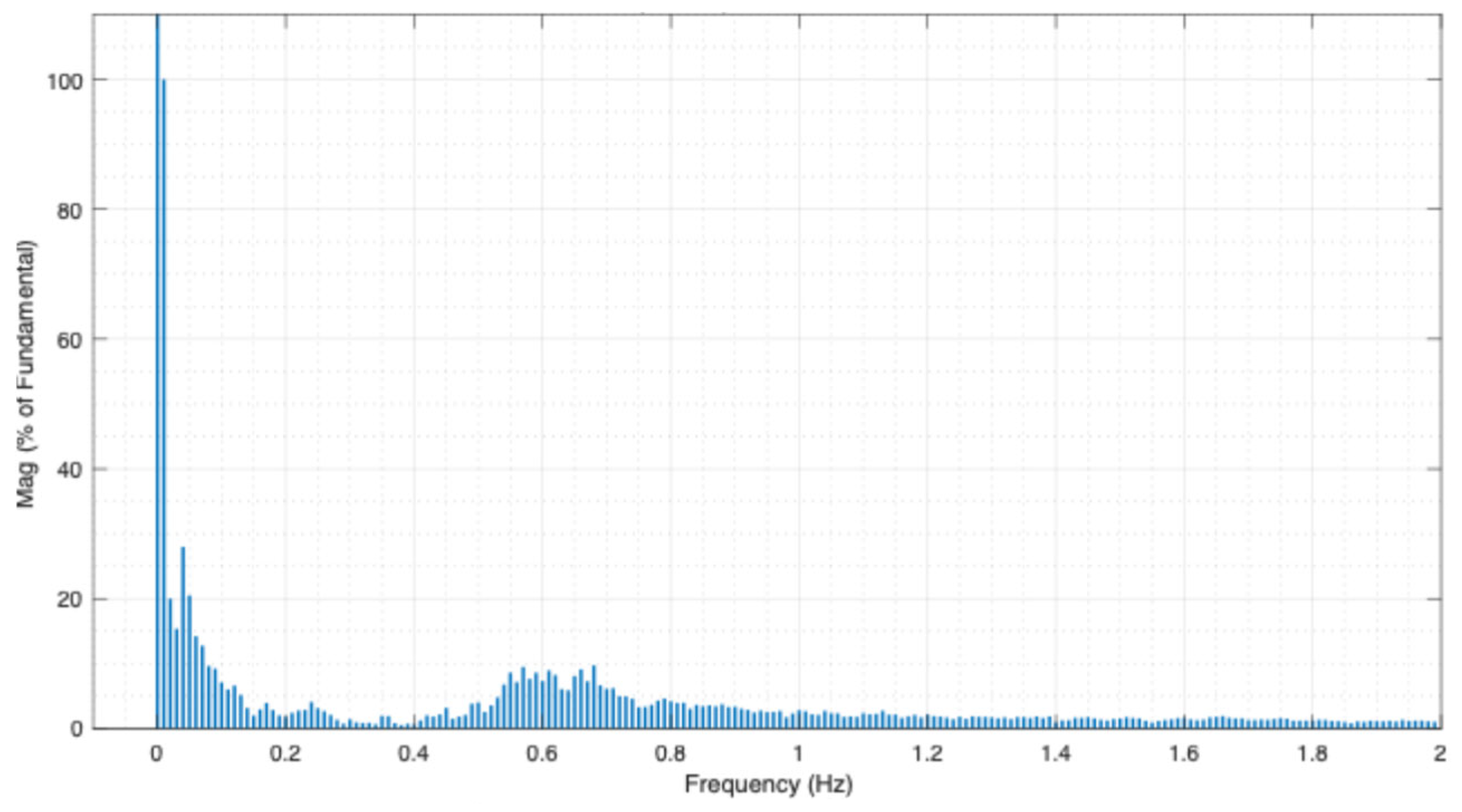
3.2. Low-Frequency Identification via FFT
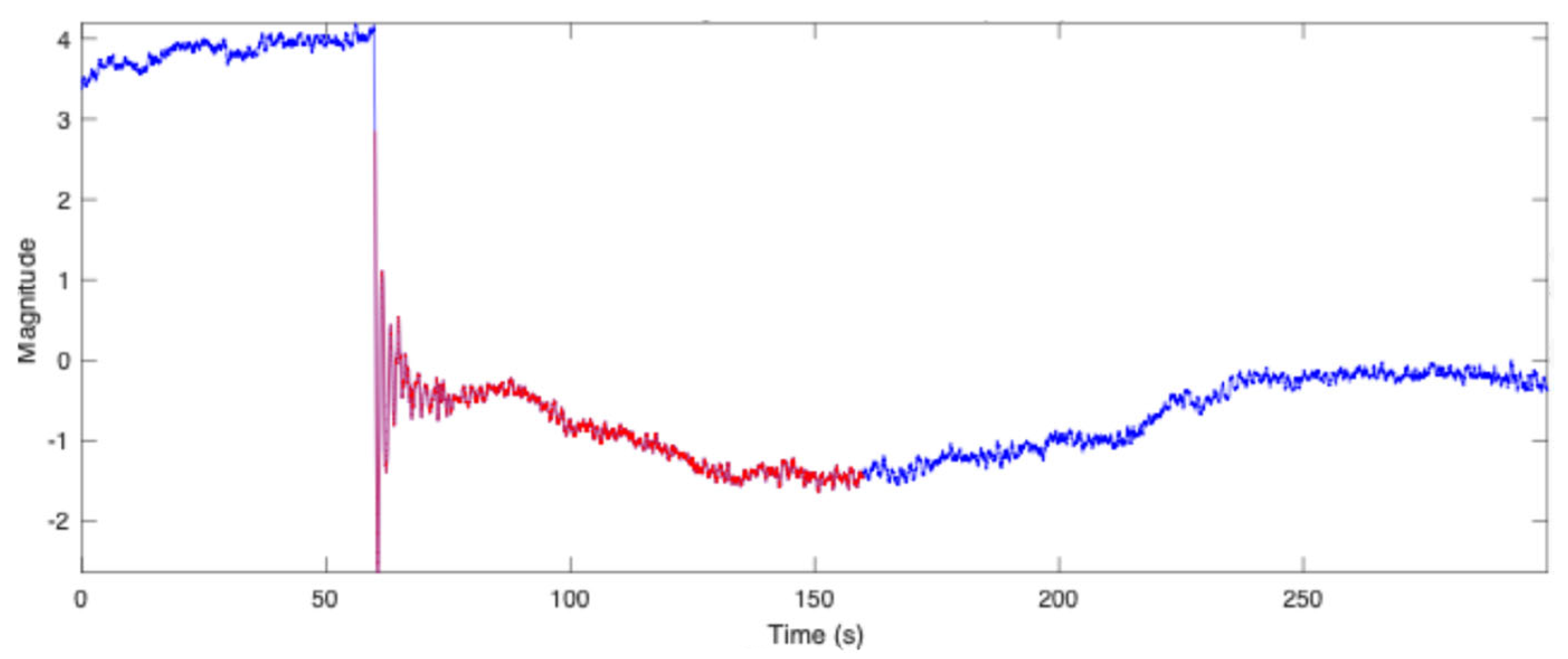
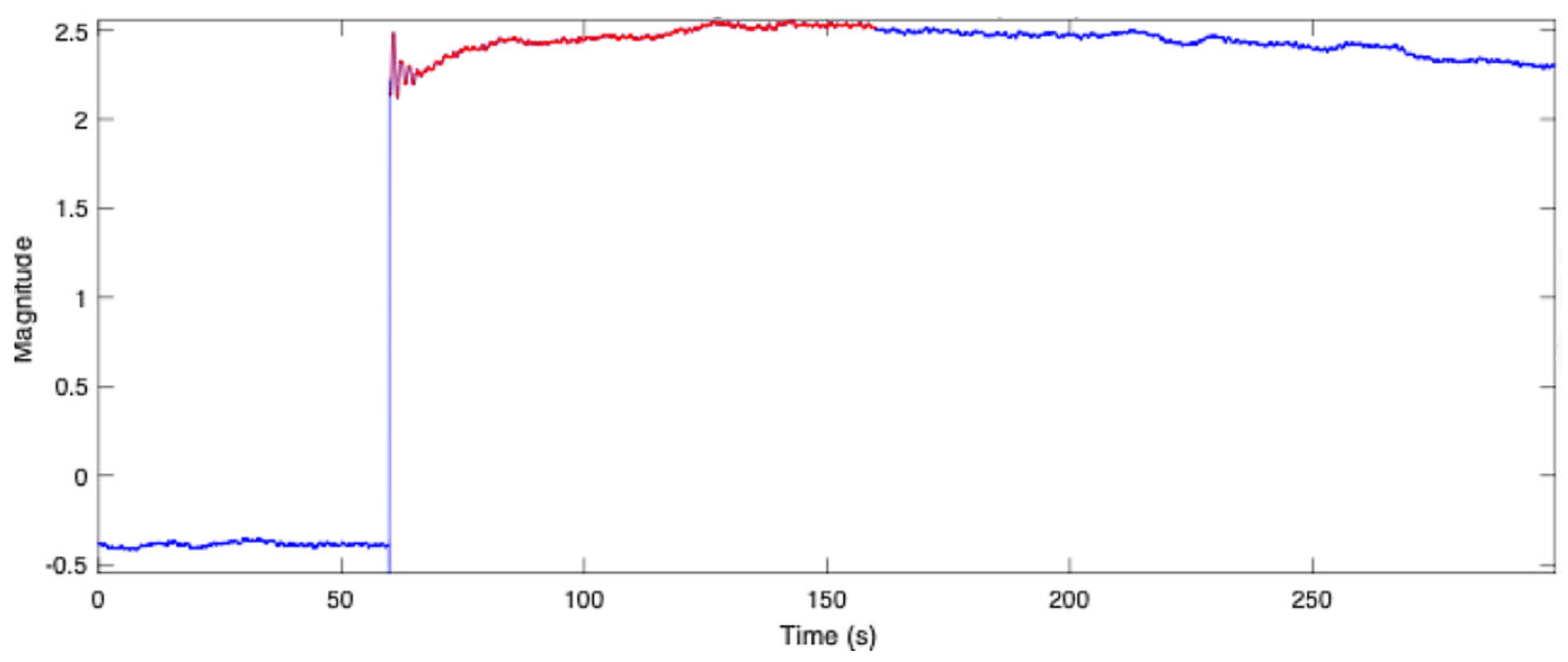
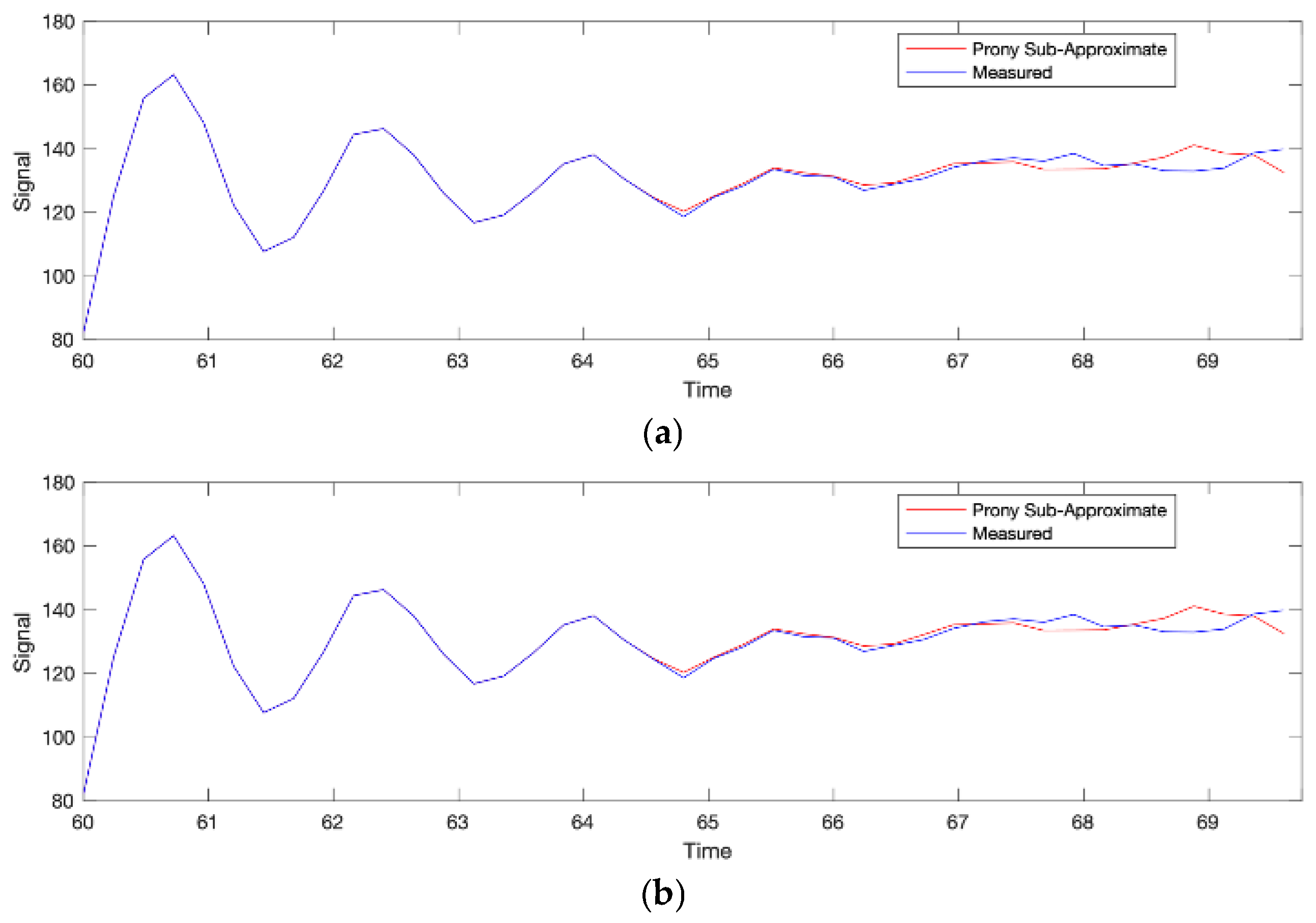
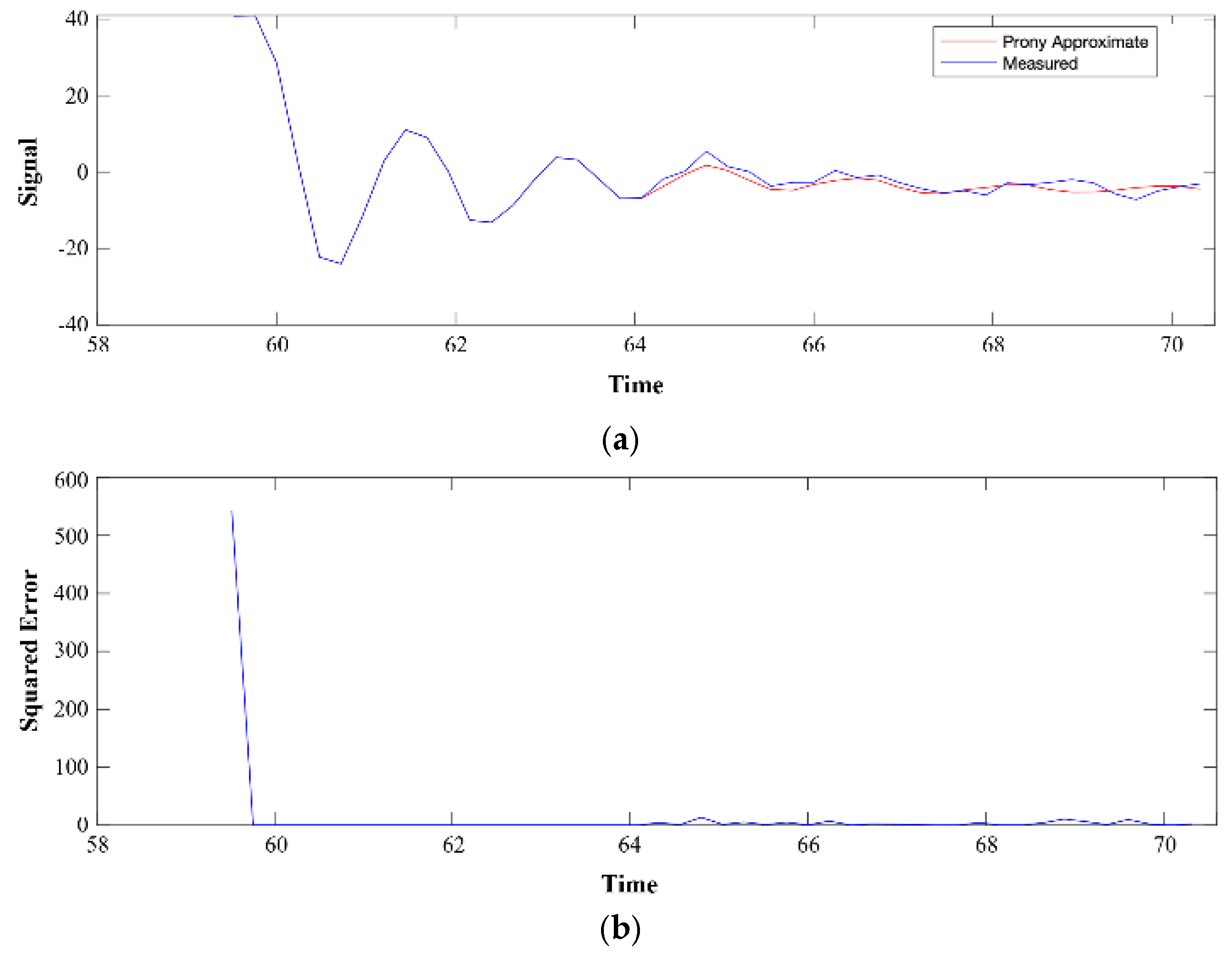
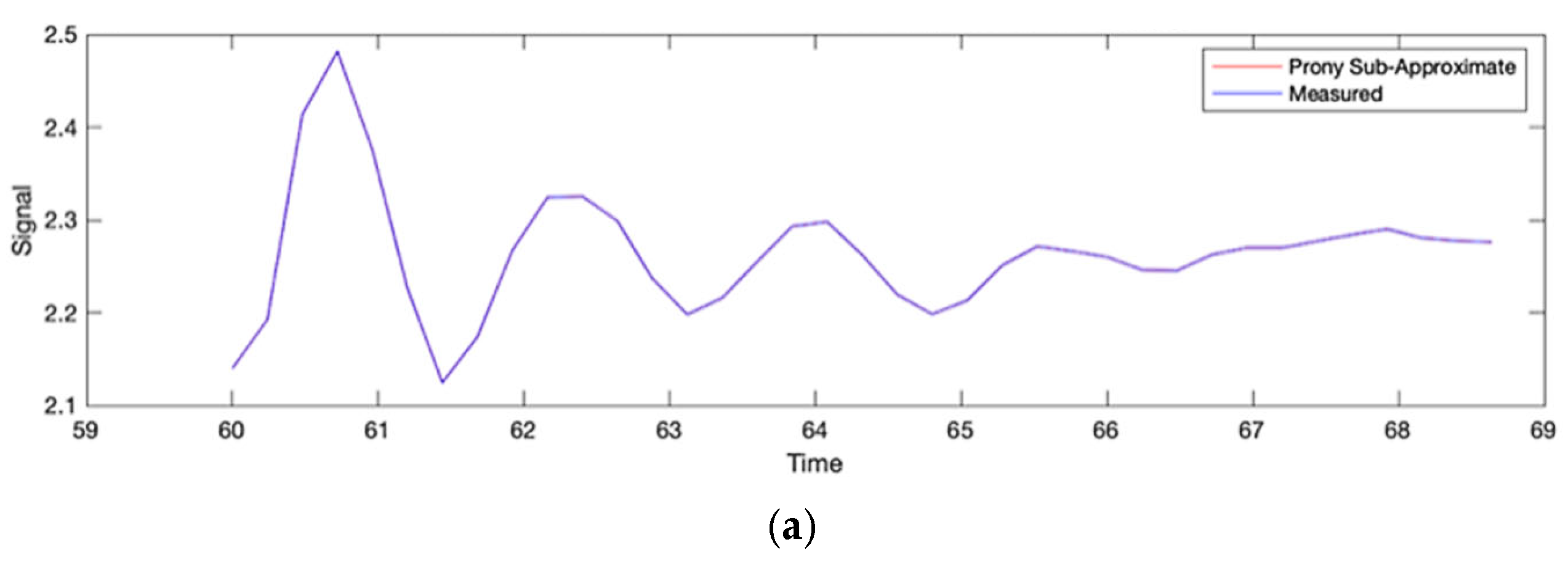
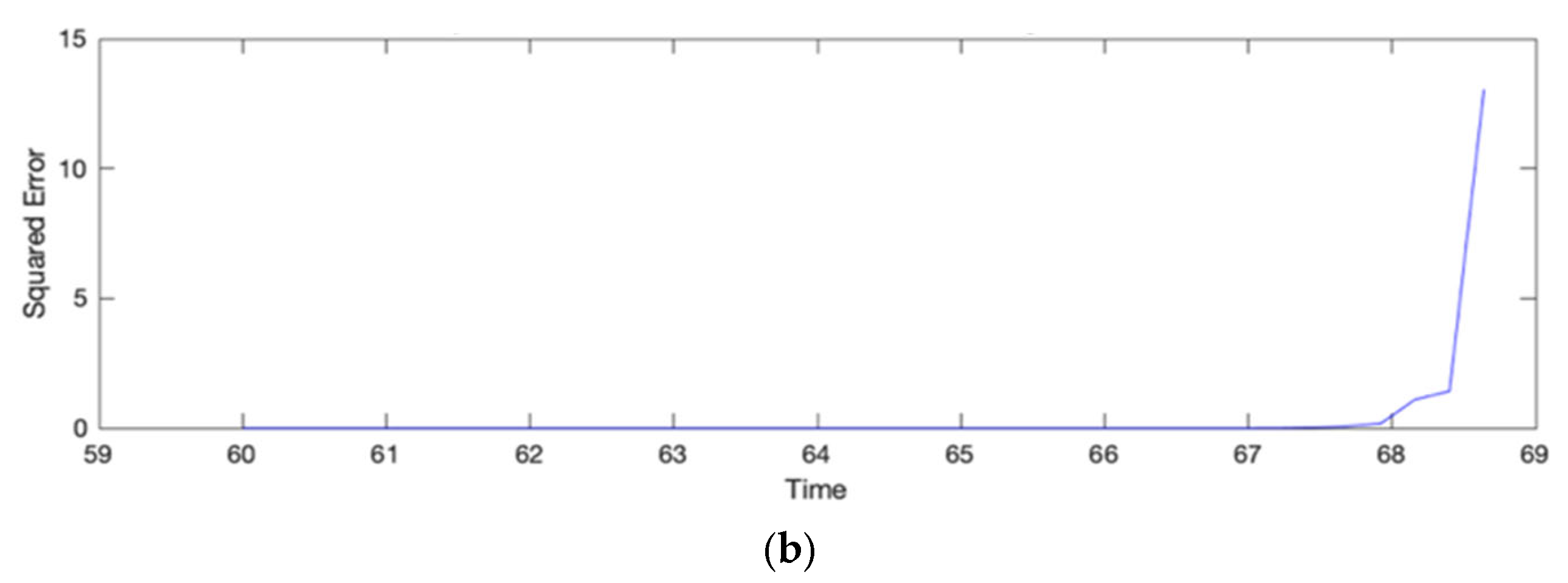
3.3. Low-Frequency Identification Using Prony’s Method
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BO | Blackout |
| CTs | Current Transformers |
| CVTs | Capacitive Voltage Transformers |
| DFT | Discrete Fourier Transform |
| DRTS | Digital Real-Time Simulators |
| DSF | Down Sampling Factor |
| EMS | Energy Management System |
| FFT | Fast Fourier Transform |
| GPS | Global Positioning System |
| IEEE | Institute of Electrical and Electronics Engineers |
| NERC | North American Electric Reliability Corporation |
| PDC | Phasor Data Concentrator |
| PMU | Phasor Measurement Unit |
| PSSs | Power System Stabilizers |
| PTs | Potential Transformers |
| PV | Photovoltaic |
| ROCOF | Rate of change of frequency |
| SCADA | Supervisory Control and Data Acquisition |
| UTC | Coordinated Universal Time |
| VRE | Variable Renewable Energy |
| VTs | Voltage Transformers |
References
- Lai, L.L.; Zhang, H.T.; Mishra, S.; Ramasubramanian, D.; Lai, C.S.; Xu, F.Y. Lessons learned from July 2012 Indian blackout. In Proceedings of the 9th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2012), Hong Kong, 18–21 November 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Gou, B.; Zheng, H.; Wu, W.; Yu, X. Probability Distribution of Power System Blackouts. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Yamashita, K.; Li, J.; Zhang, P.; Liu, C.-C. Analysis and control of major blackout events. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Hiyama, T.; Suzuki, N.; Funakoshi, T. On-line identification of power system oscillation modes by using real time FFT. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, Y.; Song, J.; Zhang, S.; Liu, H. Analysis of Forced Power Oscillation Based on FFT. IOP Conf. Ser. Earth Environ. Sci. 2019, 223, 012020. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Halang, W.A.; Zhang, B.; Chen, G. Analyzing Chaotic Spectra of DC–DC Converters Using the Prony Method. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 61–65. [Google Scholar] [CrossRef]
- Feilat, E.A. Prony analysis technique for estimation of the mean curve of lightning impulses. IEEE Trans. Power Deliv. 2006, 21, 2088–2090. [Google Scholar] [CrossRef]
- Yutthago, P.; Pattanadech, N. Improved Least-Square Prony Analysis Technique for Parameter Evaluation of Lightning Impulse Voltage and Current. IEEE Trans. Power Deliv. 2016, 31, 271–277. [Google Scholar] [CrossRef]
- Zhao, S.; Loparo, K.A. Forward and Backward Extended Prony (FBEP) Method for Power System Small-Signal Stability Analysis. IEEE Trans. Power Syst. 2017, 32, 3618–3626. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, G. A Robust Prony Method Against Synchrophasor Measurement Noise and Outliers. IEEE Trans. Power Syst. 2017, 32, 2484–2486. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Synchrophasor Estimation Using Prony’s Method. IEEE Trans. Instrum. Meas. 2013, 62, 2119–2128. [Google Scholar] [CrossRef]
- de la O Serna, J.A.; Martínez, E.V. Smart grids Part 2: Synchrophasor measurement challenges. IEEE Instrum. Meas. Mag. 2015, 18, 13–16. [Google Scholar] [CrossRef]
- Tawfik, M.M.; Morcos, M.M. On the use of Prony method to locate faults in loop systems by utilizing modal parameters of fault current. IEEE Trans. Power Deliv. 2005, 20, 532–534. [Google Scholar] [CrossRef]
- Pushkareva, A.V.; Markuleva, M.V. The Research of Noise Stability of the Prony’s Method While Processing of Cardiological Time Series. In Proceedings of the 2019 International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Novosibirsk, Russia, 21–27 October 2019. [Google Scholar] [CrossRef]
- Zhao, M.; Yin, H.; Xue, Y.; Zhang, X.-P.; Lan, Y. Coordinated Damping Control Design for Power System with Multiple Virtual Synchronous Generators Based on Prony Method. IEEE Open Access J. Power Energy 2021, 8, 316–328. [Google Scholar] [CrossRef]
- Netto, M.; Mili, L. Robust Data Filtering for Estimating Electromechanical Modes of Oscillation via the Multichannel Prony Method. IEEE Trans. Power Syst. 2017, 33, 4134–4143. [Google Scholar] [CrossRef]
- Meyer, J.-U.; Burkhard, P.M.; Secomb, T.W.; Intaglietta, M. The Prony spectral line estimation (PSLE) method for the analysis of vascular oscillations. IEEE Trans. Biomed. Eng. 1989, 36, 968–971. [Google Scholar] [CrossRef]
- Sava, H.P.; McDonnell, J.T.E. Spectral composition of heart sounds before and after mechanical heart valve implantation using a modified forward-backward Prony’s method. IEEE Trans. Biomed. Eng. 1996, 43, 734–742. [Google Scholar] [CrossRef] [PubMed]
- Jafarpisheh, B.; Madani, S.M.; Jafarpisheh, S. Improved DFT-Based Phasor Estimation Algorithm Using Down-Sampling. IEEE Trans. Power Deliv. 2018, 33, 3242–3245. [Google Scholar] [CrossRef]
- Dai, R.; Liu, G.; Stability, S.-S. Graph Database and Graph Computing for Power System Analysis; IEEE: New York, NY, USA, 2024; pp. 365–389. [Google Scholar] [CrossRef]
- Vaccaro, A. Small-Signal Stability Analysis of Uncertain Power Systems. In Interval Methods for Uncertain Power System Analysis; IEEE: New York, NY, USA, 2023; pp. 87–94. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A.; Chow, J.H.; Stability, S.-S. Power System Dynamics and Stability: With Synchrophasor Measurement and Power System Toolbox; IEEE: New York, NY, USA, 2017; pp. 183–231. [Google Scholar] [CrossRef]
- Fan, L. Interarea Oscillations Revisited. IEEE Trans. Power Syst. 2017, 32, 1585–1586. [Google Scholar] [CrossRef]
- Vournas, C.D.; Metsiou, A.; Nomikos, B.M. Analysis of intra-area and interarea oscillations in South-Eastern UCTE interconnection. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Galassi, P.H.; de Almeida, A.B.; Pesente, J.R.; Ramos, R.A. Analysis of Wide-Area Input Signals for Damping Interarea Oscillation of the Interconnected Paraguayan-Argentinean System. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 15–18 August 2021; pp. 1252–1257. [Google Scholar] [CrossRef]
- Jain, V.; Nagarajan, S.T.; Garg, R. Study of Forced Oscillations in Two Area Power System. In Proceedings of the 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 96–101. [Google Scholar] [CrossRef]
- Mantzaris, J.C.; Metsiou, A.; Vournas, C.D. Analysis of Interarea Oscillations Including Governor Effects and Stabilizer Design in South-Eastern Europe. IEEE Trans. Power Syst. 2013, 28, 4948–4956. [Google Scholar] [CrossRef]
- Nomikos, B.M.; Kotlida, M.A.; Vournas, C.D. Interarea Oscillations and Tie-line Transients in the Hellenic Interconnected System. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 68–73. [Google Scholar] [CrossRef]
- Mao, X.-M.; Zhang, Y.; Guan, L.; Wu, X.-C. Coordinated control of interarea oscillation in the China Southern power grid. IEEE Trans. Power Syst. 2006, 21, 845–852. [Google Scholar] [CrossRef]
- Breulmann, H.; Grebe, E.; Lösing, M.; Winter, W.; Witzmann, R.; Dupuis, P.; Houry, M.P.; Margotin, T.; Zerenyi, J.; Dudzik, J.; et al. Analysis and Damping of Inter-Area Oscillations in the UCTE/CENTREL Power System; Paper No 38-113; CIGRÉ: Paris, France, 2000. [Google Scholar]
- Available online: https://www.nerc.com/comm/RSTC_Reliability_Guidelines/Oscillation_Analysis_for_Monitoring_And_Mitigation_TRD.pdf (accessed on 20 March 2025).
- Available online: https://jdih.esdm.go.id/storage/document/PM%20ESDM%20No%2020%20Tahun%202020.pdf (accessed on 20 March 2025).
- Xu, Y.; Gu, Z.; Sun, K. Location and Mechanism Analysis of Oscillation Source in Power Plant. IEEE Access 2020, 8, 97452–97461. [Google Scholar] [CrossRef]
- Grigsby, L.L. (Ed.) Power System Stability and Control, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Sharma, N.; Acharya, A.; Jacob, I.; Yamujala, S.; Gupta, V.; Bhakar, R. Major Blackouts of the Decade: Underlying Causes, Recommendations and Arising Challenges. In Proceedings of the 2021 9th IEEE International Conference on Power Systems (ICPS), Kharagpur, India, 16–18 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Dinh, V.T.; Le, H.H. Vietnamese 500kV power system and recent blackouts. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Pourbeik, P.; Kundur, P.S.; Taylor, C.W. The anatomy of a power grid blackout—Root causes and dynamics of recent major blackouts. IEEE Power Energy Mag. 2006, 4, 22–29. [Google Scholar] [CrossRef]
- Andersson, G. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 2005, 20, 1922–1928. [Google Scholar] [CrossRef]
- Agustriadi; Sinisuka, N.I.; Banjar-Nahor, K.M.; Bésanger, Y. Modeling, Simulation, and Prevention of July 23, 2018, Indonesia’s Southeast Sumatra Power System Blackout. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Meng, D.Z. China’s protection technique in preventing power system blackout to world. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 1838–1844. [Google Scholar] [CrossRef]
- Singh, A.; Parida, S.K. Synchronized Measurement of Power System Frequency and Phase Angle Using FFT and Goertzel Algorithm for low-cost PMU Design. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Bucharest, Romania, 29 September–2 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, S.; Tian, B.; Liang, J.; Cheng, Y. Detection of Harmonic Components using the FFT and Instantaneous Reactive Power Theory. J. Phys. Conf. Ser. 2022, 2242, 012034. [Google Scholar] [CrossRef]
- Witzmann, R.; Rittiger, J.; Winter, W. Inter-Area Oscillations during Development of Large Interconnected Power Systems. In Proceedings of the CIGRE Symposium, Working Plant and Systems Harder, London, UK, 7–9 June 1999. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- IEEE C37.118.1-2011; IEEE Standard for Synchrophasor Measurements for Power Systems (Revision of IEEE Standard C37.118-2005). IEEE Standards Association: Piscataway, NJ, USA, December 2011.
- Gou, B.; Zheng, H.; Wu, W.; Yu, X. The Statistical Law of Power System Blackouts. In Proceedings of the 2006 38th North American Power Symposium, Carbondale, IL, USA, 17–19 September 2006; pp. 495–501. [Google Scholar] [CrossRef]
- Scutariu, M.; MacDonald, M. Industrial power system protection against transmission system blackouts. In Proceedings of the 2009 44th International Universities Power Engineering Conference (UPEC), Glasgow, UK; 2009; pp. 1–5. [Google Scholar]
- Ilic, M.D.; Allen, H.; Chapman, W.; King, C.A.; Lang, J.H.; Litvinov, E. Preventing Future Blackouts by Means of Enhanced Electric Power Systems Control: From Complexity to Order. Proc. IEEE 2005, 93, 1920–1941. [Google Scholar] [CrossRef]
- Chakraborty, N.C.; Banerji, A.; Biswas, S.K. Survey on major blackouts analysis and prevention methodologies. In Proceedings of the Michael Faraday IET International Summit 2015, Kolkata, India, 12–13 September 2015; pp. 297–302. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S.; Adamiak, M.G. A new measurement technique for tracking voltage phasors, local system frequency, and rate of change of frequency. IEEE Trans. Power Appl. Syst. 1983, 102, 1025–1038. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications, Softcover Reprint of Hardcover, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- de la O Serna, J.A.; Martin, K. Improving phasor measurements under power system oscillations. IEEE Trans. Power Syst. 2003, 18, 160–166. [Google Scholar] [CrossRef]
- Macii, D.; Petri, D.; Zorat, A. Accuracy analysis and enhancement of DFT-based synchrophasor estimators in off-nominal conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2653–2664. [Google Scholar] [CrossRef]
- Barchi, G.; Macii, D.; Petri, D. Accuracy of one-cycle DFT-based synchrophasor estimators in steady-state and dynamic conditions. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Graz, Austria, 13–16 May 2012; pp. 1529–1534. [Google Scholar]
- Gholami, A.; Chari, M.V.K. Enhanced Prony analysis using regularization techniques for oscillation mode estimation. IEEE Trans. Power Syst. 2020, 35, 1346–1354. [Google Scholar]
- Wang, Y.; Zhao, L.; Zhang, H. Robust damped sinusoids estimation using a modified matrix pencil approach. Electr. Power Syst. Res. 2021, 194, 107027. [Google Scholar]
- Liu, J.; Liu, Y.; Wang, Z. A hybrid Prony and neural network approach for oscillation analysis in wide-area monitoring systems. IEEE Access 2022, 10, 12345–12356. [Google Scholar]
- Zhang, X.; Sun, K.; Xu, Y. Deep learning-based dynamic mode decomposition for power system oscillation monitoring. Appl. Energy 2023, 335, 120732. [Google Scholar]


| Bus | Mode | Frequency [Hz] | Amplitude [% Fundamental] |
|---|---|---|---|
| AC-N | 1 (interarea) | 0.57 | 9.5 |
| 2 (interarea) | 0.66 | 9.1 | |
| 3 (interarea) | 0.68 | 9.7 | |
| AN-AQ | 1 (interarea) | 0.55 | 11.9 |
| 2 (interarea) | 0.57 | 13.4 | |
| 3 (interarea) | 0.67 | 8.7 | |
| J-H | 1 (interarea) | 0.61 | 7.7 |
| 2 (interarea) | 0.66 | 7.8 | |
| 3 (interarea) | 0.68 | 7.4 |
| Mode | Frequency [Hz] | Amplitude [MW] | Damping |
|---|---|---|---|
| 1 (interarea) | 0.61 | 510 | 0.44 |
| 2 (machine) | 1.7 | 4.8 | 0.73 |
| 3 (machine) | 0.77 | 3.7 | 0.28 |
| Mode | Frequency [Hz] | Amplitude [MW] | Damping |
|---|---|---|---|
| 1 (interarea) | 0.35 | 490 | 0.47 |
| 2 (interarea) | 0.55 | 4.9 | 0.22 |
| 3 (machine) | 0.8 | 3.8 | 0.57 |
| Mode | Frequency [Hz] | Amplitude [MW] | Damping |
|---|---|---|---|
| 1 (interarea) | 0.62 | 25 | 0.42 |
| 2 (interarea) | 0.81 | 5.6 | 0.51 |
| 3 (machine) | 1.2 | 1.7 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dakhlan, D.F.; Muslim, J.; Kurniawan, I.; Banjar-Nahor, K.M.; Anggoro Soedjarno, B.; Hariyanto, N. Comparing Fast Fourier Transform and Prony Method for Analysing Frequency Oscillation in Real Power System Interconnection. Energies 2025, 18, 2377. https://doi.org/10.3390/en18092377
Dakhlan DF, Muslim J, Kurniawan I, Banjar-Nahor KM, Anggoro Soedjarno B, Hariyanto N. Comparing Fast Fourier Transform and Prony Method for Analysing Frequency Oscillation in Real Power System Interconnection. Energies. 2025; 18(9):2377. https://doi.org/10.3390/en18092377
Chicago/Turabian StyleDakhlan, Didik Fauzi, Joko Muslim, Indra Kurniawan, Kevin Marojahan Banjar-Nahor, Bambang Anggoro Soedjarno, and Nanang Hariyanto. 2025. "Comparing Fast Fourier Transform and Prony Method for Analysing Frequency Oscillation in Real Power System Interconnection" Energies 18, no. 9: 2377. https://doi.org/10.3390/en18092377
APA StyleDakhlan, D. F., Muslim, J., Kurniawan, I., Banjar-Nahor, K. M., Anggoro Soedjarno, B., & Hariyanto, N. (2025). Comparing Fast Fourier Transform and Prony Method for Analysing Frequency Oscillation in Real Power System Interconnection. Energies, 18(9), 2377. https://doi.org/10.3390/en18092377






