Abstract
Under the goal of “dual carbon”, the power market and carbon market are developing synergistically, which is strongly promoting the transformation of the power system in a clean and low-carbon direction. In order to realise the synergistic optimisation of multi-virtual power plants, economic and low-carbon operation, and the reasonable distribution of revenues, this paper proposes a multi-VPP power–carbon sharing operation optimisation strategy considering multiple uncertainties. Firstly, a cost model for each VPP power–carbon sharing considering the uncertainties of market electricity price and new energy output is established. Secondly, a multi-VPP power–carbon sharing operation optimisation model is established based on the Nash negotiation theory, which is then decomposed into a multi-VPP coalition cost minimisation subproblem and a revenue allocation subproblem based on asymmetric bargaining. Thirdly, the variable penalty parameter alternating directional multiplier method is used for the solution. Finally, an asymmetric bargaining method is proposed to quantify the contribution size of each participant with a nonlinear energy mapping function, and the VPPs negotiate with each other regarding the bargaining power of their electricity–carbon contribution size in the co-operation, so as to ensure a fair distribution of co-operation benefits and thus to motivate and maintain a long-term and stable co-operative relationship among the subjects. Example analyses show that the method proposed in this paper can significantly increase the revenue level of each VPP and reduce carbon emissions and, at the same time, improve the ability of VPPs to cope with uncertain risks and achieve a fair and reasonable distribution of the benefits of VPPs.
1. Introduction
In order to establish a sound economic system of green, low-carbon, and recycling development, and to promote the comprehensive green transformation of economic and social development, China proposed a “dual-carbon” development commitment in 2020. Against this backdrop, with the large-scale integration of renewable energy sources, the flexibility of the power system has decreased, and the grid’s regulation and control capabilities have declined, posing a huge challenge to the safe and stable operation of the power system [1]. Virtual power plants use advanced communication technology and control technology to achieve the effective aggregation and optimal scheduling of distributed resources such as distributed power sources, controllable loads, and energy storage, unified regulation and control, and participation in grid operation and power market trading [2,3], reducing Distributed Energy Resource output fluctuations and improving the efficiency of the power system and the overall stability of the power grid [4].
In July 2021, the national carbon emissions trading market (hereinafter referred to as the carbon market) was officially launched. The carbon market is an important institutional innovation to control and reduce greenhouse gas emissions using market mechanisms. The synergistic development and joint role of the power market and the carbon market can maximise the optimisation of the market mechanism in energy resource allocation and climate governance and strongly promote the transition of the power system in a clean and low-carbon direction [5]. In the operation of China’s power system, the power market guides the allocation of power generation resources through price signals, while the carbon market relies on the carbon price to internalise the negative externalities of coal-fired power generation, and the two are coupled in both directions through the transmission of costs. Specifically, carbon quota constraints raise the marginal operating costs of high-carbon units, change their offer strategy in the electricity spot market, which in turn affects the market clearing priority and drives the adjustment of power generation structure in the low-carbon direction. At the same time, the emission reduction certificates generated from green power trading can be linked to the carbon market quota payment, building a ‘power–carbon’ market value transmission channel. VPPs can be traded in both the power market and the carbon market at the same time, and they are important carriers for the synergistic development of the power market and the carbon market [6].
As the scale of VPP construction expands, neighbouring VPP units within the regional distribution system can form a collaborative network through power exchange and carbon trading to build a VPP alliance. This collaborative model can realise the cross-domain deployment of electric energy resources and carbon allowances in the spatial and temporal dimensions and promote the efficient consumption and complementary use of renewable energy. In view of this, there is an urgent need to build a synergistic optimisation mechanism for VPP alliances, so as to improve the operational efficiency and fair benefit distribution among members through the formulation of coordinated optimisation strategies.
As the construction of the VPP alliance and the synergistic development of its depth, which involves the coordination of the interests of multiple subjects and the optimal allocation of resources, has become more and more complex, the traditional method is difficult to solve effectively. Game theory, as a theoretical tool for coordinating multi-actor cooperative optimisation and benefit distribution problems [7], has demonstrated significant value in energy system research. Two types of research paths have been formed in academia for the multi-party benefit distribution mechanism: the non-cooperative game and cooperative game frameworks. The wind–photo-hydrogen microgrid capacity optimisation model based on non-cooperative games in the article [8] can effectively improve resource allocation efficiency and achieve cost minimisation and benefit maximisation. The non-cooperative game transaction architecture designed in the work [9], on the other hand, achieves the synergistic goal of node revenue maximisation and energy storage benefit enhancement. The article [10] establishes a master–slave gaming hierarchy between distribution network investors (DSOs) and integrated energy service providers (IESs), which can reduce the cost of energy supply and improve the economic benefits of multiple parties at the same time. However, it should be noted that the Nash equilibrium solution of the non-cooperative game tends to deviate from the Pareto optimum, and individual rational strategies may lead to the loss of overall system effectiveness.
Cooperative game research, on the other hand, focuses on the optimisation of alliance benefits and mainly adopts two types of modelling: the alliance game and Nash negotiation. Under the framework of the coalition game, the day-ahead power market bidding model in the article [11] verifies the feasibility of multi-virtual power plant cooperative operation. And, the two-stage multi-objective optimisation scheme proposed in the work [12] achieves the cost sharing of shared energy storage alliance through the Shapley value method. However, the method has significant limitations: the combinatorial explosion problem of Shapley values leads to the exponential growth of computational complexity as the alliance scale expands, and the centralised information interaction model is prone to the risk of member privacy leakage. In terms of the Nash negotiation model, the integrated energy service provider operation strategy proposed in the work [13] and the joint planning scheme for multiple energy systems proposed in the article [14] confirm that the model has the advantages of reducing system costs and guaranteeing operational reliability. However, existing studies generally lack in-depth exploration of the fair distribution mechanism of the cooperative surplus, especially the establishment of the revenue distribution guidelines that take into account the contribution of cooperation and risk-bearing capacity.
In addition, guiding VPPs into the carbon trading market can effectively reduce VPP carbon emissions. The investigation [15] proposed a VPP optimal dispatch model considering step carbon trading and integrated demand response. The scientific work [16] proposed an operation mechanism for VPPs to participate in the electricity–carbon joint market. The article [17] constructed a multi-VPP electricity–carbon peer-to-peer trading mechanism model based on the Nash bargaining theory to achieve resource sharing while taking into account individual interests and coalition benefits. The work [18] considered the coupling of electricity–carbon trading and established a multi-VPP low-carbon joint optimisation model based on the Nash bargaining theory, which can effectively reduce the operating costs and carbon emissions of VPPs.
It is worth noting that existing studies are generally conducted under the assumption of a deterministic environment, failing to effectively incorporate the mechanism analysis of the impact of uncertainty factors on system operation. In the actual operation scenario of virtual power plants, the double uncertainty perturbation formed by the fluctuation in market electricity price and the stochasticity of new energy output may trigger the operation risk of the multi-VPP power–carbon synergy system. To address the uncertainty problem, three typical modelling paradigms, namely fuzzy planning [19], stochastic planning [20], and robust optimisation [21], have been developed in the academic community. The scientific article [22] constructs a dynamic decision-making framework based on robust optimisation to effectively deal with the coupling of PV output fluctuation and tariff stochasticity; the work [23] innovatively introduces a box-type uncertainty set to characterise the multidimensional source–load–price uncertainty and designs a two-stage stochastic robust hybrid optimisation model. However, it should be especially pointed out that the above results do not fully consider the transmission effect of multiple uncertainties on the multi-VPP electricity–carbon synergy network in the modelling process, especially in the operation scenario of electricity trading and carbon emission right linkage, and there is a lack of quantitative analysis of the cross-subject propagation paths of uncertainty risk. Therefore, constructing a multi-VPP synergistic optimisation model that integrates the joint uncertainty of electricity price–new energy output will become a key research direction to break through the existing theoretical limitations.
This paper is devoted to constructing a multi-VPP electricity–carbon cooperative sharing collaborative optimisation paradigm for multiple uncertainties. Firstly, we design a multi-VPP power–carbon cooperative sharing architecture and establish a VPP power-carbon cooperative sharing cost model that integrates dual uncertainties; then, we construct a multi-VPP power–carbon cooperative optimisation model based on the improved Nash negotiation theory, propose a two-stage decoupling strategy of alliance cost minimisation and revenue allocation bargaining, and apply the variable penalty parameter Alternating Direction Method of Multipliers (ADMM) to solve the problem. In the first stage, robust optimisation and opportunity constraint planning are integrated to form a hybrid uncertainty coping scheme, which effectively cracks the risk of power–carbon coalition caused by the fluctuation in electricity price and the stochasticity of renewable energy output; in the second stage, the asymmetric bargaining function is constructed to achieve the differentiated allocation of the cooperative surplus through the quantitative assessment of the contribution degree. Finally, the simulation verifies the significant advantages of this model over traditional methods.
2. Multi-VPP Electro-Carbon Sharing Architecture
In this paper, we construct a multi-VPP electricity–carbon sharing architecture based on cooperative games, as shown in Figure 1.
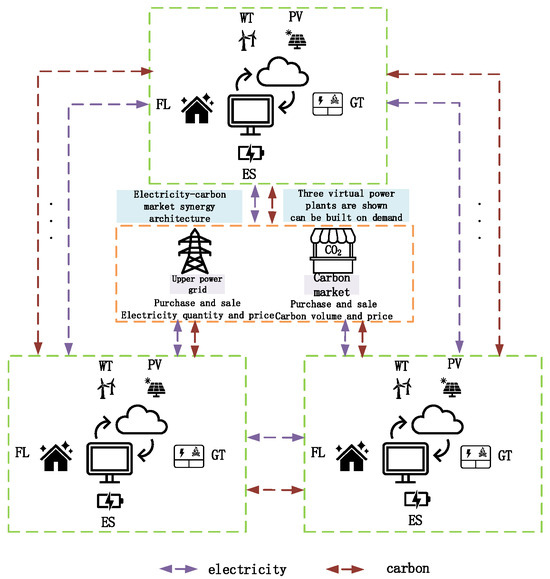
Figure 1.
Cooperative game-based multi-VPP electricity–carbon sharing architecture.
This study proposes a multi-VPP synergistic operation mechanism to form an internal electricity–carbon trading market through the construction of a regional energy alliance. The mechanism adopts a two-tier trading model of “internal priority–external supplementation”: at the alliance level, a peer-to-peer trading mechanism is established based on the principle of energy sharing, so as to achieve independent deployment of electricity and carbon resources among members and ensure the balance of supply and demand in the internal market; for the residual resources that cannot be consumed internally, they will interact with the main grid and the carbon market through the external market channel.
The overall VPP framework is shown in Figure 2.
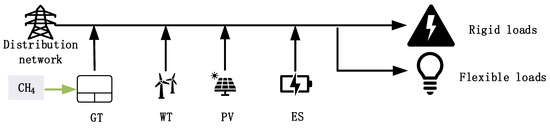
Figure 2.
VPP operational framework.
This paper constructs a VPP operation framework that aggregates distributed resources such as wind power units, photovoltaic power generation systems, gas turbine generating units, demand-side flexible load clusters, and electrochemical energy storage, which can participate in the electricity market and the carbon market at the same time and guide flexible loads to take part in the grid regulation to improve the efficiency of demand-side resource utilisation.
3. Electricity–Carbon Sharing Cost Models for Each VPP Considering Multivariate Uncertainty
This section firstly constructs the operation model of typical energy equipment within a VPP, based on which the operation model of an individual VPP is constructed considering wind power output uncertainty as well as market tariff uncertainty, and finally, the cost model of the VPP’s participation in electricity and carbon quota sharing under uncertainty is constructed to lay the model foundation for the research and analysis in Part IV.
3.1. Gas Turbine Generator Set Modelling
A gas-fired unit burns natural gas to produce electrical energy, which is mathematically modelled as
where is the electrical efficiency of the gas turbine; is the calorific value of the natural gas; and are the natural gas usage and power generation of the gas turbine at ; and are the upper and lower limits of the power generation; is the CO2 emission of the gas turbine at ; and is the carbon conversion factor of the gas turbine.
3.2. Modelling of Energy Storage Devices
The mathematical model of the energy storage device is
where is the energy storage capacity in the time period ; and are the upper and lower limits of the energy storage capacity; is the initial capacity; and are the charging and discharging power; and are the charging and discharging efficiencies; and and are the charging and discharging state variables.
3.3. Flexible Load Modelling
This subsection introduces two types of flexible loads, curtailable and transferable loads, which are mathematically modelled as
where is the VPPi electrical load in the time slot ; is the VPPi initial load demand; and are the curtailable and transferable loads in the time slot , respectively; and and are the corresponding load adjustment factors.
3.4. Single VPP Carbon Mechanism Modelling
3.4.1. Single VPP Carbon Emissions Modelling
The total carbon emissions from a single VPP are
where is the total carbon emission of the VPP in the time period ; is the power purchased from the higher grid; and is the carbon emission factor. Given that the current power system is dominated by thermal power, it is assumed in this study that the VPP purchased power is derived from fossil fuel generation from coal-fired units.
3.4.2. Single VPP Carbon Quota Modelling
The government determines the total amount of allowances for emission control enterprises through carbon emission accounting and issues them free of charge. VPPs optimise energy production based on the allowances. In this study, the baseline method is used to allocate initial quotas, and in order to promote the development of the carbon market and incentivise low-carbon power generation, quotas are allocated to wind power and photovoltaic units on the basis of equivalent consumption, which is modelled as follows:
where is the VPP carbon allowance; is the gas turbine unit carbon allowance; and are the wind power, PV, and power output in the timeframe; and is the renewable energy power unit carbon allowance.
3.5. Modelling of Market Tariff Uncertainty
Electricity price uncertainty significantly affects the decision-making of multi-VPP alliances, and given that the market complexity makes it difficult to accurately predict the distribution of electricity prices, this paper adopts a robust optimisation method that requires only confidence intervals to deal with electricity price uncertainty. Taking a single VPP as the optimisation object, the total costs include the grid electricity purchase and sale, , carbon market transaction, , natural gas purchase, , energy storage operation and maintenance, , and demand response, , costs without considering the electricity–carbon bargaining transaction. Based on the 1 h time scale, a day-ahead optimisation model is constructed considering the uncertainty of electricity price, and the objective function is to minimise the full-day operation cost of the th VPP, as follows:
where is the tariff deviation coefficient; and is the power interaction between VPP and the higher grid.
where and are the electricity purchase and sale prices for VPPi’s interactions with the upper grid in the time slot ; and are the electricity purchase and sale prices for VPPi’s interactions with the upper grid in the time slot ; and are the carbon purchase and sale prices for VPPi’s interactions with the external carbon market in the time slot ; and are the carbon purchase and sale prices for VPPi’s interactions with the external carbon market in the time slot ; is the price of purchased gas; is the unit cost of power for electric storage; and and are the unit cost of power compensation for load shedding and shifting by VPPi, respectively.
For the min-max optimisation problem with tariff uncertainty, the inner layer determines the worst-case tariff scenario through the price deviation penalty term . To simplify the solution, an auxiliary variable, , is introduced to reconstruct the inner max. problem as follows:
where is the tariff uncertainty parameter for VPPi
We set and as the dyadic variables of Equation (9), respectively, and introduce the auxiliary variable to eliminate the nonlinear term. Based on the strong dyadic theory, the equivalent optimisation form of the min-max problem is
Formula (6) can be converted to
3.6. Wind and Light Uncertainty Modelling
In view of the uncertainty of wind power and PV output, the actual output is modelled as the sum of the prediction value and the random error, in which the short-term prediction error obeys the normal distribution with a mean of 0 and the variances and .
where and are the predicted values of wind and PV output, respectively.
To ensure scheduling reliability, this paper uses the chance constraint approach to deal with such uncertainties.
The VPP electric power balance constraint based on the chance constraint can be expressed as follows:
where is the confidence level.
Let the probability cumulative distribution function of the random variable be F. According to the theory related to probability statistics, Equation (13) can be further converted into
Following the calculation of F, the solution of the inverse function is obtained by the means of the quantile points of the standard normal distribution, and the constraint Equation (14) is finally converted into
where is the inverse function of the standard normal distribution.
3.7. Model Constraints
3.7.1. VPP Operational Equilibrium and Constraints
Considering the uncertainty of wind and PV output within the VPP, this paper expresses the electric power balance constraints of the VPP in the form of opportunity constraints, as shown in Equation (15).
The carbon trading equilibrium constraints are the following:
3.7.2. Power Interaction Constraints Between VPP and Higher Grid
3.8. Electricity–Carbon Sharing Cost Models for Each VPP Considering Uncertainty
A multi-body interaction model is constructed for the power–carbon quota synergistic trading mechanism of a VPP alliance. The model has the following features: (1) it supports two-way resource trading among alliance members; (2) it realises the coupled optimisation of electricity transmission and carbon quota transfer; (3) it adopts an economic optimal decision-making algorithm. As shown in Equations (18)–(21),
is the number of members of the VPP alliance; denotes the cost of electricity paid or collected by VPPi for VPPj at the time of electricity sharing (if it is greater than 0, it means that the cost is collected, and if it is less than 0, it means that the cost is paid); and and denote the tariffs and quantities of electricity traded between VPPi and VPPj at the time , and if is greater than 0, it means that VPPi sells electricity to VPPj. Similarly, is the cost of carbon quota trading, is the carbon quota trading fee; and are the carbon quota trading price and trading volume at the time , respectively.
4. Multi-VPP Electricity–Carbon Sharing Operation Optimisation Model Based on Asymmetric Nash Negotiation
In this study, an asymmetric Nash negotiation game model is used to solve the VPP coalition revenue sharing problem. The model has two stages: (1) maximising the overall efficiency of the coalition; (2) negotiating the distribution of benefits among members. The model takes the cost of independent operation of each VPP (i.e., the cost when it is not involved in resource sharing) as the rupture point of negotiation, and its mathematical expression is the following:
Where , , , and are the cost of purchasing and selling electricity, the cost of purchasing and selling carbon, the cost of purchasing gas, the cost of operating and maintaining energy storage equipment, and the cost of demand response for VPPi when it operates independently at the time , respectively, and the last term is the price deviation penalty term.
This study sets each VPP as an independent rational decision-making subject belonging to different interest groups. Each participant determines the trading scale and price of electricity and carbon quota through strategic negotiation and establishes a fair benefit distribution mechanism to achieve cost optimisation and enhance the overall efficiency of the alliance. In order to ensure the stability of the negotiation process and prevent the negotiation from being terminated or restarted due to individual dissatisfaction with the allocation scheme, the system needs to satisfy the constraints shown in the following equation.
where is the cost of operating a single VPP independently when there is no trading of electricity and carbon allowances between virtual power plants.
It is assumed that all VPPs can reduce operating costs through collaborative negotiation. The cooperative game model constructed based on the Nash negotiation theory is shown in the following equation, and the Nash equilibrium solution can be obtained by solving the model, which is used as the basis for determining the energy trading scheme and pricing mechanism, so as to achieve the optimisation of the operation of each VPP and the maximisation of the overall benefits of the alliance.
where denotes the reduced operating cost after the co-operative gaming of VPPi participating in the Nash negotiation; and is the cost of operating VPPi after participation in the sharing of electricity and carbon allowances, net the benefits of participation in sharing.
Given that Equation (24) is non-convex and non-linear and is difficult to be solved directly, this study decomposes it into two convex optimisation subproblems: (1) the coalition cost minimisation problem Q1; (2) the asymmetric bargaining revenue sharing problem Q2. This decomposition method effectively reduces the difficulty of solving it.
4.1. Coalition Cost Minimisation Problem Q1
Since VPPs trade electricity and carbon allowances with each other in opposite directions and at equal prices, it follows that
According to the theory of “Mean Value Inequality”, when has the maximum value, the objective function of the Formula (24) obtains the maximum value, due to and , so there is
The multi-VPP coalition cost minimisation subproblem with the Nash negotiation breakdown point is fixed and is maximal when is minimal, i.e., the objective function of Equation (24) is maximal:
4.2. Asymmetric Bargaining Based Revenue Sharing Subproblem Q2
In this paper, the natural logarithm function is applied to quantify the contribution degree of each VPP in electricity and carbon quota sharing. Based on the contribution index, the P2P transaction price is determined through bargaining negotiation among VPPs to achieve a fair distribution of benefits, and its mathematical expression follows:
where and are the total amount of electricity sold and the total amount of electricity purchased by VPPi from other members in the Participation Optimisation time domain, respectively; and and are the total amount of carbon allowances sold and the total amount of carbon allowances purchased by VPPi from other members in the Participation Optimisation time domain, respectively.
An exponential function with the natural constant e as the base is chosen to construct a non-linear energy mapping model for quantifying the contribution of VPP in the sharing of electricity and carbon quotas, thus determining the bargaining power of each subject, :
where and are the contribution of electricity sharing and carbon quota sharing, respectively. Under electricity–carbon synergy, the decision-making processes influence each other, which is reflected as joint decision-making; in order to ensure that the decision-making status of the two markets is equal, and have the same weights. and are the maximum values of electricity purchased and sold during P2P trading; and are the maximum values of carbon purchased and sold during P2P trading, respectively.
According to the established quantitative model of bargaining power in Equations (29) and (30), the asymmetric bargaining revenue sharing model of multi-VPP coalition constructed based on the Nash negotiation model is shown in Equation (31):
Given that the natural logarithmic function has a strictly monotonically increasing convexity characteristic, the logarithmic solution of the original problem is transformed into a min-max optimisation problem in this study in order to facilitate the solution:
The solution determines the price of electricity for interactive electricity and the price of carbon for interactive carbon allowances.
4.3. Asymmetric Nash Negotiation Model Solution Based on Variable Penalty Parameter ADMM Distributed Algorithm
ADMM is an efficient algorithm for solving separable large-scale convex optimisation problems. Given the separable convex function properties of the cost minimisation and revenue distribution maximisation subproblems of the multi-VPP coalition, it is suitable for distributed solving using ADMM.
The traditional ADMM uses fixed penalty parameters; in order to improve the convergence speed and reduce the sensitivity of the initial value of the parameters, this study introduces a dynamic penalty factor adjustment mechanism. Referring to the method in the work [24], as shown in Equation (33), the variable penalty parameter ADMM is used to solve the above subproblems.
where is the penalty factor for the th iteration; is a scaling factor between the original residuals and the pairwise residuals to adjust the relative importance of the two; and are the original and pairwise step adjustment factors, respectively; and and are the original and pairwise residuals of the kth iteration, respectively, for assessing the quality of the solution.
4.3.1. The Specific Steps for the Distributed Solution of Subproblem Q1 Based on the Variable Penalty Parameter ADMM Algorithm Are as Follows
(1) When solving the cost minimisation subproblem for multi-VPP coalition, the objective function is to find the minimum value of , which needs to satisfy in solving the problem since the electricity–carbon trading volume is a coupled variable. The form of the augmented Lagrangian function can be constructed as shown below:
By decomposing (34), distributed optimised operational models for each VPP are obtained:
where and are the Lagrange multipliers and and are the penalty factors.
(2) Let denote the number of iterations. In each iteration, the following steps are performed.
VPPi updates its decision, or , via Equation (36):
VPPj receives the updated decision information, or , updates its decision, or :
The calculation of Equations (36) and (37) are repeated until each VPP has updated its electricity–carbon trading strategy in the current iteration.
(3) After completing one round of iterations, update the Lagrange multipliers according to Equation (38):
(4) Calculate the raw residuals and pairwise residuals from Equation (39):
(5) Update the penalty factor according to Equation (40):
(6) Update the number of iterations: k = k + 1.
(7) Determine the convergence of the algorithm according to Equation (41).
where is the convergence condition; is the maximum number of iterations.
4.3.2. Subproblem Q2 Distributed Solution Based on Variable Penalty Parameter ADMM Algorithm
(1) When solving the subproblem of cooperative revenue sharing based on asymmetric bargaining, the trading price of electricity between VPPs and the trading price of carbon allowances are coupled variables, which need to be satisfied in the solution:
The augmented Lagrangian function form can be constructed from Equation (32) as shown below:
By decomposing (43), distributed optimised operational models for each VPP are obtained:
where and are the optimal electric–carbon interactions obtained from Subproblem 1; and are the Lagrange multipliers; and and are the penalty factors, respectively.
Next, the asymmetric Nash negotiation-based revenue sharing subproblem is solved in a similar way to the multi-VPP coalition cost minimisation subproblem and will not be repeated.
The schematic of the iterative model solution for both problems is shown in Figure 3.
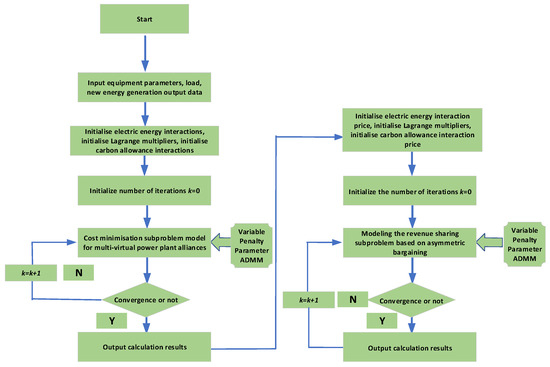
Figure 3.
Schematic diagram of iterative model solution.
5. Example Analysis
In this paper, we adopted the multi-VPP power-carbon synergy architecture shown in Figure 1 to illustrate the effectiveness of the multi-VPP power-carbon sharing optimal operation strategy considering multivariate uncertainty using the 3VPP system as an example. The model was set up with a 95% confidence level for wind and solar uncertainty, a 24-h period of tariff uncertainty, and a 15% tariff deviation rate.
5.1. Algorithm Convergence Analysis
In this paper, the improved ADMM algorithm was used to solve the cost minimisation subproblem Q1 and the benefit distribution subproblem Q2, which improves the convergence efficiency by dynamically adjusting the penalty parameter, reduces the sensitivity of the initial value of the parameter, and is widely used in the fields of variational inequalities and structural optimisation. The convergence performance of the algorithm is shown in Figure 4 and Figure 5.
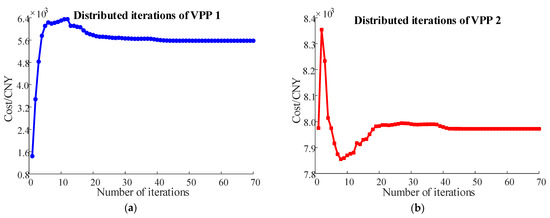
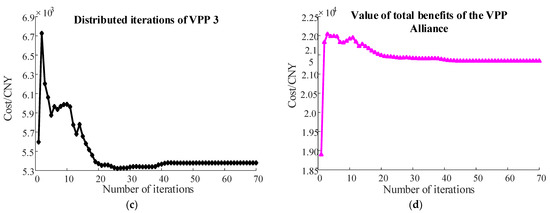
Figure 4.
(a) VPP1 cost iterations; (b) VPP2 cost iterations; (c) VPP3 cost iterations; (d) VPP alliance cost iteration status.
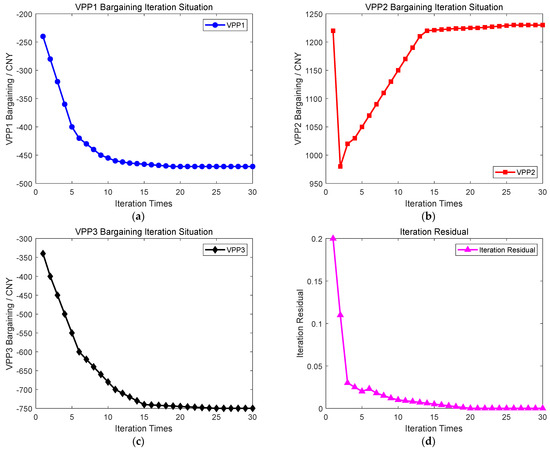
Figure 5.
(a) VPP1 bargaining iteration situation; (b) VPP2 bargaining iteration situation; (c) VPP3 bargaining iteration situation; (d) iteration residual.
Figure 4 illustrates the cost convergence process of subproblem Q1, where the algorithm converged after 70 iterations and took 279 s; Figure 5 presents the convergence of the transaction price of subproblem Q2, where the algorithm reached a 10−3 accuracy within 30 iterations and took 415 s.
Table 1 compares the computational efficiency of the variable penalty parameter ADMM with the conventional ADMM in solving Q1. The results show that the improved algorithm significantly reduced the solution time. This is attributed to the fact that the traditional ADMM suffers from the defect of slow convergence, while the variable penalty parameter ADMM improves the convergence efficiency while ensuring stability through the dynamic adjustment mechanism.

Table 1.
Comparison of solution time of each iterative algorithm with different convergence accuracies.
5.2. Multi-VPP Electricity–Carbon Sharing Benefit Analysis Considering Multivariate Uncertainties
5.2.1. Analysis of Multi-VPP Electro-Carbon Interaction Results
Considering the uncertainty of market price and new energy output, Figure 6 shows the power interactions among VPPs. VPP1 was dominated by wind power, which was sold during 00:00–7:00 and 18:00–24:00 due to abundant output and purchased during the rest of the daytime hours. VPP2 contained both wind power and PV, which were purchased during the peak load hours of 12:00–16:00 and sold during the rest of the daytime hours. VPP3 was dominated by photovoltaics and sold electricity during the 9:00–17:00 h when there was sufficient light and purchased electricity during the night hours.
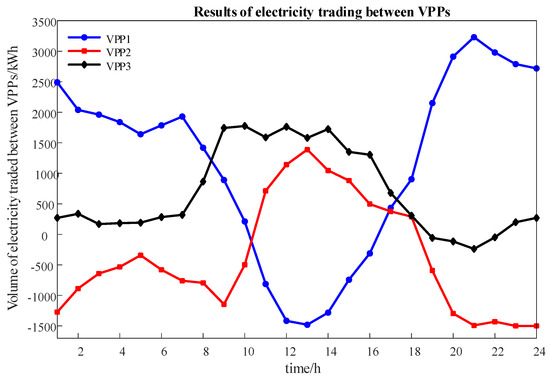
Figure 6.
Results of electricity trading between VPPs.
Figure 7 shows the carbon trading among VPPs under the uncertainty environment. The proposed carbon sharing mechanism effectively maintained the balance of carbon trading among VPPs, and each VPP rationally allocated carbon allowances according to the characteristics of power generation and energy demand. Specifically, VPP1 was in the state of purchasing carbon during 08:00–16:00 due to the demand for electricity and selling carbon during the rest of the time; VPP2 was mainly in the state of selling carbon due to the abundance of new energy generation; and VPP3 was in the state of selling carbon due to the abundance of renewable energy generation during 08:00–16:00 and purchasing carbon during the rest of the time.
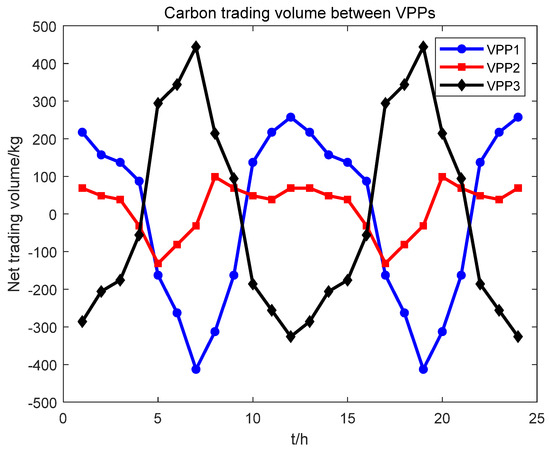
Figure 7.
Carbon trading results between VPPs.
5.2.2. Analysis of the Benefits of Multi-VPP Power-Carbon Co-Trading
Table 2 compares the operating costs before and after VPP participation in the co-operation. The results show that (1) the total benefit of the alliance was improved by CNY 2433.6 and (2) by using the asymmetric bargaining method, the benefits of each VPP were increased by CNY 212.9 (3.04%), CNY 1472.8 (18.68%), and CNY 747.9 (10.97%), respectively. This indicates that the P2P electricity–carbon sharing mechanism not only enhanced the overall efficiency but also ensured the reasonable benefits of each participant through contribution-oriented benefit distribution, achieving a win–win situation for all parties.

Table 2.
Analysis of costs and benefits before and after co-operation.
5.2.3. Analysis of Contribution-Based Revenue Sharing Methodology
Under the VPP electricity–carbon sharing optimisation framework, this study compared two revenue sharing strategies:
(1) Standard Nash bargaining.
(2) Asymmetric Nash bargaining considering the contribution degree.
The comparative analyses in Table 3 and Table 4 show that the revenue enhancement of each VPP under standard Nash bargaining was similar (about CNY809), but it did not take into account the actual contribution difference, which was a fairness defect. In contrast, in the asymmetric Nash bargaining method, VPP2 obtained a higher bargaining factor (2.4671) due to its large contribution, corresponding to a larger revenue allocation; VPP1 and VPP3 had bargaining factors of 0.891 and 1.071, respectively, due to their small new energy output, which resulted in a relatively small revenue allocation. This method effectively solves the shortcomings of the traditional method in terms of fairness.

Table 3.
Distribution of standard model benefits.

Table 4.
Distribution of benefits from asymmetric bargaining models.
5.2.4. Analysis of Carbon Emissions
Table 5 compares the carbon emissions and carbon costs before and after VPP cooperation. The results show that (1) the total carbon emissions decreased from 9758.7 kg to 6251 kg, a 35.94% reduction in emissions, and (2) the carbon cost improved from −162.4 CNY to −863.9 CNY, with an increase in benefits of 701.5 CNY. Despite the slight increase in carbon emissions from VPP2, the significant emission reductions from VPP1 and VPP3 brought about an overall improvement in benefits, mainly due to (1) reduced indirect emissions by reducing the need for purchased electricity and (2) internal carbon trading within the alliance replacing high-cost purchases from the external market. This indicates that the multi-VPP co-operation model effectively promoted carbon emission reduction and economic improvement.

Table 5.
Analysis of carbon emissions before and after VPP cooperation.
5.3. Impact of Uncertainty on Benefits of Multi-VPP Alliances
In order to assess the impact of uncertainty on electricity–carbon trading in multi-VPP alliances, four scenarios (Table 6) were designed in this study and used to validate the effectiveness of the proposed methodology.

Table 6.
Uncertainty scenario settings.
Table 7 compares the operating costs of the VPP and the coalition under different scenarios. The results show that (1) the costs of scenarios 2–4 were all higher than those of scenario 1, which did not take uncertainty into account, indicating that uncertainty management requires sacrificing some of the economic benefits, and (2) the impact of scenario 3 (tariff uncertainty) on the operating economics was significantly larger than that of scenario 2, highlighting the importance of tariff fluctuations in uncertainty management.

Table 7.
Comparison of VPP and coalition operating costs in different scenarios.
In order to verify the uncertainty handling capability of the proposed method, the operating costs of the VPP coalition are compared between the deterministic scheme 1 and scheme 4 of the method in this paper for different numbers of tariff uncertainty periods (Γ) (Table 8). The results show that (1) the cost of scheme 4 was lower than that of scheme 1 for all values of Γ and (2) the cost gap between the two schemes widened significantly as Γ increased. The reason for this is that scheme 1 did not consider the uncertainty and needed extra cost to balance the disturbance, while scheme 4 had stronger robustness and could effectively deal with the system uncertainty by integrating the tariff and new energy output uncertainty. This shows that the proposed method had a significant effect on improving the system’s ability to resist disturbances.

Table 8.
Analysis of the impact of tariff uncertainty factors on VPP operating costs.
6. Conclusions
In this paper, an optimisation strategy for multi-VPP power–carbon sharing operation was constructed, which takes into account the uncertainties of market price and new energy output. In view of the uncertainties of electricity market price and new energy generation, a multi-VPP electricity–carbon sharing operation optimisation model covering multiple uncertainties was constructed based on the Nash negotiation theory. After splitting the model into the cost minimisation subproblem of multi-VPP coalition and the revenue allocation subproblem based on asymmetric bargaining, the model was solved by applying the variable penalty parameter ADMM. In the revenue allocation subproblem based on asymmetric bargaining, an asymmetric bargaining model was constructed to distribute the revenue fairly. The main research results are the following:
(1) The variable penalty parameter ADMM algorithm proposed in this paper can dynamically adjust the penalty factor to improve the convergence speed and stability of the algorithm. It improves the computational efficiency of the model while effectively safeguarding the privacy of VPP information.
(2) The VPP alliance carried out electricity–carbon co-operation and sharing, and compared with the isolated operation of each VPP, the total benefit of the whole alliance increased by CNY 2433.6, and the carbon emission reduced by 3507.7 kg. This effectively reduced the operating cost of the VPP alliance, promoted carbon emission reduction, and achieved the low-carbon economic operation of the alliance.
(3) The constructed multi-VPP asymmetric bargaining revenue distribution model can distribute the revenue fairly after VPP cooperation. In the process of electricity–carbon sharing, the higher the contribution of VPPs is, the more benefits they accordingly obtain. As a result, VPPs are motivated to participate in energy cooperation, which not only promotes the optimal allocation and efficient use of resources, but also greatly enhances the stability of the long-term cooperative relationship between VPPs.
(4) This paper applies the robust optimisation method and the opportunity constraint method to deal with the tariff uncertainty problem as well as the wind and light output uncertainty problem in the process of multi-VPP synergistic operation, which can effectively improve the ability of the VPP alliance to cope with the uncertainty risk.
Author Contributions
Conceptualization, J.Z.; methodology, M.H. and J.Z.; formal analysis, J.Z. and X.S.; Resources, Y.C.; investigation, J.Z. and Y.Z.; data curation, J.Z. and Z.C.; writing—original draft preparation, Y.Z. and Y.L.; writing—review and editing, C.Z. and Q.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research and application of synergistic interaction technology for regional scale user-side resources (grant number: 090000KC22120002).
Data Availability Statement
The data used in this article have been given in detail in the article for the reader’s reference.
Conflicts of Interest
Authors Jun Zhan, Mei Huang, Xiaojia Sun, Yubo Zhang, Zuowei Chen, Yilin Chen and Yang Li were employed by the Shenzhen Power Supply Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Li, J.; Ai, Q.; Yin, S. Market mechanism of virtual power plant participation in peak-frequency regulation service and foreign experience. China J. Electr. Eng. 2022, 42, 37–56. [Google Scholar]
- Kang, C.; Chen, Q.; Su, J.; Ai, Q.; Ji, Y. Scientific issues and research framework of new power system scale-up flexible resource virtual power plant. Power Syst. Autom. 2022, 46, 3–14. [Google Scholar]
- Liu, S.; Ai, Q.; Zheng, J.; Wu, R. Double-layer coordination mechanism and operation strategy of multiple virtual power plants with multiple time scales. Chin. J. Electr. Eng. 2018, 38, 753–761. [Google Scholar]
- Li, R.; Wang, B.; Peng, X.; Lv, H.; Li, S. Dynamic pricing and optimal scheduling of multiple virtual power plants based on master-slave game. Renew. Energy 2024, 42, 986–994. [Google Scholar]
- Huang, Y.; Xue, Y.; Xie, M.; Huang, J.; Shi, S.; Yu, T. Optimisation method for power generation group’s decision-making on electricity-carbon synergistic trading under the price acceptance model. Power Syst. Autom. 2023, 47, 25–35. [Google Scholar]
- Fang, D.; Yang, P. Research on Trading Equilibrium Strategy of Multiple Power Producers and Consumers Under the Synergistic Mechanism of Electricity-Carbon Market. Syst. Eng. Theory Pract. 2024, 44, 1–31. [Google Scholar]
- Lu, Q.; Chen, L.; Mei, S. Typical application of game theory in power systems and some outlooks. Chin. J. Electr. Eng. 2014, 34, 5009–5017. [Google Scholar]
- Lv, H.; Qin, C. Optimal allocation of wind-photovoltaic-hydrogen microgrid capacity based on non-cooperative game. Power Eng. Technol. 2022, 41, 110–118. [Google Scholar]
- Wang, X.; Liu, J.; Wei, S. A non-cooperative game shared energy storage transaction model based on blockchain technology. J. Nanjing Univ. Inf. Eng. (Nat. Sci. Ed.) 2022, 14, 595–603. [Google Scholar]
- Liu, C.; Liu, W.; Gao, X.; Liu, Z.; Deng, S.; Liu, G. Coordinated planning of distribution network-multi integrated energy system based on master-slave game. Power Autom. Equip. 2022, 42, 45–52. [Google Scholar]
- Liu, W.; Chen, Z.; Du, P.; Chen, J.; Li, B. A model of multi-virtual power plants participating in day-ahead power market bidding based on coalition game. Power Autom. Equip. 2024, 44, 135–142. [Google Scholar]
- Jiang, C.; Ou, Q.; Wu, Z.; Zhang, J. Joint allocation and optimisation of shared energy storage in multiple microgrids based on coalition game. China Electr. Power 2022, 55, 11–21. [Google Scholar]
- Cui, M.; Xuan, M.; Lu, Z.; He, L. Operation optimisation strategy of multiple integrated energy service providers based on cooperative game. Chin. J. Electr. Eng. 2022, 42, 3548–3564. [Google Scholar]
- Li, T.; Zhao, X.; Zheng, Y.; Zhang, D. Optimal allocation of regional integrated energy system based on Nash negotiation considering energy sharing. Power Syst. Prot. Control 2023, 51, 22–32. [Google Scholar]
- Su, Z.; Li, W.; Liang, X.; Chen, T.; Zeng, S.; Yu, Z. Optimal scheduling of virtual power plants considering stepped carbon trading and integrated demand response. China Electr. Power 2023, 56, 174–182. [Google Scholar]
- Zhang, J.; Jiang, X.; Duan, S.; Li, Q. Research on bidding strategies for virtual power plants to participate in the operation of the joint electricity-carbon market. Power Syst. Prot. Control 2023, 51, 108–118. [Google Scholar] [CrossRef]
- Zhong, R.; Zhang, Y.; Zhu, S.; Xie, S. A study on low-carbon operation strategy of virtual power plant alliance and distribution network synergy based on electricity-carbon peer-to-peer trading. Grid Technol. 2024, 48, 3554–3563. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Z.; Yang, C.; Yuan, G.; Tang, L. Multi-virtual power plant electricity-carbon joint optimization modelling and solution. Power Syst. Autom 2024, 48, 29–40. [Google Scholar]
- Rostam, K.J.; Haydar, S.S. Making the optimal decision for production by using the fuzzy linear programming method. Meas. Sens. 2022, 24, 100559. [Google Scholar] [CrossRef]
- Lee, J.; Bae, S.; Kim, W.C.; Lee, Y. Value function gradient learning for large-scale multistage stochastic programming problems. Eur. J. Oper. Res. 2023, 308, 321–335. [Google Scholar] [CrossRef]
- Zdraveski, V.; Vuletic, J.; Angelov, J.; Todorovski, M. Radial distribution network planning under uncertainty by implementing robust optimisation. Int. J. Electr. Power Energy Syst. 2023, 149, 109043. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Liu, C. Research on the integrated energy production unit self dispatch offer strategy considering photovoltaic and electricity price uncertainty. Grid Technol. 2023, 47, 2713–2727. [Google Scholar]
- Zhou, L.; Yu, H.; Li, P.; Wang, C. Stochastic robust operation optimisation of an integrated energy system in a park under multi-principal market. Power Syst. Autom. 2023, 47, 100–109. [Google Scholar]
- Luo, Q.; Zhu, J. Optimal scheduling of electricity-gas integrated energy system based on improved alternating direction multiplier method. J. Electrotechnol. 2024, 39, 2797–2809. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).