Modeling Retail Buildings Within Renewable Energy Communities: Generation and Implementation of Reference Energy Use Profiles
Abstract
1. Introduction
“Industrial and commercial users may take the lead in the spread of these types of configuration, leveraging their remarkable prospect of capital investment.”
2. Materials and Methods
- EE use profile generation from the exiting database;
- Integration of the EE use profile in the RECON beta testing environment;
- Model validation.
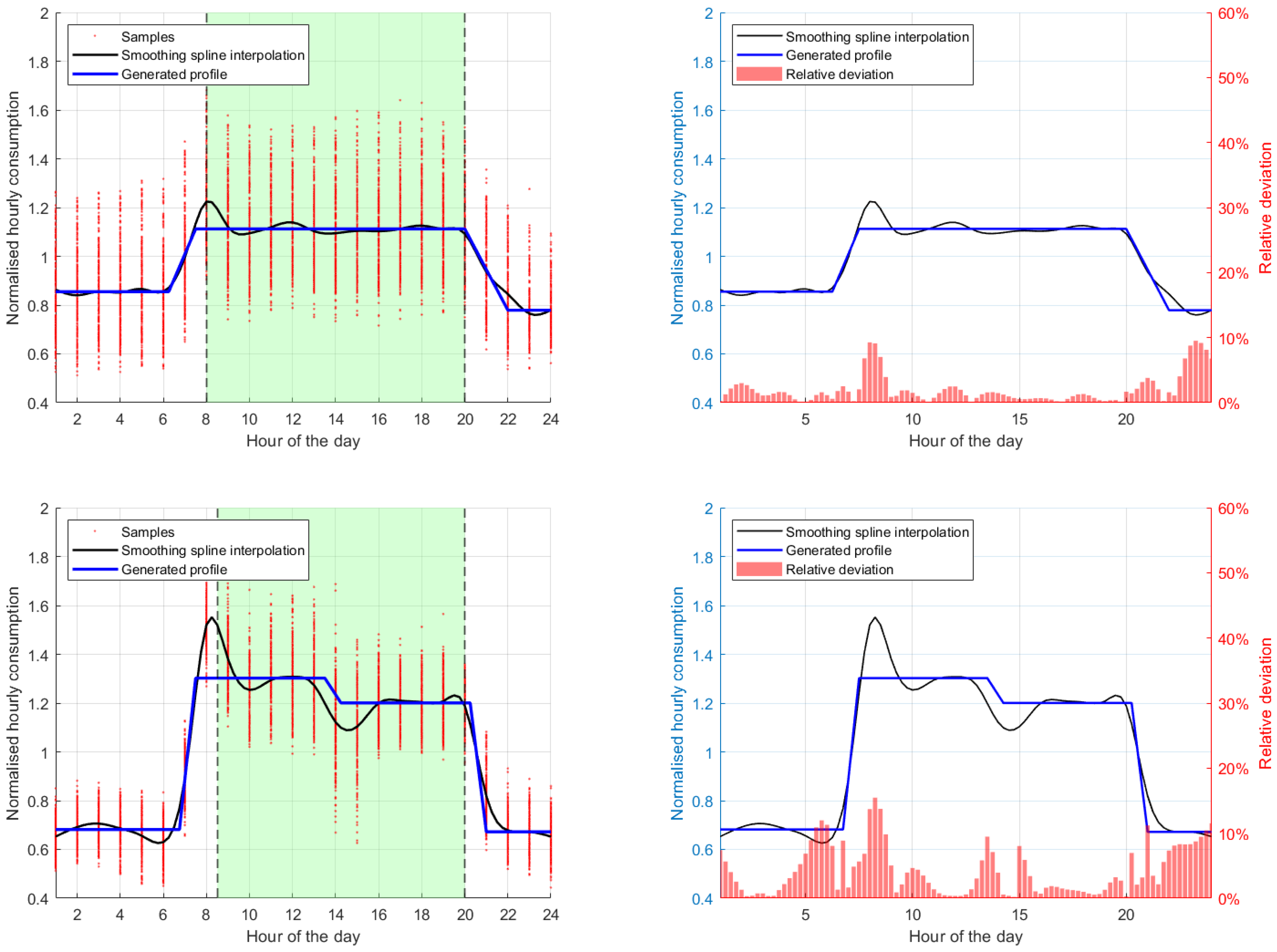
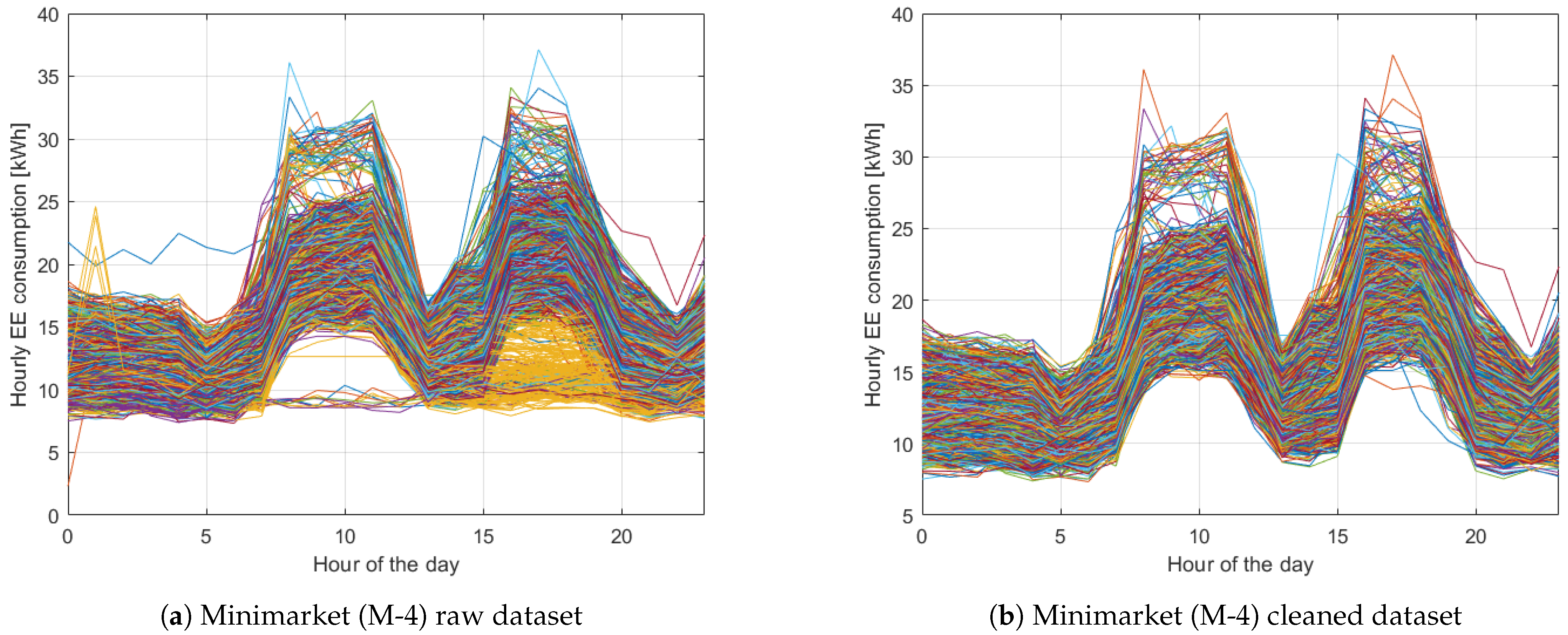
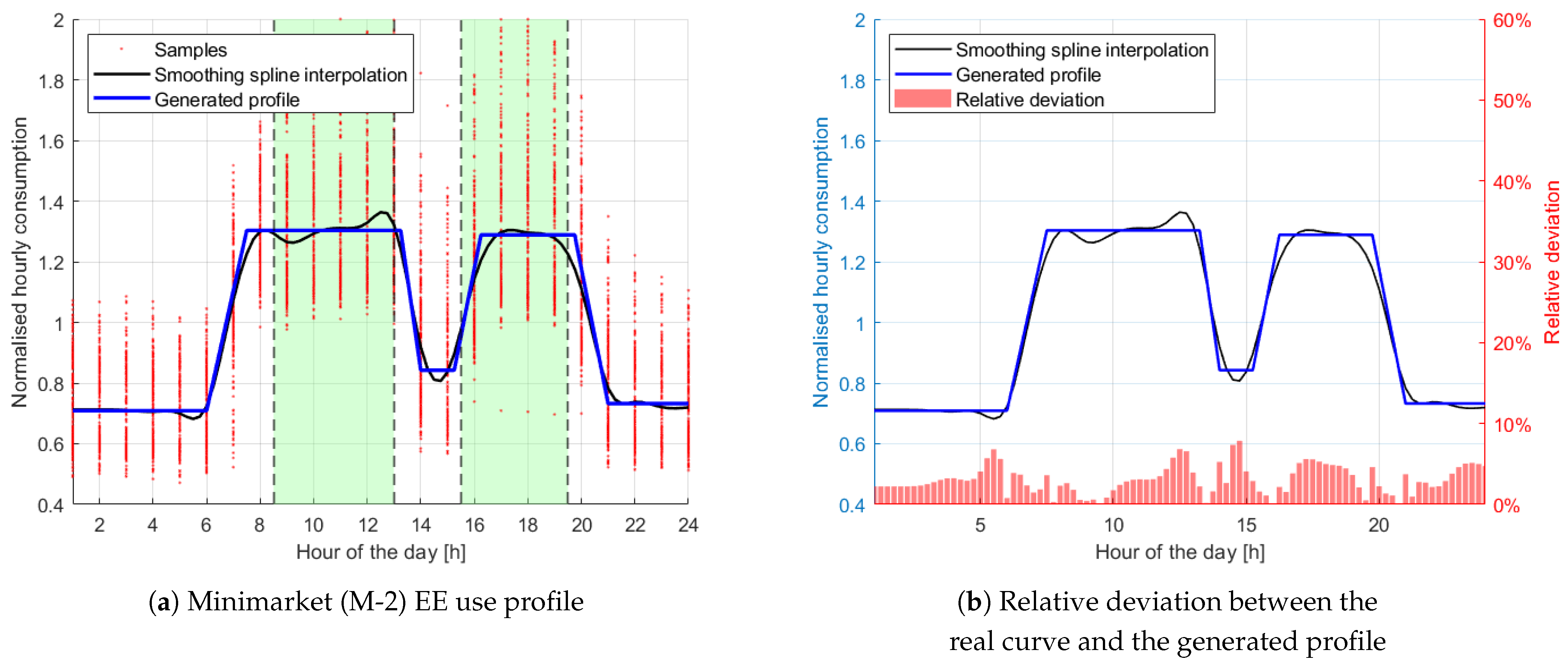
2.1. EE Use Profile Generation from Exiting Database
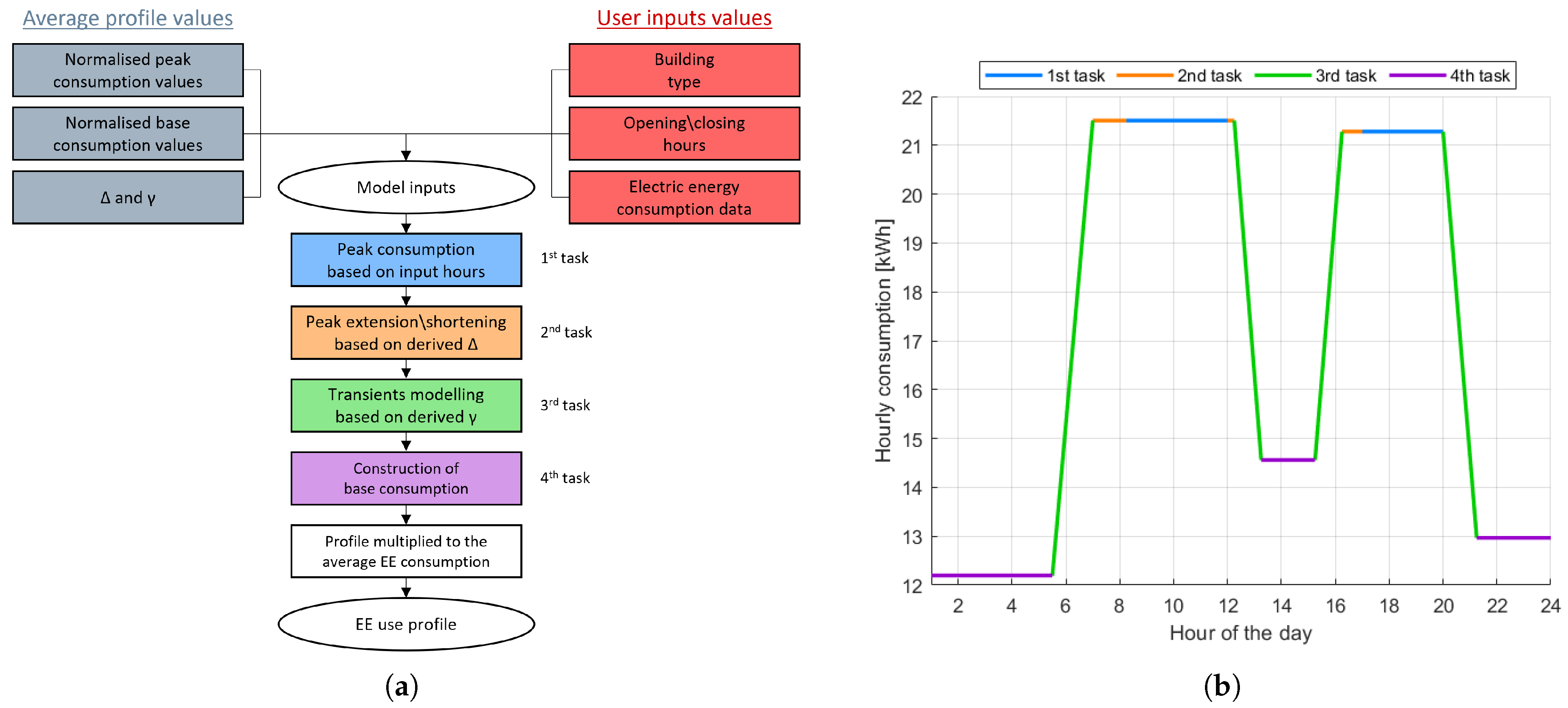
2.2. Integration of the EE Use Profile in RECON Beta Testing Environment
- -
- The normalized values of peak consumption;
- -
- The normalized values of base consumption, i.e., associated with the closing periods;
- -
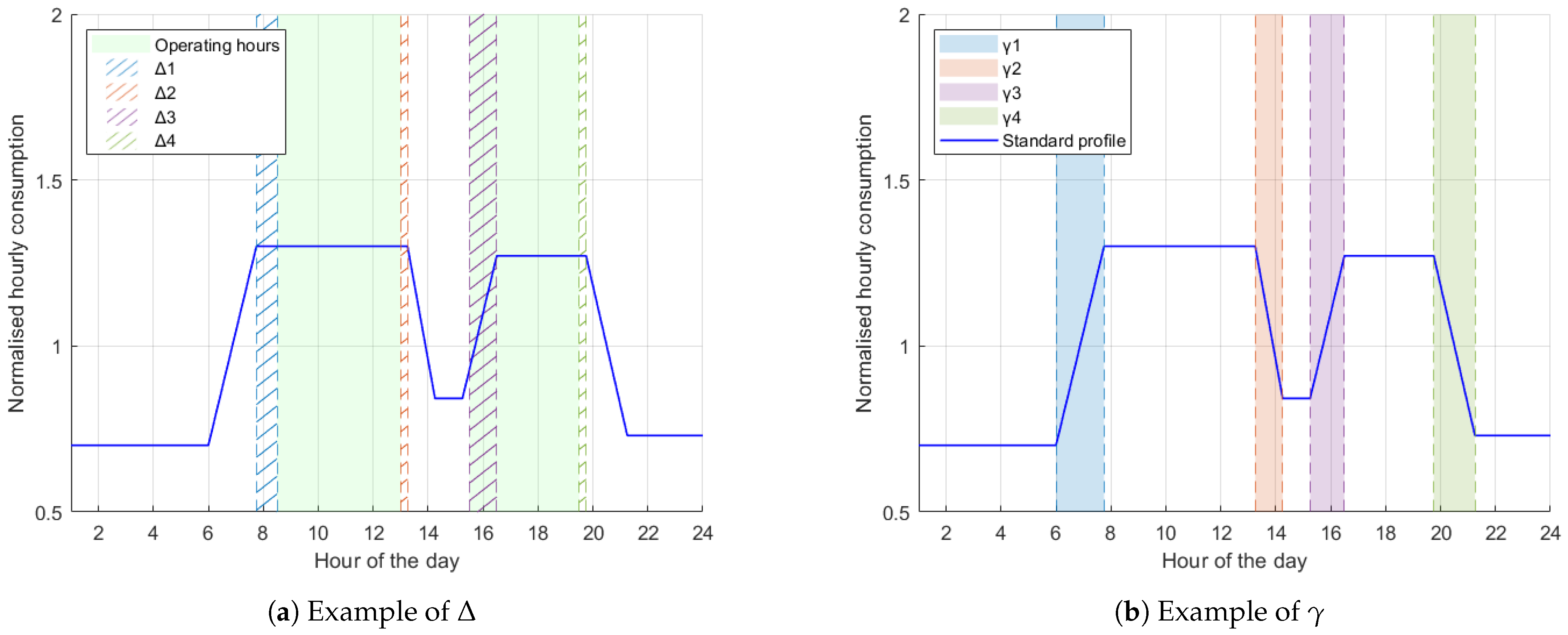
- The difference between the OLSR’s actual opening/closing hours and the opening/closing hours derived from the reference database in Section 2.1, defined as (one value for each opening/closing);
- -
- The duration of the transition periods between base load and peak load (hereinafter also called “transients” for brevity), defined as (one value for each transient).
- The duration of peak consumption is modeled using the input hours, and then, the model extends or reduces the duration of peak consumption based on the reference ;
- Then, it constructs the transients by considering their duration (), after which it fills the base segments of the remaining sections;
- Finally, the model calculates the average hourly consumption using the aggregated EE data and multiplies the modeled normalized profile with the value just obtained, in order to have an estimated hourly consumption profile on a daily basis.
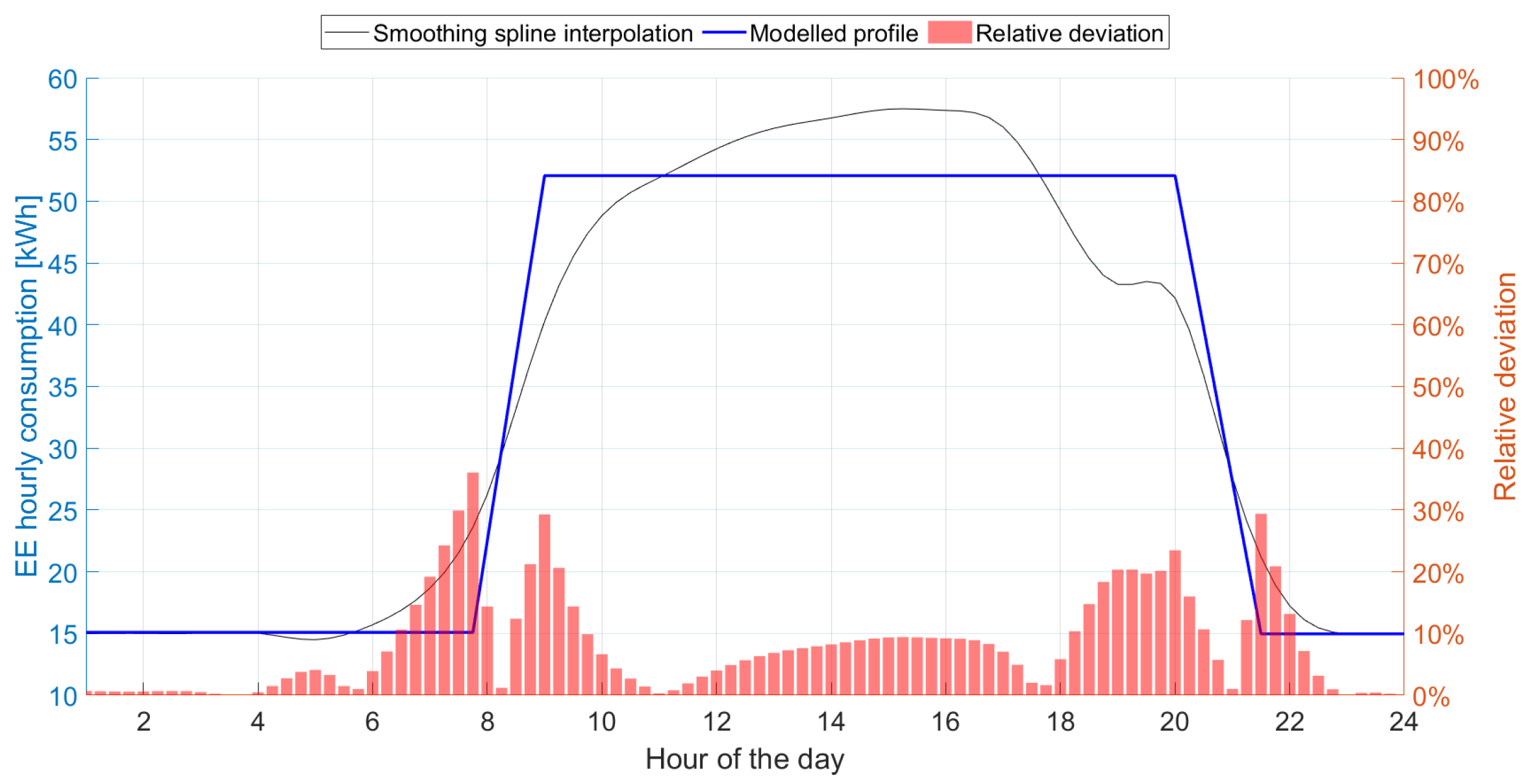
2.3. Validation of the Model
3. Results
3.1. EE Use Profile Generation from Exiting Database
3.2. Integration of the EE Use Profile into RECON Beta Testing Environment
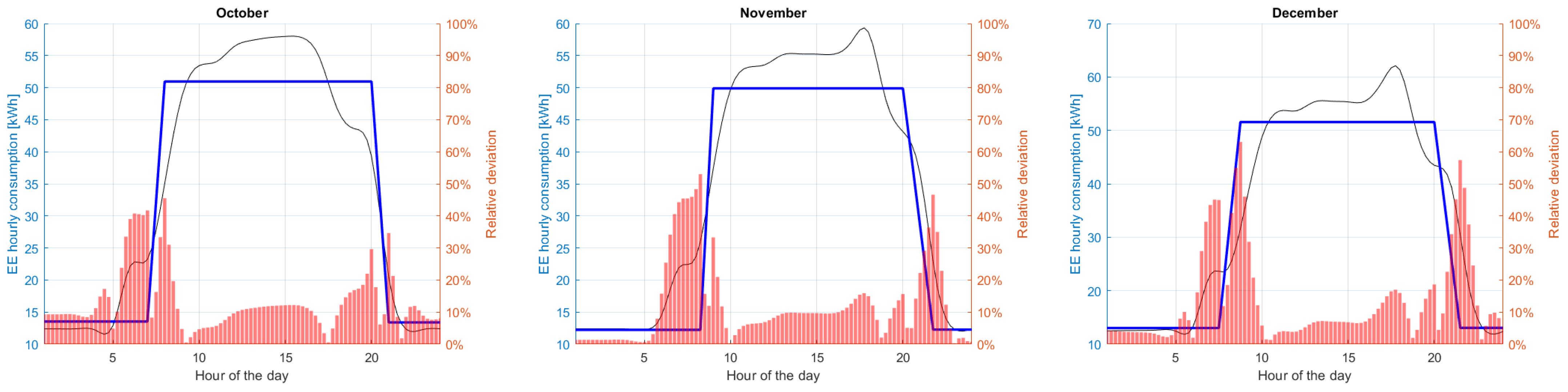
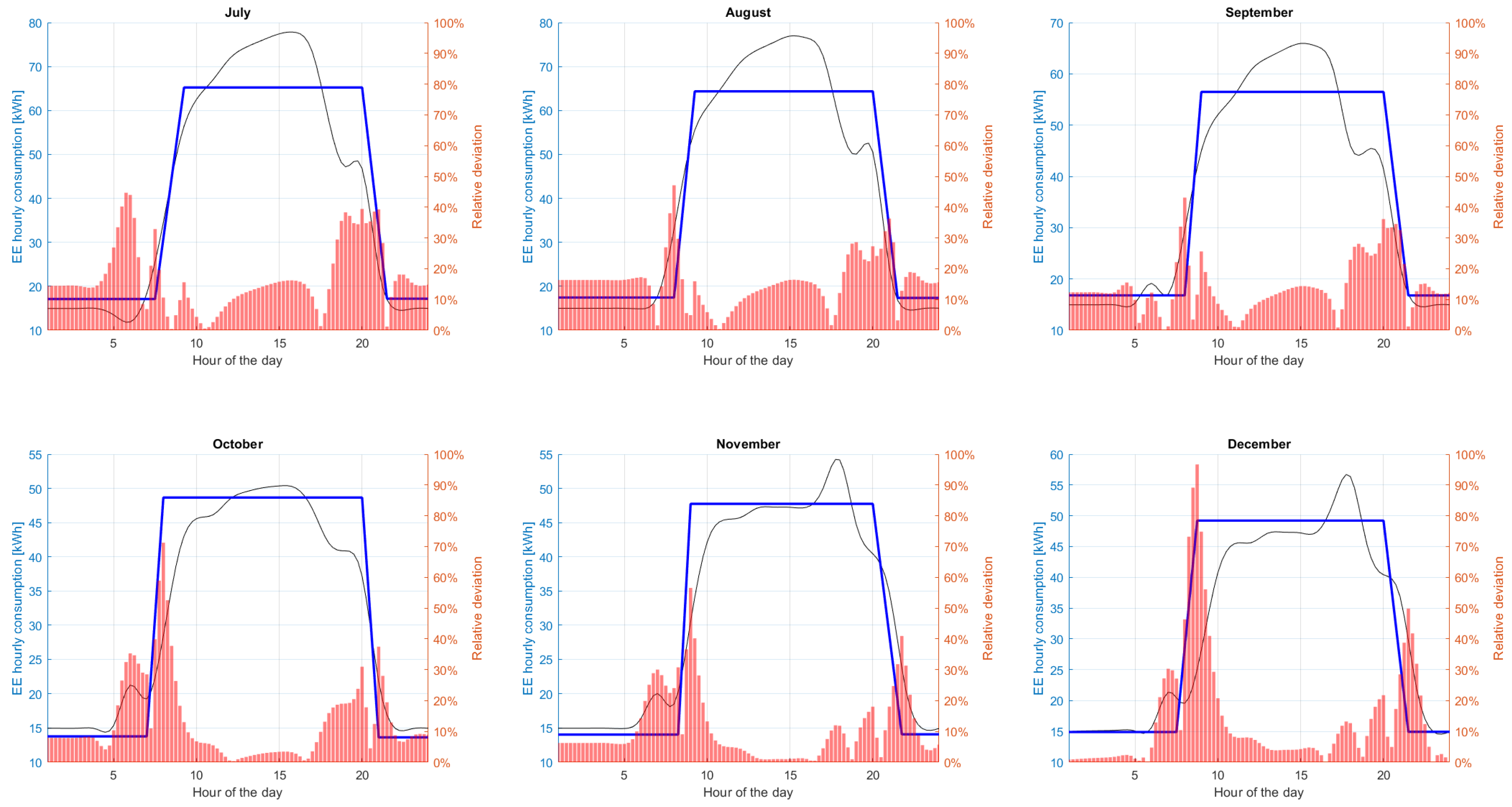
3.3. Validation of the Model
4. Discussion
5. Conclusions
- The developed algorithm successfully generates normalized EE use profiles for both minimarkets and superstores starting from raw data;
- A data-driven model was successfully developed and integrated in the RECON beta testing environment, allowing electric energy use profile generation with minimal inputs (opening/closing times, building type, and aggregated consumption);
- Validation on an annual basis demonstrated a low mean average relative deviation (approximately 4–11%), while monthly simulations highlighted larger discrepancies during cold months, likely due to heating system influences;
- These results indicate that while the model is robust for overall consumption trends, further refinement is needed to accurately capture transient behaviors and climatic factors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARERA | Autorità di Regolazione per Energia Reti e Ambiente |
| CNN | Convolutional Neural Networks |
| EE | Electric Energy |
| EU | European Union |
| EV | Electric Vehicle |
| OLSR | Organized Large-Scale Retail |
| REC | Renewable Energy Community |
| RECON | Renewable Energy Community ecONomic simulator |
| RED | Renewable Energy Directive |
| RES | Renewable Energy Source |
| SME | Small and Medium Enterprise |
| SVR | Support Vector Regression |
Appendix A

Appendix B




References
- European Commission. 2050 Long-Term Strategy. Available online: https://climate.ec.europa.eu/eu-action/climate-strategies-targets/2050-long-term-strategy_en (accessed on 2 February 2025).
- European Commission. The European Green Deal. 11 December 2019. Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:b828d165-1c22-11ea-8c1f-01aa75ed71a1.0002.02/DOC_1&format=PDF (accessed on 2 February 2025).
- Ahmad, T.; Zhang, D. A critical review of comparative global historical energy consumption and future demand: The story told so far. Energy Rep. 2020, 6, 1973–1991. [Google Scholar] [CrossRef]
- Mehedintu, A.; Sterpu, M.; Soava, G. Estimation and Forecasts for the Share of Renewable Energy Consumption in Final Energy Consumption by 2020 in the European Union. Sustainability 2018, 10, 1515. [Google Scholar] [CrossRef]
- European Commission. Directive (EU) 2018/2001 of the European Parliament and of the Council on the Promotion of the Use of Energy from Renewable Sources. 11 December 2018. Available online: https://eur-lex.europa.eu/legal-content/IT/TXT/PDF/?uri=CELEX:32018L2001 (accessed on 7 February 2025).
- European Commission. Directive (EU) 2023/2413 of the European Parliament and of the Council of 18 October 2023 Amending Directive (EU) 2018/2001, Regulation (EU) 2018/1999 and Directive 98/70/EC as Regards the Promotion of Energy from Renewable Sources, and Repealing Council Directive (EU) 2015/652. 18 October 2023. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=OJ:L_202302413 (accessed on 7 February 2025).
- Rossetto, N. Beyond Individual Active Customers: Citizen and Renewable Energy Communities in the European Union. IEEE Power Energy Mag. 2023, 21, 36–44. [Google Scholar] [CrossRef]
- Soeiro, S.; Ferreira Dias, M. Renewable energy community and the European energy market: Main motivations. Heliyon 2020, 6, e04511. [Google Scholar] [CrossRef]
- Ahmed, S.; Ali, A.; D’Angola, A. A Review of Renewable Energy Communities: Concepts, Scope, Progress, Challenges, and Recommendations. Sustainability 2024, 16, 1749. [Google Scholar] [CrossRef]
- Bauwens, T. Explaining the diversity of motivations behind community renewable energy. Energy Policy 2016, 93, 278–290. [Google Scholar] [CrossRef]
- Hanke, F.; Lowitzsch, J. Empowering Vulnerable Consumers to Join Renewable Energy Communities—Towards an Inclusive Design of the Clean Energy Package. Energies 2020, 13, 1615. [Google Scholar] [CrossRef]
- Soeiro, S.; Ferreira Dias, M. Community renewable energy: Benefits and drivers. Energy Rep. 2020, 6, 134–140. [Google Scholar] [CrossRef]
- Veronese, E.; Lauton, L.; Barchi, G.; Prada, A.; Trovato, V. Impact of Non-Residential Users on the Energy Performance of Renewable Energy Communities Considering Clusterization of Consumptions. Energies 2024, 17, 3984. [Google Scholar] [CrossRef]
- Tatti, A.; Ferroni, S.; Ferrando, M.; Motta, M.; Causone, F. The Emerging Trends of Renewable Energy Communities’ Development in Italy. Sustainability 2023, 15, 6792. [Google Scholar] [CrossRef]
- ENEA. RECON—Simulatore per Comunità Energetiche Rinnovabili. 2024. Available online: https://recon.smartenergycommunity.enea.it/ (accessed on 13 March 2025).
- Gestore dei Servizi Energetici (GSE). Portale Autoconsumo—Comunità Energetiche Rinnovabili. 2024. Available online: https://www.autoconsumo.gse.it/ (accessed on 13 March 2025).
- E-360. E-360—Soluzioni per Comunità Energetiche. 2024. Available online: https://www.e-360.it/ (accessed on 13 March 2025).
- MyGreenEnergy. Costruisci la tua Comunità Energetica—Simulatore. 2024. Available online: https://www.mygreenenergy.it/costruisci-la-tua-comunita-energetica#calcola (accessed on 13 March 2025).
- Giannuzzo, L.; Minuto, F.D.; Schiera, D.S.; Lanzini, A. Reconstructing hourly residential electrical load profiles for Renewable Energy Communities using non-intrusive machine learning techniques. Energy AI 2024, 15, 100329. [Google Scholar] [CrossRef]
- Di Silvestre, M.L.; Montana, F.; Sanseverino, E.R.; Sciumè, G.; Zizzo, G. An algorithm for renewable energy communities designing by maximizing shared energy. In Proceedings of the 2023 AEIT International Annual Conference (AEIT), Rome, Italy, 5–7 October 2023; pp. 1–6. [Google Scholar]
- Di Somma, M.; Dolatabadi, M.; Burgio, A.; Siano, P.; Cimmino, D.; Bianco, N. Optimizing virtual energy sharing in renewable energy communities of residential users for incentives maximization. Sustain. Energy Grids Netw. 2024, 39, 101492. [Google Scholar] [CrossRef]
- Belloni, E.; Fioriti, D.; Poli, D. Optimal design of renewable energy communities (RECs) in Italy: Influence of composition, market signals, buildings, location, and incentives. Electr. Power Syst. Res. 2024, 235, 110895. [Google Scholar] [CrossRef]
- Sun, Y.; Haghighat, F.; Fung, B.C. A review of the-state-of-the-art in data-driven approaches for building energy prediction. Energy Build. 2020, 221, 110022. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Data-driven estimation of building energy consumption with multi-source heterogeneous data. Appl. Energy 2020, 268, 114965. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Liu, Y.; Wu, H. A Review of Data-Driven Building Energy Prediction. Buildings 2023, 13, 532. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Ferrando, M.; Banfi, A.; Causone, F. Changes in energy use profiles derived from electricity smart meter readings of residential buildings in Milan before, during and after the COVID-19 main lockdown. Sustain. Cities Soc. 2023, 99, 104876. [Google Scholar] [CrossRef]
- Huang, Y.; Xiong, N.; Liu, C. Renewable energy technology innovation and ESG greenwashing: Evidence from supervised machine learning methods using patent text. J. Environ. Manag. 2024, 370, 122833. [Google Scholar] [CrossRef]
- Lari, A.J.; Sanfilippo, A.P.; Bachour, D.; Perez-Astudillo, D. Using Machine Learning Algorithms to Forecast Solar Energy Power Output. Electronics 2025, 14, 866. [Google Scholar] [CrossRef]
- Mikkola, J.; Lund, P.D. Models for generating place and time dependent urban energy demand profiles. Appl. Energy 2014, 130, 256–264. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T. Generating realistic building electrical load profiles through the Generative Adversarial Network (GAN). Energy Build. 2020, 224, 110299. [Google Scholar] [CrossRef]
- Lombardi, F.; Balderrama, S.; Quoilin, S.; Colombo, E. Generating high-resolution multi-energy load profiles for remote areas with an open-source stochastic model. Energy 2019, 177, 433–444. [Google Scholar] [CrossRef]
- Bayram, I.S.; Saffouri, F.; Koc, M. Generation, analysis, and applications of high resolution electricity load profiles in Qatar. J. Clean. Prod. 2018, 183, 527–543. [Google Scholar] [CrossRef]
- Rana, M.; Sethuvenkatraman, S.; Goldsworthy, M. A data-driven approach based on quantile regression forest to forecast cooling load for commercial buildings. Sustain. Cities Soc. 2022, 76, 103511. [Google Scholar] [CrossRef]
- Granell, R.; Axon, C.J.; Kolokotroni, M.; Wallom, D.C. A reduced-dimension feature extraction method to represent retail store electricity profiles. Energy Build. 2022, 276, 112508. [Google Scholar] [CrossRef]
- Orr, M. Short-Term Electrical Load Forecasting for Irish Supermarkets with Weather Forecast Data. Ph.D. Thesis, National College of Ireland, Dublin, Ireland, 2021. [Google Scholar]
- Chuan, L.; Ukil, A. Modeling and Validation of Electrical Load Profiling in Residential Buildings in Singapore. IEEE Trans. Power Syst. 2015, 30, 2800–2809. [Google Scholar] [CrossRef]
- Czétány, L.; Vámos, V.; Horváth, M.; Szalay, Z.; Mota-Babiloni, A.; Deme-Bélafi, Z.; Csoknyai, T. Development of electricity consumption profiles of residential buildings based on smart meter data clustering. Energy Build. 2021, 252, 111376. [Google Scholar] [CrossRef]
- Khan, A.N.; Iqbal, N.; Rizwan, A.; Ahmad, R.; Kim, D.H. An Ensemble Energy Consumption Forecasting Model Based on Spatial-Temporal Clustering Analysis in Residential Buildings. Energies 2021, 14, 3020. [Google Scholar] [CrossRef]
- Ramírez-Mendiola, J.L.; Grünewald, P.; Eyre, N. The diversity of residential electricity demand – A comparative analysis of metered and simulated data. Energy Build. 2017, 151, 121–131. [Google Scholar] [CrossRef]
- Khan, I.; Jack, M.W.; Stephenson, J. Identifying residential daily electricity-use profiles through time-segmented regression analysis. Energy Build. 2019, 194, 232–246. [Google Scholar] [CrossRef]
- Batra, N.; Parson, O.; Berges, M.; Singh, A.; Rogers, A. A comparison of non-intrusive load monitoring methods for commercial and residential buildings. arXiv 2014, arXiv:1408.6595. [Google Scholar] [CrossRef]
- Coakley, D.; Raftery, P.; Keane, M. A review of methods to match building energy simulation models to measured data. Renew. Sustain. Energy Rev. 2014, 37, 123–141. [Google Scholar] [CrossRef]
- MathWorks. Matlab R2024b. 2024. Available online: https://it.mathworks.com/products/new_products/latest_features.html (accessed on 27 March 2025).
- European Commission. Directive 2004/22/EC of the European Parliament and of the Council of 31 March 2004 on Measuring Instruments. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32014L0032 (accessed on 22 February 2025).
- Köppen, W. Klassification der Klimate nach Temperatur, Niederschlag und Jahreslauf. 1918. Available online: https://koeppen-geiger.vu-wien.ac.at/pdf/Koppen_1918.pdf (accessed on 17 February 2025).
- Huang, G. Missing data filling method based on linear interpolation and lightgbm. J. Phys. Conf. Ser. 2021, 1754, 012187. [Google Scholar] [CrossRef]
- Mohamed Noor, N.; Yahaya, A.S.; Ramli, N.; Abdullah, M.M.A.B. Filling Missing Data Using Interpolation Methods: Study on the Effect of Fitting Distribution. Key Eng. Mater. 2013, 594–595, 889–895. [Google Scholar] [CrossRef]
- Murti, D.M.P.; Pujianto, U.; Wibawa, A.P.; Akbar, M.I. K-Nearest Neighbor (K-NN) based Missing Data Imputation. In Proceedings of the 2019 5th International Conference on Science in Information Technology (ICSITech), Yogyakarta, Indonesia, 23–24 October 2019; pp. 83–88. [Google Scholar] [CrossRef]
- Batista, G.E.; Monard, M.C. A study of K-nearest neighbour as an imputation method. In Proceedings of the Soft Computing Systems—Design, Management and Applications, HIS 2002, Santiago, Chile, 1–4 December 2002; Volume 87, p. 48. [Google Scholar]
- Ma, X.; Han, Y.; Qin, H.; Wang, P. KNN data filling algorithm for incomplete interval-valued fuzzy soft sets. Int. J. Comput. Intell. Syst. 2023, 16, 30. [Google Scholar] [CrossRef]
- Zhang, S. Nearest neighbor selection for iteratively kNN imputation. J. Syst. Softw. 2012, 85, 2541–2552. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, S.; Cai, G.; Li, L.; Pan, Q.; Yan, J.; Ning, G. Adjusted weight voting algorithm for random forests in handling missing values. Pattern Recognit. 2017, 69, 52–60. [Google Scholar] [CrossRef]
- Tang, F.; Ishwaran, H. Random forest missing data algorithms. Stat. Anal. Data Min. Asa Data Sci. J. 2017, 10, 363–377. [Google Scholar] [CrossRef] [PubMed]
- Humaira, H.; Rasyidah, R. Determining The Appropiate Cluster Number Using Elbow Method for K-Means Algorithm. In Proceedings of the 2nd Workshop on Multidisciplinary and Applications (WMA), Padang, Indonesia, 24–25 January 2020. [Google Scholar] [CrossRef]
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration K-Means Clustering Method and Elbow Method for Identification of The Best Customer Profile Cluster. IOP Conf. Ser. Mater. Sci. Eng. 2018, 336, 012017. [Google Scholar] [CrossRef]
- Cui, M. Introduction to the K-Means Clustering Algorithm Based on the Elbow Method. Geosci. Remote Sens. 2020, 3, 9–16. [Google Scholar] [CrossRef]
- Cerquitelli, T.; Chicco, G.; Corso, E.D.; Ventura, F.; Montesano, G.; Armiento, M.; González, A.M.; Santiago, A.V. Clustering-Based Assessment of Residential Consumers from Hourly-Metered Data. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Seville, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Berggren, B.; Wall, M. Two Methods for Normalisation of Measured Energy Performance—Testing of a Net-Zero Energy Building in Sweden. Buildings 2017, 7, 86. [Google Scholar] [CrossRef]
- Wendland, H.; Rieger, C. Approximate Interpolation with Applications to Selecting Smoothing Parameters. Numer. Math. 2005, 101, 729–748. [Google Scholar] [CrossRef]
- Haszpra, L.; Prácser, E. Uncertainty of hourly-average concentration values derived from non-continuous measurements. Atmos. Meas. Tech. 2021, 14, 3561–3571. [Google Scholar] [CrossRef]
- The MathWorks, I. Fminbnd. 2006. Available online: https://it.mathworks.com/help/releases/R2024b/matlab/ref/fminbnd.html (accessed on 29 March 2025).
- ARERA. Fasce Orarie. Available online: https://www.arera.it/bolletta/glossario-dei-termini/dettaglio/fasce-orarie (accessed on 29 March 2025).
- N.R.E. Laboratory, Commercial Reference Buildings. 2014. Available online: https://en.openei.org/datasets/files/961/pub/ (accessed on 21 December 2024).
- ASHRAE Climatic Data for Building Design Standards. 2021. Available online: https://www.ashrae.org/file%20library/technical%20resources/standards%20and%20guidelines/standards%20addenda/169_2020_a_20211029.pdf (accessed on 15 October 2024).
- Deru, M.; Field, K.; Studer, D.; Benne, K.; Griffith, B.; Torcellini, P.; Liu, B.; Halverson, M.; Winiarski, D.; Rosenberg, M.; et al. Commercial Reference Building: Strip Mall. 2014. Available online: https://data.openei.org/submissions/169 (accessed on 3 October 2024).
- Deru, M.; Field, K.; Studer, D.; Benne, K.; Griffith, B.; Torcellini, P.; Liu, B.; Halverson, M.; Winiarski, D.; Rosenberg, M.; et al. Commercial Reference Building: Supermarket. 2014. Available online: https://data.openei.org/submissions/170 (accessed on 3 October 2024).
- Deru, M.; Field, K.; Studer, D.; Benne, K.; Griffith, B.; Torcellini, P.; Liu, B.; Halverson, M.; Winiarski, D.; Rosenberg, M.; et al. Commercial Reference Building: Stand-Alone Retail. 2014. Available online: https://data.openei.org/submissions/168 (accessed on 3 October 2024).




| Reference | Type | Total Area [m2] | Power at the Net Meter [kW] | Installed PV Capacity [kW] | EV Charging Station |
|---|---|---|---|---|---|
| M-1 | Minimarket 1 | 130 | 15 | - | No |
| M-2 | Minimarket | 1130 | 63 | - | No |
| M-3 | Minimarket | 1309 | 100 | - | No |
| M-4 | Minimarket | 450 | 75 | - | No |
| S-1 | Superstore | 2247 | 250 | - | No |
| S-2 | Superstore | 2730 | 250 | - | No |
| S-3 | Superstore | 9569 | 498 | 63.75 | Yes |
| Variables | Unit of Measure |
|---|---|
| Location | - |
| Opening hours | - |
| Hourly electric consumption | |
| Total area | |
| Grid meter active power | |
| Nominal installed PV power | |
| Nominal installed Electric vehicles (EV) charging station power |
| Reference | Type | Average Relative Deviation [%] |
|---|---|---|
| M-1 | Minimarket 1 | - |
| M-2 | Minimarket | 3.10 |
| M-3 | Minimarket | 2.82 |
| M-4 | Minimarket | 3.29 |
| S-1 | Superstore | 2.05 |
| S-2 | Superstore | 4.30 |
| S-3 | Superstore | 3.99 |
| Month | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| January | −1 | 0.25 | 0.75 | 0 |
| February | −1 | 0.25 | 0.75 | 0 |
| March | −1 | 0 | 0.75 | 0 |
| April | −1 | −0.25 | 0.75 | 0 |
| May | −1 | 0.25 | 0.75 | 0.25 |
| June | 0 | 0.25 | 0.75 | 0 |
| July | 0.25 | 0.25 | 0.5 | 0 |
| August | 0.25 | 0 | 0.75 | 0 |
| September | −1 | 0.25 | 0.75 | 0 |
| October | −1 | 0 | 0.75 | 0 |
| November | −1 | 0.25 | 0.75 | 0 |
| December | −1.25 | 0 | 0.75 | 0 |
| Mode | −1 | 0.25 | 0.75 | 0 |
| Month | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| January | 1.5 | 1 | 1 | 1.25 |
| February | 1 | 1 | 1 | 1.25 |
| March | 1.25 | 1 | 1 | 1.5 |
| April | 1.5 | 1 | 1 | 1.75 |
| May | 1.25 | 1 | 1 | 1.75 |
| June | 1.5 | 0.75 | 1 | 1.75 |
| July | 1.5 | 1 | 1 | 1.75 |
| August | 1.5 | 1 | 1.25 | 1.75 |
| September | 1.5 | 1 | 1 | 1.25 |
| October | 1.5 | 1.25 | 1 | 1.25 |
| November | 1.5 | 0.75 | 1 | 1.25 |
| December | 1.5 | 1 | 1.25 | 1.5 |
| Mode | 1.5 | 1 | 1 | 1.25 |
| (a) | ||||
| Month | 1 | 2 | 3 | 4 |
| January | 1.25 | - | - | 1.25 |
| February | 1.25 | - | - | 1.25 |
| March | 1.25 | - | - | 1.25 |
| April | 1 | - | - | 1.5 |
| May | 1 | - | - | 1.5 |
| June | 1.5 | - | - | 1.5 |
| July | 1.75 | - | - | 1.5 |
| August | 1.25 | - | - | 1.5 |
| September | 1 | - | - | 1.5 |
| October | 1 | - | - | 1 |
| November | 0.75 | - | - | 1.75 |
| December | 1.25 | - | - | 1.5 |
| Mode | 1.25 | - | - | 1.5 |
| (b) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozza, S.; Caldera, M.; Fava, D.; Ferrando, M.; Causone, F. Modeling Retail Buildings Within Renewable Energy Communities: Generation and Implementation of Reference Energy Use Profiles. Energies 2025, 18, 2368. https://doi.org/10.3390/en18092368
Lozza S, Caldera M, Fava D, Ferrando M, Causone F. Modeling Retail Buildings Within Renewable Energy Communities: Generation and Implementation of Reference Energy Use Profiles. Energies. 2025; 18(9):2368. https://doi.org/10.3390/en18092368
Chicago/Turabian StyleLozza, Samuele, Matteo Caldera, Daniele Fava, Martina Ferrando, and Francesco Causone. 2025. "Modeling Retail Buildings Within Renewable Energy Communities: Generation and Implementation of Reference Energy Use Profiles" Energies 18, no. 9: 2368. https://doi.org/10.3390/en18092368
APA StyleLozza, S., Caldera, M., Fava, D., Ferrando, M., & Causone, F. (2025). Modeling Retail Buildings Within Renewable Energy Communities: Generation and Implementation of Reference Energy Use Profiles. Energies, 18(9), 2368. https://doi.org/10.3390/en18092368








