A Fault Diagnosis Framework for Pressurized Water Reactor Nuclear Power Plants Based on an Improved Deep Subdomain Adaptation Network
Abstract
1. Introduction
- (1)
- proposing an improved DSAN-based fault diagnosis framework;
- (2)
- introducing weighted Focal Loss to enhance classification performance for minority-class samples, as well as incorporating a confidence-based pseudo-label calibration mechanism to improve fault classification in small-sample and class-imbalanced scenarios.
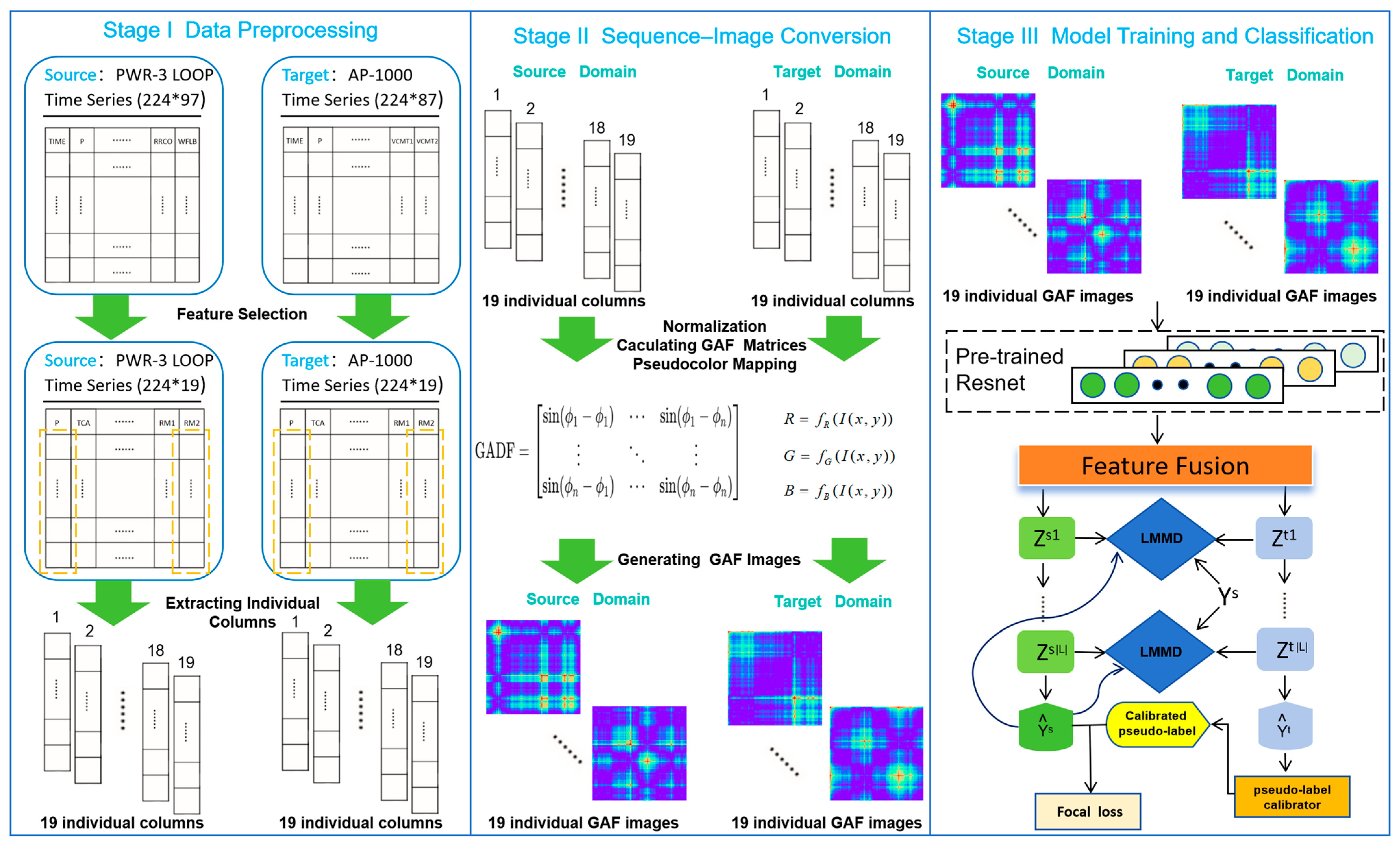
2. Fault Diagnosis Framework Based on an Improved DSAN
- Stage I—Data Preprocessing:
- Stage II—Sequence–Image Conversion:
- Stage III—Model Training and Classification:
2.1. Data Preprocessing
2.1.1. Datasets
2.1.2. Feature Selection
2.1.3. Extracting Individual Columns
2.2. Sequence–Image Conversion
2.2.1. Gramian Angular Field
2.2.2. Pseudo-Color Mapping
2.3. Model Training and Classification
2.3.1. Pre-Trained Resnet
2.3.2. Feature Fusion
- Initialization of weights
- 2.
- Hadamard product and feature weighting
- 3.
- Feature summation
- 4.
- Non-linear activation
- 5.
- Backpropagation and weight update
2.3.3. DSAN
2.4. Improvements Based on DSAN
2.4.1. Confidence-Based Pseudo-Label Calibration
2.4.2. Weighted Focal Loss
- To reduce the loss contribution of easily classified samples, thereby diminishing the dominant influence of the majority class on the loss;
- To amplify the loss contribution of hard-to-classify samples, enhancing the model’s ability to learn from minority-class samples.
2.4.3. Total Loss Function
2.4.4. Mathematical Analysis
3. Experiments and Analysis
3.1. Experimental Environment Configuration
3.2. Experimental Design
3.3. Training Strategy
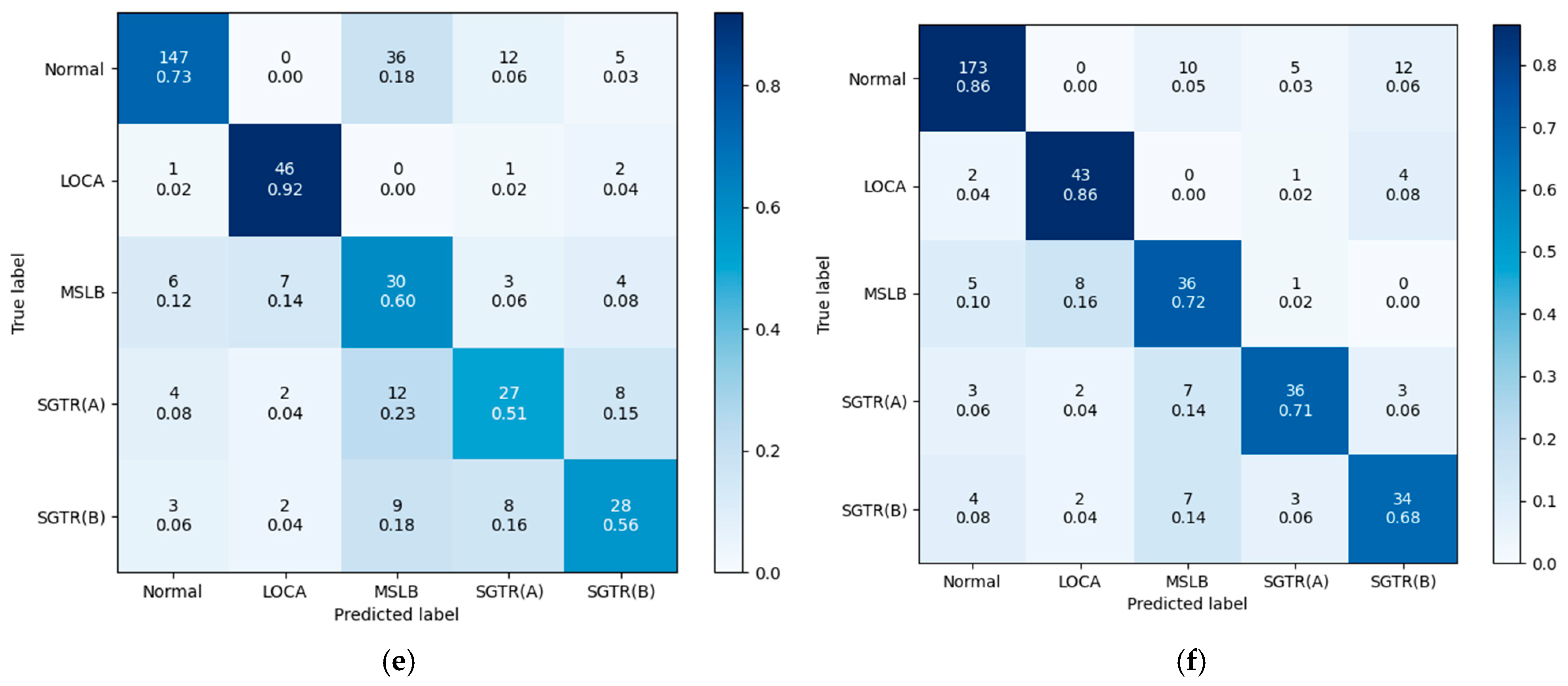
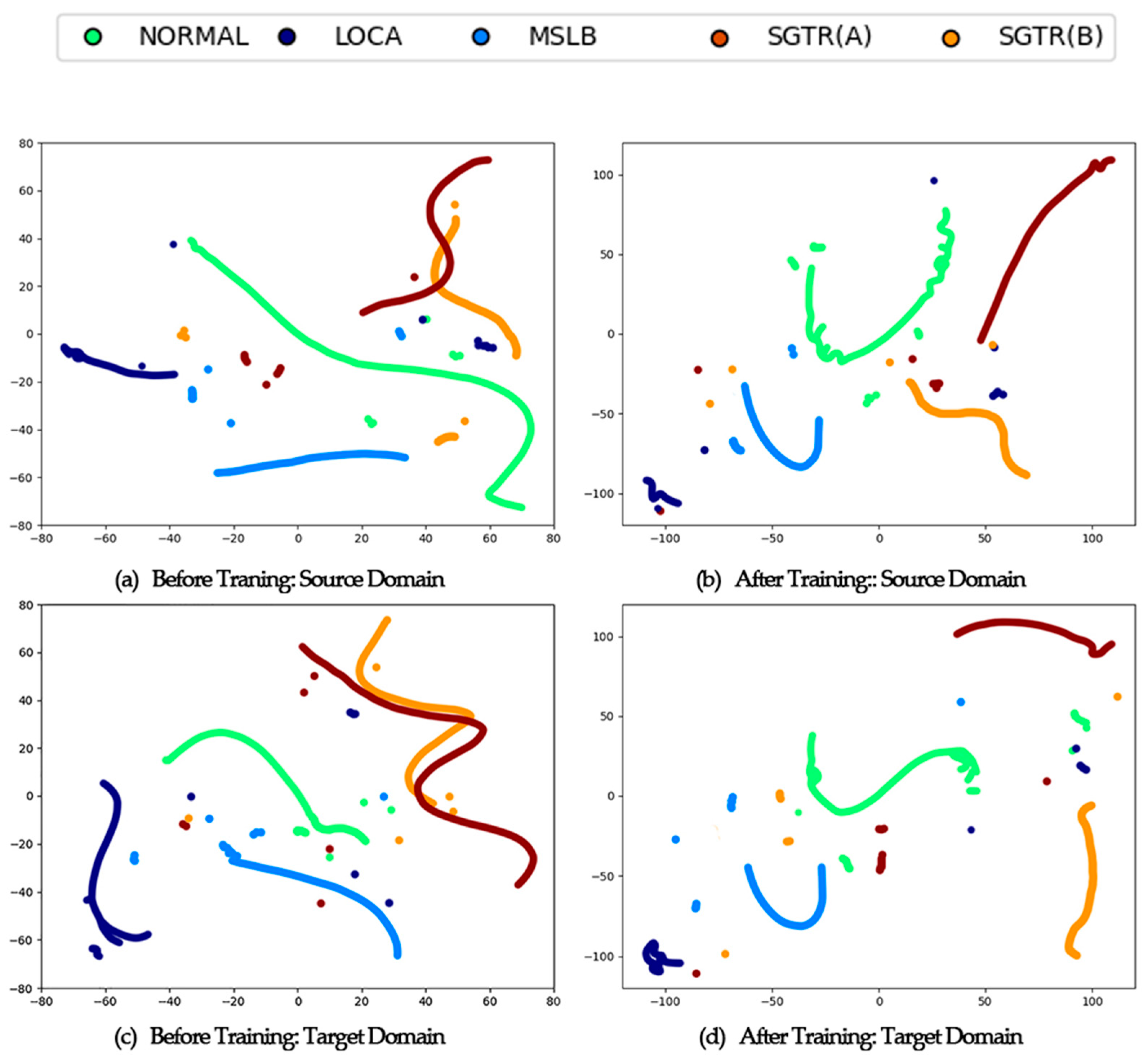
3.4. Evaluation Metrics and t-SNE Visualization
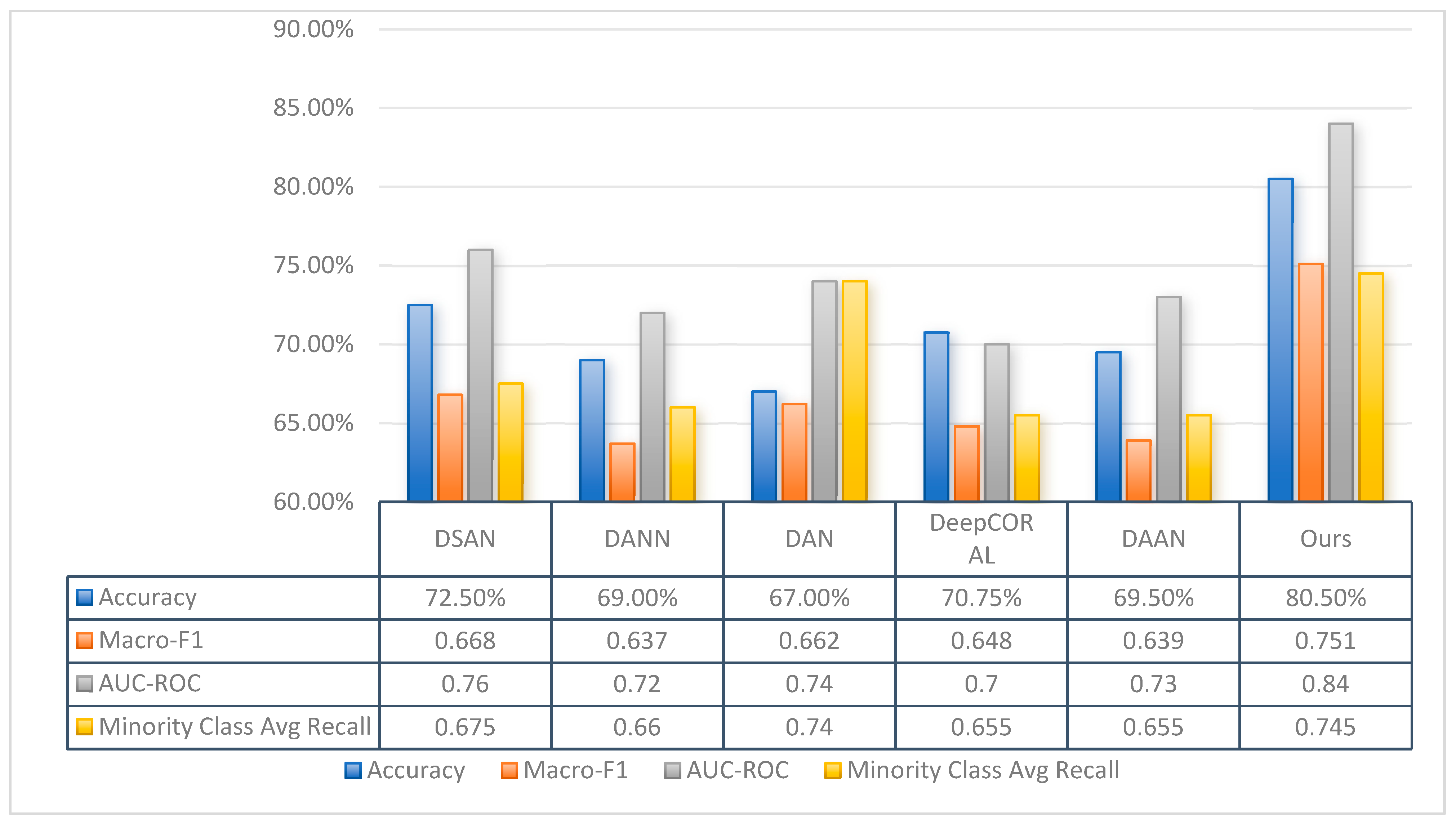
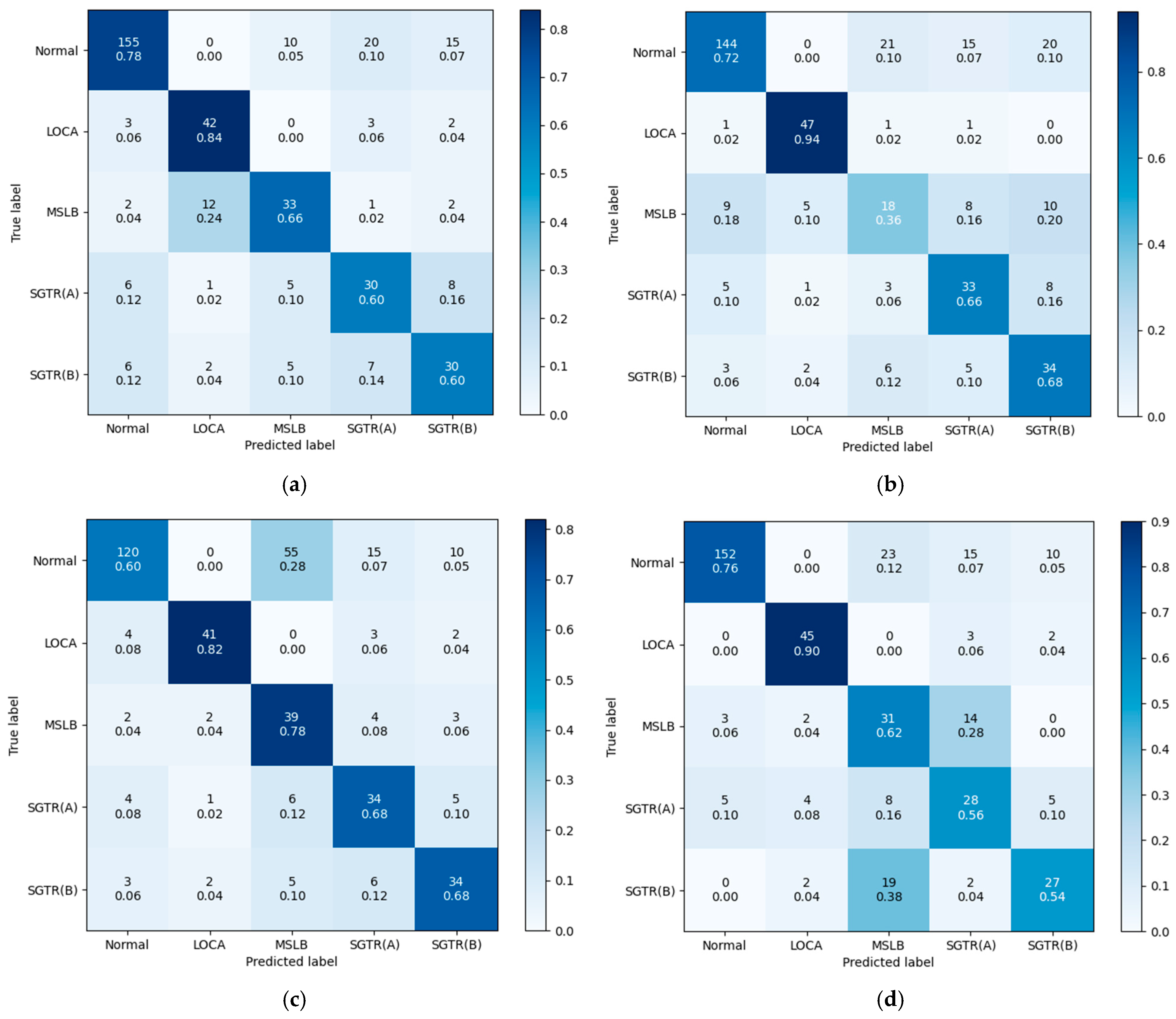
3.5. Results and Discussion
- Before Training (plots a and c):
- After Training (plots b and d):
3.6. Ablation Experiments and Results Analysis
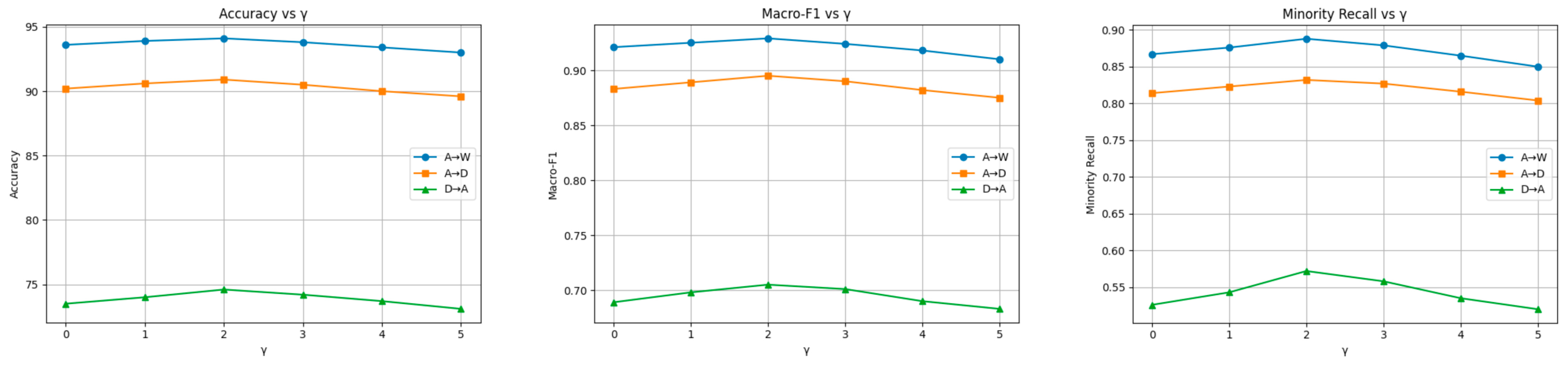
3.6.1. The Choice of γ
3.6.2. Weight Focal Loss and Confidence-Based Pseudo-Label Calibration
3.6.3. GAF and Pseudo-Color Mapping
3.7. Assessment of Online Deployability
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DBA | Design Basis Accident |
| DSAN | Deep Subdomain Adaptation Network |
| SDG | Signed directed graph |
| GAF | Gramian Angular Field |
| NPP | Nuclear power plant |
| AAKR | Auto-Associative Kernel Regression |
| CNN | Convolutional Neural Network |
| SG | Steam generator |
| DRSN | Deep Residual Shrinkage Network |
| ADASYN | Adaptive Synthetic Sampling |
| GAN | Generative Adversarial Network |
| TCA | Transfer Component Analysis |
| JDA | Joint Distribution Adaptation |
| NPPAD | Nuclear Power Plant Accident Data |
| MSLB | Main steam line break outside containment |
| LOCA | Loss of coolant accident in hot leg |
| SGTR (A) | Steam generator A tube rupture |
| SGTR (B) | Steam generator B tube rupture |
| GASF | Gramian Angular Summation Field |
| GADF | Gramian Angular Difference Field |
| LMMD | Local Maximum Mean Discrepancy |
| MMD | Maximum Mean Discrepancy |
| RKHS | Reproducing Kernel Hilbert Space |
| WFL | Weighted Focal Loss |
| CPC | Confidence-based pseudo-label calibration |
References
- Qi, B.; Liang, J.; Tong, J. Fault Diagnosis Techniques for Nuclear Power Plants: A Review from the Artificial Intelligence Perspective. Energies 2023, 16, 1850. [Google Scholar] [CrossRef]
- Min, J.H.; Kim, D.-W.; Park, C.-Y. Demonstration of the Validity of the Early Warning in Online Monitoring System for Nuclear Power Plants. Nucl. Eng. Des. 2019, 349, 56–62. [Google Scholar] [CrossRef]
- Li, X.; Fu, X.-M.; Xiong, F.-R.; Bai, X.-M. Deep Learning-Based Unsupervised Representation Clustering Methodology for Automatic Nuclear Reactor Operating Transient Identification. Knowl. Based Syst. 2020, 204, 106178. [Google Scholar] [CrossRef]
- Yue, P.; Fang, F.; Xu, P.; Xie, H.; Duan, Q.; Lin, J.; Xie, L. Noise Resistant Steam Generator Water Level Reconstruction for Nuclear Power Plant Based on Deep Residual Shrinkage Network. Ann. Nucl. Energy 2023, 193, 110038. [Google Scholar] [CrossRef]
- Tonday Rodriguez, J.C.; Perry, D.; Rahman, M.A.; Alam, S.B. An Intelligent Hierarchical Framework for Efficient Fault Detection and Diagnosis in Nuclear Power Plants. In Proceedings of the Sixth Workshop on CPS&IoT Security and Privacy, Salt Lake City, UT, USA, 18 October 2024; Association for Computing Machinery: New York, NY, USA, 2024; pp. 80–92. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, Y.; Song, L. Review of Research on Condition Assessment of Nuclear Power Plant Equipment Based on Data-Driven. J. Shanghai Jiaotong Univ. 2022, 56, 267–278. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Sun, X.; Liu, S.; Du, B. Imbalanced Data Fault Diagnosis Method for Nuclear Power Plants Based on Convolutional Variational Autoencoding Wasserstein Generative Adversarial Network and Random Forest. Nucl. Eng. Technol. 2024, 56, 5055–5067. [Google Scholar] [CrossRef]
- Yin, W.; Xia, H.; Huang, X.; Wang, Z. A Fault Diagnosis Method for Nuclear Power Plants Rotating Machinery Based on Deep Learning under Imbalanced Samples. Ann. Nucl. Energy 2024, 199, 110340. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Li, S.; Sun, S.; Wang, H.; Zhao, J.; Sun, B.; Shi, J. Self-Improving Few-Shot Fault Diagnosis for Nuclear Power Plant Based on Man-Machine Collaboration. Nucl. Eng. Des. 2024, 420, 113051. [Google Scholar] [CrossRef]
- Dai, Y.; Peng, L.; Juan, Z.; Liang, Y.; Shen, J.; Wang, S.; Tan, S.; Yu, H.; Sun, M. An Intelligent Fault Diagnosis Method for Imbalanced Nuclear Power Plant Data Based on Generative Adversarial Networks. J. Electr. Eng. Technol. 2023, 18, 3237–3252. [Google Scholar] [CrossRef]
- Li, J.; Lin, M.; Li, Y.; Wang, X. Transfer Learning with Limited Labeled Data for Fault Diagnosis in Nuclear Power Plants. Nucl. Eng. Des. 2022, 390, 111690. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer Feature Learning with Joint Distribution Adaptation. In Proceedings of the 2013 IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2200–2207. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. In Domain Adaptation in Computer Vision Applications; Csurka, G., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 189–209. ISBN 978-3-319-58347-1. [Google Scholar]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhuang, F.; Wang, J.; Ke, G.; Chen, J.; Bian, J.; Xiong, H.; He, Q. Deep Subdomain Adaptation Network for Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1713–1722. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, Q.; Macián-Juan, R. Enhancing Interpretability in Neural Networks for Nuclear Power Plant Fault Diagnosis: A Comprehensive Analysis and Improvement Approach. Prog. Nucl. Energy 2024, 174, 105287. [Google Scholar] [CrossRef]
- Park, J.H.; Jo, H.S.; Lee, S.H.; Oh, S.W.; Na, M.G. A Reliable Intelligent Diagnostic Assistant for Nuclear Power Plants Using Explainable Artificial Intelligence of GRU-AE, LightGBM and SHAP. Nucl. Eng. Technol. 2022, 54, 1271–1287. [Google Scholar] [CrossRef]
- Liu, Y.-K.; Wu, G.-H.; Xie, C.-L.; Duan, Z.-Y.; Peng, M.-J.; Li, M.-K. A Fault Diagnosis Method Based on Signed Directed Graph and Matrix for Nuclear Power Plants. Nucl. Eng. Des. 2016, 297, 166–174. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Z.; Sun, J. Applying Bayesian Networks in Nuclear Power Plant Safety Analysis. Procedia Eng. 2010, 7, 81–87. [Google Scholar] [CrossRef]
- Bensi, M.T.; Groth, K.M. On the Value of Data Fusion and Model Integration for Generating Real-Time Risk Insights for Nuclear Power Reactors. Prog. Nucl. Energy 2020, 129, 103497. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Wang, Z.; Oates, T. Imaging Time-Series to Improve Classification and Imputation 2015. arXiv 2015, arXiv:1506.00327. [Google Scholar]
- Qi, B.; Xiao, X.; Liang, J.; Po, L.C.; Zhang, L.; Tong, J. An Open Time-Series Simulated Dataset Covering Various Accidents for Nuclear Power Plants. Sci. Data 2022, 9, 766. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Pan, I.; Das, S. Fractional Order Fuzzy Control of Nuclear Reactor Power with Thermal-Hydraulic Effects in the Presence of Random Network Induced Delay and Sensor Noise Having Long Range Dependence. Energy Convers. Manag. 2013, 68, 200–218. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, K.; Chai, Y. Multiple Fault Diagnosis for Hydraulic Systems Using Nearest-Centroid-with-DBA and Random-Forest-Based-Time-Series-Classification. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020; pp. 29–86. [Google Scholar]
- Chae, Y.H.; Kim, S.G.; Choi, J.; Koo, S.R.; Kim, J. Enhancing Nuclear Power Plant Diagnostics: A Comparative Analysis of XAI-Based Feature Selection Methods for Abnormal and Emergency Scenario Detection. Prog. Nucl. Energy 2025, 185, 105759. [Google Scholar] [CrossRef]
- Wu, G.; Yuan, D.; Yin, J.; Xiao, Y.; Ji, D. A Framework for Monitoring and Fault Diagnosis in Nuclear Power Plants Based on Signed Directed Graph Methods. Front. Energy Res. 2021, 9, 641545. [Google Scholar] [CrossRef]
- Diao, X.; Zhao, Y.; Pietrykowski, M.; Wang, Z.; Bragg-Sitton, S.; Smidts, C. Fault Propagation and Effects Analysis for Designing an Online Monitoring System for the Secondary Loop of the Nuclear Power Plant Portion of a Hybrid Energy System. Nucl. Technol. 2018, 202, 106–123. [Google Scholar] [CrossRef]
- Liu, Y.; Abiodun, A.; Wen, Z.; Wu, M.; Peng, M.; Yu, W. A Cascade Intelligent Fault Diagnostic Technique for Nuclear Power Plants. J. Nucl. Sci. Technol. 2018, 55, 254–266. [Google Scholar] [CrossRef]
- Selvapriya, B.; Raghu, B. Pseudocoloring of Medical Images: A Research. Int. J. Eng. Adv. Technol. 2019, 8, 3712–3716. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How Transferable Are Features in Deep Neural Networks? In Advances in Neural Information Processing Systems 27 (NIPS 2014), Proceedings of the 28th Annual Conference on Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014; Neural Information Processing Systems Foundation, Inc. (NeurIPS): La Jolla, CA, USA, 2015. [Google Scholar]
- Wang, Z.; Oates, T. Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Hatami, N.; Gavet, Y.; Debayle, J. Classification of Time-Series Images Using Deep Convolutional Neural Networks. In Proceedings of the Tenth International Conference on Machine Vision (ICMV 2017), Vienna, Austria, 13–15 November 2017. [Google Scholar]
- Lu, J.; Wang, K.; Chen, C.; Ji, W. A Deep Learning Method for Rolling Bearing Fault Diagnosis Based on Attention Mechanism and Graham Angle Field. Sensors 2023, 23, 5487. [Google Scholar] [CrossRef]
- Styan, G.P.H. Hadamard Products and Multivariate Statistical Analysis. Linear Algebra Its Appl. 1973, 6, 217–240. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Orr, G.B.; Müller, K.-R. Efficient BackProp. In Neural Networks: Tricks of the Trade; Montavon, G., Orr, G.B., Müller, K.-R., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1524, pp. 9–50. [Google Scholar] [CrossRef]
- Le, D.N.T.; Le, H.X.; Ngo, L.T.; Ngo, H.T. Transfer Learning with Class-Weighted and Focal Loss Function for Automatic Skin Cancer Classification 2020. arXiv 2020, arXiv:2009.05977. [Google Scholar]
- Toba, M.; Uchida, S.; Hayashi, H. Pseudo-Label Learning with Calibrated Confidence Using an Energy-Based Model. arXiv 2024, arXiv:2404.09585v1. Available online: https://arxiv.org/html/2404.09585v1 (accessed on 19 April 2025).
- Long, M.; Cao, Y.; Wang, J.; Jordan, M.I. Learning Transferable Features with Deep Adaptation Networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Bach, F., Blei, D., Eds.; Proceedings of Machine Learning Research. Volume 37, pp. 97–105. [Google Scholar]
- Sun, B.; Saenko, K. Deep CORAL: Correlation Alignment for Deep Domain Adaptation. In Computer Vision—ECCV 2016 Workshops, Part III; Hua, G., Jégou, H., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 9915, pp. 443–450. [Google Scholar] [CrossRef]
- Wen, J.; He, K.; Huo, J.; Gu, Z.; Gao, Y. Unsupervised Domain Attention Adaptation Network for Caricature Attribute Recognition. In Proceedings of the Computer Vision—ECCV 2020, Glasgow, UK, 23–28 August 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2020; Volume 12353, pp. 18–34. [Google Scholar] [CrossRef]
- Saenko, K.; Kulis, B.; Fritz, M.; Darrell, T. Adapting Visual Category Models to New Domains. In Computer Vision—ECCV 2010; Daniilidis, K., Maragos, P., Paragios, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6314, pp. 213–226. [Google Scholar] [CrossRef]
| ID | Labels | Operation Conditions | Severity (Sample Number Per Category) | |
|---|---|---|---|---|
| Source Domain | Target Domain | |||
| 0 | NORMAL | Normal operation | Null (200) | Null (200) |
| 1 | LOCA | Loss of coolant accident in hot leg | 1~100% (100) | 2, 4, …, 100 (50) |
| 2 | MSLB | Main steam line break outside containment | 1~100% (100) | 2, 4, …, 100 (50) |
| 3 | SGTR (A) | Steam generator A tube rupture | 1~100% (100) | 2, 4, …, 100 (50) |
| 4 | SGTR (B) | Steam generator B tube rupture | 1~100% (100) | 2, 4, …, 100 (50) |
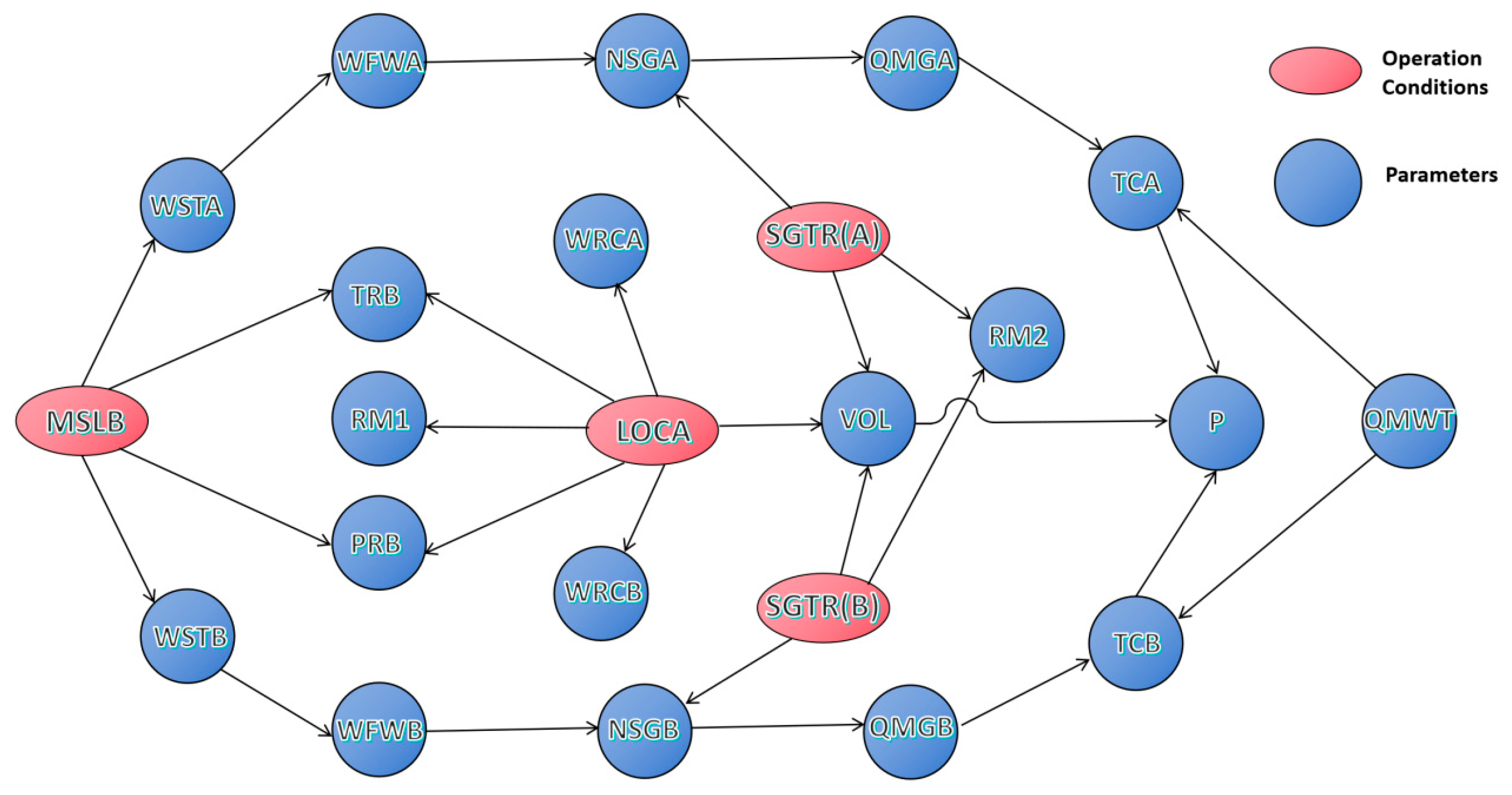
| ID | Node Label | Node Name | ID | Node Label | Node Name |
|---|---|---|---|---|---|
| 1 | P | Pressure of RCS | 11 | WRCB | Coolant flow of loop B |
| 2 | TCA | Temperature of cold leg A | 12 | WSTA | Steam flow of SG A |
| 3 | TCB | Temperature of cold leg B | 13 | WSTB | Steam flow of SG B |
| 4 | QMWT | Total thermal power | 14 | TRB | Temperature reactor building |
| 5 | QMGA | Power of SG A heat removal | 15 | PRB | Pressure reactor building |
| 6 | QMGB | Power of SG B heat removal | 16 | RM1 | Rad monitor reactor building air |
| 7 | WFWA | Feed-water flow of SG A | 17 | RM2 | Rad monitor steam line |
| 8 | WFWB | Feed-water flow of SG B | 18 | NSGA | Level SG A narrow range |
| 9 | VOL | Volume of RCS liquid | 19 | NSGB | Level SG B narrow range |
| 10 | WRCA | Coolant flow of loop A |
| G R O U P | Method | A→W | A→D | D→A | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| +WFL | +CPC (T) | Accuracy (%) | Macro-F1 | Minority Recall | Accuracy (%) | Macro-F1 | Minority Recall | Accuracy (%) | Macro-F1 | Minority Recall | |
| 1 | × | — | 93.6 | 92.1 | 86.7 | 90.2 | 88.3 | 81.4 | 73.5 | 68.9 | 52.6 |
| 2 | √ | — | 94.1 | 92.9 | 88.8 | 90.9 | 89.5 | 83.2 | 74.6 | 70.5 | 57.2 |
| 3 | × | 0.5 | 91.8 | 89.5 | 86.0 | 88.5 | 86.2 | 79.5 | 70.2 | 65.2 | 53.5 |
| 4 | × | 0.6 | 92.1 | 89.8 | 86.5 | 88.7 | 86.5 | 80.2 | 70.6 | 65.6 | 54.5 |
| 5 | × | 0.7 | 92.5 | 90.3 | 86.8 | 89.2 | 86.9 | 80.8 | 71.3 | 66.2 | 55.0 |
| 6 | × | 0.8 | 92.8 | 90.7 | 86.5 | 89.5 | 87.2 | 80.5 | 71.8 | 66.8 | 55.2 |
| 7 | × | 0.8~0.5 | 94.0 | 92.8 | 88.7 | 90.8 | 89.4 | 83.0 | 75.0 | 70.9 | 57.4 |
| 8 | √ | 0.8~0.5 | 94.3 | 93.3 | 89.2 | 91.1 | 89.9 | 84.0 | 75.4 | 71.5 | 58.2 |
| Method | Accuracy (%) | Macro-F1 | AUC-ROC | Minority Recall |
|---|---|---|---|---|
| GAF+pseudo-color | 80.5 | 0.751 | 0.84 | 0.745 |
| RP | 76.8 | 0.715 | 0.82 | 0.780 |
| CWT | 79.2 | 0.740 | 0.83 | 0.735 |
| GAF | 78.0 | 0.720 | 0.81 | 0.700 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Hu, E.; Liu, H. A Fault Diagnosis Framework for Pressurized Water Reactor Nuclear Power Plants Based on an Improved Deep Subdomain Adaptation Network. Energies 2025, 18, 2334. https://doi.org/10.3390/en18092334
Liu Z, Hu E, Liu H. A Fault Diagnosis Framework for Pressurized Water Reactor Nuclear Power Plants Based on an Improved Deep Subdomain Adaptation Network. Energies. 2025; 18(9):2334. https://doi.org/10.3390/en18092334
Chicago/Turabian StyleLiu, Zhaohui, Enhong Hu, and Hua Liu. 2025. "A Fault Diagnosis Framework for Pressurized Water Reactor Nuclear Power Plants Based on an Improved Deep Subdomain Adaptation Network" Energies 18, no. 9: 2334. https://doi.org/10.3390/en18092334
APA StyleLiu, Z., Hu, E., & Liu, H. (2025). A Fault Diagnosis Framework for Pressurized Water Reactor Nuclear Power Plants Based on an Improved Deep Subdomain Adaptation Network. Energies, 18(9), 2334. https://doi.org/10.3390/en18092334





