Orderly Charging and Discharging Strategy for Electric Vehicles with Integrated Consideration of User and Distribution Grid Benefits
Abstract
1. Introduction
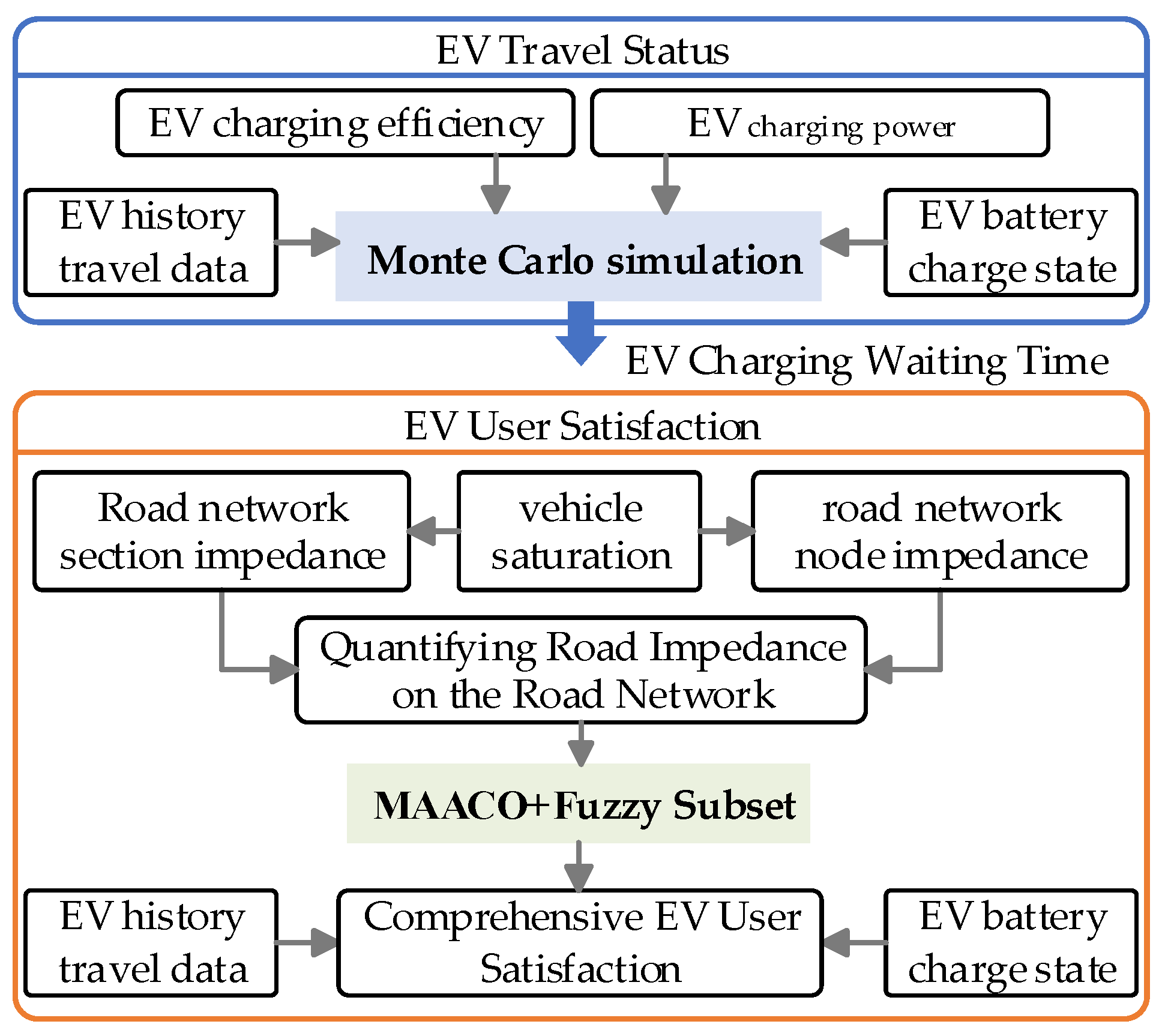
2. Comprehensive EV User Satisfaction Model That Accounts for Network Road Impedance
- (1)
- EV Users’ Travel Satisfaction
- (2)
- EV Users’ Fee Satisfaction
3. Orderly Charging and Discharging Model for Electric Vehicles with Integrated Consideration of User and Distribution Network Benefits
3.1. Objective Function
3.1.1. Minimal Operating Costs of the Distribution Network
3.1.2. Minimal Voltage Deviation in the Distribution Network
3.1.3. Best Overall EV User Satisfaction
3.2. Restrictive Condition
3.2.1. Distribution Network Current Constraints
3.2.2. Proactive Management of Device Constraints
- (1)
- OLTC Constraints
- (2)
- CB Constraints
- (3)
- SVG Constraints
- (4)
- DG Constraints
3.2.3. EV Charging Pile Charging and Discharging Constraints
3.2.4. Power Balance Constraints
4. Example Simulation and Analysis
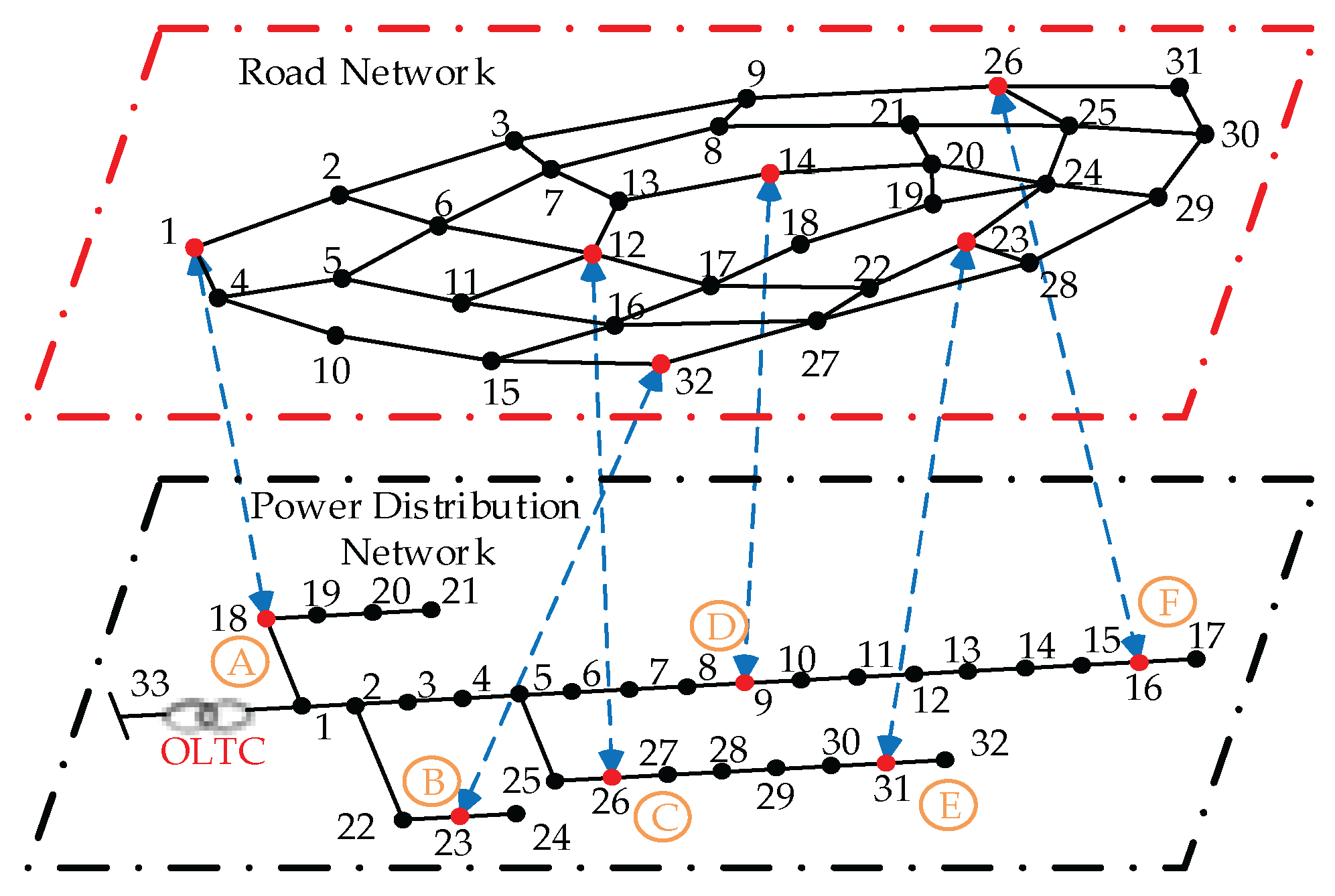
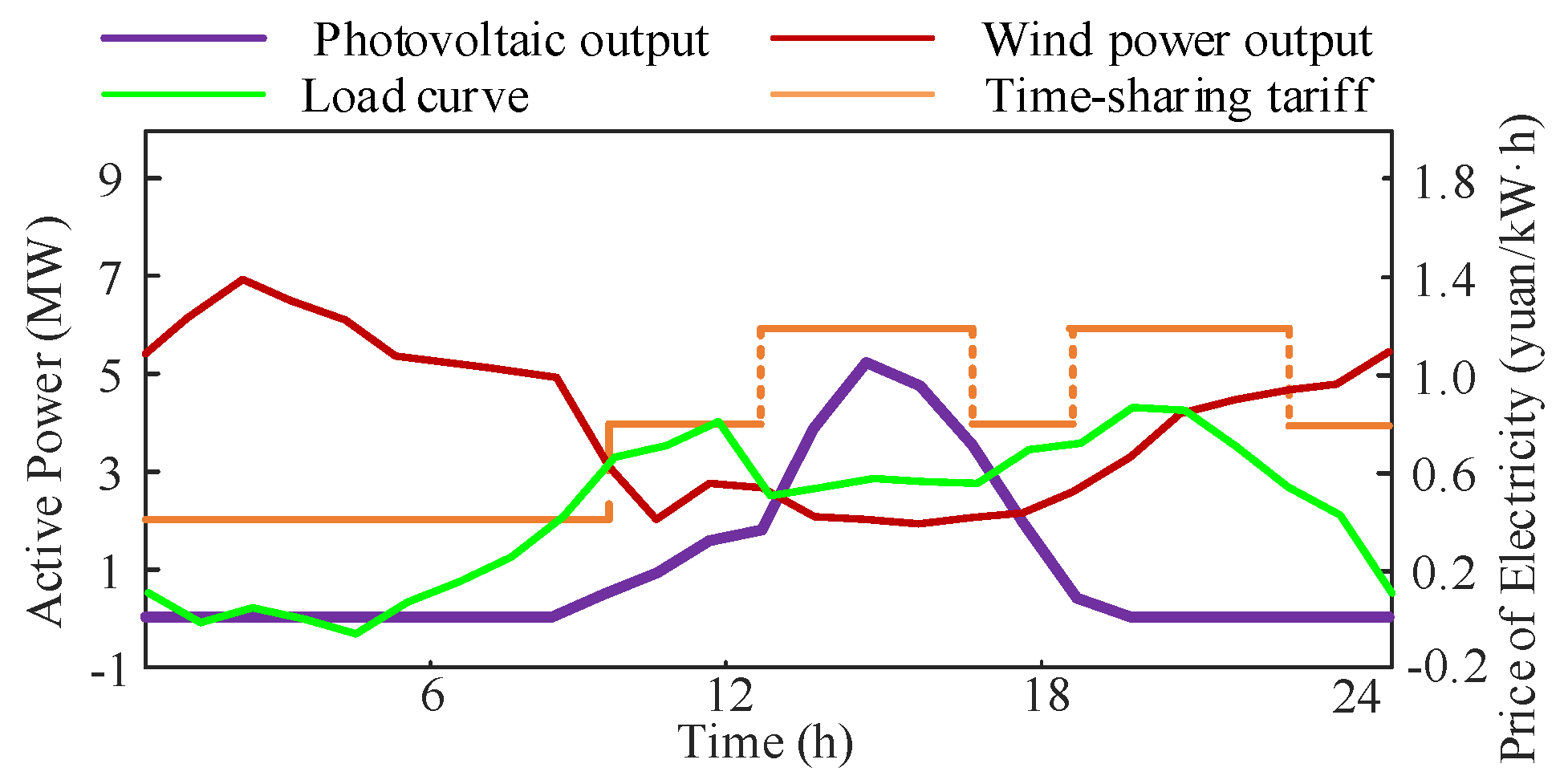
4.1. Example Overview and Parameterization
4.2. Simulation Results Analysis
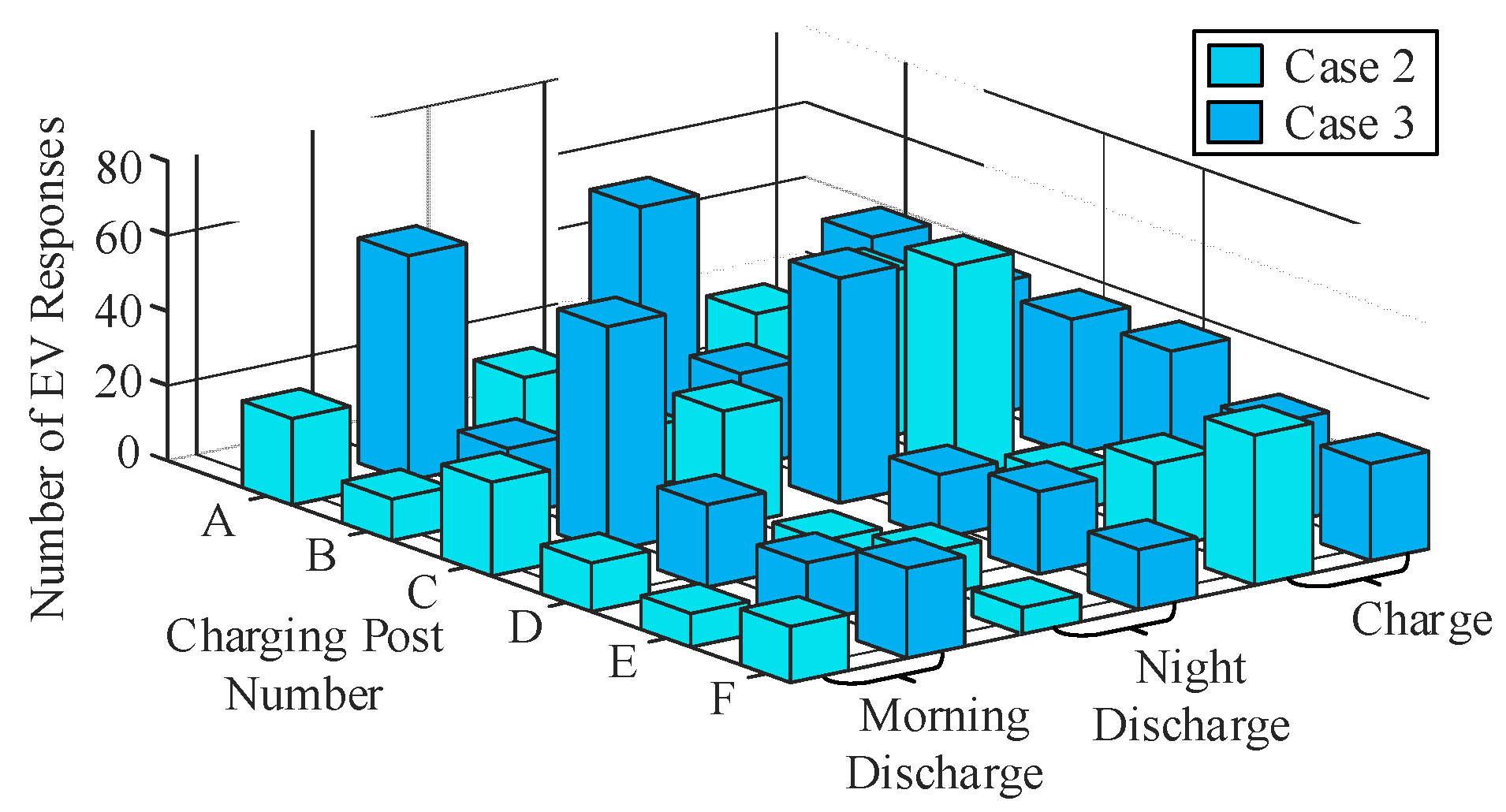
4.2.1. Results Analysis of the Economics of the Distribution Network
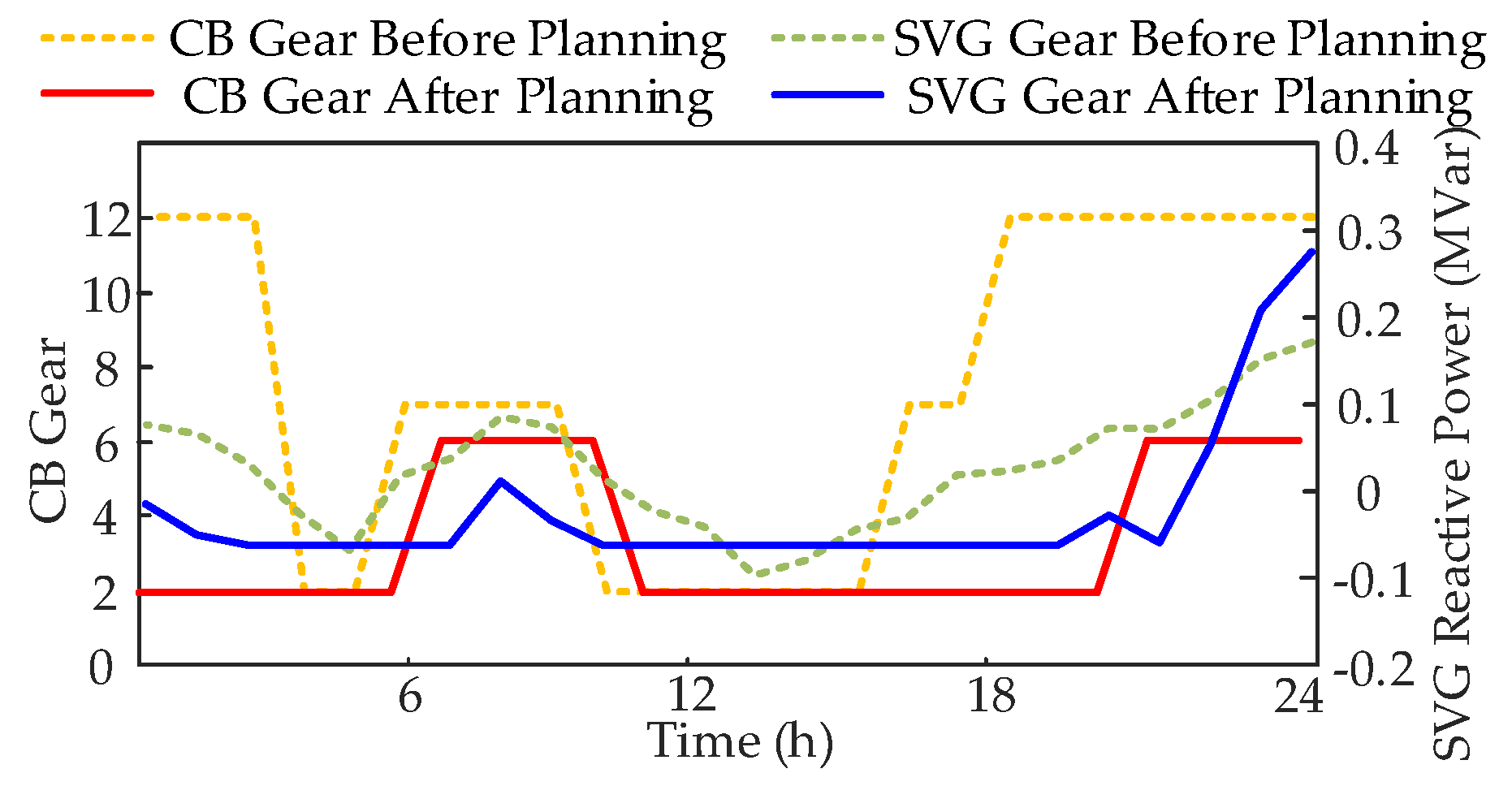
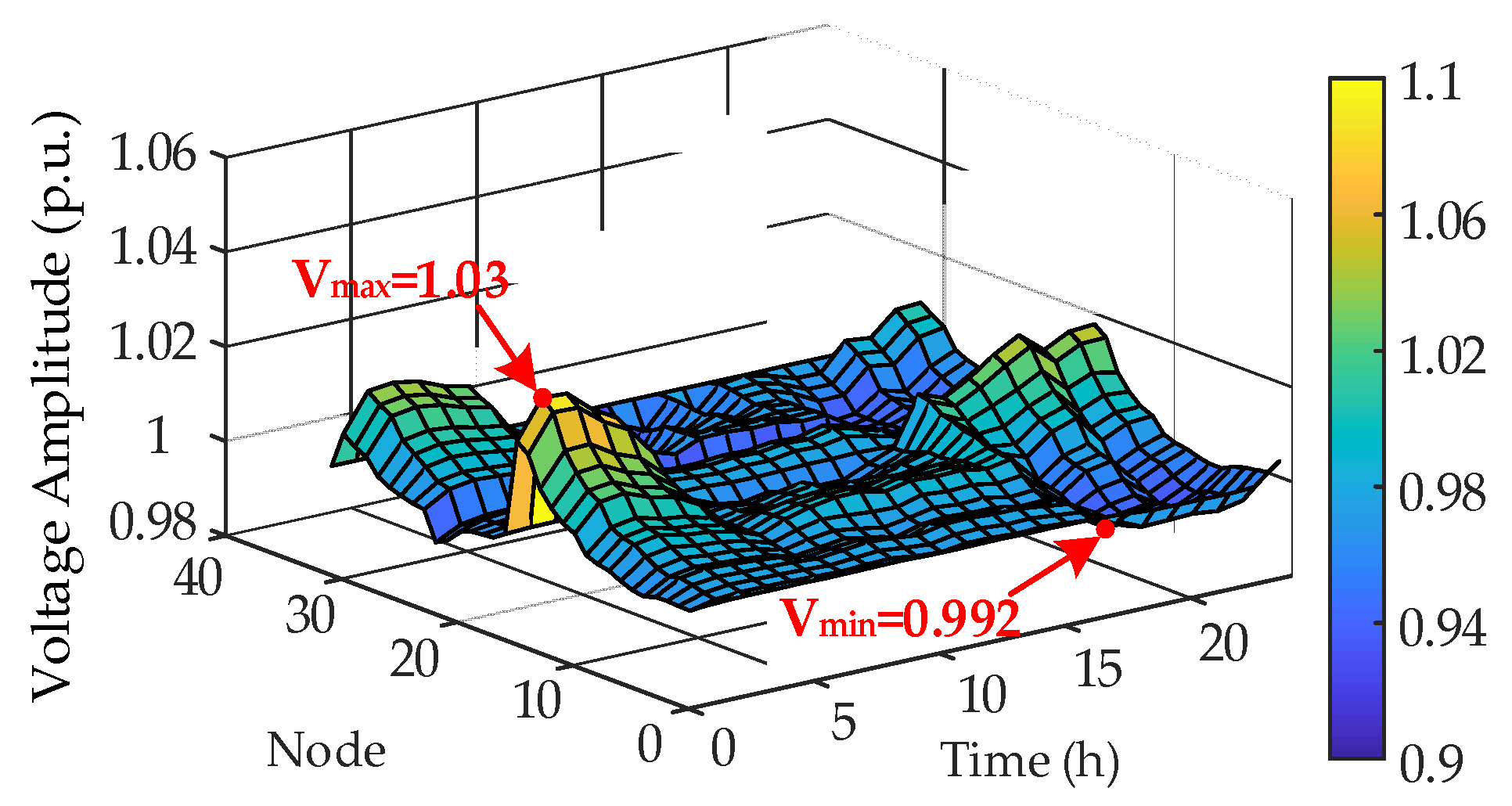
4.2.2. Analysis of Distribution Network Voltage Regulation
5. Conclusions
- (1)
- The comprehensive satisfaction of EV users is carefully quantified by introducing road network road resistance. The comprehensive satisfaction of EV users can guide EVs to actively and orderly participate in grid regulation. The peak-to-valley load difference of the distribution network under the strategy of this paper is 29.52% lower than that of the strategy involving EV non-participation in regulation. It is 6.71% lower than the traditional strategy. Therefore, the strategy of this paper can ensure that the comprehensive satisfaction of EV users is within the acceptable range. In addition, it effectively reduces the peak-to-valley load difference rate of the distribution network.
- (2)
- The strategy set out in this document takes into account the safe and economic operation of the distribution network and the good experience of electric vehicle users. Compared to a strategy where electric vehicles do not participate, this strategy can effectively reduce the cost of operating the system by 2.47% in one day. At the same time, charging costs for electric vehicles are reduced by 17.85%. The voltage reference deviation is reduced by 75.59%. The strategy presented in this paper can effectively reduce the system operation cost for one day by 6.93% compared to the traditional strategy without distribution system regulation. The cost of charging EVs for one day increased. However, the reference voltage deviation of the system has decreased by 73.48%. The approach in this document thus improves the reliability and economic efficiency of the distribution network. The strategy has practical implications for optimizing and controlling the operation of the distribution network.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| V2G | Vehicle-to-grid |
| SOC | State of charge |
| EV user travel satisfaction | |
| EV cost satisfaction | |
| MAACO | Modified Adaptive Ant Colony Optimization |
| Starting SOC for EV | |
| Expected SOC of EV | |
| Battery capacity of the EV | |
| EV charging efficiency | |
| EV charging power | |
| Ci(t) | Nodal impedance of intersection i at time t |
| Q | Roadway traffic flow |
| C | Navigational capability |
| c | Signal period |
| λ | Green letter ratio |
| q | Vehicle arrival rate of the road section |
| h | Intersection EV organization degree coefficient |
| Rij(t) | Roadway impedance between intersection i and intersection j at time t |
| t0 | Zero flow travel time |
| α and β | Impedance impact factors |
| Charging tariff costs | |
| Highest cost of charging for the user, obtained by scheduling the ith EV in charging station k to charge at the extremes of the highest and lowest tariff periods | |
| Lowest cost of charging for the user, obtained by scheduling the ith EV in charging station k to charge at the extremes of the highest and lowest tariff periods | |
| DG | Distributed generation |
| OLTC | On-load tap changer |
| CB | Capacitor banks |
| SVG | Static VAR generator |
| F | Comprehensive operation index of distribution network |
| Ctotal | Normalized value of power cost for exchanging power with the distribution network |
| Vsyn | The comprehensive level of distribution network voltage |
| Comprehensive satisfaction of EV users | |
| λi | weighting factor |
| Ctotal,real | Total distribution network operating costs |
| Ctotal,max | Maximum costs for distribution network extremes |
| Ctotal,min | Minimum costs for distribution network extremes |
| CGRI | Cost of exchanging power with the distribution network |
| CDG | DG power generation investment and operation and maintenance cost |
| CLIN | Distribution network network loss cost |
| CREA | Operation and maintenance cost of the reactive power compensation device |
| cGRI,t | Purchase and sale price of electricity from the distribution grid |
| cPV,t | Unit operation and maintenance cost of PV |
| cWD,t | Unit operation and maintenance cost of wind turbines |
| cCB,t | Unit operation and maintenance cost of CB |
| cSVG,t | Unit operation and maintenance cost of SVG |
| cLIN,t | Unit network loss price |
| PV | Photovoltaic |
| PGRI,t | Power exchanged between the distribution grid |
| PDG,t | PV output |
| PWD,t | Wind turbine output |
| QCB,t | CB output |
| QSVG,t | SVG output |
| Iij | Branch current between node i and node j |
| rij | Resistance between node i and node j |
| Vi,t | Node voltage of node i at time t |
| Nbus | Number of nodes in the distribution network |
| VN | Reference voltage |
| pj | Active power injected at node j |
| qj | Reactive power injected at node j |
| Pij | Active power flowing from node i to the next node j |
| Qij | Reactive power flowing from node i to the next node |
| xij | Reactance of the branch between node i and node j |
| gj | Conductivity to ground of node j |
| bj | Electricity generation to ground of node j |
| Iij.max | Upper limits of branch current between node i and node j |
| Iij.min | Lower limits of branch current between node i and node j |
| Vj.max | Upper limits of node voltage at node j |
| Vj.min | Lower limits of node voltage at node j |
| PGRI,t | Interactive active power of the higher-level grid |
| QGRI,t | Interactive reactive power of the higher-level grid |
| PGRI,max | Maximum interactive active power that is allowed to be passed through the branch of the contact between the distribution grid and the higher-level grid |
| PGRI,min | Minimum interactive active power that is allowed to be passed through the branch of the contact between the distribution grid and the higher-level grid |
| QGRI,max | Maximum interactive reactive power that is allowed to be passed through the branch of the contact between the distribution grid and the higher-level grid |
| QGRI,min | Minimum interactive reactive power that is allowed to be passed through the branch of the contact between the distribution grid and the higher-level grid |
| VBase,j,t | Voltage value on the high-voltage side of the transformer |
| lj,t | Square of the OLTC ratio |
| lmax,j | Squares of the upper limits of the adjustable OLTC ratio |
| lmin,j | Squares of the lower limits of the adjustable OLTC ratio |
| lj,s | Difference between the OLTC stall s and the square of the stall s-1 ratio |
| yCB,j,t | Number of groups in operation |
| YCB,max,j | Upper limit of the number of groups of CBs connected at node j |
| QCB.step,j | Compensating power of each group of CBs |
| NCB.max,j | Upper limit of the number of operations |
| QSVG,min,j | Lower limits of SVG compensation power |
| QSVG,max,j | Upper limits of SVG compensation power |
| PDG,j,t | Actual output of DG assembled at node j at time t |
| PDG.PRE,j,t | Predicted output of DG assembled at node j at period t |
| SDG,j,max | Upper bounds of the capacity of DG assembled at node j |
| SDG,j,min | Lower bounds of the capacity of DG assembled at node j |
| Pev,ch,i,t | EV charging power |
| Pev,dis,i,t | EV discharging power |
| Pev,ch,i,t,max | Maximum EV charging capacity |
| Pev,dis,i,t,max | EV Maximum Discharge |
| Tupper | Load peak times |
| Tlower | Load trough times |
| pload | Active loads at each node of the distribution network |
| qload | Reactive loads at each node of the distribution network |
References
- Harsh, P.; Das, D. Optimal coordination strategy of demand response and electric vehicle aggregators for the energy management of reconfigured grid-connected microgrid. Renew. Sustain. Energy Rev. 2022, 160, 112251. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Che, L.; Xu, Z.; Xiao, F.; Li, T.; Chen, L. A Comprehensive Control Strategy for F-SOP Considering Three-phase Imbalance and Economic Operation in ISLDN. IEEE Trans. Sustain. Energy 2025, 16, 149–159. [Google Scholar] [CrossRef]
- Yazdandoust, M.; Golkar, M.A. Participation of aggregated electric vehicles in demand response programs. In Electric Vehicles in Energy Systems: Modelling, Integration, Analysis, and Optimization; Springer: Cham, Switzerland, 2020; pp. 327–357. [Google Scholar]
- Şengör, İ.; Çiçek, A.; Erenoğlu, A.K.; Erdinç, O.; Catalão, J.P. User-comfort oriented optimal bidding strategy of an electric vehicle aggregator in day-ahead and reserve markets. Int. J. Electr. Power Energy Syst. 2020, 122, 106194. [Google Scholar] [CrossRef]
- Liu, D.; Wang, W.; Wang, L.; Jia, H.; Shi, M. Dynamic pricing strategy of electric vehicle aggregators based on DDPG reinforcement learning algorithm. IEEE Access 2021, 9, 21556–21566. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Xiao, F.; Chen, Z.; Luo, J.; Hou, Y. A Hybrid Advanced Traction Power Supply Equipment Based on Triple-Port High-Frequency Isolated Converter with its Control Strategy. IEEE Trans. Power Electron. 2025, 10038–10048. [Google Scholar] [CrossRef]
- Shojaabadi, S.; Talavat, V.; Galvani, S. A game theory-based price bidding strategy for electric vehicle aggregators in the presence of wind power producers. Renew. Energy 2022, 193, 407–417. [Google Scholar] [CrossRef]
- Hamed, A.; Torky, M.; AlJanah, S.; Alshammari, A.; Gaber, T. A blockchain-based fox optimization algorithm for optimizing and securing electrical vehicles charging. IEEE Trans. Intell. Veh. 2024, early access. [Google Scholar] [CrossRef]
- Long, T.; Jia, Q.S.; Wang, G.; Yang, Y. Efficient real-time EV charging scheduling via ordinal optimization. IEEE Trans. Smart Grid 2021, 12, 4029–4038. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S. Efficient Federated Connected Electric Vehicle Scheduling System: A Noncooperative Online Incentive Approach. IEEE Trans. Intell. Transp. Syst. 2025, 26, 3934–3946. [Google Scholar] [CrossRef]
- Yao, S.; Wang, P.; Liu, X.; Zhang, H.; Zhao, T. Rolling optimization of mobile energy storage fleets for resilient service restoration. IEEE Trans. Smart Grid 2019, 11, 1030–1043. [Google Scholar] [CrossRef]
- Li, H.; Azzouz, M.A.; Hamad, A.A. Cooperative voltage control in MV distribution networks with electric vehicle charging stations and photovoltaic DGs. IEEE Syst. J. 2020, 15, 2989–3000. [Google Scholar] [CrossRef]
- Jiang, T.; Dong, X.; Zhang, R.; Li, X. Strategic active and reactive power scheduling of integrated community energy systems in day-ahead distribution electricity market. Appl. Energy 2023, 336, 120558. [Google Scholar] [CrossRef]
- Lin, J.; Sun, J.; Feng, Y.; Zheng, M.; Yu, Z. Aggregate demand response strategies for smart communities with battery-charging/switching electric vehicles. J. Energy Storage 2023, 58, 106413. [Google Scholar] [CrossRef]
- Dahiwale, P.V.; Rather, Z.H.; Mitra, I. A comprehensive review of smart charging strategies for electric vehicles and way forward. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10462–10482. [Google Scholar] [CrossRef]
- Wang, Y.; Bi, J.; Lu, C.; Ding, C. Route guidance strategies for electric vehicles by considering stochastic charging demands in a time-varying road network. Energies 2020, 13, 2287. [Google Scholar] [CrossRef]
- Moradipari, A.; Alizadeh, M. Pricing and routing mechanisms for differentiated services in an electric vehicle public charging station network. IEEE Trans. Smart Grid 2019, 11, 1489–1499. [Google Scholar] [CrossRef]
- Salam, S.S.A.; Raj, V.; Petra, M.I.; Azad, A.K.; Mathew, S.; Sulthan, S.M. Charge scheduling optimization of electric vehicles: A comprehensive review of essentiality, perspectives, techniques and security. IEEE Access 2024, 12, 121010–121034. [Google Scholar] [CrossRef]
- Delice, Y.; Aydemir-Karadag, A.; ÖZen, H. A Heuristic Approach for the Nationwide Charging Station Location Problem for Intercity Trips. IEEE Access 2025, 13, 36348–36358. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Sun, X.; Zhao, J. Adaptive integrated planning of electricity networks and fast charging stations under electric vehicle diffusion. IEEE Trans. Power Syst. 2022, 38, 499–513. [Google Scholar] [CrossRef]
- Cheng, S.; Wei, Z.; Shang, D.; Zhao, Z.; Chen, H. Charging load prediction and distribution network reliability evaluation considering electric vehicles’ spatial-temporal transfer randomness. IEEE Access 2020, 8, 124084–124096. [Google Scholar] [CrossRef]
- Wu, J.; Su, H.; Meng, J.; Lin, M. Electric vehicle charging scheduling considering infrastructure constraints. Energy 2023, 278, 127806. [Google Scholar] [CrossRef]
- Wang, M.; Gao, H.; Pan, D.; Sheng, X.; Xu, C.; Wang, Q. Multi-energy load collaborative optimization of the active building energy management strategy. Energies 2024, 17, 2569. [Google Scholar] [CrossRef]
- Vu, L.H.; Passow, B.N.; Paluszczyszyn, D.; Deka, L.; Goodyer, E. Estimation of travel times for minor roads in urban areas using sparse travel time data. IEEE Intell. Transp. Syst. Mag. 2020, 13, 220–233. [Google Scholar] [CrossRef]
- Zhang, D.; You, X.; Liu, S.; Pan, H. Dynamic multi-role adaptive collaborative ant colony optimization for robot path planning. IEEE Access 2020, 8, 129958–129974. [Google Scholar] [CrossRef]
- Sun, X.; Qiu, J. Two-stage volt/var control in active distribution networks with multi-agent deep reinforcement learning method. IEEE Trans. Smart Grid 2021, 12, 2903–2912. [Google Scholar] [CrossRef]
- Yan, D.; Yin, H.; Li, T.; Ma, C. A two-stage scheme for both power allocation and EV charging coordination in a grid-tied PV–battery charging station. IEEE Trans. Ind. Inform. 2021, 17, 6994–7004. [Google Scholar] [CrossRef]




| Numerical Value of Affiliation | User Travel Satisfaction | Function Decision |
|---|---|---|
| μcom(w) | 1 | |
| 0 | ||
| μnor(w) | ||
| 0.6 | ||
| 0 | ||
| μanx(w) | 0.25 | |
| 0 |
| Case1 | Case2 | Case3 | |
|---|---|---|---|
| System operating cost per day/CNY | 24,658.3 | 25,839.7 | 24,048.7 |
| Total EV single-day charging cost/CNY | 4040.5 | 3277.5 | 3319.4 |
| EV user satisfaction | 0.429 | 0.457 | 0.391 |
| Voltage reference deviation | 0.553 | 0.509 | 0.135 |
| Comprehensive indicators of distribution network operation | 0.912 | 0.881 | 0.769 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Gao, Y.; Zhao, R.; Lu, J.; Li, M.; Wei, C.; Li, J. Orderly Charging and Discharging Strategy for Electric Vehicles with Integrated Consideration of User and Distribution Grid Benefits. Energies 2025, 18, 2305. https://doi.org/10.3390/en18092305
Chen Y, Gao Y, Zhao R, Lu J, Li M, Wei C, Li J. Orderly Charging and Discharging Strategy for Electric Vehicles with Integrated Consideration of User and Distribution Grid Benefits. Energies. 2025; 18(9):2305. https://doi.org/10.3390/en18092305
Chicago/Turabian StyleChen, Yizhe, Yifan Gao, Ruifeng Zhao, Jiangang Lu, Ming Li, Chengzhi Wei, and Junhao Li. 2025. "Orderly Charging and Discharging Strategy for Electric Vehicles with Integrated Consideration of User and Distribution Grid Benefits" Energies 18, no. 9: 2305. https://doi.org/10.3390/en18092305
APA StyleChen, Y., Gao, Y., Zhao, R., Lu, J., Li, M., Wei, C., & Li, J. (2025). Orderly Charging and Discharging Strategy for Electric Vehicles with Integrated Consideration of User and Distribution Grid Benefits. Energies, 18(9), 2305. https://doi.org/10.3390/en18092305





