Day-Ahead Optimal Scheduling of an Integrated Electricity-Heat-Gas-Cooling-Hydrogen Energy System Considering Stepped Carbon Trading

Abstract

Within the framework of “dual carbon”, intending to enhance the use of green energies and minimize the emissions of carbon from energy systems, this study suggests a cost-effective low-carbon scheduling model that accounts for stepwise carbon trading for an integrated electricity, heat, gas, cooling, and hydrogen energy system. Firstly, given the clean and low-carbon attributes of hydrogen energy, a refined two-step operational framework for electricity-to-gas conversion is proposed. Building upon this foundation, a hydrogen fuel cell is integrated to formulate a multi-energy complementary coupling network. Second, a phased carbon trading approach is established to further explore the mechanism’s carbon footprint potential. And then, an environmentally conscious and economically viable power dispatch model is developed to minimize total operating costs while maintaining ecological sustainability. This objective optimization framework is effectively implemented and solved using the CPLEX solver. Through a comparative analysis involving multiple case studies, the findings demonstrate that integrating electric-hydrogen coupling with phased carbon trading effectively enhances wind and solar energy utilization rates. This approach concurrently reduces the system’s carbon emissions by 34.4% and lowers operating costs by 58.6%.

1. Introduction

Accelerated industrialization and climate governance pressure to form a double forcing mechanism: the traditional energy system faces a rigid growth in demand and carbon emissions constraints of the sharp contradiction, driving many countries to turn to wind power, photovoltaic, and other renewable energy strategy layouts [1,2]. Sources of green power, symbolized by solar and wind energy, have become a key alternative to traditional fossil fuels for power generation, reducing greenhouse gas and harmful pollutant emissions due to their cleanliness and sustainability [3]. Compared to coal-fired and gas-fired power generation, sources of clean energy can significantly reduce the emission intensity of SOx, NOx, and CO₂ through zero-carbon power output, attaining the objective of cutting carbon emissions and environmental impact [4]. A comprehensive energy system through multi-energy complementary, synergistic optimization, breaking the traditional energy system of a single energy-independent supply mode, the organic integration of power, gas, heat, cooling, hydrogen, and other energy sources, and the formation of a source-network-charge-storage synergistic operation system [5,6] is a reliable way for overcoming a significant percentage of renewable energy usage [7].

Hydrogen energy is growing rapidly and has a promising development prospect [8]. Among them, the convergence of renewable energy with hydrogen technologies has garnered a great deal of interest [9]. Power-to-gas (P2G) technology turns surplus electric power into hydrogen-based fuel gasses via electrochemical conversion processes, establishing a bridge for mutual energy transfer between fossil fuel infrastructure and the electrical grid [10]. It enables high-capacity storage of excess power [11]. Giulio et al. [12] focused on evaluating the regulation capabilities of P2G in large wind farms. Wang et al. [13] constructed a coupled model of carbon capture and storage (CCS) and P2G in a wind-hydrogen energy generation system. Chen et al. [14] proposed a joint P2G-CHP-CCS operation strategy under carbon trading. Pan et al. [15] developed an integrated energy system (IES) model taking demand reaction and P2G into consideration. Zeng et al. [16] developed a coupled electricity and gas system using electricity-to-gas conversion as a hub, and the outcomes demonstrated the suggested model’s validity. Ma et al. [17] developed an IES model with P2G conversion and CCS-integrated combined heat and power (CHP) units, which synergistically addressed carbon source allocation for P2G operation and carbon emission mitigation in CHP through system optimal scheduling.

Carbon trading mechanisms are an effective measure for the creation of a society with low emissions [18,19]. The optimization of carbon trading prices has a significant role to play in promoting carbon emission reduction, energy efficiency, and technological innovation among enterprises [20]. Chen et al. [21] prove that carbon trading has a favorable effect on achieving dual-carbon goals. Zhang et al. [22] developed a regional IES model that takes carbon trading and demand response into account. Micho, P., et al. [23] carried out a number of case studies of integrated electric hydrogen markets and proposed a framework for modeling local electric hydrogen markets. Li et al. [24] synergized the running of carbon trading mechanisms with nuclear power units to improve system economics while reducing carbon emissions.

However, existing research focuses on the electricity-to-gas system, with less consideration given to the participation of hydrogen fuel cells, which fails to properly harness the advantages of hydrogen energy. The introduction of a carbon market system into the IES can effectively lessen the release of carbon from the structure, but little consideration has been given to the laddering of trading in carbon. Furthermore, although significant progress has been made in investigating electricity-heat-hydrogen integrated energy systems, the current research landscape still demonstrates scope for improvements regarding the systematic integration of cooling energy requirements.

In summary, the study provides an appropriate planning model that makes use of the stepped carbon market mechanism and applies to the IES of power, thermal energy, gas, cold, and hydrogen. The issue can be resolved using the MATLAB software CPLEX solver, which takes into account both the system’s cost-effective and environmentally friendly characteristics. By contrasting and examining the scheduling outcomes of multiple system operation techniques, the efficacy of the suggested operation strategy is confirmed. The following is a summary of this paper’s primary contributions:

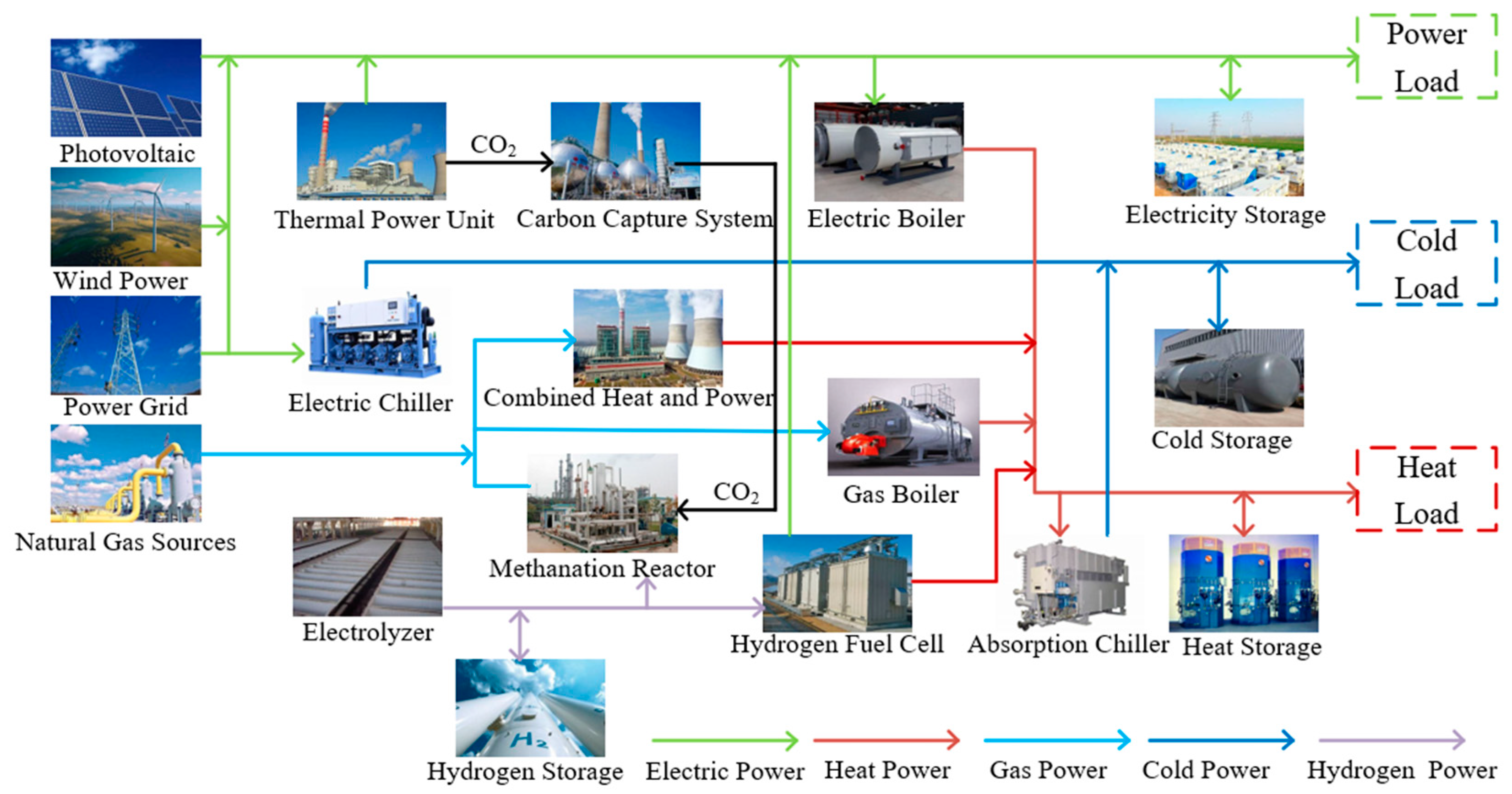
• The optimal scheduling model containing equipment such as P2G, hydrogen fuel cells, and cogeneration units is constructed, which enhances the coupling of electric, heat, gas, cold, and hydrogen subsystems.
• The refined modeling of P2G, together with the inclusion of hydrogen fuel cells and CCS, improves the utilization of renewable energy and solves the carbon source problem of the hydrogen-to-methane process while lowering the system’s carbon emissions even more.
• The implementation of a positive and negative tiered carbon trading mechanism, thereby establishing an effective market-based incentive system, demonstrates significant practical significance for advancing carbon-emission reduction through decreased CO₂ emissions in integrated energy service systems at the market level.

The main research content of this paper is as follows. First, Section 2 introduces the integrated energy system architecture and establishes mathematical models for various energy conversion and storage devices. Section 3 develops an optimal dispatch model with the objective of minimizing operational costs. In Section 4, case studies are conducted to analyze the system benefits under three operational modes. Finally, conclusions are drawn in Section 5.

2. IES Architecture and Mathematical Modelling

Figure 1 depicts the structure of the IES investigated in this article, which internally couples electricity, heat, cold, hydrogen, and natural gas and achieves the conversion between multiple forms of energy through energy conversion equipment such as cogeneration units, in addition to the traditional P2G system decomposed into two parts: electrolysis tanks and methane reactors. IES energy inputs include photovoltaic (PV), wind power (WT), thermal power unit (TPU), and the upper grid/gas grid. Equipment for energy conversion consists of CHP, gas boiler (GB), electric boiler (EB), electric chiller (EC), absorption chiller (AC), electrolyzer (EL), hydrogen fuel cell (HFC), and methane reactor (MR); equipment for energy storage comprises electricity storage (ES), hydrogen storage (H₂S), heat storage (HS), and cold storage (CS). Customer-side load, which is the energy consumed at the customer’s end. In this paper, we consider including electric load, heat load, and cold load.

2.1. IES Model Establishment

2.1.1. Electrolyzer (EL)

Electrolyzers electrolyze water using direct current to produce hydrogen and oxygen. From the perspective of energy conversion, electrolyzers transform electrical energy into hydrogen energy, and the reaction process does not emit carbon. Currently, there are four main electrolysis tank hydrogen production technologies, of which the most widely used is the production of hydrogen by inputting electrical energy in an alkaline environment [25]. Hydrogen production offers an effective method for integrating renewable energy sources. Due to its inherent physicochemical properties, hydrogen serves as an ideal energy carrier, enabling flexible energy redistribution. Furthermore, excess hydrogen can be stored in specialized tanks for interim utilization, thereby addressing intermittency challenges associated with renewable power generation [26]. This document includes the mathematical model and restrictions for producing hydrogen from electrolysis tanks:

P_EL,H2(t) = η_ELP_EL,E(t),

(1)

$$P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{E}\mathrm{L},\mathrm{E}}(t)\le P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(2)

$$\mathsf{\Delta }{P}_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{E}\mathrm{L},\mathrm{E}}(t+1)-P_{\mathrm{E}\mathrm{L},\mathrm{E}}(t)\le \mathsf{\Delta }{P}_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(3)

where P_EL,H2(t) is the electrolyzer’s ability to produce hydrogen energy at a time t, η_EL is the electrolyzer’s efficiency of generating hydrogen energy, P_EL,E(t) is the amount of electricity that the electrolyzer uses at any one time, $P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the electrolyzer’s lowest and maximum electrical power input, $P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the electrolyzer’s climbing power’s lower and upper bounds.

2.1.2. Hydrogen Fuel Cell (HFC)

HFC is an electric-heat-hydrogen coupling device in the system, and its basic working principle is that the hydrogen produced by the electrolysis tank undergoes a redox reaction in the fuel cell, generating electrical and thermal energy in the process. Therefore, the HFC is different from the traditional sense of the battery; it is actually an energy conversion device [27] rather than an energy storage device.

P_HFC,E(t) = η_HFC,EP_HFC,H2(t),

(4)

P_HFC,H(t) = η_HFC,HP_HFC,H2(t),

(5)

$$P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}\left(t\right)\le P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(6)

$$\mathsf{\Delta }{P}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}(t+1)-P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}(t)\le \mathsf{\Delta }{P}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(7)

$${\mathsf{\kappa }}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{H}\mathrm{F}\mathrm{C},\mathrm{H}}(t)/P_{\mathrm{H}\mathrm{F}\mathrm{C},\mathrm{E}}(t)\le {\mathsf{\kappa }}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(8)

where P_HFC,E(t) is the HFC’s electrical power production at a time t, η_HFC,E is the fuel cell’s ability to transform hydrogen energy into electrical energy, P_HFC,H2(t) is the hydrogen power input to the HFC at a time t, P_HFC,H(t) is the thermal power output from the HFC at a time t, η_HFC,H is the efficiency of the fuel cell in converting hydrogen energy to thermal energy, $P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the HFC’s input power’s lowest and greatest amounts. $\mathsf{\Delta }{P}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $\mathsf{\Delta }{P}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the lowest and largest amounts of the HFC’s climbing power. ${\mathsf{\kappa }}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, ${\mathsf{\kappa }}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the adjustable thermoelectric power of the HFC ratio lower and upper limits.

2.1.3. Methane Reactor (MR)

The MR is an important piece of equipment in the P2G chain. For the regular operation of the gas equipment, natural gas is delivered into the fossil fuel pipeline supply system after the carbon dioxide from the carbon capture system reacts with the hydrogen created by the electrolysis tank.

P_MR,G(t) = η_MRP_MR,H2(t),

(9)

$$P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}(t)\le P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(10)

$$\mathsf{\Delta }{P}_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}(t+1)-P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}(t)\le \mathsf{\Delta }{P}_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(11)

where P_MR,G(t) is the natural gas produced by the MR at a time t, η_MR is the energy conversion efficiency of the methane reactor, P_MR,H2(t) is the hydrogen power input to the methane reactor at a time t, $P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the maximum and minimum amounts of hydrogen power that can be added to the MR, $\mathsf{\Delta }{P}_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $\mathsf{\Delta }{P}_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the MR’s climbing power’s lower and upper bounds.

2.1.4. Carbon Capture Power Plants

Depending on the carbon capture plant’s operating conditions, some of the exhaust gas is released into the atmosphere through a flue gas bypass, while the remainder passes through the absorption tower, where the alcoholic amine solution absorbs the majority of it before it enters the rich liquid storage or regeneration tower [28].

$$\left\{\begin{array}{l}{E}_{\mathrm{G}}(t)=e_{\mathrm{g}}{P}_{\mathrm{G}}(t)\\ 0\le \delta \le 1\\ E_{{\mathrm{total},\mathrm{CO}}_2}(t)=E_{\mathrm{CG}}(t)+\beta \delta e_{\mathrm{g}}{E}_{\mathrm{G}}(t)\\ 0\le E_{{\mathrm{total},\mathrm{CO}}_2}(t)\le \eta \beta e_{\mathrm{g}}{P}_{\mathrm{G},\max }\\ P_{\mathrm{B}}(t)=\epsilon E_{{\mathrm{total},\mathrm{CO}}_2}(t)\\ P_{\mathrm{G}}(t)=P_{\mathrm{J}}(t)+P_{\mathrm{D}}(t)+P_{\mathrm{B}}(t)\\ E_{{\mathrm{total},\mathrm{CO}}_2}(t)=E_{\mathrm{f}}(t)+E_{\mathrm{U}}(t)\\ P_G^{\min }U(t)\le P_{\mathrm{G}}(t)\le P_G^{\max }U(t)\\ P_G^{\min }U(t)\le P_{\mathrm{G}}(t+1)-P_{\mathrm{G}}(t)\le P_G^{\max }U(t)\\ E_{\mathrm{U}}(t)={\beta }_{\mathrm{cc}}{P}_{{\mathrm{MR},\mathrm{H}}_2}(t)\end{array}\right.$$

(12)

where E_G(t) is TPU’s total CO₂ production at a point t, e_g is the unit’s carbon intensity, P_G(t) is the unit’s overall generation of power at a point t, and δ is the flue gas split ratio of the unit. E_total,CO2(t) is the amount of CO₂ that the unit has gathered overall at a point t, β is the degree of efficiency in carbon capture, η is the highest working condition factor of the compressor and regeneration tower, P_B(t) is the energy used by the unit operating at a point t, ε is the energy consumption of the unit for capturing a unit of CO₂, and P_J(t) is the net output power of the unit at a point t. P_D is the fixed energy consumption of the unit. E_f(t) is the total amount of carbon sequestration at a point t. E_u(t) is the total amount of carbon utilization at a point t. P_min,G, P_max,G are the minimum and maximum output of the thermal power unit, U(t) is the operating state of the thermal power unit at point t and Δ$P_{\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, Δ$P_{\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the unit’s creep rate, both uphill and downward. β_cc is the conversion coefficient of electricity and carbon.

$$\left\{\begin{array}{l}{V}_{\mathrm{CA}}(t)={\displaystyle \frac{E_{\mathrm{CG}}(t)M_{\mathrm{MEA}}}{M_{{\mathrm{CO}}_2}\theta C_{\mathrm{R}}{\rho }_{\mathrm{R}}}}\\ V_{\mathrm{FY}}(t)=V_{\mathrm{FY}}(t-1)-V_{\mathrm{CA}}(t)\\ V_{\mathrm{PY}}(t)=V_{\mathrm{PY}}(t-1)+V_{\mathrm{CA}}(t)\\ 0\le V_{\mathrm{FY}}(t)\le V_{\mathrm{CR}}\\ 0\le V_{\mathrm{PY}}(t)\le V_{\mathrm{CR}}\\ V_{\mathrm{FY}}(0)=V_{\mathrm{FY}}(24)\\ V_{\mathrm{PY}}(0)=V_{\mathrm{FY}}(24)\end{array}\right.$$

(13)

where V_CA(t) is the amount of solution needed at a time t to release CO₂ from the solution memory, M_MEA is MEA’s molar mass, M_CO2 is the molar mass of CO₂, θ is the regeneration tower resolving volume, C_R is the alkyd solution’s concentration, ρ_R is the density of the alkyd solution, V_FY(t) is the volume of the unit’s rich solution memory at time t, V_PY(t) is the volume of the unit’s lean solution memory at time t, and V_C is the unit’s solution storage capacity.

2.1.5. Combined Heat and Power (CHP)

A gas turbine, a waste heat boiler, and a generator set make up the cogeneration unit. By burning natural gas, thermal energy is converted into mechanical energy, driving the generator to generate electricity and recovering the waste heat to supply the heat load with energy.

P_CHP,E(t) = η_CHP,EP_CHP,G(t),

(14)

P_CHP,H(t) = η_CHP,HP_CHP,G(t),

(15)

$$P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}(t)\le P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(16)

$$\mathsf{\Delta }{P}_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{C}\mathrm{H}\mathrm{P},{\mathrm{H}}_2}(t+1)-P_{\mathrm{C}\mathrm{H}\mathrm{P},{\mathrm{H}}_2}(t)\le \mathsf{\Delta }{P}_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(17)

$${\mathsf{\kappa }}_{\mathrm{C}\mathrm{H}\mathrm{P}}^{\mathrm{m}\mathrm{i}\mathrm{n}}<P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{H}}(t)/P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{E}}(t)\le {\mathsf{\kappa }}_{\mathrm{C}\mathrm{H}\mathrm{P}}^{\mathrm{m}\mathrm{a}\mathrm{x}},$$

(18)

where P_CHP,E(t) is the CHP unit’s electrical energy generated at time t; η_CHP,E is the CHP unit’s power utilization; P_CHP,G(t) is the output electrical energy power of the CHP unit at a time t; P_CHP,H(t) is the output thermal energy power of the CHP unit at a time t; η_CHP,H is the thermal efficiency of the CHP unit; $P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the least and greatest natural gas power input limitations for the CHP unit; $\mathsf{\Delta }{P}_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $\mathsf{\Delta }{P}_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the creep power of the CHP unit’s lower and greater limits; ${\mathsf{\kappa }}_{\mathrm{C}\mathrm{H}\mathrm{P}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, ${\mathsf{\kappa }}_{\mathrm{C}\mathrm{H}\mathrm{P}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the CHP unit’s configurable heat-to-electricity ratio’s bottom and top bounds.

2.1.6. Gas Boiler (GB)

Gas boilers complete this energy conversion process by burning fossil fuels and transmitting thermal power to the water in the boiler via radiant heat transfer or convective heat conduction.

P_GB,H(t) = η_GBP_GB,G(t),

(19)

$$P_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{G}\mathrm{B},\mathrm{G}}(t)\le P_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(20)

$$\mathsf{\Delta }{P}_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{G}\mathrm{B},\mathrm{G}}(t+1)-P_{\mathrm{G}\mathrm{B},\mathrm{G}}(t)\le \mathsf{\Delta }{P}_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(21)

where P_GB,H(t) is the GB’s output thermal power at a time t, η_GB is the GB’s efficiency of energy conversion, P_GB,G(t) is the input natural gas power of the GB at a time t, $P_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the lowest and maximum amounts of the input natural gas energy of the GB, and $\mathsf{\Delta }{P}_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $\mathsf{\Delta }{P}_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the lowest and maximum amounts of the climbing power of the GB.

2.1.7. Electric Boiler (EB)

Electric boilers use electrical energy to heat feed water, thus utilizing high energy conversion efficiency to transform great-grade electrical energy into poor-quality thermal energy.

P_EB,H(t) = η_EB,EP_EB,E(t)

(22)

$$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{E}\mathrm{B},\mathrm{E}}(t)\le P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(23)

$$\mathsf{\Delta }{P}_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{E}\mathrm{B},\mathrm{E}}(t+1)-P_{\mathrm{E}\mathrm{B},\mathrm{E}}(t)\le \mathsf{\Delta }{P}_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(24)

where P_EB,H(t) represents the thermal energy supply of the EB at a point t, η_EB,E is the EB’s energy conversion effectiveness, P_EB,E(t) is the amount of electricity that the EB receives at point t, $P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the electrical power input to the EB’s lowest and highest levels, and Δ$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, Δ$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the EB’s climbing power’s lowest and highest levels.

2.1.8. Electric Chillers (EC)

The EC’s basic function is to use electric energy to power the compressor for refrigeration, which is effectively transformed into cold power to satisfy the system’s customers’ need for cold power [29].

P_EC,C(t) = η_EC,EP_EC,E(t)

(25)

$$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{E}\mathrm{C},\mathrm{E}}(t)\le P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(26)

$$\mathsf{\Delta }{P}_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{E}\mathrm{C},\mathrm{C}}(t+1)-P_{\mathrm{E}\mathrm{C},\mathrm{C}}(t)\le \mathsf{\Delta }{P}_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(27)

where P_EC,C(t) is the EC’s cold power output at point t, η_EC,E is the EC’s energy drilling conversion rate, P_EC,E(t) represents the EC’s input electrical energy at point t and, $P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the lowest and maximum electric power input restrictions set by the EC, Δ$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, Δ$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the EC climbing power’s lowest and highest amounts.

2.1.9. Absorption Chiller (AC)

Absorption chillers are economical and ecological [30]. It uses heat as the input energy, and in addition to the heat generated by gas boilers and cogeneration units, it can also utilize poor-quality heat, such as waste heat.

P_AC,C(t) = η_AC,HP_AC,H(t)

(28)

$$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{A}\mathrm{C},\mathrm{H}}(t)\le P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(29)

$$\mathsf{\Delta }{P}_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{A}\mathrm{C},\mathrm{H}}(t+1)-P_{\mathrm{A}\mathrm{C},\mathrm{H}}(t)\le \mathsf{\Delta }{P}_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(30)

where P_AC,C(t) is the AC’s cooling power generation at point t, η_AC,H is the AC’s energy conversion effectiveness, P_AC,H(t) is the AC’s thermal energy input at point t, $P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, Δ$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the AC’s smallest and largest constraints for cold power input, and Δ$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$Δ$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the AC’s climbing power’s lowest and highest levels.

2.1.10. Energy Storage Device

The energy device for storage for the IES established in this paper includes hydrogen storage equipment, heat storage equipment, cold storage equipment, and electricity storage equipment. It is considered that they work on the same principle.

E_i(t) = E_i(t−1)η_loss + P_i,in(t)η_i,in − P_i,out(t)/η_i,out

(31)

$$E_{\mathrm{i}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le E_{\mathrm{i}}(t)\le E_{\mathrm{i}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(32)

E_i(0) = E_i(24)

(33)

$${u_{\mathrm{i}\mathrm{n}}(t)P}_{\mathrm{i},\mathrm{i}\mathrm{n}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{i},\mathrm{i}\mathrm{n}}(t)\le {u_{\mathrm{o}\mathrm{u}\mathrm{t}}(t)P}_{\mathrm{i},\mathrm{i}\mathrm{n}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$$

(34)

$${u_{\mathrm{o}\mathrm{u}\mathrm{t}}(t)P}_{\mathrm{i},\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{i}\mathrm{n}}\le P_{\mathrm{i},\mathrm{o}\mathrm{u}\mathrm{t}}(t)\le {u_{\mathrm{o}\mathrm{u}\mathrm{t}}(t)P}_{\mathrm{i},\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(35)

u_in(t) + u_out(t) ≤ 1

(36)

where E_i(t) is the energy storage device’s capacitance at point t, i denotes the hydrogen, electricity, cold, and heat storage equipment, η_loss is the hydrogen storing tank’s wasted energy coefficient. P_i,in(t), P_i,out(t) are the energy storage device’s ability to store and release energy at a time t, and η_i,in, η_i,out are the energy storage equipment’s efficiency in storing and releasing energy. $E_{\mathrm{i}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$, $E_{\mathrm{i}}^{\mathrm{m}\mathrm{a}x}$ are the energy-storing devices with the smallest and largest capacity, and u_in(t) and u_out(t) are the binary variables that define the energy storage equipment’s ability to store and release energy at point t.

2.2. Carbon Emission Model

Carbon trading, additionally referred to as the emission of carbon trading, is a product of the carbon trading market, which is becoming more and more significant in addressing the challenge of global climate change by giving carbon emission rights a commodity attribute and allowing companies to buy or sell carbon emission rights, thereby achieving the goal of controlling emissions of carbon [31].

The following is a description of the carbon quota model:

$$\left\{\begin{array}{l}{E}_{\mathrm{all}}=E_{\mathrm{e},\mathrm{buy}}+E_{\mathrm{G}}+E_{\mathrm{CHP}}+E_{\mathrm{GB}}\\ E_{\mathrm{e},\mathrm{buy}}={\chi }_{\mathrm{e}}{\displaystyle \sum _{t=1}^T{P}_{\mathrm{e},\mathrm{buy}}(t)}\\ E_{\mathrm{G}}={\chi }_{\mathrm{e}}{\displaystyle \sum _{t=1}^T{P}_{\mathrm{G}}(t)}\\ E_{\mathrm{CHP}}={\chi }_{\mathrm{h}}{\displaystyle \sum _{t=1}^T\left({\sigma }_{\mathrm{e},\mathrm{h}}{P}_{\mathrm{CHP},\mathrm{e}}(t)+P_{\mathrm{CHP},\mathrm{h}}(t)\right)}\\ E_{\mathrm{GB}}={\chi }_{\mathrm{h}}{\displaystyle \sum _{t=1}^T{P}_{\mathrm{GB},\mathrm{h}}(t)}\end{array}\right.$$

(37)

where χ_e and χ_e represent the amount of carbon credits obtained for each unit of heat and electricity produced; σ_e,h is the factor that converts the production of electricity into the production of thermal.

The real emissions of the carbon model used by the IES are shown below:

$$\left\{\begin{array}{l}{E}_{\mathrm{all},\mathrm{a}}=E_{\mathrm{e},\mathrm{buy},\mathrm{a}}+E_{\mathrm{CHP},\mathrm{a}}+E_{\mathrm{GB},\mathrm{a}}+E_{\mathrm{G}}(t)-E_{{\mathrm{total},\mathrm{CO}}_2}\\ E_{\mathrm{e},\mathrm{buy},\mathrm{a}}={\delta }_{\mathrm{e}}{\displaystyle \sum _{t=1}^T{P}_{\mathrm{e},\mathrm{buy}}(t)}\\ E_{\mathrm{CHP},\mathrm{a}}={\delta }_{\mathrm{h}}{\displaystyle \sum _{t=1}^T(P_{\mathrm{CHP},\mathrm{e}}(t)+{\sigma }_{\mathrm{e},\mathrm{h}}{P}_{\mathrm{CHP},\mathrm{h}}(t))}\\ E_{GB,a}={\delta }_{\mathrm{h}}{\displaystyle \sum _{t=1}^T{P}_{\mathrm{GB},\mathrm{h}}(t)}\end{array}\right.$$

(38)

where E_all,a, E_e,buy,a, E_CHP,a, E_GB,a is the real carbon releases from the IES, upper power grid, CHP, and GB, δ_e, δ_h are the carbon releases per unit of electricity and heat generated.

The carbon releases market is trading as follows:

E_all,c = E_all,a − E_all

(39)

where E_all,c is the amount of carbon release traded.

The conventional carbon exchange system has a fixed carbon trading base price, while the laddered carbon exchange system divides the carbon releases involved in trading into multiple intervals of the same span, each of which sets the corresponding carbon trading price, forming a laddered price into a laddered price, thus forming a closer relationship between the systematic carbon emissions and their corresponding transaction costs [32].

$$F_{C{O}_2}=\left\{\begin{array}{l}\lambda (1+3\alpha )(E_{\mathrm{IES},\mathrm{c}}+3l)-\lambda (2+3\alpha )l, E_{IES,c}<-2l\\ \lambda (1+2\alpha )(E_{\mathrm{IES},\mathrm{c}}+l)-\lambda (1+\alpha )l, -2l<E_{\mathrm{IES},\mathrm{c}}<-l\\ \lambda (1+\alpha )E_{\mathrm{IES},\mathrm{c}}, -l<E_{\mathrm{IES},\mathrm{c}}<0\\ \lambda E_{\mathrm{IES},\mathrm{c}}, 0<E_{\mathrm{IES},\mathrm{c}}<l\\ \lambda (1+\alpha )(E_{\mathrm{IES},\mathrm{c}}-l)+\lambda l, l<E_{\mathrm{IES},\mathrm{c}}<2l\\ \lambda (1+2\alpha )(E_{\mathrm{IES},\mathrm{c}}-2l)+\lambda (2+\alpha )l, 2l<E_{\mathrm{IES},\mathrm{c}}<3l\\ \lambda (1+3\alpha )(E_{\mathrm{IES},\mathrm{c}}-3l)+\lambda (3+3\alpha )l, 3l<E_{\mathrm{IES},\mathrm{c}}<4l\\ \lambda (1+4\alpha )(E_{\mathrm{IES},\mathrm{c}}-4l)+\lambda (4+6\alpha )l, 4l<E_{\mathrm{IES},\mathrm{c}}\end{array}\right.$$

(40)

where F_CO2 is the phased carbon trading price; l is a length of the gap between carbon releases; α is the rate of rising prices for trading in carbon; and λ is the basic price of the trading of carbon cost.

3. Objective Functions and Constraint Conditions

3.1. Objective Functions

Minimizing the total cost of energy acquisition, carbon sequestration, thermal unit startup and shutdown, energy abandonment penalty, and phased carbon trading is the goal.

minF_run = F_buy + F_f + F_G + F_re + F_CO2,

(41)

where F_run is the total expense of running the system, F_buy is the network price of electricity that was purchased, F_f is the carbon storage unit cost, F_G is a start-stop cost of TPU, F_re is this network’s cost of WT and PV loss penalties, and F_CO2 is the price of exchanging carbon.

The following is the price of acquiring energy:

$$F_{\mathrm{buy}}={\displaystyle \sum _{t=1}^T{c}_e}(t)P_{e,buy}(t)+{\displaystyle \sum _{t=1}^T{c}_g}(t)P_{g,buy}(t)+{\displaystyle \sum _{t=1}^T(a_1{P}_G(t)+b_1{P}_G(t)+c_{1}U(t))}$$

(42)

where c_e(t) and c_g(t) are the time-of-day electricity and natural gas prices at a time t, P_e,buy(t), and P_g,buy(t) are the total amounts of electricity and gas purchased at point time, and a₁, b₁, and c₁ are the thermal unit coal consumption factors.

The cost of carbon sequestration is as follows:

$$F_{\mathrm{f}}={\displaystyle \sum _{t=1}^T{F}_{\mathrm{f}}(t)}{c}_{\mathrm{f}}$$

(43)

where c_f is the expense of storing carbon per unit.

The cost of starting and stopping thermal power units is as follows:

$$F_{\mathrm{G}}={\displaystyle \sum _{t=1}^T\left[U(t)(1-U(t))c_{\mathrm{u}}\right]},$$

(44)

where c_u is the cost of starting and stopping the unit.

The cost of WT and PV loss is included in the penalty cost of energy abandonment, as follows:

$$F_{\mathrm{re}}={\displaystyle \sum _{t=1}^T(c_{\mathrm{WT}}(P_{\mathrm{WT}}(t)-P_{\mathrm{WTa}}(t))}+c_{\mathrm{PV}}(P_{\mathrm{PV}}(t)-P_{\mathrm{PVa}}(t)),$$

(45)

where c_WT is the wind desertion penalty cost per unit and c_PV is the amount of the light departure penalty per unit.

3.2. Constraint Conditions

The maximum and minimum output thresholds and climbing power constraints of each energy conversion device of the system, as well as the energy-storing devices’ operational limitations, have already been covered in detail in Section 2 and will not be repeated here.

The following are the electric power equilibrium restrictions:

P_E,load(t) = P_PV(t) + P_WT(t) + P_J(t) + P_equip,E(t) − P_E,in(t)+ P_E,out(t),

(46)

P_equip,E(t) = P_HFC,E(t) − P_EL,E(t) + P_CHP,E(t) − P_EB,E(t) − P_EC,E(t)

(47)

The following are the thermal power equilibrium limitations:

P_H,load(t) + P_AC,H(t) + P_H,in(t) = P_CHP,H(t) + P_GB,H(t) + P_EB,H(t) + P_H,out(t),

(48)

The gas power equilibrium constraints are as follows:

P_G,buy(t) + P_MR,G(t) + P_G,out(t) = P_CHP,G(t) + P_GB,G(t) + P_G,in(t),

(49)

The cold power equilibrium constraints are as follows:

P_C,load(t) + P_C,in(t) = P_EC,C(t) + P_AC,C(t) + P_C,out(t),

(50)

The hydrogen power equilibrium constraints are as follows:

P_EL,H2(t) + P_H2,out(t) = P_HFC,H2(t) + P_MR,H2(t) + P_H2,in(t),

(51)

The wind and solar output constraints are as follows:

$${0\le P}_{\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{d}}\le P_{\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{d}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(52)

$${0\le P}_{\mathrm{P}\mathrm{V}}\le P_{\mathrm{P}\mathrm{V}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(53)

where P_Wind is the WT’s output power, $P_{\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{d}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum output power of the WT, P_PV is the energy that the solar power system produces, and $P_{\mathrm{P}\mathrm{V}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum output power of the solar power generation.

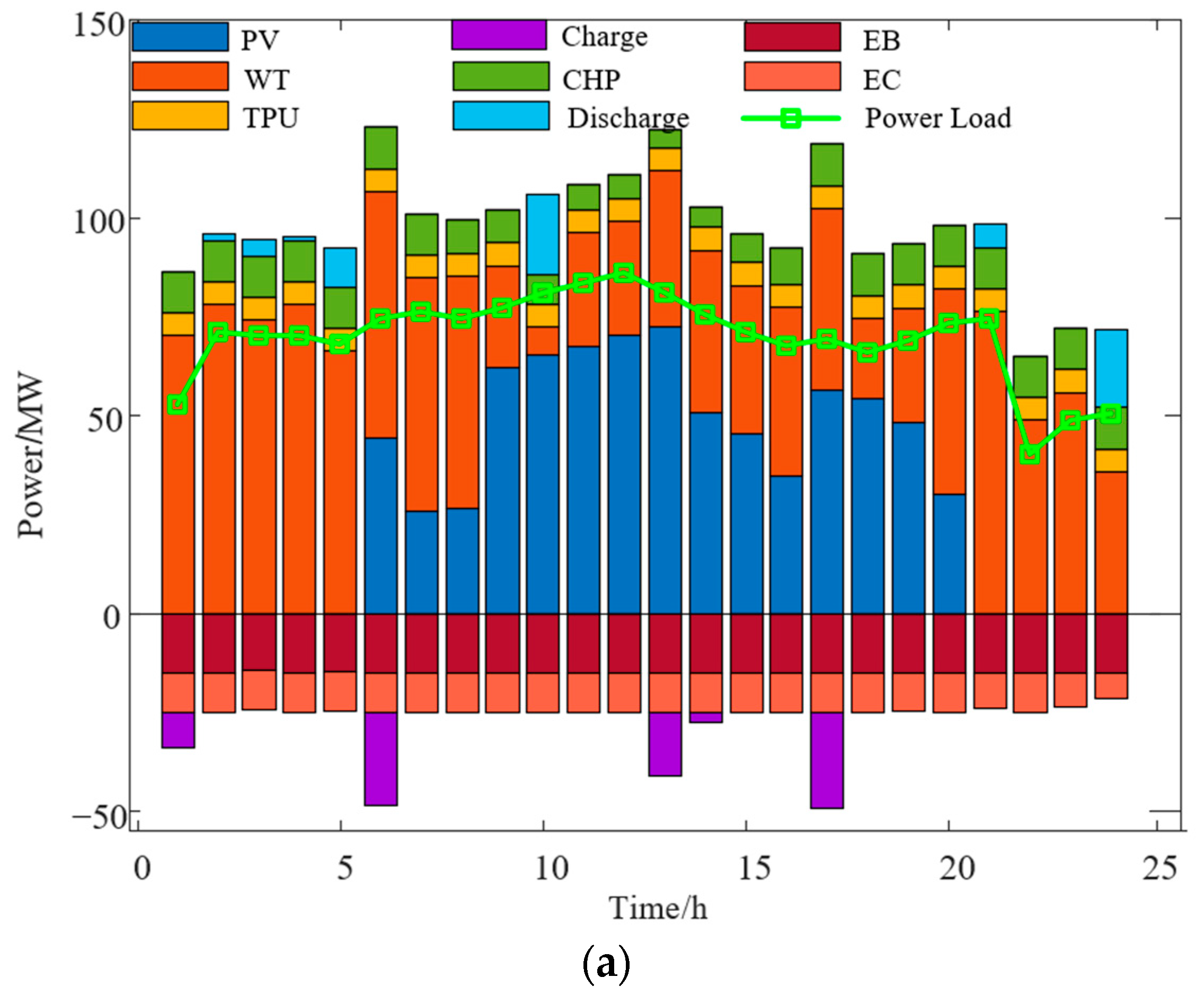
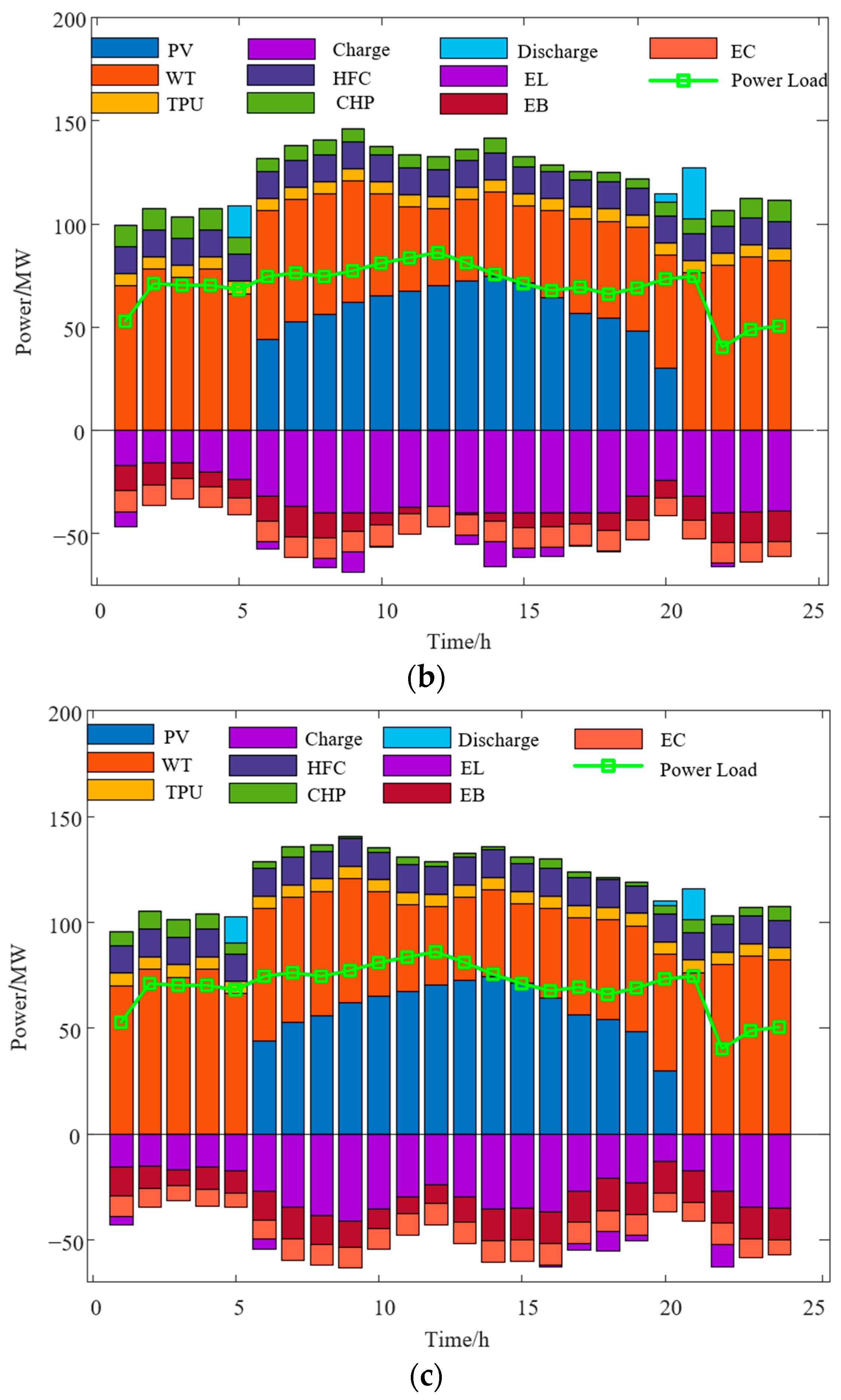
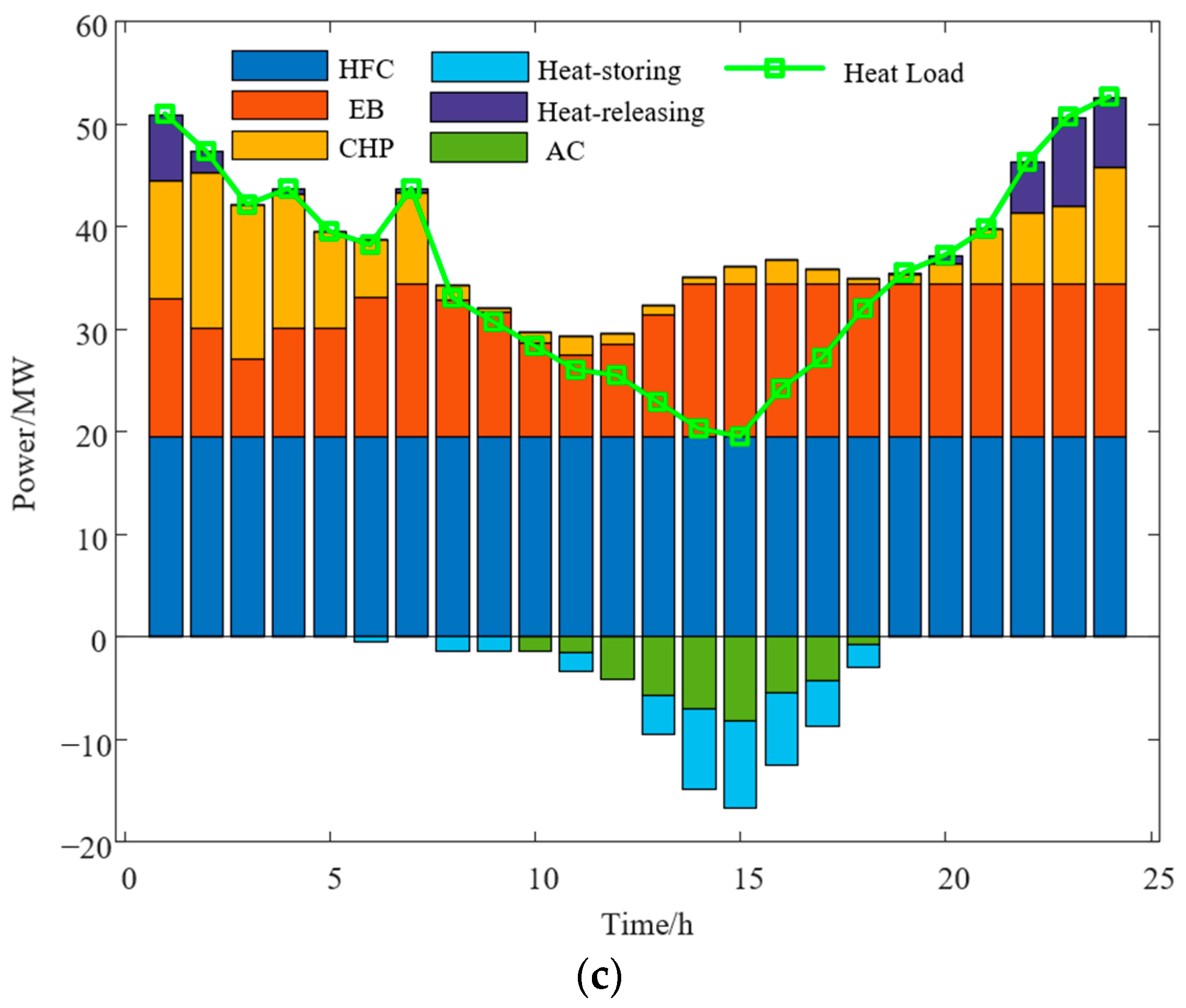
4. Case Study

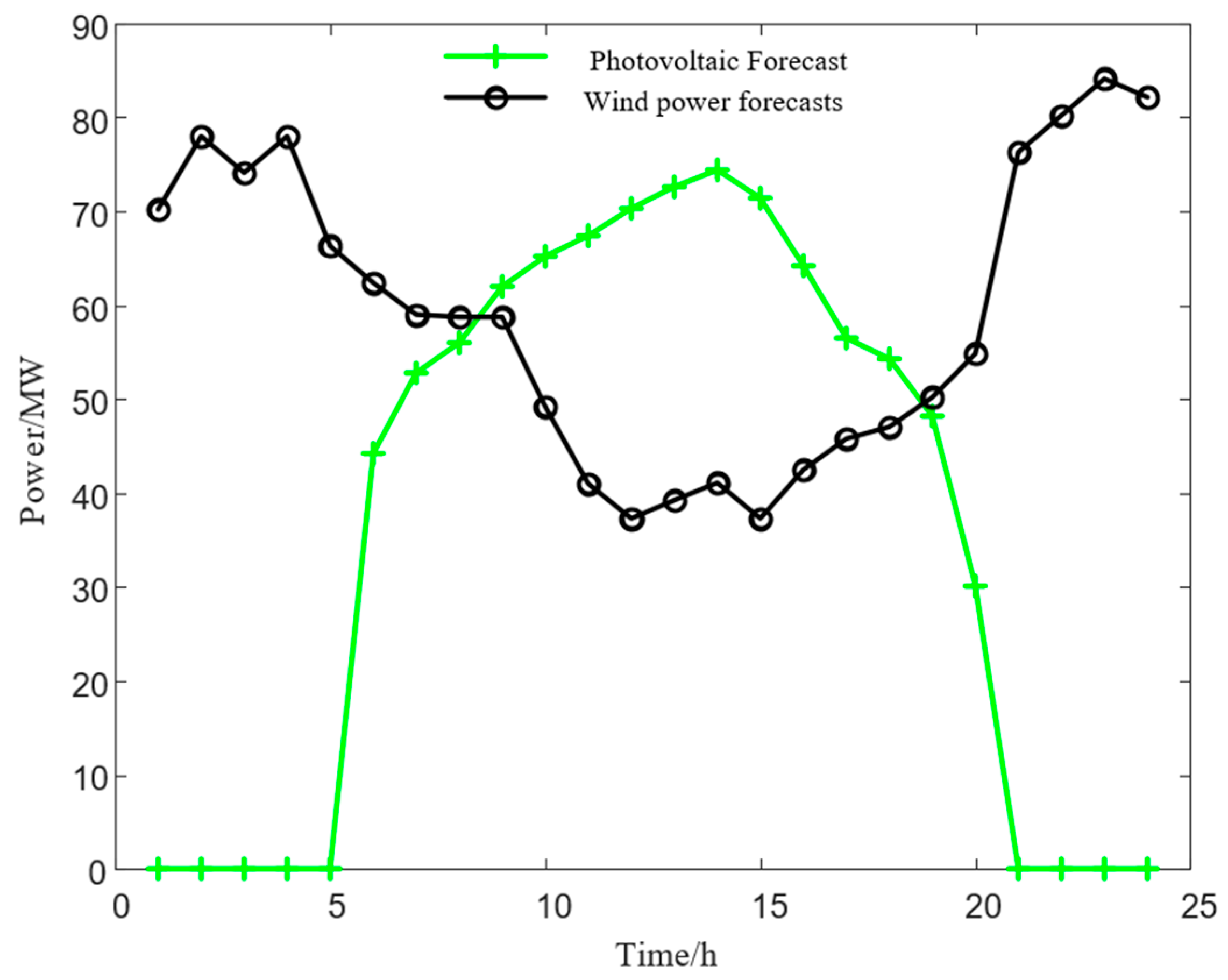
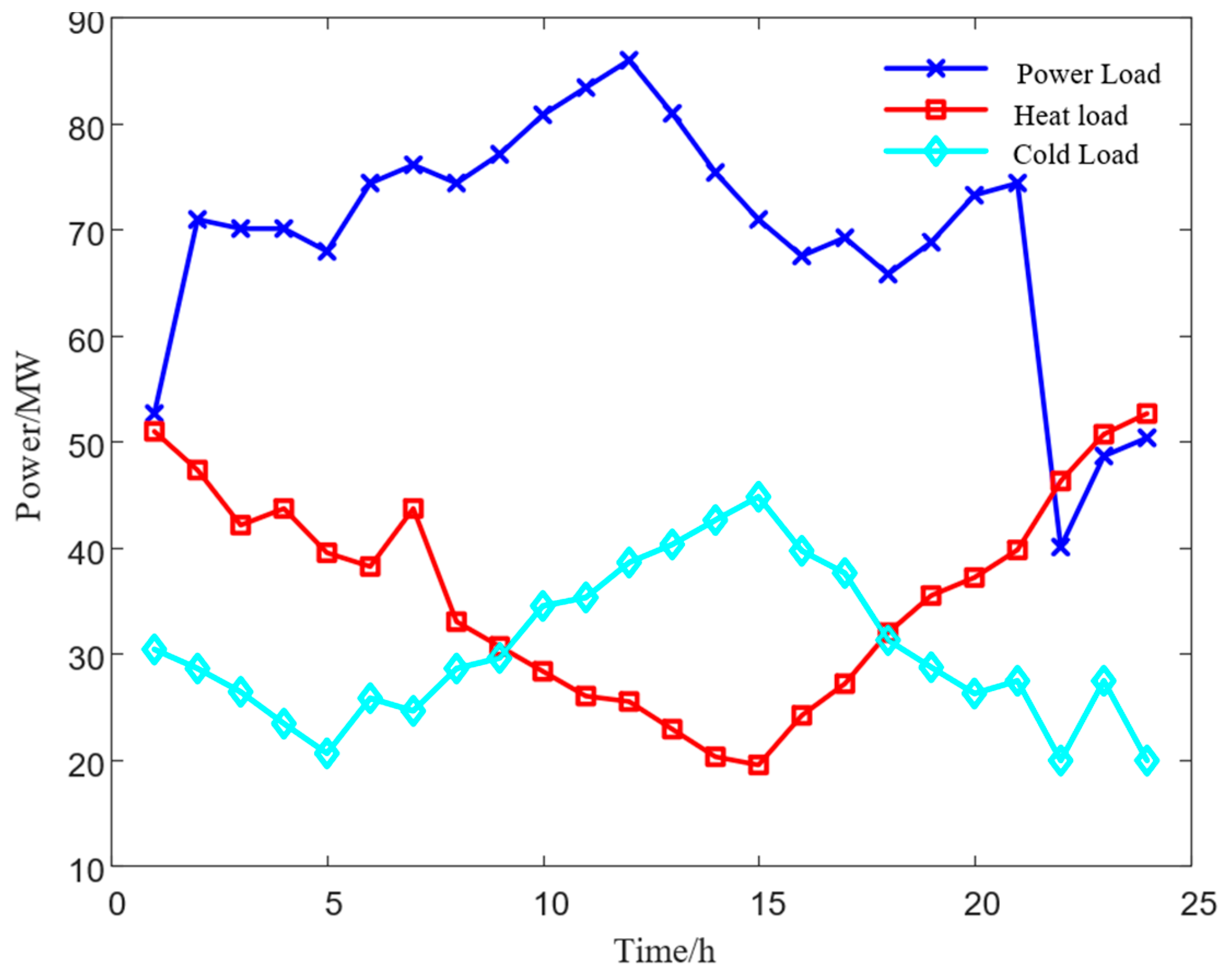
Basic Data

To confirm that the IES scheduling model developed in this paper is accurate, in this work, a park is chosen as the research site. The integrated energy system (IES) optimization dispatch model was implemented in MATLAB R2021b and executed on a computer equipped with an AMD Ryzen 7-4800U processor (Santa Clara, CA, USA) and 16 GB of RAM. The carbon trading mechanism cost was optimized using the Big-M method, rendering the problem a mixed-integer linear programming (MILP) formulation. The model was solved via the MATLAB R2021b/CPLEX 12.10.0 interface with the CPLEX solver, achieving a computational runtime of 0.670 s. Consider a 24-h day as the scheduling period, with an hourly scheduling step.

Table 1. Model parameters.

Parameters	Values	Parameters	Values
ηEL [22]	0.87	$P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW
$P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	40 MW	Δ$P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−8 MW
Δ$P_{\mathrm{E}\mathrm{L},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	8 MW	ηHFC,E	0.87
$P_{\mathrm{H}\mathrm{F}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	15 MW	$P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW
Δ$P_{\mathrm{H}\mathrm{F}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	3 MW	Δ$P_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−3 MW
${\mathsf{\kappa }}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	1.2	${\mathsf{\kappa }}_{\mathrm{H}\mathrm{F}\mathrm{C},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0.5
$P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW	ηMR	0.7 [22]
Δ$P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−4 MW	$P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	20 MW
eg [28]	1 (t/MW·h)	Δ$P_{\mathrm{M}\mathrm{R},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	4 MW
β [28]	0.9	δ [28]	0.8
ε [28]	0.269 ((MW·h)/t)	η [28]	1.05
$P_{\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	10 MW	PD	2 MW
Δ$P_{\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−60	$P_{\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	55 MW
$P_{\mathrm{C}\mathrm{H}\mathrm{P},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW	Δ$P_{\mathrm{G}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	60 MW
Δ$P_{\mathrm{C}\mathrm{H}\mathrm{P},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−4 MW	$P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	20 MW
${\mathsf{\kappa }}_{\mathrm{C}\mathrm{H}\mathrm{P},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0.5	Δ$P_{\mathrm{C}\mathrm{H}\mathrm{P},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	−4 MW
ηGB [22]	0.9	${\mathsf{\kappa }}_{\mathrm{C}\mathrm{H}\mathrm{P},{\mathrm{H}}_2}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	1.8
$P_{\mathrm{G}\mathrm{B},\mathrm{B}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	15 MW	$P_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW
Δ$P_{\mathrm{G}\mathrm{B},\mathrm{B}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	3 MW	Δ$P_{\mathrm{G}\mathrm{B},\mathrm{G}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−3 MW
$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW	ηEB,E	0.99
Δ$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−3 MW	$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	15 MW
ηEC,E [22]	3	Δ$P_{\mathrm{E}\mathrm{B},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	3 MW
$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	10 MW	$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW
Δ$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	2 MW	Δ$P_{\mathrm{E}\mathrm{C},\mathrm{E}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−2 MW
$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	0 MW	ηAC,H	1.8
Δ$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$	−6 MW	$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	15 MW
Δ$P_{\mathrm{A}\mathrm{C},\mathrm{H}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$	6 MW	l	200 t
λ [33]	250 RMB/t	α [33]	0.25
ηi,in [22]	0.95	ηi,in [22]	0.95
ηloss [15]	0.01	βcc [14]	1.02

lists the basic parameters of the system.

Table 2. Electricity costs vary depending on when it is used.

Type	Time (h)	Price (RMB/MWh)
Peak data	8:00–11:00	1000
	19:00–24:00
Off-peak data	11:00–13:00	810
	17:00–19:00
	0:00–4:00
Valley data	4:00–8:00	670
	13:00–17:00

lists the time-of-day tariffs for the system.

Table 3. Case settings.

Case	Condition
Case 1	An IES do not take into account carbon trading and hydrogen participation
Case 2	An IES consider hydrogen participation based on case 1
Case 3	An IES consider stepped carbon trading based on case 2

shows the three modes of operation of the system. Figure 2 illustrates the projected output of wind and photovoltaic installations in the park. Figure 3 shows the forecast load data for electricity, heat and cooling in the park.

Table 4. Scheduling results of each case.

Case	Renewable Energy Consumption/%	Cost/RMB	Carbon Emissions/t
1	83.16%	312,737.89	159.45
2	100.00%	186,047.03	133.00
3	100.00%	129,423.99	104.65

compares the results of the optimal scheduling of the amount of renewable energy used by the system, operating costs, and CO₂ emissions for the three cases.

Case 1 ignores the electric and gas connecting equipment or carbon trading; the system running cost is CNY 312,737.89, and CO₂ emission is 159.45 t. Case 2 considers the electric and gas coupling equipment and does not consider carbon trading; the system running cost is CNY 186,047.03, CO₂ emission is 133.00 t, the clean energy utilization rate reaches 100%, and the IES inputs the remaining solar and wind energy into the electric-hydrogen coupling equipment to achieve full utilization of clean energy. In case 3, the operating cost of the system is CNY 129,423.99, and the CO₂ emission is 104.65 t.

Figure 4 shows the electrical power equilibrium diagrams for the three cases. All three cases are mainly supplied by the WT to the system during the nighttime scheduling period, as the PV units are not working. During the daytime, wind and solar units are combined to produce power, and thermal units, cogeneration units, and storage devices take on the role of in-system peaking. EB and EC employ electrical energy to generate heat and cold energy to power the load at the customer’s location.

It is evident from comparing Cases 1 and 2 that Case 1 lacks a hydrogen-coupled unit, the PV power generation can not be better utilized in the period of 6:00–20:00, and the phenomenon of light abandonment is more serious, and the CHP unit is more out of power, which raises the system’s release of carbon. Following the fitting of P2G equipment and fuel cells into the system, the electrolyzer consumes surplus electrical energy to produce hydrogen, which makes better use of wind and light resources, and the system output is smoother, which plays the role of leveling the power load, thus facilitating the integration of large-scale renewable energy sources into the grid.

It is obvious when comparing Cases 2 and 3 that the electricity system is less affected by the implementation of phased trading of carbon. Firstly, the system reduces the output of CHP units while increasing the output of EB, thus reducing the use of natural gas and lowering the carbon emissions of the system.

In summary, from an economic standpoint, the two-stage refined modeling of the traditional electricity-to-gas equipment, followed by the introduction of HFC tanks for storing hydrogen and other apparatus, enables the hydrogen-coupled equipment to work independently, with more flexible operation and improved use of WT energy production. On the flip side, carbon dioxide from carbon capture plants is fed into MR to generate natural gas, which lowers the amount of natural gas purchased and thus the cost of purchased energy. From the perspective of the environment, HFC can use hydrogen energy to power the system, thus reducing the output of CHP units and GB, thus reducing the carbon emissions of the system.

Figure 5 displays the thermodynamic equilibrium diagrams for all three circumstances. Within the heating system, extra heat energy is stored by the heat storage apparatus during the daytime heat consumption trough time and is used for the nighttime peak period, which plays the role of system peak. AC converts heat energy into cold energy, which is delivered to the cooling system for use.

A comparison between Case 1 and Case 2 can be obtained. The system guarantees the lowest possible operational expenses, so after the introduction of hydrogen energy electrolysis tanks to dissipate the excess power, one of the uses of methanation equipment is to generate gas from natural sources, lowering the quantity of natural gas that is bought and lowering the energy expenses of the system. Excess wind energy is converted into hydrogen in this method; thus, it is a low-carbon operation. Secondly, part of the hydrogen produced is utilized by the HFC to generate electricity and heat, thus reducing the output of the CHP unit, which in turn reduces the amount of gas purchased and lowers the cost of purchasing coal and natural gas. Thirdly, the hydrogen produced in the electrolysis tank consumes a significant quantity of electrical energy, reducing the input electrical energy of the electric boiler.

A comparison between Case 2 and Case 3 can be obtained via the market for the trading of carbon. To further minimize the system’s release of carbon, the system first reduces the output of the cogeneration unit and chooses to prioritize the use of electric power equipment; in other words, the electric boiler’s output is raised, thus lowering the system’s release of carbon. In this process, the CHP unit minimizes heat output and thus reduces the system’s gas use, while the electrolyzer reduces its output.

Figure 6 depicts the cold equilibrium of power for all three cases. The electric refrigerator has a high energy conversion efficiency and therefore undertakes the main task of supplying cold to the users. Whenever the electric chiller hits its maximum power limit, the hydrogen storage tank starts to discharge the cold and performs in-system peak shifting together with the absorption refrigeration equipment. During the low peak hours, the hydrogen storage tanks store energy and realize the transfer of cold energy across time.

A comparison of Case 1 and Case 2 shows that the electric chillers are basically at full capacity to satisfy the user’s cold energy requirement. The storage tanks are not enough to fulfill peak energy consumption, so absorption refrigeration equipment is introduced to supply the system during peak hours.

Case 2 compared with Case 3 can be obtained, in the 2:00–3:00 time period, in the system of cooling in the trough section of the system for the discharge of energy. This is due to the fan, as the main source of power for equipment, solar generation, failing to operate out of power, resulting in the system power supply being tense. At this time, the electric chiller of the electric power transfer to other power-using equipment. Case 3 peak shifting is mainly met by absorption refrigeration equipment. This is due to the starting time of the day, when only the fan works to generate electricity. At this time, the system is in the tension of electricity, and in the cold peak hours, overlapping with the heat of the trough section, photovoltaic power generation and wind power generation synergistic power, thermal energy output, can be through the absorption refrigeration machine for the system to provide cold power and meet the needs for the cold load.

5. Conclusions

This study aims to enhance the capacity of the utilization of renewable energy and promote the power source carbon-neutral economic development of the energy system. By coupling electricity-heat-gas-cooling-hydrogen and other resources as a whole and integrating with the stepwise trading of carbon mechanism, an ideal scheduling model for the cooperative operation of power and heat units, electrolysis tanks, hydrogen fuel cells, and energy storage devices is established. Based on the numerical simulation study, the following results are drawn:

• The traditional P2G equipment is refined into two parts: an electrolyzer and an MR, and an HFC is introduced to reduce carbon emissions by utilizing the CO₂ produced by the system while promoting wind energy consumption. Through arithmetic simulation, the renewable energy consumption rate is increased from 83.16% to 100%, and the carbon emission is reduced from 159.45 tonnes to 133 tonnes.
• Introduced a phased carbon trading mechanism to minimize emissions by adjusting the output of each part of the system, in which the penalty and reward mechanism of the market for trading in carbon can guide participants to prioritize the use of energy with minimal environmental impact, and the data reveal that the system’s releases of carbon have been decreased from 133 tonnes to 104.65 tonnes after implementing into consideration the phased trading of carbon.

This study focuses on the low-carbon and economic aspects of integrated energy system (IES) operation, specifically examining operational costs while excluding lifecycle investment cost considerations. The research scope encompasses generation-side and grid-side operational strategies, with load-side scheduling mechanisms remaining beyond current investigation. Building upon these foundational findings, subsequent research should incorporate demand response mechanisms to achieve synergistic optimization of system efficiency and sustainability objectives.