Hybrid Method for Oil Price Prediction Based on Feature Selection and XGBOOST-LSTM
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Model Framework
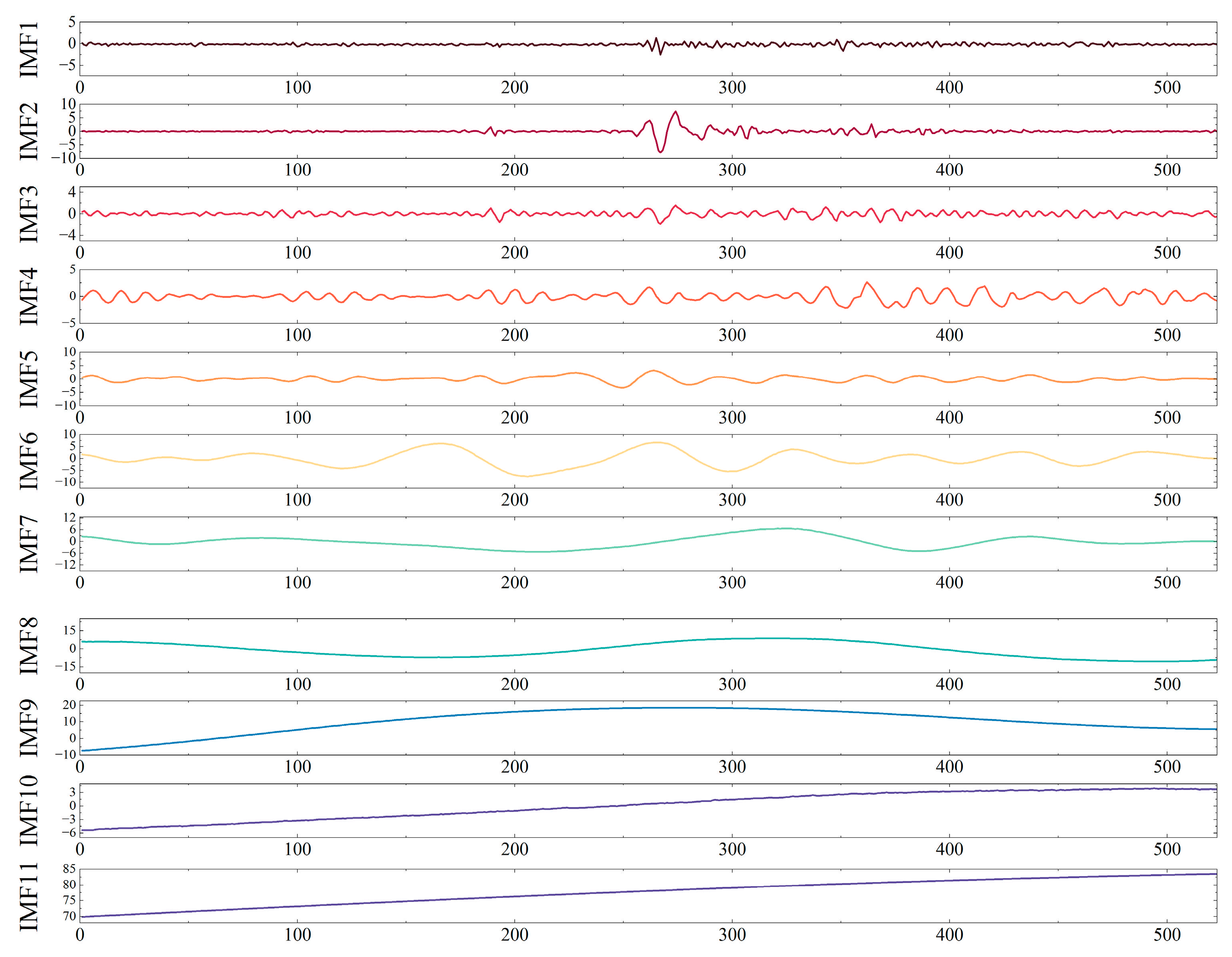
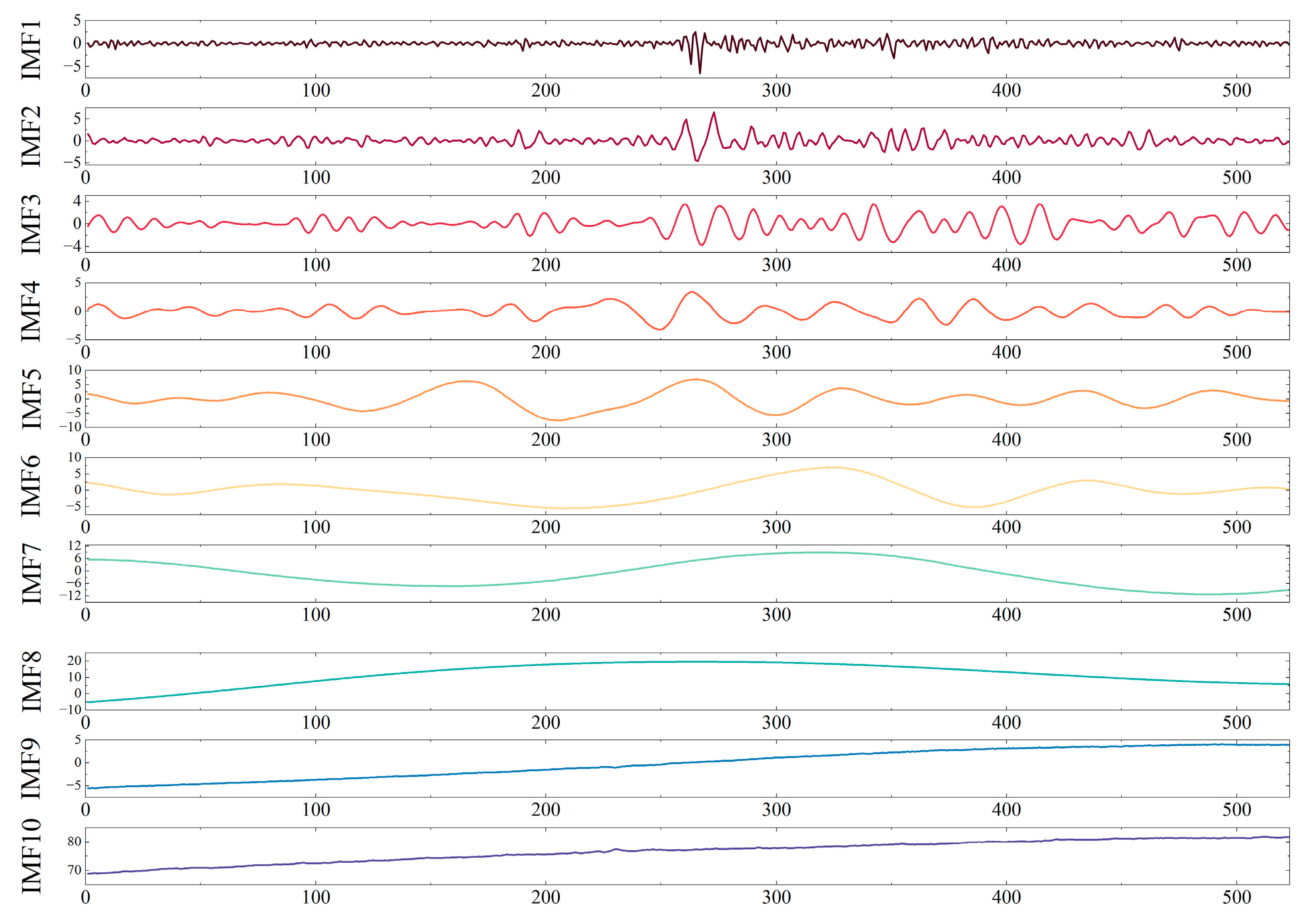
3.2. ICEEMDAN
3.3. ACBFS
3.4. Attention Mechanisms
3.5. BOHB
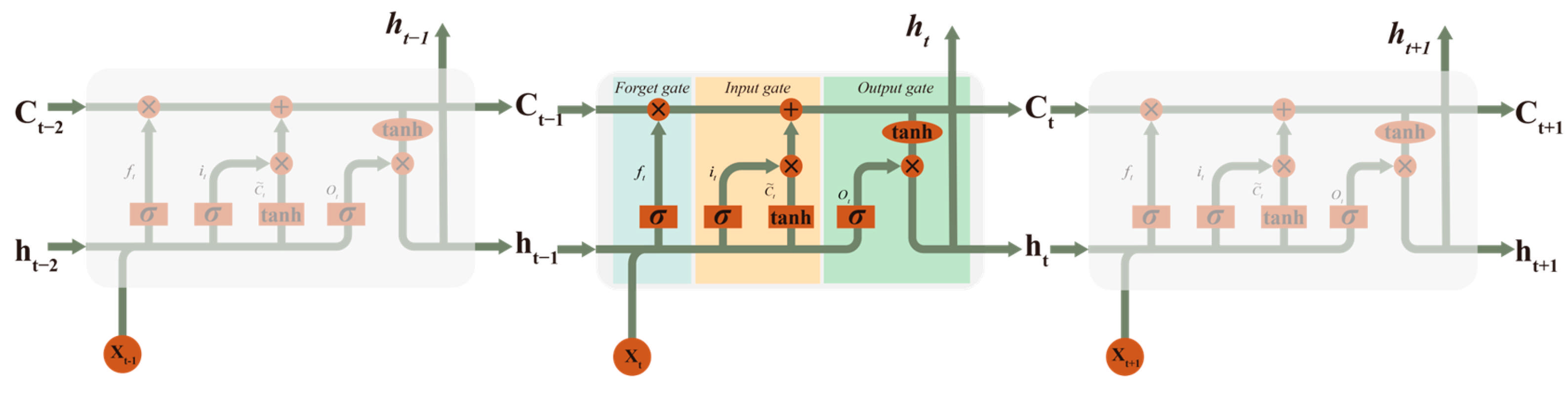
3.6. LSTM
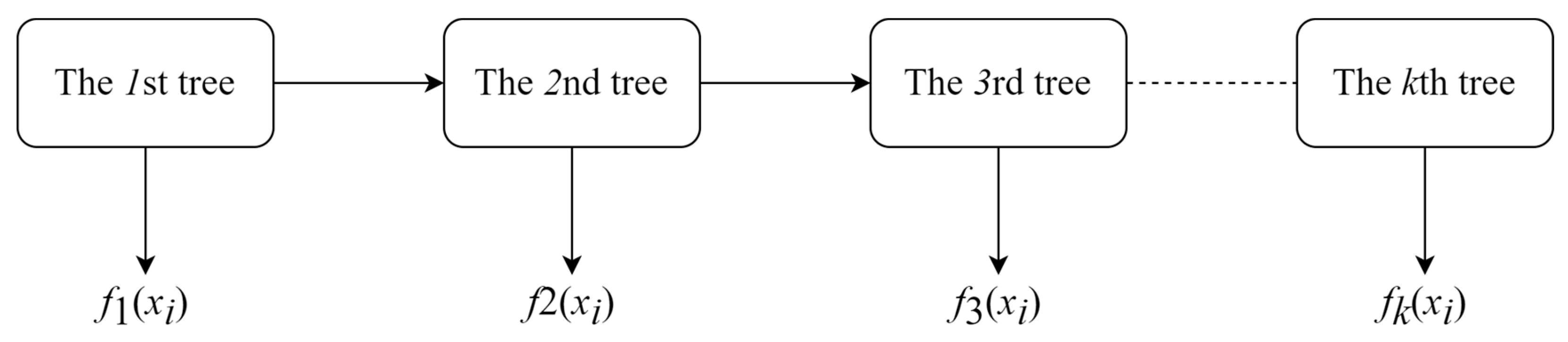
3.7. XGBoost
4. Data Preprocessing
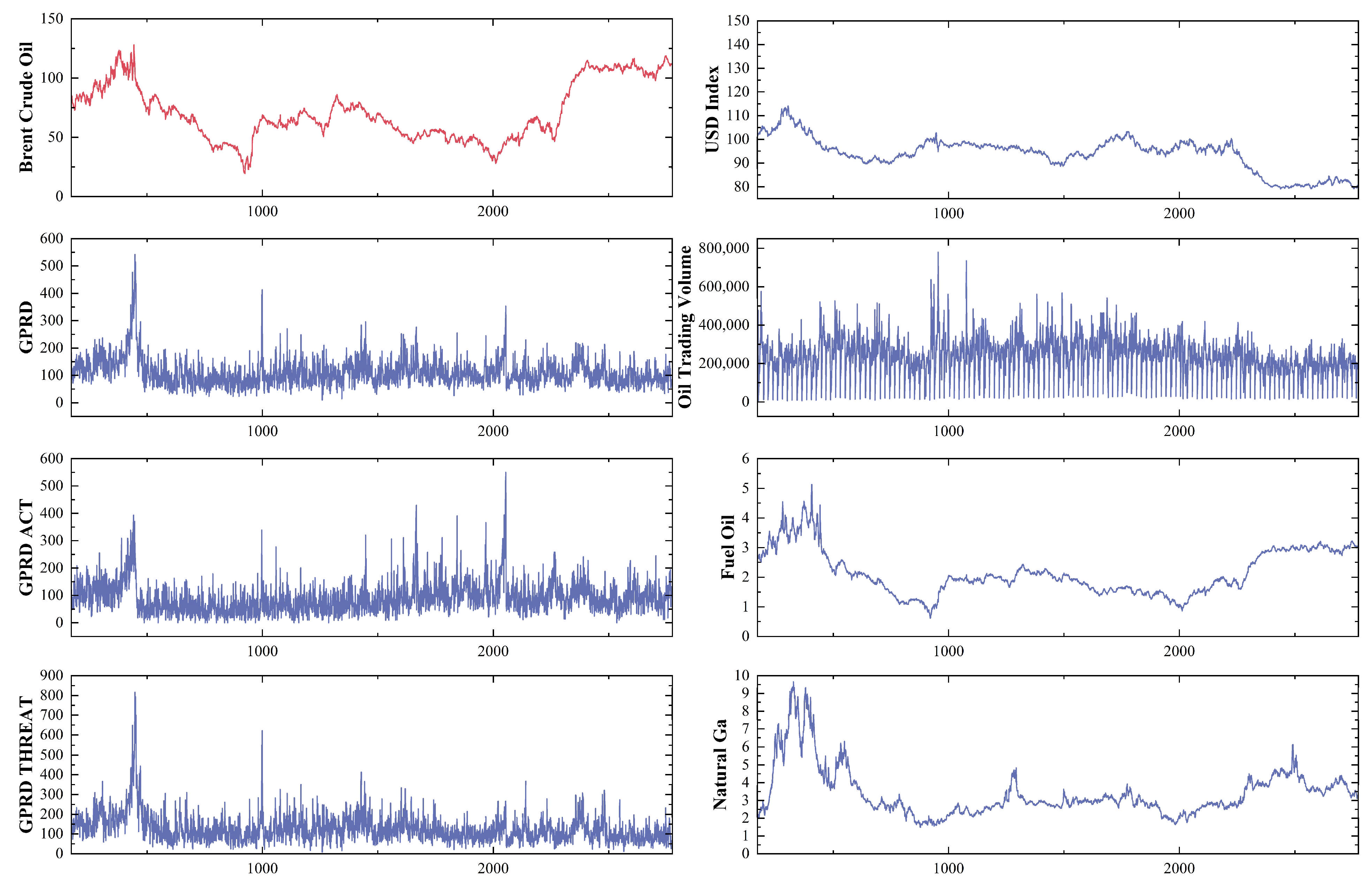
4.1. Data Selection
4.1.1. Crude Oil Price
4.1.2. Commodity Properties: Oil Futures’ Trading Volume
4.1.3. Macroeconomic Factors: United States Dollar Index
4.1.4. Geopolitical Risks
4.1.5. Alternative Energy
4.2. Evaluation Principles
4.3. Parameter Description
4.4. Benchmarking Model
5. Empirical Results
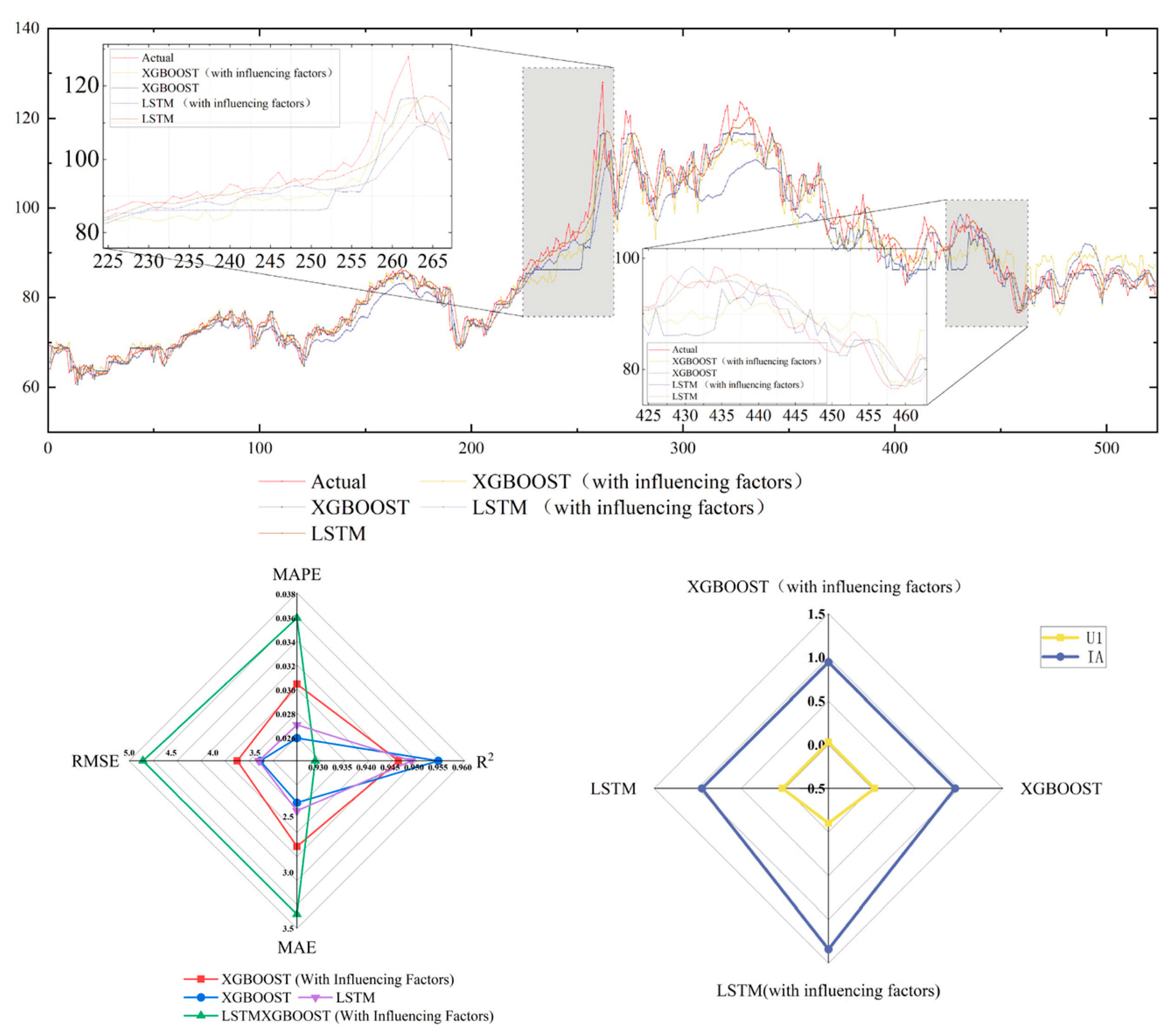
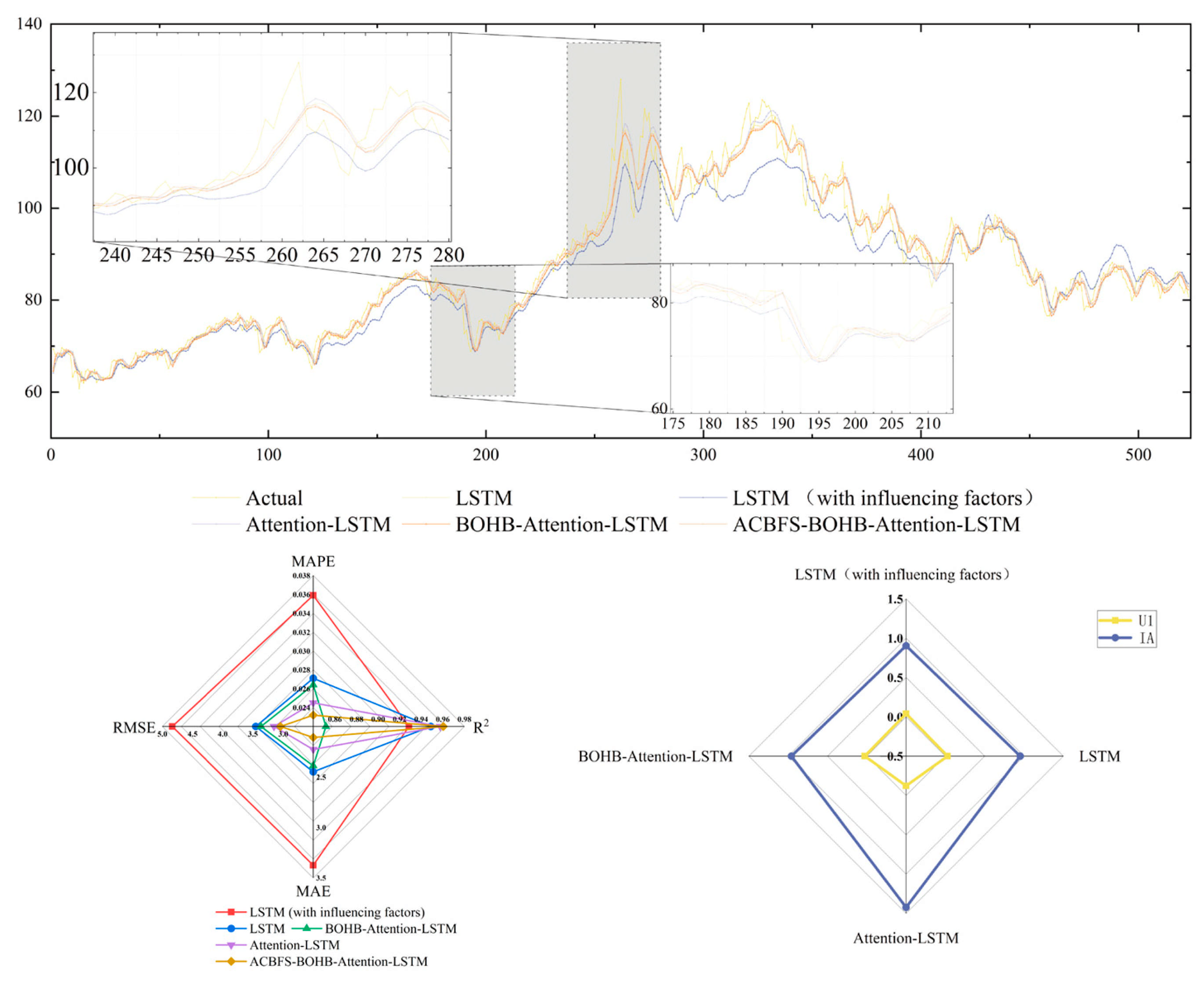
5.1. Comparison I
5.2. Comparison II
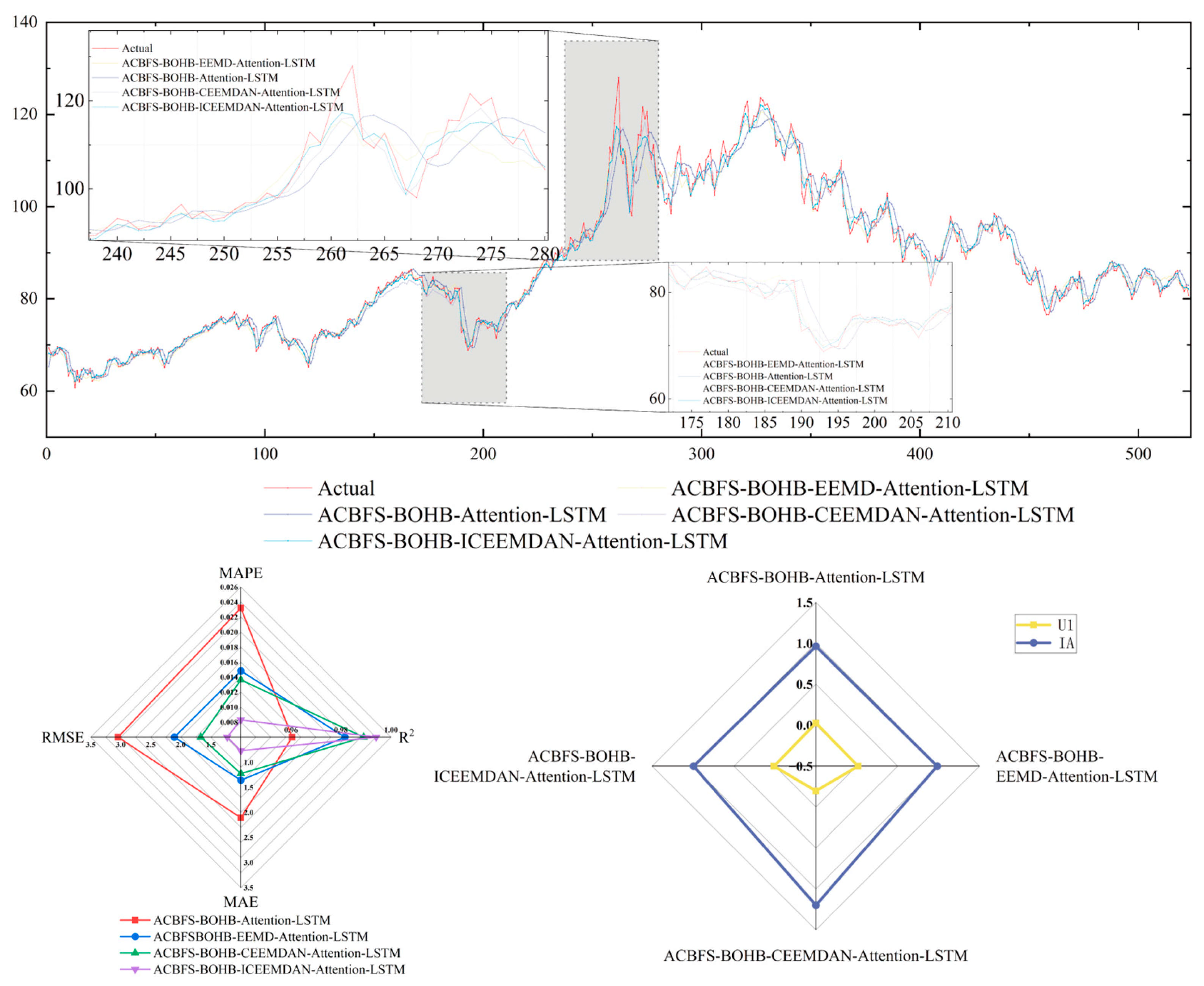
5.3. Comparison III
5.4. Comparison IV
5.5. Comparison V
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Statistical Review of World Energy 2022. 2022. Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2022-full-report.pdf (accessed on 7 May 2020).
- Xie, H.; Khurshid, A.; Rauf, A.; Khan, K.; Calin, A.C. Is Geopolitical Turmoil Driving Petroleum Prices and Financial Liquidity Relationship? Wavelet-Based Evidence from Middle-East. Def. Peace Econ. 2022, 34, 810–826. [Google Scholar] [CrossRef]
- Wu, C.; Wang, J.; Hao, Y. Deterministic and Uncertainty Crude Oil Price Forecasting Based on Outlier Detection and Modified Multi-Objective Optimization Algorithm. Resour. Policy 2022, 77, 102780. [Google Scholar] [CrossRef]
- Kisswani, K.M.; Nusair, S.A. Non-Linearities in the Dynamics of Oil Prices. Energy Econ. 2013, 36, 341–353. [Google Scholar] [CrossRef][Green Version]
- Adekoya, O.B.; Asl, M.G.; Oliyide, J.A.; Izadi, P. Multifractality and Cross-Correlation between the Crude Oil and the European and Non-European Stock Markets during the Russia-Ukraine War. Resour. Policy 2023, 80, 103134. [Google Scholar] [CrossRef]
- Ahmed, S.; Alshater, M.M.; Ammari, A.E.; Hammami, H. Artificial Intelligence and Machine Learning in Finance: A Bibliometric Review. Res. Int. Bus. Financ. 2022, 61, 101646. [Google Scholar] [CrossRef]
- Jammazi, R.; Aloui, C. Crude Oil Price Forecasting: Experimental Evidence from Wavelet Decomposition and Neural Network Modeling. Energy Econ. 2012, 34, 828–841. [Google Scholar] [CrossRef]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep Reinforcement Learning That Matters; Springer: Singapore, 2019. [Google Scholar]
- Yahya, M.; Kanjilal, K.; Dutta, A.; Uddin, G.S.; Ghosh, S. Can Clean Energy Stock Price Rule Oil Price? New Evidences from a Regime-Switching Model at First and Second Moments. Energy Econ. 2021, 95, 105116. [Google Scholar] [CrossRef]
- Nomikos, N.; Andriosopoulos, K. Modelling Energy Spot Prices: Empirical Evidence from NYMEX. Energy Econ. 2012, 34, 1153–1169. [Google Scholar] [CrossRef]
- Dash, D.P.; Sethi, N.; Bal, D.P. Is the Demand for Crude Oil Inelastic for India? Evidence from Structural VAR Analysis. Energy Policy 2018, 118, 552–558. [Google Scholar] [CrossRef]
- Niu, X.; Wang, J.; Zhang, L. Carbon Price Forecasting System Based on Error Correction and Divide-Conquer Strategies. Appl. Soft Comput. 2022, 118, 107935. [Google Scholar] [CrossRef]
- Huang, L.; Wang, J. Global Crude Oil Price Prediction and Synchronization Based Accuracy Evaluation Using Random Wavelet Neural Network. Energy 2018, 151, 875–888. [Google Scholar] [CrossRef]
- Fan, L.; Pan, S.; Li, Z.; Li, H. An ICA-Based Support Vector Regression Scheme for Forecasting Crude Oil Prices. Technol. Forecast. Soc. Change 2016, 112, 245–253. [Google Scholar] [CrossRef]
- Chen, Y.; He, K.; Tso, G.K.F. Forecasting Crude Oil Prices: A Deep Learning Based Model. Procedia Comput. Sci. 2017, 122, 300–307. [Google Scholar] [CrossRef]
- Niu, X.; Wang, J. A Combined Model Based on Data Preprocessing Strategy and Multi-Objective Optimization Algorithm for Short-Term Wind Speed Forecasting. Appl. Energy 2019, 241, 519–539. [Google Scholar] [CrossRef]
- Askarzadeh, A. Comparison of Particle Swarm Optimization and Other Metaheuristics on Electricity Demand Estimation: A Case Study of Iran. Energy 2014, 72, 484–491. [Google Scholar] [CrossRef]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and Efficient Hyperparameter Optimization at Scale. In Proceedings of the International Conference on Machine Learning PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1437–1446. [Google Scholar]
- Zhang, Y.; Liu, X.; Bao, F.; Chi, J.; Zhang, C.; Liu, P. Particle Swarm Optimization with Adaptive Learning Strategy. Knowl.-Based Syst. 2020, 196, 105789. [Google Scholar] [CrossRef]
- Soleimanzade, M.A.; Sadrzadeh, M. Deep Learning-Based Energy Management of a Hybrid Photovoltaic-Reverse Osmosis-Pressure Retarded Osmosis System. Appl. Energy 2021, 293, 116959. [Google Scholar] [CrossRef]
- Alameer, Z.; Fathalla, A.; Li, K.; Ye, H.; Jianhua, Z. Multistep-Ahead Forecasting of Coal Prices Using a Hybrid Deep Learning Model. Resour. Policy 2020, 65, 101588. [Google Scholar] [CrossRef]
- Xie, Y.; Hu, P.; Zhu, N.; Lei, F.; Xing, L.; Xu, L.; Sun, Q. A Hybrid Short-Term Load Forecasting Model and Its Application in Ground Source Heat Pump with Cooling Storage System. Renew. Energy 2020, 161, 1244–1259. [Google Scholar] [CrossRef]
- Ahmad, W.; Aamir, M.; Khalil, U.; Ishaq, M.; Iqbal, N.; Khan, M. A New Approach for Forecasting Crude Oil Prices Using Median Ensemble Empirical Mode Decomposition and Group Method of Data Handling. Math. Probl. Eng. 2021, 2021, e5589717. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, W.; Xiao, L.; Dong, Y. A Decomposition Ensemble Based Deep Learning Approach for Crude Oil Price Forecasting. Resour. Policy 2022, 78, 102855. [Google Scholar] [CrossRef]
- Zhou, F.; Huang, Z.; Zhang, C. Carbon Price Forecasting Based on CEEMDAN and LSTM. Appl. Energy 2022, 311, 118601. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Empirical Mode Decomposition Based Deep Learning for Electricity Demand Forecasting. IEEE Access 2018, 6, 49144–49156. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Wu, Q.-B.; Zhu, J.-Q. Improved EEMD-Based Crude Oil Price Forecasting Using LSTM Networks. Phys. A Stat. Mech. Its Appl. 2019, 516, 114–124. [Google Scholar] [CrossRef]
- Dolatnia, N.; Fern, A.; Fern, X. Bayesian Optimization with Resource Constraints and Production. Int. Conf. Autom. Plan. Sched. ICAPS 2016, 26, 115–123. [Google Scholar] [CrossRef]
- Rardin, R.L.; Uzsoy, R. Experimental Evaluation of Heuristic Optimization Algorithms: A Tutorial. J. Heuristics 2001, 7, 261–304. [Google Scholar] [CrossRef]
- Feng, S.-W.; Chai, K. An Improved Method for EMD Modal Aliasing Effect. Vibroeng. Proced. 2020, 35, 76–81. [Google Scholar] [CrossRef]
- Wen, J.; Zhao, X.-X.; Chang, C.-P. The Impact of Extreme Events on Energy Price Risk. Energy Econ. 2021, 99, 105308. [Google Scholar] [CrossRef]
- Zhao, D.; Sibt e-Ali, M.; Omer Chaudhry, M.; Ayub, B.; Waqas, M.; Ullah, I. Modeling the Nexus between Geopolitical Risk, Oil Price Volatility and Renewable Energy Investment; Evidence from Chinese Listed Firms. Renew. Energy 2024, 225, 120309. [Google Scholar] [CrossRef]
- Zhai, D.; Zhang, T.; Liang, G.; Liu, B. Research on Crude Oil Futures Price Prediction Methods: A Perspective Based on Quantum Deep Learning. Energy 2025, 320, 135080. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, M.; Liu, J.; Wang, P. A Functional Data Analysis Framework Incorporating Derivative Information and Mixed-Frequency Data for Predictive Modeling of Crude Oil Price. IEEE Trans. Ind. Inf. 2025, 21, 3226–3235. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Overfitting, Model Tuning, and Evaluation of Prediction Performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Switzerland, 2022; pp. 109–139. ISBN 978-3-030-89009-4. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. ISBN 978-3-642-00295-3. [Google Scholar]
- Gierlichs, B.; Batina, L.; Tuyls, P.; Preneel, B. Mutual Information Analysis. In Cryptographic Hardware and Embedded Systems—CHES 2008; Oswald, E., Rohatgi, P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5154, pp. 426–442. ISBN 978-3-540-85052-6. [Google Scholar]
- Wang, Y.; Wang, Z.; Kang, X.; Luo, Y. A Novel Interpretable Model Ensemble Multivariate Fast Iterative Filtering and Temporal Fusion Transform for Carbon Price Forecasting. Energy Sci. Eng. 2023, 11, 1148–1179. [Google Scholar] [CrossRef]
- Xiong, X.; Qing, G. A Hybrid Day-Ahead Electricity Price Forecasting Framework Based on Time Series. Energy 2023, 264, 126099. [Google Scholar] [CrossRef]
- Xu, W.; Wang, Z.; Wang, W.; Zhao, J.; Wang, M.; Wang, Q. Short-Term Photovoltaic Output Prediction Based on Decomposition and Reconstruction and XGBoost under Two Base Learners. Energies 2024, 17, 906. [Google Scholar] [CrossRef]
- Grinsztajn, L.; Oyallon, E.; Varoquaux, G. Why Do Tree-Based Models Still Outperform Deep Learning on Tabular Data? arXiv 2022, arXiv:2207.08815v1. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Zhang, G.P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Zheng, G.; Li, Y.; Xia, Y. Crude Oil Price Forecasting Model Based on Neural Networks and Error Correction. Appl. Sci. 2025, 15, 1055. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Yeh, C.-H.; Young, H.-W.V.; Hu, K.; Lo, M.-T. On the Computational Complexity of the Empirical Mode Decomposition Algorithm. Phys. A Stat. Mech. Its Appl. 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the Applications of EMD and EEMD on Time–Frequency Analysis of Seismic Signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Qin, Q.; He, H.; Li, L.; He, L.-Y. A Novel Decomposition-Ensemble Based Carbon Price Forecasting Model Integrated with Local Polynomial Prediction. Comput. Econ. 2020, 55, 1249–1273. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Comparison of Two New Intelligent Wind Speed Forecasting Approaches Based on Wavelet Packet Decomposition, Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Artificial Neural Networks. Energy Convers. Manag. 2018, 155, 188–200. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S. Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Deep Residual Model for Short-Term Multi-Step Solar Radiation Prediction. Renew. Energy 2022, 190, 408–424. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de Répartition à n Dimensions et Leurs Marges. Ann. l’ISUP 1959, 8, 229–231. [Google Scholar]
- Fleuret, F. Fast Binary Feature Selection with Conditional Mutual Information. J. Mach. Learn. Res. 2004, 5, 1531–1555. [Google Scholar]
- Peng, L.; Wang, L.; Xia, D.; Dao, Q. Effective Energy Consumption Forecasting Using Empirical Wavelet Transform and Long Short-Term Memory. Energy 2022, 238, 121756. [Google Scholar] [CrossRef]
- Florea, A.-C.; Andonie, R. Weighted Random Search for Hyperparameter Optimization. arXiv 2020, arXiv:2004.01628. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhao, L.; Li, S.; Jia, Y. Real-Time Object Detection Method Based on Improved YOLOv4-Tiny. arXiv 2020, arXiv:2011.04244. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Ali, R.; Usama, M.; Muhammad, M.A.; Khairuddin, A.S.M. A Hybrid Deep Learning Method for an Hour Ahead Power Output Forecasting of Three Different Photovoltaic Systems. Appl. Energy 2022, 307, 118185. [Google Scholar] [CrossRef]
- Guliyev, H.; Mustafayev, E. Predicting the Changes in the WTI Crude Oil Price Dynamics Using Machine Learning Models. Resour. Policy 2022, 77, 102664. [Google Scholar] [CrossRef]
- Abba Abdullahi, S.; Kouhy, R.; Muhammad, Z. Trading Volume and Return Relationship in the Crude Oil Futures Markets. Stud. Econ. Financ. 2014, 31, 426–438. [Google Scholar] [CrossRef]
- Abiad, A.; Qureshi, I.A. The Macroeconomic Effects of Oil Price Uncertainty. Energy Econ. 2023, 125, 106839. [Google Scholar] [CrossRef]
- Zhang, Z.; He, M.; Zhang, Y.; Wang, Y. Geopolitical Risk Trends and Crude Oil Price Predictability. Energy 2022, 258, 124824. [Google Scholar] [CrossRef]
- Mensi, W.; Rehman, M.U.; Vo, X.V. Dynamic Frequency Relationships and Volatility Spillovers in Natural Gas, Crude Oil, Gas Oil, Gasoline, and Heating Oil Markets: Implications for Portfolio Management. Resour. Policy 2021, 73, 102172. [Google Scholar] [CrossRef]
- Caldara, D.; Iacoviello, M. Measuring Geopolitical Risk. Am. Econ. Rev. 2022, 112, 1194–1225. [Google Scholar] [CrossRef]


| Model | Parameters |
|---|---|
| ICEEMDAN | Noise standard deviation 0.2 Number of realizations 500 Maximum number of sifting iterations 5000 |
| Hyperparameters | Range |
|---|---|
| Batch size | [32, 1024] |
| Number of hidden layers | [50, 200] |
| Learning rate | [0.001, 0.0005] |
| Evaluation Indicators | XGBOOST (With Influencing Factors) | XGBOOST | LSTM (With Influencing Factors) | LSTM |
|---|---|---|---|---|
| MAE | 2.7679 | 2.3740 | 3.3734 | 2.4492 |
| RMSE | 3.7108 | 3.4370 | 4.8361 | 3.4531 |
| R2 | 94.62% | 95.45% | 92.88% | 94.89% |
| MAPE | 3.04% | 2.59% | 3.59% | 2.70% |
| IA | 0.9436 | 0.9517 | 0.9042 | 0.9514 |
| U1 | 0.0299 | 0.0277 | 0.0393 | 0.0277 |
| Evaluation Indicators | LSTM (With Influencing Factors) | LSTM | Attention-LSTM | BOHB-Attention-LSTM | ACBFS-BOHB-Attention-LSTM |
|---|---|---|---|---|---|
| MAE | 3.3734 | 2.4492 | 2.3904 | 2.2277 | 2.1082 |
| RMSE | 4.8361 | 3.4531 | 3.3681 | 3.1534 | 3.0459 |
| R2 | 92.88% | 94.89% | 85.17% | 95.76% | 96.05% |
| MAPE | 3.59% | 2.71% | 2.64% | 2.45% | 2.32% |
| IA | 0.9042 | 0.9514 | 0.9538 | 0.9595 | 0.9622 |
| U1 | 0.0393 | 0.0277 | 0.0270 | 0.0253 | 0.0244 |
| Evaluation Indicators | ACBFS-BOHB-Attention-LSTM | ACBFSBOHB-EEMD-Attention-LSTM | ACBFS-BOHB-CEEMDAN-Attention-LSTM | ACBFS-BOHB-ICEEMDAN-Attention-LSTM |
|---|---|---|---|---|
| MAE | 2.1082 | 1.3567 | 1.2256 | 0.7699 |
| RMSE | 3.0459 | 2.1057 | 1.6666 | 1.2258 |
| R2 | 96.05% | 98.16% | 98.91% | 99.41% |
| MAPE | 2.32% | 1.48% | 1.36% | 0.83% |
| IA | 0.9622 | 0.9819 | 0.9887 | 0.9939 |
| U1 | 0.0244 | 0.0169 | 0.0134 | 0.0098 |
| imf1 | imf2 | imf3 | imf4 | imf5 | imf6 | imf7 | imf8 | imf9 | imf10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 | 3 | 3 | ||||
| 4 | 7 | 6 | 5 | 4 | 4 | ||||
| 8 | 15 | 7 | 7 | 14 | |||||
| 11 | 10 | 18 | |||||||
| 17 | 14 | ||||||||
| 20 |
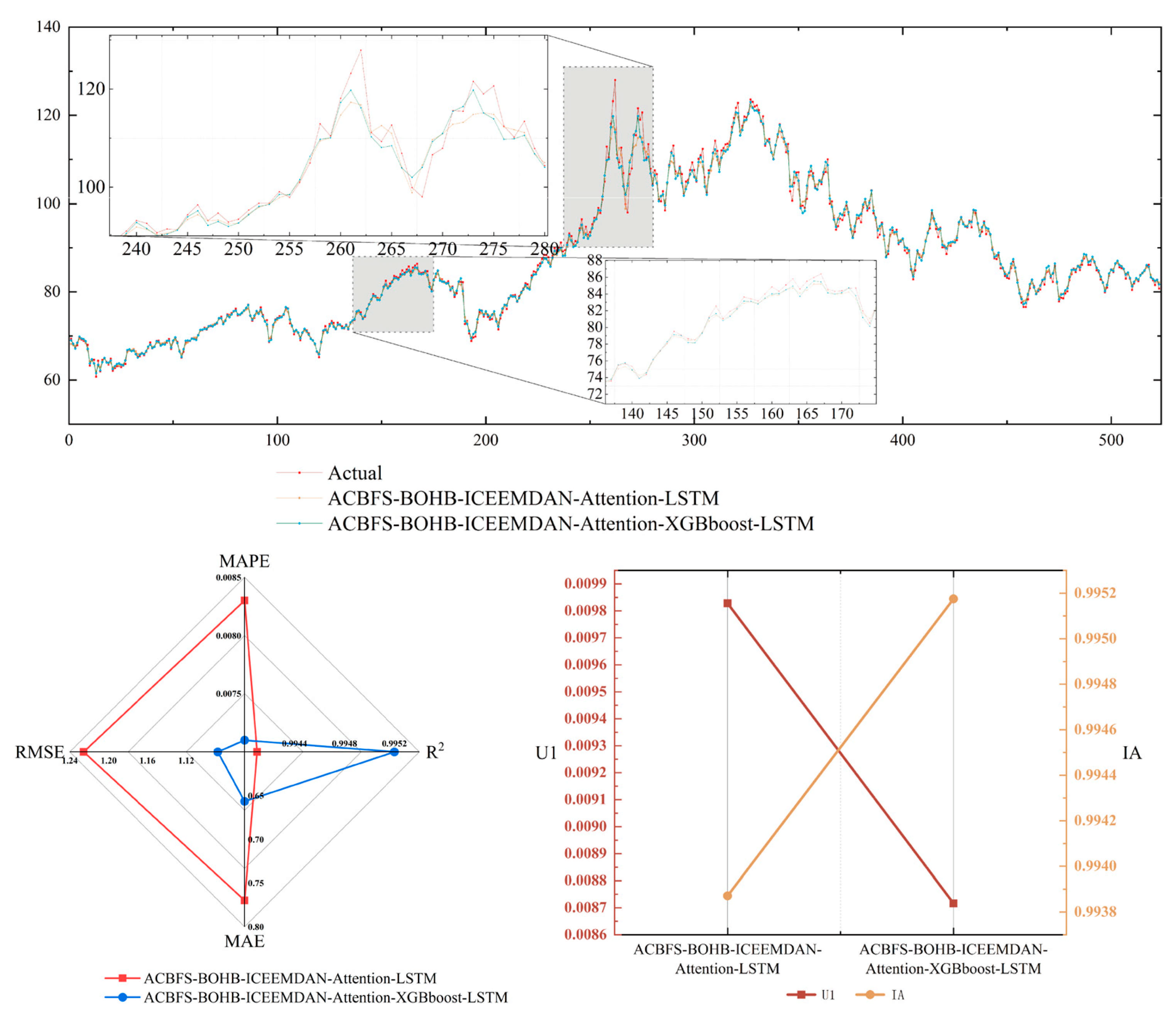
| Evaluation Indicators | ACBFS-BOHB-ICEEMDAN-Attention-LSTM | ACBFS-BOHB-ICEEMDAN-Attention-XGBboost-LSTM |
|---|---|---|
| MAE | 0.7699 | 0.6566 |
| RMSE | 1.2258 | 1.0876 |
| R2 | 99.41% | 99.52% |
| MAPE | 0.83% | 0.71% |
| IA | 0.9939 | 0.9952 |
| U1 | 0.0098 | 0.0087 |
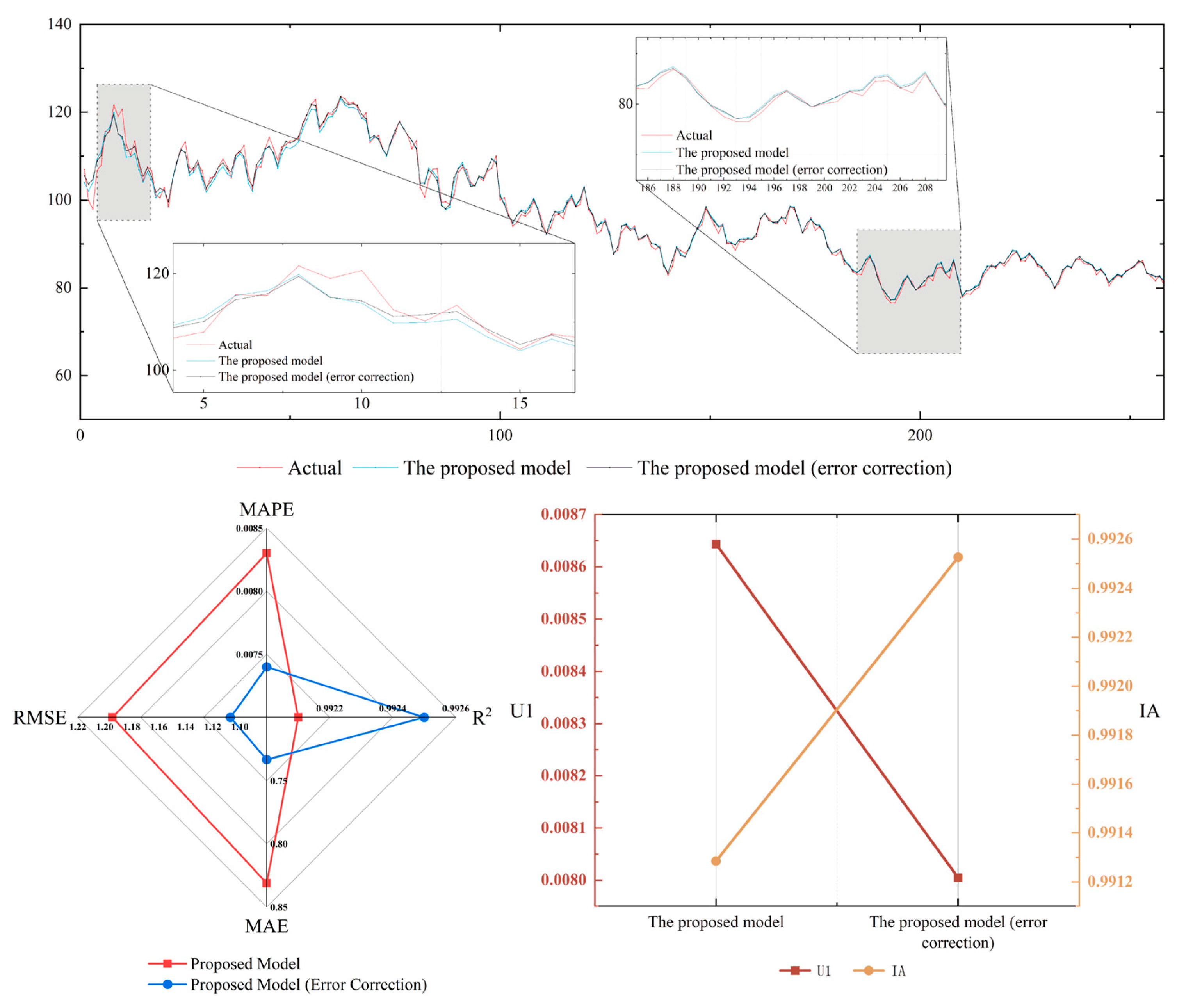
| Evaluation Indicators | Proposed Model | Proposed Model (Error Correction) |
|---|---|---|
| MAE | 0.8311 | 0.7333 |
| RMSE | 1.1944 | 1.1069 |
| R2 | 99.21% | 99.25% |
| MAPE | 0.83% | 0.74% |
| IA | 0.9913 | 0.9925 |
| U1 | 0.0086 | 0.0080 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Wang, Y.; Wei, H.; Wang, X.; Wang, Z. Hybrid Method for Oil Price Prediction Based on Feature Selection and XGBOOST-LSTM. Energies 2025, 18, 2246. https://doi.org/10.3390/en18092246
Lin S, Wang Y, Wei H, Wang X, Wang Z. Hybrid Method for Oil Price Prediction Based on Feature Selection and XGBOOST-LSTM. Energies. 2025; 18(9):2246. https://doi.org/10.3390/en18092246
Chicago/Turabian StyleLin, Shucheng, Yue Wang, Haocheng Wei, Xiaoyi Wang, and Zhong Wang. 2025. "Hybrid Method for Oil Price Prediction Based on Feature Selection and XGBOOST-LSTM" Energies 18, no. 9: 2246. https://doi.org/10.3390/en18092246
APA StyleLin, S., Wang, Y., Wei, H., Wang, X., & Wang, Z. (2025). Hybrid Method for Oil Price Prediction Based on Feature Selection and XGBOOST-LSTM. Energies, 18(9), 2246. https://doi.org/10.3390/en18092246





