Fault Diagnosis and Tolerant Control of Current Sensors Zero-Offset Fault in Multiphase Brushless DC Motors Utilizing Current Signals
Abstract
1. Introduction
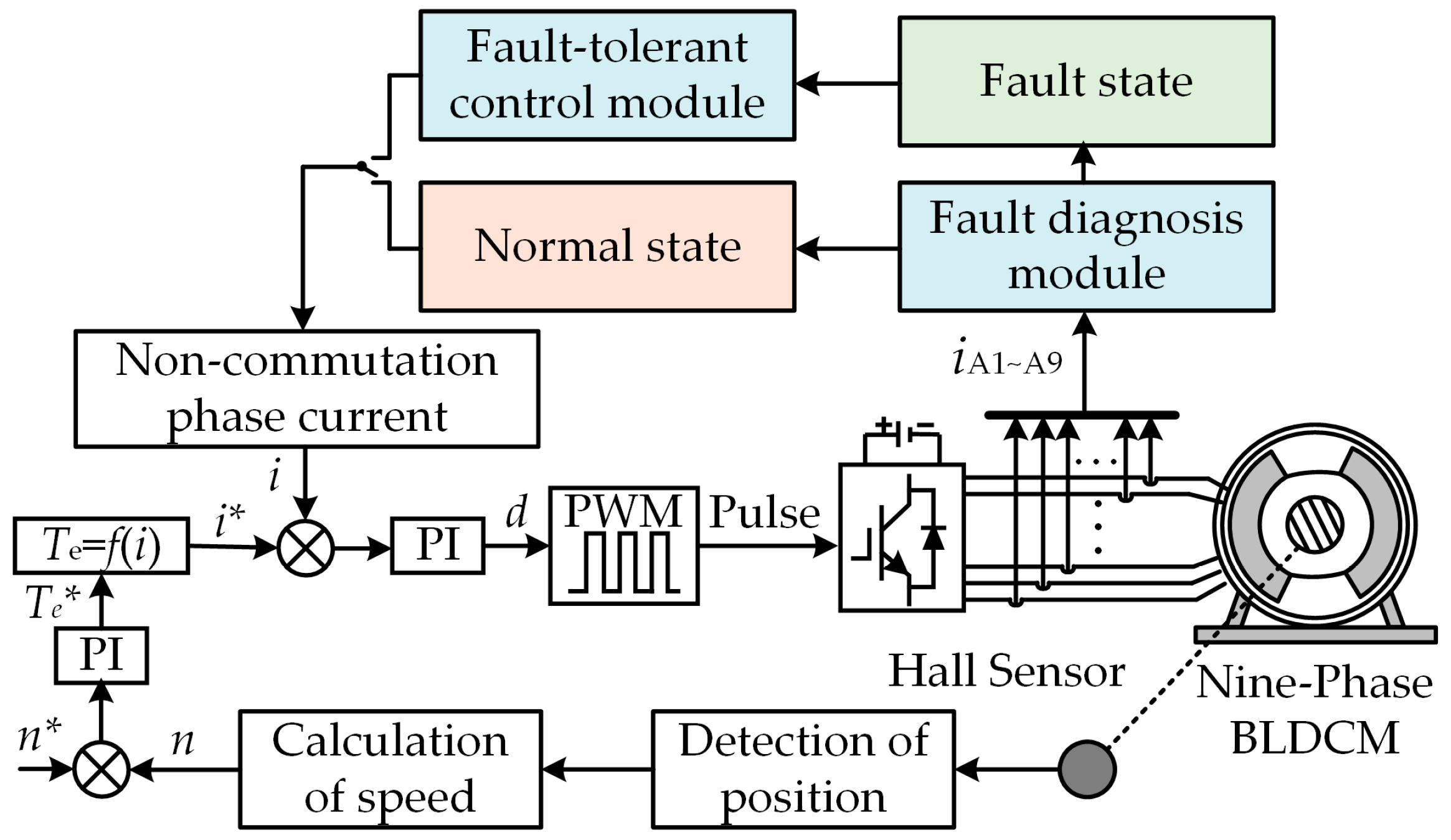
2. Operating Principle and Fault Mode Analysis of Multiphase BLDCM Drive Systems
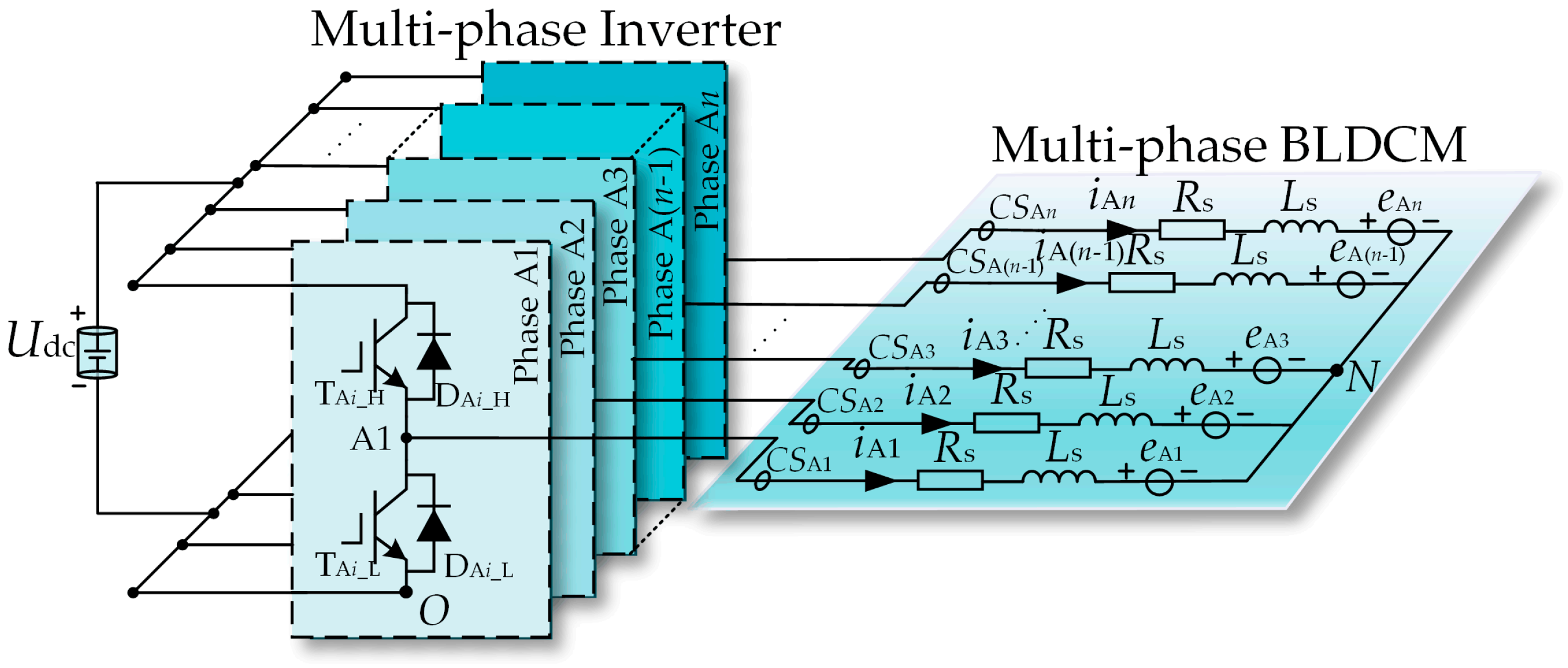
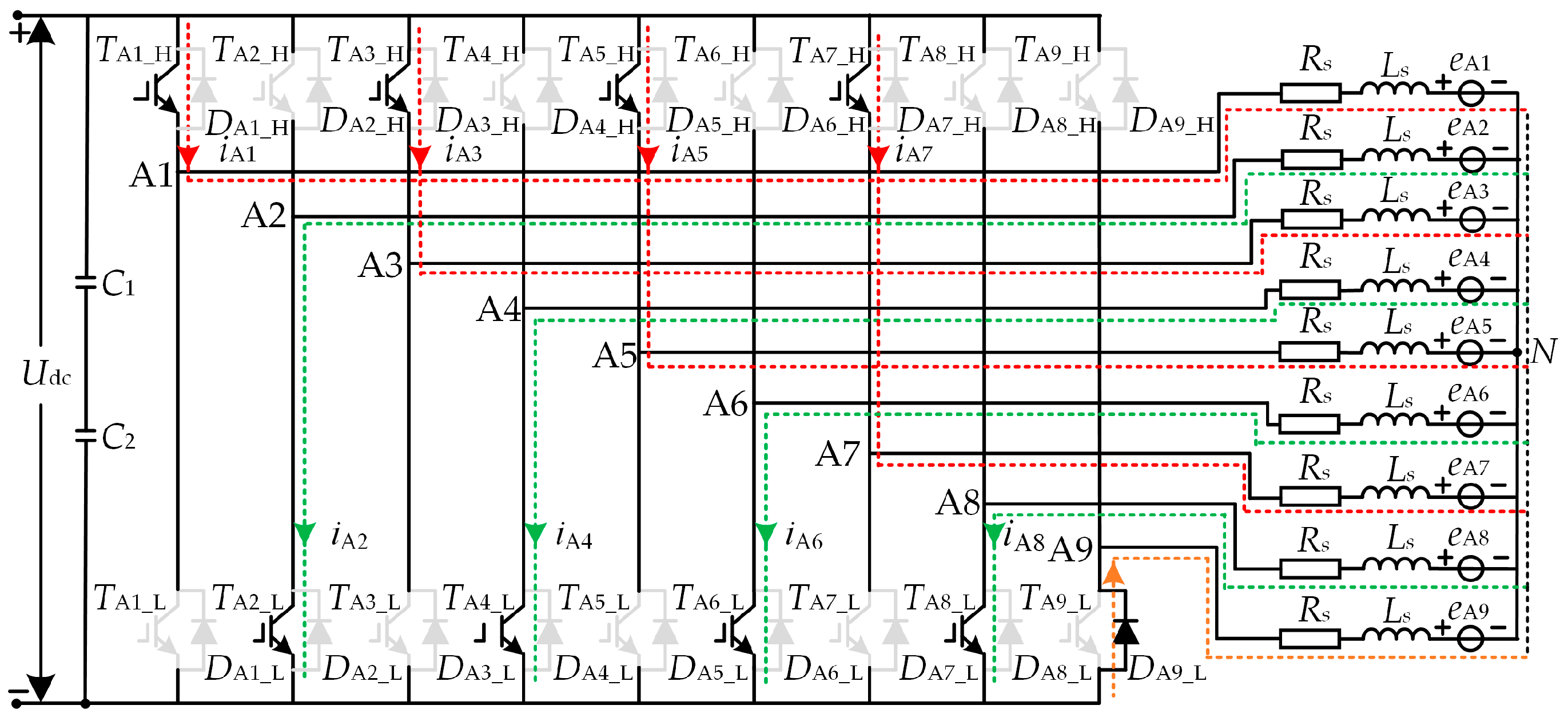
2.1. Operating Principle of Multiphase BLDCM Drive System
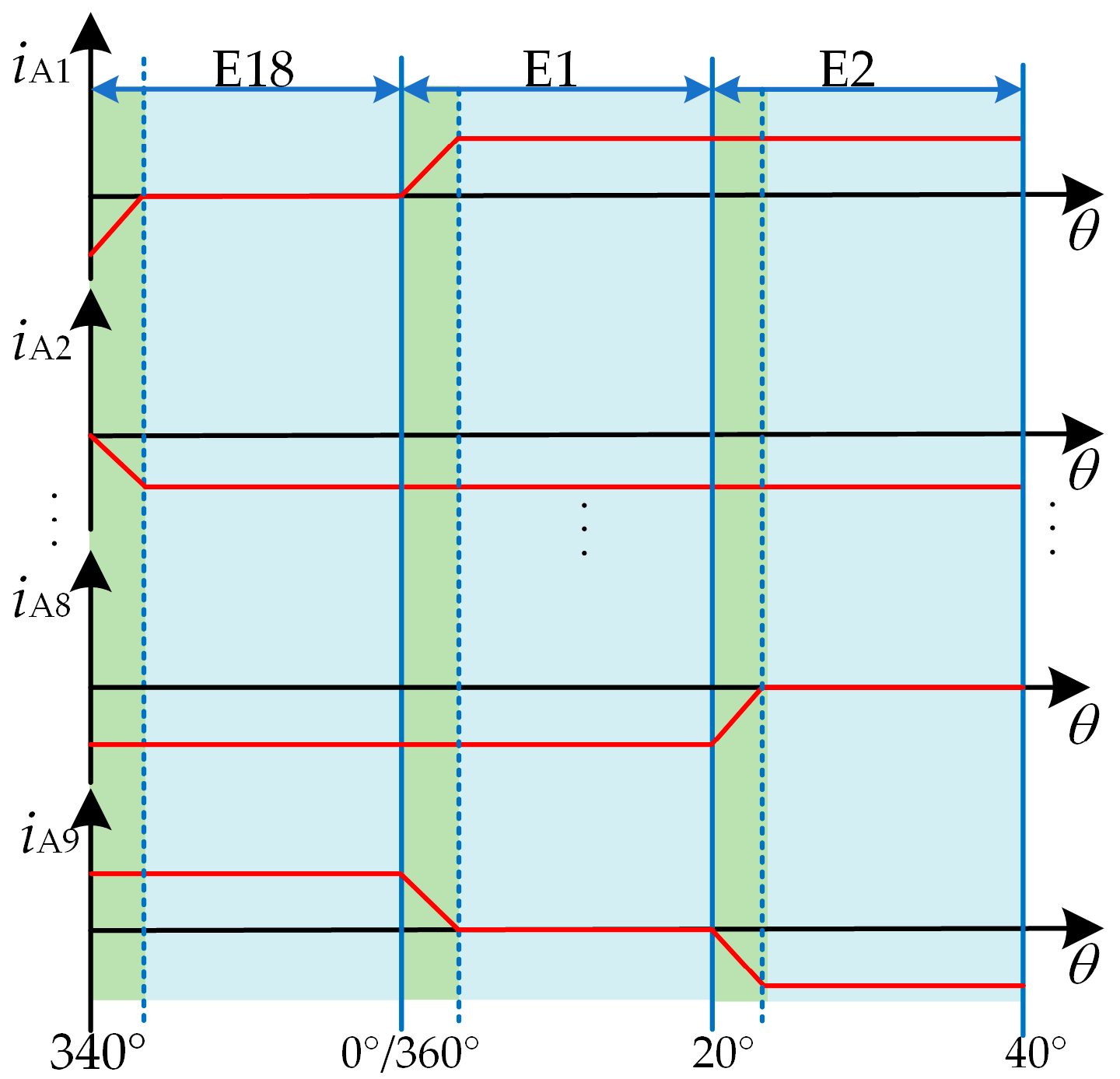
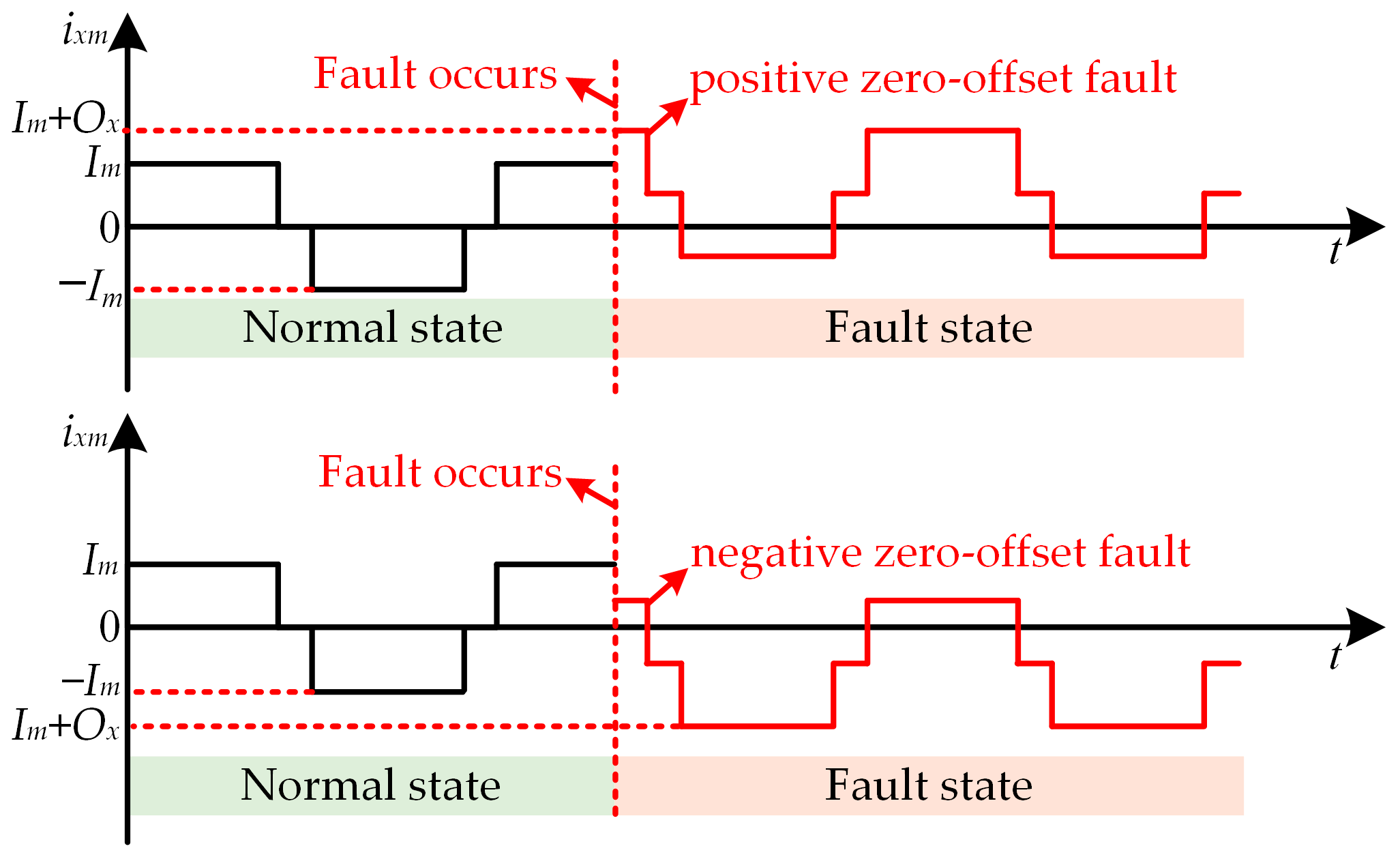
2.2. Analysis of Current Sensors Under Normal and Zero-Offset Fault Conditions
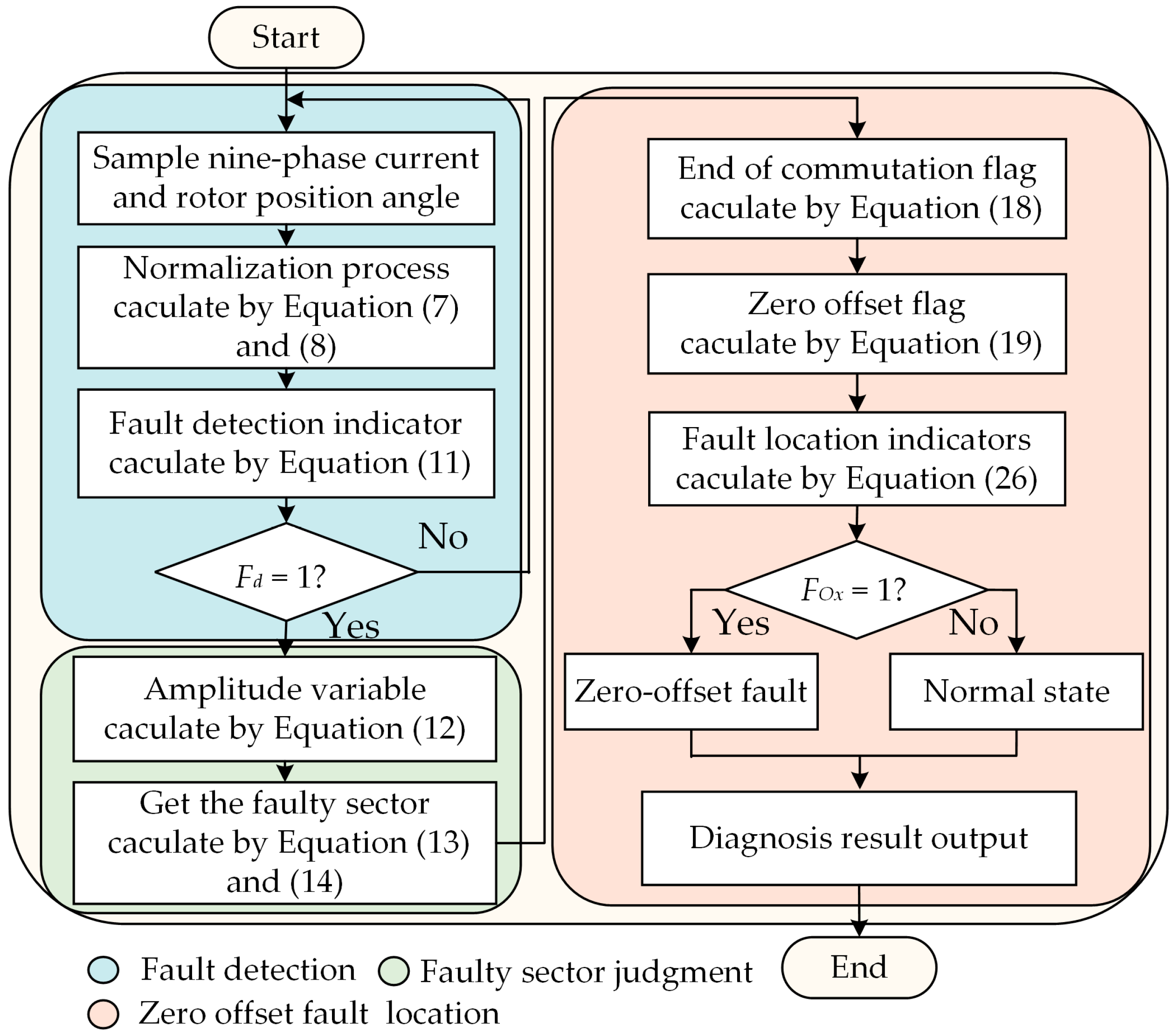
3. The Proposed Method
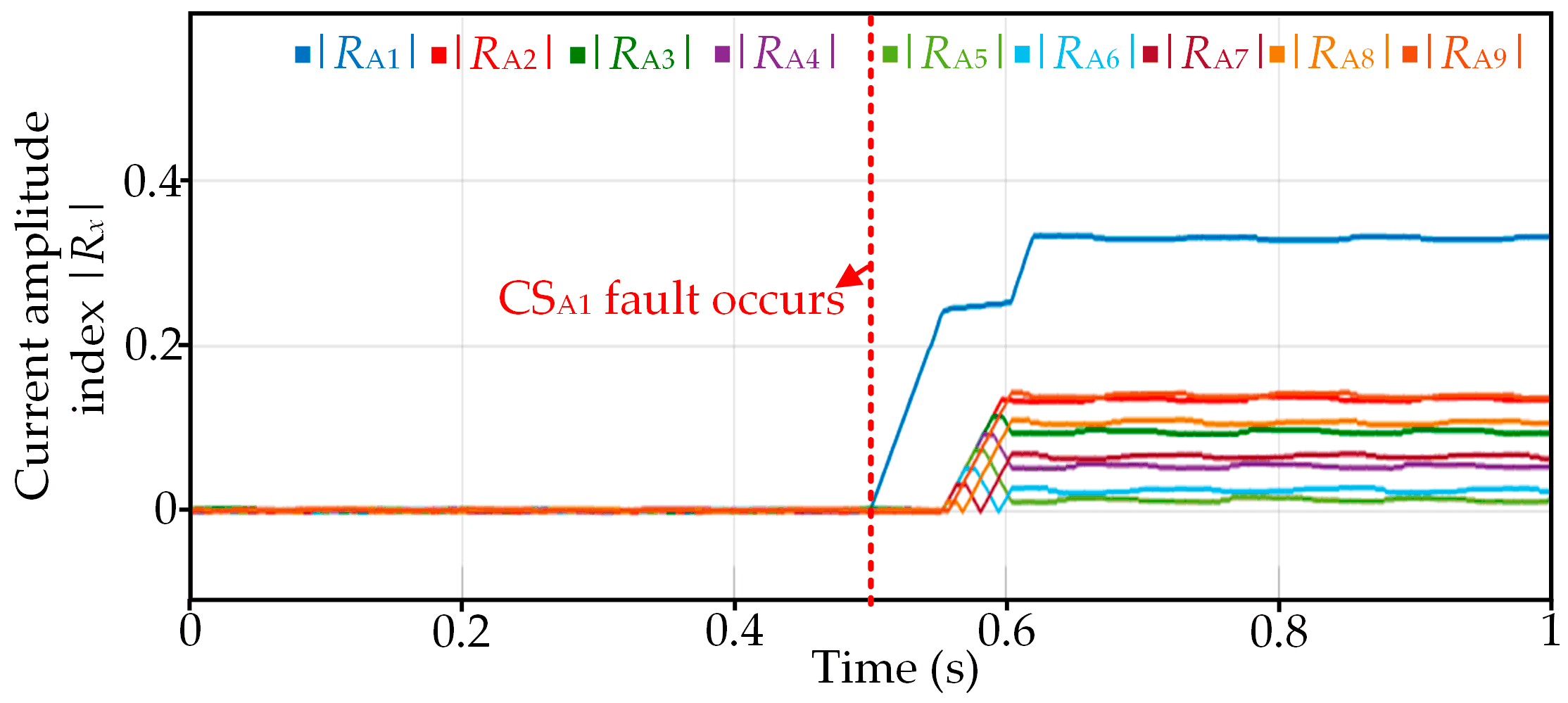
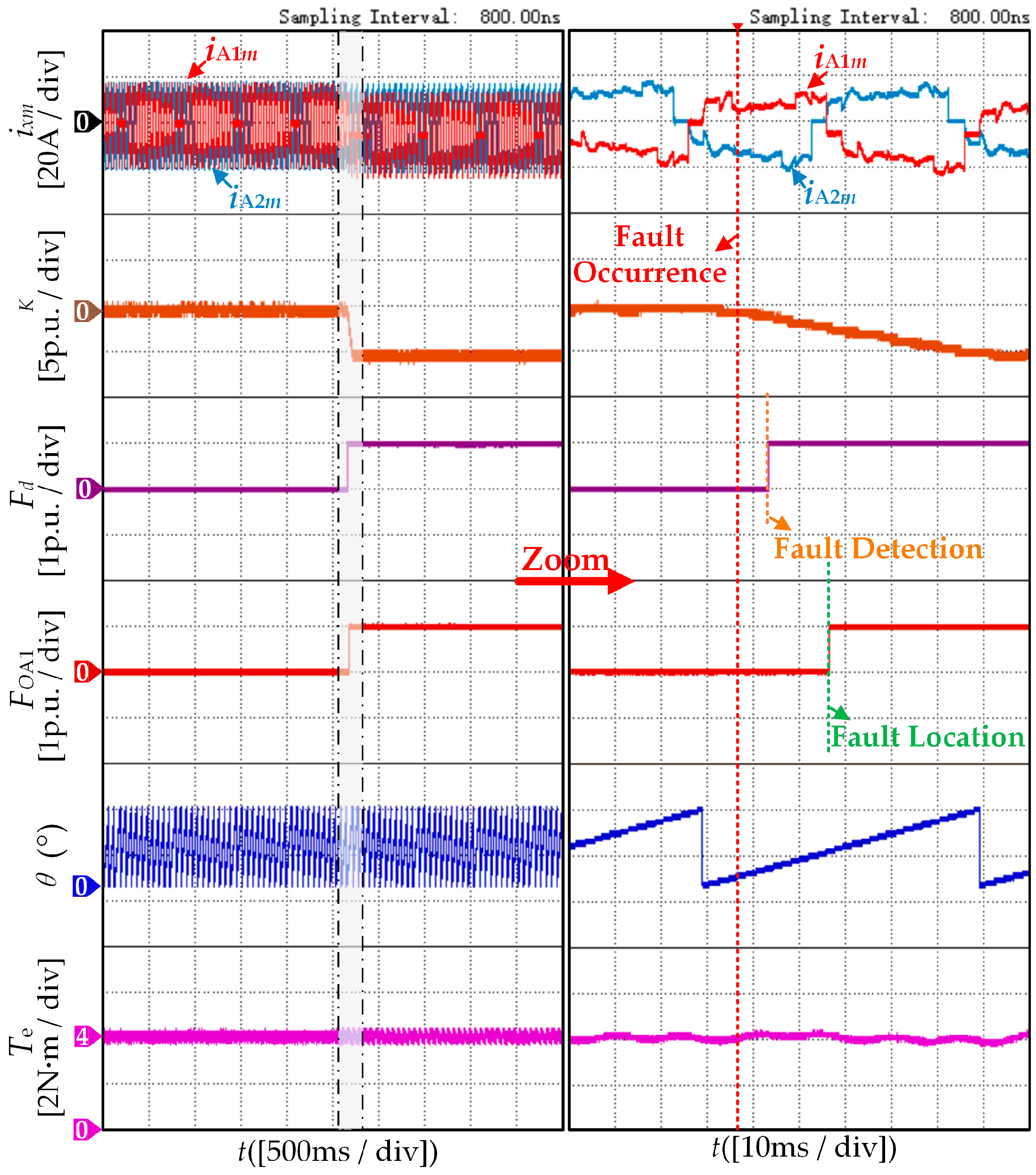
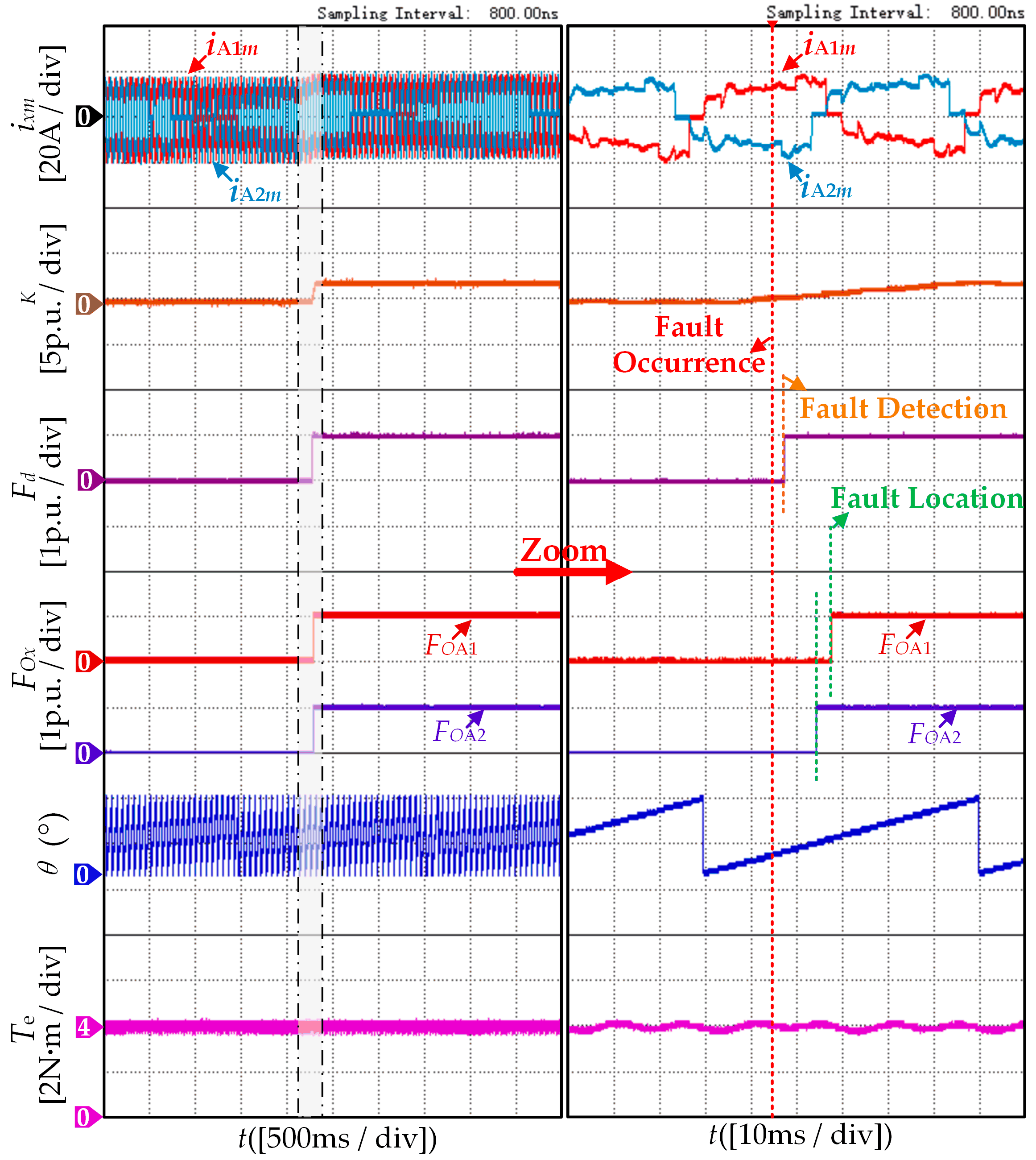
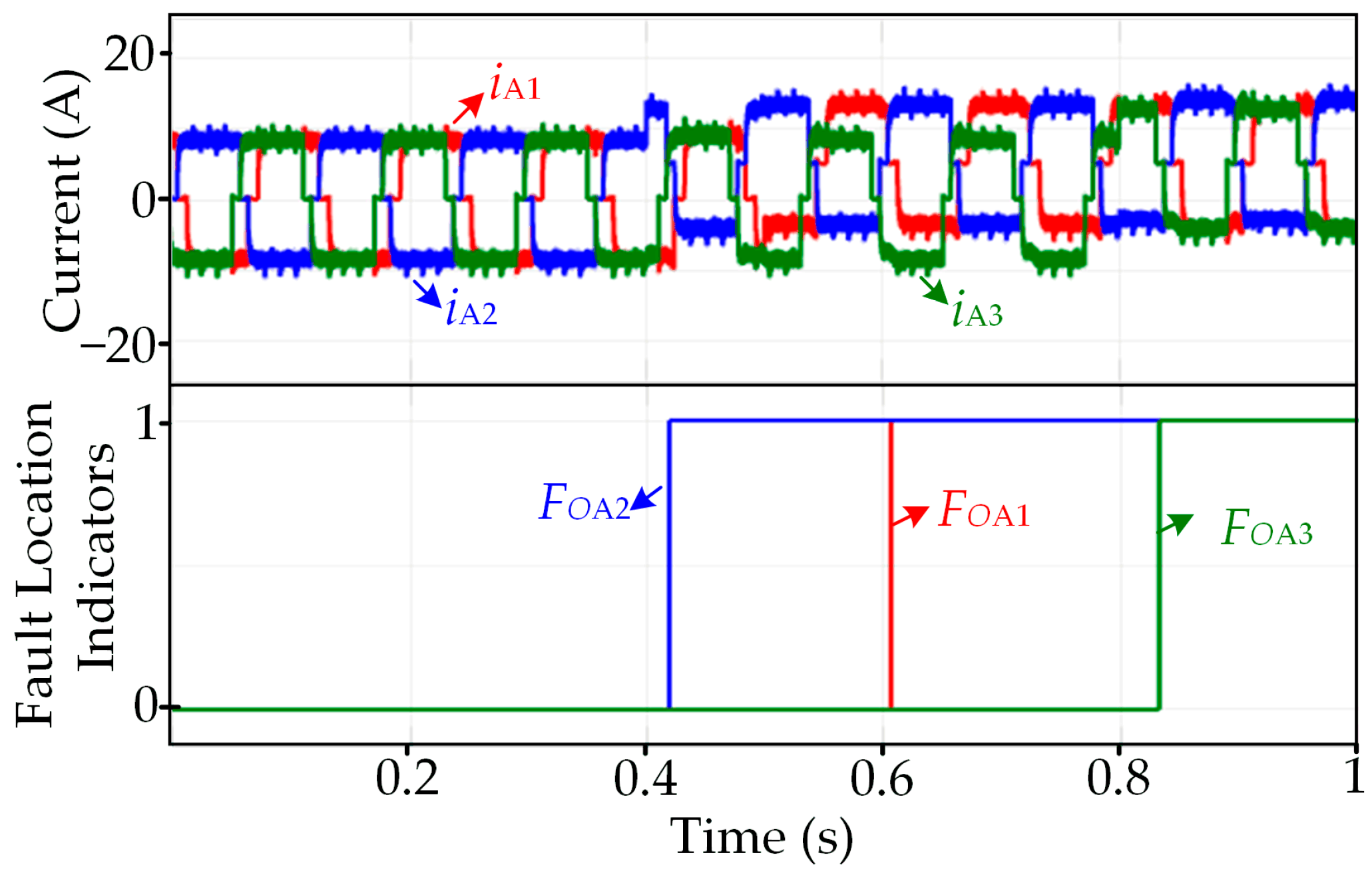
3.1. Current Sensor Fault Detection
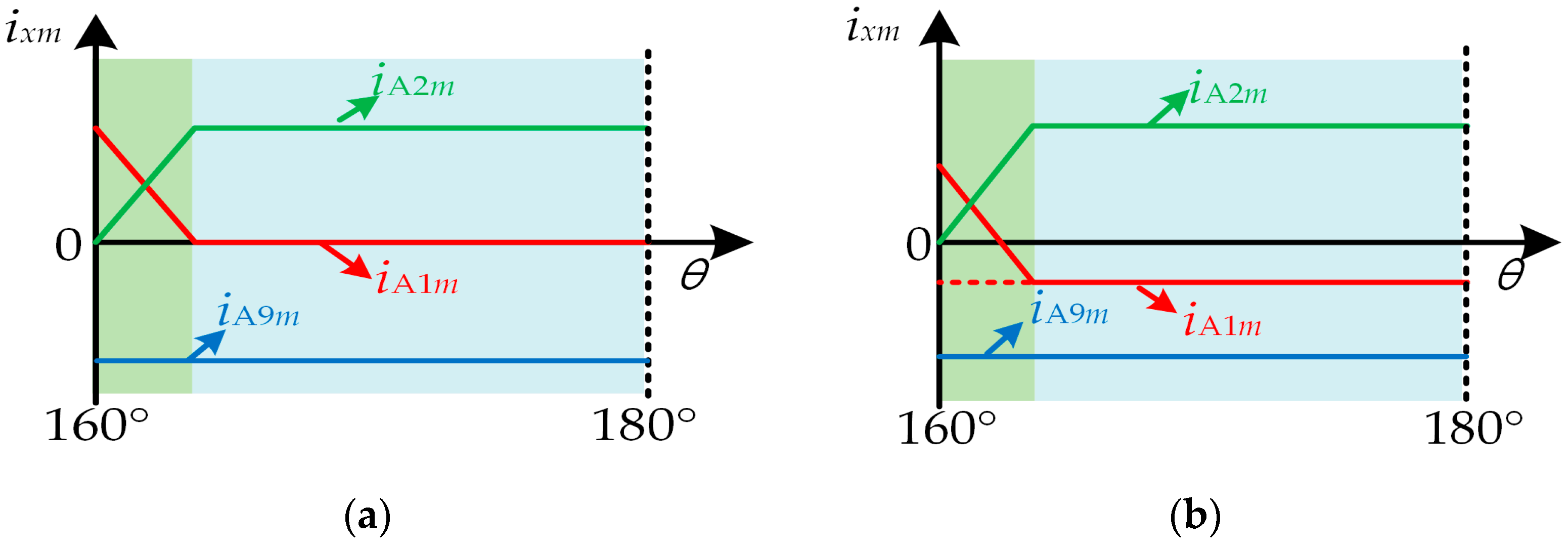
3.2. Zero-Offset Fault Detection and Localization
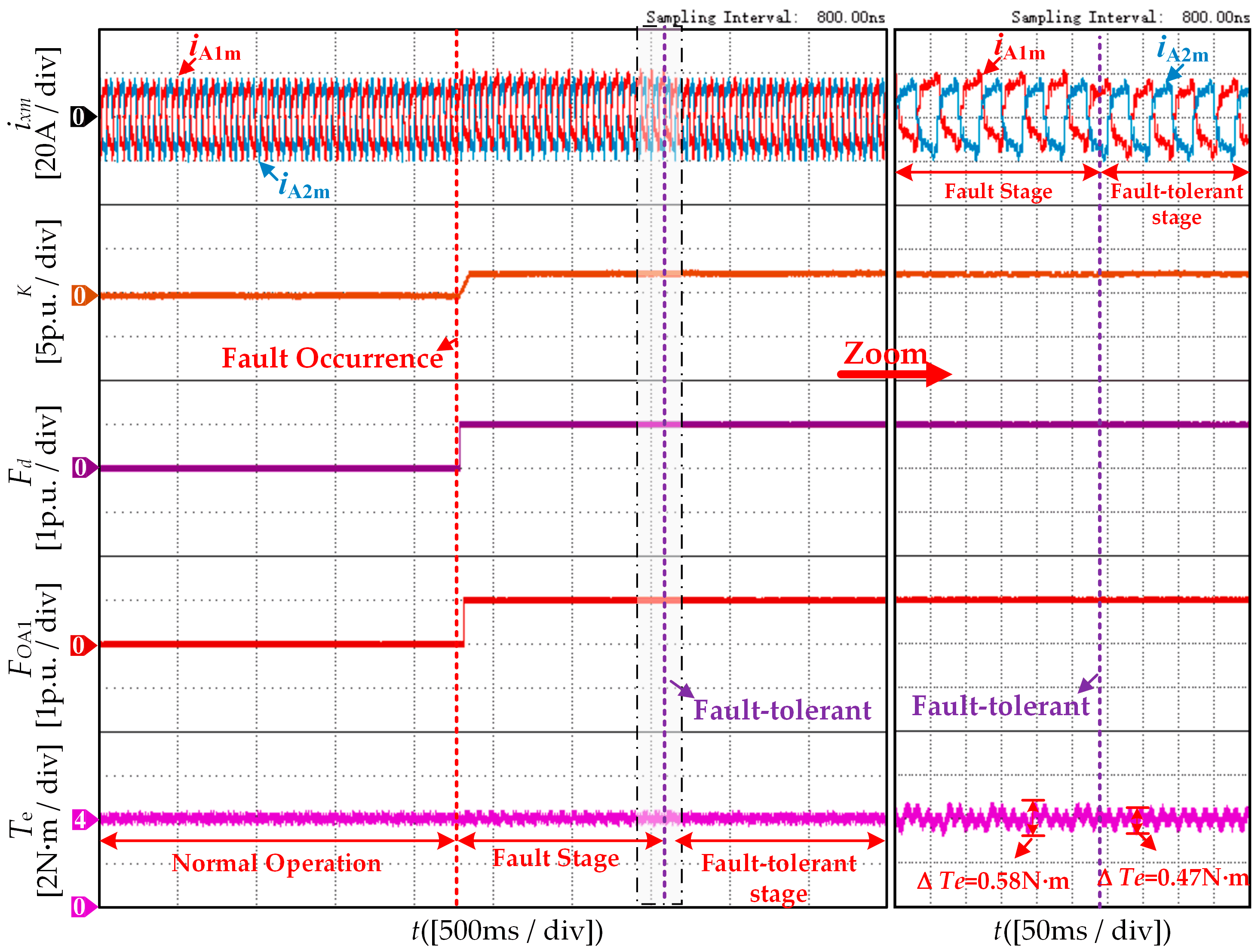
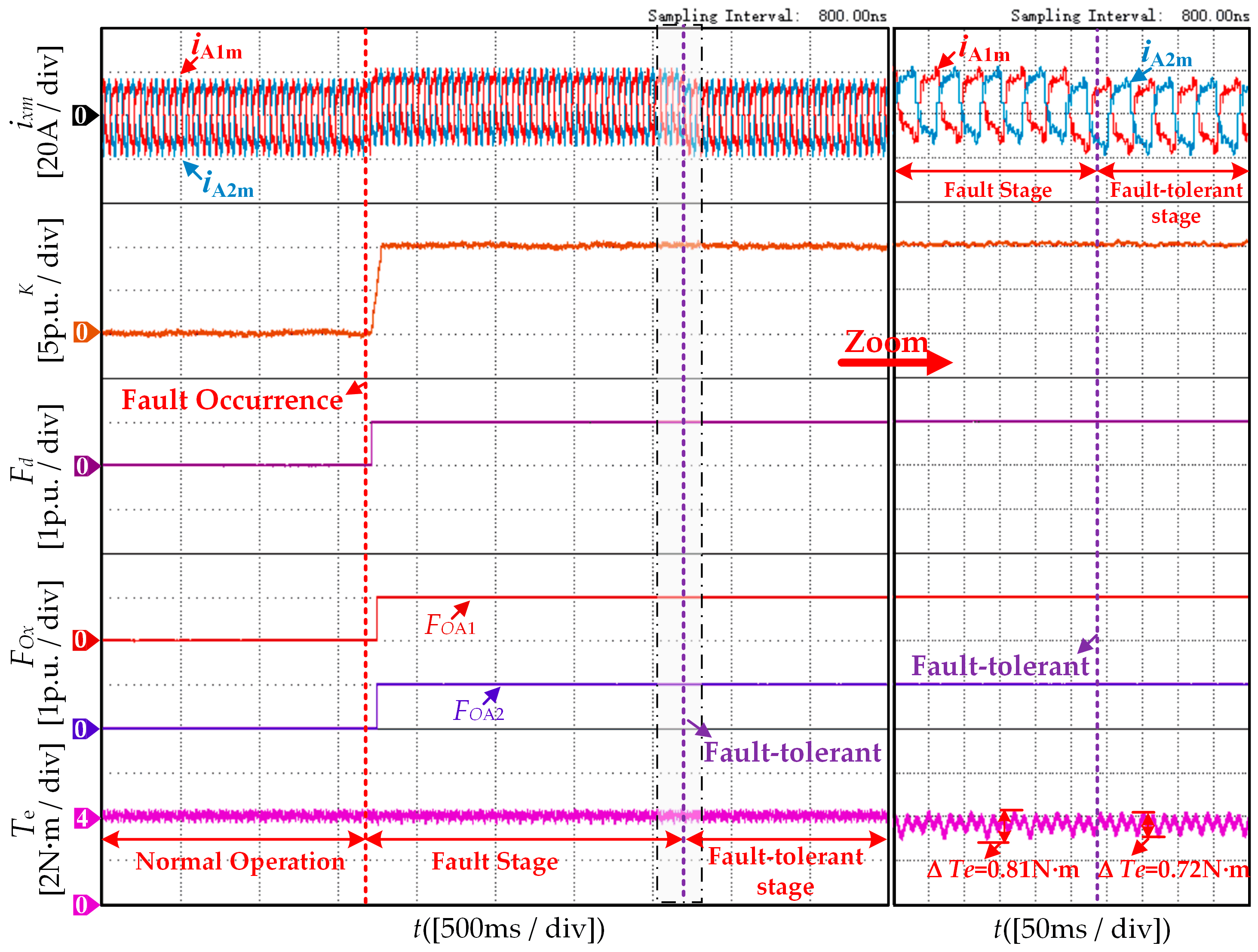
3.3. Fault-Tolerant Control
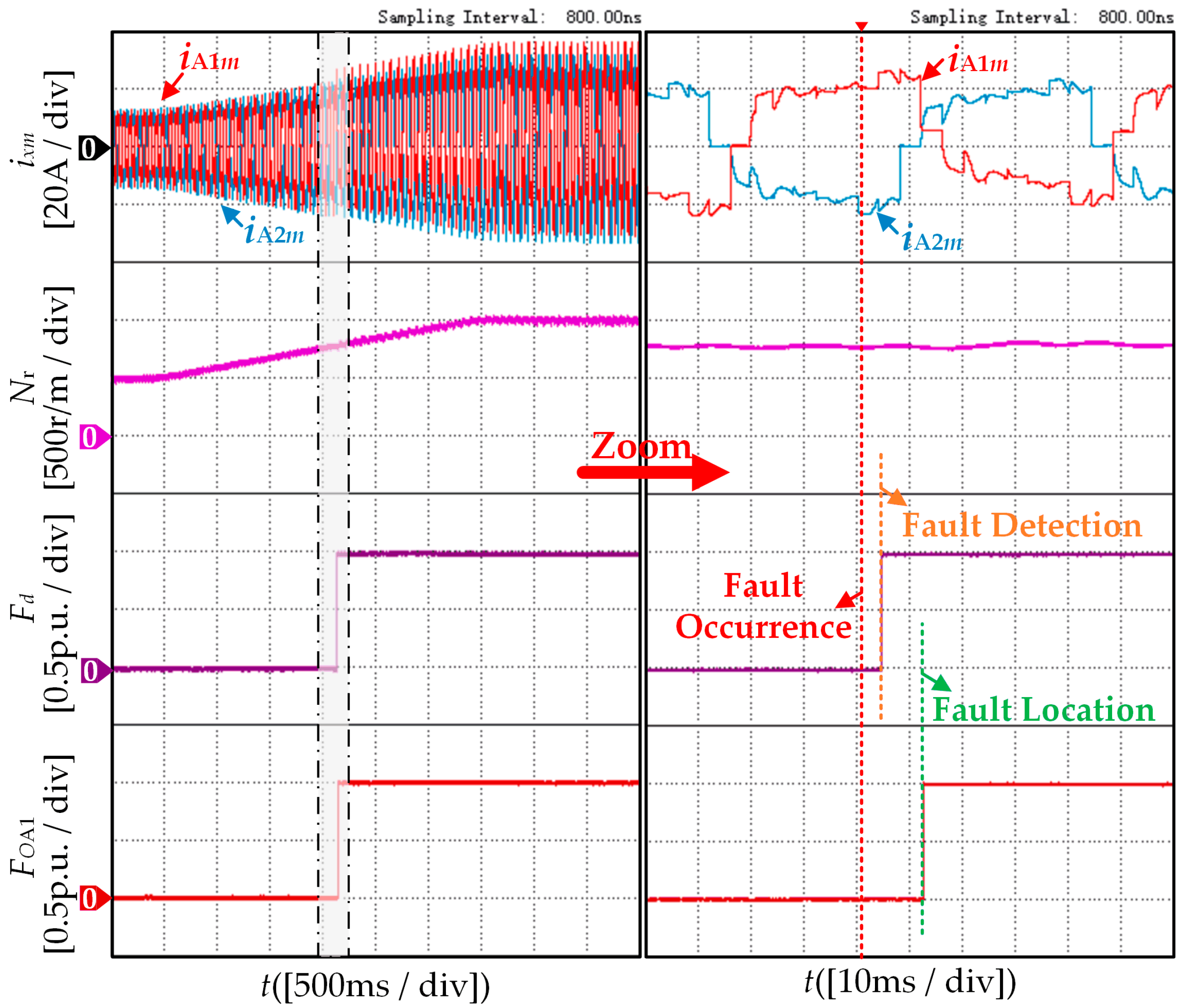
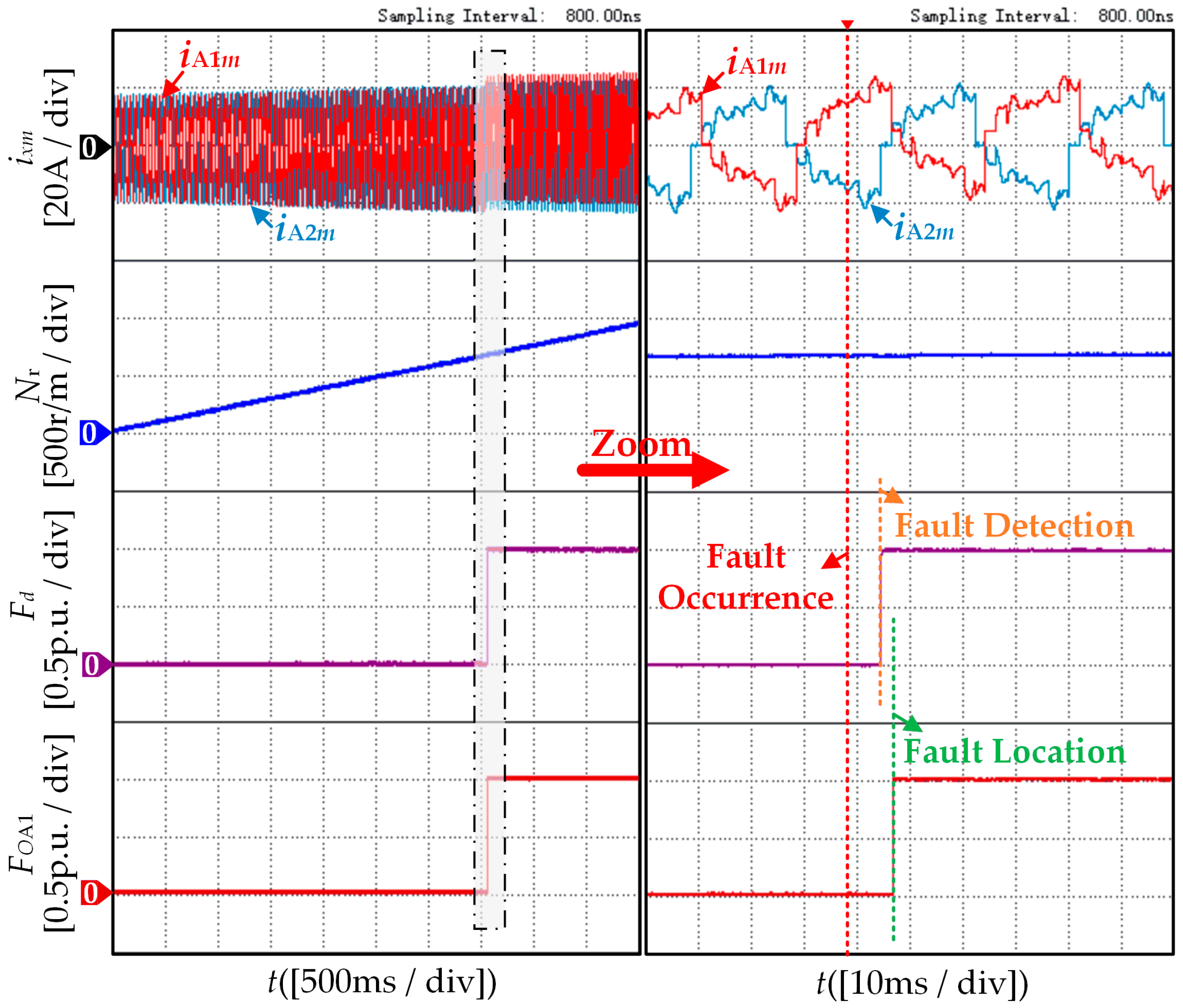
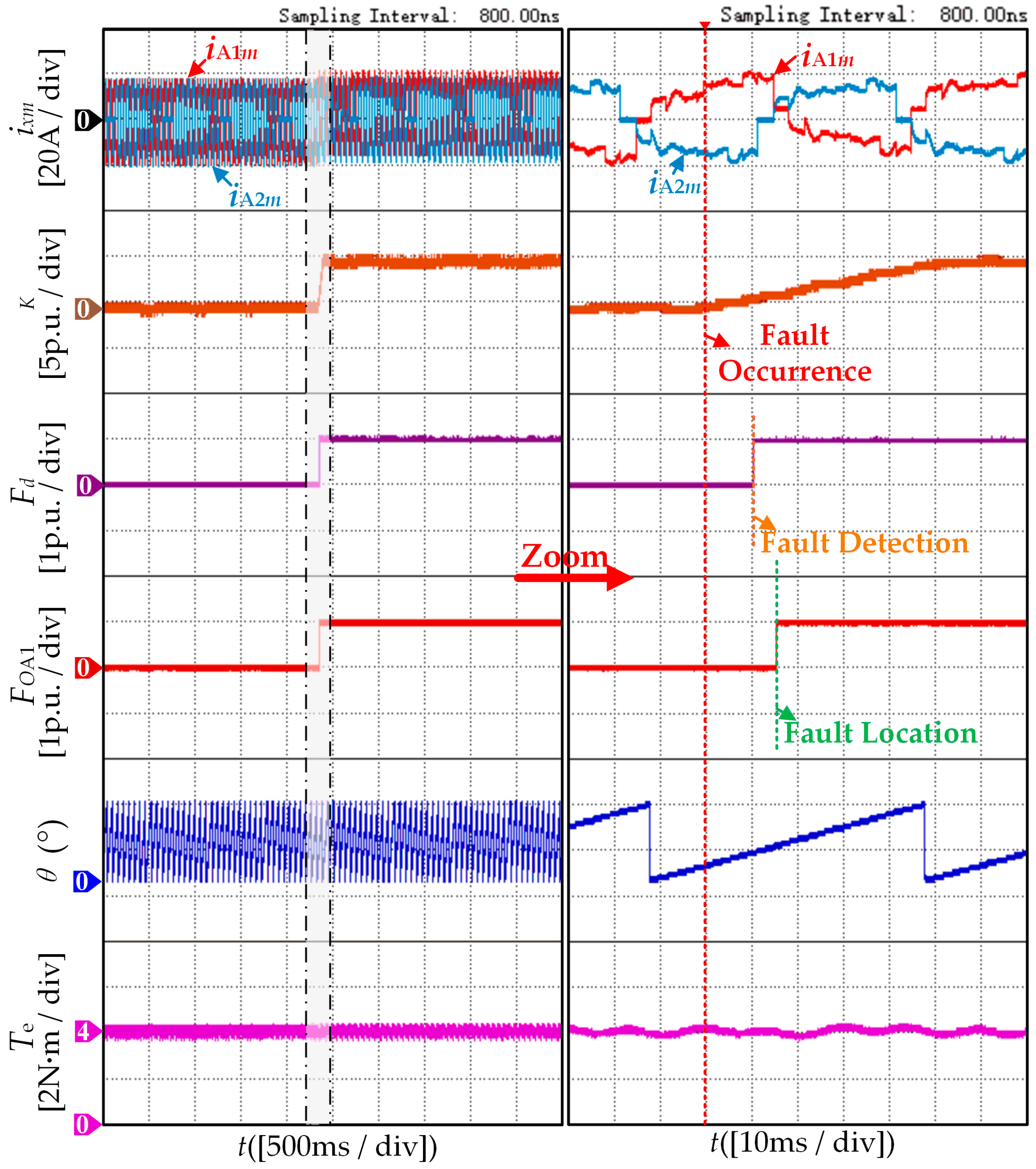
4. Experimental and Simulation Results Analysis
4.1. Validation of Robustness Results
4.2. Validation of Effectiveness Results
4.3. Simulation Results Analysis
5. Conclusions
- (1)
- The proposed method is based on the current variation characteristics, so it has strong robustness and simple implementation.
- (2)
- The method accurately estimates the fault coefficients under current sensor faults and compensates for faulty current sensors, realizing fault-tolerant operation of the system.
- (3)
- The proposed method has been experimentally proven to be effective in a nine-phase BLDCM system and possesses scalability for application in systems with analogous square-wave driving structures. However, in practical applications, it still needs to be combined with specific structural adaptability design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barrero, F.; Duran, M.J. Recent advances in the design, modeling, and control of multiphase machines—Part I. IEEE Trans. Ind. Electron. 2015, 63, 449–458. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F. Recent advances in the design, modeling, and control of multiphase machines—Part II. IEEE Trans. Ind. Electron. 2015, 63, 459–468. [Google Scholar] [CrossRef]
- Bodo, N.; Levi, E.; Subotic, I.; Espina, J.; Empringham, L.; Johnson, C.M. Efficiency evaluation of fully integrated on-board EV battery chargers with nine-phase machines. IEEE Trans. Energy Convers. 2016, 32, 257–266. [Google Scholar] [CrossRef]
- Salem, A.; Narimani, M. A review on multiphase drives for automotive traction applications. IEEE Trans. Transp. Electrific. 2019, 5, 1329–1348. [Google Scholar] [CrossRef]
- Frikha, M.A.; Croonen, J.; Deepak, K.; Benômar, Y.; El Baghdadi, M.; Hegazy, O.J.E. Multiphase motors and drive systems for electric vehicle powertrains: State of the art analysis and future trends. Energies 2023, 16, 768. [Google Scholar] [CrossRef]
- Chen, W.; Zhu, L.; Li, X.; Shi, T.; Xia, C. Comparing the performance of parallel multi-phase brushless dc motors: A comprehensive analysis. IEEE Trans. Power Electron. 2023, 38, 11290–11303. [Google Scholar] [CrossRef]
- Park, H.; Kim, T.; Suh, Y. Fault-tolerant control methods for reduced torque ripple of multiphase BLDC motor drive system under open-circuit faults. IEEE Trans. Ind. Electron. 2022, 58, 7275–7285. [Google Scholar] [CrossRef]
- Choi, K.; Kim, Y.; Kim, S.-K.; Kim, K.-S. Current and position sensor fault diagnosis algorithm for PMSM drives based on robust state observer. IEEE Trans. Ind. Electron. 2020, 68, 5227–5236. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Wang, G.; Huo, J.; Zhu, L.; Xu, D. Fault diagnosis method of current sensor for permanent magnet synchronous motor drives. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018—ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 1206–1211. [Google Scholar] [CrossRef]
- Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Di Noia, L.P. Current signature modeling of surface-mounted PMSM drives with current sensors faults. IEEE Trans. Energy Convers. 2023, 38, 2695–2705. [Google Scholar] [CrossRef]
- Chung, D.-W.; Sul, S.-K. Analysis and compensation of current measurement error in vector-controlled AC motor drives. IEEE Trans. Ind. Appl. 1998, 34, 340–345. [Google Scholar] [CrossRef]
- Lee, K.-W.; Kim, S.-I.J. Dynamic performance improvement of a current offset error compensator in current vector-controlled SPMSM drives. IEEE Trans. Ind. Electron. 2018, 66, 6727–6736. [Google Scholar] [CrossRef]
- Foo, G.H.B.; Zhang, X.; Vilathgamuwa, D.M. A sensor fault detection and isolation method in interior permanent-magnet synchronous motor drives based on an extended Kalman filter. IEEE Trans. Ind. Electron. 2013, 60, 3485–3495. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, Y.; Wang, B.; Huang, X.; Xu, D. Current sensor fault diagnosis and tolerant control for VSI-based induction motor drives. IEEE Trans. Power Electron. 2017, 33, 4238–4248. [Google Scholar] [CrossRef]
- Huang, P.; Liu, J.; Wang, J. Fault Diagnosis for Current Sensors in Charging Modules Based on an Adaptive Sliding Mode Observer. Sensors 2025, 25, 1413. [Google Scholar] [CrossRef]
- Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Di Noia, L.P. Model-based detection and estimation of dc offset of phase current sensors for field oriented PMSM drives. IEEE Trans. Ind. Electron. 2023, 70, 6316–6325. [Google Scholar] [CrossRef]
- Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Di Noia, L.P. Isolation, Detection and Estimation of Current Sensors Faults in PMSM Drives Based on Current Signature Modeling. IEEE Trans. Energy Convers. 2024, 40, 653–664. [Google Scholar] [CrossRef]
- El Khil, S.K.; Jlassi, I.; Cardoso, A.J.M.; Estima, J.O.; Mrabet-Bellaaj, N. Diagnosis of open-switch and current sensor faults in PMSM drives through stator current analysis. IEEE Trans. Ind. Appl. 2019, 55, 5925–5937. [Google Scholar] [CrossRef]
- Lu, J.; Hu, Y.; Chen, G.; Wang, Z.; Liu, J. Mutual calibration of multiple current sensors with accuracy uncertainties in IPMSM drives for electric vehicles. IEEE Trans. Ind. Electron. 2020, 67, 69–79. [Google Scholar] [CrossRef]
- Wu, C.; Guo, C.; Xie, Z.; Ni, F.; Liu, H. A signal-based fault detection and tolerance control method of current sensor for PMSM drive. IEEE Trans. Ind. Electron. 2018, 65, 9646–9657. [Google Scholar] [CrossRef]
- Chakraborty, C.; Verma, V. Speed and current sensor fault detection and isolation technique for induction motor drive using axes transformation. IEEE Trans. Ind. Electron. 2014, 62, 1943–1954. [Google Scholar] [CrossRef]
- Wang, G.; Hao, X.; Zhao, N.; Zhang, G.; Xu, D. Current sensor fault-tolerant control strategy for encoderless PMSM drives based on single sliding mode observer. IEEE Trans. Transport. Electrific. 2020, 6, 679–689. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, H.; Wang, G.; Li, C.; Xu, D. Current sensor fault-tolerant control for encoderless IPMSM drives based on current space vector error reconstruction. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 8, 3658–3668. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, H.; Sun, Z.; Yao, C.; Ren, G.; Xu, S. Current sensor fault localization and identification of PMSM drives using difference operator. IEEE J. Emerg. Sel. Topics Power Electron. 2023, 11, 1097–1110. [Google Scholar] [CrossRef]
- Feng, X.; Wang, B.; Wang, Z.; Hua, W. Investigation and Diagnosis of Current Sensor Fault in Permanent Magnet Machine Drives. IEEE Trans. Ind. Electron. 2024, 72, 1261–1270. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, B.; Fang, W.; Chen, W. A fault diagnosis method for current sensor of doubly salient electromagnetic motor. IEEE Trans. Ind. Electron. 2023, 71, 4419–4428. [Google Scholar] [CrossRef]
- Fang, W.; Zhou, B.; Zhang, Y.; Yu, X.; Jiang, S.; Wei, J. A Fault Diagnosis and Fault-Tolerant Control Method for Current Sensors in Doubly Salient Electromagnetic Motor Drive Systems. IEEE J. Emerg. Sel. Topics Power Electron. 2024, 12, 2234–2248. [Google Scholar] [CrossRef]
- Dong, L.; Jatskevich, J.; Huang, Y.; Chapariha, M.; Liu, J. Fault diagnosis and signal reconstruction of hall sensors in brushless permanent magnet motor drives. IEEE Trans. Energy Convers. 2015, 31, 118–131. [Google Scholar] [CrossRef]


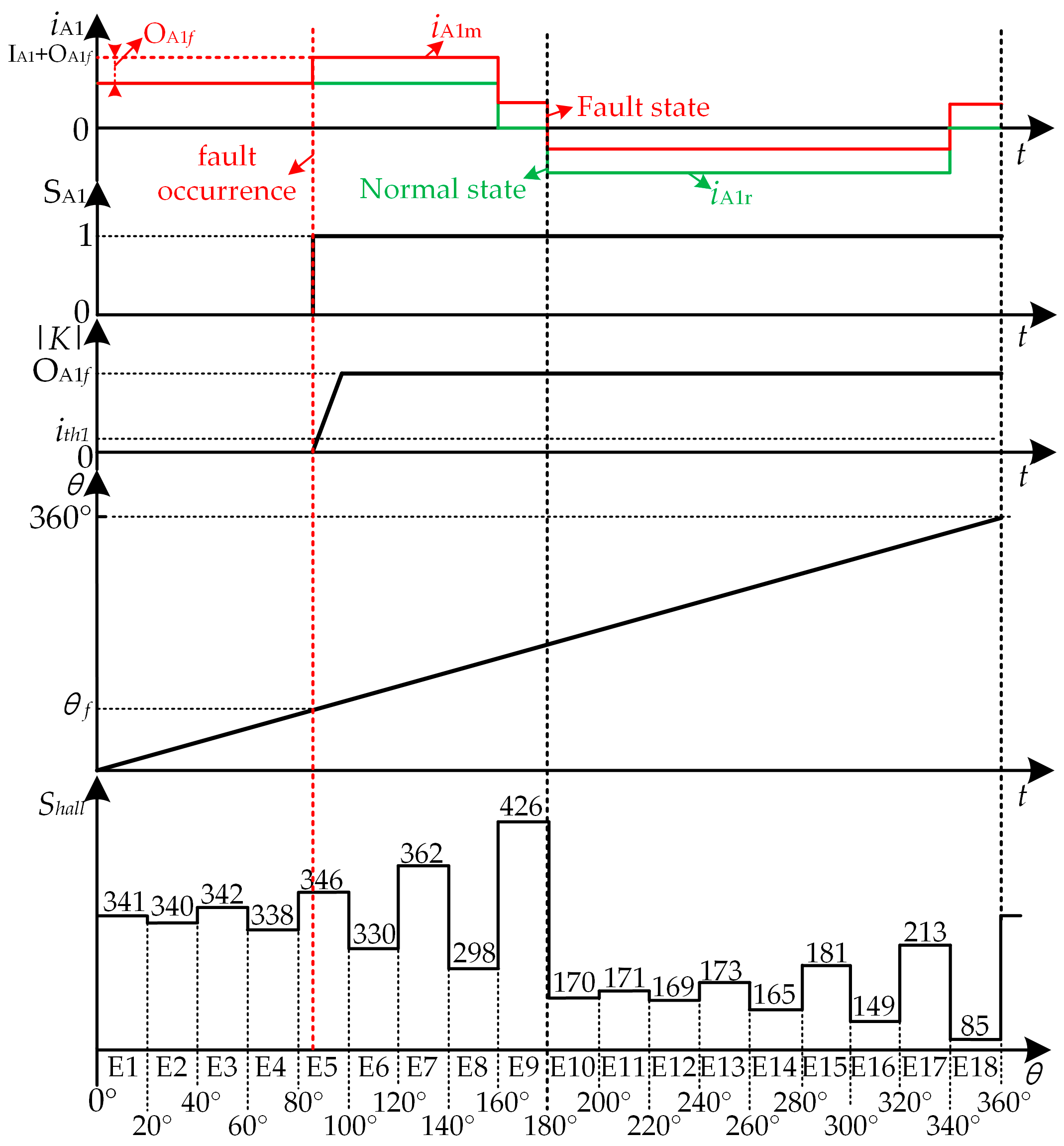






| Hall State | Sector | Conduction Phase | Suspended Phase |
|---|---|---|---|
| 341 | E1 | p = {A1,A3,A5,A7}; n = {A2,A4,A6,A8} | A9 |
| 340 | E2 | p = {A1,A3,A5,A7}; n = {A2,A4,A6,A9} | A8 |
| 342 | E3 | p = {A1,A3,A5,A8}; n = {A2,A4,A6,A9} | A7 |
| 338 | E4 | p = {A1,A3,A5,A8}; n = {A2,A4,A7,A9} | A6 |
| 346 | E5 | p = {A1,A3,A6,A8}; n = {A2,A4,A7,A9} | A5 |
| 330 | E6 | p = {A1,A3,A6,A8}; n = {A2,A5,A7,A9} | A4 |
| 362 | E7 | p = {A1,A4,A6,A8}; n = {A2,A5,A7,A9} | A3 |
| 298 | E8 | p = {A1,A4,A6,A8}; n = {A3,A5,A7,A9} | A2 |
| 426 | E9 | p = {A2,A4,A6,A8}; n = {A3,A5,A7,A9} | A1 |
| 170 | E10 | p = {A2,A4,A6,A8}; n = {A1,A3,A5,A7} | A9 |
| 171 | E11 | p = {A2,A4,A6,A9}; n = {A1,A3,A5,A7} | A8 |
| 169 | E12 | p = {A2,A4,A6,A9}; n = {A1,A3,A5,A8} | A7 |
| 173 | E13 | p = {A2,A4,A7,A9}; n = {A1,A3,A5,A7} | A6 |
| 165 | E14 | p = {A2,A4,A7,A9}; n = {A1,A3,A6,A8} | A5 |
| 181 | E15 | p = {A2,A5,A7,A9}; n = {A1,A3,A6,A8} | A4 |
| 149 | E16 | p = {A2,A5,A7,A9}; n = {A1,A4,A6,A8} | A3 |
| 213 | E17 | p = {A3,A5,A7,A9}; n = {A1,A4,A6,A8} | A2 |
| 85 | E18 | p = {A3,A5,A7,A9}; n = {A2,A4,A6,A8} | A1 |
| Fault Phase | Rotor Position Angle θc in Suspended State |
|---|---|
| A1 | 160° < θc < 180°; 340° < θc < 360° |
| A2 | 140° < θc < 160°; 320° < θc < 340° |
| A3 | 120° < θc < 140°; 300° < θc < 320° |
| A4 | 100° < θc < 120°; 280° < θc < 300° |
| A5 | 80° < θc < 100°; 260° < θc < 280° |
| A6 | 60° < θc < 80°; 240° < θc < 260° |
| A7 | 40° < θc < 60°; 220° < θc < 240° |
| A8 | 20° < θc < 40°; 200° < θc < 220° |
| A9 | 0° < θc < 20°; 180° < θc < 200° |
| Parameter | Symbol | Value |
|---|---|---|
| Rated voltage | UN | 42.5 V |
| Rated power | PN | 2 kW |
| Rated current | IN | 23 A |
| Rated load | TN | 8 N⋅m |
| Rated speed | nN | 2500 r/min |
| Phase resistance | Rs | 3.2 Ω |
| Phase inductance | Ls | 0.064 mH |
| Phase back-EMF coefficient | Ke | 0.06 V/(rad/s) |
| Pairs of poles | Pn | 2 |
| Fault Phase | Offset Value | Tef | Teft | Reduction |
|---|---|---|---|---|
| A1 | 5A | 14.5% | 11.8% | 2.7% |
| A1 | 10A | 27.2% | 21% | 6.2% |
| A1 and A2 | 5A | 20.25% | 18% | 2.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Liu, Z.; Wang, Z.; Li, C. Fault Diagnosis and Tolerant Control of Current Sensors Zero-Offset Fault in Multiphase Brushless DC Motors Utilizing Current Signals. Energies 2025, 18, 2243. https://doi.org/10.3390/en18092243
Chen W, Liu Z, Wang Z, Li C. Fault Diagnosis and Tolerant Control of Current Sensors Zero-Offset Fault in Multiphase Brushless DC Motors Utilizing Current Signals. Energies. 2025; 18(9):2243. https://doi.org/10.3390/en18092243
Chicago/Turabian StyleChen, Wei, Zhiqi Liu, Zhiqiang Wang, and Chen Li. 2025. "Fault Diagnosis and Tolerant Control of Current Sensors Zero-Offset Fault in Multiphase Brushless DC Motors Utilizing Current Signals" Energies 18, no. 9: 2243. https://doi.org/10.3390/en18092243
APA StyleChen, W., Liu, Z., Wang, Z., & Li, C. (2025). Fault Diagnosis and Tolerant Control of Current Sensors Zero-Offset Fault in Multiphase Brushless DC Motors Utilizing Current Signals. Energies, 18(9), 2243. https://doi.org/10.3390/en18092243







